地球物理学报  2013, Vol. 56 Issue (12): 4226-4233   PDF    
引用本文
唐晓明, 钱玉萍, 陈雪莲. 孔隙、裂隙介质弹性波理论的实验研究. 地球物理学报, 2013, 56(12): 4226-4233, doi: 10.6038/cjg20131225.  
Tang X M, Qian Y P, Chen X L. Laboratory study of elastic wave theory for a cracked porous medium using ultrasonic velocity data of rock samples. Chinese J. Geophys. (in Chinese), 2013, 56(12): 4226-4233, doi: 10.6038/cjg20131225.  
孔隙、裂隙介质弹性波理论的实验研究
唐晓明 , 钱玉萍 , 陈雪莲     
中国石油大学(华东)地球科学与技术学院, 青岛 266555
收稿日期 2012-10-26, 2013-11-21 收修定稿
基金项目: 国家自然科学基金(41174088)资助
作者简介: 唐晓明，男，1955年生，教授，1982年获北京大学地球物理学士；1984年获中国国家地震局地球物理研究所地球物理硕士；1986年起，在美国麻省理工学院地球资源实验室从事声波测井研究工作，1990年获麻省理工学院理学博士.一直致力于地球物理（特别是声波）测井、岩石物理学、地震波传播及测量等方面的研究和技术开发工作.E-mail：tangxiam@aliyun.com
摘要: 近年来发展起来的“孔隙、裂隙介质弹性波理论”提高了人们对实际岩石声学性质的模拟和预测的能力.作为对这一理论的实验验证和重要应用，我们将它用来模拟和解释岩石超声实验中测得的干燥和饱和岩石弹性波速度随压力的变化曲线.理论模拟的重要参数，如岩石的裂隙密度等是从实验数据反演得到的.结果表明：无论是孔隙度较高的砂岩，还是孔隙度很小的致密岩石，如花岗岩，该理论都能很好地描述岩石在干燥和饱和状态下纵、横波速度随压力的变化.造成波速变化的原因是岩石中裂隙在压力作用下的闭合和裂隙密度的减少.本文的结果还指出了将岩石裂隙密度作为描述岩石的重要物性参数，并给出了从实验室超声测量中确定这一参数的方法.
关键词: 岩石物理      孔裂隙介质      弹性波理论     
Laboratory study of elastic wave theory for a cracked porous medium using ultrasonic velocity data of rock samples
TANG Xiao-Ming, QIAN Yu-Ping, CHEN Xue-Lian     
School of Geosciences, China University of Petroleum, Qingdao 266555, China
Abstract: The recent development of the elastic wave theory for a cracked porous medium significantly enhances our ability to model and predict acoustic response of real rocks. As an important application and verification of the theory, we apply it to model and interpret laboratory ultrasonic velocity data of rock samples measured under pressure loading conditions. The important model parameters, such as crack density and aspect ratio, are obtained by inverting the velocity versus pressure data. The results show that the theory can well describe the elastic velocity variation with pressure under dry and saturated conditions. The theory is applicable for both porous sandstone and very tight granite. The cause of the velocity variation with pressure is the closure of microcracks and the decreasing of crack density within the rock under pressure loading. This paper also suggests using crack density as an important rock property parameter and provides a method for determining the crack parameter..
Key words: Rock physics      Cracked porous media      Elastic wave theory     
1 引言

描述在实际岩石中传播的弹性波理论一直是地球物理学研究的重要课题, 实际岩石中往往是既含孔隙又含裂隙, 这对弹性波传播产生重大影响.综合经典的Biot孔隙介质弹性波理论和O'Connell和Budiansky [1]的裂隙弹性力学, 及Thomsen[2]的低频的孔、裂隙介质相恰理论, 唐[3]最近提出了"含孔隙、裂隙介质弹性波动理论"并进一步将其完善[4].相对于经典的Biot理论, 新的理论增加了裂隙密度和裂隙纵横比这两个描述裂隙介质的重要参数.该理论能很好地解释波在实际岩石中的衰减和频散, 并被用来模拟孔、裂隙地层中的井孔声场[5]和解释致密性砂岩和页岩地层声波测井数据中的油气显示[4].本文的目的在于运用该理论来模拟和解释实验室压力条件下弹性波的超声测量数据, 并由此来估计岩石中裂隙密度和裂隙纵横比这两个重要参数及其随压力的变化.

孔隙、裂隙介质弹性波动理论中描述的裂隙的尺度很小, 与岩石颗粒的尺度相当.用纵横比这个参数来度量, 把岩石颗粒中纵向与横向尺度差别不超过一个数量级, 或纵横比约等于1的空间称为孔隙, 而把纵横比远小于1的空间称为裂隙.相对于孔隙而言, 形状狭小而扁平的裂隙在外力(如弹性波动)作用下很容易变形, 把其中的流体挤入相邻的孔隙, 这种局部的流体流动称为挤喷流[3], 是造成弹性波衰减和频散的重要原因.显然, 控制挤喷流发生的时间尺度(称为弛豫时间)是裂隙的纵横比, 而控制挤喷流效应的大小的重要参数是岩石中的裂隙密度.此外, 裂隙密度还直接影响岩石的弹性模量, 这种影响在Thomsen[2]的理论中有很好的描述, 并被包括在孔隙、裂隙弹性波理论之中.

由于该理论中岩石的裂隙对弹性波速具有灵敏度很高的控制作用, 可以将此理论用来预测和模拟裂隙变化条件下的弹性波速测量数据.实验室中所做的岩石超声弹性波速随压力的变化曲线提供了所需的实验数据.岩石受压时, 狭长和扁平的裂隙首先闭合, 造成裂隙尺度(或纵横比)的减少和裂隙密度的降低.与此相应, 测得的纵、横波速度随着压力的增加而上升.相比而言, 纵横比约等于1的孔隙在压力作用下很少变化, 作为近似, 可以认为这类孔隙的孔隙度是不随压力变化的[6], 故随着压力增加及纵横比很小的裂隙闭合后, 弹性波速的增加趋缓, 甚至不再变化, 这一点可以从以下实际数据中看到.

上述的岩石波速随压力的变化曲线由裂隙弹性理论得到了很好的模拟和解释[7-8].值得一提的是, Cheng [7]用Kuster & Toksöz[9]裂隙弹性理论模拟了实验数据并反演了岩石的裂隙参数.然而, 对于本文所述的孔隙、裂隙弹性波动理论而言, 我们更加关心的是该理论是否能很好地模拟这些实验数据.理论对实验室数据的成功应用不但为该理论提供了实验验证, 而且还提供了一种确定岩石裂隙参数的实验室测量和计算方法.

2 实验室数据的反演和理论模拟

在实验室可控条件下测得的干燥和饱和岩石弹性波速(即纵、横波速)随压力的变化为验证上述的"孔隙、裂隙弹性波理论"提供了所需的数据, 这是因为波速的变化直接反映了岩石中裂隙的数量(由裂隙密度控制)和裂隙结构(由裂隙纵横比控制)随压力的变化.根据理论中的裂隙与波速的函数关系可以从波速测量数据中反演出裂隙的参数, 反过来又可以将裂隙参数代入理论公式来模拟和预测波速随压力的变化.

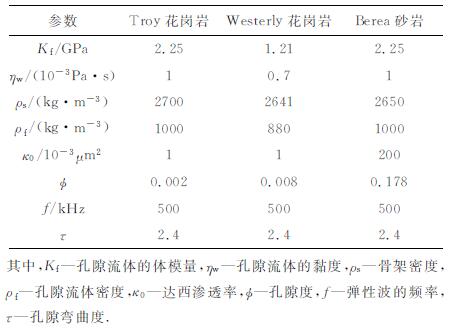
我们将采用几套已发表的岩石波速随压力变化的经典实验数据[6, 10], 其中有孔隙度几乎为零的Troy花岗岩石, 也有孔隙度较高的Berea砂岩(φ=0.178), 以及孔隙度很小的Westerly花岗岩的纵横波速度的实验数据, 来验证孔隙、裂隙弹性波理论的正确性和适用性.有关这几种岩石的实验和理论计算参数在表 1中列出.

表 1 Troy花岗岩、Westerly花岗岩和Berea砂岩的理论模型参数 Table 1 Model parameters of Troy granite, Westerly granite and Berea sandstone
2.1 灵敏度分析

孔隙、裂隙弹性波理论的推导见唐[3]和Tang等[4].为讨论方便起见, 我们将该理论的主要结果放在附录中.由附录中的讨论可知, 该理论计算所得的岩石纵横波速度受以下参数的影响:孔隙度、裂隙密度、裂隙纵横比、孔隙流体和岩石基质的体模量Kf和Ks、岩石基质的剪切模量μs以及弹性波的频率.

要从声速测量数据反演岩石的弹性模量及裂隙参数, 必须考虑理论模型中波速对这些参数的灵敏度, 对模型中的某一参数p, 其灵敏度的定义为:

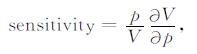
其中, 波速V可以是纵波或横波的速度.一般而言, 波速对基质弹性模量Ks和μs, 以及裂隙密度的灵敏度是较高的, 因为这些参数直接影响弹性波速度, 但对于裂隙纵横比这一参数, 却取决于纵横比的取值范围、波速测量所用频率及岩石处于饱和或干燥状态.

根据附录中的理论及前述的讨论可知, 裂隙纵横比控制了裂隙流体向孔隙挤喷的弛豫时间(或频率).如果测量的频率范围在此弛豫频率附近, 则波速对裂隙纵横比有较大灵敏度, 否则, 灵敏度会很低甚至消失.

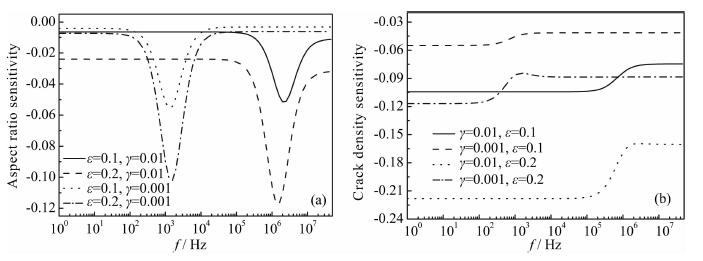
以Troy花岗岩为例, 图 1a和图 1b计算了Troy花岗岩纵波速度分别对纵横比和裂隙密度在0~10000kHz频率范围内的灵敏度曲线.灵敏度的绝对值的大小说明波速对此参数是否灵敏, 而灵敏度的符号说明波速随此参数增加(灵敏度为正值)还是降低(灵敏度为负值).

图 1 纵波速度对裂隙纵横比的灵敏度及对裂隙密度的灵敏度曲线(以Troy花岗岩为例) (a)对Troy花岗岩, 在ε=0.1和ε=0.2两种情况下纵波速度对γ=0.01和0.001时的灵敏度曲线; (b)对Troy花岗岩, 在γ=0.01和γ=0.001两种情况下纵波速度对ε=0.1和ε=0.2时的灵敏度曲线. Fig. 1 Sensitivity analysis example for Troy granite (a) Sensitivity to aspect ratio atγ=0.01 and γ=0.001 for two crack density values of ε=0.1 and ε=0.2, respectively; (b) Sensitivity to crack density atε=0.1 and ε=0.2 for two aspect ratio values of γ=0.01 and γ=0.001, respectively.

从图 1a可以看到, 对Troy花岗岩, 若纵横比的取值为0.01, 当裂隙密度取值为0.1时, 对裂隙纵横比的灵敏度在2%左右, 当裂隙密度达到0.2, 它在实验室给定的超声测量频率下(~500kHz)对纵横比灵敏度增加, 大约为8%左右.相比之下, 对于裂隙纵横比的取值为0.001时, 无论裂隙密度是0.1还是0.2, 在500kHz的超声测量频率下对裂隙纵横比的灵敏度都很小, 不超过2%.

类似地, 以同样方式分析纵波速度对裂隙密度的灵敏度, 见图 1b.若裂隙密度的取值为0.1, 当裂隙纵横比取值为0.01时, 对裂隙密度的灵敏度在10%左右, 当裂隙纵横比为0.001, 它在实验室给定的测量频率下(~500kHz)对裂隙密度灵敏度大约为5%左右.相比之下, 对于裂隙密度的取值为0.2时, 无论裂隙纵横比是0.01还是0.001, 在500kHz的超声测量频率下对裂隙密度的灵敏度都很大, 超过10%, 甚至达到20%.可以看到对裂隙密度的灵敏度明显要大于对裂隙纵横比的灵敏度.

同样根据以上对图 1a所做的灵敏度分析可知, 在裂隙密度大幅度减少后岩石波速对纵横比灵敏度变得很低, 所以当在压力增加到很大时(裂隙密度会降低), 将造成对裂隙纵横比的反演结果可靠性降低, 而对裂隙密度的灵敏度一般是较高的, 可以有效地反演出裂隙密度.

2.2 反演方法

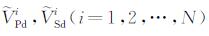
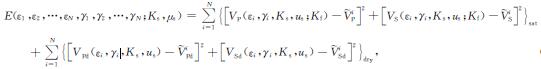
对孔隙、裂隙弹性介质波动理论的模型参数(如裂隙密度等)进行反演是通过用理论公式对实验室测量数据做最小二乘拟合得到的.对同一岩石样品在干燥和流体饱和状态下分别测量波速随压力的变化.在压力加载范围内进行N次测量, 测得的干燥和饱和岩石的纵、横波速分别为和.理论和实验数据拟合所得的均方误差即可作为反演所需的目标函数, 如下所示.

(1)

其中, Ks和μs分别为岩石基质的体模量和剪切模量, εi(i=1, 2, …, N)和γi(i=1, 2, …, N)分别为从1到N个压力点下待求的裂隙密度和裂隙纵横比.式(1)中计算理论波速的参数Kf为岩石中流体的体模量, 在实验中是已知的.计算干燥岩石的理论波速时, 取Kf=0.调节各个参数使式(1)中的目标函数达到最小值时所得的参数值便取为模型的参数值.反演所需的理论模型, 即纵、横波速的正演计算, 由附录所述的孔隙、裂隙弹性波理论公式给出.理论模型的计算参数例子见表 1.式(1)所表示的反演是-多参数的反演过程.对N个压力测量点的纵、横波速度数据, 共有2N+2个未知参数待求, 反演的目标函数(1)也可能存在多个极小值.为解决这个问题, 我们采用了求全局极小值的GA最优化方法[11].通过求目标函数的全局极小值来减少反演结果的非唯一性.经过反演得到模型参数后, 再代入理论模型, 模拟出不同压力下纵横波速度的值.模拟结果与实测数据的符合程度可以用来检验理论的正确性和适用性.

2.3 应用举例

我们首先用以上方法处理博伊西砂岩(Berea sandstone)在0~100 MPa压力区间测得的干燥和水饱和状态下的纵横波速度数据.这种砂岩的物性特征是高孔高渗, 孔隙度为17.8%, 渗透率为200×10-3 μm2(见表 1).图 2a的测量数据显示, 无论是干燥和饱和, 弹性波速随压力的增加均有所上升, 低压时上升较快.图 2b是反演得到的裂隙密度随压力的变化, 从反演结果可以看出, 随着压力的增加, 裂隙密度明显地降低, 而从图 2c中可以看到, 裂隙纵横比却随压力增加而呈现上升趋势.二者的变化在低压时最为显著.这说明岩石受压时, 狭长和扁平的裂隙首先闭合, 从而造成了裂隙尺度(或纵横比)的减少和裂隙密度的降低.(这一物理现象在下述的低孔的花岗岩的数据处理结果中表现的尤为突出.)反演得到的岩石基质的体积和剪切模量分别为40.67 GPa和35.27GPa.将这些反演结果用于纵横波的理论计算得出图中的干燥和水饱和状态下纵横波速度随压力的变化曲线, 该曲线与实测的数据吻合得相当好.这一吻合说明孔隙、裂隙弹性波理论对于实验室条件下测量的超声频率范围内的岩石弹性波速也是适用的.从实验与理论的吻合及反演的裂隙密度随压力增加而下降的趋势, 说明了弹性波速度随着压力增加而上升是由于岩石中裂隙在外力作用下的闭合造成的这一物理事实.

图 2 Berea砂岩的实验数据的反演和理论模拟 (a)干燥和水饱和条件下Berea砂岩的纵横波速度数据与理论拟合结果; (b) Berea砂岩纵横波速度数据反演得到的裂隙密度值; (c) Berea砂岩纵横波速度数据反演得到的裂隙纵横比. Fig. 2 Theoretical inversion of crack parameters using Berea sandstone laboratory velocity data (a) Inversion-fitting between theoretical (curves) and the laboratory (markers) velocities of Berea sandstone under dry (open circles) and water-saturated (solid dots) conditions; (b) Crack density versus pressure from inverting the laboratory data; (c) Aspect ratio versus pressure by inverting the laboratory data.

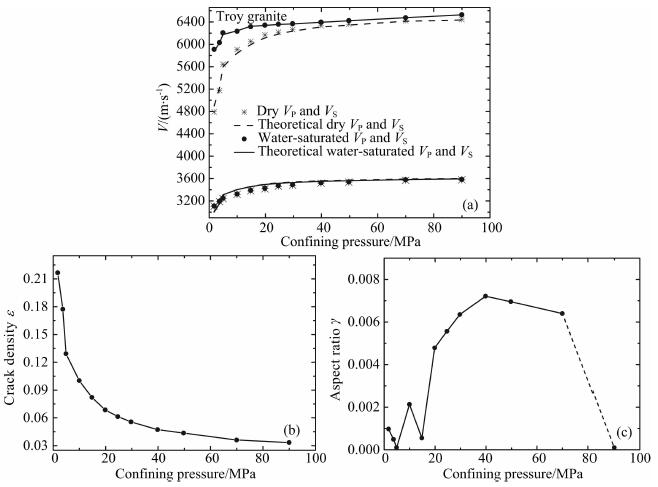
图 3a是特洛伊花岗岩(Troy granite), 在0~100 MPa的压力下, 测得的干燥和水饱和状态下纵横波速度数据(星状和实心圆点), 以及相应的理论拟合数据(曲线).值得注意的是, 该岩石非常致密, 孔隙度仅有0.2%.图 3b是反演得到的裂隙密度随压力的变化, 反演结果表明裂隙密度在低压下较高, 达到0.22, 这意味着该岩石在未加压力时, 微裂隙比较发育, 随着压力增加, 裂隙密度大幅度减少达一个量级, 由此对应的是弹性波速随着压力增加而显著上升.根据图 1a所做的灵敏度分析可知, 在给定频率下, 当裂隙密度一定, 纵横比很小或裂隙密度大幅度减少后岩石波速对纵横比灵敏度很低.我们可以在图 3c中看到反演出的裂隙纵横比在低压时的变化很不稳定, 这正是由于低压时的微裂隙纵横比很小, 导致速度对其灵敏度很低, 从而造成反演结果的不可靠; 而高压时, 裂隙密度已经降到很小, 导致速度对纵横比的灵敏度也降低, 因此也造成了反演结果的不可靠, 如图 3c中的虚线所表示的(与理论分析相悖的)下降趋势所示.反演所得到的岩石基质的体模量和剪切模量分别为75GPa和37GPa.由这些参数和反演的裂隙密度数据代入附录中的理论公式, 计算得出的纵横波速度与压力变化曲线, 与实测的数据吻合得很好(见图 3a), 这说明孔隙、裂隙波动理论对致密性岩石的超声波速测量也是适用的.

图 3 Troy花岗岩的实验数据的反演和理论模拟 (a)干燥和水饱和条件下Troy花岗岩的纵横波速度数据与理论拟合结果; (b) Troy花岗岩纵横波速度数据反演得到的裂隙密度值; (c) Troy花岗岩的纵横波速度数据反演得到的裂隙纵横比. Fig. 3 Theoretical inversion of crack parameters using Troy granite laboratory velocity data (a) Inversion-fitting between theoretical (curves) and the laboratory (markers) velocities of Troy granite under dry (open circles) and water-saturated (solid dots) conditions; (b) Crack density versus pressure from inverting the laboratory data; (c) Aspect ratio versus pressure by inverting the laboratory data.

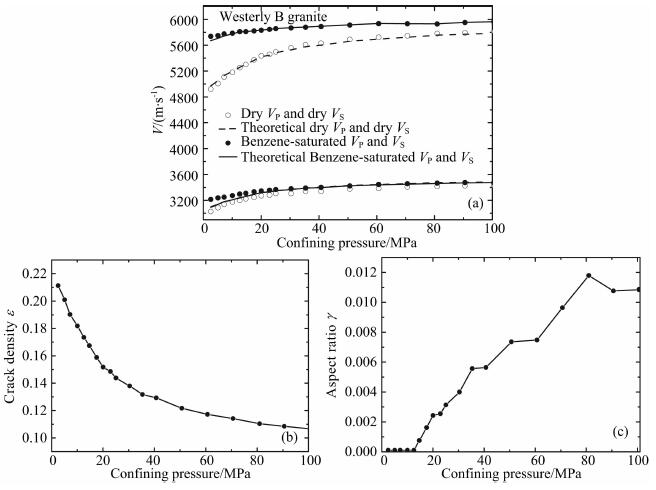
前面两组岩石都是用水饱和与干燥条件下的数据联合反演裂隙密度、纵横比及基质模量, 下面是利用Westerly花岗岩的干燥和苯饱和条件下的纵横波速度数据联合反演裂隙密度、纵横比和基质模量.该岩石也很致密, 孔隙度仅有0.8%.相关参数仍见表 1.反演结果如图 4b和4c所示.反演结果表明裂隙密度随压力增加而降低, 而裂隙纵横比呈上升趋势, 二者的变化趋势比Troy花岗岩要缓慢些.这意味着该岩石在所加压力范围内, 微裂隙还未完全压实, 由此对应的弹性波速在高压下还有缓慢增加趋势.反演得到的体模量和剪切模量分别为66.7GPa和38.3GPa, 将这些反演结果用于纵横波的理论计算得出图中的干燥和苯饱和状态下纵横波速度随压力的变化曲线, 该曲线与实测的数据吻合相当好(见图 4a).

图 4 Westerly花岗岩的实验数据的反演和理论模拟 (a)干燥和苯饱和条件下Westerly花岗岩的纵横波速度数据与理论拟合结果; (b) Westerly花岗岩纵横波速度数据反演得到的裂隙密度值; (c) Westerly花岗岩的纵横波速度数据反演得到的裂隙纵横比. Fig. 4 Theoretical inversion of crack parameters using Westerly granite laboratory velocity data (a) Inversion-fitting between theoretical (curves) and the laboratory (markers) velocities of Westerly granite under dry (open circles) and benzene-saturated (solid dots) conditions; (b) Crack density versus pressure from inverting the laborator ydata; (c) Aspect ratio versus pressure by inverting the laboratory data.
2.4 讨论

将孔隙、裂隙弹性波理论应用于实验室压力条件下的超声波速测量数据, 我们看到了岩石中裂隙对弹性波速的巨大影响, 特别对非常致密的低孔岩石, 更是如此; 同时还看到由于裂隙的存在, 使得岩石的声学响应在干燥和饱和状态下有着较大的差别, 即存在相当的流体敏感性或灵敏度, 这种流体灵敏度已被用来解释致密油气储层中的声波测井数据[4].理论与对实验数据的反演结果表明, 无论对高孔砂岩还是致密性低孔岩石, 该理论均能较好地描述干燥和饱和状态下岩石的声学响应.

由于裂隙对岩石弹性响应产生的重大影响及流体灵敏度, 根据本文及大量实验室和野外测量数据的结果, 我们提出应当将岩石的裂隙参数, 如裂隙密度和裂隙纵横比(特别是前者)作为重要的岩石物性参数.对于致密性岩石, 这一物性参数(即裂隙密度)的作用, 有时比孔隙度更为重要.本文所述的理论和反演方法为在常规岩石物理实验条件下确定这一岩石物性参数提供了一种方法.

3 结语

岩石中普遍存在的裂隙不仅对岩石的弹性响应产生重大的影响, 而且使这种响应具有可观的流体灵敏度.将孔隙、裂隙介质的弹性波动理论应用于实验室的超声波速测量数据, 我们看到, 这种影响由介质两个重要的参数所控制, 即裂隙密度和裂隙纵横比.鉴于裂隙的重要影响, 我们提出, 除了岩石的孔隙度外, 应当将岩石裂隙参数, 特别是裂隙密度, 作为一个重要的物性参数, 对于致密性的低孔岩石这一物性参数尤为重要.本文的结果表明:孔隙、裂隙介质弹性波动理论对实验室条件下的超声波速测量数据也是适用的, 可以用来从实验室数据中反演得到岩石的裂隙参数, 从而为确定这一物性参数提供了一种行之有效的方法.

附录

唐[3]和Tang等[4]提出了在孔隙、裂隙并存条件下计算弹性波速和衰减的理论和方法, 在这种介质中的快慢纵波和横波波数由(A1)式给出:

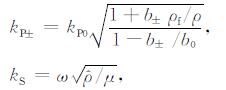
(A1)

其中, 下标P和S分别表示纵波和横波, +号和-号分别表示快、慢纵波,

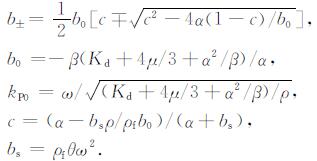
(A2)

其中, ω为角频率,

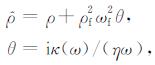
(A3)

式中的动态渗透率κ为:

其中, κ0为达西渗透率, τ为介质孔隙弯曲度, η为流体黏度.

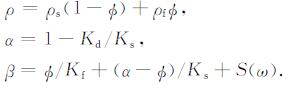
(A4)

其中, μ和kd分别为介质的剪切和干燥体模量, φ是孔隙度, ρf和Kf分别为流体密度和体模量; ρs和Ks分别为岩石骨架的密度和体模量.

上述理论公式为经典Biot孔隙弹性波动理论的结果, 裂隙的存在对上述理论有三个重要修正, 其一是产生了孔隙与裂隙之间的挤喷流, 由下述的挤喷流项来表征:

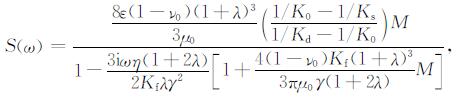
(A5)

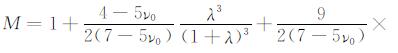
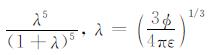
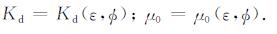
其中, , λ为孔隙与裂隙的大小之比, γi是裂隙纵横比, η是孔隙流体黏度; K0、μ0和ν0分别为背景介质的体模量、剪切模量和泊松比.第二个修正是介质的弹性模量μ0和kd变为ε和φ的函数:

(A6)

裂隙的存在将大大降低岩石的模量.在Biot相恰理论中描述了这种影响[2], 并可以从Biot相恰理论中求解得到.第三个修正是对频率有依赖性的剪切模量, 局部挤喷效应造成明显的频散, 这一频散体现在流体饱和时的体积模量K因挤喷流效应变化到频率域中.对于挤喷流机制, Mavko和Jizba[12]证明了介质剪切模量的频散可以从体积模量的频散推导出来, 公式如下:

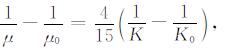
(A7)

其中μ0和K0取为介质中不存在挤喷流时(即S(ω)=0)的模量.对频率有依赖性的μ可以代入公式(A1)中来计算横波波数.随频率变化的速度由(A8)式计算:

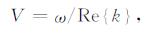
(A8)

其中, k为公式(A1)中任一种波的波数, Re{k}为复波数的实部.上述理论中有关参数的例子参见表 1.

参考文献
[1] O'Connell R J, Budiansky B. Seismic velocities in dry and saturated cracked solids. J. Geophys. Res. , 1974, 79(35): 5412-5426. DOI:10.1029/JB079i035p05412
[2] Thomsen L. Biot-consistent elastic moduli of porous rocks:Low-frequency limit. Geophysics , 1985, 50(12): 2797-2807. DOI:10.1190/1.1441900
[3] 唐晓明. 含孔隙、裂隙介质弹性波动统一理论--Biot理论的推广. 中国科学:地球科学 , 2011, 41(6): 784–795. Tang X M. A unified theory for elastic wave propagation through porous media containing cracks-An extension of Biot's poroelastic wave theory. Sci. China Earth Sci. (in Chinese) , 2011, 41(6): 784-795.
[4] Tang X M, Chen X L, Xu X K. A cracked porous medium elastic wave theory and its application to interpreting acoustic data from tight formations. Geophysics , 2012, 77(6).
[5] 陈雪莲, 唐晓明. 孔、裂隙并存地层中的声波测井理论及多极子声场特征. 地球物理学报 , 2012, 55(6): 2139–2140. Chen X L, Tang X M. Numerical study on the characteristics of acoustic logging response in the fluid-filled borehole embedded in crack-porous medium. Chinese J. Geophys. (in Chinese) , 2012, 55(6): 2139-2140.
[6] 陈顒, 黄庭芳, 刘恩如. 岩石物理学. 合肥: 中国科技大学出版社, 2009 . Chen Y, Huang T F, Liu E R. Rock Physics (in Chinese). Hefei: China University of Science and Technology Press, 2009 .
[7] Cheng C H. Seismic velocities in porous rocks:direct and inverse problems. Cambridge: Massachusetts Institute of Technology, 1978 .
[8] Cheng C H, Toks z M N. Inversion of seismic velocities for the pore aspect-ratio spectrum of a rock. J. Geophys. Res. , 1979, 84(B13): 7533-7543. DOI:10.1029/JB084iB13p07533
[9] Kuster G T, Toks z M N. Velocity and attenuation of seismic waves in two-phase media:I. Theoretical formulation. Geophysics , 1974, 39(5): 587-606.
[10] Coyner K B. Effects of stress, pore pressure, and pore fluids on bulk strain, velocity, and permeability in rocks. Cambridge: Massachusetts Institute of Technology, 1984 .
[11] Goldberg D E. Genetic Algorithms in Search, Optimization & Machine Learning. Boston: Addison-Wesley Publishing Co, 1989 .
[12] Mavko G, Jizba D. Estimating grain-scale fluid effects on velocity dispersion in rocks. Geophysics , 1991, 56(12): 1940-1949. DOI:10.1190/1.1443005