近年来大地震的发生及其造成的近断层区的严重破坏引起人们对近断层地震动的极大关注[1-3].近断层地震动的显著特征之一是断层破裂的方向性效应[4],这类地震动一般具有高速度幅值、短持时和明显的速度脉冲等特征[5-6].研究表明,近断层脉冲型地震动会造成长周期结构的严重破坏[7-8].随着越来越多的高层建筑、大跨度桥梁、海洋平台等长周期结构的大量建造,近断层地震动已成为长周期工程结构抗震设计必须考虑的内容[9-10].
为定量地分析近断层地震动的工程特性,许多学者研究了近断层脉冲型地震动的等效以及单自由度和多自由度体系等效脉冲地震动作用下的弹性及非弹性动力响应[11-12].Makris[13]将近断层地震动中的长周期脉冲分为三类,并分别给出了函数表达. Alavi[14]和Bozorgnia[15]分别采用三角形和长方形模型用于等效地震动中的长周期分量.徐龙军[4]对四类不同的等效地震动脉冲模型进行了对比分析,为工程中等效地震动模型的选取提供了参考依据.需要注意的是,简单的等效地震动模型虽然能够定性地表征近断层地震动的长周期特性,但却忽略了实际地震动时程中的高频成分.为了分析近断层地震动的组成特性,Baker[16]采用连续小波变换,把地震动中的长周期分量从原始时程中分离出来,为区分脉冲型地震动和非脉冲型地震动提出了判别准则.Yaghmaei-Sabegh[17-18]、Mollaioli[19]和谢俊举[20]等采用了Baker[16]所提出的方法分别对近断层地震动的位移比谱、脉冲特性与结构反应的关系以及地震动参数特征进行了分析.Ghahari[21]采用“移动平均值”的分解方法进行近断层地震动的组成分析,并论证了方法的可行性,与Baker[16]得到的结果进行了对比.此外,许多学者对脉冲型地震动的位移谱进行了研究,为工程结构设计提供了宝贵的参考资料[22-23].为了进一步分析近断层地震动的组成及其长周期分量随场地、断层距等影响因素的变化规律,本文基于小波分析中多尺度分析的概念以及Mallat分解与重构算法提出了一个按照频率由低到高的顺序对地震动加速度时程逐次分解的方法,用于实际近断层地震动的组成分析;先从频域、时域以及动态响应三个方面阐述了该方法的精确性与有效性;进而采用这种方法对近期12次大地震中的53条典型近断层长周期地震动进行了分解,得到了266条地震动加速度分量;讨论了场地条件、断层距影响下近断层地震动的频谱组成和幅值特征,以期能为近断层地震动的工程特性认识和应用提供些新的参考依据.
2 多尺度分解方法及精度与有效性分析小波变换是信号处理领域一种比较理想的数学工具,在地震动数据处理中也得到了较为广泛的应用[24].本文基于小波分析中多尺度分析的理论,分离地震动中的长周期分量.空间L2(R)中的多尺度分析是将L2(R)空间做逐级二分解产生一组逐级包含的子空间:…,V0=V1⊕W1,V1=V2⊕W2,V2=V3⊕W3,….记Vj空间中的离散序列为{x}j,Wj空间中的离散序列为{d}j.离散信号经过j次分解,最终分为空间W1,W2,…Wj,Vj,它们分别包含了信号从高频到低频的不同频带的信息.文中采用Mallat算法进行信号的分解与重构.记由{x}j重构到V0空间的信号为aj,由{d}j重构到V0空间的信号为dj,则离散序列x经j次分解和重构后可以表示为x=d1+d2+ … +dj+aj.dj仅具有信号的高频信息,不是本文的研究内容.虽然aj能表示低频信息,但是aj包含aj+1的频率信息,这样得到的低频序列是依次包含的.为获取频率范围各不相同的低频分量,对序列{x-aj}进行(j-1)次分解,并将Vj-1空间的低频信号重构到V0空间,记为a′j-1,则重构得到的a′j-1不包含aj的信息,文中采用该方法对地震动由低频到高频逐次分解,依次得到aj,a′j-1,…,a′2,a′1.此外,考虑到近断层地震动脉冲的特点,在进行地震动分解时选用db4小波函数.
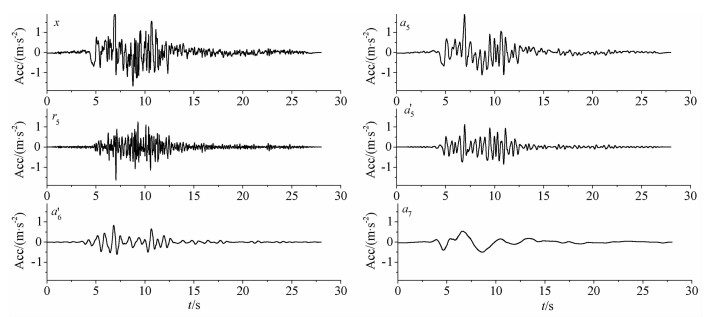
以Kocaeli,Turkey地震Gebze台站地震动为例,将实际地震动加速度时程分解得到一组加速度分量时程(见图 1).其中x为原始地震动序列,x=a5+r5;a5为通过对尺度空间V5中的低频系数重构得到的分量;a′6为对(x-a7)进行多尺度分解,由V6中低频系数重构得到;a′5为对(x-a7-a′6)进行多尺度分解,由V5中低频系重构得到.经验证a5≈a′5+ a′6+a7,且误差可忽略不计.
|
图 1 Kocaeli,Turkey地震Gebze台站多尺度分解各分量时程图 Fig. 1 Time-histories of components through multiscale decompose, Gebze, Kocaeli, Turkey earthquake |
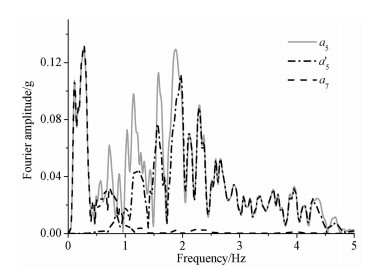
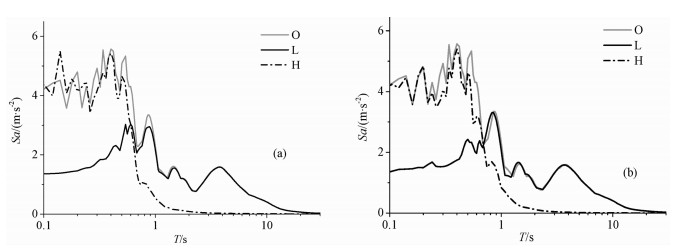
为说明各分量在频域上相互之间的独立性及其与原始地震动的关系,对各分量的傅里叶谱和反应谱进行了对比分析.从分量的傅里叶谱(见图 2)可看出,a′5与a7的傅里叶谱的相交面积很小,说明分解得到的各分量分布在不同的频率范围.同时,a′5、a7分别与a5在低频和高频范围内基本重合.傅里叶分析能够精确定位信号的频域信息,且通过傅里叶滤波可以得到信号的高低频分量.为进一步体现多尺度分解在频域上的精确性,对比分析了由两种方法得到的分量的反应谱(见图 3).在多尺度分解方法中低频采用a7,高频采用r7=x-a7;在傅里叶方法中,低频成分是通过阻断频率为1.67 Hz的低通滤波得到,高频由相同截断频率的高通滤波得到.两种方法获得的分量反应谱表明,多尺度分解方法与傅里叶方法在频域上具有相同的精确性.
|
图 2 a5,a′5,a7傅里叶幅值谱 Fig. 2 Fourier amplitude spectra of a5, a′5, a7 |
|
图 3 反应谱对比图 (a)傅里叶方法分解各分量反应谱图形;(b)多尺度分解方法分解各分量反应谱图形;O-原始地震动;L-低频成分;H-高频成分. Fig. 3 Response spectra comparison diagram (a) By Fourier method; (b) By multiscale decompose method; O-Original ground motion; L-Low frequency component; H-High frequency component. |
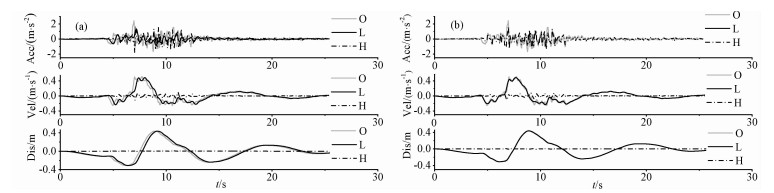
结构的动态响应大多采用激励的时域信息进行计算,所以有必要探讨多尺度分解方法得到的分量在时域上的准确性.图 4对比了由两种方法得到的高低频分量与原始地震动的时程曲线.采用多尺度分析方法得到的高低频分量的时程与原始地震动时程始终保持一致,所以,多尺度分解方法得到的分量在时域内也是准确的.而由傅里叶方法得到的分量时程与原始时程产生了明显的偏差.
|
图 4 时程对比图 (a)傅里叶分解方法时程图;(b)多尺度分解方法时程图;O-原始地震动;L-低频成分;H-高频成分. Fig. 4 Time-histories comparison diagram (a) Time-histories through Fourier method; (b) Time-histories through multiscale decompose method; O-Original ground motion; L-Low frequency component; H-High frequency component. |
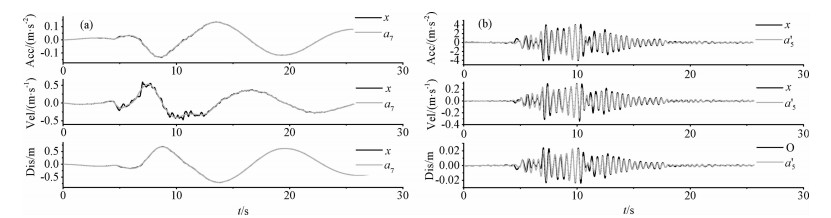
由动力学的基本知识可知,长周期体系对低频分量和原始地震动的动态响应应该一致;短周期体系对高频分量和原始地震动的动态响应应该一致. 图 5a为原始地震动与a7分量作用在周期为14.5 s的单自由度体系上计算得到的加速度、速度与位移时程.图 5b为原始地震动与a′5分量作用在周期为0.5 s的单自由度体系上计算得到的响应时程.图 5表明通过多尺度分解方法得到的各频率分量,除与原始地震动在时域和频域内皆吻合外,在对体系的动态响应方面也能与原始地震动保持一致.
|
图 5 反应时程对比图 (a)a7与原始地震动反应时程对比;(b)a′5与原始地震动反应时程对比. Fig. 5 Response time-histories comparison diagram (a) Comparison between a7 and original ground motion; (b) Comparison between a′5 and original ground motion. |
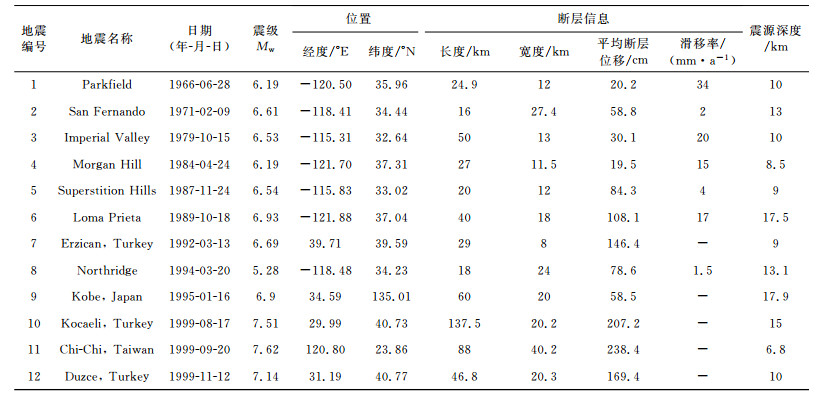
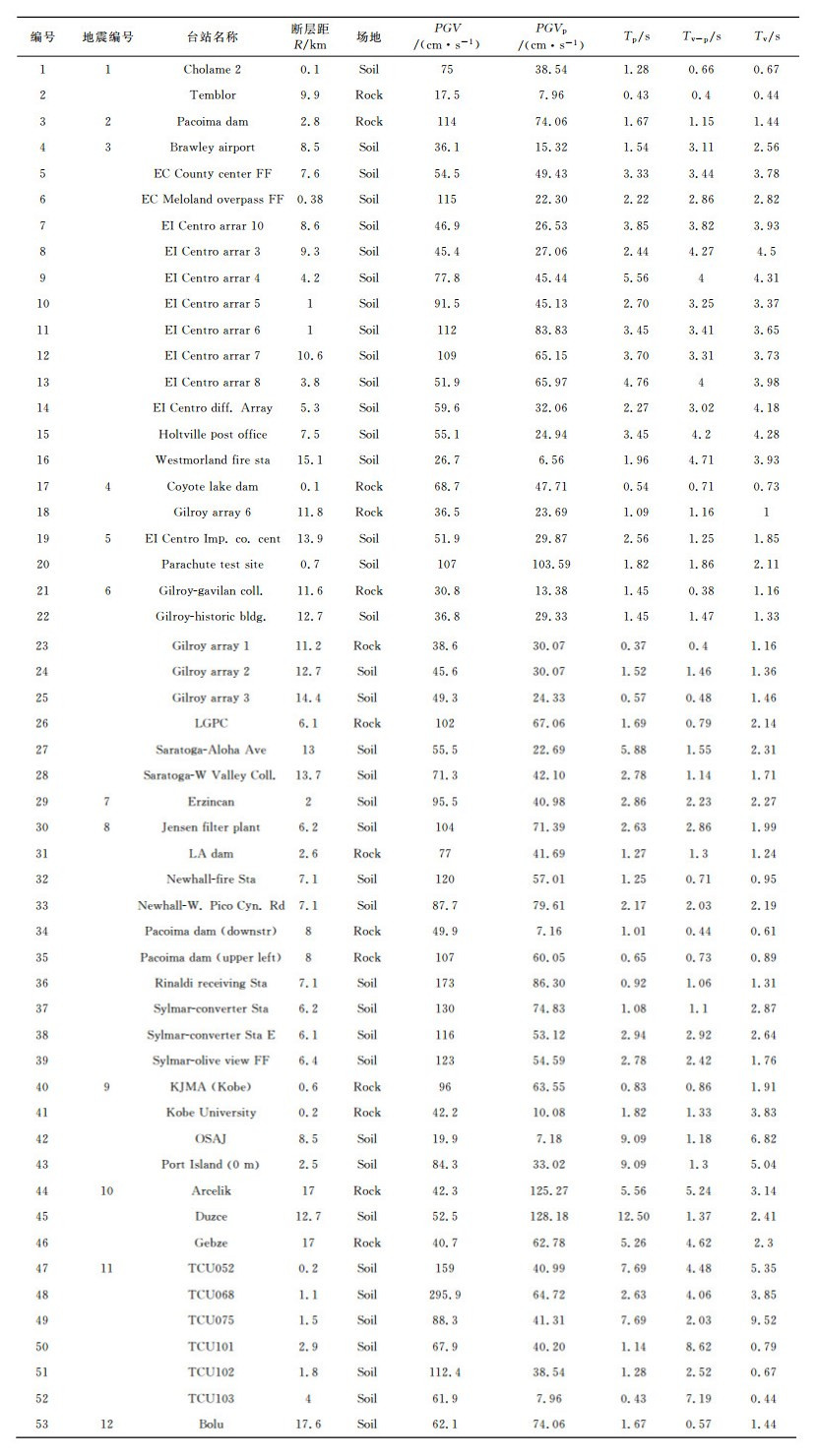
文中对文献[4]和文献[25]中采用的53条近断层长周期地震动进行了分解,这些数据全都来自PEER强地震动数据库(http://peer.berkeley.edu/[2013-01-25]).这些记录都是处于活断层上的浅源地震记录.其中,14条位于岩石场地,震级介于6.1和7.4之间,39条位于土层场地,震级介于6.1和7.6之间.地震与地震动信息分别见表 1和2.由于讨论的主要对象是长周期分量,分解过程中选取的分量频率均小于5 Hz.对于最小分解尺度的确定:经分析,一般经过4尺度的分解就能获得频率小于5 Hz的分量,所以所有地震动都进行了4层以上分解;对于最大分解尺度的确定:如果进行j+1次分解之后,aj+1不再呈现震荡特性,或者aj+1的幅值小于原始地震动幅值的千分之一,或者序列长度受限不能再分解,则“j”即为最大分解尺度.每条地震动按逆序依次获取a′4,a′5,…,a′j-1,aj,共(j-3)个分量.通过这种分解方式共获取了266条地震动分量.由分解结果可知,地震动平均分解次数约为5次,即将一条地震动分解成5个较为简单的地震动分量,为后文的理论分析提供了数据基础.
|
|
表 1 地震信息表 Table 1 Earthquake information |
|
|
表 2 地震动信息表 Table 2 Ground motion information |
由于结构的反应受到脉冲周期与结构自振周期之间比率的影响,地震动的脉冲周期是工程领域中一个极其重要的参数[26-29].由于通过多尺度分解方法所获取的分量在频域上是一个窄带过程,文中采用与分量加速度时程傅里叶幅值谱的幅值对应的周期作为分量的周期.
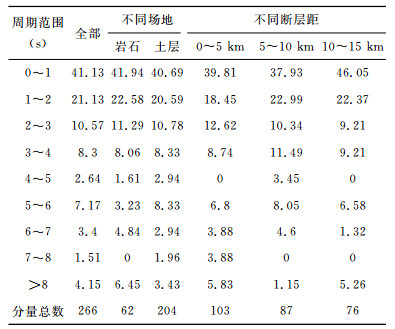
本文对266条地震动分量的周期进行了统计分析,按周期的大小分为0.2~1 s、1~2 s、2~3 s、3~4 s、4~5 s、5~6 s、6~7 s、7~8 s以及大于8 s共9个区间;按照场地的不同分为岩石场地和土层场地;按照断层距的大小划分为0~5 km、5~10 km、10~15 km三个区域.文中依次从总体、不同场地和不同断层距三个方面给出了分量周期的统计结果(见表 3).表 3给出了各类别不同周期范围地震动分量所占的百分比以及各类别分量总数.
|
|
表 3 分量周期统计表 Table 3 Statistical table of components period |
由全部地震动分量统计结果知:(1)近断层长周期地震动中长周期分量的周期一般都在8 s以内,周期超过8s的分量仅占4.15%;(2)0~2 s的分量是长周期分量的主要组成部分,占62.26%;(3)在0~5 s的范围内,各分量的比重逐渐下降,当周期介于5~6 s时分量的比重突然上升,然后再逐渐下降.
由不同场地统计结果可知:(1)岩石场地和土层场地中,地震动中周期为0.2~2 s的分量分别占有64.52%和61.28%,基本相当;(2)在周期为3~8 s的每一个区间段,土层场地中分量的比重都多于岩石场地;(3)岩石场地地震动中周期大于8 s的分量的比重是土层场地的1.5倍,表明近断层土层场地地震动中的长周期分量明显增加,但周期大于8 s的超长周期分量主要出现在岩石场地.虽然岩石场地中超过8 s的超长周期的比例比土层场地大,但由于所采用的岩石场地地震动数据偏少,所得到的结果有待将来在更多强震观测记录的基础上做进一步的分析验证.
由不同断层距统计结果可知:(1)断层距为0~5 km、5~10 km、10~15 km的地震动中周期为0~2 s的分量分别占58.26%、60.92%、68.42%,呈现随断层距的增大比重递增的趋势;(2)2~3 s的分量分别占12.62%、10.34%、9.21%,呈现随断层距的增大比重递减的趋势;(3)周期为3~8 s的分量不论总体还是各区间段大都呈现出中间大两端小的特点;(4)周期大于8 s的分量分别占5.83%、1.15%、5.26%,表现为中间小两端大.因此,在近断层区域,随断层距的增加,地震动中长周期分量的比重减小,周期大于8 s的超长周期分量主要集中在断层处.
5 地震动脉冲特性分析 5.1 参数确定国内外较多学者围绕近断层长周期地震动的脉冲特性开展了研究工作,给出了脉冲周期、峰值速度等重要参数随场地、震级、断层距等影响因素的变化规律.由于脉冲本身的复杂性,大都采用简单的几何函数对最大脉冲进行等效或简化.分析发现,在近断层长周期地震动各低频分量中,速度幅值最大的一条分量能够很好地表征原始地震动速度时程中最大脉冲在时域以及频域内的特征.为获得更为可靠的信息,将最大分量定义为:与原始脉冲幅值方向相同的各分量中速度幅值最大的分量,简称为卓越分量.文中通过卓越分量研究地震动的脉冲特性.
速度幅值与脉冲周期是表征近断层长周期地震动脉冲特性最重要的两个参数[25].在研究中,大都认为PGV能够较好地反应脉冲的时域特征,文中直接对卓越分量的速度时程峰值PGVp进行分析.
目前对地震动脉冲周期的定义尚不统一.有学者采用零交法或者用等效脉冲模型的方法计算脉冲周期.还有对速度时程中有效脉冲循环的周期加权平均计算脉冲周期.这些方法虽能在一定程度上体现脉冲周期的特征,但受主观因素(零交法中零点的选取,起止点的确定;等效脉冲模型的选择;权系数的确定等)的影响明显.上文已经论述,经多尺度分解得到的各分量在频域内是一个窄带过程,采用傅里叶幅值谱最大幅值对应的周期就可以较为精确地标定分量的周期.
5.2 参数对比由于忽略了其他频率组分的作用,PGVp与PGV之间在幅值上必然存在一定的差异,文中对PGVp与PGV进行了对比分析.分析结果(见图 6)表明,PGVp约为PGV的0.6倍,并且PGVp与PGV之间存在明显的线性关系.

|
图 6 PGVp与PGV对比图 Fig. 6 PGVp versus PGV |
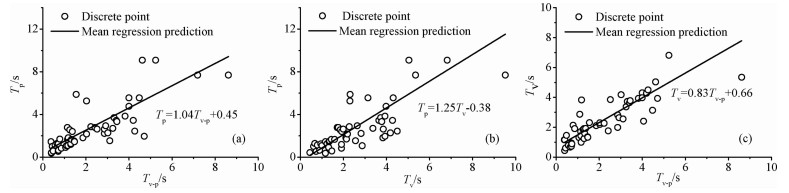
零交法和速度谱幅值方法是确定脉冲周期最常见的两种方法.Rodriguez-Marek[25]采用这两种方法计算了文中提到的53条近断层地震动的周期,指出零交法得到的脉冲周期Tv约为速度谱幅值法脉冲周期Tv-p的0.84倍.文中对三种方法得到的周期进行了对比分析,分析结果见图 7.结果表明,在三种方法得到的周期中Tp>Tv-p>Tv,并且三种周期两两之间都存在明显的线性关系.此外,相对于零交法本文方法得到的周期与速度谱幅值法得到的周期更为接近.
|
图 7 三种周期(Tp、Tv-p、Tv)对比图 (a)Tp与Tv-p对比;(b)Tp与Tv对比;(c)Tv-p与Tv对比. Fig. 7 Comparison between three kinds of period, Tp、Tv-p、Tv (a)Tp versus Tv-p; (b)Tp versus Tv; (c)Tv-p versus Tv. |
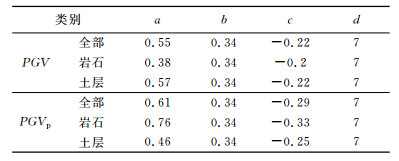
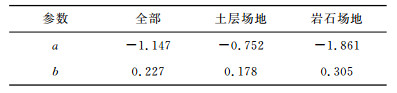
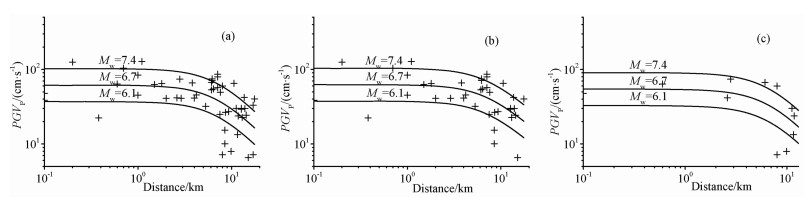
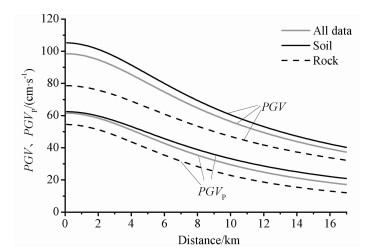
考虑到近断层地震动的复杂性,为获得更可靠的速度幅值的预测结果,采用方程(1)分别对PGVp和PGV进行了回归分析.这种数学模型在断层距较小时斜率为0,并随断层距的增大而逐渐增大,衰减特点与PGVp以及PGV的变化趋势吻合,此外,合理地确定参数d可以减小断层区地震动对预测结果的不利影响.方程的可靠性与数据随断层距和震级的分布相关,由于岩石场地的数据较少,为提高模型的可靠性,震级参数b采用全部数据回归计算的结果.方程中各参数取值见表 4,回归曲线分别见图 8-9.可以看出,PGVp和PGV皆随断层距的增大而逐渐减小,随震级的增大而增大,并且土层场地中的值大于岩石场地.
|
|
表 4 PGVp和PGV回归分析参数表 Table 4 Parameters from the regression analyses of PGVp and PGV |
|
图 8 PGVp衰减关系 (a)全部;(b)土层;(c)岩石. Fig. 8 Attenuation relationship for PGVp (a) All data; (b) Soil; (c) Rock. |
|
图 9 PGVp和PGV衰减关系对比图 Fig. 9 Comparison graph of attenuation relationship between PGVp and PGV |
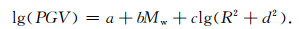
|
(1) |
文中采用方程(2)对Tp与震级的关系进行了回归分析,各参数取值见表 5.回归曲线(见图 10a)表明,Tp随震级的增大而增大,且土层场地卓越分量的周期大于岩石场地,与文献[25]中脉冲周期Tv的分布特征相同.
|
|
表 5 Tp回归分析参数表 Table 5 Parameters from the regression analyses of Tp |
|
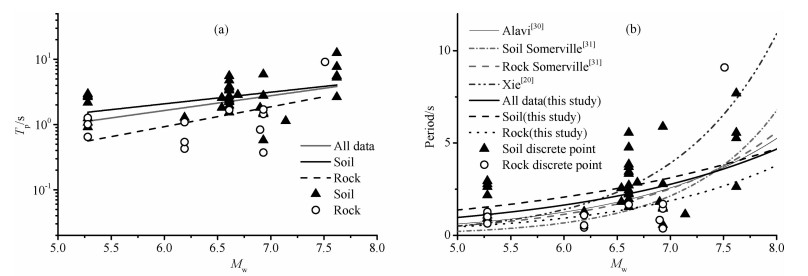
图 10 周期衰减关系 (a)-本文Tp衰减关系;(b)-本文回归得到的脉冲周期和震级的经验关系与前人结果的比较. Fig. 10 Attenuation relationship of period (a) Attenuation relationship of Tp(in this study); (b) Variation formula of pulse period with moment magnitude obtained in this study compared with former relationship. |

|
(2) |
图 10b将回归得到的周期和震级的预测模型与Alavi[30]、Somerville[31]以及谢俊举[20]给出的经验模型进行了对比.由图可见,文中得到的经验模型除与谢俊举[20]给出的经验模型相差较大外,与其余的经验模型相差不大.但是,在震级较小的范围内文中的经验模型比其他模型的值都偏大.由于谢俊举[20]的分析中含有较多的汶川地震动数据,所以其对地震动周期的预测值偏大.
6 结论为了深入探讨近断层长周期地震动的组成及其脉冲特性,基于多尺度分析理论提出了一种用于分析地震动组成的分解方法,检验了该分析方法的有效性,并应用于典型近断层方向性效应地震动的分解,通过对实际地震动及其组成分量的分析,得到一些新的认识,主要结果如下:
(1) 多尺度分解方法可以将一条地震动分解为多个不同频率的分量,并具有较高的精度和计算效率.但由于地震动本身的复杂性,仍需通过其他计算方法确定地震动分量的周期参数.
(2) 通过分解方法可以定量地评估近断层脉冲型地震动的频率组成在场地、断层距等影响因素下的变化规律.所得到的分析结果可为近断层区域建筑结构设计中场地的选取、结构周期的确定等提供参考依据.
(3) 采用多尺度分解方法可以对近断层地震动的脉冲特性进行更为有效的分析.由分解得到的卓越分量可以作为最大脉冲的有效简化,且计算简便,相关参数的物理意义明确.
(4) 通过分量分离的方法可以获取地震动更为详细的细节信息,但对于指导近断层区域建筑结构设计仍需要结合其他领域的相关知识进行更为深入的研究.
| [1] | Galal K, Ghobarah A. Effect of near-fault earthquakes on North American nuclear design spectra. Nuclear Engineering and Design , 2006, 236(18): 1928-1936. DOI:10.1016/j.nucengdes.2006.02.002 |
| [2] | Luco N, Cornell C A. Structure-specific scalar intensity measures for near-source and ordinary earthquake ground motions. Earthquake Spectra , 2007, 23(2): 357-392. DOI:10.1193/1.2723158 |
| [3] | Akkar S, Yazgan U, Gulkan P. Drift estimates in frame buildings subjected to near-fault ground motions. Journal of Structural Engineering , 2005, 131(7): 1014-1024. DOI:10.1061/(ASCE)0733-9445(2005)131:7(1014) |
| [4] | Xu L J, Rodriguez-Marek A, Xie L L. Design spectra including effect of rupture directivity in near-fault region. Earthquake Engineering and Engineering Vibration , 2006, 5(2): 159-170. DOI:10.1007/s11803-006-0636-8 |
| [5] | Rupakhety R, Sigurdsson S U, Papageorgiou A S, et al. Quantification of ground-motion parameters and response spectra in the near-fault region. Bull Earthquake Engineering , 2011, 9(4): 893-930. DOI:10.1007/s10518-011-9255-5 |
| [6] | Zamora M, Riddell R. Elastic and inelastic response spectra considering near-fault effects. Journal of Earthquake Engineering , 2011, 15(5): 775-808. DOI:10.1080/13632469.2011.555058 |
| [7] | Adanur S, Altunisik A C, Bayraktar A, et al. Comparison of near-fault and far-fault ground motion effects on geometrically nonlinear earthquake behavior of suspension bridges. Nat Hazards , 2012, 64(1): 593-614. DOI:10.1007/s11069-012-0259-5 |
| [8] | Cavdar O. Probabilistic sensitivity analysis of two suspension bridges in Istanbul, Turkey to near-and far-fault ground motion. Natural Hazards and Earth System Science , 2012, 12(2): 459-473. DOI:10.5194/nhess-12-459-2012 |
| [9] | 谢礼立, 周雍年, 胡成祥, 等. 地震动反应谱的长周期特性. 地震工程与工程振动 , 1990, 10(1): 1–19. Xie L L, Zhou Y N, Hu C X, et al. Characteristics of response spectra of long-period earthquake ground motion. Earthquake Engineering and Engineering Vibration (in Chinese) , 1990, 10(1): 1-19. |
| [10] | Takewaki I, Murakami S, Fujita K. The 2011 off the Pacific coast of Tohoku earthquake and response of high-rise buildings under long-period ground motions. Soil Dynamics and Earthquake Engineering , 2011, 31(11): 1511-1528. DOI:10.1016/j.soildyn.2011.06.001 |
| [11] | Xie L L, Xu L J, Rodriguez-Marek A. Representation of near-fault pulse-type ground motions. Earthquake Engineering and Engineering Vibration , 2005, 4(2): 191-199. DOI:10.1007/s11803-005-0002-2 |
| [12] | Sehhati R, Rodriguez-Marke A, Gawady M E, et al. Effects of near-fault ground motions and equivalent pulses on multi-story structures. Engineering Structures , 2011, 33(3): 767-779. DOI:10.1016/j.engstruct.2010.11.032 |
| [13] | Makris N. Rigidity-plasticity-viscosity: can electrorheological dampers protect base-isolated structures from near-source ground motions. Earthquake Engineering and Structural Dynamics , 1997, 26(5): 71-91. |
| [14] | Krawinkler H, Alavi B. Development of an improved design procedure for near-fault ground motions. SMIP 98 seminar on utilization of strong motion data, Oakland, CA, 1998. |
| [15] | Bozorgnia Y, Mahin S A. Ductility and strength demands of near-fault ground motions of the Northridge earthquake. Proceedings of the 6th US national conference on earthquake engineering, Earthquake Engineering Research Institute, Seattle, 1998. |
| [16] | Baker J W. Quantitative classification of near-fault ground motions using wavelet analysis. Bulletin of the seismological society of America , 2007, 97(5): 1486-1501. DOI:10.1785/0120060255 |
| [17] | Yaghmaei-Sabegh S. Application of wavelet transforms on characterization of inelastic displacement ratio spectra for puls-like ground motions. Journal of Earthquake Engineering , 2012, 16(4): 561-578. DOI:10.1080/13632469.2011.640739 |
| [18] | Yaghmaei-Sabegh S. Detection of pulse-like ground motions based on continues wavelet transform. Journal of Seismology , 2010, 14(4): 715-726. DOI:10.1007/s10950-010-9193-8 |
| [19] | Mollaioli F. Wavelet analysis for the characterization of forward-directivity pulse-like ground motions on energy basis. Meccanica , 2012, 47(1): 203-219. DOI:10.1007/s11012-011-9433-1 |
| [20] | 谢俊举, 温增平, 李小军, 等. 基于小波方法分析汶川地震近断层地震动的速度脉冲特性. 地球物理学报 , 2012, 55(6): 1963–1972. Xie J J, Wen Z P, Li X J, et al. Analysis of velocity pulses for near-fault strong motions from the Wenchuan earthquake based on wavelet method. Chinese Journal of Geophysics (in Chinese) , 2012, 55(6): 1963-1972. |
| [21] | Ghahari S F, Jahankhah H, Ghannad M A. Study on elastic response of structures to near-fault ground motions through record decomposition. Soil Dynamics and Earthquake Engineering , 2010, 30(7): 536-546. DOI:10.1016/j.soildyn.2010.01.009 |
| [22] | Iervolino I, Chioccarelli E, Baltzopoulos G. Inelastic displacement ratio of near-source pulse-like ground motions. Earthquake Engineering and Structural Dynamics , 2012, 41(15): 2351-2357. |
| [23] | Maniatakis C A, Spyrakos C C. A new methodology to determine elastic displacement spectra in the near-fault region. Soil Dynamics and Earthquake Engineering , 2012, 35: 41-58. DOI:10.1016/j.soildyn.2011.10.005 |
| [24] | 高静怀, 汪文秉, 朱光明, 等. 地震资料处理中小波函数的选取研究. 地球物理学报 , 1996, 39(3): 392–400. Gao J H, Wang W B, Zhu G M, et al. On the choice of wavelet functions for seismic data processing. Chinese J. Geophys (in Chinese) , 1996, 39(3): 392-400. |
| [25] | Bray J D, Rodriguez-Marek A. Characterization of forward-directivity ground motions in the near-fault region. Soil Dynamics and Earthquake Engineering , 2004, 24(11): 815-828. DOI:10.1016/j.soildyn.2004.05.001 |
| [26] | Alavi B, Krawinkler H. Effects of near-fault ground motions on frame structures. Blume Earthquake Engineering Research Center, Report No.138, Stanford, California, 2001. |
| [27] | Mavroeidis G P, Dong G. Near-fault ground motions, and the response of elastic and inelastic single-degree-of-freedom (SDOF) systems. Earthquake Engineering and Structural Dynamics , 2004, 33(9): 1023-1049. DOI:10.1002/(ISSN)1096-9845 |
| [28] | Yang D X, Wang W. Nonlocal period parameters of frequency content characterization for near-fault ground motions. Earthquake Engineering and Structural Dynamics , 2012, 41(13): 1793-1811. DOI:10.1002/eqe.v41.13 |
| [29] | James C A, Vitelmo V B. Uncertainties in establishing design earthquakes. Journal of Structural Engineering , 1987, 113(8): 1709-1724. DOI:10.1061/(ASCE)0733-9445(1987)113:8(1709) |
| [30] | Alavi B, Krawinkler H. Consideration of near-fault ground motion effects in seismic design.//Proceedings 6th World Conference on Earthquake Engineering. New Zealand: The New Zealand Society for Earthquake Engineering, 2000, 2665: 1-8. |
| [31] | Somerville P G. Magnitude scaling of the near fault rupture directivity pulse. Physics of the Earth and Planetary Interiors , 2003, 137(1-4): 201-212. DOI:10.1016/S0031-9201(03)00015-3 |
 2013, Vol. 56
2013, Vol. 56