强震发生后,作为可利用的直接信息,余震序列的早期活动特征被用于序列类型判定[1]、强余震预测[2]和余震短期概率预测[3-4]等方面,在抗震救灾、区域地震危险性评估和对地震序列本身的认识上均具有重要的科学价值和现实意义.作为Omori-Utsu公式[5-6]的推广,“传染型余震序列”(Epidemic Type Aftershock Sequence,简称ETAS)模型[7-9]得到长足发展.ETAS模型除可对地震序列参数进行接近真实的估计,还可基于其模型参数,以及“瘦化算法”(thinning algorithm)[10-11]进行序列模拟和余震概率预测.
由于多采用统计地震学的方法,余震序列早期活动特征和余震概率预测研究可能受到截止震级Mc设定的影响.一些研究表明,表征地震监测能力的完整性震级可在强震发生后的短期内在余震区甚至更大范围内发生显著降低[12],余震区增设临时台站和区域地震台网固定台站运行状态的改变也可造成完整性震级的实时、动态变化[13].除客观的监测能力/完整性震级的变化,Mc的人为设定将对ETAS模型参数估计造成影响[14-16],其中一个原因是由于ETAS模型假定任何一个地震都可能触发其后发生的任何大小的地震,Mc的设定可能切断了M<Mc的地震与其他地震的触发关系,从而造成“链接缺失”(missing link)现象[16].由此,在强震发生后,面对完整性震级的可能变化,如何科学、合理地设定ETAS模型计算所用的截止震级Mc,以及评估这种设定对相关的应用有何影响具有重要的现实意义.
本研究将基于ETAS模型,以新近发生的2013年7月22日甘肃岷县-漳县6.6级地震序列为例,探讨截止震级Mc对序列参数估计和余震概率预测应用效果的可能影响.
2 研究所用资料和序列目录完整性分析本研究所用的2013年甘肃岷县-漳县6.6级地震序列目录,来自中国地震台网中心“全国地震编目系统”提供的《甘肃地震台网速报目录》1).选用主震发生至之后3天内的0级以上地震,限定地震序列的空间范围分别为34.4°N-34.7°N,104.0°E-104.4°E.
1) 全国地震编目系统.http://10.5.202.22/bianmu/index.jsp[2013-07-24].
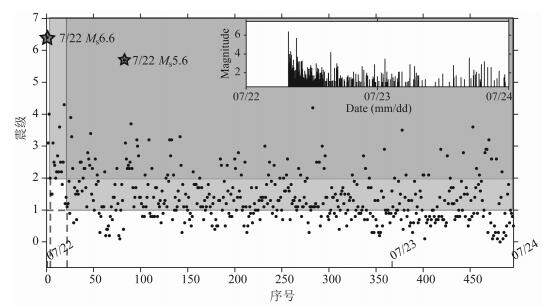
2013年甘肃岷县-漳县6.6级地震序列目录的完整性震级是采用“震级-序号”法[17-19]进行定性讨论.震级-序号法按地震发生时间的先后顺序排序,地震密度较大的区域的连线大致为Mc的时序变化.这种分析一方面避免了短期内大量发生、密集分布的余震在时间轴上难以分析对其监测能力的快速变化,另一方面,由于Mc在短期内常具有分段和不连续的变化特征,由此可以给出信噪比和人为因素引起的监测能力变化.对甘肃岷县-漳县6.6级地震序列的分析结果如图 1所示.由图可见,主震发生后1天内,Mc由ML3.0逐渐降低至ML0.5左右,反映了对余震序列的监测能力逐渐提升过程.当截止震级Mc=ML1.0和Mc=ML2.0时,地震序列目录完整的位置分别为主震后0.021天和0.006天.对2013年四川芦山7.0级地震序列,蒋长胜等[20]同样利用震级-序号法进行了完整性震级分析,结果表明在震后0.031天,序列完整性震级可达ML2.0.
|
图 1 甘肃岷县-漳县MS6. 6地震序列目录的震级-序号图 图中五角星标出了主震和MS5.6最大余震的位置,两条垂直虚线分别标出了当截止震级为MLl.0和ML2.0时地震目录完整的位置,即分别为主震后0.021天和0.006天.子图为ML1.0以上地震的震级-时间(M-t)图. Fig. 1 Catalogue completeness of the Minxian-Zhangxian MS6. 6 earthquake sequence Grey stars are the position of mainshock and its largest aftershock, respectively. The two vertical dashed lines indicate the starting time of the aftershocks with completeness magnitude of ML2.0 and ML1.0, respectively, corresponding to 0.006 day and 0.021 day, respectively, after the mainshock. The subplot shows the M-t plot with magnitude no less than ML1.0. |
对一维的余震序列随时间的衰减关系,在统计地震学的“时间点过程”(temporal point-process)研究中常使用泊松模型、应力释放模型以及修正的Omori-Utsu公式等进行研究,其中修正的Omori-Utsu公式[5-6]最为普遍使用.其表达式为
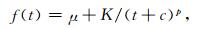
|
(1) |
其中t为主震发生后的离逝时间,f(t)为t时刻的余震发生率,μ为背景地震的发生率,p表示余震序列衰减的快慢,c为主震后余震频次达到峰值时对应的时间,K表示余震的活跃程度.上式中μ、K、c和p为非负的常数.
实际上真实的余震序列远比修正的Omori-Utsu公式描述的简单衰减关系复杂.为解决每个余震都可激发次级余震的情况,Ogata[7-9]在Omori-Utsu公式基础上,提出了ETAS模型.ETAS模型假设余震遵从Omori-Utsu公式激发自己的余震,且震级的分布是独立的,在主震的发生为初始零时刻情况下,观测时间段[0,T]内的地震序列{(ti,Mi);i=1,2,…,N}的条件强度函数(conditional intensity function)可表示为[7]
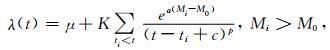
|
(2) |
其中Mi和ti分别为第i个事件的震级和发生时间,M0为参考震级,这里取为截止震级.p与修正的Omori-Utsu公式中的p有相同的物理含义,均表示序列衰减的快慢,p越大衰减越快,反之越慢.α表示触发次级余震的能力[8, 21].
3.2 ETAS模型参数的最大似然估计和残差分析ETAS模型的参数一般通过最大似然法(MLEs)进行估计.在地震序列目录完整的时间段[tc,T]内,0<tc<T,似然函数L的形式为
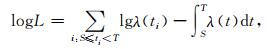
|
(3) |
将(2)式带入上式,即可对待估参数[μ,K,c,α,p]进行最大似然估计.
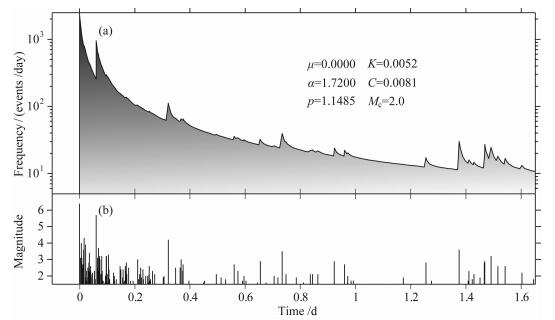
强震发生后,尽快获得对地震序列活动特征的认识在时效性上有重要显示意义.在本文对甘肃岷县-漳县6.6级地震序列参数早期特征的考察中,选定2013年7月22日07:45至24日00:00的ML1.0以上地震序列目录,设定参数拟合时段为震后0.021~1.677天(7月24日00:00),进行不同截止震级Mc下的ETAS模型参数的最大似然估计.作为示例,图 2给出了甘肃岷县-漳县6.6级地震序列在Mc=ML2.0情况下的ETAS模型参数结果,其中μ=0.0000,K=0.0052,c=0.0081,α=1.7200和p=1.1485.图 2a为相应ETAS模型条件强度曲线,即单位时间内的地震发生率随时间的变化.由图可见,在震后1.677天内,较大余震事件引起的强度曲线的变化较为明显.
|
图 2 利用ETAS模型拟合给出的岷县-漳县MS6.6地震序列ML2.0以上地震的条件强度曲线 (a)条件强度曲线;(b)M-t图. Fig. 2 Temporal evolution of the conditional intensity from fitting the ETAS model to the Minxian-Zhangxian MS6.6 earthquake sequence, with cutoff magnitude ML2.0 (a) Conditional intensity curve; (b)M-t plot. |
为考察ETAS模型的拟合效果,常使用在“转换时间”域的“残差分析”方法[7, 22].“残差分析”方法可将复杂的地震序列{ti}转换为齐次泊松过程:
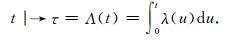
|
(4) |
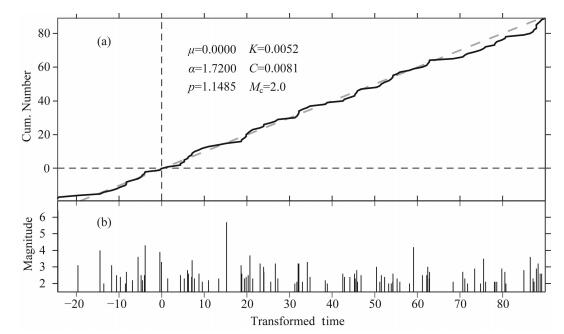
(4)式中经过转化的数据被称为“残差点过程”(RPP).如果模型与数据拟合的较好,RPP在转换时间-累积频次图上就表现为线性,接近标准的稳态泊松过程的理论直线[19],而实际上对一般的强余震预测,在“转换时间”域{τ}的预测和效能检验可能更有意义[23].图 3a给出了甘肃岷县-漳县6.6级地震序列累积地震数与ETAS拟合曲线在“转换时间”域{τ}的比较情况.在图 3b中,地震序列在“转换时间”域{τ}已被转换为稳态泊松分布.
|
图 3 利用ETAS模型对岷县-漳县MS6.6地震序列ML2.0以上地震的拟合情况利用ETAS模型对岷县-漳县MS6.6地震序列ML2.0以上地震的拟合情况 (a)累积地震数与ETAS拟合曲线在“转换时间”(τ)域的比较;(b)M-τ图,τ为将时间转换为稳态泊松分布的“转换时间”. Fig. 3 Comparison of the observed and modeled cumulative number of M≥ML2.0 earthquakes of the Minxian-Zhangxian MS6.6 earthquake sequence (a) Observation (dark blue curve) and ETAS modeled curve (thick gray dashed line) in the transformed time (τ) domain; (b)M-τ plot, in which τ is the transformed time which is according to the stationary Poisson process. |
由于真实地震序列的复杂性,ETAS模型对地震序列的拟合是否优于修正的Omori-Utsu公式还需要根据定量的判据、进行比较研究[21, 24-25].如果序列整体的衰减特征相对简单,则修正的Omori-Utsu公式可能拟合效果更好.为考察ETAS模型是否适用于甘肃岷县-漳县6.6级地震序列,这里使用修正的Omori-Utsu公式进行比较,并使用赤池准则[26](Akaike information criteria,简写为AIC)进行判断:
(5)式中计算获得的AIC值越小表示适用效果越好.由于AIC准则包括了待定拟合参数/模型自由度的数量,因此考虑了对增加模型参数个数提高拟合效果的“惩罚”.
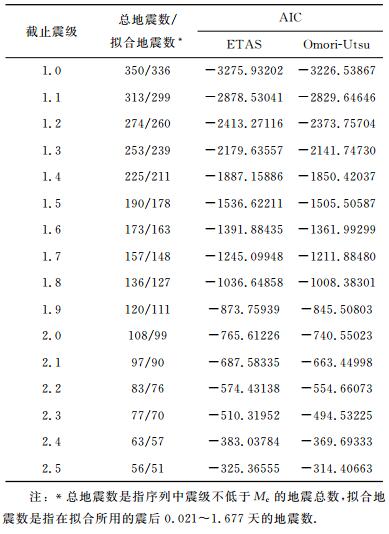
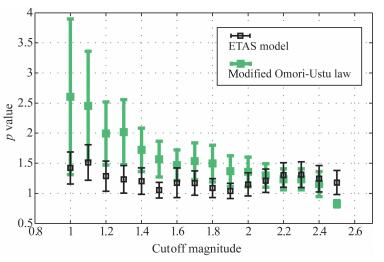
在对两个模型的比较研究中,分别考察了Mc=ML1.0,1.1,…,2.5时的AIC值的比较情况,结果如表 1所示.由表 1可见,在不同的截止震级下,ETAS模型的AIC值均小于修正的Omori-Utsu公式的结果.图 4给出了两个模型在不同截止震级Mc下的参数p值,及其基于对数似然函数的Hessian矩阵[27]估计拟合参数的标准差的结果.由图可见,ETAS模型给出的p值在不同截止震级Mc下相对震数是指在拟合所用的震后0.021~1.677天的地震数.稳定、误差更小,而修正的Omori-Utsu公式给出的p值变化范围可达0.8~2.6,表现出较强的不稳定性.由此表明ETAS模型更适合对此时段的序列拟合.
|
|
表 1 不同截止震级下ETAS模型和修正的Omori-Utsu公式模型拟合效果的比较 Table 1 Fitting results of ETAS model and modified Omori-Utsu law model with deferent cutoff magnitude |
|
图 4 ETAS模型和修正的Omori-Utsu公式在不同截止震级下的p值拟合结果比较 图中给出了基于Hessian矩阵估计的误差. Fig. 4 Estimated p values of ETAS model and modified Omori-Utsu law with deferent cutoff magnitude The Hessian matrix based error is also shown. |
为考察Mc的选取对ETAS模型参数估计的影响,研究中设定Mc=ML1.0,1.1,…,2.5,将拟合时间固定为主震后0.021~1.677天,分别考察最大似然估计结果.此外,作为对比还同时考察了2013年芦山7.0级地震序列在震后相同时段的参数情况.受序列目录完整性的影响,仅对Mc=ML2.0,2.1,…,3.0情况下的参数进行考察.
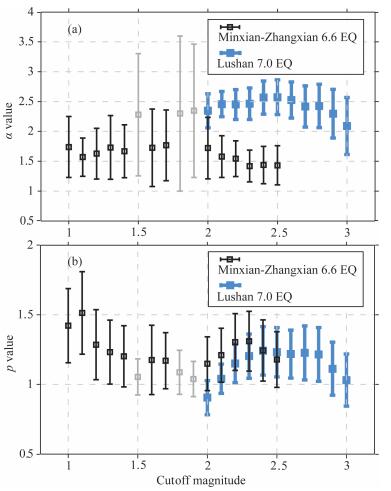
图 5给出了ETAS模型中的α值和p值随Mc的变化情况.由图 5a可见,除当Mc=ML 1.5、1.8和1.9时误差较大、数值较高外,α值随Mc变化在1.4~1.8之间.而芦山7.0级地震的α值较大,在2.1~2.6之间.由图 5b可见,甘肃岷县-漳县6.6级地震的p值在1.2~1.5之间,芦山7.0级地震的p值在0.9~1.2之间.由于不同类型的地震序列α值差异较大,而p值平均1.0左右、差异相对较小.
|
图 5 ETAS模型参数α值(a)和p值(b)随截止震级的变化 图中给出了2013年芦山MS7.0地震的结果用于比较,灰色标出了α值拟合误差较大的结果,分别为Mc=ML1.5、1.8和1.9. Fig. 5 Parameter α (a) and p (b) against the cutoff magnitude in ETAS fitting The blue ones show the fitting result of 2013 Lushan MS7.0 earthquake sequence, and grey ones show the larger error fitting results corresponding to Mc=ML1.5, 1.8 and 1.9. |
图 5结果显示,两次地震的α值随Mc的变化相对稳定,甘肃岷县-漳县6.6级地震的α值明显低于芦山7.0级地震,显示了对次级余震相对较强的激发能力,而其p值则相对高于芦山7.0级地震,显示了相对较快的衰减.两次地震的p值则随Mc的变化较大,由此可知,在考察地震序列参数的早期特征,尤其是衰减特征时,需要考虑在何种截止震级下进行讨论和对比.
5 对余震短期概率预测的影响 5.1 基于ETAS模型和瘦化算法的余震短期概率预测由于余震的短期概率预测需要基于“过去”的序列参数,在给定的时间间隔[t,t+l(t)]内外推时间相依(time-dependent)的、未来余震序列的发生情况,这种预测可通过对点过程模型(point process model)的多次模拟来实现.点过程模型模拟的关键技术是在给定的强度函数情况下确定下一次事件的发生时刻,一般采用逆解法(inverse method)或瘦化算法(thinning algorithm,也称“Lewis’ law”)[10-11]进行.目前,基于ETAS模型的余震短期概率预测主要采用Ogata[11]“修正的瘦化算法”(文中不加区分地使用“瘦化算法”)进行.“瘦化算法”将地震序列转化为齐次泊松过程,并对强度函数进行多次模拟,利用模拟获得的地震序列的平均结果描述预测情况.此外,一些研究还使用高斯空间核函数,基于“瘦化算法”和复杂的时-空ETAS模型开展地震短期概率预测尝试[28-30].
“瘦化算法”的计算基本步骤如下:
(1) 在进行预测/随机模拟的时段[tsta,tend]内,条件强度函数λ*的计算模型参数使用tsta时刻获得的ETAS模型参数[μ,K,C,α,p];
(2) 地震序列模拟事件的发生时刻t=tsta为起点,设定序列模拟事件的“前进”时间步长函数l(t),在[t,t+l(t)]内进行齐次泊松过程模拟.其中,模拟获得的条件强度函数λ*的,需满足其上限低于起始时刻的条件强度函数m(t),即:

|
(6) |
(6)式中s为随机变量.同时,在[0, 1]中产生另一个独立的均匀随机变量U1,此时l(t)采用如下形式:
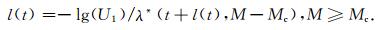
|
(7) |
(3) 震级的分布函数采用:
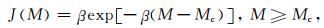
|
(8) |
其中的β与G-R关系中的b值有关,β=blog(10).上述震级关系确保了随机模拟目录的震级分布,也实现了随机目录中次级余震的产生;
(4) 如果s>l(t),设定t=t+l(t);如果t+s>tend或者U1>λ*(t+s)/m(t),则t=t+s.否则,n=n+1,tn=t+s,t=t+s;
(5) 重复上述步骤,直至t+s>tend;此时生成的随机目录的时间序列为{t1,t2,…,tn}.
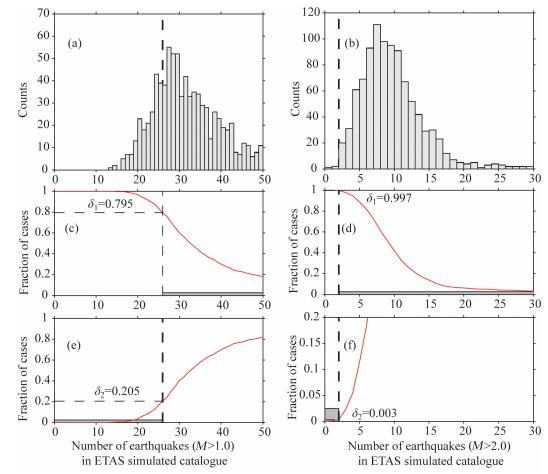
在本研究中,使用上述的“瘦化算法”,对震后1.677~2.677天期间进行1000次的地震目录随机模拟,并通过生成目录中各震级档地震的平均发生率情况,进行余震序列短期预测.图 6a和6b分别给出了Mc=ML1.0和Mc=ML2.0时的预测结果的统计分布.由图中实际发生的地震数目与随机模拟获得的地震的统计分布的比较可见,Mc=ML1.0的结果优于Mc=ML2.0时的结果.
|
图 6 基于ETAS模型和“瘦化算法”方法给出的余震短期概率预测结果和N-test统计检验 左侧的图(a)、(c)和(e)为Mc=ML1.0的结果,右侧的图(b)、(d)和(f)为Mc=ML2.0的结果;图(a)和(b)为震后1.677~2.677天的1000次余震序列随机预测模拟结果的分布,垂直虚线为实际发生的截止震级以上地震数;图(c)和(d)为N-test检验中的δ1评分情况,图(e)和(f)为δ2评分情况,图中红色曲线为余震序列随机预测模拟结果的累积概率曲线,垂直虚线为实际发生的截止震级以上地震数,灰色矩形为显著性水平αeff=0.025的范围. Fig. 6 Aftershock probability forecast based on ETAS model and thinning algorithm with N-test of their performance Left and right column show the results of Mc=ML1.0 and Mc=ML2.0, respectively.Fig. 6(a) and (b) present the stochastic forecast results with 1000 samples simulation of the 1.677~2.677 days after mainshock, the vertical dashed lines show the number of actual earthquakes occurred.Fig. 6(c) and (d) show the results of δ1 evaluation.Fig. 6(e) and (f) show the results of δ2 evaluation.The red curves show the cumulative probability of simulation results, the vertical dashed lines indicate the number of actual earthquakes occurred, and the grey rectangle show the region of significance level with αeff=0.025. |
为更定量化地考察预测的余震数目与实际发生地震数是否存在偏离,这里使用了地震发生数检验的N-test方法[31-33].N-test方法一般借助模拟地震目录进行检验[31-32],模拟地震目录一般基于累积泊松分布函数生成,并可进行任何置信度的检验[31].当预测地震发生数为Nfore,实际地震发生数为Nobs,累积分布函数为F时,可通过两个评分量δ1和δ2分别回答发生“至少”和“不超过”Nobs个地震事件的概率:
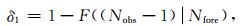
|
(9) |
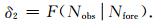
|
(10) |
对于N-test检验结果可使用有效显著性水平 αeff下的单边检验进行解读,其中αeff=0.5α,α为一般意义上的置信水平.当δ1<αeff时表明预测的地震数目过少;当δ2<αeff时表明预测的地震数目过多.目前,正在进行的国际“地震可预测性合作研究”(Collaboratory for the Study of Earthquake Predictability,CSEP)计划(http://www.cseptesting.org[2013-01-25])中,已将N-test方法作为地震预测效能评估的常规方法.
在本研究中,由于已生成1000次随机模拟地震目录,因此,直接将这些符合ETAS模型参数分布的随机目录,进行累积频次的归一化并作为累积概率.此外,设定置信水平α=0.05时,则有效显著性水平αeff=0.025.图 6(c-f)给出了Mc=ML1.0和Mc=ML2.0时的N-test方法预测效能的检验结果示例.由图可见,在Mc=ML1.0时,评分变量δ1和δ2均未出现<αeff的情况,而在Mc=ML2.0时,δ2=0.003<αeff,由此表明基于ETAS模型的随机预测结果“过多”地预测了ML2.0以上地震的数量.
进一步考察截止震级的选取对余震短期概率预测结果的影响,图 7给出了当截止震级Mc=ML1.0,1.1,…,2.5情况下的N-test检验结果.由图 7a给出的δ1评分结果可见,不同Mc下均未出现预测结果“过少”的情况.在图 7b中,当Mc=ML1.0~2.0时,出现了预测结果“过多”的情况,而当Mc=ML2.1~2.5时尽管通过了评分检验,但评分变量δ1与αeff较为接近.由此可见,对于2013年甘肃岷县-漳县6.6级地震序列,在震后1.677天进行的1天尺度的余震预测中,仅当选取截止震级Mc=ML1.0或ML1.1时可获得较好的余震预测结果.

|
图 7 不同截止震级下的余震短期概率预测的N-test统计检验结果 (a)δ1评分情况;(b)δ2评分情况. Fig. 7 N-test results of short-term probabilistic forecast of after shocks against the cutoff magnitude (a)δ1 evaluation results; (b)δ2 evaluation results. |
在主震发生后较短时间的地震序列早期阶段,地震波速、地表变形、渗透率以及余震速率等参数均发生快速变化[34-35],而流体、矿物和变形构造均可影响断层的愈合行为[36-38],此时的地震序列活动及其控制因素非常复杂.本研究针对此阶段对余震序列类型判定和强余震预测、余震序列短期概率预测等的紧迫需求,讨论了截止震级Mc的选取对ETAS模型应用研究的影响.而实际上,准确把握此阶段地震序列活动特征/趋势或震源区应力状态的变化,统计地震学仅能反映一个侧面,更为直接的约束条件还需要直接面向断层和震源区的震后快速钻探[39]等工作进行佐证.
为使研究问题简化,本研究采用了时间序列的ETAS模型.实际上,目前已有多种形式的ETAS模型,例如基于随机除丛法的时-空ETAS模型[40-41],考虑变化的背景地震活动的时间序列ETAS模型[42]等.因此采用更为接近真实地描述地震活动特征的模型,是本研究讨论的问题可进一步开展之处.
本研究针对ETAS模型在地震序列参数的早期特征和余震短期概率预测研究中的应用问题,重点考察了不同截止震级Mc选取对结果的影响.其中,为考察ETAS模型对甘肃岷县漳县6.6级地震序列的适用性,使用了AIC准则,并与修正的Omori-Utsu公式进行对比研究.为考察不同截止震级Mc的选取对ETAS模型参数估计的影响,设定Mc=ML1.0,1.1,…,2.5,分别考察了α值和p值的稳定性,并与2013年芦山7.0级地震序列进行了对比.为考察不同截止震级Mc的选取对基于ETAS模型和“瘦化算法”的余震短期概率预测结果,设定Mc=ML1.0,1.1,…,2.5,并利用N-test方法进行了预测效能检验.上述研究获得了如下认识:
(1) 对甘肃岷县-漳县6.6级地震序列,由于序列早期阶段的复杂性,ETAS模型相比修正的Omori-Utsu公式更适用于对序列的拟合;
(2) 截止震级Mc对序列参数影响较大,其中对α值的影响相对较小,p值影响较大.因此,在地震序列早期,对序列参数存在序列类型判定、后续强余震估计等应用中,需要进行多个时间段和截止震级的比较,谨慎应用.此外,由于Mc对选取的影响,对不同的地震序列进行比较研究时,需要在相同的Mc下进行分析、考察;
(3) 截止震级Mc的设定对余震短期概率预测影响较大,对甘肃岷县-漳县6.6级地震,仅当Mc=ML1.0或ML1.1时可获得较好的预测结果.由此,在使用不同的Mc均可进行序列参数估计的情况下,如何获得好的余震预测能力,需要分别考察不同的Mc下的预测效果,再进行“向前”的预测实践.
致谢研究中使用了中国地震台网中心“全国地震编目系统”提供的区域地震台网速报目录,日本统计数理研究所庄建仓教授在访问地球物理研究所期间编制、提供了ETAS模型和余震短期概率预测程序,并予以了指导.两位评审专家的意见对本文质量的提升帮助很大,在此表示感谢.
| [1] | 蒋海昆, 郑建常, 吴琼, 等. 传染型余震序列模型震后早期参数特征及其地震学意义. 地球物理学报 , 2007, 50(6): 1778–1786. Jiang H K, Zheng J C, Wu Q, et al. Earlier statistical features of ETAS model parameters and their seismological meanings. Chinese J. Geophys. (in Chinese) , 2007, 50(6): 1778-1786. |
| [2] | Omi T, Ogata Y, Hirata Y, et al. Forecasting large aftershocks within one day after the main shock. Scientific Report , 2013, 3: 2218. DOI:10.1038/srep02218 |
| [3] | Reasenberg P A, Jones L M. Earthquake hazard after a mainshock in California. Science , 1989, 243(4895): 1173-1176. DOI:10.1126/science.243.4895.1173 |
| [4] | Gerstenberger M C, Wiemer S, Jones L M, et al. Real-time forecasts of tomorrow's earthquakes in California. Nature , 2005, 435(7040): 328-331. DOI:10.1038/nature03622 |
| [5] | Omori F. On aftershocks of earthquakes. J. Coll. Sci. Imp. Univ. Tokyo , 1894, 7: 11-200. |
| [6] | Utsu T. A statistical study on the occurrence of aftershocks. Geophys. Mag. , 1961, 30: 521-605. |
| [7] | Ogata Y. Statistical models for earthquake occurrences and residual analysis for point processes. J. Amer. Statist. Assoc. , 1988, 83(401): 9-27. DOI:10.1080/01621459.1988.10478560 |
| [8] | Ogata Y. Statistical model for standard seismicity and detection of anomalies by residual analysis. Tectonophysics , 1989, 169(1-3): 159-174. DOI:10.1016/0040-1951(89)90191-1 |
| [9] | Ogata Y. Increased probability of large earthquakes near aftershock regions with relative quiescence. J. Geophys. Res. , 2001, 106(B5): 8729-8744. DOI:10.1029/2000JB900400 |
| [10] | Lewis P A W, Shedler G S. Simulation of nonhomogeneous Poisson processes by thinning. Naval Research Logistics Quarterly , 1979, 26(3): 403-413. DOI:10.1002/(ISSN)1931-9193 |
| [11] | Ogata Y. On Lewis' simulation method for point processes. IEEE Transactions on Information Theory , 1981, 27(1): 23-31. DOI:10.1109/TIT.1981.1056305 |
| [12] | Iwata T. Low detection capability of global earthquakes after the occurrence of large earthquakes: Investigation of the Harvard CMT catalogue. Geophys. J. Int. , 2008, 174(3): 849-856. DOI:10.1111/gji.2008.174.issue-3 |
| [13] | Schorlemmer D, Mele F, Marzocchi W. A completeness analysis of the national seismic network of Italy. J. Geophys. Res. , 2010, 115: B04308. DOI:10.1029/2008JB006097 |
| [14] | Sornette D, Werner M J. Apparent clustering and apparent background earthquakes biased by undetected seismicity. J. Geophys. Res. , 2005, 110: B09303. DOI:10.1029/2005JB003621 |
| [15] | Schoenberg F P, Chu A, Veen A. On the relationship between lower magnitude thresholds and bias in epidemic-type aftershock sequence parameter estimates. J. Geophys. Res. , 2010, 115: B04309. DOI:10.1029/2009JB006387 |
| [16] | Wang Q, Jackson D D, Zhuang J C. Missing links in earthquake clustering models. Geophys. Res. Lett. , 2010, 37: L21307. DOI:10.1029/2010GL044858 |
| [17] | Huang Q. Search for reliable precursors: A case study of the seismic quiescence of the 2000 western Tottori prefecture earthquake. J. Geophys. Res. , 2006, 111(B4): B04301. DOI:10.1029/2005JB003982 |
| [18] | 蒋长胜, 吴忠良. 2010年玉树Ms7.1地震前的中长期加速矩释放(AMR)问题. 地球物理学报 , 2011, 54(6): 1501–1510. Jiang C S, Wu Z L. Intermediate-term medium-range Accelerating Moment Release (AMR) priori to the 2010 Yushu Ms7.1 earthquake. Chinese J. Geophys. (in Chinese) , 2011, 54(6): 1501-1510. |
| [19] | Zhuang J C, Harte D, Werner M J, et al. Basic models of seismicity: temporal models. Community Online Resource for Statistical Seismicity Analysis , 2012. DOI:10.5078/corssa-79905851 |
| [20] | 蒋长胜, 庄建仓, 龙锋, 等. 2013年芦山7.0级地震序列参数的早期特征:传染型余震序列模型计算结果. 地震学报 , 2013, 35(5): 661–669. Jiang C S, Zhuang J C, Long F, et al. Statistical analysis of ETAS parameters in the early stage of the 2013 Lushan Ms7.0 earthquake sequence. Acta Seismologica Sinica (in Chinese) , 2013, 35(5): 661-669. |
| [21] | Ogata Y. Detection of precursory relative quiescence before great earthquakes through a statistical model. J. Geophys. Res. , 1992, 97(B13): 19845-19871. DOI:10.1029/92JB00708 |
| [22] | Daley D J, Vere-Jones D. An Introduction to the Theory of Point Processes-Volume I: Elementary Theory and Methods. (Second Edition). New York: Springer, 2003 : 17 -33. |
| [23] | Jiang C S, Wu Z L. Testing the forecast of aftershocks: a simple method with an example of application. Research in Geophysics , 2012, 2(1): 29-33. |
| [24] | Guo Z Q, Ogata Y. Statistical relations between the parameters of aftershocks in time, space, and magnitude. J. Geophys. Res. , 1997, 102(B2): 2857-2873. DOI:10.1029/96JB02946 |
| [25] | Zhuang J C. Statistical modelling of seismicity patterns before and after the 1990 Oct 5 Cape Palliser earthquake, New Zealand. N. Z. J. Geol. Geophys. , 2000, 43(3): 447-460. DOI:10.1080/00288306.2000.9514901 |
| [26] | Akaike H. A new look at the statistical model identification. IEEE Trans. Automat. Control , 1974, AC-19(6): 716-723. |
| [27] | Ogata Y. The asymptotic behaviour of maximum likelihood estimators for stationary point processes. Annals of the Institute of Statistical Mathematics , 1978, 30(1): 243-261. DOI:10.1007/BF02480216 |
| [28] | Helmstetter A, Kagan Y Y, Jackson D D. Comparison of short-term and time-independent earthquake forecast models for southern California. Bull. Seismol. Soc. Am. , 2006, 96(1): 90-106. DOI:10.1785/0120050067 |
| [29] | Werner M J, Helmstetter A, Jackson D D. High-resolution long-term and short-term earthquake forecasts for California. Bull. Seismol. Soc. Am. , 2011, 101(4): 1630-1648. DOI:10.1785/0120090340 |
| [30] | Zhuang J C. Next-day earthquake forecasts for the Japan region generated by the ETAS model. Earth Planets Space , 2011, 63(3): 207-216. DOI:10.5047/eps.2010.12.010 |
| [31] | Kagan Y Y, Jackson D D. New seismic gap hypothesis: Five years after. J. Geophys. Res. , 1995, 100(B3): 3934-3959. |
| [32] | Schorlemmer D, Gerstenberger M C, Wiemer S, et al. Earthquake likelihood model testing. Seismol. Res. Lett. , 2007, 78(1): 17-29. DOI:10.1785/gssrl.78.1.17 |
| [33] | Zechar J D. Evaluating earthquake predictions and earthquake forecasts: a guide for students and new researchers. Community Online Resource for Statistical Seismicity Analysis , 2010. DOI:10.5078/corssa-77337879 |
| [34] | Kitagawa Y, Fujimori K, Koizumi N. Temporal change in permeability of the rock estimated from repeated water injection experiments near the Nojima fault in Awaji Island, Japan. Geophys. Res. Lett. , 2002, 29(1): 1483. DOI:10.1029/2001GL014030 |
| [35] | Brenguier F, Campillo M, Hadziioannou C, et al. Postseismic relaxation along the San Andreas fault at Parkfield from continuous seismological observations. Science , 2008, 321(5895): 1478-1481. DOI:10.1126/science.1160943 |
| [36] | Hickman S, Sibson R, Bruhn R. Introduction to special section: Mechanical involvement of fluids in faulting. J. Geophys. Res. , 1995, 100(B7): 12831-12840. DOI:10.1029/95JB01121 |
| [37] | Ohtani T, Fujimoto K, Ito H, et al. Fault rocks and past to recent fluid characteristics workshop reports from the borehole survey of the Nojima fault ruptured in the 1995 Kobe earthquake, southwest Japan. J. Geophys. Res. , 2000, 105(B7): 16161-16171. DOI:10.1029/2000JB900086 |
| [38] | Ma K F, Tanaka H, Song S R, et al. Slip zone and energetics of a large earthquake from the Taiwan Chelungpu-fault Drilling Project. Nature , 2006, 444(7118): 473-476. DOI:10.1038/nature05253 |
| [39] | Brodsky E E, Ma K F, Mori J, et al. Rapid response fault drilling past, present, and future. Scientific Drilling , 2009, 8: 66-74. |
| [40] | Zhuang J, Ogata Y, Vere-Jones D. Stochastic declustering of space-time earthquake occurrences. J. Amer. Stat. Assoc. , 2002, 97(458): 369-380. DOI:10.1198/016214502760046925 |
| [41] | Zhuang J, Ogata Y. Properties of the probability distribution associated with the largest event in an earthquake cluster and their implications to foreshocks. Physical Review E. , 2006, 73(4): 046134. DOI:10.1103/PhysRevE.73.046134 |
| [42] | Peng Y J, Zhou S Y, Zhuang J C, et al. An approach to detect the abnormal seismicity increase in Southwestern China triggered co-seismically by 2004 Sumatra Mw9.2 earthquake. Geophys. J. Int. , 2012, 189(3): 1734-1740. DOI:10.1111/gji.2012.189.issue-3 |
 2013, Vol. 56
2013, Vol. 56