2. 武汉大学电子信息学院, 武汉 430072
2. School of Electronic Information, Wuhan University, Wuhan 430072, China
考虑大气阻力影响的卫星轨道模拟计算,对于低轨卫星(1000 km高度以下)的轨道设计和飞行轨道预测以及轨道衰落预警具有重要的意义.大气阻力系数和沿飞行轨道的热层大气总质量密度,是影响低轨卫星轨道高度衰减的重要参数;对复杂形状卫星的阻力系数的精确估计和热层大气总质量密度的高精度预测,目前仍然是国际热点与难点问题.
我们在进行暴前平静大气相对标定时发现[1],对于CHAMP这样具有复杂构形的卫星,阻力系数在2.4至3.6之间变化.Moe & Moe[2]研究了不同形状飞行器在不同高度上的阻力系数,据此可外推得到类长柱状复杂形状飞行器在400 km高度处的大气阻力系数大于3.0;并指出,在较大高度上飞行的卫星,由于表面材料被原子氧逐渐蚀化,可能会造成阻力系数随时间而增长.
Jacchia大气模型[3]系列是20世纪60年代后发展建立起来的国际标准大气模式,其77版一直沿用到21世纪;同时,在1977年以后MSIS系列模式[4-5]被广泛使用;20世纪后期,美国海军实验室对MSIS模式加以改进形成NRLMSISE-00模式[6],在科学界与工程上获得重要应用.近年来,Bowman等人对Jacchia模型加以改进建立了JB-2006模型[7].该模型相对Jacchia模型的主要改动是太阳辐射通量的输入,以及大气密度半年变化和地方时变化的修正.该模型中输入的太阳辐射由三个分量组成,分别是:基于SOHO卫星EUV传感器数据的S10;基于FUV MgⅡ传感器数据的Mg10;以及10.7 cm波长微波辐射通量F10.7.用于建立该模型的大气密度数据来自从1978-2004年的多颗卫星,这些卫星的近地点高度范围在175~1100 km之间.之后,Bowman等人在JB-2006模式的基础上,引进Dst指数作为磁暴期间大气密度变化的控制和预测参数,发展建立了JB-2008模式[8];目前它已经被提议作为120 km高度以上大气总质量密度的最新国际大气标准.
本文以德国低轨道卫星CHAMP[9]为例,联合考虑地球扁率和大气阻力摄动的影响,对相应摄动方程进行数值积分,计算轨道根数变化,并进而计算得到卫星空间位置坐标,由此考察大气阻力引起的轨道高度的衰减.在大气阻力摄动的模拟中,使用综合考虑了太阳辐射和磁暴等多种因素影响的最新国际大气标准JB-2008模式;参照国际最新研究成果,并考虑CHAMP卫星的特殊几何构形与表面材料以及热层温度条件,调整大气阻力系数为在2.8~3.5之间变化以探寻较佳取值.
2 基本公式本文模拟计算使用的受摄二体问题与相关摄动力基本公式依据文献[10]和[11].
2.1 受摄二体问题卫星在地球引力场中的运动方程为
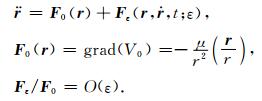
|
(1) |
式中,r是卫星的位置矢量;F0是中心天体(地球,假设为等密度球体,看作位于地心的质点)引力加速度;μ是地球引力常数;Fε是各种摄动力(加速度)之和,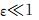
只考虑地球中心引力加速度时,运动方程化为
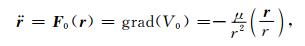
|
(2) |
V0为相应于均匀密度球体的引力位,此方程即表示一个二体问题,而方程(1)则表示受摄二体问题.对于方程(2)所表示的无摄二体问题,相应的运动轨迹解为平面二次曲线(圆锥曲线),包括椭圆、抛物线和双曲线;对于围绕地球运动的卫星,其轨道为不变椭圆.椭圆轨道在空间中的位置和卫星在椭圆轨道上的位置由方程的6个积分常数确定,即轨道根数,包括半长轴a、偏心率e、倾角i、升交点赤经Ω、近地点幅角ω以及过近地点的时刻τ;第6个根数τ常由平近点角M=n(t-τ)来代替,此处n为卫星平均角速度,n=2π/T,T是轨道周期;轨道平面内卫星位置与时间的关系由开普勒方程描述.
如前所述,Fε是各种摄动力(加速度)之和,包括地球非球形引力摄动、日月等第三体引力摄动以及非保守力摄动(例如大气阻力、太阳辐射压、姿态调整喷气动力摄动等).
2.2 简化的摄动方程利用常数变易法可将问题(1)转化为以椭圆轨道根数σ(六维列向量)描述的小参数方程,即摄动方程
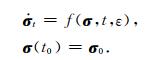
|
(3) |
本文主要考察大气阻力引起的低轨卫星轨道衰减,这里只考虑地球扁率(非球形引力摄动J2项)和大气阻力摄动的影响,忽略高阶保守力和太阳辐射压等非保守力项.采用文献[10]中关于旋转大气阻力摄动方程式(11.58)至(11.63),形式如下:
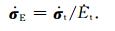
|
(4) |
以上各式中,右端含有与A1ρ或A2ρ成比例的项,它们代表大气阻力摄动.其中ρ是大气总质量密度,系数A1和A2的表达式为
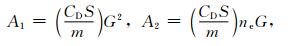
|
(5) |
其中

|
(6) |
式中,r和v分别是卫星的地心高度和线速度大小;rp0是卫星近地点的初始地心高度;vp0是卫星过近地点的初始速度值;ne是大气旋转角速度(假定等于地球自转角速度);CD是阻力系数;S是卫星有效面积;m是卫星质量.
地球扁率引起的轨道进动采用以下公式(参见文献[11]中的(4.5-63)式):
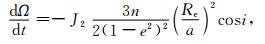
|
(7a) |
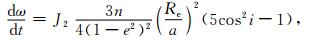
|
(7b) |
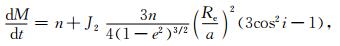
|
(7c) |
式中,J2=0.0010826,Re是地球赤道半径,轨道参数Ω,ω,M,a,e,i,n等的含义如前所述.
3 CHAMP轨道衰减模拟计算 3.1 计算方法与流程对大气阻力摄动方程(4)和地球扁率摄动方程(7)做数值积分,时间步长为10 s,获得ti时刻σ(轨道根数)的变化量ΔXi=ΔXi,drag+ ΔXi,J2,其中ΔXi,drag和ΔXi,J2分别是大气阻力和地球扁率引起的轨道根数的变化,将变化量ΔXi累加给上一个根数值Xi,得到ti+1时刻的轨道根数Xi+1=Xi+ΔXi;每获得一个新的根数,计算卫星位置坐标,并利用JB-2008模式计算该位置的大气密度,用以计算大气阻力摄动,如此循环至结束.计算流程如图 1所示.
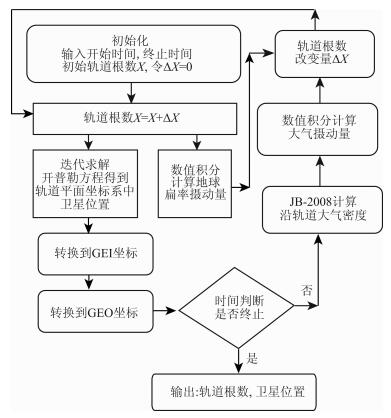
|
图 1 卫星轨道衰减模拟计算流程框图 Fig. 1 Flow chart for numerical simulation of satellite orbit decay |
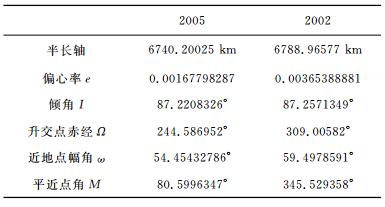
使用德国地学中心GFZ发布的快速科学轨道(Rapid Science Orbit,RSO)数据文件(http://www-app2.gfz-potsdam.de/pub/op/champ)计算卫星初始轨道根数,并以RSO数据作为实测轨道,将数值模拟得到的轨道衰减与其进行对比.RSO数据利用地面GPS网和CHAMP星载GPS数据,采用简化动力学模型计算得到卫星位置与速度,在传统地球参考坐标系(Conventional Terrestrial reference System,CTS)中给出,时间分辨率为10 s.本文模拟计算以2005年为例进行,这一年CHAMP卫星没有进行提升轨道高度和重要姿态调整的燃料点火,其轨道经历自然衰减.为了考察不同年份轨道衰减情况,对2002年1-3月处在较大高度(平均高出约50 km)的轨道也进行了模拟.模拟输入的初始轨道参数参见表 1.
|
|
表 1 卫星初始轨道根数 Table 1 Initial satellite orbit eleme nTs |
卫星受到的大气动力加速度为[12]:
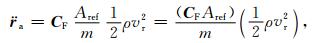
|
(8) |
式中,CF是气动力系数矢量;Aref是卫星参考面积(它总是伴随着CF);m是卫星质量;ρ是大气质量密度;vr是大气相对于卫星的速度.忽略气动升力和侧向力时,大气动力加速度简化为阻力加速度,用aD表示,其方向与卫星相对于大气的速度相反,系数矢量CF变为阻力系数标量CD,即
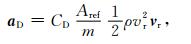
|
(9) |
阻力系数CD与卫星形状、表面材料、背景大气状况(分子质量与温度等)等因素有关.CD与卫星表面各平板的面积Ai及其法方向ni、各平面单元阻力系数Cdi、各平板法向与卫星相对于大气飞行速度方向矢量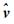
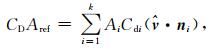
|
(10) |
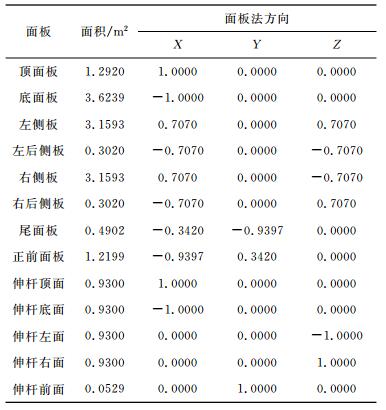
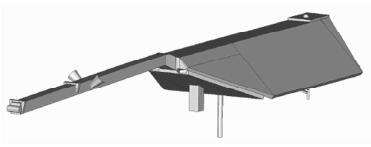
式中k为卫星分解后的平面(板)个数.要得到CD,需要知道卫星宏观几何模型以及平面单元阻力系数Cdi.CHAMP具有复杂的特殊外形,参见图 2;宏观结构可分解为13块(也有一种是分为15块)平板,表 2中给出了各平面的面积和法向矢量(卫星固定参考系中).
|
图 2 CHAMP卫星外形 Fig. 2 CHAMP satellite figuration |
|
|
表 2 CHAMP卫星各平面的面积和法向矢量 Table 2 Area and normal direction of each panel of CHAMP satellite |
各平面单元的阻力系数可以采用基于物理学的模式计算求得,由下面的公式表示[13]:
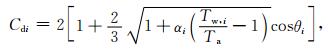
|
(11) |
式中,αi为调节系数;Ta为大气的温度;Tw,i为卫星各个面的温度;θi为大气流过卫星各个面的入射角.由于卫星温度很低,假设大气分子再入主要是扩散性的,于是调节系数可近似为
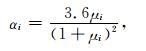
|
(12) |
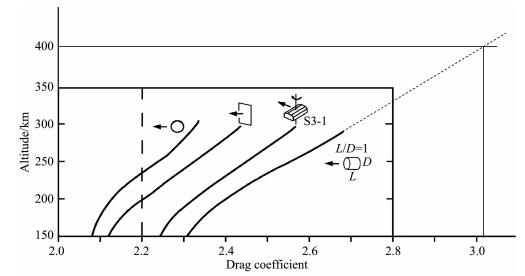
其中,μi为入射的大气原/分子质量与卫星表面原/分子质量之比.我们利用NRLMSISE-00大气模式计算得到的热层大气温度和平均分子量,假定卫星表面材料温度为300 K,利用物理模式计算得到2005年某一天CHAMP卫星的CD系数约为2.8±0.2.以前我们在进行暴前平静大气相对标定[1]时发现,对于CHAMP这样具有复杂构形的卫星,阻力系数CD在2.4至3.6之间变化.另外,Moe等人[2]对不同形状飞行器阻力系数研究得到的CD,在某些情况下比以往所认为的要高,根据他们得到的阻力系数随高度的变化曲线,外推得到外形比较接近CHAMP的卫星在350 km以上高度的阻力系数大于2.8,参见图 3;Moe等人还指出卫星表面材料被原子氧的蚀化可能使阻力系数增大.考虑以上情况以及CHAMP卫星的飞行高度与特殊外形,我们在数值模拟中取CD在2.8至3.5之间变化.模拟计算所需的卫星质量数据,取自CHAMP卫星内务数据;卫星面积则以最初发布的面质比和初始质量计算得到.
|
图 3 不同形状卫星阻力系数随高度的变化[2] 图中虚线是本文所作的外推. Fig. 3 Altitude depende nT air drag coefficie nTs for different satellite shapes[2] The dotted line is an extrapolation made by the author of this paper. |
2008年,Bowman等人在JB-2006模式[7]的基础上,发展建立了JB-2008模式[8].与以往的Jacchia系列大气模式相比,这两个模式使用了新的太阳指数[14]以计算太阳辐射对大气的作用,包括基于SOHO卫星极紫外EUV传感器数据的S10,基于远紫外FUV MgⅡ传感器数据的Mg10,以及F10.7;JB-2008还利用地磁Dst指数,亦即磁层环电流指数,作为暴时大气密度变化的驱动参数,模拟暴时大气密度的变化.对于平静时大气密度,JB-2006预测的误差已下降到约10%,而JB-2008在此基础上又利用CHAMP/GRACE卫星高精度加速度仪测量得到的大气密度数据改进了暴时的预测.这是目前提议的最新国际大气标准.在轨道衰减模拟计算中我们采用此模式计算沿轨道的热层大气密度,借以计算大气阻力摄动.图 4给出2005年5月15-16日大磁暴(min.Dst=-256 nT)和2005年6月12-14日大磁暴(min.Dst=-106 nT)期间JB-2008模式预测的沿模拟轨道的大气密度和CHAMP卫星实测的大气密度.
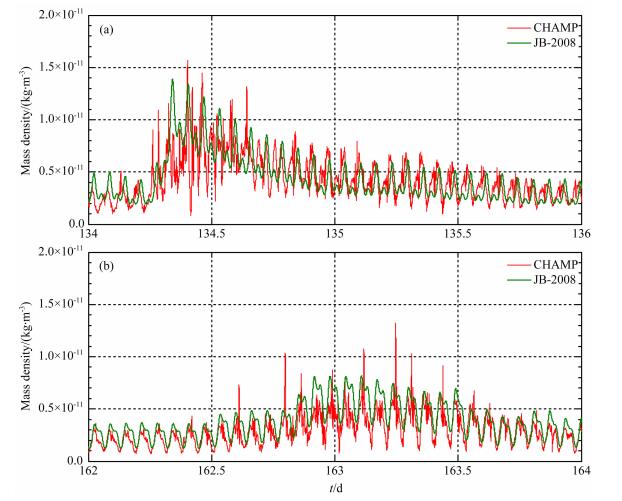
|
图 4 两次大磁暴期间JB-2008模式预测的沿模拟轨道的热层大气密度(绿色)和CHAMP卫星沿真实轨道的实测(红色)大气密度 (a)2005年5月15-16日;(b)2005年6月12-13日.图中横坐标的天数以2005年1月1日为零计. Fig. 4 Thermospheri cmass densities predicted by JB-2008 model along simulated orbit (green line) and observed by CHAMP along real orbit (red) during two great magnetic storms (a) Storm of May 15-16, 2005;(b) Storm of June 12-13, 2005.The day number of zero in the abscissa presents Jan 1, 2005. |
模拟中令阻力系数在2.8至3.5之间变化以寻找最佳取值,结果表明,对于所模拟的2005年,当阻力系数取2.91时,模拟得到的卫星轨道衰减与真实情况符合得较好.图 5a给出此种情况下模拟计算的与真实的轨道高度参数的比较,这里轨道高度参数包括半长轴、近地点和远地点的地心高度;实测轨道参数是指由实时RSO轨道位置与速度数据确定的轨道根数与导出参数.2005年模拟计算的与实测的半长轴的差,其全年统计标准偏差为81.3 m,细致分析发现引起此偏差的主要原因是实测半长轴的短周期起伏(在图上表现为实测半长轴的棕黄色曲线较宽),而模拟的半长轴不含这种周期变化;模拟得到的最后一天卫星轨道半长轴(取日均值)比第一天下降了20.868 km,实际CHAMP轨道半长轴下降了20.690 km,二者相差178 m,此值显著大于标准偏差,这是因为在2005年的最后一个多月时间里,模拟与实际的半长轴彼此符合的程度在整个一年中最差.模拟计算得到CHAMP卫星远地点首尾两天相比降低了约20.903 km,实际轨道远地点(消除其3个月周期起伏后)一年中下降21.403 km,模拟与实际的下降量相差-0.5 km;模拟与实际轨道近地点下降量相差0.845 km.可见,模拟的与实际的轨道高度平均衰减率符合得比较好.明显的差别是,实际轨道远/近地点高度有周期约3个月的波浪型起伏,模拟结果未含此种周期变化.这可能是因为在模拟计算中保守力摄动只简单地考虑了扁率的长期影响,没有考虑高阶周期性保守力摄动所致.
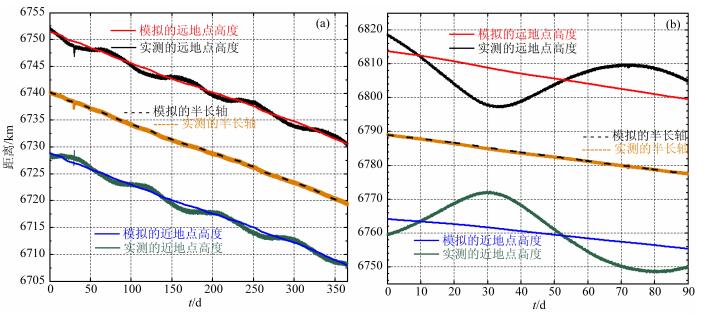
|
图 5 模拟计算的与真实的轨道高度参数的比较 (a)2005年全年;(b)2002年1-3月. Fig. 5 Comparison of simulated orbit altitude with real orbit altitude (a) During 2005 year; (b) During Jan To Mar in 2005. |
为了考察其他年份卫星处在较大高度上阻力系数的可能变化,我们对2002年1-3月的轨道也进行了模拟,此间卫星飞行高度比2005年平均高约50 km,卫星未进行提升高度的燃料点火.结果表明,当阻力系数取3.0时,模拟得到的卫星轨道衰减与真实情况符合得最好.图 5b给出此种情况下模拟计算的与真实的轨道高度参数的比较.以半长轴,近/远地点地心高度表征的轨道高度的衰减率(不考虑周期性起伏)的模拟结果与实测数据符合得很好.
4.2 讨论 4.2.1 模拟的轨道位置参数及其对高度衰减的影响图 6给出模拟计算得到的在初始两日(2005年1月2-3日)和结束前两日(2005年12月30-31日),卫星在地球参考坐标系(本文中记为GEO坐标系)中位置(三个直角坐标分量)与实际位置的比较.可以看出,二者的轨道总体上大致符合,随着时间的累积,相位差别逐渐显现出来.从精密轨道的角度来说,本文的模拟还是很粗略的,所得卫星空间位置与实际还有较大误差,由于真近点角误差的累积,模拟与真实卫星位置的纬度相差逐渐增大,在模拟的后期最大可相差约20°;近地点幅角的误差和上述真近点角误差引起的纬度误差会影响模拟计算的地表高度,最大可有十几公里的误差.这些会造成作为位置的函数的大气密度的模型计算误差,因而影响大气阻力摄动引起的轨道高度衰减的模拟结果.因为本文的主要目的是考察大气阻力引起的轨道高度的衰减,而不是卫星位置的精密预测,而大气阻力效应是个长期项,主要依赖于沿轨道的积分,因此本文的模拟方法对于考察有限时间内轨道高度的衰减还是有效的.在以后进一步的模拟工作中,需要考虑太阳辐射压等非保守力项,特别是需要精细考虑保守力摄动(涉及地球高阶重力场和日、月引力)模型.
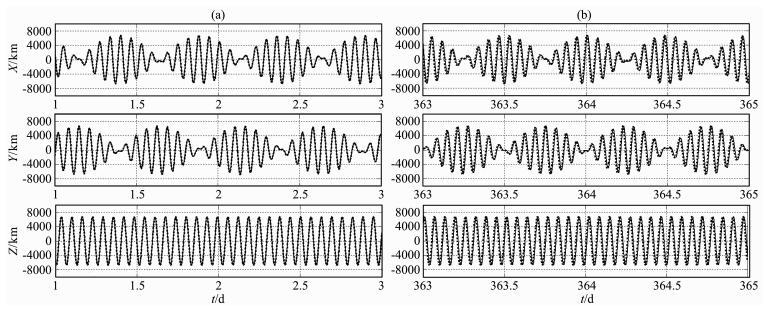
|
图 6 模拟计算的卫星轨道坐标(点)与实际轨道坐标(线)的比较 (a)2005年1月2-3日;(b)模拟结束前两日:2005年12月30-31日.图中由上至下依次为卫星在地球参考坐标系中位置矢量的X分量、Y分量和Z分量. Fig. 6 Comparison between simulated (dot) and real (line) satellite position (a) For the period of Jan 2-3, 2005;(b) For the period of Dec 30-31, 2005, just before the simulation end. From top to bottom the three rows are separately for X, Y, and Z components in the GEO reference frame. |
本文不是从阻力系数的物理模型(如3.3节所述)对其进行计算的,而是作为大气摄动的一个参数,利用模拟轨道衰减来求取最佳阻力系数.由2.2节所述可知,大气阻力摄动量正比于阻力系数与大气密度的乘积,本文采用最新提议的国际大气标准JB-2008模型来计算模拟轨道的大气密度,如果改用其他大气密度模型,结果会有所不同.如果大气密度估计值偏高,将使模拟得到的最佳阻力系数取值偏小,反之则使系数偏大.我们考察了按欧空局技术报告[12]由加速度仪测量数据迭代计算得到的2005年CHAMP轨道大气密度,将其与JB-2008模型计算的该轨道大气密度进行比较,发现实测全年平均值为2.28×10-12 kg/m3,而JB-2008模型全年平均值为2.78×10-12 kg/m3,模型比实测大气密度总体上要高出20%以上.这样,如果将大气密度降低20%,要使模拟与实际轨道高度衰减比较一致,阻力系数则要相应增大20%,即为约3.5.在以后进一步的模拟研究中,如果能利用更准确的实测大气密度数据,无疑是很有益的.
5 结论考虑大气阻力影响的卫星轨道模拟计算对低高度卫星轨道设计和在轨卫星轨道预测与精确定轨具有重要意义.
本文以德国低轨道卫星CHAMP为例,联合考虑地球扁率和大气阻力摄动的影响,对相应摄动方程进行数值积分,计算大气阻力引起的轨道根数变化,并进而计算得到卫星空间位置坐标,由此考察卫星轨道衰减.模拟中使用综合考虑了太阳辐射和磁暴等多种因素影响的最新国际大气标准JB-2008模式;考虑到CHAMP卫星的具体几何构形与表面材料以及热层温度条件,参照国际有关研究新成果,采用阻力系数大于2.8,并在一定范围内变化.模拟结果表明,在使用JB-2008热层大气模式条件下,对于2005年的CHAMP飞行轨道环境与卫星状况,阻力系数为2.91(远大于传统采用的值2.2)时模拟得到的与实际的轨道高度衰减符合得最好,模拟与实际轨道半长轴的全年标准偏差为81 m.对于卫星飞行在较大高度(比2005年平均高出约50 km)的2002年1-3月,模拟得到最佳阻力系数为3.0.
应该指出,本文模拟是在选用JB-2008大气密度模型情况下进行的,若改用其他大气模型,最佳阻力系数会有所改变.而且,阻力系数实际上是随时间(即随飞行所在热层大气环境和卫星状态)不断变化的,本文得到的阻力系数是一段时间(一年或3个月)里的平均效果.另外,目前模拟计算采用的保守力摄动模型比较简单,模拟结果未含有如实际轨道高度所呈现的周期起伏,且预测与实测的卫星位置之间还有较大误差,有待在下一步的模拟工作中考虑精细重力场模型等因素加以改进.
致谢感谢德国地学研究中心(GFZ,Potsdam)提供CHAMP卫星数据.
| [1] | Zhou Y L, Ma S Y, Lühr H, et al. An empirical relation to correct storm-time thermospheric mass density modeled by NRLMSISE-00 with CHAMP satellite air drag data. Adv. Space Res. , 2009, 43(5): 819-828. DOI:10.1016/j.asr.2008.06.016 |
| [2] | Moe K, Moe M M. Gas-surface interactions and satellite drag coefficients. Planetary and Space Science , 2005, 53: 793-801. DOI:10.1016/j.pss.2005.03.005 |
| [3] | Jacchia L G. New static models of the thermosphere and exosphere with empirical temperature profiles. SAO Special Report. 1970. |
| [4] | Hedin A E, Salah J E, Evans J V, et al. A global thermospheric model based on mass spectrometer and incoherent scatter data MSIS: 1.N2 density and temperature. J. Geophys. Res. , 1977, 82(16): 2139-2147. DOI:10.1029/JA082i016p02139 |
| [5] | Hedin A E, Reber C A, Newton G P, et al. A global thermospheric model based on mass spectrometer and incoherent scatter data MSIS. Ⅱ-Composition. J. Geophys. Res. , 1977, 82(16): 2148-2156. DOI:10.1029/JA082i016p02148 |
| [6] | Picone J M, Hedin A E, Drob D P, et al. NRLMSISE-00 empirical model of the atmosphere: statistical comparisons and scientific issues. J. Geophys. Res. , 2002, 107(A12): 1468. |
| [7] | Bowman B R, Tobiska W K, Marcos F A. A new empirical thermospheric density model JB-2006 using new solar indices. AIAA 2006-6166. 2006. |
| [8] | Bowman B R, Tobiska W K, Marcos F A, et al. A new empirical thermospheric density model JB-2008 using new solar and geomagnetic indices. AIAA/AAS, Astrodynamics Specialist Conference , 2008: 18-21. |
| [9] | Reigber C, Luehr H, Schwintzer P. CHAMP mission status. Adv. Space Res. , 2002, 30: 129-134. DOI:10.1016/S0273-1177(02)00276-4 |
| [10] | 刘林. 航天器轨道理论. 北京: 国防工业出版社, 2000 . Liu L. Orbit Theory of Spacecraft (in Chinese). Beijing: National Defense Industry Press, 2000 . |
| [11] | 杨嘉墀主编.航天器轨道动力学与控制(上).北京:中国宇航出版社, 2009. Yang J X Chief Ed. Dynamics and Control of Spacecraft Orbit (Part 1) (in Chinese). Beijing: Chinese Astronautics Press, 2009. |
| [12] | Doornbos E, Förster M, Fritsche B, et al. Air density models derived from multi-satellite drag observations. Final report, ESTEC contract 21022/07/NL/HE. 2009. |
| [13] | Sutton E K, Forbes J M, Nerem R S. Global thermospheric neutral density and wind response to the severe 2003 geomagnetic storms from CHAMP accelerometer data. J. Geophys. Res. , 2005, 110: A09S40. DOI:10.1029/2004JA010985 |
| [14] | Tobiska W K, Bouwer S D, Bowman B R. The development of new solar indices for use in thermospheric density modeling. J. Atmos. Solar-Terr. Phys. , 2008, 70: 803-819. DOI:10.1016/j.jastp.2007.11.001 |
 2013, Vol. 56
2013, Vol. 56