利用地面发射大功率高频电波进行电离层人工扰动,是近30多年来空间物理和电子科技领域研究的一个重要课题[1-2].其中,通过VLF调幅的高频波对电离层进行加热,形成等效的电离层虚拟天线,可以作为激发VLF波的一种有效手段.这种虚拟辐射源辐射的VLF波向下传播可以进入地球-电离层波导,在授时、导航、军用通信以及地下目标探测等方面具有潜在的应用价值,这种下行VLF波已经由全波解等方法建立了其辐射模型[3-4].而上行VLF波则可以进入磁层.磁层是一个位于地球周围的天然的巨大的等离子体实验室,其中各种等离子体波以及波与粒子相互作用的研究是近年来空间物理的前沿和热点课题.磁层空间充满大量的高能电子,主要被地球磁场捕获于L=1.2~8的内外辐射带里,这些电子的能量大部分在~100 keV到几个MeV之间,其中能量较高的电子被称为“相对论电子”,也叫“杀手电子”,对于运行于其中的卫星、航天器以及航天员是一个潜在的威胁.这些由电离层调制加热激发的VLF波进入磁层,参与磁层波粒相互作用,对于人工沉降高能粒子、消除自然辐射带或者高空核爆所产生的人工辐射具有很大的实际意义[5-6].美国HAARP计划就将此作为实验项目之一,试验中使用407MW的高频发射功率对电离层进行调制加热,激发的低频信号在DEMETER卫星和位于Alaska的地基接收站同时被接收到[7-8].
由于电离层调制加热产生的低频信号源位于较低的电离层,需要经过较大的磁层空间区域传播到高L-shell参与磁层电子动力学过程,其在磁层中的传播路径和各种特性对波粒相互作用有直接的影响.低频波(VLF)在磁层中的相折射指数远大于1,波长也比在自由空间中短很多,因此磁层中适宜运用射线理论处理低频波的传播问题.Haselgrove基于费马原理推导出电磁波传播的三维射线方程[9],Budden利用程函概念也推导出了同样的返程[10-11]. Walter在非管道哨声的研究中,通过引入一个新的变量,给出了一组新的二维射线追踪方程[12-13],这是一组易于求解的方程组.徐继生等(1984)[14]通过该射线追踪方程对低纬赤道异常区的非导管哨声进行了模拟,Horne(1989)等基于该方程组在FORTRON语言环境下建立了低频波传播模型[15],Bortnik(2005)使用该模型对闪电激发的磁层哨声进行了研究[16].
磁层辐射带粒子同时存在着三种运动方式,绕磁力线的回旋运动,沿着磁力线的弹跳运动,以及围绕地球的漂移运动.大量研究表明,回旋共振波粒相互作用在辐射带电子动力学过程中发挥着重要的作用,共振可以导致粒子的投掷角散射和动量扩散,使得辐射带粒子沿着磁力线沉降在大气中.当前针对波粒相互作用发展出了两种理论:准线性理论和测试粒子理论,这两种理论被广泛用于研究磁层高能电子与各种天然等离子体波,有哨声模式的和声、等离子体嘶声、电磁粒子回旋波(EMIC)等共振作用所驱动的电子通量演化[16-17]等,例如STEERB模型[17-19]、VERB模型[20],而人工激发的VLF波与磁层粒子的共振作用的研究较少,且基本集中在位于某空间区域的VLF波发射机所产生的人工波[21],对于由电离层加热产生的VLF波如何进入磁层并参与波粒相互作用的研究极其有限.另外,无论使用哪一种波粒共振理论,共振能否发生都取决于电子与波的回旋共振条件,在大量研究中,都首先需要确定波的各种参数和粒子的初始条件,比如波法向角、频率(频带)、粒子能量、投掷角等应满足波粒共振条件,进而计算散射作用效果.这些参数的确定或根据一定的观测数据,或根据以往文献的经验值.
本文基于Walter的二维射线追踪方程组,在MATLAB环境下建立自己的代码,模拟电离层调制激发的VLF波在磁层的传播路径和各种特性.该模型与Horne模型基于同样的二维射线方程组,但是不同于Horne主要利用预测矫正方法求解方程组(其中前几个点用4阶Runga-Kutta求解),本文采用5阶Cash-Karp Runga-Kutta方法对方程组进行求解,同样取得了较好的求解效率,具有稳定性和准确性.本文对射线追踪的模拟结果进行分析,探讨了影响VLF波传播路径和传播特性的参数,并基于低频波的色散方程和波粒共振条件,探讨人工激发的VLF波在传播路径上与磁层高能粒子相互作用的最低共振能及其分布.这些研究既是对电离层调制激发的低频信号沉降磁层粒子的空间位置和能量范围的初步预测,对磁层辐射带的人工改变有一定的参考意义,也为相应的波粒共振研究(例如利用准线性或者测试粒子理论研究人工激发波对磁层粒子的投掷角散射和动量扩散作用)中的波参数和粒子初始条件的确定提供一定的理论依据.
在本文第二部分,介绍本文所用的地球磁场模型和背景粒子模型,对射线追踪方程组和色散方程进行简单的描述,最后介绍波粒共振条件,并对共振椭圆以及由共振椭圆求得最低共振能进行推导和介绍.第三部分陈述模拟结果,包括由射线追踪得到的低频波的传播路径及特性,路径上点在磁层发生波粒相互作用的共振椭圆,以及最低共振能的分布情况,并对模拟结果进行分析和探讨.第四部分是本文内容的一个总结,也有对不足地方的讨论.
2 理论方法和模型 2.1 背景磁层模型磁层作为低频波传播介质,影响电波传播的主要是介质中的地球磁场大小和方向,以及介质中各粒子成分的组成和百分比.本文涉及的区域主要在磁层内部(L≤6,L是地球空间常用的距离单位,L=r/Recos2λ,λ是地磁纬度,Re是地球半径),地球中心偶极子模型是一种较好的近似.本文的背景粒子分布采用冷等离子体扩散平衡模型[12],计入四种粒子成分:电子[e-]、氢离子[H+]、氦粒子[He+]和氧粒子[O+].该模型下,电子密度为
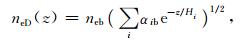
|
(1) |
其中z是位势高度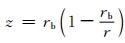

电子密度和离子密度写成下面形式:
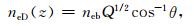
|
(2) |
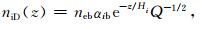
|
(3) |
其中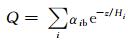
在忽略碰撞的情况下,从费马原理出发并利用折射指数面与射线面的性质可以建立射线轨道与波法轨道方程,本文采用Walter(1969)的二维射线追踪方程:
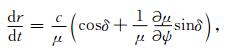
|
(4) |
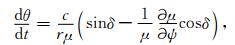
|
(5) |
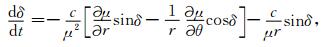
|
(6) |
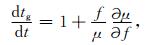
|
(7) |
r,θ分别为以地心为中心的距离和余纬,δ是波法线与径向的夹角,tg是群时延,c是光速,f是波频率,ψ为波法线与背景磁场矢量的夹角,即波法向角,ψ与δ关系为:ψ=δ-γ,其中γ是磁场方向与径向的夹角,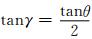
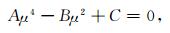
|
(8) |
式中
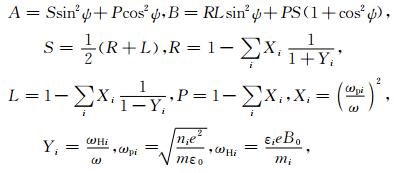
|
其中ωpi和ωHi分别为第i类粒子的等离子体频率和回旋频率,ω为电波角频率,ε0是真空介电常数,εi为第i类粒子电量的符号,e为电子电量的绝对值,B0为背景磁场的大小,mi为第i类粒子的质量.
2.3 波粒相互作用理论波粒共振相互作用是磁层中存在的最为广泛的物理机制,对于磁层辐射带的形成具有基础性作用.波与电子发生共振相互作用的条件为:

|
(9) |
ω是波的频率,k为波数,ψ是波法向角,α是电子的投掷角,γ为相对论因子,γ=(1-β 2)-1/2,β=v/c,Ωe是非相对论电子回旋频率,N(=1,2,…)为共振回旋谐数.
引入两个无量纲的量
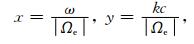
|
(10) |
于是,共振条件可以写成
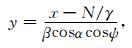
|
(11) |
代入γ=(1-β2)-1/2,整理得到

|
(12) |
其中,β∥=v∥/c,β⊥=v⊥ /c,v∥和v⊥分别是电子速度平行于和垂直于磁场线的分量,可以看出,在(β∥,β⊥)平面内存在一个以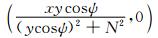
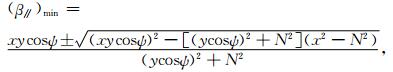
|
(13) |
可以求得相应的最小共振能量:
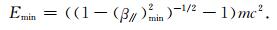
|
(14) |
低频辐射源所在的高度为人工调制电离层的中心高度75 km,在电离层中尤其是较低的电离层高度,电子密度在一个波长距离上变化较大,并且电子与中性粒子的碰撞也不可忽略,这些使得射线追踪方法误差较大.所以,本文所有的射线都从800 km出发(800 km以下的电离层高度,我们使用全波解处理),另外,基于过去使用全波解方法对于VLF波的研究[3-4],以及Helliwell(1965)所指出的射线在开始阶段基本上为竖直向上[24],所以,本文所有射线出发时波法线与径向的夹角δ取为0°.
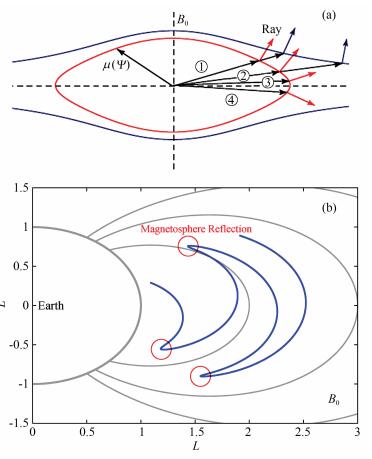
背景磁层介质对电波传播的影响,主要通过粒子密度分布和地球磁场,反映在等离子体频率ωpi以及回旋频率ωHi当中,并且与波的角频率归一化,从而影响折射指数的大小.射线方程遵从几何光学原理,意味着折射指数对波的传播具有决定性作用.某一频率的波,在磁层中某一固定点,ωpi、ωHi和ω都是固定的,唯一的变量只有波法向角ψ,于是折射指数成为波法向角ψ的函数.通过折射指数面可以定性地分析低频波在磁层中传播的重要特性-磁层的反射.因为,对于任意波法向角ψ下的波能量的传播方向(射线方向),与折射指数向量μ(ψ)末端所在的折射指数面的切线是垂直的[9],如图 1a中所示.因此,射线的方向取决于波法向角,并涉及到整个射线路径,从而影响ELF/VLF波的能量在磁层中的分布情况.在图 1a中,从①到④,在较短的时间尺度内波法向角转过90°,对于红色的闭合的折射指数曲面,射线相应改变方向,即发生磁层反射,而对于蓝色的开放的折射指数曲面,当法向角较接近90°时,折射指数趋于无穷大,低频波是无法传播的,法向角也无法进一步增大,会转而远离90°.低频波在磁层中的传播,折射指数面必须是闭合的,这样法向角才能转过90°,射线随之改变方向,即发生磁层反射,如图 1b所示.二维射线追踪方程组忽略经度,得到的是在一个子午面内低频波在磁层中的射线路径,从图 1b可以看出低频波在磁层中传播的典型路径,即通过在南北半球来回反射向更高的L-shell传播,磁层反射是低频波在磁层传播的重要特点.
|
图 1 折射指数面和磁层反射示意图 Fig. 1 Refraction index and magnetosphere reflection |
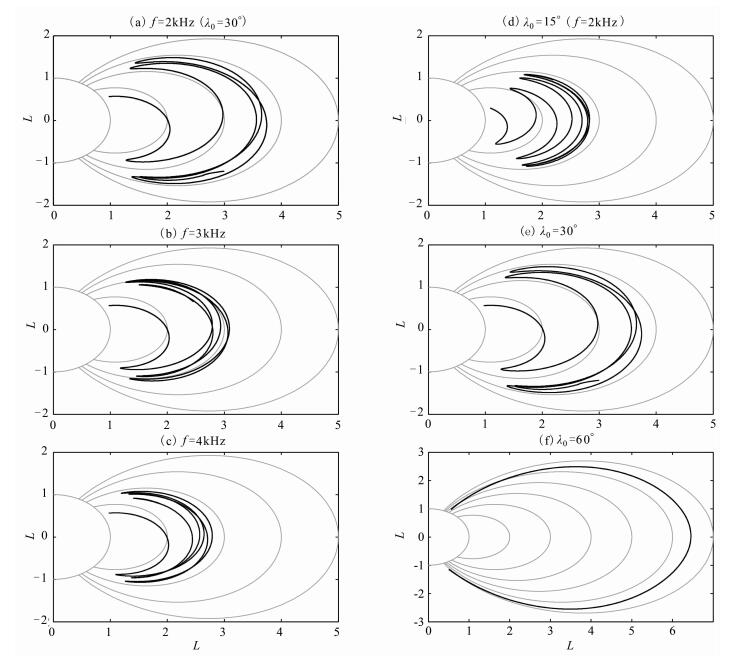
图 2给出了从磁纬30°出发,调制频率分别为2、3、4 kHz,以及调制频率为2 kHz时,从不同纬度激发的VLF波的射线路径.从图中可以看出,不同频率的低频波从不同纬度出发,经过多次磁层反射传播到了更高的L-shell,并最终在某一L值附近趋于稳定.低频波的频率和激发纬度对最终到达的磁层区域具有显著影响.从同一纬度激发的低频波,频率越低,能够传播到越高的L-shell;在同一调制频率下,从越高的纬度激发,能够传播到越高的L-shell.在其他条件不变的情况下,调制频率和激发纬度在很大程度上决定了低频波在磁层中的传播路径,这一特性对于人工沉降辐射带高能粒子具有重要意义.根据所要沉降的辐射带区域,在电离层调制中,选择合适的调制频率和激发纬度,使该低频信号能够通过磁层反射传播到目标区域,从而实现人工沉降辐射带高能粒子.
|
图 2 从磁纬30°激发不同频率的低频波(a-c),以及频率为2 kHz从不同纬度激发的低频波(d-f)的射线路径 Fig. 2 Ray path of the three indicated frequency waves launched from fixed latitude 30°, and waves from the three indicated initial latitude for fixed wave frequency 2 kHz |
另外,从图 2f中我们可以看出,当低频波的出发纬度较高时,如从纬度60°激发的2 kHz的低频波,当到达另外半球时,没有发生磁层反射,而直接进入了电离层和大气层,在那里,低频波的能量将会由于碰撞而损失掉.由于在极区上空存在着较大的自然电流,所以很多电离层电流人工扰动的工作主要集中在高纬地区和极区.但是对于调制加热而言,如果要使激发的VLF波能够在磁层中来回反射传播、参与波粒相互作用,则不宜选取较高的纬度位置进行激发,事实上,大量实验观测表明,低纬地区由于赤道电急流的存在,同样也可以通过高频调制加热激发VLF波.
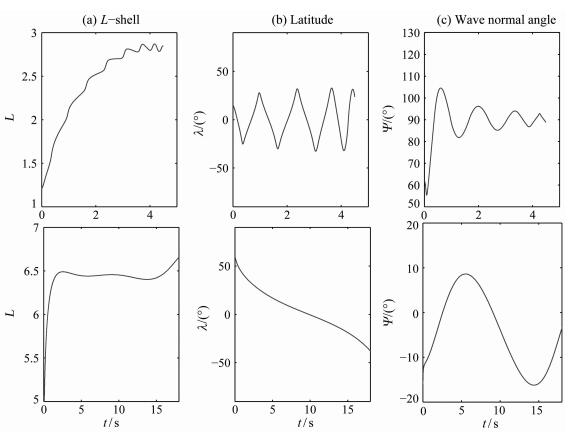
图 3分别给出了图 2d和图 2f,即出发磁纬度分别为15°和60°低频信号在磁层传播过程中的L值、纬度和法向角的变化.从这两幅图我们可以更直观地看出低频波发生磁层反射和不发生反射的传播特性的不同.图 3(上)中的L值、纬度和波法向角的变化具有低频波磁层反射传播的一般规律,即震荡和稳定.其中L逐渐变大,最后趋于某一值,并在这个值周围轻微振荡;纬度和波法向角分别以0°(赤道)和90°为中心振荡变化,其中法向角振幅逐渐变小,最后趋近于90°;图 3b中纬度变化曲线中每个波峰处(最高纬度处)即为低频波的磁层反射点,对应于图 3c中波法向角变化曲线的波谷(90°).不难推论,图 3(上)所在的相折射指数面必为闭合的,每当法向角转过90°,射线转过平行于磁场的方向,随着波的传播,法向角最终趋近于90°,射线趋于平行于磁场的方向传播,这与低频波在传播过程中有沿着地球磁场传播的特性相符合.而图 3(下)中,L值和纬度都未出现震荡变化,法向角也从未达到90°,即从未发生磁层反射.这些结论可以指导人工激发波对磁层粒子共振作用研究中的波参数选取,例如L-shell和相应波频率的选取,波法向角的选取等.
|
图 3 从磁纬15°和60°激发的2000 Hz的低频波的传播特性 Fig. 3 Propagation properties of 2 kHz waves launched at latitude of 15° and 60° |
3.1节中用射线追踪得到了电离层调制激发的低频波在磁层的传播路径以及路径上每一点的折射指数、波法向角、电子磁旋频率等,依据(12)式,可求得各点的共振椭圆.低频波所经过的磁层区域存在大量高能电子,这些电子能量不同,投掷角各异;其中,满足(12)式所示的共振椭圆的电子则能与该低频波在相应点处发生共振相互作用.而椭圆离原点的最近距离代表着共振能量的最小值,是能与该低频波发生共振相互作用的电子的能量下限.
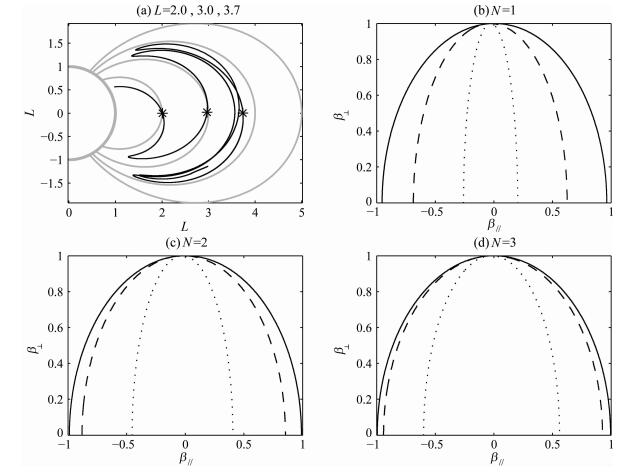
图 4给出了频率为2 kHz,从纬度30°激发的低频波的传播路径中不同L值处的共振椭圆.图 4a可知,射线路径上选取的三个点都在近赤道处,有着不同的L值.图 4(b,c,d)对应不同的共振谐数N=1,2,3.从图中可以看出,L值越大,椭圆的次轴越短,意味着最小共振能量越小.不同的共振谐数下,都有着这一规律.而同一点,共振谐数越高,椭圆的次轴越长,也就是最低共振能量越大.
|
图 4 不同L值点的共振椭圆(实线:L=2.0,点划线:L=3.0,点线:L=3,7) Fig. 4 Resonance ellipse for three indicated points with different L and similar latitude λ≈0° |
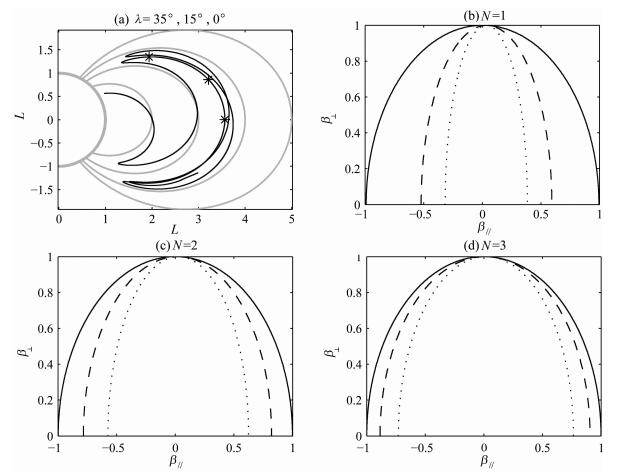
图 5给出了上例中的低频波的传播路径中不同纬度处的共振椭圆.图 5a中,射线路径上选取的三个点大致在同一L上,有着不同的纬度.图 5(b,c,d)对应不同的共振谐数N=1,2,3.从图中可以看出,越接近赤道处,椭圆的次轴越短,意味着低纬地区最低共振能量较小,高纬地区的最低共振能量较大;同一点处,与图 4一样,共振谐数越高,椭圆的次轴越长,也就是最低共振能量越大.
|
图 5 不同纬度点的共振椭圆(实线:λ=35°,点划线:λ=15°,点线:λ=0°) Fig. 5 Resonance ellipse for three indicated points with different latitude and similar L≈3.5 |
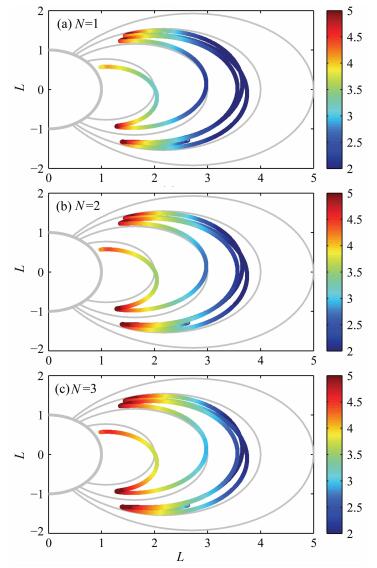
如果求出射线路径上每一点的最低共振能量,我们就可以了解低频波在传播路径中能够与之发生共振相互作用的电子的大致能量范围.图 6给出了图 4和图 5中的低频波的传播路径上各点在不同的共振谐数下的最低共振能量,色棒是指数棒,表示从102~105 keV能量范围.从图 6中可以更清楚地看出低频波传播路径上能与之发生共振相互作用的电子的能量分布情况.本例中的低频波(2 kHz,激发纬度30°)在较低的L-shell(L<2.5)或者较高纬地区,能够与MeV~100 MeV能量的电子发生共振作用,在较高的L-shell并且低纬地区,能够与~100 keV的电子发生共振作用.
|
图 6 低频波传播路径上电子的最低共振能量 Fig. 6 The minimum resonance energy of electrons along the ray path |
我们还可以得到图 2中其他的VLF波(或者其他初始条件下的VLF波)进入磁层发生波粒共振相互作用的共振椭圆和最低共振能量,了解其能达到的磁层区域和能够作用到的粒子能量范围以及分布(由于篇幅所限,这里不一一列举).
4 总结与讨论本文选取地球中心偶极子磁场模型和计入4种粒子成分的冷等离子体扩散平衡模型,利用射线追踪方法得到电离层调制激发的VLF波在磁层中的传播路径,分析传播路径对于调制频率和激发纬度的依赖关系,基于波粒共振条件,通过共振椭圆得到传播路径上各点的最小共振能量,分析能与之发生共振的电子的能量范围以及分布,主要得到以下几点结论:
(1) 同一地点出发的VLF波,频率越低,能够传播到越高的L-shell.
(2) 从较高纬度激发的VLF波能够传播到更高的L-shell,但是高纬地区出发的低频波沿着磁力线到达另外半球时,容易不发生磁层反射,而直接进入电离层和大气层.
(3) VLF波在磁层的传播过程中,在较低的L-shell或者较高纬地区能够与较高能量的电子发生共振相互作用,在较高的L-shell并且低纬地区,能够与较低能量的电子发生共振作用.共振谐数越大,波粒共振的电子能量越高.
总之,电离层调制激发的VLF波进入磁层,通过多次磁层反射向更高的L-shell传播,磁层反射发生于波法向角转过90°时,最后低频波稳定于某一L-shell附近,法向角趋于90°,低频波趋于沿着磁力线传播.这些人工VLF波在磁层传播路径主要由调制频率和激发纬度决定,传播路径上,在不同的L-shell和不同的纬度,能够与不同能量范围的电子发生共振相互作用.以上结论,一方面,能为人工激发波与磁层粒子散射作用研究中的参数选取提供一定的理论依据;另一方面,这些结论对于人工沉降辐射带高能粒子具有一定的参考价值.例如,如果知道辐射带中高能电子的能量和投掷角分布情况,就可以依据目标辐射带位置以及目标电子的能量范围,选取适当的调制频率和激发位置,使电离层加热产生的低频波到达目标区域与目标电子发生共振相互作用,实现辐射带的人工改变.当然,这只是较简单的理论研究,实际中需要考虑的问题还有很多,比如人工VLF波的辐射效率问题等.
本文的射线追踪所用的背景模型是冷等离子体扩散平衡模型,一些观测和模拟结果显示在较大L区域电子背景密度显著偏离扩散平衡模型,具体来说,电子密度在L=4.5左右呈现陡峭的下降,尽管在本文所涉及的绝大部分磁层区域(L<4),平衡扩散模型仍不失为较合理的近似,但是若计算极低频(ELF)或者较高纬度激发的低频信号时,仍需要引入含磁层顶的更精确的粒子扩散平衡模型.此外,冷等离子忽略粒子的碰撞和低频波能量的变化,而低频波在实际传播过程中,由于能量的衰减,有可能不能到达最终的L-shell,所以引入热等离子体模型,建立能够同时计算低频波传播路径和能量变化的模型,是有待努力的方向.
| [1] | Barr R, Stubbe P. ELF and VLF wave generation by HF heating: A comparison of AM and CW techniques. J. Atmos. Terr. Phys. , 1997, 59(18): 2265-2279. DOI:10.1016/S1364-6826(96)00121-6 |
| [2] | Hansen J D, Morales G J, Duncan L M, et al. Large-scale HF-induced ionospheric modifications: Experiments. J. Geophys. Res. , 1992, 97(A1): 113-122. DOI:10.1029/91JA02403 |
| [3] | 常珊珊, 赵正予, 汪枫. 电离层人工调制激发的下行ELF/VLF波辐射. 地球物理学报 , 2011, 54(10): 2458–2467. Chang S S, Zhao Z Y, Wang F. The downward ELF/VLF waves radiation excited by ionospheric artificial modulation. Chinese J. Geophys. (in Chinese) , 2011, 54(10): 2458-2467. |
| [4] | 汪枫, 赵正予, 常珊珊, 等. 电离层人工调制在水平分层电离层中所激发的ELF波辐射. 地球物理学报 , 2012, 55(7): 2167–2176. Wang F, Zhao Z Y, Chang S S, et al. Radiation of ELF waves by ionospheric artificial modulation into a stratified ionosphere. Chinese J. Geophys. (in Chinese) , 2012, 55(7): 2167-2176. |
| [5] | Cairó L, Lefeuvre F. Localization of sources of ELF/VLF hiss observed in the magnetosphere: three-dimensional ray tracing. J. Geophys. Res. , 1986, 91(A4): 4352-4364. DOI:10.1029/JA091iA04p04352 |
| [6] | Gu X D, Zhao Z Y, Ni B B, et al. Statistical analysis of pitch angle distribution of radiation belt energetic electrons near the geostationary orbit: CRRES observations. J. Geophys. Res. , 2011, 116: A01208. DOI:10.1029/2010JA016052 |
| [7] | Platino M, Inan U S, Bell T F, et al. DEMETER observations of ELF waves injected with the HAARP HF transmitter. Geophys. Res. Lett. , 2006, 33: L16101. DOI:10.1029/2006GL026462 |
| [8] | Piddyachiy D, Inan U S, Bell T F, et al. DEMETER observations of an intense upgoing column of ELF/VLF radiation excited by the HAARP HF heater. J. Geophys. Res. , 2008, 113: A10308. DOI:10.1029/2008JA013208 |
| [9] | Haselgrove J. Report of the Physical Society Conference on the Physics of the Ionosphere. Cambridge: Cambridge University Press, 1954 . |
| [10] | Budden K G. Radio Waves in the Ionosphere. Cambridge: Cambridge University Press, 1961 . |
| [11] | Budden K G. The Propagation of Radio Waves. New York: Syndicate of the University of Cambridge Press, 1985 . |
| [12] | Walter F. Non-ducted VLF propagation in the magnetosphere. California: Stanford Electronics Laboratories, 1964 . |
| [13] | Walter F, Angerami J. Nonducted mode of VLF propagation between conjugate hemispheres; Observations on OGO's 2 and 4 of the "walking-trace" whistler and of Doppler shifts in fixed frequency. J. Geophys. Res. , 1969, 74(26): 6352-6370. DOI:10.1029/JA074i026p06352 |
| [14] | 徐继生, 保宗悌, 梁百先. 赤道异常区内非管道哨声的射线跟踪. 地球物理学报 , 1984, 27(5): 407–416. Xu J S, Bao Z D, Liang B X. Ray tracing of non-ducted whistler mode waves in the region of equatorial anomaly. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1984, 27(5): 407-416. |
| [15] | Horne R B. Ray tracing of electrostatic waves in a hot plasma and its application to the generation of Terrestrial Myriametric Radiation. Geophys. Res. Lett. , 1988, 15(6): 553-556. DOI:10.1029/GL015i006p00553 |
| [16] | Bortnik J. Precipitation of radiation belt electrons by lightning-generated magnetospherically reflecting whistler waves [Ph.D.thesis]. California: Stanford University 2005. |
| [17] | Su Z P, Xiao F L, Zheng H N, et al. STEERB: A three-dimensional code for storm-time evolution of electron radiation belt. J. Geophys. Res. , 2010, 115: A09208. DOI:10.1029/2009JA015210 |
| [18] | Su Z P, Xiao F L, Zheng H N, et al. Radiation belt electron dynamics driven by adiabatic transport, radial diffusion, and wave-particle interactions. J. Geophys. Res. , 2011, 116: A04205. DOI:10.1029/2010JA016228 |
| [19] | Su Z P, Xiao F L, Zheng H N, et al. CRRES observation and STEERB simulation of the 9 October 1990 electron radiation belt dropout event. Geophys. Res. Lett. , 2011, 38: L06106. DOI:10.1029/2011GL046873 |
| [20] | Shprits Y Y, Subbotin D, Ni B B. Evolution of electron fluxes in the outer radiation belt computed with the VERB code. J. Geophys. Res. , 2009, 114: A11209. DOI:10.1029/2008JA013784 |
| [21] | Inan U S, Bell T F, Bortnik J, et al. Controlled precipitation of radiation belt electrons. J. Geophys. Res. , 2003, 108: A51186. DOI:10.1029/2002JA009580 |
| [22] | Stix T H. The Theory of Plasma Waves. New York: McGraw-Hill, 1962 . |
| [23] | Summers D, Thorne R M, Xiao F L. Relativistic theory of wave-particle resonant diffusion with application to electron acceleration in the magnetosphere. J. Geophys. Res. , 1988, 103(A9): 20487-20500. |
| [24] | Helliwell R A. Whistlers and Related Ionospheric Phenomena. California: Stanford University Press, 1965 . |
 2013, Vol. 56
2013, Vol. 56

