2. 中国石油大学(北京), 北京市地球探测和信息技术重点实验室, 北京 102249
2. Key Laboratory of Earth Prospecting and Information Technology, China University of Petroleum, Beijing 102249, China
NMR测井利用氢原子核与磁场相互作用发生的共振现象来实现井下油气储层信息的观测.NMR所产生的自旋回波串能观测到常规测井仪器难以提供的岩石孔隙流体体积、流体特性等重要信息, 提供孔隙度、流体类型、渗透率等重要参数, 已成为应用广泛的地球物理测井新方法[1-4].然而NMR测井是在高温、高压的极端条件下进行采集, 样品为切片内的流体, 样品体积小, 回波幅度微弱(通常只有几十纳伏), 受到来源非常复杂的噪声影响, 信噪比很低, NMR信号通常被淹没在噪声中.因此, 如何有效提取微弱的NMR信号、压制噪声, 提高数据信噪比, 一直是NMR测井研究的关键课题之一.
提高NMR测井数据信噪比的常用方法是回波串数据的累加平均.然而, 累加平均会降低NMR测井的纵向分辨率[5].Edwards[6]提出了时间依赖滤波方法, 利用滤波器宽度正比于时间的矩形窗口平均来实现滤波处理, 噪声功率谱可以衰减1/4.小波变换由于具有优异的时频分析性能, 已经广泛应用于NMR信号的降噪分析中.Wood等[7]应用小波包分析(Wavelet Package Analysis)为低信噪比(小于5)的MRI (Magnetic Resonance Imaging)图像进行降噪, 能有效改善MRI图像质量, 而小波复数降噪方法能得到更清晰的边缘效果, 对于密度较低的成像部分能取得更好的分辨率.Ahmed等[8]基于小波变换提出了"Critically-sampled"时频变换算法为NMR信号降噪, 通过小波分解后对小波系数进行阈值降噪, 该算法计算过程简便, 能有效抑制噪声, 得到较高信噪比的NMR数据.Wu等[9]采用硬阈值法为NMR测井数据进行降噪处理, 降噪结果更优于IIR (Infinite Impulse Response)滤波器, 能有效提高测井数据的信噪比.Lin等[10]采用小波能量谱分析NMR信号的特征, 当脉冲扳倒角达到最优的时候小波能谱能得到最大值, 用于优化NMR实验参数.郑传行等[11-12]讨论了基于小波变换的UDWT (Undecimated Wavelet Transform)方法, 在保持回波信号峰值的同时为低场NMR信号降噪.谢庆明等[13]将SURE (Stein Unbiased Risk Estimation)算法应用于岩芯NMR测量的降噪处理, 能进一步改善测量数据的信噪比, 有效提高致密砂岩孔隙度计算的准确性.
NMR测井是在极端条件的井眼环境中, 与实验室测量相比, 噪声的来源更为复杂多样, 且不能像实验室测量可以进行成百上千次的累加以提高信噪比, 因此NMR测井数据的信噪比很低, 要求降噪方法不仅能有效压制噪声, 而且需要考虑地层孔隙结构、孔隙流体等影响因素.
本文提出一种正则化-启发式阈值降噪方法, 结合地层孔隙结构、原始回波串信噪比等多种影响NMR测井信噪比的因素, 通过正则化方法控制不同孔隙结构、不同信噪比数据的小波细节系数阈值, 选取的阈值与孔隙结构和原始信噪比等因素相关, 有效提高NMR测井数据的信噪比, 反演后的结果更准确地反映了地层孔隙结构特征.
2 R-Heuresure算法原理 2.1 NMR测井回波串的小波分析小波变换主要分为连续小波变换CWT (Continuous Wavelet Transform)和离散小波变换DWT (Discrete Wavelet Transform).CWT即把基本小波(母小波)作位移后, 在不同的尺度下与带噪信号作内积[14-15].而DWT对尺度因子和位移因子以2的幂次离散采样, 经过Mallat快速分解[14]原信号被分解为近似系数(低频分量)和细节系数(高频分量)的集合, 细节系数主要反映了小孔(或者微孔)响应和噪声, 而近似系数主要反映中孔和大孔的NMR响应.采用DWT分析回波串信号时, 需要综合考虑母小波函数、尺度因子、分解层次以及采用适用于NMR指数衰减特征的阈值算法, 以期望得到更好的降噪效果.
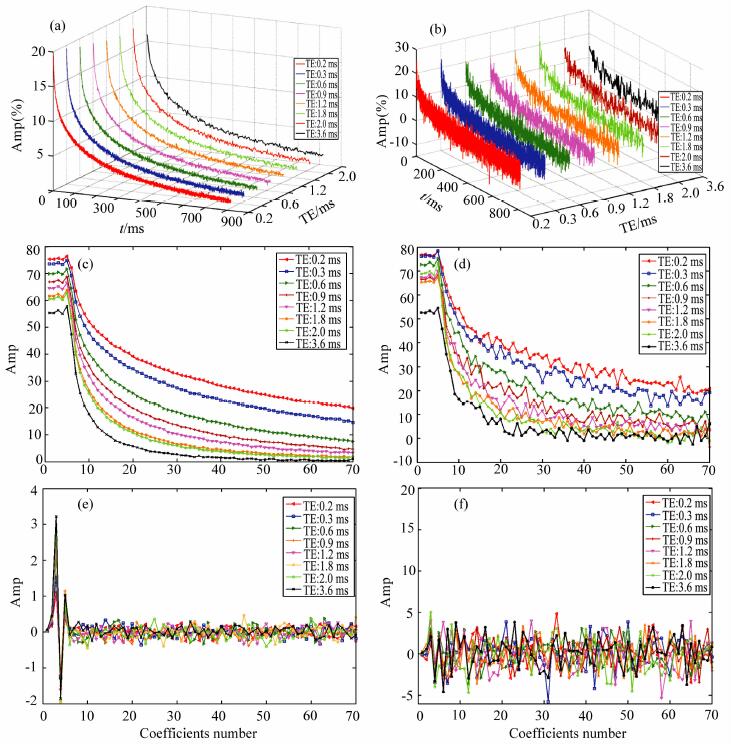
建立具有双峰特征、油水两相、孔隙度为20%的T2谱模型, 第一个峰为7 ms, 流体为束缚水, 束缚水饱和度为35.6%;第二个峰在323ms, 流体为轻质油, 含油饱和度为64.4%, 采用Daubchies小波进行小波变换, 比较分析信噪比分别100和10时、8组不同回波间隔(TE)近似系数和细节系数的变化, 如图 1所示.由图 1中可以看出:
|
图 1 不同回波间隔(TE)下的近似系数和细节系数(信噪比分别为100和10) Fig. 1 Detail coefficients with the various TE (SNR is 100 and 10 respectively) |
(1) 随着信噪比的降低, 近似系数逐渐呈现不光滑, 这是由噪声所引起的; 而细节系数的幅值发生了较大变化, 且具有随机统计特性, 说明噪声主要集中在细节系数;
(2) NMR微孔响应由于弛豫时间短、衰减快, 具有高频特性, 主要集中在细节系数, 因此在对细节系数进行降噪处理时需要考虑微孔的信息, 在采用不同阈值做降噪处理时需要有效分离微孔响应与噪声;
(3) 即使信噪比发生了较大变化(从100降到了10), 近似系数仍能较好的反映NMR回波串的衰减特性, 噪声的增大对于近似系数的影响不大;
(4) 近似系数对于回波间隔(TE)的选取较为灵敏, 具有很好的时间分辨特性, 且随着TE的增大, 系数幅度逐渐减低, 但衰减趋势相似; 而细节系数不具有时间分辨特性, 具有随机分布的特征, 系数幅度随着信噪比的降低而增大;
基于小波变换的降噪方法主要有Mallat[16]提出的模极大值重构降噪、Xu等[17]提出的空域相关法降噪、Donoho[18-20]提出的阈值降噪等.阈值降噪方法直接对各分解层次的小波系数进行阈值处理, 其关键是确定阈值, 噪声能得到很好的抑制, 且信号的特征突变点能得到很好的保留.Donoho曾提出通用阈值选取公式[21], 在任何尺度和分解层次下选用统一的阈值:
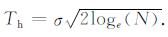
|
(1) |
潘泉等[22]对阈值选取公式做了一些改进:
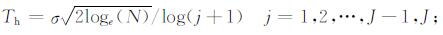
|
(2) |
式中, σ为噪声方差, N为数据采样点数, J为小波分解层次.
SURE[13]算法采用自适应软取阈值的方法, 针对多尺度、不同分解层次下的回波信号选取不同的阈值降噪, 能较好的消除回波串中的噪声.SURE算法的阈值选取简述如下:
假设Wj为第j层分解后的小波细节系数, 将Wj按升序排列得到新的系数C(k), 令
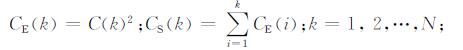
|
(3) |
其中N为第j层细节系数的长度, CE(k)为第k个系数的能量, 而CS(k)为前k个系数能量的累加, 则可以得到第k个系数的SURE无偏估计R(k):
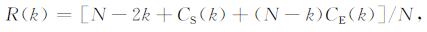
|
(4) |
而第j层分解的SURE阈值为
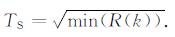
|
(5) |
如果采集的回波串较为光滑(即较高的信噪比), 那么信号能量主要集中在近似系数上, 而细节系数主要为幅度较小的噪声, 根据中值定理可以得到噪声水平的稳健估计, 可采用硬阈值法进行降噪; 当测井数据中含有多种来源的噪声时, 其功率谱密度并非常数, 噪声水平随着小波尺度的变化而变化, 因此需要在不同的分解层次上采用不同的阈值降噪; 此外, 阈值的选取还需考虑地层孔隙结构特征、测井仪器响应特征等因素.
分别定义第j层细节系数的目标函数Ta, j和比较函数Ca, j为
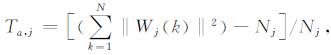
|
(6) |
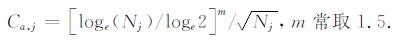
|
(7) |
式中, Nj为第j层细节系数的个数, Wj(k)为第j层、第k个小波细节系数.由上式可知, 比较函数Ca, j主要与数据长度有关, 而Ta, j是对第j层小波系数能量的统计平均, 反映了细节系数的起伏程度.而启发式阈值的选取为[15]
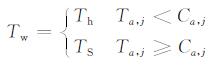
|
(8) |
式中, Th为根据式(2)计算的硬阈值, TS为根据式(5)计算的SURE阈值.为了控制选取的阈值刚好大于噪声水平, 在第j层选取的阈值中加入正则化因子λ:
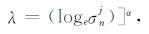
|
(9) |
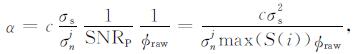
|
(10) |
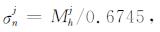
|
(11) |
式中, σs为原始NMR测井数据经相位旋转后噪声道的标准差, σnj为第j层小波细节系数噪声的估计, 反映了小波分解后噪声的统计水平; Mhj为第j层小波细节系数的中值.由于NMR回波信号是呈指数衰减的, logσnj可以对指数信号起平滑作用; 此外, 为了避免小孔信息被误判为噪声, 所选取的阈值只能刚好大于噪声水平, logσnj可以避免阈值过大造成信号失真.指数因子α与地层孔隙结构、测量回波幅度和噪声水平相关, 反映NMR测井中各种因素对测量数据的影响.常数c与反演算法相关, 廖广志等[23]认为, SVD反演算法的稳定区间为40 < SNR < 10000, 当信噪比大于20, SVD反演方法可获得较为准确的束缚水和可动水体积, 却不能准确分辨出黏土束缚水和毛管束缚水体积, 因此, 当测井信噪比SNRP > 20时, c=0, 否则, c=1.
在微孔(或小孔)地层, 原始测量的回波幅度和信噪比低, 回波串衰减快, 除了前几个回波, 大部分数据落在基线附近, λ就要大才能达到压制噪声的目的; 而在中孔(或大孔)地层, 由于NMR测井仪器切片内所含流体多, 回波幅度和信噪比相对较大, 回波串衰减慢, 为了减小信号失真, 阈值的选取就要小, λ的取值也要小.通过正则化函数λ可以控制每一个分解层次下的阈值, 既能自适应于信噪比的变化, 又能避免选取的阈值过大而损失小孔(或微孔)信息, 这对于低孔地层的信噪比提高非常重要.结合硬阈值法、软阈值法和地层孔隙结构特征信息, R-Heursure算法所选取的阈值为
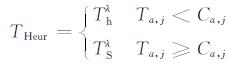
|
(12) |
R-Heursure算法降噪的步骤简述如下:
(1) 将NMR测井仪采集的回波串信号进行相位旋转, 得到信号道和噪声道;
(2) 根据信号道和噪声道估算回波幅度、原始信噪比和受信噪比影响的反演结果;
(3) 采用Symlets小波作为R-Heursure算法的母小波函数;
(4) 结合2.2节所建立的图版和相位旋转后的结果选择小波分解的层次;
(5) 采用小波分解对NMR回波串分解到最细的尺度, 得到近似系数和细节系数;
(6) 根据式(8)判断采用硬阈值法还是软阈值法, 计算阈值;
(7) 根据式(9)和式(10)计算指数因子α和正则化因子λ;
(8) 根据式(12)更新步骤6的阈值;
(9) 将各层细节系数与新阈值进行比较, 保留大于新阈值绝对值的系数, 小于新阈值绝对值的系数根据式(12)重新计算;
(10) 保存各分解层次新的细节系数;
(11) 采用隔点插零法重构信号, 得到降噪后的NMR回波串信号;
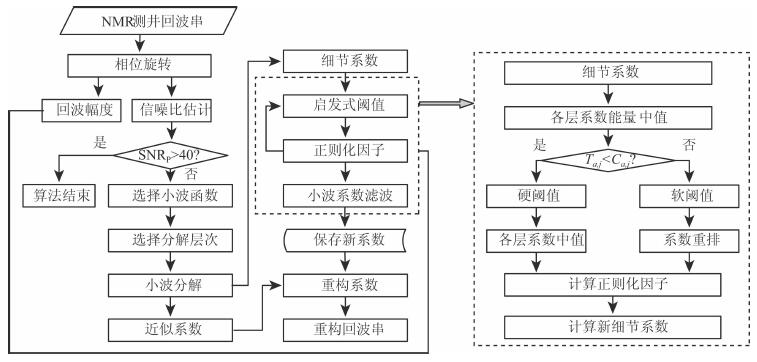
经过对近似系数和新的细节系数进行小波重构, 从而得到R-Heursure算法降噪后的NMR回波串信号, 算法的降噪流程如图 2所示.
|
图 2 R-Heursure算法的降噪流程 Fig. 2 Flow chart of de-noising with R-Heursure |
通常, NMR测井信号是两道相互正交的信号构成.为了能对正交信号构成的自旋回波串进行降噪, 应该选用具有正交特性的母小波函数对NMR测井信号进行时频分析.由于不同的母小波函数具有不同的函数形状和正交特性, 因此对降噪的效果均有不同的影响.为了能选择更优的母小波函数, 本文通过最大系数能量的方法选取母小波函数.定义最大相关系数能量MECC (Maximum Energy of Correlative Coefficients)为
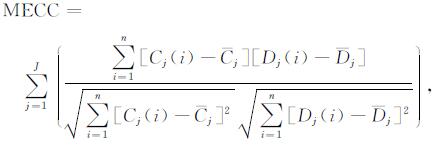
|
(13) |
式中, J为分解层数, 珚Cj和珡Dj分别为第j层分解近似系数和细节系数的均值, Cj(i)和Dj(i)分别为第j层分解的近似系数和细节系数.
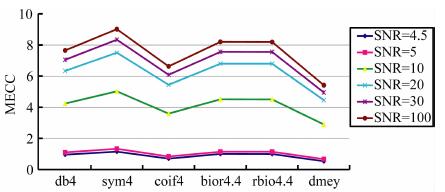
图 3为不同母小波函数在不同信噪比时的系数能量.不失一般性, 具有最大能量的母小波函数最适合于NMR测井数据的降噪处理.由图可以看出, 在不同信噪比下Symlets小波具有最大的小波系数能量, 而且小波系数随着信噪比的提高而能量越大, 因此, 建议NMR测井数据的小波降噪处理采用Symlets小波.当信噪比低到5以下时, 不同母小波函数的能量变化并不大, 说明当NMR测井数据的信噪比低于5时, 信号已经完全被噪声淹没, 已经不能从带噪数据中正确分离出NMR信号.
|
图 3 不同信噪比、不同母小波函数下的最大相关系数能量. 分解层次从1层到10层, 采用的尺度因子为4. Fig. 3 Maximum energy of correlative coefficients with various SNR and different mother wavelet functions. Decomposition level is from 1 to 10, and the scale is 4. |
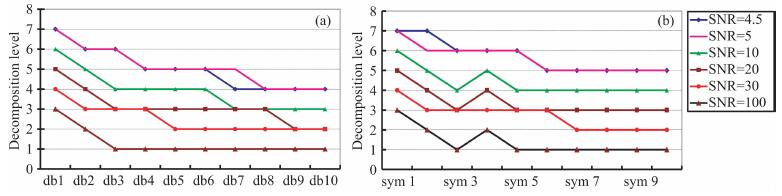
小波分解时, 消失矩和分解层次的选择对于回波信号的降噪处理非常重要.消失矩决定了母小波函数的宽度, 而分解层次决定了小波分解后的精细程度.当信噪比高时, 所需的分解层次就应该小, 从而保证信号的损失最小.当信噪比低时, 为了有效分离信号与噪声, 需要在多个分解层次分析回波信号.以2.1节所建模型为例, 分别选取Daubechies小波和Symlets小波计算不同分解层次的最大系数能量, 如图 4所示.由图可知, 随着消失矩的增大所需的分解层次越小; 随着信噪比的降低, 回波信号所需分解的层次越来越多; 当消失矩在7以后, 分解层次将不再变化, 说明母小波函数过度的伸缩对于带噪信号的总能量没有变化, 也不能精细刻画原信号.
|
图 4 Daubechies小波(a)和Symlets小波(b)不同消失矩的分解层次 Fig. 4 Decomposition level with various vanishing moments for Daubechies (a) and Symlets (b) |
综合以上分析, 使用小波变换对NMR测井数据降噪处理时, 建议使用"sym4"小波, 根据图 4不同回波串的原始信噪比自适应选择分解层次.
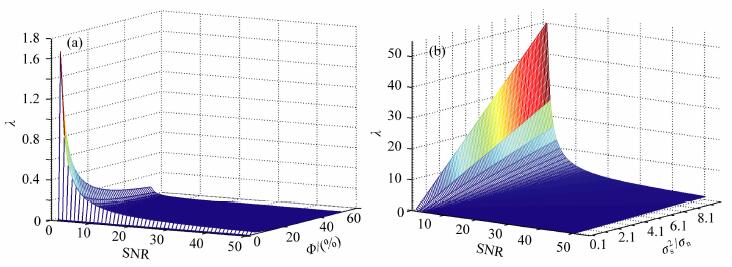
3.3 正则化因子R-Heursure算法选取的正则化因子与孔隙结构和NMR测井原始信噪比有关.图 5为不同信噪比、不同孔隙度下正则化因子的变化.由图 5a中可以看出, 随着信噪比和孔隙度的不断增加, 正则化因子λ逐渐趋于0, 选取的阈值也越接近于0, 也即对回波串不做降噪处理; 在信噪比和孔隙度很低的情形下, 正则化因子的取值要大于估计的噪声水平, 选取的阈值要大才能达到压制噪声的目的.当信噪比大于20时, 反演方法已经能得到较为准确的孔隙度信息, 为了避免降噪后的回波串失真, 因此选取的阈值要小, 降噪效果不明显.图 5b反映了不同信噪比下估计的噪声和正则化因子的关系, 正则化因子随着信噪比的增大而减小, 随着噪声比的增大的而增大.
|
图 5 正则化因子的影响因素 (a)不同信噪比、不同孔隙度下的正则化因子; 噪声比值假定为5;(b)不同噪声比值、不同信噪比下的正则化因子; 假定孔隙度为20% Fig. 5 Influence factors of regularization factor (a) Regularization factor with the various SNR and porosity, and noise ratio is assumed to 5; (b) Regularization factor with the various SNR and noise ratio, and porosity is assumed to 20% |
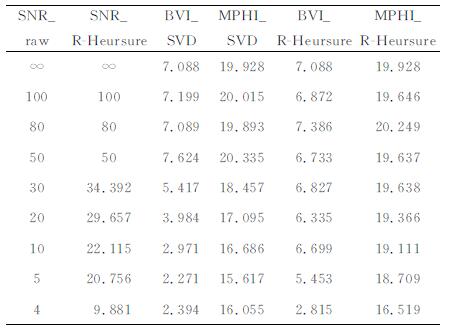
表 1为2.1节所建模型采用R-Heursure算法降噪结果对比.表中第1列和第2列分别为降噪前后的回波串信噪比, 第3列和第4列分别为降噪前计算的束缚水孔隙体积和NMR有效孔隙度, 第5列和第6列为采用R-Heursure算法降噪后计算的束缚水孔隙体积和NMR有效孔隙度, 采用截断奇异值(truncated singular value decomposition, TSVD)反演方法.由表 1可知:
|
|
表 1 R-Heursure降噪前后模型对比 Table 1 Comparison of before and after the de-noising with R-Heursure |
(1) 当信噪比大于50, 反演算法已经能准确的反映真实的孔隙度信息, R-Heursure算法不实施降噪处理; 当信噪比低于30后, 正则化因子自适应于测量数据的信噪比和孔隙特征, 约束阈值的变化, 从而提高数据的信噪比;
(2) 当信噪比大于50, 反演结果能得到准确的总孔隙度; 当信噪比低于30后, 总孔隙度开始减小, 这是由于反演算法逐渐不能正确反映束缚水体积; 降噪后随着信噪比的提高有所改善, 受到正则化因子的影响, 小孔(或微孔)响应的细节系数与噪声分离出来, 因此总孔隙度的计算与模型较为接近;
(3) 算法的适用范围:当信噪比低于5后, NMR测井信号已经完全淹没在噪声中, 算法的降噪效果不明显, 反演后不能得到正确的束缚水体积, 计算的孔隙度与模型有较大的差异, 说明算法失效.
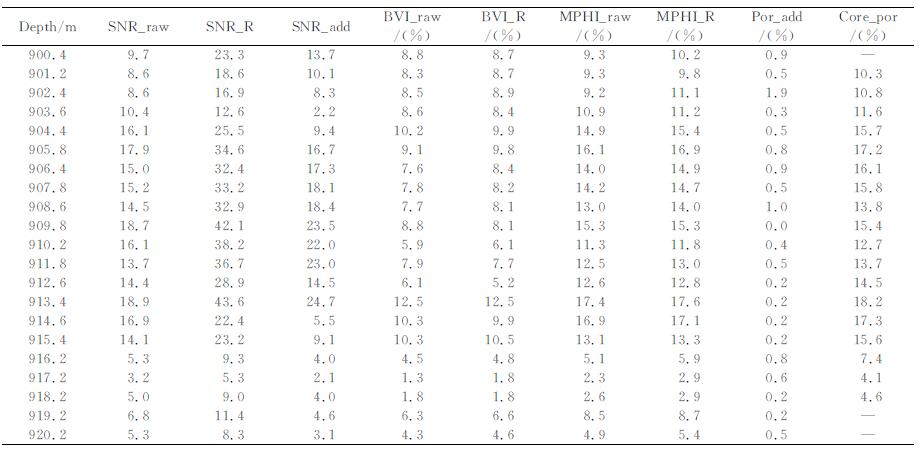
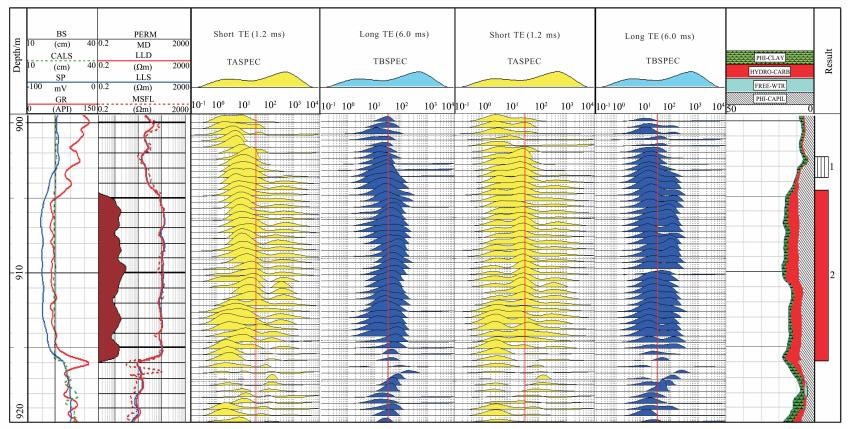
4 降噪实例分析对内蒙古二连盆地白音查干凹陷地区X井的NMR测井原始数据运用R-Heursure降噪方法进行处理, 处理井段为900~920 m, 降噪前后反演结果如图 6所示.图中, 第1道为深度, 第2道为岩性曲线, 第3道为电阻率曲线, 第4道、第5道分别为降噪前短TE (1.2 ms)和长TE (6.0 ms)的回波串反演结果, 第6道、第7道分别为采用R-Heursure降噪后的短TE (1.2 ms)和长TE (6.0 ms)的回波串反演结果, 第8道为综合处理结果.
|
图 6 X井R-Heursure降噪处理结果 Fig. 6 De-noising results with R-Heursure algorithm for X well |
由图 6可以看出, 常规测井曲线显示该段物性较好.NMR测井观测模式选用DTWEADC412, 长TE (6.0 ms)的T2谱比短TE (1.2 ms)前移明显, 且比较整齐.在T2截止值(33 ms)附近有很强的峰, 短TE部分在目的层显示为双峰, 长TE呈单峰显示, 集中在33 ms附近, 不能有效区别BVI和FFI.降噪前, 905~915m段的短TE (1.2ms)部分T2谱主要呈双峰显示, 能有效分离束缚水和可动流体, 但是不能分辨出黏土束缚水峰和毛管束缚水峰; 长TE (6.0ms)部分T2谱主要呈单峰显示, 且峰值幅度较大, 但不能分辨出黏土束缚水峰和毛管束缚水峰.这是由于长TE采集的回波个数只有80个, 回波个数太少, 采集的回波信号衰减没有结束, 长弛豫组分采集不完整, 使得反演结果不能真实反映长T2组分的信息, 如图第5道和第7道数据所示.经过R-Heursure方法降噪后, 信噪比得到了提高, 目的层段(904.5~916.0 m)短TE (1.2 ms)部分T2谱呈三峰显示, 黏土束缚水峰在4 ms附近, 毛管束缚水峰幅度较强, 峰值在33ms附近, 可动流体峰幅度微弱, 呈拖拽现象, 峰值在400 ms左右.长TE (6.0ms)部分T2谱呈双峰显示, 束缚水峰在20ms附近, 可动流体峰值在100 ms左右, 两峰的幅度都较强, 已经能有效分离束缚水体积和可动流体体积, 且峰值幅度增大.NMR测井计算的孔隙度与岩芯测量孔隙度的平均误差为1.4%, 采用R-Heursure算法降噪后计算的孔隙度与岩芯测量孔隙度的平均误差为0.8%, 降噪前后的处理结果如表 2所示.
|
|
表 2 NMR测井降噪前后对比-X井为例 Table 2 De-noising results of NMR well logging with R-Heursure algorithm-X well |
表中第1列为深度, 第2、3、4列分别为降噪前后的信噪比和信噪比增量(SNR_add), 第5、6列分别为以33 ms为截止值计算的降噪前后束缚水体积, 第7、8、9列分别为降噪前后的NMR有效孔隙度和孔隙度增量(por_add), 第10列为岩芯测量孔隙度.由表 2可知, 目的层段(904.5~916.0 m)的物性较好, NMR有效孔隙度(MRIL porosity, MPHI)都在10%以上, 原始NMR测井数据的信噪比大部分都在15以上; 经R-Heursure算法降噪处理后, 信噪比均有较大改善, 而孔隙度增量(por_add)主要与黏土束缚水体积和毛管束缚水体积部分相关.在降噪前受到信噪比的影响, 不能有效分离黏土束缚水体积和毛管束缚水体积, 降噪后长、短TE的T2谱显示束缚水部分有很好的双峰显示, 如第6道和第7道所示.而在916.2~918.2m层段, 物性较差, 原始NMR测井数据的信噪比在5左右, 降噪前后反演结果变化不大, 信噪比没有明显改善, 仍然不能有效分辨出黏土束缚水峰和毛管束缚水峰.此外, 测井计算的孔隙度与岩芯孔隙度相比总体偏小, 这是由于实验室测量时采用岩芯饱和盐水测量, 盐水黏度与储层原油相差较大, 致使T2谱向左偏移, 计算的孔隙度值偏小[24].该井试油层段为904.5~915.5m, 试油密度为0.9463g/cm3, 原油黏度1184.4mPa·s, 渗透率为614.687×10-3 μm2, 试油结果表明该层段为物性较好的稠油储层.
5 结论基于地层岩石孔隙结构、原始回波串信噪比等影响NMR测井信噪比的多种因素, 提出R-Heursure算法并应用于NMR测井的降噪处理, 有效增强NMR测井数据的信噪比.通过数值模拟和实际测井资料处理验证, 得到以下结论:
(1) 建立的阈值与地层孔隙结构相关的正则化方法, 通过正则化因子约束阈值, 使选取的阈值能够刚好大于噪声水平而不损失小孔(或微孔)的响应信息.
(2) 通过数值模拟, 对不同信噪比的NMR测井数据降噪, Symlets小波在不同信噪比时具有最大的相关系数能量, 建议在采用算法降噪时值得选用该小波.
(3) R-Heuresure算法能有效提高NMR测井数据的信噪比, 反演后的结果能有效分离出束缚水和可动流体体积, 更准确地反映地层孔隙结构特征.
(4) 当NMR测井数据的信噪比低于5时, 信号已经完全被噪声淹没, 算法不能从原始测井数据中正确分离出NMR信号和噪声.在孔隙度极低(低于5%)的致密地层, 建议降低测井速度, 采用点测或多次累加的方式以提高测井信噪比, 从而得到更准确的地层信息.
| [1] | Coates G R, Xiao L Z, Prammer M G. NMR Logging:Principles and Applications. Texas:Gulf Professional Publishing , 1999. |
| [2] | 肖立志, 陆大卫, 柴细元, 等. 核磁共振测井资料解释与应用导论. 北京: 石油工业出版社, 2001 . Xiao L Z, Lu D W, Chai X Y, et al. NMR Logging Interpretation and China Case Studies (in Chinese). Beijing: Petroleum Industry Press, 2001 . |
| [3] | 肖立志, 谢然红, 廖广志. 复杂油气藏的核磁共振测井新方法. 北京: 科学出版社, 2011 . Xiao L Z, Xie R H, Liao G Z. New Methods of NMR Well Logging for Complex Reservoir (in Chinese). Beijing: Science Press, 2011 . |
| [4] | Dunn K J, Bergman D J, Latorraca G A. Nuclear Magnetic Resonance:Petrophysical and Logging Applications. Pergamon:Elsevier Science , 2002. |
| [5] | 刘双惠, 肖立志, 胡法龙, 等. 核磁共振测井地层界面响应特征研究. 地球物理学报 , 2008, 51(4): 1262–1269. Liu S H, Xiao L Z, Hu F L, et al. Studies on NMR logging responses at formation boundary. Chinese J. Geophys. (in Chinese) , 2008, 51(4): 1262-1269. |
| [6] | Edwards C M, Chen S H. Improved NMR well logs from time-dependent echo filtering. SPWLA 37th Annual Logging Symposium , 1996. |
| [7] | Wood J, Johnson K. Wavelet packet denoising of magnetic resonance images:importance of Rician noise at low SNR. Magnetic Resonance in Medicine , 1999, 41(3): 631-635. DOI:10.1002/(ISSN)1522-2594 |
| [8] | Ahmed O, Fahmy M. NMR signal enhancement via a new time-frequency transform. IEEE Transactions on Medical Imaging , 2001, 20(10): 1018-1025. DOI:10.1109/42.959299 |
| [9] | Wu L, Kong L, Cheng J J. Wavelet de-noising algorithm for NMR logging application. Journal of Information and Computational Science , 2011, 8(5): 747-754. |
| [10] | Lin Y L, Peng L, Chen S, et al. Wavelet analysis of nuclear magnetic resonance signal characteristics. International Conference on Wavelet Analysis and Pattern Recognition , 2007, 4: 1891-1895. |
| [11] | Zheng C X, Zhang Y M. Noise reduction for low-field pulsed NMR signal via stationary wavelet transform. The Eighth International Conference on Electronic Measurement and Instruments, ICEMI , 2007: 746-750. |
| [12] | Zheng C X, Zhang Y M. Low-field pulsed NMR signal denoising based on wavelet transform. Signal Processing and Communications Applications, SIU , 2007: 1-4. |
| [13] | 谢庆明, 肖立志, 廖广志. SURE算法在核磁共振信号去噪中的实现. 地球物理学报 , 2010, 53(11): 2776–2783. Xie Q M, Xiao L Z, Liao G Z. Application of SURE algorithm to echo train de-noising in low field NMR logging. Chinese J. Geophys. (in Chinese) , 2010, 53(11): 2776-2783. |
| [14] | Mallat S. A Wavelet Tour of Signal Processing. Burlington:Elsevier Science , 2009. |
| [15] | 杨福生. 小波变换的工程分析与应用. 北京:机械工业出版社 , 1999. Yang F S. Wavelet Analysis and Its Engineering Applications (in Chinese). Beijing:China Machine Press (in Chinese) , 1999. |
| [16] | Mallat S. A theory for multi-resolution signal decomposition:the wavelet representation. IEEE TPAMI , 1989, 11(7): 674-693. DOI:10.1109/34.192463 |
| [17] | Xu Y S, Weaver J B, Healy D M, et al. Wavelet transform domain filters:a spatially selective noise filtration technique. IEEE Transactions on Image Processing , 1994, 3(6): 747-758. DOI:10.1109/83.336245 |
| [18] | Donoho D L, Johnstone I M. Idearl spatial adaptation via wavelet shrinkage. Biometrika , 1994, 81(12): 425-455. |
| [19] | Donoho D L, Johnstone I M. Adapting to unknown smoothness via wavelet shrinkage. J. American Statist. Assoc. , 1995, 90(432): 1200-1224. DOI:10.1080/01621459.1995.10476626 |
| [20] | Donoho D L, Johnstone I M, Kerkyacharian G, et al. Wavelet shrinkage:asymptopia? J. Royal Stat. Soc. B. , 1995, 57(2): 301-369. |
| [21] | Donoho D L, Mallat S, Von Sachs R. Estimating covariances of locally stationary processes:consistency of best basis methods. In Proc. of Time-Freq. and Time-Scale Symp. , 1996: 337-340. |
| [22] | 潘泉, 张磊, 孟晋丽, 等. 小波滤波方法及应用. 北京:清华大学出版社 , 2005. Pan Q, Zhang L, Meng J L, et al. Wavelet Filtering Method and Its Applications (in Chinese). Beijing:Tsinghua University Press (in Chinese) , 2005. |
| [23] | 廖广志, 肖立志, 谢然红, 等. 孔隙介质核磁共振弛豫测量多指数反演影响因素研究. 地球物理学报 , 2007, 50(3): 932–938. Liao G Z, Xiao L Z, Xie R H, et al. Influence factors of multi-exponential inversion of NMR relaxation measurement in porous media. Chinese J. Geophys. (in Chinese) , 2007, 50(3): 932-938. |
| [24] | 谢然红, 肖立志, 刘天定. 原油的核磁共振弛豫特性. 西南石油大学学报 , 2007, 29(5): 21–24. Xie R H, Xiao L Z, Liu T D. NMR relaxation properties of crude oils. Journal of Southwest Petroleum University (in Chinese) , 2007, 29(5): 21-24. |
 2013, Vol. 56
2013, Vol. 56