2. 中石油西部钻探测井公司, 克拉玛依 834000
2. CNPC West Drilling and Logging Company, Karamay 834000, China
在定向井及水平井钻井过程中, 由于钻前资料不足或者地质情况复杂等因素影响, 先导地层模型具有一定的不确定性[1-4].因此需要根据随钻测井数据对地层模型进行实时更新[5-6], 为实时调整井眼轨迹提供依据, 以降低钻井风险、提高油层钻遇率、最大限度地发挥地质导向的作用[7-8].
地层模型更新的关键在于实时确定地层界面和产状.基于先导地层模型, 采用合适算法对测井响应进行正演模拟, 并与实测数据进行比较可有效确定地层界面和产状.国内现有常见随钻测井资料以电阻率和自然伽马为主, 随钻电阻率与自然伽马测井资料相比具有更深的径向探测深度, 因此不少学者通过正演模拟来研究不同地层模型的随钻电阻率测井响应特征[9-13]并用于确定地层界面[14-18]; 由于其受上下围岩的影响比伽马测井更为严重, 因此在薄互层及低阻地层中不利于识别地层界面[18].国内随钻地质导向钻井常用于薄互层, 由于伽马测井曲线具有更高的纵向分辨率, 可较好地反映薄砂体和隔夹层, 因此对自然伽马测井响应进行正演模拟并与实测结果对比是提高薄互层地层模型实时更新精度的有效方法.目前对伽马测井响应正演多采用蒙特卡罗方法[19-21], 但该方法计算量大、速度慢, 一般用于测井响应影响因素分析和测井仪器的优化设计[22-25], 尚难以满足井场地层模型实时更新需求, 因此需要寻求一种快速正演算法.
实现随钻伽马测井响应快速正演计算的关键在于得出伽马探头在地层不同位置的响应方程.本文根据伽马探头探测范围与地层界面的不同空间关系, 将不同位置地层在探头处的伽马射线通量贡献分别进行积分, 得出了不同空间关系下的自然伽马测井响应正演算法.数值测试和实例表明该方法计算速度快, 能根据随钻伽马测井资料实时确定地层界面和产状、为地层模型实时更新提供依据.
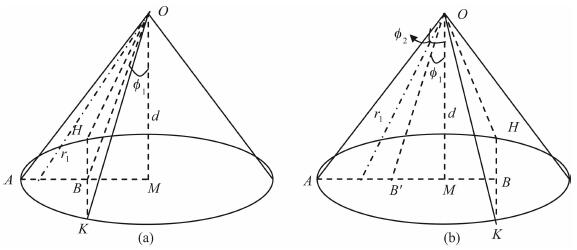
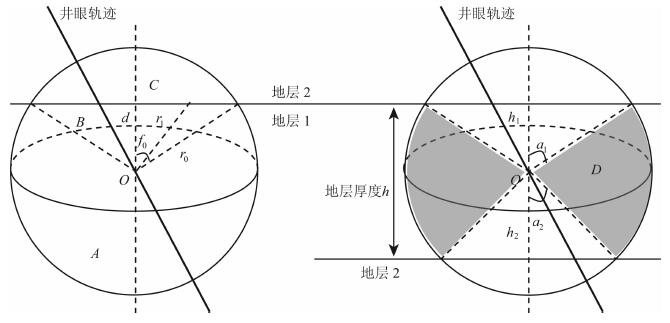
2 随钻伽马测井响应快速正演算法 2.1 规则地层界面模型的正演解析算法 2.1.1 物理模型为简化问题, 设地层模型为如图 1所示水平层状.图中阴影圆代表伽马射线贡献范围, 圆心处为探测器(图 2中O点)的位置.
|
图 1 水平层状地层模型 ` Fig. 1 Horizontal layered strat amodel |
|
图 2 探测器与地层界面相交情况 Fig. 2 Two cases of the detector intersect with formation boundary |
设图 1模型满足:(1)地层为水平层状均匀介质; (2)井眼无明显扩径, 鉴于随钻测井中泥饼成熟度较低, 因此忽略井眼和泥饼影响; (3)探测器中的计数管位于仪器中心, 没有方位; (4)地层中放射性强度为当量强度.
根据探测器的探测范围和距地层界面的距离可以分为两种情况:(1)探测器位于某地层中, 探测范围不受邻近地层的影响; (2)探测器位于某地层中, 探测范围受相邻地层的影响(如图 2所示).
2.1.2 正演解析计算模型若探测器探测范围不受邻层影响, 探测器O点处的伽马射线通量可根据如下均匀地层中的计算公式得到[26]:
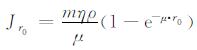
|
(1) |
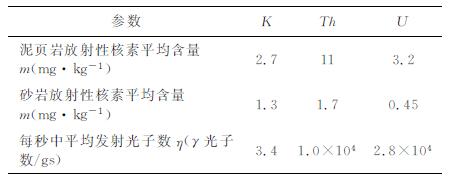
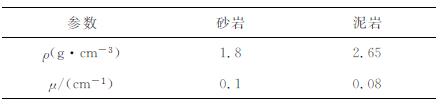
其中, r0为探测器的探测半径, ρ(g/cm3)为地层密度, m(g/g)为岩石中放射性物质的含量, η(伽马光子/g·s)为放射性物质伽马射线的平均放射强度, μ(cm-1)为介质对伽马射线的平均吸收系数.
若探测范围受到邻层影响(图 2), 可分不同贡献区域进行计算.当贡献区域为两地层时(图 2左), 可分别对界面两侧的扇形体(图中A区)、圆锥体(图中B区)和弓形体(图中C区)进行积分, 然后将各区域相加得到总的伽马射线通量值.各区域在探测器O点处的伽马射线通量计算公式如下:
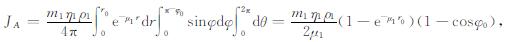
|
(2) |
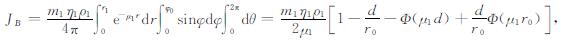
|
(3) |
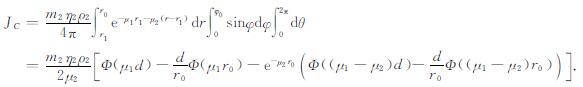
|
(4) |
当中间地层厚度小于探测半径2倍时(图 2右), 图 2左中的A区表现为图 2右的中间环形体(D区), 其他跨地层界面区域与B、C区域相同.
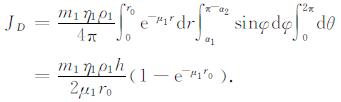
|
(5) |
式(2)至(5)中的JA、JB、JC和JD分别表示图 2中A-D四个区域在O点处伽马射线通量, 参数ρ、m、η和μ的下标与图 2中地层的标号一致, r0为探测半径, d为探测器到地层边界的距离, h为地层厚度.另外, (3)、(4)两式在推导过程中用到了金格函数[27]: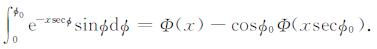
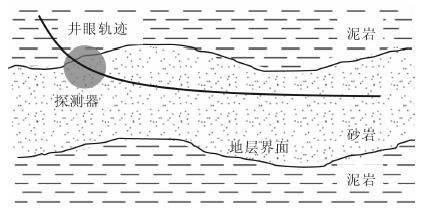
由于水平层状地层模型与实际地层情况相差较远, 考虑到自然伽马测井探测范围在米级[26], 因此可以将地层界面视为不同倾斜面的组合:即沿井眼轨迹最大延伸方向做地层纵剖面, 地层界面与纵剖面的交线由若干折线段组成; 沿垂直井眼轨迹最大延伸方向作横剖面, 地层界面与剖面的交线为直线.此时地层界面不再是水平的, 仅在小范围内为一平面, 其走向与纵剖面垂直(图 3).当探测范围跨地层界面时, 伽马射线贡献区域类型可归纳为如图 4所示三段折线情况.据图 4可以将整个探测范围球体分解为地层界面以上的扇形体OAD区域(含整个上半球体)、几何体AOB区域、几何体BOC区域、几何体COD区域及地层界面以下的几何体ABF区域、几何体BCEF区域和几何体CDE区域.其中, OAD区域为一类, AOB区域和COD区域为一类, ABF区域和CDE区域为一类, BOC区域为一类, BCEF区域为一类.
|
图 3 地层界面为曲面时地层模型 Fig. 3 The strata model with curved formation boundaries |

|
图 4 地层界面为曲面时与探测器位置关系图 Fig. 4 The detector intersect with a curved formation boundary |
根据图 4不同区域几何特点, 可导出不同类型区域在探测器处的伽马射线通量计算方法.
(1) OAD区域
该区域可根据规则地层界面模型中扇形体的计算公式(2)进行近似计算.
(2) AOB及COD区域
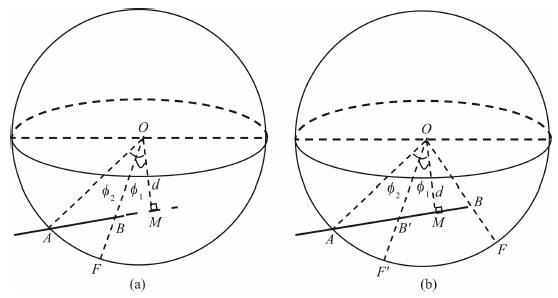
根据AOB三点相对位置关系可以将该类区域分为两种情况(见图 5), 此时很难导出其具体解析计算公式, 所以得出体积元贡献方程后再采取数值积分的方法进行计算.
|
图 5 AOB区域的两种情况((a)中AB≤AM, (b)中AB > AM, B'M=BM) Fig. 5 Two cases of region AOB |
图 5中d为OM的距离, φ1为∠BOM的大小, φ2为∠AOM的大小.图 6为图 5两种情况下AOB区域(图 6中OHAK所围成的区域)的侧视图; 图 7为图 5两种情况下的俯视图, 给出了图 6中过AB界面与贡献球体相交截面⊙M上各个量的关系; 图 5、图 6和图 7中(a)、(b)一一对应.
|
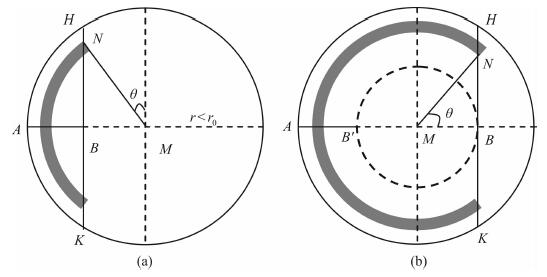
图 7 AOB区域两种情况下⊙M上各量的关系 Fig. 7 The relationship among each value in ⊙ M in two cases of region AOB |
图 7中, r为⊙M的半径, r0为探测半径, r < r0, 需要注意的是(a, b)中θ的位置不同.
(1) 对于第一种情况(图 7a), MN以一定步长dr从r变化到BM, 对于每次计算, φ从φ'1到φ'2.其中各量之间的关系为
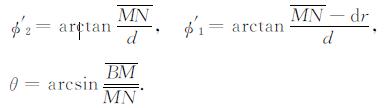
|
以O点为顶点、以图 7中阴影部分为底的体积元在O点的伽马射线通量JAOB*的计算公式为:
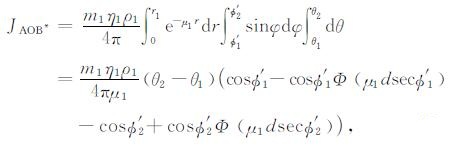
|
(6) |
式中, θ1=θ, θ2=π-θ, 则θ2-θ1=π-2θ, r1表示O点到⊙M上相同径向距离处的长度(图 6), 参数ρ、m、η和μ的下标与图 4中地层标号一致.
(2) 对于第二种情况(图 7b), MN从r变化到BM的计算过程与(1)中相同, 体积元伽马射线通量JAOB*的计算公式也相同, 只是由于两种情况下θ的位置不同, 此时(6)式中的θ2 -θ1=2π-2θ.另外, 当MN小于BM时几何体BOB'为一个规则的圆锥体, 其在O点处的伽马射线通量计算公式如下:
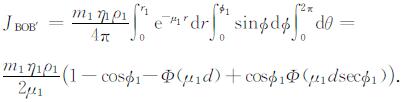
|
(7) |
COD区域对探测器的贡献积分思路与AOB相同, 不再赘述.
(3) ABF及CDE区域
该区域具体分解情况和计算方法与AOB区域类似.与AOB区域中的积分体元相对应, ABF区域的体积元在O点的伽马射线通量计算公式为
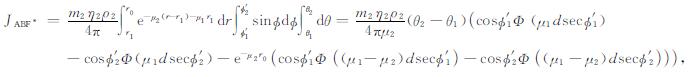
|
(8) |
式中θ1和θ2的取值与AOB区域一致, 其他参数的意义与前述相同.对于第二种情况, 几何体BFF'B'在O点的伽马射线通量为:
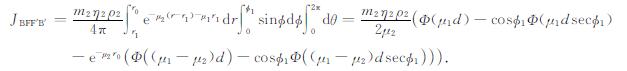
|
(9) |
CDE区域体积元贡献积分可参照上述思路得出.
(4) BOC区域
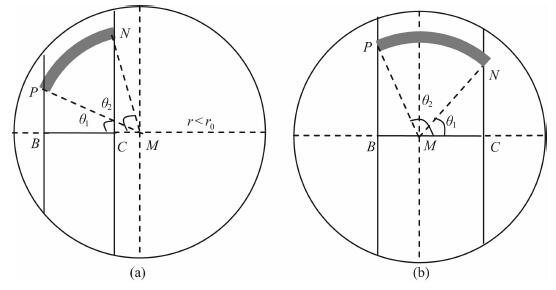
与AOB区域类似, 根据BC和BM的不同大小可以将BOC区域分为两种情况, 具体分解情况可以参照AOB区域, 下面给出BOC区域每个小体元的计算方法.图 8表示过BC地层界面与贡献球体相交的截面⊙M上各个量的关系.
|
图 8 BOC区域两种情况下⊙M上各量的关系 Fig. 8 The relationship among each value in ⊙ M in two cases of BOC region |
对于BOC区域, 图 8中以BC为界上下两部分是对称的, 所以只需对上半部分计算, 然后再乘以2即可.其中以O点为顶点、以阴影部分为底的体元在O点的伽马射线通量可根据式(6)进行计算.图 8a中θ1=∠BMP, θ2=∠BMN, BM以一定步长从r变化到CM, θ1和θ2的大小也随之发生变化, 当MN≤BM时, θ1=0;图 8b中设CM > BM, MN以一定步长从r变化到0MN > CM时, θ1=∠CMN, 否则θ1=0, MN > BM时, θ2=∠CMP, 否则θ2=π.
(5) BCEF区域
对于BCEF区域, 过BC地层界面与贡献球体的截面与图 8相同, 两种情况下MN的积分长度和θ的大小均与BOC区域对应情况相同.其体元以BC为界呈对称分布(图 8), 在O点的伽马射线通量的计算方法与ABF区域类似, 可参考式(8)并乘以2进行计算.
以上讨论假设探测范围内的地层界面为三段折线, 如果地层界面为两段折线, 则分解后的计算区域中不包括BOC区域和BCEF区域; 如果地层界面超过三段折线, 分解后的计算区域则包括多个与BOC和BCEF类似的区域; 这两种情况下的其他区域与三段折线时完全一致.
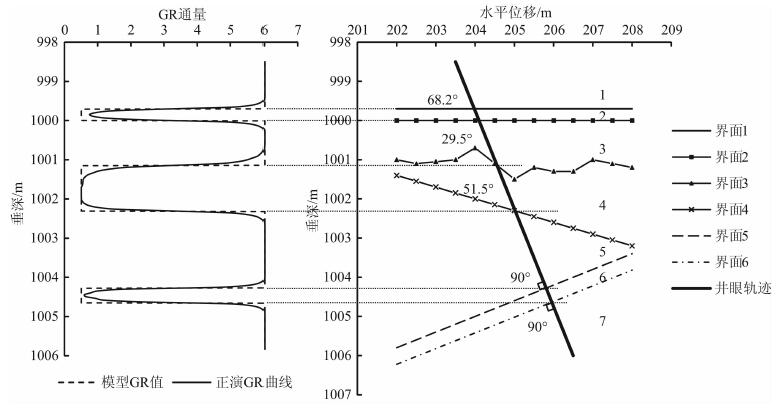
3 快速正演算法在实时地质导向中的应用 3.1 数值地层模型随钻伽马测井响应正演模拟为检验本文正演算法的正确性, 在考察地层厚度和井眼轨迹与地层夹角对伽马响应影响基础上, 设计了如图 9右侧所示地层和井眼轨迹模型; 其中1、3、5、7号地层为泥岩, 2、4、6号地层为砂岩, 地层界面与井眼轨迹的相交纵剖面如右图所示, 井眼轨迹与4种不同倾角地层界面的夹角如图中标注.设地层放射性参数如表 1和表 2所示, 以Halliburton DGR探测半径30cm为例[28], 算出纯泥岩层的伽马射线通量为6.0122, 纯砂岩层的伽马射线通量为0.5063.根据本文正演算法得到如图 9左侧所示结果.
|
图 9 地层模型及其伽马正演曲线 Fig. 9 The strata model and forward GR curve |
从图 9左侧正演结果中可以看出:当地层厚度大于2倍探测半径时, 正演伽马极值(砂岩最小值、泥岩最大值)与模型值相等(地层1、3、4、5、7), 当地层厚度小于2倍探测半径时, 由于围岩影响, 正演伽马极值达不到模型值(地层2、6);在地层界面附近正演伽马值受井眼轨迹与地层界面的夹角影响, 夹角越小、界面附近伽马测井响应变化越平缓; 另外正演曲线所示地层界面位置与模型相当(当层厚或井眼轨迹与地层的夹角大于一定值时).上述正演结果验证了本文算法的正确性.
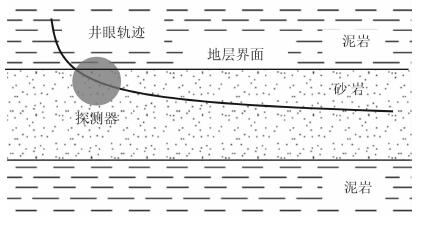
3.2 地质导向应用 3.2.1 实际地层伽马射线通量方程参数的确定对实际地层进行正演模拟, 需要得到不同地层中ρ、m、η和μ参数.由于实际岩石组分的复杂性, 难以准确获得这些参数, 因此利用实际地层自然伽马测井值进行工程简化求取.
在式(1)中, 令A=mηρ, 则有:
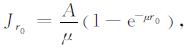
|
(10) |
对于足够厚地层, 设99%的自然伽马测井贡献都来自探测半径以内, 则有方程1-e-μr0=0.99, 代入随钻伽马测井仪器探测半径r0则得到μ值; 然后利用足够厚地层中自然伽马测井值根据(10)式便可求出不同地层的A值.
虽然这样在砂泥岩地层会得出相同吸收系数μ值, 但A值会有相应差异, 另外实际上砂岩和泥岩的μ值也相差很小, 所以对结果影响甚微.
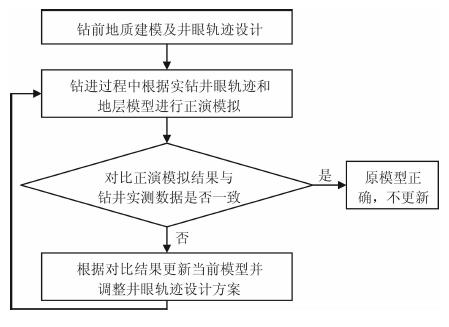
3.2.2 基于随钻伽马测井正演的地层模型实时更新与导向流程通过对比基于地层模型的伽马测井正演响应曲线与随钻实测伽马测井曲线的差别可对地层模型进行实时更新与调整, 从而实现地质导向钻井, 具体流程如图 10所示.
|
图 10 地层模型更新与导向流程 Fig. 10 The flow of the strata model updating and steering |
(1) 实例1-A井
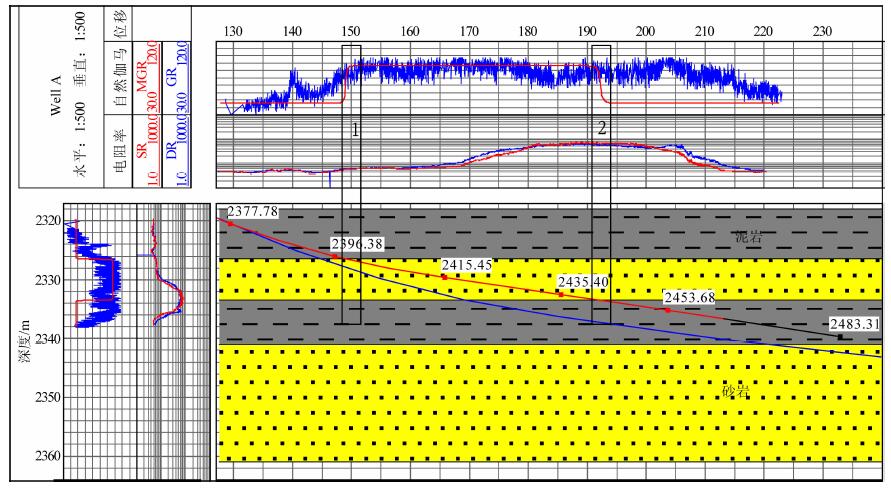
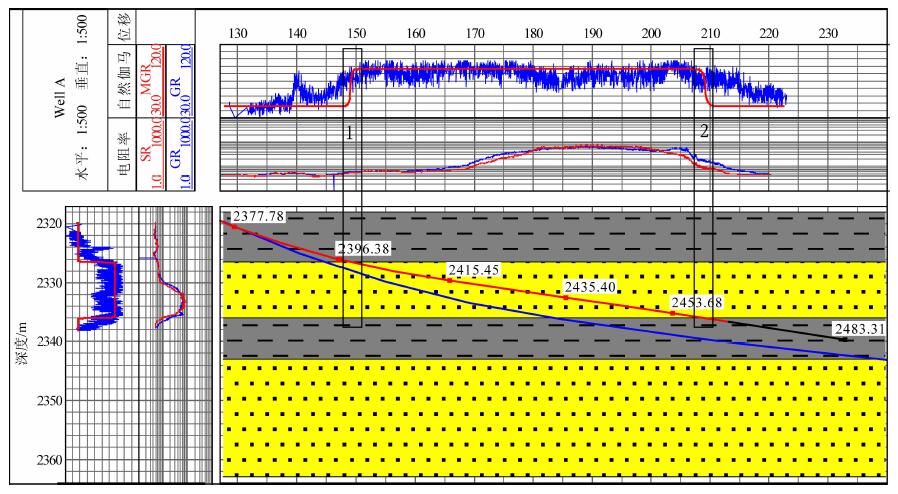
图 11、图 12、图 13是应用上述算法和流程对新疆油田某A井的应用结果.图中左上角为图头和测井曲线头; 右下角是地层模型, 蓝色实线为设计井眼轨迹, 红色线为实钻井眼轨迹; 地层模型上侧和左侧分别为按照井眼轨迹水平和垂直位移标注的测井曲线显示区, 自然伽马测井道中MGR (红色实线)为根据地层模型和实钻井眼轨迹得到的正演伽马测井曲线、GR (蓝色实线)为实际伽马测井曲线.由于特殊地质原因, 该井砂岩层的伽马测井值高于泥岩层的伽马测井值.
|
图 11 align="center"井调整前的地层模型、井眼轨迹及测井曲线综合图 Fig. 11 The strata model, well path and log curves before updating of well |
|
图 12 A井调整后的地层模型、井眼轨迹及测井曲线综合图 Fig. 12 The updated strata model, well path and log curves of well |
|
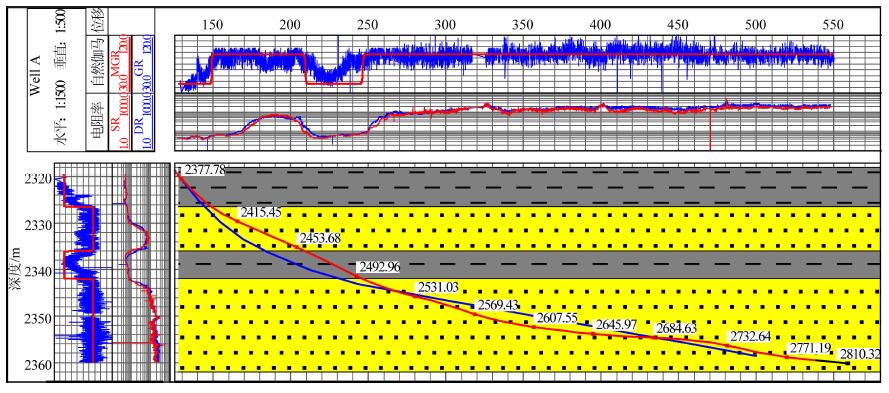
图 13 A井完钻后的模型、井眼轨迹及测井曲线综合图 Fig. 13 The strata model, well path and log curves after finished drilling of well |
如图 11所示, 在钻进过程中第1个地层界面处伽马测井值增大, 电阻率值也开始增大, 基于先导地层模型由实钻轨迹得到的伽马测井正演结果与实测资料较为吻合, 说明界面位置是正确的、无需修改.而对于第2个界面, 正演伽马测井响应与实测值差异较大、实测曲线明显滞后正演结果; 另外, 虽然在地层模型中直观显示钻头已经进入下一地层, 但实测伽马测井值及电阻率值基本没有变化, 说明模型地层界面超前实际地层界面; 通过调整地层模型、比较正演与实测伽马测井曲线的差异, 最后将地层模型界面下调2.5m, 如图 12所示.图 12中根据更新后的地层模型和实钻井眼轨迹得到的伽马测井正演响应曲线与实测曲线变化趋势一致, 表明调整后的地层界面符合实际地层情况.
图 13为完钻后的最终结果, 可以看到根据更新后的地层模型和实钻轨迹得到的正演伽马测井曲线与实测曲线吻合, 综合随钻电阻率资料分析表明实时更新后的地层模型与实际地层一致.
(2) 实例2-B井
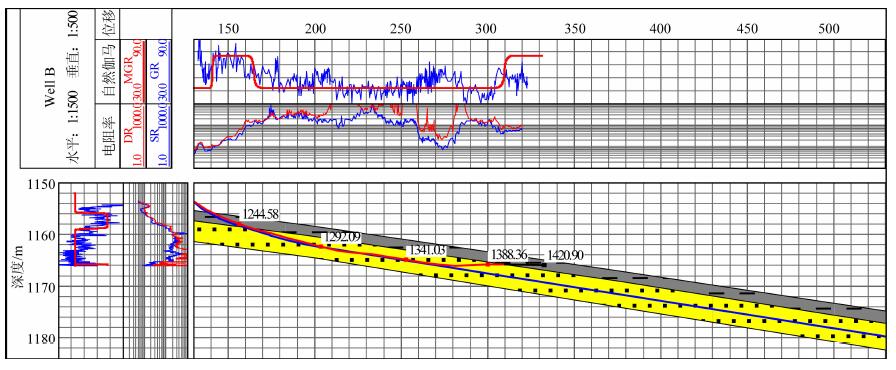
该井为新疆油田某B井, 为泥岩伽马测井值高于砂岩的正常地层.图 14、图 15、图 16是应用本文算法和流程对其处理的结果, 图中每个绘图区域及曲线所表示的意义与图 11相同.
|
图 14 B井地层模型调整前的模型、井眼轨迹及测井曲线综合图 Fig. 14 The strata model, well path and log curves before updating of well B |
|
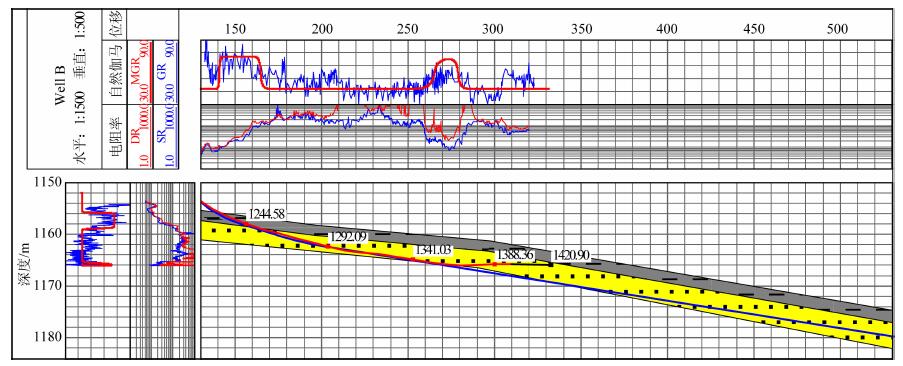
图 15 B井地层模型调整后的模型、井眼轨迹及测井曲线综合图 Fig. 15 The updated strata model, well path and log curve sof well B |
|
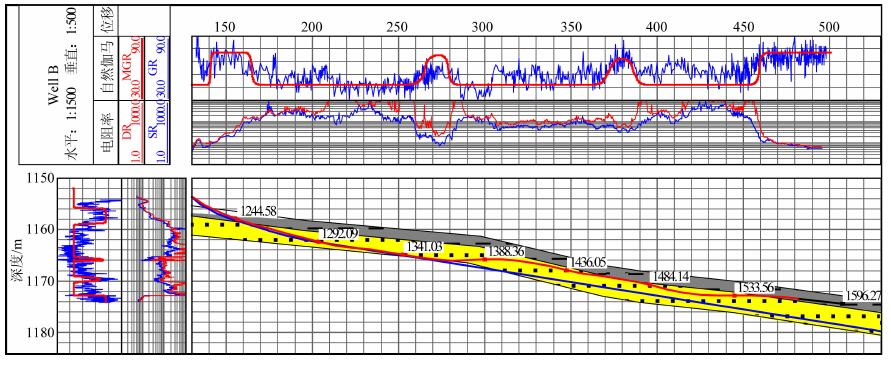
图 16 B井完钻后的模型、井眼轨迹及测井曲线综合图 Fig. 16 The strata model, well path and log curves after well B was finished drilling |
如图 14所示, 根据实钻井眼轨迹和先导地层模型、通过正演得到的伽马测井响应曲线与实测随钻伽马测井曲线大体一致; 但是在水平位移260~280m处, 随钻电阻率测井值明显降低、实际伽马测井值明显高于正演值, 综合判定此处已钻出目的层、进入下部泥岩层.经可视化分析, 调整地层模型、比较正演与实测伽马测井曲线的差异, 在保持原模型趋势下将该处附近地层界面上移2m, 得到如图 15所示结果.图 15中根据调整后的地层模型和实钻井眼轨迹得到的伽马测井正演曲线与实测曲线变化趋势相同, 表明地层界面的调整符合实际地层情况.
图 16为完钻后的最终结果, 可以看到根据更新后的地层模型和实钻轨迹得到的正演伽马测井响应曲线与实际伽马测井曲线形态相同, 综合随钻电阻率测井资料分析认为实时更新后的地层模型正确再现了实际地层形态.
4 结论(1) 利用地层中伽马射线通量衰减方程, 通过积分得到的伽马测井响应正演算法速度快、能满足现场实时正演需求.
(2) 基于地层模型和实钻轨迹, 通过正演得到伽马测井响应曲线并与实测曲线进行对比、可为钻进过程中实时调整地层模型及井眼轨迹提供依据.
(3) 无论泥岩层伽马测井值相对砂岩层为低值还是高值, 本文正演算法都能得到正确结果、在地层模型更新和井眼轨迹优化调整过程中起到较好指导作用, 没有明显误差变化.
(4) 地层模型的实时更新调整要根据钻进情况进行反复修正, 直至正演伽马测井曲线与实测伽马测井曲线形态吻合为止, 并非一次更新调整所能完成.
对于严重扩径和三维各向异性地层情况下的快速正演算法有待另行研究和论述.
致谢本文得到了国家油气科技重大专项"复杂油气藏精细表征及剩余油分布预测"(2011ZX05009-003)与中石油、中石化企业资金资助, 得到了学报编辑部和审稿人的指导, 在此一并致谢.
| [1] | Jackson C E, Ⅲfelder H, Pineda G. Filed Implementation of Geological Steering Techniques Optimizes Drilling in Highly-Deviated and Horizontal Wells. SPE International Conference on Horizontal Well Technology, Calgary, Alberta, Canada, November 1998: SPE 50381. https://www.onepetro.org/conference-paper/SPE-50381-MS |
| [2] | Chabuel H T, Fejerskov M. Geosteering Diagnosis: A New Approach to Monitor the Well Position Within a 3D Geological Model. SPE Annual Technical Conference and Exhibition, San Antonio, Texas, USA, September 2006: SPE 102602-MS. https://www.onepetro.org/conference-paper/SPE-102602-MS |
| [3] | Solomon S T, Ross K C, Burton R C, et al. A multidisciplined approach to designing targets for horizontal wells. Journal of Petroleum Technology , 1994, 46(2): 143-149. DOI:10.2118/25506-PA |
| [4] | Konstantakopoulos I K, Stamataki S K. A Computerized Method for the Real-Time WellPath Monitoring and Placement in 3-D Space. SPE International Conference on Horizontal Well Technology, Calgary, Alberta, Canada, November 1996: SPE 37099-MS. https://www.onepetro.org/conference-paper/SPE-37099-MS |
| [5] | 张伟, 林承焰, 周明晖, 等. 地质模型动态更新方法在关家堡油田的应用. 石油勘与开发 , 2010, 37(2): 220–224. Zhang W, Lin C Y, Zhou M H, et al. Application of geological model dynamic updating method in Guanjiapu oilfield, Dagang. Petroleum Exploration and Development (in Chinese) , 2010, 37(2): 220-224. DOI:10.1016/S1876-3804(10)60027-4 |
| [6] | Efnik M S, Hamawi M, Al Shamri A, et al. Using New Advances in LWD technology for Geosteering and Geologic Modeling. SPE/IADC Middle East Drilling Technology Conference, Abu Dhabi, United Arab Emirates, 1999: SPE 57537-MS. https://www.onepetro.org/conference-paper/SPE-57537-MS |
| [7] | 测井重点实验室编著. 测井新技术培训教材. 北京: 石油工业出版社, 2003 : 186 -194. Well Logging Laboratory. New Logging Technology Training Materials (in Chinese). Beijing: Petroleum Industry Press, 2003 : 186 -194. |
| [8] | 张辛耘, 王敬农, 郭彦军. 随钻测井技术进展和发展趋势. 测井技术 , 2006, 30(1): 10–15. Zhang X Y, Wang J N, Guo Y J. Advances and trends in logging while drilling technology. Well Logging Technology (in Chinese) , 2006, 30(1): 10-15. |
| [9] | 李辉, 刘得军, 刘彦昌, 等. 自适应hp-FEM在随钻电阻率测井仪器响应数值模拟中的应用. 地球物理学报 , 2012, 55(8): 2787–2797. Li H, Liu D J, Liu Y C, et al. Application of self-adaptive hp-FEM in numerical simulation of resistivity logging-while-drilling. Chinese J. Geophys. (in Chinese) , 2012, 55(8): 2787-2797. |
| [10] | 孙向阳, 聂在平, 赵延文, 等. 用矢量有限元方法模拟随钻测井仪在倾斜各向异性地层中的电磁响应. 地球物理学报 , 2008, 51(5): 1600–1607. Sun X Y, Nie Z P, Zhao Y W, et al. The electromagnetic modeling of logging-while-drilling tool in tilted anisotropic formations using vector finite element method. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1600-1607. |
| [11] | 杨震, 范宜仁, 文艺, 等. 三维频率域随钻电磁波测井数值模拟. 地球物理学进展 , 2009, 24(5): 1833–1838. Yang Z, Fan Y R, Wen Y, et al. Three-dimensional numerical simulation of electromagnetic logging-while-drilling tool response in frequency domain. Progress in Geophysics (in Chinese) , 2009, 24(5): 1833-1838. |
| [12] | Yang J, Liu C B, Li Q M, et al. Bed-Boundary Effect Removal to Aid Formation Resistivity Interpretation from LWD Propagation Measurements at All Dip Angles. SPWLA 46th Annual Logging Symposium , 2005. |
| [13] | 杨震, 刘庆成, 岳步江, 等. 随钻电磁波测井中极化角的形成机理及其影响因素模拟分析. 测井技术 , 2010, 34(3): 211–214. Yang Z, Liu Q C, Yue B J, et al. On mechanism of polarization angle of electromagnetic logging while drilling and its influence factors simulation. Well Logging Technology (in Chinese) , 2010, 34(3): 211-214. |
| [14] | 魏宝君, 田坤, 张旭, 等. 定向电磁波传播随钻测量基本理论及其在地层界面预测中的应用. 地球物理学报 , 2010, 53(10): 2507–2515. Wei B J, Tian K, Zhang X, et al. Physics of directional electromagnetic propagation measurements-while-drilling and its application for forecasting formation boundaries. Chinese J. Geophys. (in Chinese) , 2010, 53(10): 2507-2515. |
| [15] | 陈华, 范宜仁, 邓少贵, 等. 水平井中随钻电阻率实时确定地层界面方法. 吉林大学学报(地球科学版) , 2011, 41(5): 1623–1628. Chen H, Fan Y R, Deng S G, et al. Methods for real-time determination of formation boundary with LWD resistivity logs in horizontal wells. Journal of Jilin University (Earth Science Edition) (in Chinese) , 2011, 41(5): 1623-1628. |
| [16] | 史晓锋. 水平井中随钻电阻率测量仪定位和预测地层界面的方法. 测井技术 , 2006, 30(2): 119–122. Shi X F. Methods for orientation of formation layerings and formation boundary prediction with LWD resistivity logs in HZ wells. Well Logging Technology (in Chinese) , 2006, 30(2): 119-122. |
| [17] | 杨锦舟, 魏宝君, 林楠. 倾斜线圈随钻电磁波电阻率测量仪器基本原理及其在地质导向中的应用. 中国石油大学学报(自然科学版) , 2009, 33(1): 44–49. Yang J Z, Wei B J, Lin N. Basic theory of electromagnetic wave resistivity measurement while drilling tool with tilted antennas and its application for geo-steering. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese) , 2009, 33(1): 44-49. |
| [18] | 郝以岭, 杜志强. OnTrak随钻测井资料在冀东油田地质导向中的应用. 测井技术 , 2009, 33(2): 148–149. Hao Y L, Du Z Q. Application of geosteering service based on ontrak MWD/LWD platform in Jidong oilfield. Well Logging Technology (in Chinese) , 2009, 33(2): 148-149. |
| [19] | Mendoza A, Ellis D V, Rasmus J C. Why the LWD and Wireline Gamma Ray Measurements May Read Different Values in the Same Well. First International Oil Conference and Exhibition, Cancun, Mexico, 2006: SPE 101718. https://www.onepetro.org/conference-paper/SPE-101718-MS |
| [20] | Yin H Z, Zhou J J, Guo P J. A Hybrid Solution for Fast 3D Gamma Ray Tool Modeling in High Angle and Horizontal Wells. SPWLA 49th Annual Logging Symposium, Edinburgh, Scotland, 2008: SPWLA 2008-YYY. http://www.freepatentsonline.com/8731888.html |
| [21] | Yin H Z, Han X G, Xu L B, et al. Field and Benchmark Studies of LWD Nuclear Tool Response in High Angle and Horizontal Wells. SPWLA 47th Annual Logging Symposium, Veracruz, Mexico, 2006: SPWLA 2006-AAA. https://www.researchgate.net/publication/237340657_FIELD_AND_BENCHMARK_STUDIES_OF_LWD_NUCLEAR_TOOL_RESPONSE_IN_HIGH_ANGLE_AND_HORIZONTAL_WELLS |
| [22] | 吴文圣, 黄隆基. 三探测器密度测井的Monte Carlo模拟. 地球物理学报 , 2004, 47(1): 164–170. Wu W S, Huang L J. Monte Carlo simulation of three-detector density logging. Chinese J. Geophys. (in Chinese) , 2004, 47(1): 164-170. |
| [23] | 吴文圣, 付赓, 张智, 等. 小井径双源距碳氧比C/O测井的影响因素及处理. 地球物理学报 , 2005, 48(2): 459–464. Wu W S, Fu G, Zhang Z, et al. Study of influence factor for dual-detector C/O logging in slim holes. Chinese J. Geophys. (in Chinese) , 2005, 48(2): 459-464. |
| [24] | 张锋, 徐建平, 胡玲妹, 等. PNN测井方法的蒙特卡罗模拟结果研究. 地球物理学报 , 2007, 50(6): 1924–1930. Zhang F, Xu J P, Hu L M, et al. Monte Carlo simulation result for the pulsed neutron-neutron logging method. Chinese J. Geophys. (in Chinese) , 2007, 50(6): 1924-1930. |
| [25] | Al-Harbi A, Ersoz H, AbdRabAlreda S H. Influence of Sodium/Potassium Formate-Based Drilling Fluids on Nuclear Logs. SPE Latin American and Caribbean Petroleum Engineering Conference, Rio de Janeiro, Brazil, 2005: SPE 94693. http://www.halliburton.com/en-US_tech-papers_public/abstracts/spe_94693.page |
| [26] | 黄隆基. 放射性测井原理. 北京: 石油工业出版社, 1985 : 38 . Huang L J. Radioactive Logging Principle (in Chinese). Beijing: Petroleum Industry Press, 1985 : 38 . |
| [27] | 章晔. 放射性方法勘查. 北京: 原子能出版社, 1990 : 128 -130. Zhang Y. Radioactive Prospecting (in Chinese). Beijing: Atomic Energy Press, 1990 : 128 -130. |
| [28] | DGR Sensor Manual, Sperry-Sun, a Halliburton Company, 1999. |
| [29] | 庞巨丰. 核测井物理基础. 北京: 石油工业出版社, 2005 : 54 -93. Pang J F. Nuclear Logging Physical Basis (in Chinese). Beijing: Petroleum Industry Press, 2005 : 54 -93. |
| [30] | Yin H Z, Guo P J, Alberto M. Comparison of Processing Methods to Obtain Accurate Bulk Density Compensation and Azimuthal Density Image from Dual-detector Gamma Density Measurements in High Angle and Horizontal Wells. SPWLA 49th Annual Logging Symposium, Edinburgh, Scotland, 2008: SPWLA 2008-M. |
| [31] | 王斌, 范晓敏. 围岩对自然伽马测井影响的数值模拟. 吉林大学学报(地球科学版) , 2006, 36(Special): 166–168. Wang B, Fan X M. Application of numerical simulation in the rocks influence the gamma-ray logging. Journal of Jilin University (Earth Science Edition) (in Chinese) , 2006, 36(Special): 166-168. |
| [32] | Lott S J, Dalton C L, Bonnie J, et al. Use of Networked Geosteering Software for Optimum High-Angle/Horizontal Wellbore Placement: Two U. K. North Sea Case Histories. SPE/PS-CIM International Conference on Horizontal Well Technology, Calgary, Alberta, Canada, 2000: SPE 65542. https://www.researchgate.net/publication/254511096_Use_of_Networked_Geosteering_Software_for_Optimum_High-AngleHorizontal_Wellbore_Placement_Two_UK_North_Sea_Case_Histories |
 2013, Vol. 56
2013, Vol. 56