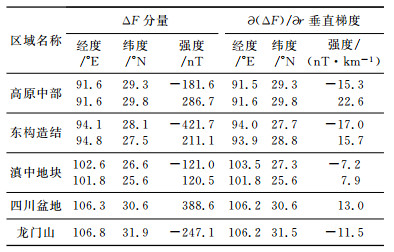
位于青藏高原东南端、印度次大陆东北和缅甸西北角地带的喜马拉雅东构造结(南迦巴瓦)地区, 是印度板块与欧亚大陆碰撞的前缘, 也是喜马拉雅造山带构造变形最强烈的地区之一(图 1方框).它对周围地域的构造运动、物质运移及其动力学过程均有着重要作用[1-4].研究东构造结及周围地区的地壳磁异常空间分布特征, 对认识该地区的地质构造演化及磁性物质分布有重要意义.
|
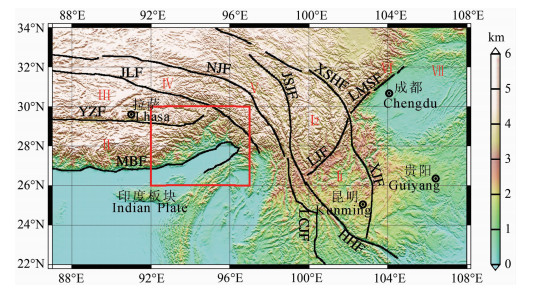
图 1 东构造结周围地区地质构造简图 Ⅰ1-滇中地块Central Yunnan Block; Ⅰ2-川西北地块Northwest Sichuan Block; Ⅱ-喜马拉雅地块Himalayan Block; Ⅲ-拉萨地块Lhasa Block; Ⅳ-羌塘地块Qiangtang Block; Ⅴ-巴颜喀拉地块Bayankala Block; Ⅵ-龙门山地块Longmenshan Block; Ⅶ-四川盆地Sichuan Basin.MBF-主边界断裂Mainboundary Fault; YZF-雅鲁藏布江断裂Yarluzangbu Jiang Fault; JLF-嘉黎断裂Jiali Fault; NJF-怒江断裂Nu jiang Fault; JSJF-金沙江断裂Jinshajiang Fault; XSHF-鲜水河断裂Xianshuihe Fault; LMSF-龙门山断裂LongmenshanFault; LJF-丽江-小金河断裂Lijiang-Xiao jinhe Fault; LCJF-澜苍江断裂Lan cang jiang Fault, HHF-红河断裂Honghe Fault; XJF-小江断裂Xiaojiang Fault. Fig. 1 Schematic tectonic map around the eastern Himalayan tectonic syntaxis |
对东构造结及周围地区地磁场的观测和研究, 过去的工作已有所涉及.例如, 分别利用地面磁测、航空磁测和卫星磁测资料给出的青藏高原磁异常图、中国地磁图都包括了东构造结周围地区[5-9].这些观测和研究给出了青藏高原磁异常分布的基本轮廓.青藏高原地区整体磁异常较弱, 中西部以东西向分布为主, 喜马拉雅造山带分布着强的负磁异常带[10].由于受自然条件限制, 这个地区地面磁测点数目少, 航空磁测并没有完全覆盖东构造结周边地区, 卫星磁测只能反映大尺度异常分布特征.因此, 对这个地区地壳磁场仍然缺乏系统的认识.
随着卫星磁测和数据处理技术的进步, 将卫星、航空、地面和海洋磁测资料融合在一起, 构建地磁场高阶球谐模型, 可以方便地计算地磁场各个要素, 研究地磁场的各种成分及时空演变规律.近10多年来, 构建地磁场高阶球谐模型取得重要进展, 国际上已建立了多种高阶磁场模型.其中一些模型仅使用卫星资料构建, 更多的则是将卫星、航空、地面和海洋磁测资料融合在一起构建高阶地磁场球谐模型[11-16].其中, 波茨坦地磁场模型(POMME)和美国地球物理数据中心(NGDC)给出的NGDC-720模型球谐阶次高达720阶, 并且随着观测资料增加和数据处理方法的改进, 球谐系数随之更新, 给出不同版本的模型.这两种模型采用组合方式给出球谐系数, 低阶球谐项(长波长部分)用卫星磁测、中高阶球谐项(中等波长和短波长部分)则利用卫星、地面、海洋和航空磁测资料给出的地球磁异常网格EMAG2[17-20]构建.例如, NGDC-EMM-720-V3模型, 16~120阶球谐系数是用CHAMP卫星磁测资料构建的岩石圈磁场模型MF6来代替, 121~720阶球谐系数根据EMAG2构建; POMME-6.2模型1~45阶球谐系数使用2000年6月到2009年7月CHAMP卫星磁测资料构建, 46~720阶则取自NGDC-EMM-720-V3模型.此外, 确定121~720阶球谐系数使用的EMAG2网格数据在青藏高原等部分地区缺少航磁资料[20], 在一定程度上影响了模型精度.但在没有航磁测量资料的地区, 模型也还有CHAMP卫星磁测资料, 因此, 它们是到目前为止较为全面的高阶磁场模型.
本文根据波茨坦地磁场模型POMME-6.2[21], 计算东构造结及周围地区地壳磁场总强度ΔF在不同高度的异常分布.利用二维小波变换对地面磁异常进行小波分解, 分析小波细节组合和逼近信号的异常特征.研究磁异常与地质构造的关系, 讨论东构造结对周围地区地壳磁异常分布的影响.
2 地壳磁场计算根据地磁场位函数理论, 地磁位可以表达为球谐级数:
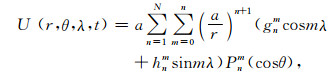
|
(1) |
式中λ和θ分别为经度和余纬, a为地球半径(6371.2 km), r是地心距, Pnm
(cosθ)是n阶m次Schmidt准归一化缔合Legendre函数, gnm和hnm是地磁位的球谐系数.在球坐标系下对磁位函数求导, 可得到地磁场北向X、东向Y和垂直向Z方向3个直角坐标分量[22], 地磁场总强度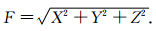
根据地磁场能谱随谐波阶次的变化规律, 通常认为球谐阶次n≤13为地核场, n=14~15为地核和地壳磁场的过渡, n≥16阶主要是地壳磁场[23]. POMME-6.2模型最大截止阶数N=740阶.由于721~740阶球谐系数较小, 几乎为零, 本文计算中取截止阶数N=720阶.对地壳磁场总强度ΔF的计算, 首先分别计算出n=1~720阶的总磁场和n=1~15阶的地核磁场, 再用总磁场减去地核场, 所得差值部分即为地壳磁场ΔF.将地磁场总强度对地心距r求导数[24], 可得到地壳磁场的垂直梯度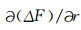
考虑到东构造结对周围地区的影响范围较大, 本文计算区域为22°N-34°N, 87°E-108°E, 计算网格为0.1°×0.1°.在地域上涉及青藏高原中部、东构造结地区、川滇地区、印度北部和缅甸西北部地区.图 2分别给出采用地心球坐标系计算的地表(h=0 km)地壳磁场ΔF及其垂直梯度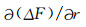
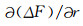

|
图 2 不同高度的地壳磁异常分布图 Fig. 2 Distributions of the crustal magnetic anomaly at different altitudes |
从图 2a可以看出, 研究区地表磁异常分布有明显的地域特点.四川盆地正磁异常强度大、分布广.喜马拉雅造山带、四川盆地北部的龙门山、大巴山地区分布着近东西向的强负磁异常带.东构造结西北部的青藏高原中部分布着近东西向的正负磁异常条带.滇中地块的正负磁异常为团状、带状分布.其他地区磁异常相对较弱, 但在弱磁异常背景下, 东构造结北东向的正负磁异常呈弧形状分布.最外层的弧形状磁异常带大致沿金沙江-红河断裂带分布, 其展布方向(走向)与断裂构造走向基本一致.
地表磁异常ΔF和垂直梯度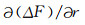
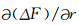
为了定量了解磁异常强弱特点, 表 1列出ΔF和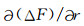
|
|
表 1 地表各地块的ΔF和∂(ΔF)/∂r的主要异常焦点位置和强度 Table 1 The location and intensity of magnetic anomaly centers of ΔF and ∂(ΔF)/∂r for the blocks on the earth′s surface |
通过磁异常的衰减特点, 可以了解磁异常源的埋藏深浅.我们将地表磁异常向上延伸, 计算了地表以上不同高度的磁异常分布.图 2c和图 2d分别给出地表以上25 km和100 km高度的磁异常分布.观察不同高度的磁异常分布可以看出, 随着高度增加, 不同地区的磁异常衰减有明显差异.四川盆地、喜马拉雅-东构造结-龙门山地区的正负磁异常衰退减慢.在100 km高度, 四川盆地正异常为椭圆状分布, 与盆地构造相吻合.其他地区为负异常, 喜马拉雅-东构造结-龙门山地区仍然分布着强负磁异常带, 与青藏高原负异常区连成一片.青藏高原中部和滇中地块带状、团状磁异常衰减快, 在25 km高度处磁异常几乎完全消失, 表明它们是叠加在负异常背景上的浅源局部异常.
3.3 磁异常二维小波分解上述磁异常随高度的变化表明, 不同地区磁异常衰减有较大差异, 反映了磁异常场是地下不同深度层次、规模、形态的磁源体引起的异常的叠加.近年来发展起来的小波变换方法, 可以把位场分解为不同尺度的成分, 在重力场、航磁异常等研究中有较好的应用[25-26].由于局部磁异常埋藏浅, 区域场埋藏深, 它们在不同尺度上小波变换的衰减速率不同.因此, 选择合适的分解尺度, 有可能把它们区分开来.
3.3.1 磁异常二维小波分解特点根据二维小波变换原理[27-28], 可以将位场分解为不同尺度的细节信号Dn[f(x, y)]和逼近信号(光滑近似)An[f(x, y)], 进行N阶小波分解的异常信号可以表示为
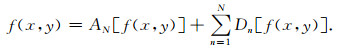
|
(2) |
在地壳磁异常小波分解中, 关键是选择合适的小波函数.通过试算对比几种小波函数, 我们采用正交性较好的Daubechies (db5)小波函数对地面磁异常进行分解[29-31].根据低阶小波细节不变性原理[32], 观察磁异常小波分解的各阶细节和逼近信号分布特点, 选择合适的分解尺度及其组合.利用db5小波分解的地面磁异常结果显示, 1~3阶小波细节异常空间尺度小, 分布形态相近.4~5阶细节异常空间尺度较大, 分布特征类似.因此, 选取小波截止阶数为5阶, 并将1~3阶和4~5阶小波细节分别组合.
图 3(a, b, c)给出地面磁异常1~3阶(D1+D2+ D3)、4~5阶小波细节(D4 +D5)组合和5阶小波逼近(A5)的异常分布图.可以看出, 1~3阶小波细节组合的异常空间尺度较小, 以带状、团状为主.其中, 青藏高原中部的异常为东西向, 龙门山地块的异常为北东向.图 3b显示的4~5阶细节组合, 四川盆地为正异常, 其南北两边为负异常带.喜马拉雅强负异常带北部为与之平行的正异常带, 它一直延伸至东构造结弧顶地区, 并包围着喜马拉雅负异常带.沿东构造结弧顶的北东方向, 分布着正、负相间的弧形状弱异常带.5阶逼近反映的区域异常分布形态简单, 四川盆地为正异常, 其他地区为负异常或弱异常带.此外, 小波细节显示的东构造结北东方向的弧形状异常在5阶逼近中完全消失.

|
图 3 小波组合(左列)和不同波长带(右列)磁异常分布图 Fig. 3 The magnetic anomaly distribution for wavelet (left) and different wavelength bands (right) |
小波变换是一种数学工具, 可以把磁异常分解为不同尺度的成分, 但不能给出各种成分的地球物理意义.为了认识小波分解得到的异常分布的地球物理意义, 我们对小波组合进行径向功率谱分析, 确定小波组合异常对应的磁源深度.并将小波细节组合磁异常与不同波长带的磁异常进行对比分析.根据位场波数域理论, 功率谱斜率增大正比于场源埋藏深度的增加.因此, 由功率谱斜率可以计算出小波细节及逼近对应的场源深度, 使小波分析结果有对应的深度概念.从统计意义上看, 磁异常的径向平均功率谱拟合直线反映异常场源的等效深度[33-34].
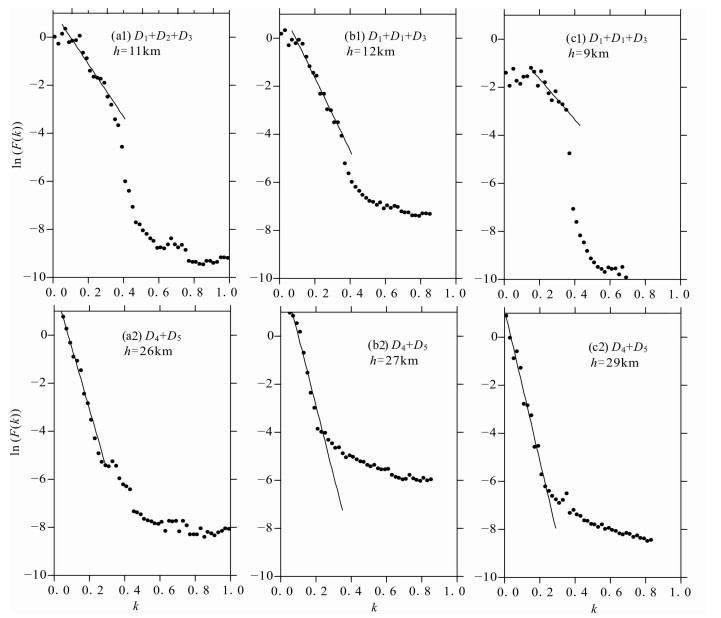
因为研究区磁异常强弱和分布不均匀, 说明磁异常源的规模和深浅不一.根据小波细节组合磁异常的分布特点, 我们将研究区分为青藏高原中部(26°N-34°N, 87°E-97°E)、四川盆地-龙门山(28°N-34°N, 98°E-108°E)和滇中(22°N-28°N, 98°E-108°E)3个片区, 利用径向功率谱方法分别计算各片区磁异常体的等效深度(图 4)[35-36].图 4中a, b和c分别代表高原中部、四川盆地-龙门山和滇中片区.各个片区1~3阶小波细节组合的等效深度为9~12 km之间, 4~5阶小波细节组合等效深度在26~29 km之间.滇中片区1~3阶小波细节组合异常的等效深度相对较浅(9 km), 但4~5阶细节组合异常等效深度相对较深(29 km).从功率谱线性拟合效果看, 4~5阶细节组合优于1~3阶细节组合, 表明上地壳磁源体空间分布的不均性更为强烈.
|
图 4 小波细节组合功率谱图 Fig. 4 The power spectra of the wavelet details reconstruction |
由小波细节组合给出的等效磁源体深度与地震学揭示的地壳分层基本一致.张智等利用地震面波频散重建川滇地区壳幔S波速度[37], 得出云南地区地壳可分为上下两层, 上地壳变化不大, 大多介于10~15 km之间.彭淼等利用接收函数和大地电磁数据联合反演喜马拉雅东构造结地区壳幔结构[38], 给出东构造结中部地区的壳幔结构分为上、中、下3层, 上地壳都存在9~14 km厚的高阻高速层, 中地壳平均埋藏深度为28 km.可以看出, 小波细节1~3阶组合和4~5阶组合的磁源体平均等效深度基本一致.
3.3.3 不同波长带磁异常与小波分解磁异常的对应关系计算地壳磁异常的球谐阶数为16~720阶, 对应的空间波长大约在2500~56 km范围[23].根据地壳磁场能谱变化[10], 地壳磁场可以分为长波长带(16~60阶)、中等波长带(61~220阶)和短波长带(221~720阶).图 3(d, e, f)分别给出3种波长带的磁异常分布.比较不同波长带磁异常与小波分解磁异常可以看出, 1~3阶小波细节组合与短波长带异常、4~5阶小波细节组合与中等波长带异常、5阶逼近与长波长带异常分布形态有很好的对应关系.表明小波分解的磁异常是不同空间波长磁异常的具体反映.
3.4 磁异常与地质构造的联系上述分析表明, 除四川盆地外, 研究区内地壳磁异常都是在负磁或弱磁异常背景上叠加着中短波长的异常, 这些磁异常与地质构造有密切联系.
在东构造结西北的青藏高原中部, 地质、地貌和地球物理场研究表明[7, 39], 大型的东西向构造是最明显的构造特征.喜马拉雅造山带以北的青藏高原中部地区, 东西向的磁异常条带相对较强, 与高原构造走向一致.特别在28°N-32°N, 87°E-94°E之间, 东西向的磁异常条带尤其明显.
在东构造结地区, 由于印度板块以47 mm/a (约NE23°)的速度向青藏高原汇聚[40].特别是印度板块东北角好似一个“尖楔”向北东方向插入高原东南边缘的东构造结地区, 对周边地区产生了重要影响.GPS水平位移[41-42]、地震波速度结构[43-44]、大地电磁观测[45]的研究显示, 东构造结北侧和东侧地块总体上围绕构造结发生顺时针旋转, 形成孤形状构造.在东构造结北东向方向, 小波细节组合和中短波长带的磁异常(图 3)都呈现弧形状、正负相间分布, 反映了中上地壳磁源体呈弧形状构造特征.
在东构造结以东、龙门山-小金河-红河断裂带以西的川西北、滇西、三江造山带地区, 地壳磁异常较弱.大约98°E-101°E范围, 磁异常值较小, 形成近南北向的弱磁异常带.这个地带是我国南北地震带的中南部地区, 也是最年轻的造山带.
由于近南北向俯冲的印度板块和欧亚大陆碰撞, 青藏高原北面受西伯利亚地台阻挡, 物质东流, 受高强度块体四川盆地的阻挡分叉为东北向和东南向.在四川盆地以北的龙门山地区, 反映中上地壳磁源体异常的垂直梯度异常(图 2), 1~3阶小波细节组合和短波长带异常具有明显北东向特征, 与地质构造走向一致.DenghaiBai等[45]通过大地电磁层析成像对青藏高原东南部地区下地壳流进行了研究, 进一步给出了下地壳流的位置.在青藏高原东部存在两条巨大的中下地壳低阻异常带, 一条从拉萨地块沿雅鲁藏布缝合带向东延伸, 环绕喜马拉雅东构造结向南转折; 另一条从羌塘地体沿金沙江-鲜水河断裂带向东延伸, 在四川盆地西缘向南转折, 最后通过小江断裂和红河断裂之间的川滇菱形块体(滇中块体).在四川盆地南部的滇中地块, 正负磁异常相对较强, 以带状和团状形式分布.它们随高度的衰减规律与青藏高原中部的条带状异常相同.由此说明滇中地块磁源体可能是青藏高原物质流向东南的一部分.
对比磁异常与断裂带分布可以看出, 龙门山断裂带、丽江-小金河断裂带和红河断裂带是磁异常强弱的明显分界.而鲜水河断裂带、怒江断裂、澜沧江断裂带两侧的地壳磁异常强弱没有明显差别, 说明这些断裂两侧的磁性物质分布变化不大.
4 结论(1) 根据POMME6.2模型给出的东构造结周边地区地面磁异常有明显的地域特点.四川盆地和东构造结分布有强的正磁异常, 喜马拉雅和龙门山地块分布有强的负磁异常.青藏高原中部和滇中地块磁异常相对较强, 呈带状、团状分布, 其他地区磁异常较弱.
(2) 东构造周围地区的地壳磁异常与地质构造有密切联系.通过对不同高度、不同波长带磁异常分布、小波分解的细节组合和逼近异常分析表明, 东构造结周围地区(除四川盆地外)的磁异常都是在负磁或弱磁异常背景上叠加中短波长的正负磁异常.这些中小尺度磁异常由中、上地壳磁性物质产生, 异常走向与地质构造走向相同.龙门山断裂带、丽江-小金河断裂带和红河断裂带是正负磁异常分界或强弱过渡带.
(3) 东构造结对周围地区地壳磁异常有重要影响.青藏高原中部东西向的磁异常条带, 在东构造结弧顶地区呈弧形状分布, 与地质和相关地球物理场给出的构造形态一致.东构造结地区的正磁异常主要是中上地壳产生的.本文给出的东构造结周围地区地壳磁异常的各种分布形态特征, 为地质和地球物理学研究印度板块与欧亚板块碰撞、青藏高原抬升及其物质运移提供了地壳磁异常依据.
致谢感谢审稿专家提出的宝贵意见.
| [1] | Schoenbohm L M, Burchfiel B C, Chen L Z. Propagation of surface uplift, lower crustal flow, and Cenozoic tectonics of the southeast margin of the Tibetan Plateau. Geology , 2006, 34(10): 813-816. DOI:10.1130/G22679.1 |
| [2] | 王二七, BarchfielB C, 季建清. 东喜马拉雅构造结新生代地壳缩短量的估算及其地质依据. 中国科学(D辑) , 2001, 31(1): 1–9. Wang E Q, Barchfiel B C, Ji J Q. Estimation of Cenozoic crust shortening and its geological evidence in Himalayas structure knot. Science in China (Seies D) (in Chinese) , 2001, 31(1): 1-9. |
| [3] | 宋键, 唐方头, 邓志辉, 等. 喜马拉雅东构造结周边地区主要断裂现今运动特征与数值模拟研究. 地球物理学报 , 2011, 54(6): 1536–1548. Song J, Tang F T, Deng Z H, et al. Study on current movement characteristics and numerical simulation of the main faults around Eastern Himalayan Syntaxis. Chinese J. Geophys. (in Chinese) , 2011, 54(6): 1536-1548. |
| [4] | 滕吉文, 王谦身, 王光杰, 等. 喜马拉雅"东构造结"地区的特异重力场与深部地壳结构. 地球物理学报 , 2006, 49(4): 1045–1052. Teng J W, Wang Q S, Wang G J, et al. Specific gravity field and deep crustal structure of the "Himalayas east structural knot". Chinese J. Geophys. (in Chinese) , 2006, 49(4): 1045-1052. |
| [5] | 安振昌. 青藏高原地磁场模型的研究. 地球物理学报 , 2000, 43(3): 339–345. An Z C. Studies on geomagnetic field models of Qinghai-Xizang plateau. Chinese J. Geophys. (in Chinese) , 2000, 43(3): 339-345. |
| [6] | 贺日政, 高锐, 郑洪伟, 等. 青藏高原中西部航磁异常的匹配滤波分析与构造意义. 地球物理学报 , 2007, 50(4): 1131–1140. He R Z, Gao R, Zheng H W, et al. Matched-filter analysis of aeromagnetic anomaly in mid-western Tibetan Plateau and its tectonic implications. Chinese J. Geophys. (in Chinese) , 2007, 50(4): 1131-1140. |
| [7] | 薛典军, 姜枚, 吴良士, 等. 青藏高原区域重磁异常的东西向分区及其构造地质特征. 中国地质 , 2006, 33(4): 912–919. Xue D J, Jiang M, Wu L S, et al. East-west division of regional gravity and magnetic anomalies on the Qinghai-Tibet plateau and its tectonic features. Geology of China (in Chinese) , 2006, 33(4): 912-919. |
| [8] | 熊盛青, 周伏洪, 姚正煦, 等. 青藏高原中西部航磁概查. 物探与化探 , 2007, 31(5): 404–407. Xiong S Q, Zhou F H, Yao Z X, et al. Aero magnetic survey in central and western Qinghai Tibet Plateau. Geophysics & Geochemical Exploration (in Chinese) , 2007, 31(5): 404-407. |
| [9] | 张昌达. 由卫星磁异常推断西藏高原地壳的磁性特征. 地球物理学进展 , 2002, 17(2): 325–330. Zhang C D. The magnetic characteristics of crust beneath Xizang (Tibetan) plateau deduced from satellite magnetic anomaly. Progress in Geophysics (in Chinese) , 2002, 17(2): 325-330. |
| [10] | Kang G F, Gao G M, Bai C H, et al. Characteristics of the crustal magnetic anomaly and regional tectonics in the Qinghai-Tibet Plateau and the adjacent areas. Sci. China-Earth Sci. , 2012, 55(6): 1028-1036. DOI:10.1007/s11430-011-4323-x |
| [11] | 徐文耀, 白春华, 康国发. 地壳磁异常的全球模型. 地球物理学进展 , 2008, 23(3): 641–651. Xu W Y, Bai C H, Kang G F. Global models of the Earth's crust magnetic anomalies. Progress in Geophysics (in Chinese) , 2008, 23(3): 641-651. |
| [12] | Hemant K, Thébault E, Mandea M, et al. Magnetic anomaly map of the world: merging satellite, airborne, marine and ground-based magnetic data sets. Earth Planet Sci. Lett. , 2007, 260(1-2): 56-71. DOI:10.1016/j.epsl.2007.05.040 |
| [13] | Olsen N, Lühr H, Sabaka T J, et al. CHAOS-a model of the Earth's magnetic field derived from CHAMP, ?rsted and SAC-C magnetic satellite data. Geophys. J. Int. , 2006, 166(1): 67-75. DOI:10.1111/gji.2006.166.issue-1 |
| [14] | Olsen N, Mandea M, Sabaka J T, et al. CHAOS-2 a geomagnetic field model derived from one decade of continuous satellite data. Geophys. J. Int. , 2009, 179(3): 1477-1487. DOI:10.1111/gji.2009.179.issue-3 |
| [15] | Sabaka T J, Olsen N, Purucker M E. Extending comprehensive models of the Earth's magnetic field with rsted and CHAMP Data. Geophys. J. Int. , 2004, 159(2): 521-547. DOI:10.1111/gji.2004.159.issue-2 |
| [16] | Hamoudi M, Thébault E, Lesur V, et al. Geoforschungs Zentrum anomaly magnetic map (GAMMA): A candidate model for the world digital magnetic anomaly map. Geochem. Geophys. Geosyst. , 2007, 8(6). DOI:10.1029/2007GC001638 |
| [17] | Maus S, Rother M, Stolle C, et al. Third generation of the Potsdam magnetic model of the Earth (POMME). Geochem. Geophys. Geosyst. , 2006, 7(7). DOI:10.1029/2006GC001269 |
| [18] | Maus S. An ellipsoidal harmonic representation of Earth's lithospheric magnetic field to degree and order 720. Geochem. Geophys. Geosyst. , 2010, 11: Q06015. DOI:10.1029/2010GC003026 |
| [19] | Maus S, Lühr H, Rother M, et al. Fifth-generation lithospheric magnetic field model from CHAMP satellite measurements. Geochem. Geophys. Geosyst. , 2007, 8(5). DOI:10.1029/2006GC001521 |
| [20] | Maus S, Barckhausen U, Berkenbosch H, et al. EMAG2: A2-arc min resolution Earth Magnetic Anomaly Grid compiled from satellite, airborne, and marine magnetic measurements. Geochem. Geophys. Geosyst. , 2009, 10(8): Q08005. DOI:10.1029/2009GC002471 |
| [21] | Maus S, Manoj C, Rauberg J, et al. NOAA/NGDC candidate models for the 11th generation international geomagnetic reference field and the concurrent release of the 6th generation Pomme magnetic model. Earth, Planets and Space , 2010, 62(10): 729-735. DOI:10.5047/eps.2010.07.006 |
| [22] | 徐文耀. 地球电磁现象物理学. 合肥: 中国科技大学出版社, 2009 : 93 -101. Xu W Y. Physics of Electromagnetic Phenomena of the Earth (in Chinese). Hefei: University of Science and Technology of China Press, 2009 : 93 -101. |
| [23] | Thébault E, Purucker M, Kathryn A, et al. The magnetic field of the Earth's lithosphere. Space Sci. Rev. , 2010, 155(1-4): 95-127. DOI:10.1007/s11214-010-9667-6 |
| [24] | 高国明, 康国发, 白春华, 等. 主磁场梯度的空间分布和长期变化特征. 地球物理学报 , 2012, 55(8): 2651–2659. Gao G M, Kang G F, Bai C H, et al. Characteristics of the spatial distribution and the secular variation of the main geomagnetic field gradients. Chinese J. Geophys. (in Chinese) , 2012, 55(8): 2651-2659. |
| [25] | Hornby P, Boschetti F, Horowitz H G. Analysis of potential field data in the wavelet domain. Geophys. J. Int. , 1999, 137(1): 175-196. DOI:10.1046/j.1365-246x.1999.00788.x |
| [26] | 武奥, 孟小红, 李淑玲. 小波分析及其在我国地球物理学研究中的应用进展. 地球物理学进展 , 2012, 27(2): 750–760. Wu A, Meng X H, Li S L. Wavelet analysis and its application in geophysics of China. Progress in Geophysics (in Chinese) , 2012, 27(2): 750-760. |
| [27] | 侯遵泽, 杨文采. 中国重力异常的小波变换与多尺度分析. 地球物理学报 , 1997, 40(1): 85–95. Hou Z Z, Yang W C. Wavelet transform and multi-scale analysis on gravity anomalies of China. Chinese J. Geophys. (in Chinese) , 1997, 40(1): 85-95. |
| [28] | Chambodut A, Panet I, Mandea M, et al. Wavelet frames an alternative to spherical harmonic representation of potential fields. Geophys. J. Int. , 2005, 163(3): 875-899. DOI:10.1111/gji.2005.163.issue-3 |
| [29] | Daubechies I. The wavelet transform, time-frequency localization and signal analysis. IEEE Transactions on Information Theory , 1990, 36(5): 961-1006. DOI:10.1109/18.57199 |
| [30] | Daubechies I, Sweldens W. Factoring wavelet transforms into lifting steps. J. Fourier Anal. Appl. , 1998, 4(3): 247-269. DOI:10.1007/BF02476026 |
| [31] | Marlet G, Sailhac F, Moreau F, et al. Characterization of geological boundaries using 1-D wavelet transform on gravity data: Theory and application to the Himalayas. Geophysics , 2001, 66(4): 1116-1129. DOI:10.1190/1.1487060 |
| [32] | 侯遵泽, 杨文采. 塔里木盆地多尺度重力场反演与密度结构. 中国科学(D辑) , 2011, 54(3): 399–409. Hou Z Z, Yang W C. Multi-scale inversion of density structure from gravity anomalies in Tarim Basin. Science in China (Seies D) (in Chinese) , 2011, 54(3): 399-409. DOI:10.1007/s11430-011-4169-2 |
| [33] | Bhattacharyya B K, Leu L K. Spectral analysis of gravity and magnetic anomalies due to two-dimensional structures. Geophysics , 1975, 40(6): 993-1013. DOI:10.1190/1.1440593 |
| [34] | Spector A, Grant F S. Statistical models for interpreting aeromagnetic data. Geophysics , 1970, 35(2): 293-302. DOI:10.1190/1.1440092 |
| [35] | 张先, 赵丽. 功率谱用于计算不同尺度磁性体场源深度的分析. 物探与化探 , 2007, 31(Suppl.): 53–56. Zhang X, Zhao L. An analysis of the power spectrum for computing field source depths of magnetic bodies of different scales. Geophysical & Geochemical Exploration (in Chinese) , 2007, 31(Suppl.): 53-56. |
| [36] | Vallée M A, Keating R S, Smith R S, et al. Estimating depth and model type using the continuous wavelet transform of magnetic data. Geophysics , 2004, 69(1): 191-199. DOI:10.1190/1.1649387 |
| [37] | 张智, 陈赟, 李飞. 利用地震面波频散重建川滇地区壳幔S波速度. 地球物理学报 , 2008, 51(4): 1114–1122. Zhang Z, Chen Y, Li F. Reconstruction of the S-wave velocity structure of crust and mantle from seismic surface wave dispersion in Sichuan-Yunnan region. Chinese J. Geophys. (in Chinese) , 2008, 51(4): 1114-1122. |
| [38] | 彭淼, 谭捍东, 姜枚, 等. 利用接收函数和大地电磁数据联合反演南迦巴瓦构造结中部地区壳幔结构. 地球物理学报 , 2012, 55(7): 2281–2291. Peng M, Tan H D, Jiang M, et al. Joint inversion of receiver functions and magnetotelluric data: Application to crustal and mantle structure beneath central Namche Barwa, eastern Himalayan syntaxis. Chinese J. Geophys. (in Chinese) , 2012, 55(7): 2281-2291. |
| [39] | 张进, 马宗晋. 西藏高原西、中、东的分段性及其意义. 地质学报 , 2004, 78(2): 218–227. Zhang J, Ma Z J. East-West segmentation of the Tibetan plateau and its implication. Acta Geologica Sinica (in Chinese) , 2004, 78(2): 218-227. |
| [40] | Paul J, Bürgmann R, Gaur V K, et al. The motion and active deformation of India. Geophysical Research Letters , 2001, 28(4): 647-650. DOI:10.1029/2000GL011832 |
| [41] | 曹建玲, 石耀霖, 张怀, 等. 青藏高原GPS位移绕喜马拉雅东构造结顺时针旋转成因的数值模拟. 科学通报 , 2009, 54(8): 1398–1410. Cao J L, Shi Y L, Zhang H, et al. Numerical simulation of GPS observed clockwise rotation around the eastern Himalayan syntax in the Tibetan Plateau. Chinese Science Bulletin (in Chinese) , 2009, 54(8): 1398-1410. |
| [42] | Wang Q, Zhang P Z, Freymueller J T, et al. Present-day crustal deformation in China constrained by global positioning system measurements. Science , 2001, 294(5542): 574-577. DOI:10.1126/science.1063647 |
| [43] | 崔仲雄, 裴顺平. 青藏高原东构造结及周边地区上地幔顶部Pn速度结构和各向异性研究. 地球物理学报 , 2009, 52(9): 2245–2254. Cui Z X, Pei S P. Study on Pn velocity and anisotropy in the upper most mantle of the Eastern Himalayan syntaxis and surrounding regions. Chinese J. Geophys. (in Chinese) , 2009, 52(9): 2245-2254. |
| [44] | Wang C Y, Han W B, Wu J P, et al. Crustal structure beneath the eastern margin of the Tibetan plateau and its tectonic implications. J. Geophys. Res. , 2007, 112: B07307. DOI:10.1029/2005JB003873 |
| [45] | Bai D H, Unsworth M J, Meju M A, et al. Crustal deformation of the eastern Tibetan plateau revealed by magnetotelluric imaging. Nature Geoscience , 2010, 3(5): 358-362. DOI:10.1038/ngeo830 |
 2013, Vol. 56
2013, Vol. 56