航空电磁法是一种基于机载方式,以电磁感应为基础的地球物理探测方法,广泛用于油气探测、矿体勘察和地下水普查等方面.根据机载形式,航空电磁系统可分为固定翼航空电磁系统和直升机航空电磁系统.与直升机时间域航空电磁系统相比,固定翼航空电磁系统具有探测深度深、工作效率高等特点.航空电磁系统在飞行探测过程中,由于飞机姿态、速度、风速等因素,引起线圈俯仰、摇摆、偏航旋转以及吊舱摆动,导致系统参数发生改变,严重影响观测数据的一致性[1-5].
Holladay等[6]在利用直升机时间域航空电磁系统探测冰层厚度时,提出吊舱摆动不仅引起接收线圈姿态发生改变,同时引入雷达高度计误差;Deszcz-Pan等[7]讨论了直升机吊舱摆动与反演结果误差的关系;Yin等[8]利用直升机频率域航空电磁正演算法,研究了吊舱姿态变化对航空电磁响应的影响,并给出了几何校正方法;2010年,嵇艳鞠[9]采用几何校正方法实现了直升机时间域航空电磁数据的姿态校正;Davis等[10-11]利用视频信息及GPS信息,研究了频率域直升机航空电磁系统吊舱的周期性摆动特征及由此带来的高度误差,并给出了高度随吊舱摆动变化的解析表达式和吊舱摆动校正的滤波算法.但上述文献中关于姿态变化和吊舱摆动的研究,均针对直升机航空电磁探测系统,由于直升机航空电磁系统发射线圈与接收线圈固定在同一支架上,在实际飞行过程中,发射线圈与接收线圈的姿态角度相同,且其相对位置不变,因此直升机航空电磁系统线圈的姿态变化与校正方法相对简单[8-9].
固定翼时间域航空电磁系统采用偶极-偶极方式[12],发射线圈架设于飞机四周,接收吊舱以吊绳连接,悬挂在飞机后下方.在实际飞行过程中,发射线圈与接收线圈可能产生不同的姿态,同时由于吊舱摆动,其相对位置(即系统的收发距)也发生变化.因此,当固定翼航空电磁系统线圈姿态以及吊舱摆动状态发生变化时,发射磁矩方向、接收分量方向和位置以及系统的收发距均发生改变.国内外学者对固定翼航空电磁系统的线圈姿态以及吊舱摆动的影响研究较少.Brodie和Sambridge[13-15]指出固定翼时间域航空电磁系统的线圈姿态和吊舱摆动状态对数据反演结果影响严重.但关于固定翼时间域航空电磁系统的线圈旋转及吊舱摆动对电磁响应影响分析与校正方法的研究,尚未见相关文献.
本文基于固定翼时间域航空电磁正演理论,采用层状大地模型,推导了任意发射、接收线圈姿态角度以及任意吊舱摆动角度情况下的固定翼航空三分量电磁响应计算表达式,分别研究了发射线圈、接收线圈的旋转姿态和吊舱摆动对x分量和z分量接收线圈接收到的电磁响应的影响,分析了姿态角度和摆动角度同时存在时对z分量接收线圈接收到电磁响应的影响.提出了相应的校正算法,并通过准二维大地模型校正前后反演结果与理论模型的对比,验证了方法的正确性.
2 正演计算方法
为计算固定翼时间域航空电磁响应,建立如图 1所示系统坐标系,原点为发射线圈中心在地面的投影,飞机飞行方向为x轴方向.发射线圈中心位于(0,0,h0),接收线圈中心位于(x0,y0,z0),系统的水平收发距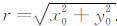
若发射线圈内通以角频率为ω,强度为I=eiωt的电流,则接收线圈(x0,y0,z0)处的三分量二次磁场频率域表达式为[12]

|
(1) |
式中m为发射磁矩矢量,G为格林张量,
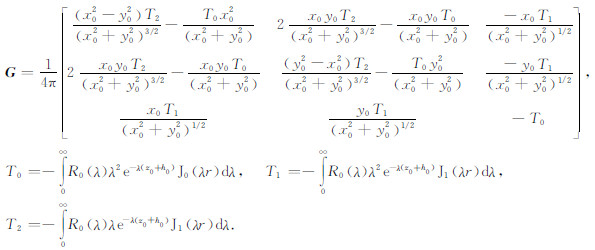
|
其中,J0和J1分别为零阶和一阶贝塞尔函数,λ为积分变量,反射系数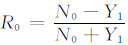
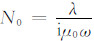

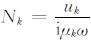

当固定翼航空电磁系统在平稳状态下(图 1)飞行测量时,发射磁矩m0为z方向,三分量接收线圈接收到的磁场分别为x、y、z方向,接收线圈(x0,y0,z0)处的二次场三分量表达式为但是,在实际飞行测量过程中,固定翼航空电磁系统很难保持在平稳状态下飞行,当线圈旋转或吊舱摆动时,不能采用式(2)计算接收线圈接收到的二次场响应,因此本文推导了发射线圈姿态、接收线圈姿态和吊舱的摆动状态改变时,三分量接收线圈接收到的二次场电磁响应表达式.

|
图 1 固定翼航空电磁系统坐标系示意 Fig. 1 Sketch of coordinates of the fixed-wing time-domain electromagnetic system |
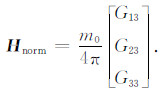
|
(2) |
但是,在实际飞行测量过程中,固定翼航空电磁系统很难保持在平稳状态下飞行,当线圈旋转或吊舱摆动时,不能采用式(2)计算接收线圈接收到的二次场响应,因此本文推导了发射线圈姿态、接收线圈姿态和吊舱的摆动状态改变时,三分量接收线圈接收到的二次场电磁响应表达式.
2.1 发射、接收线圈旋转线圈绕x轴旋转,为摇摆(roll)旋转(逆时针为正),旋转前后线圈平面间的角度δR即为摇摆姿态角度;绕y轴旋转,产生俯仰(pitch)姿态角度δP;绕z轴旋转,产生偏航(yaw)姿态角度δY [6].文献[8]采用双直角坐标系变换算法,通过线性变换将旋转向量aR表示为系统坐标系下的向量aO,即

|
(3) |
其中,旋转矩阵R可由线圈各姿态角度的三角函数计算,
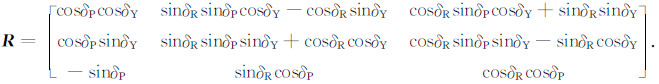
|
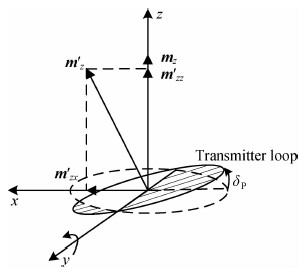
发射线圈产生姿态旋转,使发射磁矩方向发生变化.以z分量发射线圈俯仰姿态为例,如图 2所示.系统平稳飞行时z分量发射线圈(虚线)的发射磁矩mz只含有z分量;线圈发生俯仰旋转后,发射磁矩m′z不仅存在z分量发射磁矩m′zz,同时产生x分量发射磁矩m′zx.根据式(3),旋转后的发射磁矩m′z在系统坐标系下可表示为RTXm′z(RTX为仅包含发射线圈俯仰姿态角度的旋转矩阵),即RTXm′z=sinδP·m′z+cosδP·m′z=m′zx+m′zz.因此,当发射线圈同时产生摇摆、俯仰和偏航姿态旋转后,在系统坐标系下,三分量发射磁矩m′可表示为
|
图 2 发射线圈俯仰旋转磁矩变化示意 Fig. 2 Change of transmitter loop magnetic moment |

|
(4) |
式中RTX为由发射线圈姿态角度计算的旋转矩阵.
接收线圈姿态改变,引起接收分量的方向发生变化.x分量接收线圈俯仰姿态如图 3所示.系统平稳飞行时,x分量接收线圈(虚线)只接收到x分量磁场Hx;线圈发生俯仰后,x分量接收线圈不仅接收到系统坐标系下的x分量电磁响应H′xx,而且接收到z分量电磁响应H′xz,即H′x.由式(3),三分量接收线圈旋转后接收到的电磁响应H′在系统坐标系下可表示为H=RRXH′,则三分量接收线圈旋转后,接收到的磁场H′为
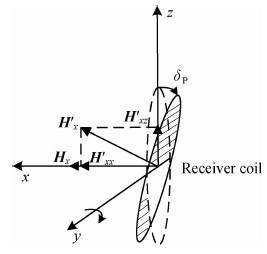
|
图 3 接收线圈俯仰旋转线圈接收到的电磁响应变化示意 Fig. 3 Change of receiver coil electromagnetic response |
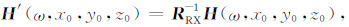
|
(5) |
式中RRX是由接收线圈姿态角度计算的旋转矩阵,且正定矩阵RRX满足RRX-1=RRXT.
根据式(4)、(5)得到,当发射线圈、接收线圈姿态以各自的姿态角度发生旋转时,三分量接收线圈接收到的二次场表达式为
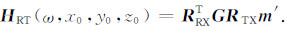
|
(6) |
吊舱的摆动状态可分解为沿飞行方向的摆动(即同向摆动)和沿飞行正交方向的摆动(垂向摆动),如图 4、图 5所示.吊舱摆动改变了接收线圈相对于发射线圈的位置,即系统的水平与垂直收发距发生变化,在正演计算公式(1)中,表现为接收线圈坐标(x0,y0,z0)的变化.

|
图 4 吊舱同向摆动示意 Fig. 4 In-line swing of the bird |

|
图 5 吊舱垂向摆动示意 Fig. 5 Cross-line swing of the bird |
由图 4可以看到,吊舱沿飞行方向前后摆动时(向前摆动为负,向后摆动为正),产生摆动角度α.根据几何关系,同向摆动情况下,接收线圈坐标(x′0,y′0,z′0)为
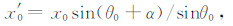
|
(7) |

|
(8) |

|
(9) |
其中θ0为平稳飞行时悬绳与z轴的夹角.
沿飞机飞行方向观察,如图 5(后视图)所示,吊舱沿飞行正交方向左右摆动时(向左摆动为正,向右摆动为负),产生摆动角度β.同理,可得到接收线圈坐标(x′0,y′0,z′0)
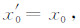
|
(10) |

|
(11) |
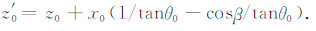
|
(12) |
整理式(7)-式(12),得到吊舱摆动前后,接收线圈位置的变化关系,即

|
(13) |
将式(13)代入式(1)格林张量G中,得到吊舱发生摆动时的格林张量Gswing为
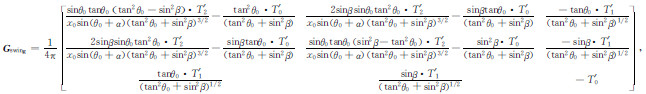
|
其中
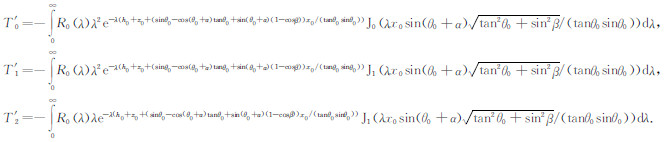
|
当吊舱发生摆动时,三分量接收线圈内接收到的二次场表达式为

|
(14) |
综合式(6)、(14)得到,固定翼航空电磁系统在任意发射、接收线圈姿态角度和任意吊舱摆动角度情况下,三分量接收线圈接收到的二次场频域响应HRTS为

|
(15) |
s代替式(15)中jω,得到航空电磁响应的s域表达式:HRTS(s)=HRTS(ω)|jω=s,则阶跃电流的s域响应可表示为HRTS=HRTS(s)/s.
由于接收线圈内的感应电动势vRTS(t)=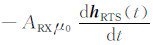

|
(16) |
式(16)中的拉普拉斯逆变换通过G-S变换[19]计算,格林张量中零阶和一阶贝赛尔函数的无限积分(汉克尔变换)分别利用Guptasarma120点和140点数字滤波算法[20-21]计算.
3 吊舱摆动、发射和接收线圈姿态对航空电磁响应的影响分析设航空电磁系统平稳飞行时,z分量发射线圈距离地面高度h0=100 m,三分量接收线圈位于(70,0,70)m,悬绳长L=76 m,系统水平收发距r=70m,悬绳与z轴的夹角θ0=66.8°.发射和接收线圈的有效面积为归一化面积即ATX=1 m2,ARX=1 m2,阶跃发射电流强度I=1 A.三层大地模型的各层电导率分别为σ1=0.02 S/m,σ2=0.2 S/m,σ3=0.02 S/m,厚度d1=50 m,d2=50 m,d3→ ∞,各层磁导率与空气磁导率一致,即μ1=μ2=μ3=μ0.
为研究不同接收线圈姿态和吊舱摆动状态对航空电磁响应的影响,将非平稳飞行探测状态(vRTS)与平稳状态(vnorm)在某一时刻的感应电动势(正比于电磁响应)的比值,定义为响应系数K

|
(17) |
响应系数K表示非平稳飞行时的电磁响应为平稳飞行状态的K倍,当K>1时,非平稳大于平稳状态的电磁响应;反之,则小于平稳状态的电磁响应.
本文以电流关断后0.14 ms采样时刻为例,计算了发射、接收线圈各姿态角度(由于发射线圈偏航姿态角度对接收线圈电磁响应无影响,此处省略)及摆动角度在-20~20°之间变化时的K值,结果如图 6所示.可以看到,线圈旋转以及吊舱摆动对z分量、x分量接收线圈接收到的电磁响应均有影响,且角度变化越大,影响(K值)越大.图 6a显示,吊舱同向摆动对z分量线圈接收到的电磁响应值影响最大,且呈现准线性趋势,吊舱向前摆动角度每增大5°,电磁响应增加量为平稳飞行时电磁响应的0.12倍;向后摆动角度每增大5°,电磁响应减小量略小.接收线圈俯仰姿态角度与发射线圈俯仰姿态角度的影响居于其次,电磁响应随接收线圈俯仰角的正向增大而减小,随发射线圈俯仰角的正向增大而增大,角度负向增大变化趋势相反.吊舱垂向摆动以及发射线圈、接收线圈的摇摆姿态角度对z分量接收线圈接收到的电磁响应影响较弱;接收线圈偏航姿态角度对z分量接收线圈接收到的电磁响应无影响.由图 6b可以看到,接收线圈俯仰角度对x分量接收线圈接收到的电磁响应影响最大,但变化规律与z分量接收线圈相反,x分量接收线圈接收到的电磁响应随接收线圈俯仰角的正向增大而增大;吊舱同向摆动角度与发射线圈俯仰姿态角度的影响居于其次,且变化规律与z分量接收线圈的类似.综上,可以得出发射线圈、接收线圈的俯仰姿态和吊舱同向摆动对航空电磁响应影响最大.

|
图 6 K值随吊舱摆动角度和发射、接收线圈姿态角度的变化规律 Fig. 6 Changes of K due to transmitter loop rotation, receiver coils rotation and swinging of the bird |
在实际飞行测量过程中,线圈旋转以及吊舱摆动可能会同时存在.根据各角度单独变化时对电磁响应的影响情况,本文计算了发射线圈、接收线圈的俯仰姿态角度和吊舱同向摆动角度同时存在时,对z分量接收线圈接收到的电磁响应的影响.图 7给出了三个角度在-20~20°之间变化时,任意组合情况下的K值,x轴为接收线圈俯仰姿态角度,y轴为发射线圈俯仰姿态角度,z轴为吊舱同向摆动角度.可以看出,随吊舱同向摆动角度和接收线圈俯仰角度的负向增大、发射线圈俯仰角度的正向增大,z分量接收线圈接收到的电磁响应呈增大趋势;反之,电磁响应呈减小趋势,其变化规律与各角度单独作用时一致.图中Plane1是发射线圈俯仰姿态角度为-10°时,接收线圈俯仰姿态角度和吊舱同向摆动角度分别在-20°~20°范围内变化情况下的K值. Plane1的色彩沿z轴呈条带状变化,因此,可以得出z分量接收线圈接收到的电磁响应随吊舱同向摆动变化更大.在接收线圈俯仰姿态角度、发射线圈俯仰姿态角度及吊舱摆动角度分别为-20°、-10°和-20°时,响应系数值最大,为1.37;三个角度分别为20°、-10°和20°时,响应系数值最小,为0.52. Plane1与Plane2交线是发射线圈和接收线圈俯仰姿态角度都为-10°时,吊舱同向摆动角度对z分量接收线圈内电磁响应的影响,吊舱摆动角度从-20°~20°变化时,K值从1.36变化到0.70,与图 6a中×线变化规律相似.当接收线圈俯仰姿态角度、发射线圈俯仰姿态角度及吊舱摆动角度分别为-20°、20°和-20°时,电磁响应为平稳飞行时的1.68倍,测量误差达到68%.

|
图 7 吊舱摆动角度和发射、接收线圈姿态角度同时存在时K值三维切片图 Fig. 7 3D slice graph of K for co-existing transmitter loop pitch, receiver coils pitch and in-line swing angles |
通过以上分析,若将非平稳状态下的电磁响应数据除以相应的响应系数K,可获得系统平稳飞行状态下的电磁响应,从而实现了线圈姿态以及吊舱摆动的校正.但从正演公式可知,响应系数K与大地电导率有关.为此,本文分别计算了当接收线圈的俯仰角度为-5°、-10°、-15°、-20°时,电导率在0.0002~100 S/m范围的均匀半空间模型的响应系数K,如图 8所示.明显看出,对于固定翼电磁探测系统,K随大地电导率的增大而增大,但变化趋势缓慢.特别当电导率在0.0002~0.001 S/m及1~100 S/m之间变化时,K值几乎与电导率无关;而当电导率在0.001~1 S/m时,K值随电导率的对数变化呈准线性趋势,如俯仰角度为-10°时,电导率每增大10倍,K仅增大0.025.则在10倍电导率范围内的大地模型,K可近似为同一个值,因此可以采用同一个K值进行校正.

|
图 8 不同大地电导率对K值的影响 Fig. 8 Change of K due to different earth conductivities |
为研究校正时不同电导率的K值对校正结果的影响,以电导率σ1=0.02 S/m、σ2=0.2 S/m、σ3=0.02 S/m,厚度d1=100 m、d2=50 m、d3→∞的三层大地模型为例进行说明.设非平稳飞行测量时,接收线圈俯仰角度为3°,吊舱同向摆动角度为12°,分别计算了平稳与非平稳的电磁响应,如图 9所示,其均方相对误差为3.05%.以电导率为0.008~0.08 S/m的均匀半空间模型的响应系数K对其进行校正,结果见图 9中多种颜色曲线.可以看出,层状模型的非平稳飞行测量数据,在利用不同电导率模型的响应系数进行校正时,均获得与平稳飞行数据基本一致的校正结果,校正后数据均方相对误差如表 1所示.

|
图 9 利用不同电导率大地模型的K值校正后电磁响应曲线 Fig. 9 Electromagnetic response curves corrected by K for different earth conductivity models |
|
|
表 1 不同电导率模型K值校正后与平稳飞行时电磁响应的均方相对误差 Table 1 Relative mean-square-root errors of electromagnetic response curves corrected by different K for different earth conductivity models |
因此,固定翼航空电磁系统线圈姿态与吊舱摆动的校正,仅需要已知线圈旋转角度、吊舱摆动角度信息和大地电导率的大致范围.在实际应用中,线圈旋转角度、吊舱摆动角度可通过视频和GPS进行记录[8];大地电导率信息可根据已知的地质资料、CDI(Conductivity Depth Imaging)成像结果[22-23]或未校正数据的反演结果确定.但是,若反演获得的电导率信息与校正模型电导率值相差较大,则需利用初步反演结果的电导率信息再次计算K值,并进行校正,经反复迭代直到满足精度要求,即可实现精确校正.
本文采用50个三层大地模型相互连接,仿真构造准二维倾斜导电夹层大地模型,如图 10a所示.中间导电夹层电导率为0.2 S/m,厚度为50 m,埋深从50 m变化到150 m,周围基岩电导率为0.02 S/m.根据文献[10]中RESOLVE系统在维多利亚Sunraysia地区实测飞行时,记录的接收线圈俯仰姿态角度和吊舱摆动角度信息,经式(16)计算了固定翼航空电磁系统的z分量电磁响应数据,并在数据中加入10%的高斯噪声.

|
图 10 校正前后反演结果对比图 (a)大地准二维理论模型;(b)校正前;(c)校正后. Fig. 10 Comparison of pseudo-2D models before and after correction inversions with Occam′s (a) Pseudo-2D earth model; (b) Before correction; (c) After correction. |
采用二阶粗糙度因子的Occam方法[24-25]对其反演,初始模型采用电导率为0.1 S/m的均匀半空间,反演结果如图 10b所示,黑色虚线示意了理论模型的导电夹层位置.利用图 10b中反演结果的大地电导率信息,计算相应响应系数K,对非平稳状态下的仿真数据进行校正,校正后电磁响应数据与平稳飞行时基本一致,对其进行反演,结果如图 10c所示.对比图 10b、10c可以看出,校正前反演结果对地下导电薄层的埋深及厚度信息描述不准确,与理论模型存在一定偏差,尤其在第1~20测点,导电薄层深度明显变深,且厚度变薄.计算了各测点各层电导率反演结果相对均方误差的平均值,数据校正前反演结果平均相对均方误差为46.5%,校正后,反演结果平均相对均方误差达到13.4%,提高了33.1%.
5 结论本文根据电磁场理论,推导了固定翼航空电磁系统在发射、接收线圈旋转以及吊舱摆动情况下,三分量接收线圈接收到的电磁响应的计算表达式.该表达式以发射、接收线圈的双旋转矩阵以及摆动格林张量的形式,建立了线圈旋转以及吊舱摆动的数学模型,揭示了线圈旋转及吊舱摆动产生的发射磁矩方向、接收分量方向以及系统收发距的变化实质.
对于固定翼航空电磁系统,吊舱同向摆动、接收线圈和发射线圈的俯仰旋转对航空电磁响应的影响最大,且角度变化越大,对电磁响应的影响越大.吊舱同向摆动对z分量接收线圈接收到的电磁场影响最大,由于同向摆动直接改变系统的水平和垂直收发距,离发射线圈越近,接收高度越低,响应越大;而接收线圈的俯仰旋转对x分量接收线圈接收到的电磁场影响最大,由于x分量接收线圈绕y轴旋转时,引入与发射磁矩方向一致的幅度较大的z分量.
在实际应用中,当固定翼航空电磁系统精确记录线圈姿态角度以及吊舱摆动角度时,可根据本文推导的响应系数进行校正.对于直升机频率域航空电磁系统,其偶极距约为飞机的飞行高度的1/4,可以将发射、接收偶极近似为重叠偶极,消除了大地电性参数对响应系数的影响[4],但固定翼航空电磁探测系统的收发距较大,不满足重叠偶极近似条件,难以消除大地电性参数对响应系数的影响.由于大地电导率对响应系数的影响较小,则固定翼航空电磁系统计算响应系数时,可根据地质资料、CDI成像结果或测量数据的反演结果确定大地电导率范围.文中采用10倍电导率范围内的多组均匀半空间模型计算的响应系数,对层状模型的单测点off-time电磁数据进行校正,校正误差均在0.36%内,满足实际需要.准二维模型仿真实例校正前后的反演结果说明,数据校正有效地去除了固定翼航空电磁系统中由于线圈旋转和吊舱摆动对反演结果的影响,提高了反演精度.
致谢感谢吉林大学地球信息探测仪器教育部重点实验室提供了研究平台,感谢吉林大学时间域航空电磁组嵇艳鞠老师和刘长胜老师在线圈姿态及校正问题中给予的指导.
| [1] | Annan A P. Effect of differential transmitter/receiver motion on airborne transient EM interpretation. 53rd Annual International Meeting, Society Exploration Geophysics, Expanded Abstract, 1983: 622-623. |
| [2] | 薛国强, 李貅, 底青云. 瞬变电磁法理论与应用研究进展. 地球物理学进展 , 2007, 22(4): 1195–1200. Xue G Q, Li X, Di Q Y. The progress of TEM in theory and application. Progress in Geophysics (in Chinese) , 2007, 22(4): 1195-1200. |
| [3] | 赵国泽, 陈小斌, 汤吉. 中国地球电磁法新进展和发展趋势. 地球物理学进展 , 2007, 22(4): 1171–1180. Zhao G Z, Chen X B, Tang J. Advanced geo-electromagnetic methods in China. Progress in Geophysics (in Chinese) , 2007, 22(4): 1171-1180. |
| [4] | 张保祥, 刘春华. 瞬变电磁法在地下水勘查中的应用综述. 地球物理学进展 , 2004, 19(3): 537–542. Zhang B X, Liu C H. Summarization on applications to groundwater exploration by using transient electromagnetic methods. Progress in Geophysics (in Chinese) , 2004, 19(3): 537-542. |
| [5] | 嵇艳鞠, 林君, 朱凯光, 等. 利用瞬变电磁技术进行地下水资源勘察. 地球物理学进展 , 2005, 20(3): 828–833. Ji Y J, Lin J, Zhu K G, et al. Underground water prospecting by Transient electromagnetic method. Progress in Geophysics (in Chinese) , 2005, 20(3): 828-833. |
| [6] | Holladay J S, Lo B, Prinsenberg S K. Bird orientation effects in quantitative airborne electromagnetic interpretation of pack ice thickness sounding. Oceuns'97, Marine Technology Society Institute of Electrical and Electronic Engineers Conference Proceedings, 1997, 2, 1114-1116. |
| [7] | Deszcz-Pan M, Fitterman D, Labson V F. Reduction of inversion errors in helicopter EM data using auxiliary information. Exploration Geophysics , 1998, 29(2): 142-146. DOI:10.1071/EG998142 |
| [8] | Yin C, Fraser D C. Attitude corrections of helicopter EM data using a superposed dipole model. Geophysics , 2004, 69(2): 431-439. DOI:10.1190/1.1707063 |
| [9] | 嵇艳鞠, 林君, 关珊珊, 等. 直升机航空TEM中心回线线圈姿态校正的理论研究. 地球物理学报 , 2010, 53(1): 171–176. Ji Y J, Lin J, Guan S S, et al. Theoretical study of concentric loop coils attitude correction in helicopter-borne TEM. Chinese Journal of Geophysics (in Chinese) , 2010, 53(1): 171-176. |
| [10] | Davis A C, Macnae J, Robb T. Pendulum motion in airborne HEM systems. Exploration Geophysics , 2006, 37(4): 355-362. DOI:10.1071/EG06355 |
| [11] | Davis A C, Macnae J, Hodges G. Predictions of bird swing from GPS coordinates. Geophysics , 2009, 74(6): F119-F126. DOI:10.1190/1.3237143 |
| [12] | Wait J R. Geo-electromagnetism. New York: Academic Press Inc., 1982 . |
| [13] | Brodie R, Sambridge M. Holistically calibrating, processing and inverting frequency domain AEM surveys. 17th Geophysical Conference and Exhibition, Australian Society of Exploration Geophysicists, Extended Abstracts, 2004. |
| [14] | Brodie R C, Sambridge M. A holistic approach to inversion of frequency-domain airborne EM data. Geophysics , 2006, 71(6): G301-G312. DOI:10.1190/1.2356112 |
| [15] | Brodie R C. Holistic inversion of airborne electromagnetic data[Ph. D. thesis]. Australian National University, 2010. |
| [16] | 汤井田, 任政勇, 化希瑞. 地球物理学中的电磁场正演与反演. 地球物理学进展 , 2007, 22(4): 1181–1194. Tang J T, Ren Z Y, Hua X R. The forward modeling and inversion in geophysical electromagnetic field. Progress in Geophysics (in Chinese) , 2007, 22(4): 1181-1194. |
| [17] | 薛国强, 李貅, 底青云. 瞬变电磁法正反演问题研究进展. 地球物理学进展 , 2008, 23(4): 1165–1172. Xue G Q, Li X, Di Q Y. Research progress in TEM forward modeling and inversion calculation. Progress in Geophysics (in Chinese) , 2008, 23(4): 1165-1172. |
| [18] | 李建慧, 朱自强, 曾思红, 等. 瞬变电磁法正演计算进展. 地球物理学进展 , 2012, 27(4): 1393–1400. Li J H, Zhu Z Q, Zeng S H, et al. Progress of forward computation in transient electromagnetic method. Progress in Geophysics (in Chinese) , 2012, 27(4): 1393-1400. |
| [19] | Knight J H, Raich A P. Transient electromagnetic calculations using the Gaver-Tehfest inverse Laplace transfer method. Geophysics , 1982, 47(1): 47-50. DOI:10.1190/1.1441280 |
| [20] | Guptasarma D, Singh B. Computation of the time-domain response of a polarizable ground. Geophysics , 1982, 47(11): 1574-1576. DOI:10.1190/1.1441307 |
| [21] | Guptasarma D, Singh B. New digital linear filters for Hankel J0 and J1 transforms. Geophysical Prospecting , 1997, 45(5): 745-762. DOI:10.1046/j.1365-2478.1997.500292.x |
| [22] | 陈小红, 段奶军. 时间域航空电磁快速成像研究. 地球物理学进展 , 2012, 27(5): 2123–2127. Chen X H, Duan N J. Study on fast imaging of airborne time-domain electromagnetic data. Progress in Geophysics (in Chinese) , 2012, 27(5): 2123-2127. |
| [23] | 朱凯光, 林君, 韩悦慧, 等. 基于神经网络的时间域直升机电磁数据电导率深度成像. 地球物理学报 , 2010, 53(3): 743–750. Zhu K G, Lin J, Han Y H, et al. Research on conductivity depth imaging of time domain helicopter-borne electromagnetic data based on neural network. Chinese Journal of Geophysics (in Chinese) , 2010, 53(3): 743-750. |
| [24] | Constable S C, Parker R L, Constable C G. Occam's inversion: a practical algorithm for generating smooth models from electromagnetic sounding data. Geophysics , 1987, 52(3): 289-300. DOI:10.1190/1.1442303 |
| [25] | Farquharson C G, Oldenburg D W. Inversion of time-domain electromagnetic data for a horizontally layered Earth. Geophysical Journal International , 1993, 114(3): 433-442. DOI:10.1111/gji.1993.114.issue-3 |
 2013, Vol. 56
2013, Vol. 56



