地面磁共振法(Magnetic Resonance Sounding,MRS)[1-2]具有直接确定含水层深度、厚度及含水量大小的能力,近年来已得到广泛应用[3-4].在影响磁共振勘探效果的众多因素中,地下电阻率信息是其中一个非常重要的因素[5-6],传统的MRS数据反演方法[7-12],通常依据地质情况,采用某种平均方法估算地下电阻率值,导致反演结果受人为因素影响;然而,针对复杂多变的多层导电模型,这种等效均匀半空间的方法会使含水量反演结果严重偏离真实地质构造[5].因此,地层电阻率分布的有效获取,是MRS准确进行含水量反演解释的必要条件.
国际上的相关研究起步于2002年,Hertrich和Yaramanci[13]利用模拟退火法实现了MRS和垂直电测深法(Vertical electric sounding,以下简称VES)的联合反演.MRS技术可获取地下100或150 m深度的含水构造,但利用VES方法获取相同深度的电阻率分布信息,需要铺设很长的供电导线,工作费时,耗力,并严重受地形、地物的限制.为弥补这一不足Braun和Yaramanci[14]试图直接通过MRS相位反演得到地下电阻率分布情况.理论仿真取得了不错的效果,但由于相位信息数据量少,且实际测量中受硬件系统及环境干扰影响,反演得到的电阻率分布不准确.
瞬变电磁法(Transient Electromagnetic,TEM)[15-18]利用不接地回线发射一次磁场,在一次磁场间歇期间接收由地下良导体受激励引起的涡流所产生的二次感应磁场.与其他电法勘探技术(直流电法、垂向电测深)相比,具有高效率、高分辨率、大探测深度等优点,能够获取地下几百米范围内的电阻率信息. 2009年,Legchenko [19]研究了复杂地质情况下MRS与TEM的联合探测问题,通过两种方法解释上的取长补短,一定程度实现了地下含水层位置的准确划分.尽管这一研究未建立方法间的内部制约关系,依然提示了MRS与TEM联合反演解释应是进行准确地下水定位的最理想手段.
国内有关研究报道较少,相对滞后.翁爱华等人于2007年研究了导电性对MRS反演的影响[5],提出在介质电阻率分布已知情况下,MRS感应电动势的平方是含水量的二次型形式,实际工作中可利用电法勘探结果作为先验信息,参与MRS反演.这种方法在反演过程中MRS核函数恒定,若获取的电阻率分布信息不准确,则很难对MRS反演结果进行实时修正.2012年刘道涵,胡祥云[20]等人在进行考虑椭圆极化效应的磁共振找水理论研究中发现,当地下电阻率较小时,由于椭圆极化效应导致垂直激发场严重畸变,进一步说明了电阻率分布信息对磁共振反演解释的重要性.
本文借助瞬变电磁法获取地下电阻率信息的优势,提出MRS与TEM联合反演方法.构建了具有光滑模型约束的加权联合问题目标函数.采用自适应遗传算法(Adaptive Genetic Algorithm,AGA)进行反演,通过对遗传算子的自适应调整,保证算法全局最优解搜索能力及收敛速度.同时,依据Archie定律进一步缩小模型参数搜索空间,降低反演问题的多解性.
文章首先通过理论模型对比MRS-TEM联合反演及MRS单独反演差异,凸显联合反演优势,验证AGA反演算法的稳定性.其次,针对内蒙古正镶白旗野外实测数据进行反演解释,与钻井资料进行一致性分析,全面验证MRS-TEM联合反演的实际意义.
2 TEM、MRS正演数值模拟 2.1 TEM正演计算将层状大地上方磁偶极子dx′,dy′产生的磁场分别沿矩形发射回线各边积分,得到回线源发射,地面任一点接收的二次感应电动势为[21]
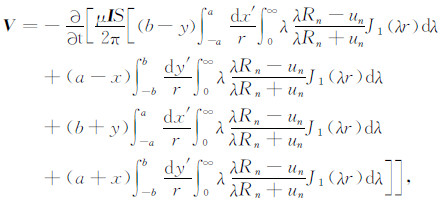
|
(1) |
其中,μ=4π×10-7为磁导率;I为发射电流;S为接收线圈面积;a、b分别为矩形发射线圈长和宽;(x,y)为以发射线圈中心为原点的测点位置坐标;r为收发距;Rn是表征多层介质的函数:
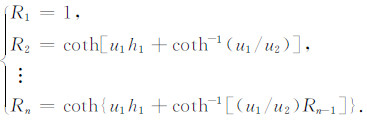
|
(2) |
其中hn为第n层厚度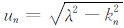
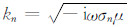
公式(1)内层积分中的贝塞尔函数采用F.N. Kong241点数字滤波法[22]计算,外层积分采用Guass48点积分法[23]以提高计算速度和精度,最后利用D.Guptasarma提出的线性滤波方法实现频率域到时间域的转换[18].
2.2 MRS正演计算MRS方法是向地下通以激发频率为拉莫尔频率fL的交变电磁场(其中fL=0.04258×|B0|,B0为测点实际地磁场强度),使地下水中的氢质子绕地磁场进动,当激发电流断开后,用同一线圈或其它接收线圈进行测量[24-26].采用固定激发脉冲矩q(q=I0τ为电流振幅与持续时间的乘积),只能进行地下某一深度的含水量分布探测.选择一系列递增的q,即可得到由浅到深的地下各深度含水量分布.
激发停止时刻MRS信号幅值大小为
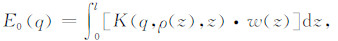
|
(3) |
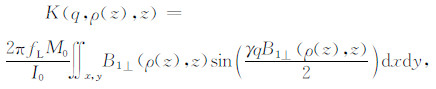
|
(4) |
其中,w(z)为含水量分布,ρ(z)为地层电阻率分布;M0为磁化强度;γ=2.675×108 s-1T-1为氢质子磁旋比;B1⊥为层状介质中激发磁感应强度在地磁场垂直方向的分量;K(q,ρ(V),z)为核函数,代表接收线圈对地下空间各位置处含水体的灵敏度大小.E0为信号初始振幅,其大小与被激发的地下氢质子数量成正比.
经过一系列激发脉冲矩测量后,对初始振幅反演即可得到测区内地下含水量分布.由公式(3)可见,核函数的计算直接影响MRS解释结果的准确度.
考虑到磁场分布具有柱对称性,核函数的计算采用柱坐标系实现[24].对公式(4)离散化,得到
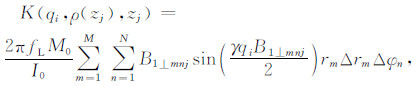
|
(5) |

|
(6) |
其中,qi为第i个激发脉冲矩;zj为第j个含水层顶面埋深;Δrm、Δφn分别为点(rm,φn)位置剖分单元的径向与切向长度;M、N分别为径向与切向剖分单元个数;α为地磁倾角;B1r、B1z分别为磁感应强度的径向与垂向分量,文献[27]详细介绍了二者的计算方法.
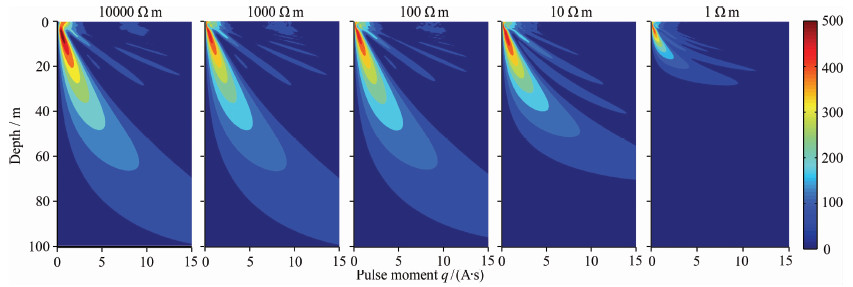
采用上述方法,分别计算了几种均匀半空间模型的MRS核函数.发射线圈边长100 m,地磁场强度53600 nT,地磁倾角60°N时,计算结果如图 1所示.由图可见,电阻率信息直接影响核函数计算结果,核函数随地层导电性增强而降低.
|
图 1 不同均匀半空间模型的MRS核函数 Fig. 1 Kernels for different homogeneous half-space model |
实现MRS-TEM联合反演与进行MRS或TEM单一反演有很大的不同,根本原因在于联合反演内部两种方法彼此约束.联合反演的目标函数由MRS与TEM两部分数据组成:MRS信号,通常为纳伏级;TEM信号,动态范围大,通常为几微伏到几伏.采用响应归一化处理方法,建立具有光滑模型约束的MRS-TEM加权联合目标函数:

|
(7) |
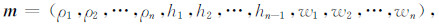
|
(8) |
其中Vobs为TEM响应的观测数据;ATEM由TEM正演算子计算得到的理论数据;Eobs为MRS观测数据中提取的初始振幅;AMRS由MRS正演算子计算得到的理论数据;C为平滑度矩阵[28];m为联合反演待解模型参数向量,包括各层电阻率、层厚度及含水量.wTEM、wMRS分别为TEM和MRS的加权系数,代表联合反演侧重关系,权系数的选择主要依赖实测数据噪声水平,在MRS信噪比较高时,可相对提高MRS数据权重.
λ为正则化参数,λ=0,主要拟合数据目标函数,导致反演过程不稳定;λ→∞,主要拟合模型目标函数,严重降低了解的分辨率.因此,本文参照文献[29]得到一种兼顾反演结果稳定性与算法计算效率的正则化参数自动调整方法,即
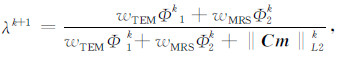
|
(9) |
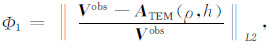
|
(10) |
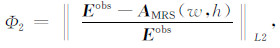
|
(11) |
其中λk+1为第k+1次迭代正则化参数,Φ1、Φ2分别代表TEM、MRS数据目标函数.这种正则化参数自适应调整方案能够使反演结果满足总体目标函数极小的同时,近似满足数据目标函数和模型约束目标函数极小的条件.且调整过程无需人为输入初值,避免了反演结果受人为因素影响.
4 自适应遗传反演方法遗传算法(GA)是一种借鉴生物界自然选择和自然遗传机制的随机搜索算法[30].其基本运算流程:首先对模型参数进行编码形成一条染色体,并随机产生初始种群(染色体的集合),通过适应度函数对种群中个体进行评价,按“优胜劣汰”标准决定个体取舍.对存活的个体按概率执行交叉、变异等繁殖操作,产生新一代模型群体(子代群体).利用适应度函数不断对群体中个体进行评价,更新模型群体,直至得到全局最优解模型.
地球物理反问题大多是非线性的,反演容易出现多解性和局部最优解问题.GA采用群体操作模式并行搜索多个极值,同时使用随机转移规则引导搜索,一定程度上降低了陷入局部极值的概率,已成为地球物理资料反演的主要方法之一[31-32].然而,标准GA,采用恒定的遗传算子(交叉概率和变异概率)繁殖后代,当搜索到包含全局最优解区域后,会花费大量时间进行局部精确解搜索,导致算法收敛慢,且一旦陷入局部极值,将很难跳出.鉴于此,本文针对MRS-TEM联合反演问题,提出了一套自适应遗传反演算法(AGA),对影响GA性能的几个主要因素:染色体长度、搜索空间,适应度函数,遗传算子等给出了相应的设计方法,保证收敛性的同时,提高算法全局最优解搜索能力.
4.1 染色体长度及搜索空间确定对于n层地电断面而言,MRS-TEM联合反演问题求解参数如公式(8)所示,包括地下各层电阻率、层厚度及各层含水量共3n-1个模型参数.将这些模型参数进行二进制编码并顺序连接形成一条染色体.设第i个模型参数mi的搜索空间为(mmini,mmaxi),模型参数最小分辨率为|Δmi|min,则染色体长度l为
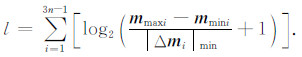
|
(12) |
可见,染色体长度取决于模型参数最小分辨率及搜索空间,在参数最小分辨率固定情况下,可通过缩小搜索空间减小染色体长度,提高算法效率,降低反演问题多解性.
文献[13]中,Hertrich等人根据Archie定律推导出地层总含水量与含水地层电阻率的直接关系:
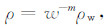
|
(13) |
其中,w为地层总含水量,包括自由水和束缚水含量;ρ为含水地层电阻率;m为胶结指数,通常m∈ [1.3,2.5];ρw为地下水电阻率.
原则上,地层电阻率ρ和层厚度h的取值范围即搜索空间为(0,+ ∞),含水量w的搜索空间为[0, 1],但根据实际地质情况或钻井资料信息,可以缩小这一空间.同时,MRS探测得到的含水量被定义为地下自由水含量占总体积的百分比[2],因此,w的取值应小于按公式(13)计算得到的地层总含水量大小.这样,各模型参数的搜索空间可缩小为
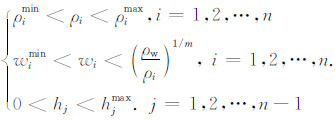
|
(14) |
适应度函数是遗传算法用于评价群体中个体优良程度的标准,是决定个体能否被遗传到下一代的唯一判定依据.适应度越大的个体,其再生概率越大.
适应度函数可由目标函数变换得到,其设计依据需满足非负标准,同时以能体现群体平均性能为最佳.综合考虑个体目标函数值及所在群体的分散程度,本文适应度函数定义为
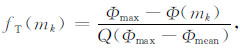
|
(15) |
其中,Q表示群体规模;Φmax、Φmean分别为群体中个体目标函数的最大值和平均值;Φ(mk)为群体中个体mk的目标函数值;fT(mk)为个体mk的适应度值.个体适应度越强,说明其表达的模型参数越接近真实模型.以此为判定依据,高适应度个体将继续参与子代繁殖,而低适应度个体将从子代中移除.
4.3 遗传算子的自适应调整交叉操作和变异操作是产生新个体的主要方法,是遗传算法的核心部分.交叉概率Pc和变异概率Pm分别控制着交叉操作和变异操作被使用的频率.
Pc越大,交叉操作越频繁,新模型产生的速度越快,但Pc过大,将导致接近真实模型的个体很容易被破坏.在算法初始阶段模型群体中个体差异较大,与真实模型的接近程度相对离散,此时,应采用较小的Pc限制个体间的信息交换,随着迭代过程进行,逐渐增大Pc避免进化停滞.因此,Pc应按进化状态自适应调整,若群体平均适应度逐代递增,则降低Pc,否则增加Pc,其调整公式为
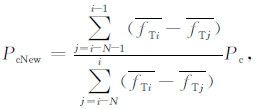
|
(16) |
其中,i为当前迭代数;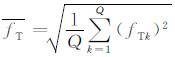

Pm越大,变异操作越频繁,将导致算法的随机性过强;Pm过小,不宜产生新的个体,易产生未成熟收敛.因此,Pm应根据个体适应度自适应调整.降低接近真实模型个体的变异概率,确保优良个体直接进化;同时,增加偏离真实模型个体的变异概率,确保个体多样性,其调整公式为
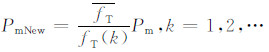
|
(17) |
其中fT(k)为个体k的适应度;Pm为父代个体变异概率;PmNew为调整后的当代个体变异概率.
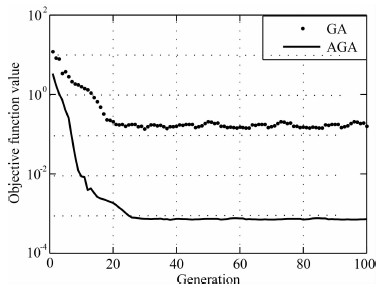
4.4 算法验证以四层大地模型的TEM数据反演为例,验证自适应遗传算法的收敛性及全局最优解搜索能力.设置的模型参数及搜索空间如表 1所示.以理论数据与实测数据平均相对误差最小为目标函数,分别采用标准遗传算法和自适应遗传算法进行反演.图 2给出了反演过程中最佳个体目标函数值随迭代次数变化曲线,可以看出,GA与AGA均有很快的收敛速度,但AGA搜索到最优解的目标函数值明显优于GA搜索到的最优解.图 3给出了两种反演方法得到的最优模型,GA得到的第三层电阻率和层厚度与实际模型偏差较大,电阻率拟合误差达19.4%,而AGA得到的模型与实际模型具有很好的一致性,电阻率拟合误差仅为0.28%,充分说明AGA具有更强的收敛性及全局最优解搜索能力.
|
|
表 1 模型参数 Table 1 Model parameters |
|
图 2 最佳个体目标函数值随迭代次数变化曲线 Fig. 2 Variations of objective function values of the best individuals with iteration numbers |
|
图 3 反演结果图 Fig. 3 Inversion results |
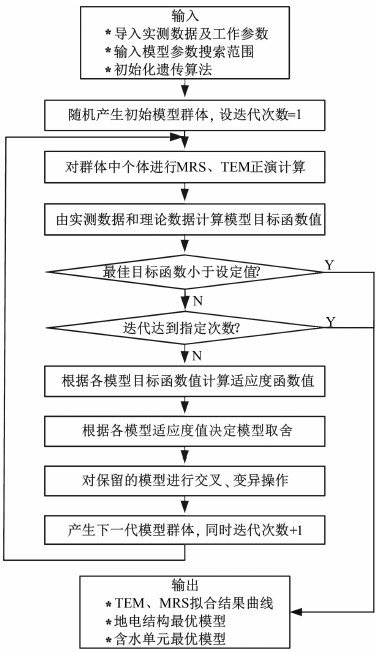
反演算法流程如图 4所示.其具体操作步骤如下:
|
图 4 MRS-TEM联合反演流程图 Fig. 4 Flowchart of MRS-TEM joint inversion |
(1)导入实测数据及工作装置参数;输入MRS、TEM模型参数搜索空间,初始化遗传算法;随机产生初始模型群体,并设迭代次数为1;
(2)对群体中个体进行MRS、TEM正演计算,根据实测数据与理论数据计算相应的目标函数;
(3)根据个体目标函数值计算适应度函数值,依据适应度大小决定个体取舍,对保留的个体按遗传算子自适应调整方案进行交叉、变异等操作,生成新一代模型群体,同时迭代次数加1;
(4)重复执行步骤2~3,直到最佳目标函数值小于设定值或迭代达到指定次数,输出反演结果.
5 理论模型算例用自适应遗传算法分别对均匀半空间模型和层状大地模型按传统MRS单独反演方式、MRS-TEM联合反演方式进行反演,验证AGA反演算法的稳定性及MRS-TEM联合反演优势.
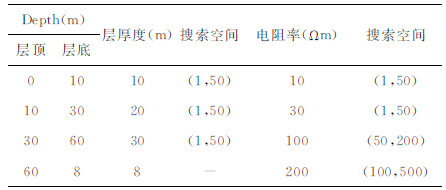
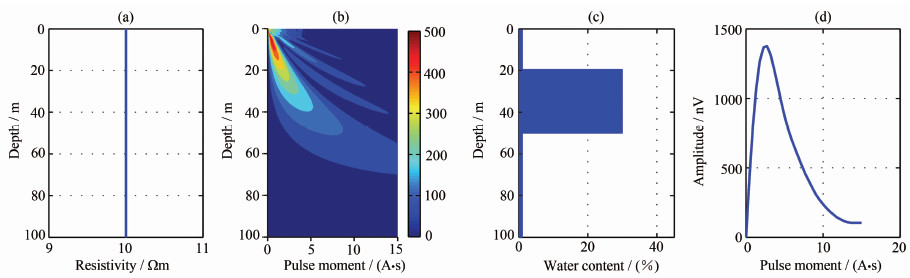
5.1 均匀半空间模型MRS、TEM模拟观测数据按照如下条件获得:MRS采用边长为100 m的方形发射线圈,地磁场强度48000 nT,地磁倾角60°N,拉莫尔频率2044 Hz,激发最大脉冲矩15 As;TEM采用边长为40 m的方形发射线圈,中心回线工作方式,发射线圈中心与MRS发射线圈中心重合.设置的实际模型参数如表 2所示,均匀半空间电阻率为10 Ωm(图 5a),地下水在20 m和50 m间均匀分布,含水量为30%,含水层厚度为30 m(图 5c).图 5b、d分别为模型的MRS核函数和初始振幅曲线.
|
|
表 2 均匀半空间模型参数 Table 2 Parameters of homogeneous half-space model |
|
图 5 均匀半空间模型 (a)电阻率结构;(b)核函数;(c)含水单元结构;(d)初始振幅曲线. Fig. 5 Homogeneous model (a) Resistivity structure; (b) Kernel function; (c) Water-bearing structure; (d) Initial amplitude. |
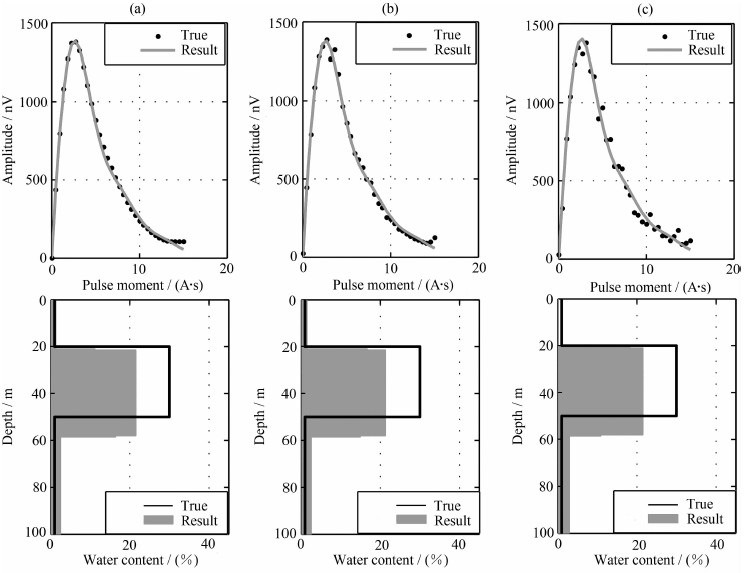
首先对MRS数据单独反演,采用500 Ωm的均匀半空间模型,反演结果如图 6a所示.图中红线为设置的实际含水单元模型,蓝色填充区域为反演结果.由图可见,反演结果与实际模型偏差较大,反演得到的含水量比实际小,含水层位置比实际埋深深,含水量拟合误差达13.6%.
|
图 6 MRS数据单独反演结果 (a)无噪声数据;(b)5%噪声数据;(c)10%噪声数据. Fig. 6 Single inversion result of MRSdata (a) no noise; (b)5% noise; (c)10% noise applied on synthetic data. |
野外工作中MRS探测受噪声影响较大,为使理论仿真更接近实际,在MRS理论数据中分别加入了5%和10%的Guass噪声,反演结果如图 6b、c所示,含水量拟合误差分别为13.9%和13.2%.对不同信噪比数据反演,得到了接近一致的反演结果,说明反演算法未过度拟合含噪声数据,验证了反演算法的稳定性.
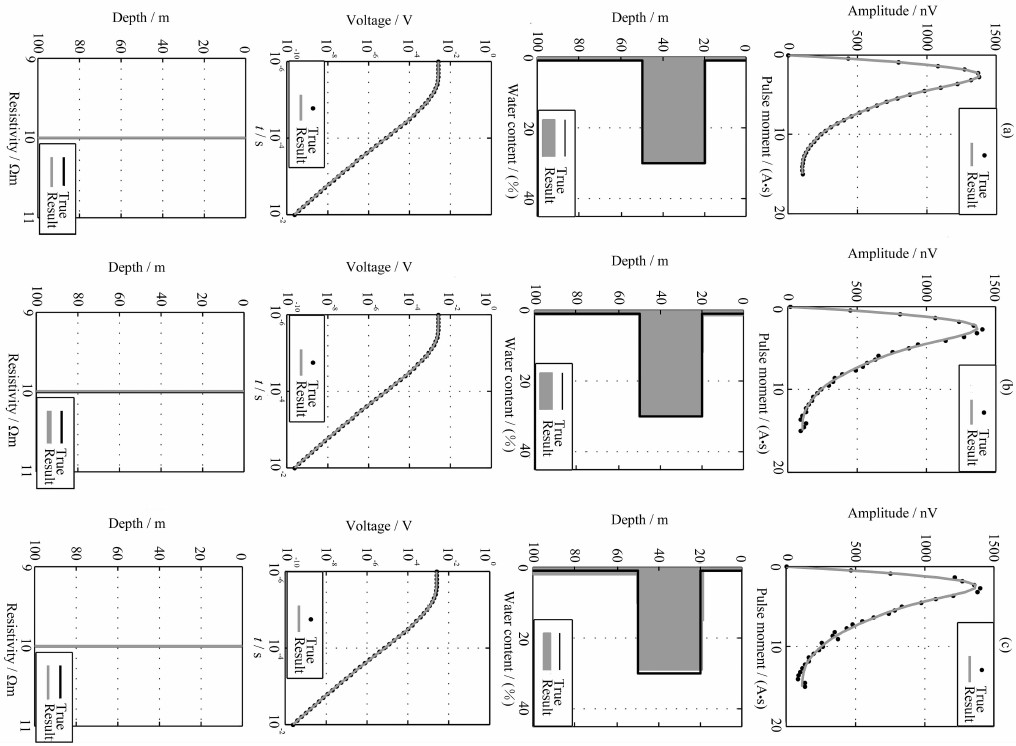
针对上述模型,采用MRS-TEM联合反演方法,结果如图 7所示.由图可见,在加入10%噪声情况下,反演结果仍与实际模型保持很好的一致性,含水量拟合误差仅为1.15%.对比MRS数据单独反演结果,MRS-TEM联合反演得到的含水量分布与实际模型更接近,优势明显.
|
图 7 MRS-TEM数据联合反演结果 (a)无噪声数据;(b)5%噪声数据;(c)10%噪声数据. Fig. 7 Joint inversion results of MRS-TEM data (a) No noise; (b)5% noise; (c)10% noise applied on synthetic data. |
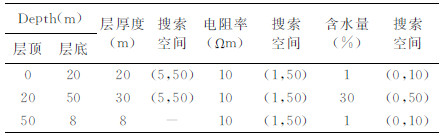
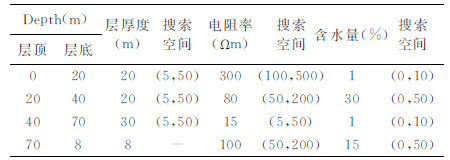
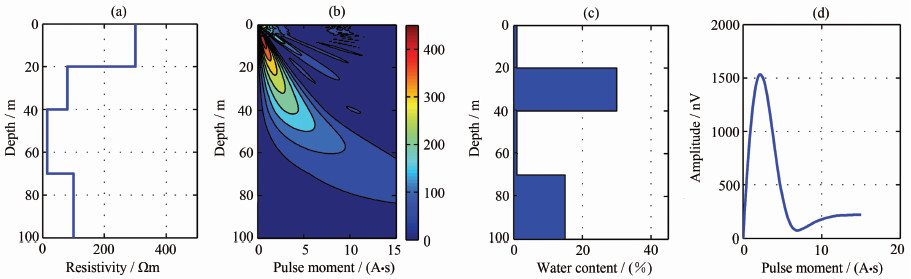
在均匀半空间模型基础上,采用更接近实际地质情况的层状大地模型进行联合反演优势验证. MRS、TEM模拟观测数据采用如下条件获得:MRS采用边长为100 m的方形发射线圈,地磁场强度54627 nT,地磁倾角60°N,拉莫尔频率2326 Hz,激发最大脉冲矩15As;TEM采用边长为40 m的方形发射回线,中心回线工作方式,发射线圈中心与MRS发射线圈中心重合.设置的实际模型参数如表 3所示,采用四层大地模型(图 8a),地表模拟电阻率为300 Ωm的高阻覆盖层,含水量1%(图 8c);第二层模拟20 m厚的含水砂砾石层,电阻率80 Ωm,含水量30%;第三层模拟30 m厚的粘土隔水层,电阻率15 Ωm,含水量1%;底层模拟含水量相对较小的砂砾石层,电阻率100 Ωm,含水量15%.图 8b、d分别为模型的MRS核函数和初始振幅曲线.
|
|
表 3 层状大地模型参数 Table 3 Parameters of layering earth model |
|
图 8 层状大地模型 (a)电阻率结构;(b)核函数;(c)含水单元结构;(d)初始振幅曲线. Fig. 8 Layered model (a) Resistivity; (b) Kernel; (c) Water content; (d) Initial amplitude. |
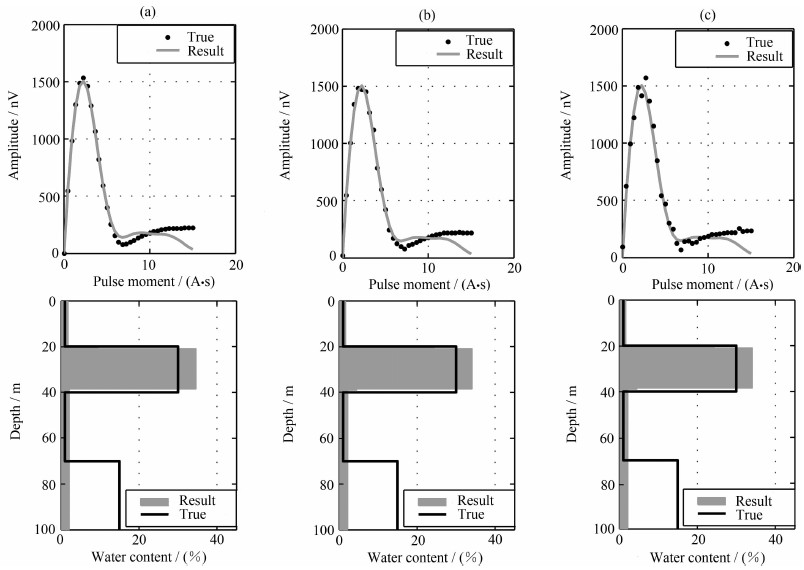
首先采用300 Ωm均匀半空间模型进行MRS数据单独反演,结果如图 9所示.可见,反演结果与实际模型偏差较大,加入10%噪声时含水量拟合误差达21.9%.反演结果中主含水层含水量与实际模型浅部主含水层含水量稍有差别,含水层位置基本一致.但深部含水层信息未能良好体现,说明传统MRS单独反演,虽然采用了与实际电阻率模型浅部一致的均匀半空间模型,但深层电阻率分布信息对MRS数据反演结果的影响依然存在.
|
图 9 MRS数据单独反演结果 (a)无噪声数据;(b)5%噪声数据;(c)10%噪声数据. Fig. 9 Single inversion result of MRS data (a) No noise; (b)5% noise; (c)10% noise applied on synthetic data. 3736 |
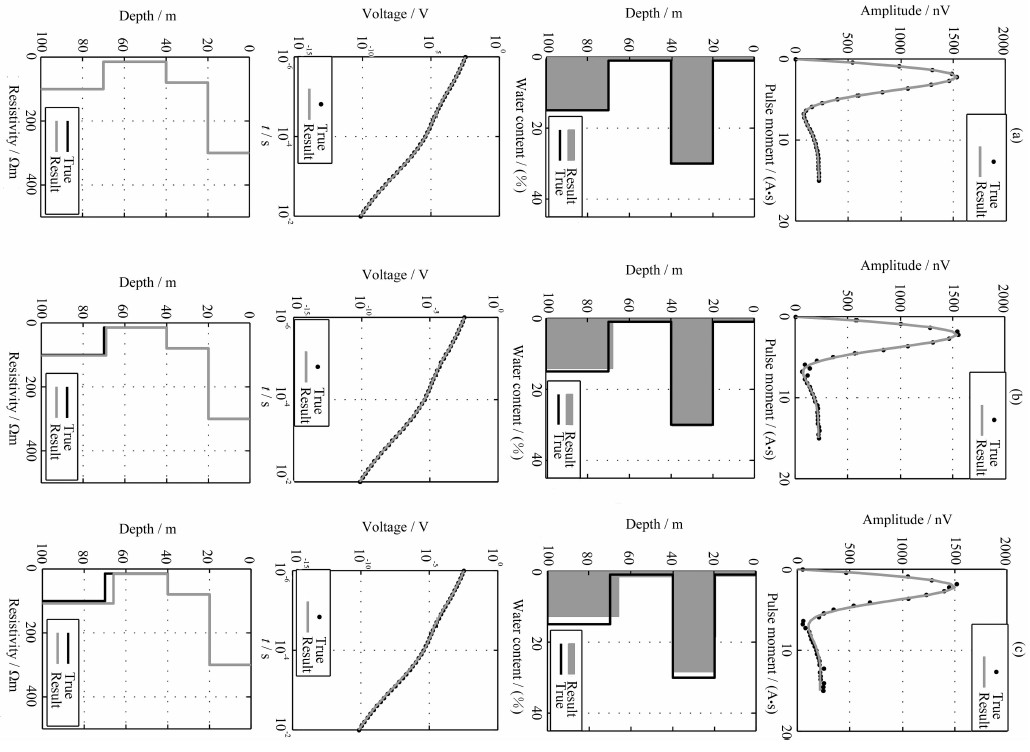
联合反演结果如图 10a所示,可见,反演结果与实际模型基本一致,含水量拟合误差为0.26%,对含噪5%和10%数据反演结果如图 10b、c所示,得到的含水量拟合误差分别为2.25%和4.26%,反演得到的含水量分布与实际模型吻合较好.不同信噪比数据接近一致的反演结果再次验证了AGA反演算法的稳定性.
|
图 10 MRS-TEM数据联合反演结果 (a)无噪声数据;(b)5%噪声数据;(c)10%噪声数据. Fig. 10 Joint inversion results of MRS-TEM data (a) No noise; (b)5% noise; (c)10% noise applied on synthetic data. |
综合均匀半空间模型和层状大地模型仿真结果可见,基于AGA的联合反演结果能够稳定、准确地反映真实含水单元结构,不过于平滑反演模型,也不过度拟合含噪声观测曲线.
6 实测数据处理应用本文所述自适应遗传反演算法对野外实测数据进行反演解释,验证算法的实用性及MRS-TEM联合反演的实际意义.
在内蒙古正镶白旗采用自主研制的ATEM瞬变电磁系统和JLMRS核磁共振系统分别进行了地下水探测.测试点地磁场强度56000 nT,地磁倾角39°N,拉莫尔频率2385 Hz.图 12d为探测后钻探取芯结果,0~15 m为第四系粉砂层,含水层厚度约10 m,类型为孔隙潜水;15~73 m为断裂带充填物,岩性以砂砾石、粘土、中细砂为主,含水层厚度约28.7 m,类型为孔隙自流承压水;下部岩性以中粗砂、红色泥岩为主,含水层厚度约20 m.
|
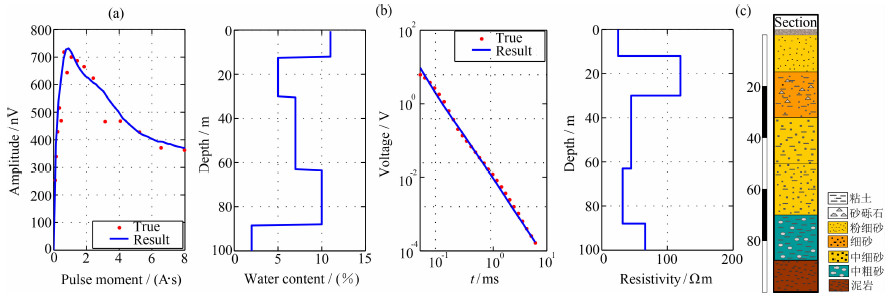
图 12 白旗测点MRS-TEM联合反演结果 (a)MRS数据拟合结果及含水量分布;(b)TEM数据拟合结果及电阻率结构;(c)钻井成图. Fig. 12 Joint inversion results of MRS-TEM data at Baiqi test site (a) MRS data fitting result and water content; (b) TEM data fitting result and resistivity; (c) Drillhole column. |
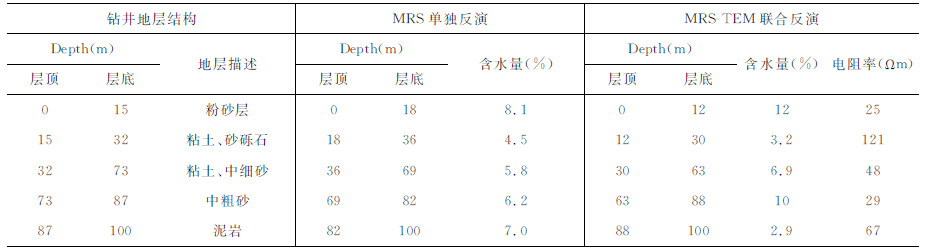
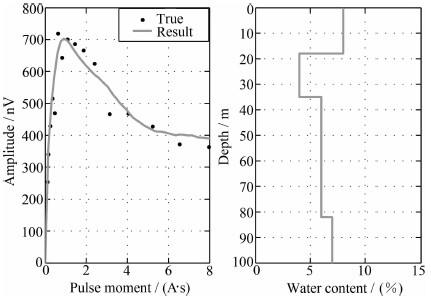
野外工作中,TEM采用重叠回线工作装置,与MRS同采用100 m×100 m发射线圈,MRS数据信噪比为13.29 dB(磁共振反演中,以信噪比高于6.02 dB的数据为可信[33]).首先进行MRS单独反演,采用电阻率为100 Ωm的均匀半空间模型,结果如图 11所示.然后对MRS-TEM数据联合反演,结果如图 12(a-c)所示.表 4给出了钻井地层结构与两种方法的反演结果对比情况.MRS数据单独反演得到地表至18 m一个主含水层,与钻井资料浅部第四系粉砂层对应,但含水层厚度偏大;深部含水层分界面划分不明确.由于MRS数据信噪比较高,联合反演取数据拟合权重wMRS:wTEM=3:2,反演结果得到浅部地表至12 m,深层30~63 m,63~88 m三个主含水层,分别对应钻井资料中含水层厚度为10 m的浅部含水层及含水层厚度为28.7 m和20 m的两个深部含水层,同时由MRS-TEM联合反演得到的电阻率分布信息能清晰的反映地下岩石结构.实测数据处理结果表明,联合反演结果无论是含水层位置、厚度还是电阻率分布信息反映的地下岩石结构均与钻井结果均具有很好的一致性.
|
图 11 白旗测点MRS数据单独反演结果 Fig. 11 MRS single inversion results of Baiqi test site |
|
|
表 4 测试点钻井结果与反演结果对比 Table 4 Comparison of drilling results and inversion results |
本文详细介绍了MRS-TEM联合反演方法的原理和步骤.构建了具有光滑模型约束的加权联合问题目标函数.采用自适应遗传算法对MRS-TEM数据进行联合反演,根据个体目标函数值及群体分散程度建立了适应度函数,全面评价个体性能.通过遗传算子的自适应调整,解决了GA在交叉概率和变异概率选择不当时,易于陷入局部极值问题.依据Archie定律,进一步缩小模型参数搜索空间,降低了反演问题的多解性.以TEM数据反演为例,证实了AGA反演算法优于GA,并且具有很强的全局最优解搜索能力及收敛速度.
联合反演优势在均匀半空间模型、层状模型反演算例中均得以体现.在理论信号中分别加入不同信噪比噪声,反演结果稳定.且MRS-TEM联合反演方法即使在加入10%噪声情况下,结果仍能较真实地反映地下含水单元模型结构,相对于传统MRS单独反演,优势明显.
利用该反演方法,对内蒙古白旗野外观测数据进行反演.与MRS单独反演结果相比,MRS-TEM联合反演得到的含水层分界面更明确、含水层位置精度更高,充分验证了本文所述自适应遗传反演算法的实用性及MRS、TEM两种探测方法联合反演的实际意义.
| [1] | 潘玉玲, 张昌达. 地面核磁共振找水理论和方法. 北京: 中国地质大学出版社, 2000 . Pan Y L, Zhang C D. Theories and Methods of Surface Nuclear Magnetic Resonance (in Chinese). Beijing: Publishing House of Geology University of China, 2000 . |
| [2] | 林君, 段清明, 王应吉, 等. 核磁共振找水仪原理与应用. 北京: 科学出版社, 2010 . Lin J, Duan Q M, Wang Y J, et al. Theory and Design of Magnetic Resonance Sounding Instrument for Groundwater Detection and Its Applications (in Chinese). Beijing: Science Press, 2010 . |
| [3] | Nielsen L, Jørgensen N O, Peter G. Mapping of the freshwater lens in a coastal aquifer on the Keta Barrier (Ghana) by transient electromagnetic soundings. Journal of Applied Geophysics , 2007, 62(1): 1-15. DOI:10.1016/j.jappgeo.2006.07.002 |
| [4] | Chalikakis K, Nielsen M R, Legchenko A. MRS applicability for a study of glacial sedimentary aquifers in Central Jutland, Denmark. Journal of Applied Geophysics , 2008, 66(3-4): 176-187. DOI:10.1016/j.jappgeo.2007.11.005 |
| [5] | 翁爱华, 王雪秋, 刘国兴, 等. 导电性影响的地面核磁共振反演. 地球物理学报 , 2007, 50(3): 890–896. Weng A H, Wang X Q, Liu G X, et al. Nonlinear inversion of surface nuclear magnetic resonance over electrically conductive medium. Chinese J. Geophys. (in Chinese) , 2007, 50(3): 890-896. |
| [6] | Braun M, Yaramanci U. Inversions of Surface-NMR signals using complex kernels. Proceedings of the 9th EEGS conference, Prague/Czech Republic. 2003. |
| [7] | 戴苗, 胡祥云, 吴海波, 等. 地面核磁共振找水反演. 地球物理学报 , 2008, 51(6): 1876–1882. Dai M, Hu X Y, Wu H B, et al. Inversion of surface nuclear magnetic resonance. Chinese J. Geophys. (in Chinese) , 2008, 51(6): 1876-1882. |
| [8] | Walsh D O. Multi-channel surface NMR instrumentation and software for 1D/2D groundwater investigations. Journal of Applied Geophysics , 2008, 66(3-4): 140-150. DOI:10.1016/j.jappgeo.2008.03.006 |
| [9] | Mohnke O, Yaramanci U. Smooth and block inversion of surface NMR amplitudes and decay times using simulated annealing. Journal of Applied Geophysics , 2002, 50(1-2): 163-177. DOI:10.1016/S0926-9851(02)00137-4 |
| [10] | Braun M, Yaramanci U. 1D inversion of resistivity and water content of magnetic resonance sounding.//Proceedings of Near Surface 2006-12th European Meeting of Environmental and Engineering Geophysics. Helsinki, Finland, 2006. |
| [11] | Lehmann-Horn J A, Hertrich M, Greenhalgh S, et al. Three-dimensional magnetic field and NMR sensitivity computations incorporating conductivity anomalies and variable-surface topography. IEEE Transactions on Geoscience and Remote Sensing , 2011, 49(10): 3878-3891. DOI:10.1109/TGRS.2011.2135861 |
| [12] | Lehmann-Horn J A, Walbrecker J O, Hertrich M, et al. Imaging groundwater beneath a rugged proglacial moraine. Geophysics , 2011, 76(5): B165-B172. DOI:10.1190/geo2011-0095.1 |
| [13] | Hertrich M, Yaramanci U. Joint inversion of surface nuclear magnetic resonance and vertical electrical sounding. Journal of Applied Geophysics , 2002, 50(1-2): 179-191. DOI:10.1016/S0926-9851(02)00138-6 |
| [14] | Braun M, Yaramanci U. Inversion of resistivity in magnetic resonance sounding. Journal of Applied Geophysics , 2008, 66(3-4): 151-164. DOI:10.1016/j.jappgeo.2007.12.004 |
| [15] | Nabighian N M.电磁法勘探-理论卷.赵经祥等译.北京:地质出版社, 1992. Nabighian N M. Electromagnetic Methods in Applied Geophysics (Volume 1) (in Chinese). Translated by Zhao J X, et al. Beijing: Geology Publishing House, 1992. |
| [16] | 薛国强, 李貅, 底青云. 瞬变电磁法理论与应用进展研究. 地球物理学进展 , 2007, 22(4): 1195–1200. Xue G Q, Li X, Di Q Y. The progress of TEM in theory and application. Progress in Geophysics. (in Chinese) , 2007, 22(4): 1195-1200. |
| [17] | Raiche A P. Transient electromagnetic field computations for polygonal loops on layered earths. Geophysics , 1987, 52(6): 785-793. DOI:10.1190/1.1442345 |
| [18] | 刘桂芬.回线源层状大地航空瞬变电磁场的理论计算[硕士论文].长春:吉林大学, 2008. Liu G F. Theoretical calculation of airborne transient electromagnetic field for loop source[Master] (in Chinese). Changchun: Jilin University, 2008. |
| [19] | Legchenko A, Ezersky M. Joint use of TEM and MRS methods in a complex geological setting. C. R. Geoscience , 2009, 341(10-11): 908-917. DOI:10.1016/j.crte.2009.07.013 |
| [20] | 刘道涵, 胡祥云, 李耀国, 等. 基于椭圆极化的核磁共振找水理论研究. 应用地球物理学报 , 2012, 9(4): 365–377. Liu D H, Hu X Y, Li Y G, et al. Understanding the effect of elliptical polarization in surface nuclear magnetic resonance method. Applied Geophysics. (in Chinese) , 2012, 9(4): 365-377. DOI:10.1007/s11770-012-0348-y |
| [21] | Podder M. A rectangular loop source of current on multilayered earth. Geophysics , 1983, 48(1): 107-109. DOI:10.1190/1.1441398 |
| [22] | Kong F N. Hankel transform filters for dipole antenna radiation in a conductive medium. Geophysical Prospecting , 2007, 55(1): 83-89. DOI:10.1111/gpr.2007.55.issue-1 |
| [23] | Abramowitz M, Stegun I A. Handbook of mathematical functions with formulas graphs and mathematical tables. The Fifth Printing Washington: U. S. Government Printing Office, 1964: 919-924. |
| [24] | 翁爱华, 李舟波, 王雪秋. 层状导电介质中地面核磁共振响应特征理论研究. 地球物理学报 , 2004, 47(1): 157–163. Weng A H, Li Z B, Wang X Q. A study on surface nuclear magnetic resonance over layered conductive earth. Chinese J. Geophys. (in Chinese) , 2004, 47(1): 157-163. |
| [25] | Legchenko A, Valla P. A review of the basic principles for proton magnetic resonance sounding measurements. Journal of Applied Geophysics , 2002, 50(1-2): 3-19. DOI:10.1016/S0926-9851(02)00127-1 |
| [26] | 蒋川东, 林君, 段清明, 等. 二维阵列线圈核磁共振地下水探测理论研究. 地球物理学报 , 2011, 54(11): 2973–2983. Jiang C D, Lin J, Duan Q M, et al. A study on 2D magnetic resonance sounding with an array loop for groundwater exploration. Chinese J. Geophys. (in Chinese) , 2011, 54(11): 2973-2983. |
| [27] | 翁爱华, 李舟波, 王雪秋. 地表大回线源在任意层状介质中产生磁场的计算. 物探化探计算技术 , 2000, 22(3): 245–249. Weng A H, Li Z B, Wang X Q. The magnetic field computation for large loop source. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 2000, 22(3): 245-249. |
| [28] | 张文权, 翁爱华. 地面正则化核磁共振反演方法研究. 吉林大学学报(地球科学版) , 2007, 37(4): 809–813. Zhang W Q, Weng A H. On regularization inversion method of surface nuclear magnetic resonance data. Journal of Jilin University (Earth Science Edition) (in Chinese) , 2007, 37(4): 809-813. |
| [29] | 陈小斌, 赵国泽. 大地电磁自适应正则化反演算法. 地球物理学报 , 2005, 48(4): 937–945. Chen X B, Zhao G Z. An adaptive regularized inversion algorithm for magnetotelluric data. Chinese J. Geophys. (in Chinese) , 2005, 48(4): 937-945. |
| [30] | 雷英杰, 张善文, 李续武, 等. MATLAB遗传算法工具箱及应用. 西安: 西安电子科技大学出版社, 2005 . Lei Y J, Zhang S W, Li X W, et al. MATLAB Genetic Algorithms Toolbox and Application (in Chinese). Xi'an: Publishing House of Xidian University, 2005 . |
| [31] | 李帝铨, 王光杰, 底青云, 等. 基于遗传算法的CSAMT最小构造反演. 地球物理学报 , 2008, 51(4): 1234–1245. Li D Q, Wang G J, Di Q Y, et al. The application of Genetic Algorithm to CSAMT inversion for minimum structure. Chinese J. Geophys. (in Chinese) , 2008, 51(4): 1234-1245. |
| [32] | 何飞, 张效信, 陈波, 等. 遗传算法反演地球等离子体层离子密度分布. 地球物理学报 , 2012, 55(1): 29–35. He F, Zhang X X, Chen B, et al. Inversion of the Earth's plasmaspheric density distribution from EUV images with genetic algorithm. Chinese J. Geophys. (in Chinese) , 2012, 55(1): 29-35. |
| [33] | Legchenko A. MRS measurements and inversion in presence of EM noise. Boletín Geológicoy Minero , 2007, 118(3): 489-508. |
 2013, Vol. 56
2013, Vol. 56