具有顺磁性的氢原子核能够产生核磁共振弛豫现象[1-3],富水地下介质中氢原子丰度相对较高,因此,只要能探测到核磁共振信号,就可以证明地下水的存在;另外,核磁共振信号的强弱与地下水的含量成正比,所以,根据核磁共振信号的强弱,不打钻就能了解到地下水的含量.磁共振测深(Magnetic Resonance Sounding,简称MRS)就是一种应用核磁共振现象探测地下水的地球物理方法.
过去20年,一维核磁共振探测理论日趋完善[4-5],法国、德国、中国先后成功研制出了商业化的核磁共振地下水探测仪器[6-7],利用同一发射/接收线圈,按水平层状地下水介质模型的概念探测地下水,在全世界范围内开展了广泛应用[8-10].然而,一维方法技术在对复杂地质环境中非一维地下水体探测显得无能为力.最近十年,核磁共振技术取得了重大进展,Weichman修正了一维探测的基本理论公式[11-12],从而能够准确计算发射、接收线圈分离时感应出的核磁共振信号[13-14].Yaramanci等人随后提出了二维核磁共振地下水探测理论[15-17],在模型仿真中准确反演了非层状地下水边界,凸显了二维磁共振测量的优势.他们引用了医学影像学中的概念,赋予二维MRS反演新的定义---磁共振断层成像(magnetic resonance tomography,MRT)技术.遗憾的是,由于当时仪器水平的限制,这些方法在实际测量中,仅能利用一维探测仪器多次拖动接收线圈得以完成.2008年,Walsh开发了MRS多通道仪器[18]使MRT探测成为可能,而这款仪器仅有4个采集通道,工作效率及其横向分辨率均具有局限性.
与国际上MRS前沿性探索相比,国内相关研究起步较晚.2003年,潘玉玲等人报导了地面核磁共振找水方法在中国的应用效果[19].翁爱华等人计算了层状导电介质中地面磁共振的响应特征[20-21]和导电性影响的核磁共振反演方法[22].然而,这些研究均基于未修正的一维探测基本理论公式,对于正演模型和反演结果都存在误差.蒋川东等人在国内率先研究了二维阵列线圈磁共振地下水探测正演理论,并提出了阵列式线圈的工作模式[23],但该研究仅限于水平大地的二维正演理论推导,未考虑存在探测角度的二维正演方法修正.国内MRT反演研究如今刚刚起步,尚未见有影响力的成果.
针对上述问题,本文开展了二维MRS理论研究,引入旋转坐标系数矩阵,首次推导了天线沿不同方位测线铺设对应的激发场垂直分量;在二维正演的基础上,探索了基于Occam算法的二维反演方法,为复杂地质条件下非层状地下水精细定位与定量解释奠定了基础.在二维探测剖面的正反演方法基础上,吉林大学仪电学院成功研发了可扩展至8个甚至更多的通道个数的分布式MRS探测仪,并通过野外实验证实了所研制系统的有效性.
2 二维测线倾角的正演推导 2.1 核函数的二维表达式推导地面磁共振探测地下水的理论已经在很多文献中进行了阐述[11-14],MRS信号的表达式为:
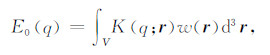
|
(1) |
其中,E0是MRS信号的初始振幅;q=I0 ·τ是激发脉冲矩,即激发电流I0和激发时间τ的乘积;w(r)是空间任意一点r的含水量大小;K(q;r)称为核函数,代表了位置r处MRS信号的灵敏度.核函数的三维形式K3D(q;r)由下式表示:
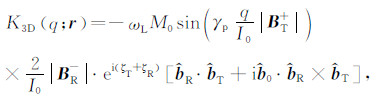
|
(2) |
其中,ωL是Larmor频率;M0是氢质子的净磁化强度;γp是质子旋磁比;BT+是激发场垂直分量BT⊥的同向分量;BR-是接收场垂直分量BR⊥的反向分量;ζT和ζR分别是激发场和接收场椭圆极化的相位分量;单位向量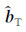
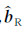
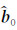
对于二维磁共振探测,可将二维核函数K2D(q;r)在某一方向(如±y)上先进行积分(见式(3)),再计算磁共振信号的感应电动势(见式(4)):
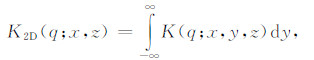
|
(3) |
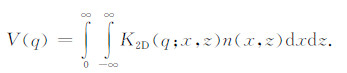
|
(4) |
实际探测中,对于分布式探测模式,激发场垂直分量BT⊥不但要考虑地磁倾角,还应考虑测量剖面线与地磁场磁北方向的夹角α(地磁方位角,简称方位角).设α代表测线由北向东偏转的角度,0<α<2π.如图 1所示,α分别为0°N(正北方向),45°N和90°N(东西方向).
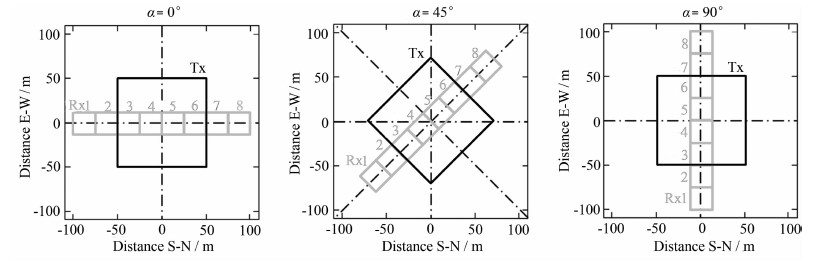
|
图 1 分布式线圈采集模式和剖面方位角变化示意图 Fig. 1 Schematic diagram of distributed coils acquisition mode and changes of profile azimuth |
设α0=0°代表地磁场的磁北方向,当测量剖面的方位角逆时针旋转α时,旋转前的发射场BT⊥(α0)可由旋转后的BT⊥(α)和旋转矩阵Rα表示:
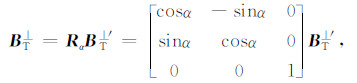
|
(5) |
因此,可以获得:
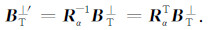
|
(6) |
根据(1)-(6)式,可计算在地磁场环境下沿任意方位剖面线的激发场.
3 二维含水量Occam反演方法地面核磁共振信号的初始振幅E0与地下介质含水量w线性相关,见表达式(1).其中核函数K既代表了地下空间灵敏度大小,也可作为雅可比矩阵.为了利用观测的二维MRS信号数据获得二维地下水模型的含水量分布图像MRT,本文采用Occam反演方法[24],即,将地下空间分解成固定几何形状的单元,分别计算这些单元内的含水量大小.反演算法的目标为寻找最优的含水量分布,使其正演信号Kw与观测信号初始振幅E0obs的差值最小,可用二阶范数表示为:
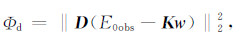
|
(7) |
其中,D是数据的权值,可用观测数据或观测噪声的不确定度计算获得.
由于直接对式(7)寻优是不稳定的,为了获得高分辨率且稳定的成像结果,反演的目标函数需要引入平滑限制条件:
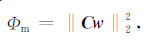
|
(8) |
其中,C是平滑度矩阵.因此,最终优化问题可以描述为
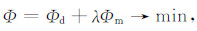
|
(9) |
其中,λ称为正则化参数.为了求解这个优化问题,将表达式(9)重新表示成迭代格式:
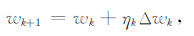
|
(10) |
其中,k是当前迭代次数,ηk是搜索步长.新的模型增量Δwk可用高斯牛顿方法求解:
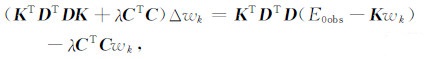
|
(11) |
其中,T代表矩阵的转置.
在每次迭代过程中,搜索步长ηk的选择用来防止反演过程迭代过度.首先建立含有ηk值的正演计算表达式:

|
(12) |
然后通过对Φd(f(η))+λΦm(η)求解最优化问题得到当前迭代的最优搜索步长ηk.
3.1 正则化参数选择正则化参数λ是权衡数据吻合误差和模型平滑程度的权重,小λ会得到粗糙的成像结果,反演数据过度吻合含有噪声的观测数据;相反,大的λ会得到过于光滑的成像结果,而反演数据与观测数据吻合度较低.因此,合适的选择正则化参数对于反演结果的可信性和稳定性非常重要.有多种考虑数据吻合和模型平滑程度的正则化方法[25],其中差异原则是已知噪声估计时只考虑数据吻合误差的方法,L曲线法是一种无需先验信息但是不完全稳定的方法.当计算一系列λ时,数据吻合误差Φd与模型平滑度Φm曲线呈现出L形状,如图 2所示.显然,L曲线“拐角”对应的λ应该是权衡Φd与Φm的最优值,而“拐角”的位置可由L曲线的最大曲率获得,如图中λ=7017.
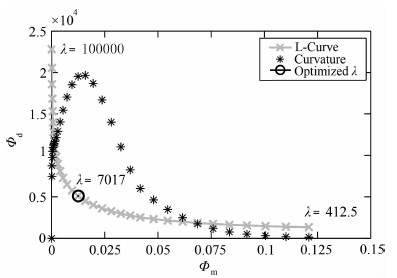
|
图 2 L曲线法确定模型平滑度 Fig. 2 Model smoothness determined by L-curve method |
由于该优化问题在强正则化时比较稳定,本文首先采用相对较大的λ进行反演,然后逐渐减小λ值,直到L曲线的曲率出现衰减.同时,根据差异原则
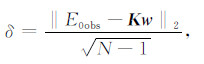
|
(13) |
其中,N是数据个数.当δ小于环境噪声估计,则此时的λ为最优正则化参数.因此,可以同时进行两种方法,当满足其中一种方法时停止,此时的λ既不会过度吻合,也不会欠吻合观测数据.
3.2 参数约束条件的确定由于野外观测数据均为实数,而核函数K是复数,在反演时通常对计算结果进行取模处理,即
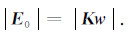
|
(14) |
此时,式中数据和模型是非线性的,需要首先进行线性化.本文采用雅可比矩阵法,计算数据对模型的导数,通过推导获得:
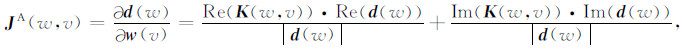
|
(15) |
其中,d=Kw,Re和Im分别代表实部和虚部.接着,可用该雅可比矩阵JA来限定反演变量的取值范围.对于地下含水量w,其取值范围为[0, 1],因此需要将w映射到一个全空间变量f(w)∈ [-∞,∞].应用tan函数,并应用上边界约束条件ub,则:
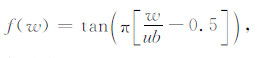
|
(16) |
而对于JA表示为:

|
(17) |
因此,反演过程每一步迭代所要求解的表达式为
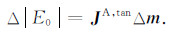
|
(18) |
地面磁共振响应核函数代表了接收线圈对地下含水体的灵敏度大小.为研究分布式系统多个接收线圈的灵敏度差异,本文对磁共振响应核函数进行了仿真.首先建立模型,采用100 m单匝正方形发射线圈,8个双匝25 m边长正方形接收线圈组成测量剖面;发射脉冲矩q,范围为0.1~10 A·s;地磁场B0设为54000 nT,Larmor频率fL为2044 Hz;地磁倾角I为60°;采用电阻率ρ为100 Ωm的均匀半空间模型;测量剖面的方位角α分别为0°N,45°N和90°N.
图 3所示为二维分布式磁共振响应核函数仿真结果,图中仅列出一个脉冲矩(q=1 A·s)的结果,第一行到第三行分别代表α=0°N,45°N与90°N,分别对应图 1中的三种测线布置.分布式磁共振测深具有较高的灵敏度,特别是在发射线圈Tx附近.脉冲矩q较小时,每个接收线圈Rx下方地表浅部具有最高灵敏度,随着q的增加,逐渐向下扩展到达较深区域.发射线圈Tx外的接收线圈Rx1、Rx2、Rx7和Rx8同样具有较高灵敏度,可以提供较宽的横向范围,这一点优于同一线圈和分离线圈测量模式.对于不同的测量剖面方位角α,核函数呈现出不同的特征.当α为0°时,接收线圈Rx1-Rx8的核函数相对于发射线圈Tx中心是不对称的,因为计算核函数时主要用到激发场垂直于地磁场B0的分量,而此时地磁场的方向与α在同一平面上,因此地磁倾角影响最大,导致发射线圈Tx内部的接收线圈Rx3-Rx6的总灵敏度逐渐减小;当α为45°时,地磁场方向不在α所在平面上,这种不对称性减弱,但接收线圈Rx3-Rx6的总灵敏度仍然逐渐减小;当α为90°时,地磁场方向与α所在平面垂直,地磁倾角I无影响,所以核函数相对于发射线圈的中心是对称的,接收线圈Rx1-Rx4的总灵敏度分别近似等于Rx8-Rx5的总灵敏度.
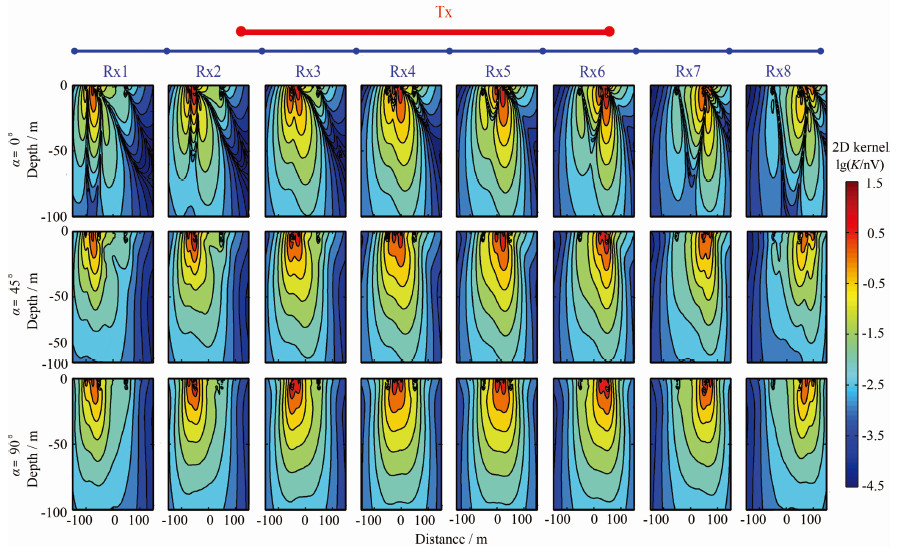
|
图 3 二维磁共振核函数仿真 Fig. 3 Two-dimensional MRS kernel function simulation |
这种特性也体现在分布线圈的磁共振信号的初始振幅E0上.设地下10 m到20 m有一层状含水层,含水量100%,图 4所示即为不同方位角α的测线上8个接收线圈采集的磁共振信号初始振幅E0的仿真结果.对于α=90°,发射线圈Tx内的接收线圈Rx3到Rx6的磁共振信号初始振幅E0是对称的,且E0最大值对应的脉冲矩q基本一致,发射线圈Tx外的接收Rx1、Rx2、Rx7和Rx8的信号初始振幅E0也分别对称.但对于α=0°和45°,发射线圈内Rx3到Rx6的信号初始振幅E0最大值和其对应的脉冲矩q均逐渐下降.发射线圈外Rx1、Rx2、Rx7和Rx8的信号变化较复杂,但是幅度均低于α=90°时.综上,对于同一深度的含水层,东西方向测量时,产生磁共振信号初始振幅最大值所需的脉冲矩基本相同,而其他方向测量时,偏南的接收线圈所需脉冲矩大,信号初始振幅也较大;偏北的所需脉冲矩小,信号初始振幅也较小.因此,测线方位角是二维分布式磁共振正演的重要参数,也是MRT成像时所需的关键参数.
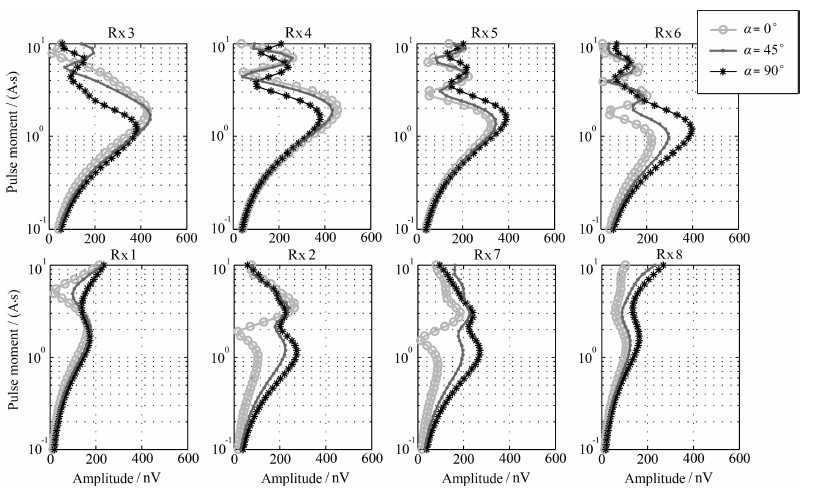
|
图 4 分布式接收线圈的磁共振响应 Fig. 4 MRS resonance signal of distributed receiver coils |
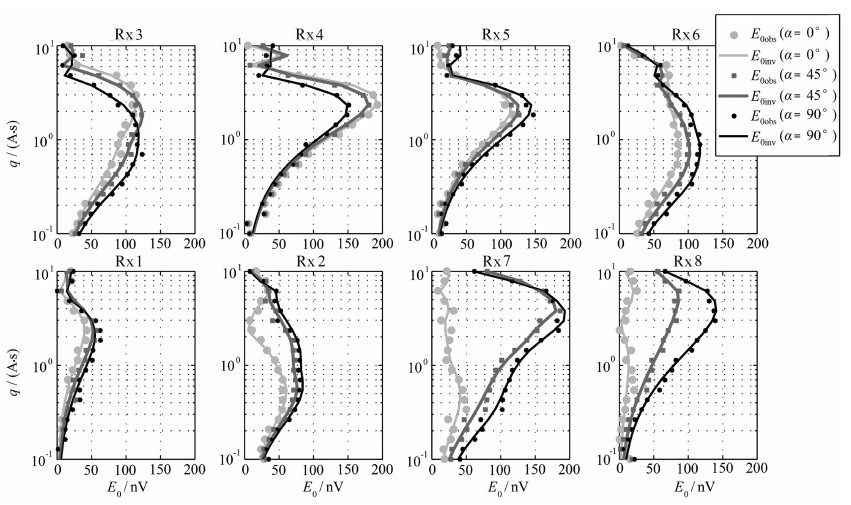
为了验证分布式磁共振系统进行二维地下水分布解释的效果,再设计一个更为复杂的地下含水体模型,如表 1和图 5a所示,含水体模型在不同测线上的分布保持一致.通过正演计算可以得到8个接收线圈在具有不同方位角α的测线上测量的磁共振信号初始振幅E0对脉冲矩q的曲线,如图 6所示.为了模拟野外环境,对信号初始振幅叠加了方差为5 nV的高斯噪声.图 5b、c和d分别是不同测线方位角对应的二维初始振幅反演结果.通过比较三个反演结果的差异,可以分析不同测线方位角对应的二维分布式磁共振系统对地下含水体的反演分辨率.
|
|
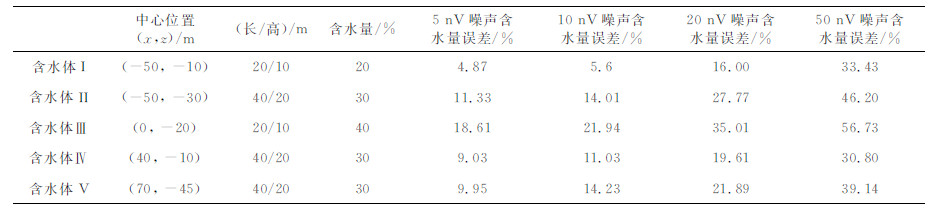
表 1 不同噪声水平下的含水量反演结果误差(α=0°) Table 1 Water content inversion errors with different noise levels (α=0°) |

|
图 5 模型设定与反演结果.(a)含水模型;(b)α=0°N反演结果;(c)α=45°N反演结果;(d)α=90°N反演结果 Fig. 5 Modeling of aquifer and inversion results.(a) Water-bearing model; (b) Inversion results for α=0°N; (c) Inversion results for α=45°N; (d) Inversion results for α=90°N |
|
图 6 二维剖面角度变化的E0-q的曲线 Fig. 6 E0-q curves of two-dimensional profile angle variations |
对于α=0°N南北测量剖面,含水体I和含水体Ⅱ的位置和含水量能够准确反映原始模型,说明发射线圈边框下方的分辨率较高;针对含水量最大的含水体Ⅲ的水平位置发生偏差,且含水量值偏低,表明发射线圈中心位置分辨率最低;含水体IV的位置和含水量均能与原始模型基本一致,说明对发射线圈外部的浅层含水体分辨率较高;含水体Ⅴ的位置和含水量与原始模型相近,但是两侧向外延伸,与含水体Ⅲ和Ⅳ相接,说明即使是发射线圈边框下,分辨率随深度增加亦逐渐下降.
对于α=45°N测量剖面,含水体Ⅰ和Ⅱ的反演效果仍然较好,含水体Ⅳ的反演效果较粗糙,但是基本符合原始模型.含水体Ⅲ和Ⅴ的反演效果较差,两者连成一个含水体,位置均偏离原始模型,同样说明发射线圈中心和深层的分辨率很差.
对于α=90°N东西测量剖面,含水体Ⅰ和Ⅱ的反演效果最好,与南北测量剖面的结果相当.含水体Ⅲ的垂直位置发生偏移,且含水量估计过低,再次证明中心位置分辨率较低.含水体Ⅳ的反演效果较好,优于南北测量剖面.含水体Ⅴ的反演效果较差,再次证明深层分辨率较低.
综合以上结果可以得出:发射线圈边框下方的反演分辨率最高,边框外浅部的分辨率较好,发射线圈中心的分辨率较差,随着深度增加,分辨率均下降.对比图 6中三种测量剖面反演结果计算的磁共振信号初始振幅曲线与仿真信号曲线,两者吻合程度较高,误差均在噪声水平(5 nV)范围内,说明Occam方法反演结果能够准确反映观测曲线,既不获取过于平滑的反演模型,也不过度吻合含噪声观测曲线.
如图 7所示,二维磁共振反演结果还与环境噪声水平密切相关,环境噪声增大时,反演分辨率迅速下降.图 7所示是对同样的模型上南北测量剖面的磁共振信号初始振幅的仿真结果,分别加入了10 nV、20 nV和50 nV的高斯噪声.与环境噪声5 nV时的反演结果相比,10 nV噪声下的反演结果能较好地反映原始模型的含水体Ⅰ、Ⅱ和Ⅳ,而对于含水体Ⅴ,只能大致反映出该含水体位置,而含水量和范围无法准确确定,而对于含水体Ⅲ则完全没有反映.在20 nV噪声下,只有含水体Ⅰ和Ⅳ能够有所反映,而含水体Ⅱ和Ⅴ的位置、范围和含水量均出现偏差,含水体Ⅲ同样无反映.50 nV噪声下的反演结果最差,几乎无法与原始模型对应,所有的含水体位置和含水量不准确,而此时的噪声水平已经相当于仿真信号最大值25%,即多数MRS信号均淹没到噪声水平之下.综上所述,随着环境噪声的增加,反演分辨率显著下降,对于分辨率极低的中心探测位置,噪声带来的影响被认为是“致命”的.表 1中以α=0°为例,详细列举了不同噪声水平下的模型含水量拟合误差.

|
图 7 噪声影响下的反演结果.(a)含水模型;(b)10 nV噪声反演结果;(c)25 nV噪声反演结果;(d)50 nV噪声反演结果 Fig. 7 Inversion results under effect of noise.(a) Water-bearing model; (b) Inversion results for 10 nV noise; (c) Inversion results for 20 nV noise; (d) Inversion results for 50 nV noise |
综上所述,该分布式探测模式,采用同一线圈发射,多个单元分布式接收,实现对地下二维水体的探测,能够有效地提高横向分辨率.这种探测与多通道仪器分离线圈模式相比具有更高的探测效率,通过一次发射可同时获取多组MRS信号.
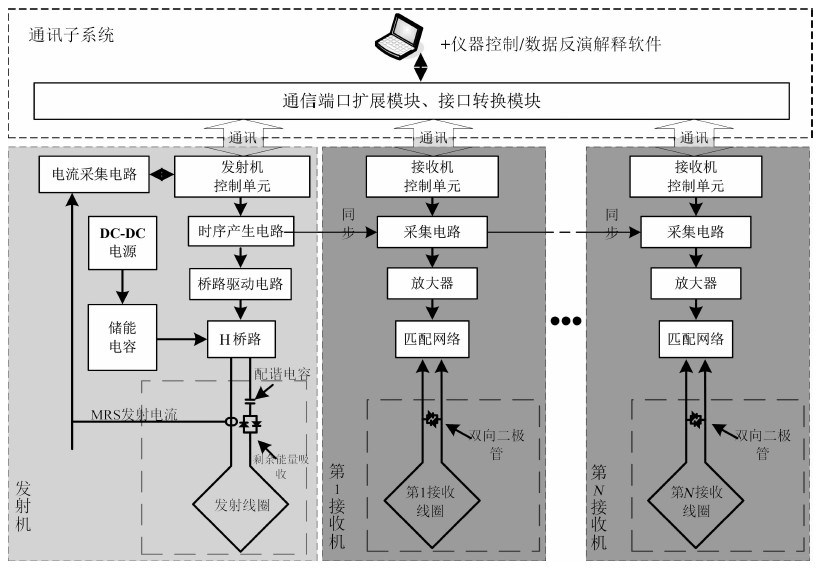
而上述收发模式也对分布式磁共振地下水探测系统的研制提出了一系列难题,包括:(1)实现中心发射线圈(100 m)的大电流发射,以最大程度地提高探测深度.(2)降低放大器的噪声水平,使相对较小的探测线圈(如25 m)能最大程度地获取有效信号,并使得放大器随环境噪声强度自动调整.(3)进行各采集站放大器标定与校正,以满足正演理论计算的各线圈标准水平,使得反演结果更为准确、可靠.(4)降低仪器死区时间,以探测粘土束缚状地下水(弛豫时间一般小于30 ms).
在2010年验收的国家十一五科技支撑计划重大项目课题《核磁共振找水仪的研制与开发》中,吉林大学完成了JLMRS-I型收发共线模式(同一线圈)仪器的研制(表 2),其各项性能指标优于同类型法国仪器NumisPLUS.借助已有的仪器开发平台,结合正反演研究结果,针对上述亟待解决的问题,本文开展了分布式磁共振地下水探测仪器系统的研发,如图 8所示,突破了如下关键技术:(1)基于大容量高压电容的瞬态大功率电源技术,在兼顾仪器重量和电容容量的情况下,选用0.132F的高压电容作为储能电容,实现了最大激发脉冲矩为20000 A·ms、最大发射电流为500 A的发射系统研制;(2)通过弱信号检测与窄带滤波技术,实现了测量范围为5~104 nV,中心频率调整范围为1.3~3.7 kHz,前置放大器增益调整范围0~40 dB,总增益调整范围为70~150 dB,本底噪声为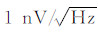
|
|
表 2 国际上MRS仪器参数对比 Table 2 Comparison of parameters of three MRS instruments in the world |
|
图 8 分布式核磁共振地下水探测系统总体结构框图 Fig. 8 Block diagram of Distributed Surface Magnetic Resonance Sounding system |
为了验证分布式磁共振地下水探测仪器的探测效果,本文在吉林省长春市烧锅镇测试地点进行了完整的二维磁共振数据采集(图 9).

|
图 9 分布式核磁共振地下水探测系统野外工作场景图 Fig. 9 Photograph showing work site of MRS distributed groundwater detection system |
测试地点的地磁场强度为54627 nT,Larmor频率为2326 Hz,地磁倾角60°.测量时,发射线圈采用单匝100 m正方形线圈,接收线圈采用8个25 m方形线圈边对边排成一行,其中发射线圈内的4个接收线圈为双匝,而发射线圈外两边各两个接收线圈,为了提高信号幅度,匝数设为四匝.测量剖面的方向角度为-39°N.发射脉冲矩为16个,范围从0.4 A·s到10 A·s.考虑到该分布式线圈配置和较低的电阻率分布(瞬变电磁探测法显示地下电阻率为100 Ωm),反演深度由此设为60 m.测量弛豫信号的时间长度为250 ms,在发射停止后经过18 ms的死区时间开始测量.
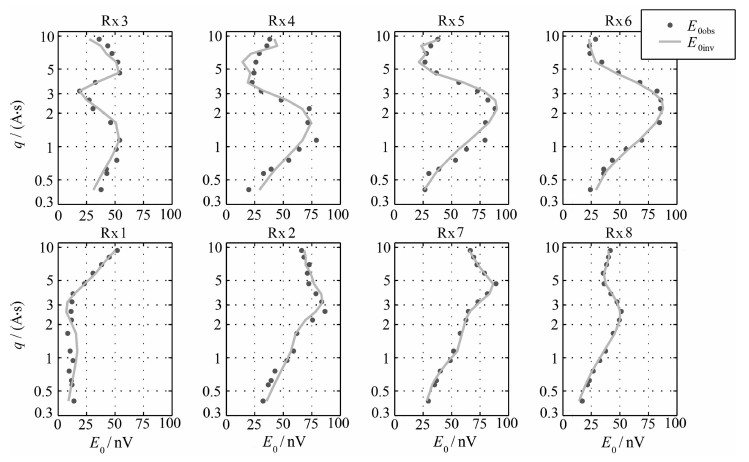
8个接收线圈采集到的磁共振信号初始振幅见图 10(绿色点)所示.测量数据的信噪比较高,环境噪声水平为9.7 nV.接收线圈Rx3-Rx5的信号初始振幅最大值对应的脉冲矩逐渐增加,与上文讨论的测量剖面方向角度与信号对称性的关系一致.发射线圈外的接收线圈Rx1、Rx2、Rx7和Rx8由于增加了匝数,采集的信号质量较好.利用采集到的所有磁共振信号数据进行MRT反演,设置含水量最大值为20%,初始模型为地下空间均为含水量5%的含水层,正则化参数通过L曲线方法和差异原则共同选取.二维反演结果计算的磁共振测量信号初始振幅如图 10(蓝色线)所示,与观测结果吻合较好.二维反演结果可以清晰地看出在地下-10~-20 m之间的层状含水层,含水量不完全均匀,但几乎没有间断.而在深层-30~-40 m的位置,只有水平位置为-100~-50 m处存在主要含水层,其他位置的含水量很低,反演结果仍然体现为二维含水构造,而并不是完整的层状水.将该反演结果与该测点附近存在的已知钻孔结果比对,如图 11所示.测试地点的地质结构由砂层和第四系地层的互层组成,钻孔结果显示地下存在一个浅层的含水层(深度位于13~25 m)和两个含水薄层(深度分别位于37.5~39 m和45~50 m).所有的含水层都是不均匀的,由不同岩性的薄层相互重叠组成,特别是浅层含水层包含了从细砂到粗砂和砾质砂层.二维Occam反演结果趋近于层状分布,含水层反演位置与钻孔结果能够良好对应.
|
图 10 接收线圈(Rx1-Rx8)的初始振幅曲线E0obs与反演拟合曲线E0inv Fig. 10 Initial amplitude curve E0obs and inversion fitting curve E0inv of receiving coil (Rx1-Rx8) |

|
图 11 烧锅地区2D反演结果图与钻井资料 Fig. 11 2D inversion results and the drilling data in Shaoguo area |
本文建立了二维分布式磁共振测量的正反演方法,利用研制分布式磁共振系统,结合野外实测数据,得出如下结论:
(1)研究首先定义了地磁场环境中,实际二维测量中的剖面方位角α,建立了分布式接收线圈MRS响应核函数表达式,实现了二维正演计算,仿真结果显示,进行东西方向剖面测量时,产生磁共振信号初始振幅最大值所需的脉冲矩基本相同,而剖面位于其他方向时,偏南接收线圈所需的脉冲矩大,信号初始振幅也较大;偏北的所需脉冲矩小,信号产生的初始振幅也较小.
(2)本文实现了Occam反演方法,用于MRT磁共振断层成像之中.通过不同测量角度,设定多个含水层模型,均得出相似反演结果,即分布式探测模式在发射线圈边框下方分辨率最高,边框外浅部的分辨率较好,而发射线圈中心分辨率较差,随着深度增加,分辨率均下降.反演解释还与环境噪声水平相关,当噪声为50 nV时,结果已无法与模型相对应,含水量反演误差极大.
(3)研制了8通道分布式探测系统,结合正反演理论,用于长春市郊区烧锅镇地下水评价之中,通过与钻井资料的比对,验证了二维分布式探测方法与仪器系统的有效性.
8 展望美国多通道磁共振系统GeoMRI的诞生,突破了传统一维探测模式,是国际MRS仪器发展至今的里程碑.吉林大学仪器科学与电气工程学院核磁共振课题组研制的MRS分布式探测系统,靶向国际前沿技术,弥补了我国在MRS领域二维探测仪器研制的空白.因其开发了多个拓展通道,从而具备相对GeoMRI更高的工作效率.同时,本文建立的分布式MRS探测相关理论将为该系统在复杂地质环境中进行地下水探测,奠定更为坚实的基础.
| [1] | Schirov M, Legchenko A, Greer G. A new direct non-invasive groundwater detection technology for Australia. Exploration Geophysics , 1991, 22(22): 333-338. |
| [2] | Legchenko A, Valla P. A review of the basic principles for proton magnetic resonance sounding measurements. Journal of Applied Geophysics , 2002, 50(1-2): 3-19. DOI:10.1016/S0926-9851(02)00127-1 |
| [3] | Legchenko A, Baltassat J M, Beauce A, et al. Nuclear magnetic resonance as a geophysical tool for hydrogeologists. Journal Applied Geophysics , 2002, 50(1-2): 21-46. DOI:10.1016/S0926-9851(02)00128-3 |
| [4] | Legchenko A, Valla P. Processing of surface proton magnetic resonance signals using non-linear fitting. Journal of Applied Geophysics , 1998, 39(2): 77-83. DOI:10.1016/S0926-9851(98)00011-1 |
| [5] | Legchenko A, Shushakov O. Inversion of surface NMR data. Geophysics , 1998, 63(1): 75-84. DOI:10.1190/1.1444329 |
| [6] | 林君. 核磁共振找水技术的研究现状与发展趋势. 地球物理学进展 , 2010, 25(2): 681–691. Lin J. Situation and progress of nuclear magnetic resonance technique for groundwater investigations. Progress in Geophysics (in Chinese) , 2010, 25(2): 681-691. |
| [7] | 林君, 段清明, 王应吉. 核磁共振找水仪原理与应用. 北京: 科学出版社, 2010 . Lin J, Duan Q M, Wang Y J. Theory and Design of Magnetic Resonance Sounding Instrument for Groundwater Detection and Its Applications (in Chinese). Beijing: Science Press, 2010 . |
| [8] | Yaramanci U, Lange G, Hertrich, M. Aquifer characterisation using Surface NMR jointly with other geophysical techniques at the Nauen/Berlin test site. Journal of Applied Geophysics , 2002, 50(1-2): 47-65. DOI:10.1016/S0926-9851(02)00129-5 |
| [9] | Chalikakis K, Nielsen M, Lechenko A. MRS applicability for a study of glacial sedimentary aquifers in central Jutland, Denmark. Journal of Applied Geophysics , 2008, 66(3-4): 176-187. DOI:10.1016/j.jappgeo.2007.11.005 |
| [10] | Vouillamoz J, Faverau G, Massuel S, et al. Contribution of magnetic resonance sounding to aquifer characterization and recharge estimate in semiarid Niger. Journal of Applied Geophysics , 2008, 64(3-4): 99-108. DOI:10.1016/j.jappgeo.2007.12.006 |
| [11] | Weichman P B, Lavely E M, Ritzwoller M. Surface nuclear magnetic resonance imaging of large systems. Physical Review Letters , 1999, 82(20): 4102-4105. DOI:10.1103/PhysRevLett.82.4102 |
| [12] | Weichman P B, Lavely E M, Ritzwoller M H. Theory of surface nuclear magnetic resonance with applications to geophysical imaging problems. Physical Review E , 2000, 62(1, Part B): 1290-1312. DOI:10.1103/PhysRevE.62.1290 |
| [13] | Hertrich M. Magnetic resonance sounding with separated transmitter and receiver loops for the investigation of 2d water content distributions. Berlin: School of Civil Engineering and Applied Geosciences, Technical University, 2005. |
| [14] | Hertrich M, Braun M, Yaramanci U. Magnetic resonance soundings with separated transmitter and receiver loops. Near Surface Geophysics , 2005, 3(3): 141-154. |
| [15] | Hertrich M, Braun M, Günther T, et al. Surface nuclear magnetic resonance tomography. IEEE Transactions on Geoscience and Remote Sensing , 2007, 45(11): 3752-3759. DOI:10.1109/TGRS.2007.903829 |
| [16] | Mueller-Petke M, Hertrich M, Yaramanci U. Analysis of magnetic resonance tomographic (MRT) kernels for optimized field layouts.// 3rd Magnetic Resonance Sounding Workshop, A reality in applied hydrogeophysics. Spain, Madrid, 2006: 37-40. |
| [17] | Hertrich M, Yaramanci U. Magnetic resonance sounding data inversion.// 3rd Magnetic Resonance Sounding Workshop, A reality in applied hydrogeophysics. Spain, Madrid, 2006: 15-20. |
| [18] | Walsh D O. Multi-channel surface NMR instrumentation and software for 1D/2D groundwater investigations. Journal of Applied Geophysics , 2008, 66(3-4): 140-150. DOI:10.1016/j.jappgeo.2008.03.006 |
| [19] | 潘玉玲, 贺颢, 李振宇. 地面核磁共振找水方法在中国的应用效果. 地质通报 , 2003, 22(2): 135–139. Pan Y L, He H, Li Z Y. Surface detection of groundwater with the nuclear magnetic resonance method and its application results in China. Regional Geology of China (in Chinese) , 2003, 22(2): 135-139. |
| [20] | 翁爱华, 李舟波, 王雪秋. 层状导电介质中地面核磁共振响应特征理论研究. 地球物理学报 , 2004, 47(1): 156–163. Weng A H, Li Z B, Wang X Q. A study on surface nuclear magnetic resonance over layered conductive earth. Chinese Journal of Geophysics (in Chinese) , 2004, 47(1): 156-163. |
| [21] | 翁爱华, 李舟波, 王雪秋. 地面核磁共振响应数值模拟研究. 物探化探计算技术 , 2002, 24(2): 97–101. Weng A H, Li Z B, Wang X Q. Numerical simulation of surface NMR. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 2002, 24(2): 97-101. |
| [22] | 翁爱华, 王雪秋, 刘国兴, 等. 导电性影响的地面核磁共振反演. 地球物理学报 , 2007, 50(3): 890–896. Weng A H, Wang X Q, Liu G X, et al. Nonlinear inversion of surface nuclear magnetic resonance over electrically conductive medium. Chinese Journal of Geophysics (in Chinese) , 2007, 50(3): 890-896. |
| [23] | 蒋川东, 林君, 段清明, 等. 二维阵列线圈核磁共振地下水探测理论研究. 地球物理学报 , 2011, 54(11): 2973–2983. Jiang C D, Lin J, Duan Q M, et al. A study on 2D magnetic resonance sounding with an array loop for groundwater exploration. Chinese Journal of Geophysics (in Chinese) , 2011, 54(11): 2973-2983. |
| [24] | Constable S C, Parker R L, Constable C G. Occam's inversion: A practical algorithm for generating smooth models from electromagnetic sounding data. Geophysics , 1987, 52(3): 289-300. DOI:10.1190/1.1442303 |
| [25] | Farquharson C G, Oldenburg D W. A comparison of automatic techniques for estimating the regularization parameter in non-linear inverse problems. Geophysical Journal International , 2004, 156(3): 411-425. DOI:10.1111/gji.2004.156.issue-3 |
 2013, Vol. 56
2013, Vol. 56