2. 中海石油(中国)有限公司上海分公司研究院, 上海 200030;
3. 中海油田服务股份有限公司, 天津 300451
2. Institute of ShangHai Branch, CNOOC Ltd., XuHui Area, Shanghai 200030, China;
3. China Oilfield Services Limited (COSL), Tianjin 300451, China
地震资料的不连续信息在断层、河道、盐丘等地质体的解释过程中具有重要地位,因此,实现对地震数据不连续性信息的检测是一项重要任务.目前,相干体、曲率体技术[1-2]等很多方法都能够实现地震资料不连续性检测.
边缘检测是起源于图像处理领域的一门重要技术,主要用于检测图像中灰度值突变区域.引申到地震勘探领域,地震资料中的不连续性区域反映在图像中即为边缘特征[3].因此将边缘检测技术用于地震资料不连续信息的检测非常有意义.
边缘检测技术在地震资料处理中的应用已经有了十几年的历史.众多学者对边缘检测技术的实际应用做了大量研究,提出了多种基于不同算法的、适用于不同尺度地质体的边缘检测技术,如基于高阶伪希尔伯特变换算法的边缘检测技术、小尺度特征地震边缘检测技术[4-5]等.国内边缘检测技术方面的文章多数应用于二维地震图像,包括薄地层识别、剖面同相轴自动识别及检测、初至波同相轴提取、裂缝检测以及砂体边界识别等[3, 6-11],对于其在三维地震资料中的应用未作出深入研究;国外方面,一些学者提出将边缘检测技术应用到三维地震资料处理中的方法,涉及到盐丘边界识别、断层边界识别等[12-14].
梯度极大值边缘检测具有原理简单、计算量小的优点,被广泛应用于图像处理领域,代表算子有Sobel算子、Facet模型曲面拟合算子等.上述常规算子如果直接用于三维地震数据地质体边界识别,并不能取得良好的效果,其原因有两点:1)常规算子将地震资料的不连续性信息不加筛选的全部检测出来,这导致地震资料中连续性很好的地层边界信息对小断层、微裂缝边界的检测有着很强的干扰.2)常规边缘检测算子检测梯度值为绝对梯度值,这使得小地质体边界的弱反射信息淹没在强背景地层边界反射信息中.
Y.Luo(1996)提出了差分算子思想,该思想对沿层边缘检测的实现有着重要的指导意义.基于该思想,Aqrawi(2011)利用互相关方法求取地层倾角,然后将倾角约束Sobel边缘检测算子应用于断层和盐丘边界检测中,取得很好效果.本文借鉴Aqrawi(2011)思想,利用梯度结构张量方法[15]估计地层倾角和方位角,给出结构导向梯度属性算子计算公式,通过与结构导向方差属性检测结果对比分析,验证了该方法的可行性.
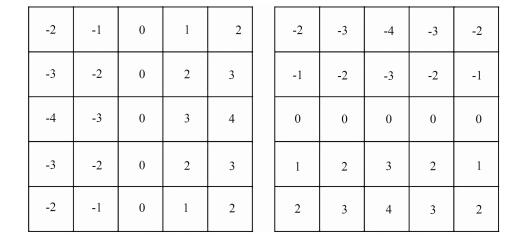
2 方法原理 2.1 常规Facet模型曲面拟合算子梯度极大值边缘检测技术通过利用差分模板对原始地震图像进行检测来获得梯度模值图像.由于边缘存在的区域通常表现为局部梯度极大值,可以根据模值图像中模值的大小判断边缘发育情况.常规5×5Sobel差分模板如图 1所示.Sobel模板数值的确定往往凭借经验,因此不易进行扩展.
|
图 1 Sobel算5×5窗口大小两个方向卷积模板 Fig. 1 5×5 convolution template of Sobel operator for two direction |
1984年,Haralick提出了基于多项式曲面拟合的Facet模型边缘检测算子[16].Facet检测算子的基本思想可以描述为如下过程:
I(r,c)表示局部邻域S内数据,利用式(1)所示二元三次多项式对I(r,c)进行最小二乘拟合求取拟合系数,利用求得的拟合系数构建拟合函数f(r,c),最终对拟合函数f(r,c)求取梯度模值.这样,原来直接对图像邻域数据进行的模板操作转化为对拟合函数的处理.该方法能够在抑制噪声的同时提高边缘定位精度,而且算子更易扩展.拟合函数为
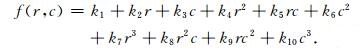
|
(1) |
式中ki为拟合系数.为了方便拟合系数的计算,通常将式(1)用正交多项式组合来代替,即:
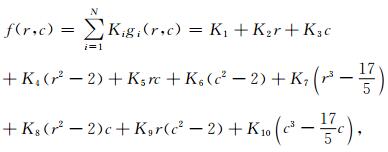
|
(2) |
其中gi(r,c)代表第i个正交多项式.利用最小二乘法可以得到式(3):
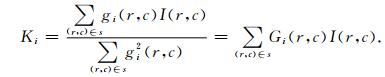
|
(3) |
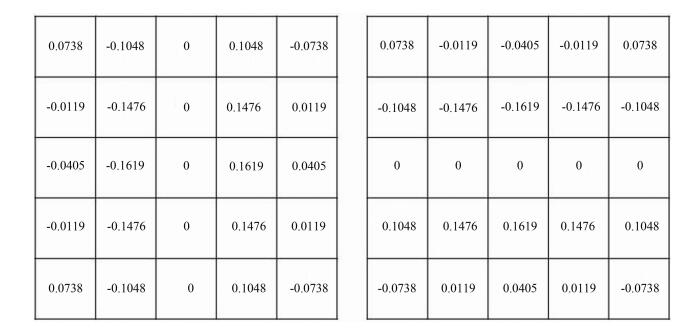
可见每一个Ki都可以单独由I(r,c)的线性组合表达,其中Gi为Ki对应的卷积模板.对比式(1)和式(2)可知,ki可以由Ki线性表示.因此,为了求取f(r,c)的梯度幅值,只需要求得k2和k3.k2和k3对应的卷积模板Gr和Gc则可以由Gi卷积模板线性表示.通过上述转换和推导,曲面拟合方法求取梯度最终转化为利用两个相互正交的模板Gr和Gc对原始图像局部邻域进行模板卷积的过程,5×5窗口大小模板系数如图 2所示:
|
图 2 Facet模型算子5×5窗口大小两个方向卷积模板 Fig. 2 5×5 convolution template of Facet operator for two direction |
利用背斜模型验证Facet模型算子检测效果. 图 3所示为背斜模型,图中加入了5db高斯白噪,图 3a为抽取的一条纵测线剖面,图 3b为时间切片.为了对比分析Facet检测结果,同时利用Sobel算子进行检测,处理中Facet模板和Sobel模板均为3×3.

|
图 3 原始背斜模型 (a)纵测线背斜剖面; (b)时间切片. Fig. 3 Original Anticline model (a) Anticline section of inline; (b) Time slice. |
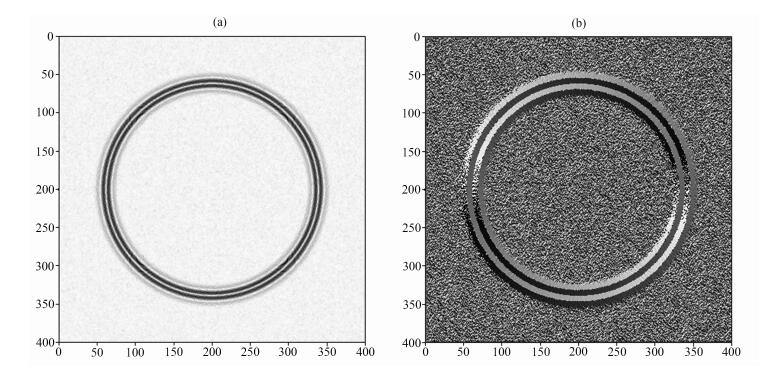
Sobel算子检测结果和Facet算子检测结果分别如图 4和图 5所示.对比图 4和图 5可以发现,Facet模型算子检测结果不但具有定位精度高的优点,而且相比其他算子抑噪性能更好,在噪声压制和定位精度上都有很大提高.

|
图 4 Sobel算子背斜模型检测结果 (a)梯度值; (b)幅角. Fig. 4 Sobel operator detection result of Anticline model (a) Gradient magnitude result; (b) Argument result. |
|
图 5 Facet算子背斜模型检测结果 (a)梯度值; (b)幅角. Fig. 5 Facetoperator detection result of Anticline model (a) Gradient magnitude result; (b) Argument result. |
常规边缘检测算子输出绝对梯度模值,导致地震资料中小地质体边界弱反射信息在地震剖面上没有良好的响应特征.基于此,通过引入能量归一化因子对常规算子进行改进,以r方向为例,绝对梯度值计算公式由式(4)
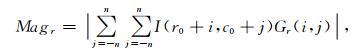
|
(4) |
改进为式(5):
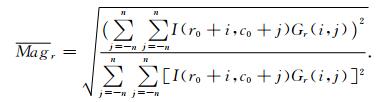
|
(5) |
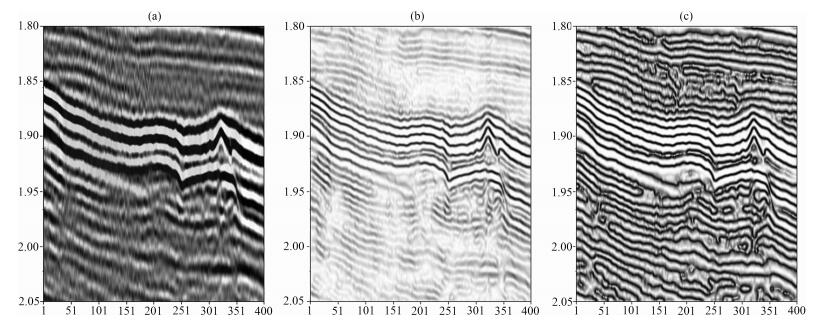
利用常规Facet算子和能量归一化后的Facet模型算子对某地震剖面进行处理,处理前后如图 6所示.从原始剖面上可以看到,上覆巨厚石膏夹盐岩层经过后期构造运动,地层褶皱变形,在该地层下方存在的若干礁体,由于石膏夹盐岩层的波阻抗差太大,地震波能量难以穿透巨厚强反射界面,导致岩层下方礁体反射信息微弱.常规Facet模型算子对下层的弱信息无法突出显示,能量归一化Facet算子检测结果中,强的上覆地层信息和弱的礁体反射信息都得到了很好的显示.
|
图 6 常规算子和能量归一化算子处理效果对比 (a)原始剖面; (b)常规算子处理结果; (c)能量归一化算子处理结果 Fig. 6 Comparing of conventional operator and energy unified operator (a) Original profile; (b) Processing result of conventional operator; (c) Processing result of energy unified operator. |
引入能量归一化使得弱反射信号得到了增强显示,但是强的背景地层信息仍然存在,本文采用沿层思想,利用结构张量矩阵估计局部地层倾角和方位角信息,然后沿着局部地层发育方向提取分析窗口,再利用能量归一化梯度算子进行处理,以实现边界不连续性信息的识别和刻画,在下一节对该方法展开详细论述.
2.3 结构导向梯度属性的计算方法为了研究相干滤波,1999年Weickert提出了各向异性非线性扩散滤波技术,处理过程中通过利用结构张量的特征向量控制扩散方向,同时利用结构张量的特征值控制特征方向上的扩散量,实现对原始地震图像的平滑处理,增强具有一致性的同相轴及其所反映的重要地质结构,同时实现地震图像边缘信息的保护.处理中在地震资料局部结构特征分析的基础上进行扩散参数的调整,从而实现边界信息完整性的保持和噪音最大限度的消除[17].梯度结构张量算法所构建的梯度结构张量矩阵包含了丰富的局部地层信息,因此本文利用该算法估计局部地层结构倾角和方位角信息.令f(x,y,t)代表某三维地震数据体,如叠后偏移处理后的数据体或瞬时相位等地震属性体等,梯度结构张量矩阵定义为

|
(6) |
其中Gρ表示尺度为ρ的三维高斯函数,*表示褶积,fσ=Gσ*f, fσ为梯度.
梯度结构张量的求取过程可以用如下流程描述:
(1) 利用尺度为σ的三维高斯函数对f进行滤波,得到平滑后的数据体fσ,σ可以根据所要研究的地质体大小和数据体噪声水平综合确定,σ值越小,分析得到的地质体信息越精细,但噪声影响越大;σ值越大,分析得到的地质体信息越粗糙,但噪声压制效果越好;
(2) 对fσ求取梯度矢量和梯度张量;
(3)利用尺度为ρ的高斯函数对梯度张量进行高斯滤波,进一步抑制噪声,使得到的局部地层结构信息更准确.
从求取过程可以看出,最终局部地层结果的精细程度由尺度σ和ρ共同决定,一般选取较小的σ值(如0.5)和较大的ρ(如1.5).
不难证明实对称矩阵Tρ为半正定矩阵,它的特征值为不小于零的实数,并且不为零的特征值对应的特征向量相互正交.利用矩阵分解,Tρ可以变为
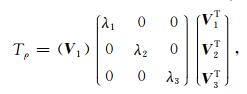
|
(7) |
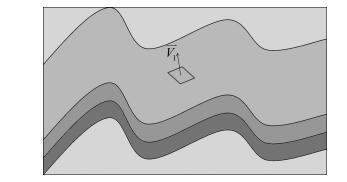
其中λ1≥λ2≥λ3≥0为Tρ的三个特征值,其各自对应的特征向量为V1、V2和V3.这些特征值和特征向量具有明显的物理意义,三个特征向量可以构成一个局部三维坐标系,V1是局部地层结构变化最快的方向,可以近似代表局部地层的法线方向(图 7),变化率为λ1;V2和V3所构成的平面垂直于V1,该平面上局部地层结构变化最快的方向为V2,变化率为λ2,变化最慢的方向为V3,变化率为λ3.
|
图 7 局部地层结构的法线方向 Fig. 7 The normal direction of local formation structure |
通过计算每个目标点所在层位的局部法线方向V1,可以求取x(横测线)方向和y(纵测线)方向的延迟时间τx(x,y,t)和τy(x,y,t),根据延迟时间可以提取局部地层分析窗口,在该分析窗口进行能量归一化算子处理,就可以消除背景地层边界信息的干扰.
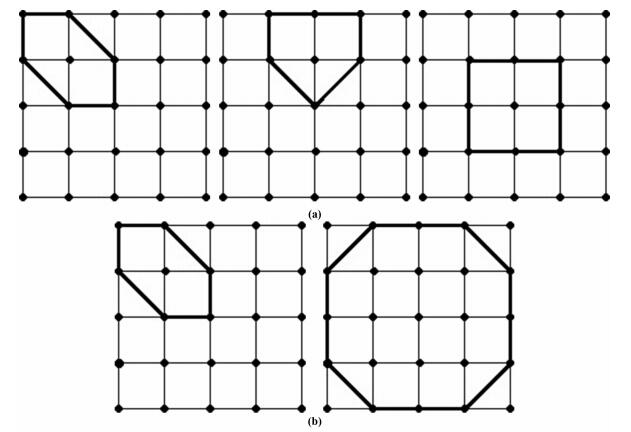
为了提高梯度属性的解释精度,抑制地震数据体中的噪声,文中采用多窗口划分思想进行局部地层分析窗口的提取.1976年Kuwahara首次提出多窗口滤波思想,其后,众多学者通过研究,给出了不同的多窗口划分方案.以5×5窗口为例,图 8给出了Y.Luo等的窗口划分方案和Rugumira Georgia等[18]的窗口划分方案.本文选用Y.Luo等提出的窗口划分方法,即图 8a所示,将5×5大小的窗口划分为9个小多边形,包括中央一个矩形,四个顶点处的四个六边形和四条边上的四个五边形.
|
图 8 二维多窗口保边滤波窗口划分示意图[18] (a) Y.Luo等人窗口划分思想, 在5×5邻域内包含四个五边形, 四个六边形和一个矩形; (b) RugumiraGeorgia等窗口划分思想, 在5×5邻域内包含四个六边形和一个八边形. Fig. 8 Window dividing diagram of two-dimensional multi-window edge-preserving filter (a) Window dividing method of Y.Luo, there are four pentagon, four hexagon and one rectangle in 5×5 neighborhood; (b) Window dividing method of Rugumira Georgia, there are four hexagon and one octagon in 5×5 neighborhood. |
利用延迟时间,可以提取局部沿层数据.延迟时间的求取可以采用以下两种方法:
(1)利用V1直接求取τx(x,y,t)和τy(x,y,t);
(2)根据几何关系,计算得到倾角数据体θ(x,y,t)和方位角数据体Φ(x,y,t),将θ(x,y,t)和Φ(x,y,t)转化为沿x方向和y方向的延迟时间τx(x,y,t)和τy(x,y,t),转化公式为
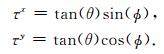
|
(8) |
本文采用第二种计算方法,该方法能够避免较大倾角情况下异常大值延迟时间的产生.
为了验证Facet检测算子检测效果,同时利用方差算子、Sobel算子进行处理.本文给出结构导向方差属性,结构导向Sobel梯度属性和结构导向Facet模型梯度属性三种属性计算公式.
结构导向方差属性的求取采用以下方法:
(1) 分别求取每个局部窗口均值,根据均值求取方差;
(2) 沿法线方向对各局部分析窗口求得的方差结果作和;
(3) 按能量对结果进行归一化处理.
为了增加输出结果的稳定性,处理中采用垂向2K+1个样点的叠加求均值作为输出,2K+1一般取一个子波延续时间内的样点数,具体计算公式为
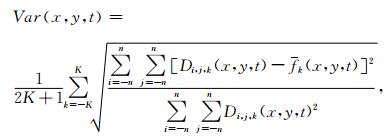
|
(9) |
其中x、y分别代表横测线和纵测线方向,D代表局部分析窗口所有样点在原始数据f(x,y,t)中的取值,f -代表窗口内所有样点均值,对于原始数据中无法采集的整数样点,可以采用插值算法求取近似值.
具有边缘保持效果的插值方法有多种,如基于边缘保持滤波器的多项式拟合插值算法[19],三次样条插值算法等.其中三次样条插值算法在边缘提取过程中抑制噪声和边缘定位精度的综合性能相对较为优秀,因此本文采用三次样条插值算法获取近似值.D和f的计算公式为

|
(10) |
其中Δt为采样率,τ i,j,kx(x,y,t)和τ i,j,ky(x,y,t)分别为与局部窗口中心点所对应的纵测线和横测线相同层位的延迟时间,标识含义如下式所示:
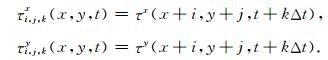
|
(11) |
在同样窗口大小和窗口数目的情况下,结构导向Sobel梯度属性计算公式为

|
(12) |
其中My和Mx代表Sobel算子两个正交方向模板.
结构导向Facet模型梯度属性计算公式为
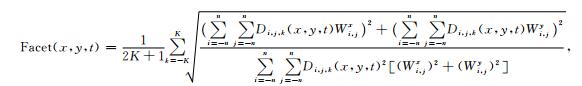
|
(13) |
其中Wy和Wx代表Facet模型算子两个正交方向模板.
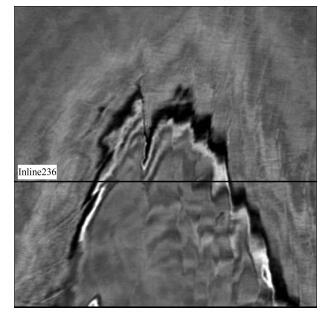
3 实际资料处理为了验证Facet算子检测结果,选取实际地震数据进行处理.选取来自荷兰境内北海F3区块三维地震数据体的一部分,该区域内发育大量东西走向断层,抽取原始资料第1560ms时间切片,如图 9所示.由于原始数据体噪声比较严重,为了抑制噪声,首先进行三维边缘保持滤波,对滤波后数据利用结构张量矩阵求取倾角和方位角数据体.
|
图 9 1560ms处的时间切片 Fig. 9 Time slice of 1560 ms |
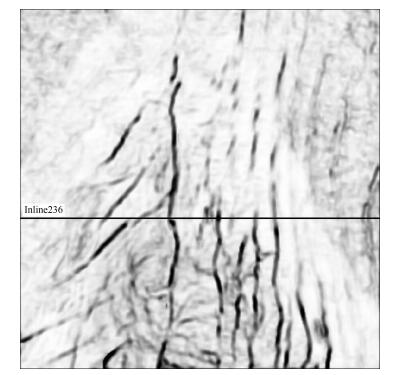
图 10~12为滤波后数据体结构导向方差属性、Sobel梯度属性和Facet模型梯度属性1560ms时间切片.图 13为局部放大对比图.三种属性的计算采取相同参数,窗口大小5×5,垂向时窗包含15个样.
|
图 10 结构导向的方差属性在1560ms处的时间切片 Fig. 10 Structure directed variance attribute slice of 1560 ms |

|
图 11 结构导向的Sobel梯度属性在1560ms处的时间切片 Fig. 11 Structure directed Sobel gradient attribute slice of 1560 ms |

|
图 12 结构导向的Facet模型梯度属性在1560 ms处的时间切片 Fig. 12 Structure directed Facet gradient attribute slice of 1560 ms |
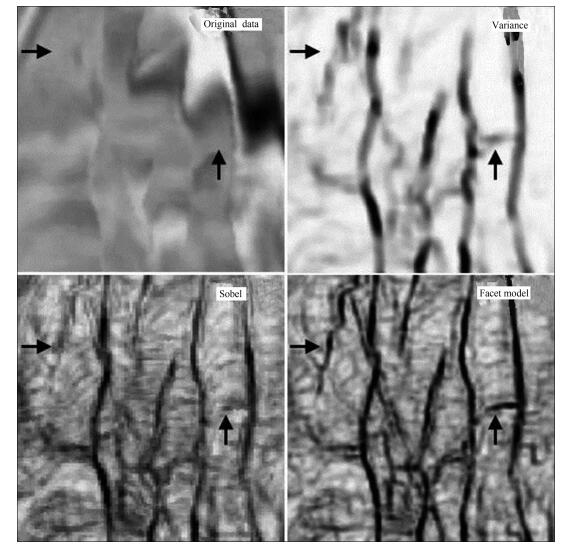
|
图 13 原始切片和三种属性不连续性检测结果的局部放大图 Fig. 13 Enlargement of original slice and three kinds of un-continuity detection |
由图 10方差属性结果可以看出,原始资料中的大断层信息基本得到展现,获取的属性在噪声抑制方面效果较好.对比图 11Sobel梯度属性,Sobel属性断层细节展现更好,一些弱的断层得到较好显示.将以上两种属性与本文提出的Facet模型梯度属性对比分析,Facet梯度属性具有更好的噪声抑制效果,细节信息最为丰富.
观察图 13局部放大对比图,Facet模型梯度属性对原始断层展示最为清晰,尤其对于反射信息较弱的小断裂发育区,刻画信息最为清晰,箭头所指区域给出良好展示.
4 结论为了实现储层小断裂、微裂缝等地震不连续性信息的边缘检测,本文对常规边缘检测算子进行了改进,一是引入能量归一化因子,突显了地震资料中小地质体边界弱反射信息,二是利用局部地层结构倾角和方位角信息约束,使边缘检测算子在增强弱信息的同时消除背景地层信息的干扰.利用结构导向方差属性算子,结构导向Sobel梯度属性算子和结构导向Facet模型梯度属性算子对实际数据进行处理,证明结构导向Facet模型梯度属性边缘检测算子检测结果最精细,包含边界信息最丰富,对小断层、微裂缝的识别最准确,可以作为一种地震资料精细解释工具.
| [1] | Bahorich M, Farmer S. 3-D seismic discontinuity for faults and stratigraphic features: The coherence cube. The Leading Edge , 1995, 14(10): 1053-1058. DOI:10.1190/1.1437077 |
| [2] | Wang Y S, Yang P J. Orientation steering fault preserving filtering. SEG Technical Program Expanded Abstracts , 2010, 29(1): 1550-1554. |
| [3] | 孙夕平, 杜世通. 边缘检测技术在河道和储层小断裂成像中的应用. 石油物探 , 2003, 42(4): 469–472. Sun X P, Du S T. Using edge detection technique to image channels and minor faults. Geophysical Prospecting for Petroleum (in Chinese) , 2003, 42(4): 469-472. (in Chinese) |
| [4] | 陈学华, 贺振华, 黄德济. 地震资料的高阶伪希尔伯特变换边缘检测. 地球物理学进展 , 2008, 23(4): 1106–1110. Chen X H, He Z H, Huang D J. Seismic data edge detection based on higher-order pseudo Hilbert transform. Progress in Geophysics (in Chinese) , 2008, 23(4): 1106-1110. (in Chinese) |
| [5] | 孙夕平, 周超. 小尺度边缘特征地震检测技术研究. 石油地球物理勘探 , 2011, 46(1): 121–125. Sun X P, Zhou C. Small-scale edge characteristic seismic detection technique. Oil Geophysical Prospecting (in Chinese) , 2011, 46(1): 121-125. (in Chinese) |
| [6] | 唐向宏, 贺振华. 图像边缘检测方法在薄地层识别中的应用. 石油地球物理勘探 , 2002, 37(2): 163–165. Tang X H, He Z H. Study for application of image edges detection to thin-layer recognition. Oil Geophysical Prospecting (in Chinese) , 2002, 37(2): 163-165. (in Chinese) |
| [7] | 李红星, 刘财, 陶春辉.图像边缘检测方法在地震剖面同相轴自动检测中的应用研究.地球物理学进展, 2007, 22(5): 1607-1610. Li H X, Liu C, Tao C H. The study of application of edge measuring technique to the detection of phase axis of the seismic section. Progress in Geophysics (in Chinese), 2007, 22(5):1607-1610, doi:1004-2903(2007)05-1607-04. http://www.cqvip.com/qk/98047x/200705/25854822.html |
| [8] | 苟量, 彭真明. 小波多尺度边缘检测及其在裂缝预测中的应用. 石油地球物理勘探 , 2005, 40(3): 309–313. Gou L, Peng Z M. Multi-scale edge detection of wavelet and application in fracture prediction. Oil Geophysical Prospecting (in Chinese) , 2005, 40(3): 309-313. (in Chinese) |
| [9] | 李辉峰, 邹强, 金文昱. 基于边缘检测的初至波自动拾取方法. 石油地球物理勘探 , 2006, 41(2): 150–155. Li H F, Zou Q, Jin W Y. Method of automatic first breaks pick-up based on edge detection. Oil Geophysical Prospecting (in Chinese) , 2006, 41(2): 150-155. (in Chinese) |
| [10] | 许辉群, 桂志先. 边缘检测技术砂体边界识别方法研究. 石油天然气学报 , 2009, 31(5): 75–77. Xu H Q, Gui Z X. Method to identify sandstone boundary with edge detection. Journal of Oil and Gas Technology (J.JPI) (in Chinese) , 2009, 31(5): 75-77. (in Chinese) |
| [11] | 熊会军, 管业鹏, 于蕴杰, 等. 基于图像边缘检测方法提取地震剖面同相轴. 地球物理学进展 , 2009, 24(6): 2250–2254. Xiong H J, Guan Y P, Yu Y J, et al. Extraction of cophasal axes on seismic sections based on the edge detection method. Progress in Geophysics (in Chinese) , 2009, 24(6): 2250-2254. DOI:10.3969/j.issn.1004-2903.2009.06.045 (in Chinese) |
| [12] | Luo Y, Higgs W G, Kowalik W S. Edge detection and stratigraphic analysis using 3D seismic data. SEG Technical Program Expanded Abstracts , 1996, 15(1): 324-327. |
| [13] | Aqrawi A A, Boe T H, Barros S. Detecting salt domes using a dip guided 3D Sobel seismic attribute. SEG Technical Program Expanded Abstracts , 2011, 30(1): 1014-1018. |
| [14] | Aqrawi A A, Boe T H. Improved fault segmentation using a dip guided and modified 3D Sobel filter. SEG Technical Program Expanded Abstracts , 2011, 30(1): 999-1003. |
| [15] | Weickert J. Coherence-enhancing diffusion filtering. International Journal of Computer Vision , 1999, 31(2-3): 111-127. |
| [16] | Haralick R M. Digital step edges from zero crossing of second directional derivatives. IEEE Transactions on Pattern Analysis and Machine Intelligence , 1984, 6(1): 58-68. |
| [17] | 王绪松, 杨长春. 对地震图像进行保边滤波的非线性各向异性扩散算法. 地球物理学进展 , 2006, 21(2): 452–457. Wang X S, Yang C C. An edge-preserving smoothing algorithm of seismic image using nonlinear anisotropic diffusion equation. Progress in Geophysics (in Chinese) , 2006, 21(2): 452-457. (in Chinese) |
| [18] | Georgia R, Gao J H, Wang L L, et al. Discontinuities detection on edge preserved smoothed seismic image using directional masks. Progress in Geophysics , 2008, 23(5): 1398-1405. |
| [19] | 陆艳洪, 陆文凯, 翟正军. 一种边缘保持的地震数据插值方法. 地球物理学报 , 2012, 55(3): 991–997. Lu Y H, Lu W K, Zhai Z J. An edge-preserving seismic data interpolation method. Chinese Journal of Geophysics (in Chinese) , 2012, 55(3): 991-997. DOI:10.6038/j.issn.0001-5733.2012.03.029 (in Chinese) |
 2013, Vol. 56
2013, Vol. 56

