2. 英国地质调查局, Edinburgh EH9;
3. 北京旭日奥油技术有限公司, 北京 100101
2. British Geological Survey, Edinburgh EH9;
3. SunRise PetroSolutions Tech Inc, Beijing 100101, China
水力压裂技术是页岩气开发过程中最为重要的增产措施之一,该技术利用流体传压特性,将流体高压注入地层,使岩石破裂以改善地层渗透率,从而达到提高油气产量的目的[1].水力压裂模拟技术近几十年间得到了迅猛发展,先后提出了Perkins-Kern-Nordgren(PKN)、Khristianovic-Geertsma-de Klerk(KGD)、拟三维(P3D)和三维(3D)等计算模型[2],对油气开采具有重要的指导意义.微地震监测技术通过观测、分析微地震事件来监测生产活动及地下状态;该技术可用于水力压裂分析,水驱前缘监测和储层描述等,在储层开发监测中发挥重要作用[3].
水力压裂过程中,定位后的微地震信号能够指示裂缝分布,并用于指导下一阶段的压裂操作和制定相应的开发策略,因此定位结果的精度对于油气开发极为关键.微地震定位技术经历了数十年的发展,已从基于射线走时反演发展至基于概率和波形反演[4-5],目前已实现了实时定位技术[6-7]和基于高斯束、逆时偏等偏移理论的定位方法[8-9].尽管微地震定位方法已比较成熟,但反演过程中的速度模型往往忽略地层各向异性和压裂、生产过程引起的变化,这些因素会影响反演结果的可靠性[5].微地震反演中采用的速度模型一般根据地震、声波测井、VSP等资料构建[3];由于反演过程同时需要纵横波速度信息,因此基于测井资料构建速度模型的方法较为常用[10].由于测井资料受泥浆侵入等因素影响,基于测井数据构建的地层速度往往与实际情况存在偏差,需要进行校正,在压裂前常采用标定炮来校正初始速度模型.由于标定炮的位置和激发时间已知,根据各检波器的接收时间及相应的优化算法能够求取最佳速度模型[10-12],并在整个反演过程中采用该速度模型进行定位.标定炮数据在压裂前采集,因此基于标定炮优化的速度模型只能够表征压裂前的地层速度.实际上,在水力压裂过程中,高压流体会产生裂缝,同时通过渗流作用改变压裂缝附近地层的孔隙压力,新增裂缝和孔隙压力的改变都会引起地层速度的变化[13-14].Block等[15]在上世纪90年代就关注了该问题,他们在对LosAlamos地热储层研究中发现,考虑压裂带速度变化的定位误差要比基于压裂前速度模型的定位误差下降11%~15%. Block等[15]针对该问题提出了能够同步反演微地震信号和压裂带速度的分步算法,但由于该方法需要较高的检波器覆盖程度[11],在实际采集过程中,尤其是井中观测很难满足该要求,使得该方法没有得到推广.目前,包括斯伦贝谢的实时定位方法在内[6],微地震定位过程中所采用的速度模型多根据地震、测井、VSP资料或标定炮构建,并没有考虑压裂过程对地层速度的影响.
研究中首先综合应力、流量信息,基于物质守恒和渗流方程正演三维流体压力扩散,并结合断裂力学理论模拟裂缝破裂.继而根据Coates-Schoenberg等效理论和裂缝柔量分别计算裂缝和孔隙压力对地层弹性模量的影响,获得压裂过程中的实时速度场信息.得到破裂位置和速度场后,借助三维射线追踪方法正演微地震数据,得到纵波、横波走时和方位信息,最后采用基于走时的常规微地震定位方法反演震源位置并进行误差对比分析.
2 理论基础 2.1 三维水力压裂模拟对于含裂缝地层的渗流模拟,目前主要分为整体模拟和分别模拟两种思路.整体模拟就是综合考虑裂缝渗透率和基质渗透率,计算含裂缝岩石的等效渗透率并用于渗流模拟.考虑孔隙压力对裂缝闭合度和传导能力的影响,模拟中可采用幂指数函数等近似等效渗透率随孔隙压力的变化[17-18].石油工程专业在水力压裂研究中往往采用分别模拟方法[19],即将注入地层的流体分为两部分,一部分储存在裂缝内,一部分渗流到基质中,在模拟过程中分别分析.
整体模拟思路中的等效渗透率计算过程和渗透率随孔隙压力变化过程都采用近似算法,会引入一定误差,该方法往往应用于大规模的油藏模拟.本文采用水力压裂模拟中更为常用的分别模拟思路.压裂过程中,缝内储存量与漏失量之和等于注入量[19]:
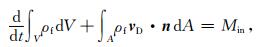
|
(1) |
式中,ρf为流体密度,V为裂缝体积,vD为达西渗流速度,A为裂缝面积,n表示裂缝面法向方向,Min表示单位时间注入流体质量.
式(1)为压裂过程中的流量守恒关系,如果要获得基质中的孔隙压力变化,需结合渗流方程进行模拟[20].渗流方程基于物质守恒原理和达西定律,综合考虑了应力、流量信息,其三维表达式如下:
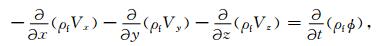
|
(2) |
式中,Vx,Vy,Vz为x,y,z方向上的流速,Φ为孔隙度.假设流体运动符合达西定律,则Vx,Vy,Vz的表达式如下:
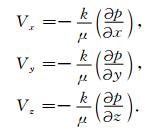
|
(3) |
式中,p为孔隙流体压力,k为渗透率,μ为流体黏度.联立式(2)、(3)并考虑渗透率的各向异性,式(2)变为

|
(4) |
式中,kx,ky,kz为x,y和z方向的渗透率.
获得地下孔隙压力分布后,需要选择合适的判别准则进行岩石破裂分析.研究中假设地应力、岩石性质在压裂过程中保持稳定,并采用断裂力学作为破裂判别准则.与最大应变破裂、最大应力破裂、Mohr-Coulomb等破裂准则相比,断裂力学既分析了破裂点的应力状态,又考虑了已存在裂缝的影响,广泛用于水力压裂分析[21-23].根据断裂力学理论,当裂缝尖端的应力强度因子达到岩石临界应力强度因子时,岩石发生破裂[23]:
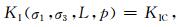
|
(5) |
式中,KI为裂缝尖端的应力强度因子,与最大地应力σ1、最小地应力σ3、孔隙流体压力p和已存在裂缝的长度L有关,KIC为岩石临界应力强度因子.
模拟过程中,首先基于物质守恒(式(1))和渗流方程(式(4))模拟压裂过程中的孔隙压力分布.得到孔隙压力分布后,如果压裂缝尖端不满足破裂条件(式(5)),则直接将计算得到的孔隙压力、裂缝分布作为初始条件用于下一时刻模拟;如果裂缝满足破裂条件,需要计算破裂后缝内的平衡流体压力[19],并将更新后的流体压力和裂缝分布用于下一时刻模拟.
2.2 压裂带等效弹性参数根据Coates-Schoenberg等效理论,裂缝可以视为地层中高柔性界面,该界面上位移不连续,应力保持连续[13].含裂缝岩石的柔量S由围岩柔量Sb和裂缝柔量Sf组成,关系式如下:
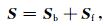
|
(6) |
C=S-1,对柔量矩阵S求逆即可得到弹性参数矩阵C,裂缝介质的等效弹性矩阵如下[13]:
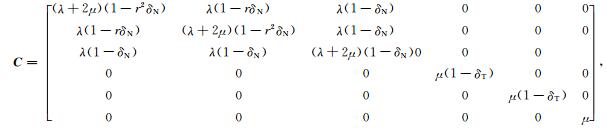
|
(7) |
式中,λ,μ为拉梅系数,δT,δN,r表达式为:
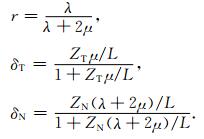
|
(8) |
式中,ZT,ZN为裂缝切向、垂向柔量,1 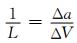
压裂液泵入地层引起孔隙流体压力增大,地层有效压力随之减小[14]:
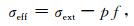
|
(9) |
式中,σeff为地层有效压力,σext为上覆压力,p为孔隙流体压力,f为有效压力系数.
裂缝柔量ZT,ZN随有效地层压力变化而改变,可表示为[14, 17]:
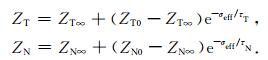
|
(10) |
式中,ZT∞,ZN∞为异常高压对应的柔量值,ZT0,ZN0为异常低压对应的柔量值,σeff为有效压力,τT、τN为衰减系数.
模拟得到孔隙压力分布后,根据式(9)计算有效地层压力,继而通过式(10)更新ZT、ZN,并结合裂缝分布联立式(7)、(8)得到不同压裂阶段压裂带的等效弹性参数,获得实时速度信息.
2.3 微地震正反演微地震反演技术多基于纵横波走时和方位信息进行微地震事件定位[3, 5],研究中采用射线追踪方法正演微地震信号的走时、方位信息,并用于进一步的反演研究.射线追踪技术是指给出发射点、接收点和速度模型后,求取发射点到接收点的射线轨迹及走时等信息.该技术在地球物理方面应用极为广泛,从计算走时和射线路径的运动学到计算振幅信息的动力学追踪,各种方法层出不穷.运动学方面,传统的方法有打靶法和弯曲法,随后发展起来的有基于程函方程、惠更斯原理的波前扩展类方法和基于图论和费马原理的最短路径算法[24].这些方法中,最短路径方法和基于程函方程的有限差分算法只能计算节点位置的走时和传播信息[24-25],由于节点位置的离散性,无法得到精确的传播方位.而有些微地震定位方法依靠传播方向来确定震源方位[5],需要准确的方位信息,这两种方法无法满足要求.与之相比,四方打靶法基于Snell定律计算射线路径,不受节点约束,能够提供精确的走时和方位信息,研究中采用该方法作为正演算法.
微地震的定位方法大致可分为以下三类[5, 8]:(1)当只有单个三分量检波器时,通过极化方向确定震源方位,并根据纵横波时差计算传播距离,从而获得震源位置.(2)当有多个检波器时,可基于多点走时信息构建方程组来求解震源位置.(3)借助偏移思路,在空间寻找能够使微地震特定相位叠加得到极大值的点,并将其作为震源位置.方法1和方法2基于射线理论,计算效率高且广泛应用于实际生产,本文采用这两种方法定位微地震事件并研究水力压裂过程对其的影响.
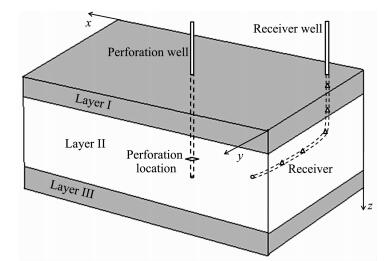
3 模型试算 3.1 水力压裂模拟研究中,模型大小为200m×50m×50m,网格大小为1m×1m×1m,模拟时间间隔为10ms,模型分为三层(如图 1所示),z方向上1~10m(Ⅰ层)和41~50m(Ⅲ层)为过渡层,11~40m为压裂层(Ⅱ层),图中压裂井上的菱形符号表示压裂位置,监测井上的三角形符号表示检波器.模型中,基质的拉梅系数为λ=9.312×109kg·m-1·s-2,μ=6.144× 109kg·m-1·s-2,地层密度为ρ=2.4g·cm-3.压裂过程中注水点的位置为(100m,25m,25m),注水速率为Vinj=3m3·min-1,地层初始孔隙流体压力为ppor=19MPa,最大水平地应力pmax沿x方向,pmax=25MPa,最小水平地应力pmin沿y方向,pmin=20MPa,第Ⅱ层临界强度因子KIC=2MN·m-3/2.考虑地层渗透率的各向异性,压裂层三个方向的渗透率依次设为:kx=15×10-3 μm2,ky=10× 10-3 μm2,kz=5×10-3 μm2.模型边界位置(z=1,50m)临界应力强度因子K IC*=5MN·m-3/2,边界位置的渗透率依次为:k x*=6×10-3 μm2,k y*=4× 10-3 μm2,k z*=2×10-3 μm2,过渡层的临界应力强度因子及渗透率参数通过边界和压裂层反距离线性内插构建.
|
图 1 模型示意图 Fig. 1 The schematic diagram of fracturing model |
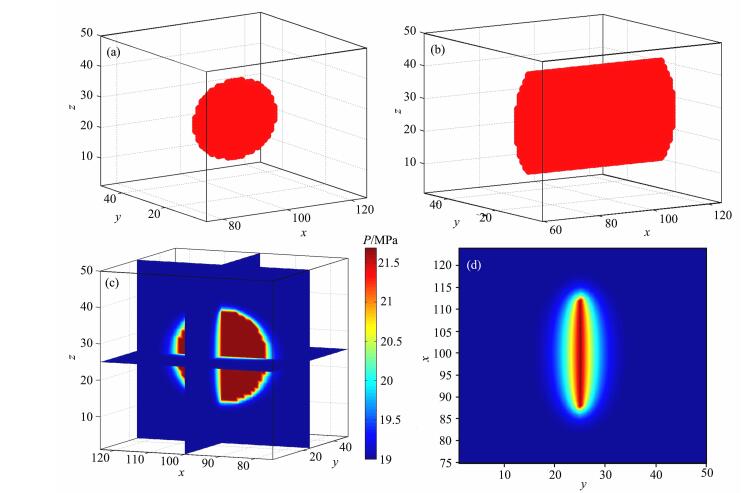
正演模拟迭代次数48000次,时长为480s,模拟得到的成果数据包括三维裂缝和孔隙流体压力分布.图 2展示水力压裂模拟得到三维裂缝和孔隙流体压力分布,其中图 2a、2b为50s、350s时刻的裂缝分布,图中红色网格表示裂缝;图 2c为50s时刻三维孔隙流体压力分布,图 2d为压力分布的x-y剖面.裂缝破裂初期,由于破裂点位于储层内,各方向上临界应力强度因子相同,即破裂难度相当,所以裂缝呈圆形形态(如图 2a所示).随着裂缝进一步扩展,垂向上破裂至过渡层,由于过渡层的临界应力强度因子大于储层,其在储层内破裂更加容易.因此裂缝在储层内沿横向破裂,近似椭圆形态(如图 2b所示).从图 2c和图 2d可以看到,裂缝分布控制孔隙压力的形态,地层的孔隙压力分布在二维和三维剖面上呈现扁长的椭圆和椭球形态.
|
图 2 (a)50s时刻裂缝分布; (b)350s时刻裂缝分布; (c)50s时刻三维孔隙压力分布; (d)50s时刻孔隙压力分布x-y剖面 Fig. 2 (a) The fracture distribution at 50 s; (b) The fracture distribution at 350 s; (c) The 3D pore pressure distribution at 50 s; (d) The x-y profile of porepressure at 50 s |
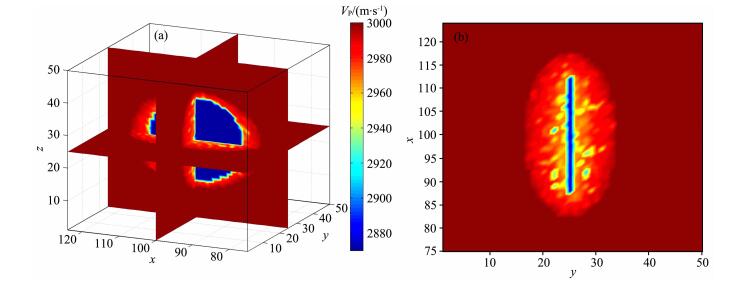
根据Coates-Schoenberg理论(式(7)、(8))计算等效弹性参数时,需要知道网格内裂缝的面积Δa.研究中,假设水力压裂缝贯穿网格,即压裂缝所在网格的裂缝面积等于网格面积.在非压裂位置,由于注入液从裂缝中漏失导致周边岩石的孔隙流体压力上升,该过程会降低骨架有效压力并进一步引起裂隙的滑移或破裂[26-27],也会产生裂隙.研究中假设非压裂缝位置但孔隙压力发生改变的网格也会出现裂缝,且裂缝面积满足幂律分布[28].模拟中,基质纵、横波速度为3000m/s和1600m/s,ZT0=5.681× 10-10Pa-1,ZT∞=ZT0/5,ZN0=2.8409×10-11Pa-1,ZN∞=ZN0/2,τT=τN=1.35MPa[14].图 3a展示50s时刻的三维纵波速度场分布,图 3b展示速度场的x-y剖面.由于缝内孔隙压力高且裂缝面积Δa大,因此压裂缝的速度最低.非压裂位置的裂缝尺度满足幂律分布且随机分配至各网格,在速度剖面上表现为随机的速度扰动;由于速度场同时受控于孔隙压力,而孔隙压力距离压裂缝越近数值越大,因此压裂带速度朝压裂缝方向具有递减趋势(如图 3a,图 3b所示).
|
图 3 (a)50s时刻三维纵波速度场; (b)50s时刻纵波速度场x-y剖面 Fig. 3 (a) The 3D P-wave velocity model at 50 s; (b) The x-y profile of P-wave velocity at 50 s |
模拟中,射孔点位置为(100m,25m,25m),五个检波点的空间位置依次为R1(5m,5m,5m),R2(5m,5m,18m),R3(5m,5m,30m),R4(10m,17m,30m),R5(15m,30m,30m),分布如图 1所示.其中R1到R3的x、y坐标相同,z坐标不同,近似垂直观测系统;R3到R5的z坐标相同,x、y坐标不同,近似水平观测系统.裂缝破裂的同时会产生微地震信号,因此研究中从50s,150s和480s时刻的破裂点中各选取三个位置作为微地震震源.水力压裂过程中,裂缝会同时向井两侧破裂,研究中从远离监测井那一侧的破裂位置中选取震源,其中50s时刻的震源位置为S1(103m,25m,37m),S2(108m,25m,15m),S3(112m,25m,28m),150s时刻的震源位置为S4(115m,25m,13m),S5(112m,25m,40m),S6(119m,25m,22m),480s时刻的震源位置为S7(159m,25m,11m),S8(160m,25m,35m),S9(161m,25m,25m).
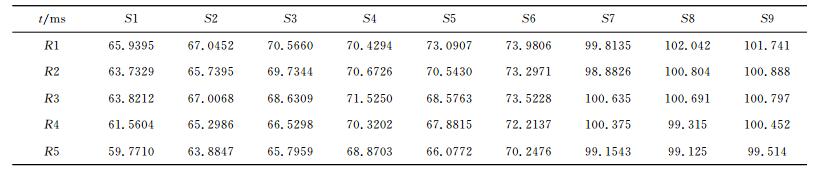
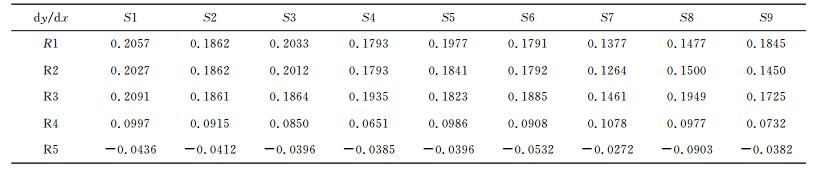
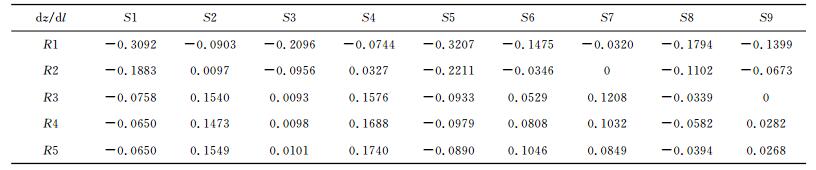
得到检波点、炮点位置后,根据50s、150s和480s时刻的裂缝及孔隙压力分布,能够计算该时刻的速度场,然后基于该速度场采用四方打靶方法进行射线追踪,即可得到纵、横波走时和方位信息.表 1为纵波传播时间,表 2为横波传播时间.表 3为dy/dz,表示检波器位置单位时间y方向上传播距离与x方向上传播距离之比,即传播方向的y分量与x分量之比.表 4为dz/dl,表示检波器位置单位时间z方向上传播距离和水平方向上传播距离之比,即传播方向的z分量与水平分量之比.所有信号在x方向上都是沿递减方向传播,因此文中没有列举出该参数.结合dy/dx,dz/dl和x方向传播方位即可确定射线的三维传播方位.
|
|
表 1 纵波走时 Table 1 P-wave travel time |
|
|
表 2 横波走时 Table 2 S-wave travel time |
|
|
表 3 dy/dx Table 3 dy/dx |
|
|
表 4 dz/dl Table 4 dz/dl |
研究中采用单点极化法和多点反演法对微地震信号进行定位,反演速度采用压裂前的纵横波速度.
(1) 单点极化法,根据单个检波器的纵横波走时差和极化方向反推震源位置.假设检波器的位置为(A,B,C),震源的位置为(X,Y,Z),纵横波时差为Δt,纵波出射方向为(1,dy/dx,dz/dl),则震源位置的计算公式如下:
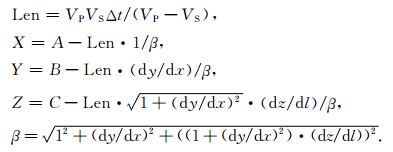
|
(11) |
式中,Len是检波点到震源的位置,VP是纵波速度,VS是横波速度.
(2) 多点反演法,根据多个检波器纵横波时差对震源位置进行定位.设三个检波器位置依次为(A1,B1,C1),(A2,B2,C2)和(A3,B3,C3),震源的位置为(X,Y,Z),三个检波器纵横波时差依次为Δt1,Δt2和Δt3.根据纵横波时差计算各检波器到震源距离:
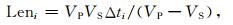
|
(12) |
继而构建关于震源坐标的方程组:
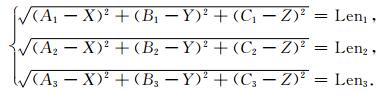
|
(13) |
求解该方程,即可获得震源位置.
图 4(a-c)分别显示50s、150s和480s的反演误差对比,图中纵坐标表示反演误差,横坐标表示反演采用的数据和方法.单点反演法利用极化方向(polarization)指示震源方位,图中用Pol表示该方法;多点反演法利用多点(Multi-point)数据构建矩阵反演震源位置,图中用Mp表示该方法.图 4a、4b、4c中黑点表示x方向的反演误差,红圈表示y方向反演误差,绿三角表示z方向反演误差.图 4d为length-error关系,其中length表示射线路径在裂缝带中的传播距离,error表示反演误差.

|
图 4 (a)50s时刻误差对比; (b)150s时刻误差对比; (c)480s时刻误差对比; (d) Length-error关系 Fig. 4 (a) The error comparison at 50 s; (b) The error comparison at 150 s; (c) The error comparison at 480 s; (d) The length-error relation |
从图中可以得出以下结论:(1)x,y,z三个方向上的误差相比,x方向误差最大.由于压裂缝沿x方向破裂(图 2),微地震信号从破裂位置传播至检波器的过程中,射线路径通过压裂带距离的x分量最大,因此受到的影响最为严重.(2)在极化反演结果中(图 4(a-c)中Pol),R5误差最大,R4误差次之,R1、R2、R3的误差相对较小,最大反演偏差约为最小偏差的3~4倍.根据检波器分布可知,R4、R5检波器在y方向上距离压裂缝最近,微地震信号传播到这两个检波器受到压裂带的影响要大于其它检波器位置,从而导致反演精度最低.(3)多点反演法的精度受控于反演数据的质量;从图中可以看到,(R1,R2,R3)组合的反演精度最高,(R3,R4,R5)组合的反演误差最大,与单点极化法反演精度对应.(4) 对比多点反演法和单点极化法反演结果,多点约束并没有明显降低反演误差,反演精度一般位于所用数据中最佳单点极化反演和最差单点极化反演之间.(5)图 4d展示射线路径在压裂带中传播距离与反演误差的关系,图中只展示50s,150s和480s的数据,因此在中间一段距离上存在空缺.如图 4d所示,传统定位方法的反演误差随射线路径在压裂带中传播距离的增加而不断变大.在实际生产中,我们虽然无法准确获得压裂带分布,却可以利用常规微地震的定位结果近似压裂带;根据压裂带的近似分布和震源-检波器组合计算射线路径穿过压裂带的距离,可将其作为定位误差的一个评判标准.
4 结论与认识本文综合物质守恒、渗流方程、断裂力学、Coates-Schoenberg理论和裂缝柔量参数计算水力压裂过程对速度的实时影响,继而利用四方打靶法正演微地震走时和传播方位,并进一步研究了压裂带对常规定位方法(单点极化法和多点反演法)的影响.通过以上的理论分析和数值模拟,可以得到以下结论:
(1) 水力压裂过程中,由于缝内渗透率远高于基质渗透率,裂缝的分布控制孔隙压力的整体分布,孔隙压力分布在二维和三维剖面上分别呈现扁长的椭圆和椭球形态.
(2) 水力压裂过程产生压裂缝,同时缝内流体向基质渗流提高地层孔隙压力,引起有效应力下降.压裂过程中,压裂带的速度变化受裂缝和孔隙压力的共同影响.
(3) 模型试算表明,如果忽略压裂过程中的速度变化,反演结果将与实际震源之间产生偏差,且偏差值会随着射线路径在压裂带中传播距离的增加而变大.
(4) 忽略压裂带的情况下,多点反演法与单点极化法在不同压裂阶段的反演精度相当;多点反演法的准确性取决于参与反演的数据质量,反演精度位于各检波器单点极化反演的精度范围内.
(5) 相同震源,不同检波器或检波器组合的反演偏差很大,表明检波器位置是影响微地震定位精度的重要因素.
(6) 反演误差与射线路径在压裂带中的传播距离有关;实际生产中可用常规微地震定位结果近似压裂带分布,并根据该分布对定位结果进行可靠性分析.
对页岩气储层的开发过程是通过技术进步和创新来降低开发成本的典型体现.如果因为检波器的排列导致定位精度不准,由此引起的误差则会进一步增加压裂和开发成本.因此在实际进行微地震监测前,需要进行观测系统及采集方案的设计,以提高数据的采集质量和实时监测效果.本文数值模拟中得到的一个重要认识就是,各检波器位置在微地震监测过程中受到压裂过程的影响不同,并对应于不同的定位精度.因此,在采集系统设计过程中,除了考虑信噪比、有效信号强度等因素外,还需要综合考虑压裂过程中速度变化对微地震传播和定位的影响,以确保获得最佳微地震信号.
致谢本研究同时得到了国家重点基础研究发展计划(973)项目(2013CB228603),中国石油大学(北京)引进人才科研启动基金资助(YJRC-2011-03)和中国石油大学(北京)科研基金资助(YJRC-2013-36)的资助.
| [1] | 张广明. 水平井水力压裂数值模拟研究. 合肥: 中国科学技术大学, 2010 . Zhang G M. A Numerical Simulation Study on Hydraulic Fracturing of Horizontal Wells (in Chinese). Hefei: University of Science and Technology of China, 2010 . |
| [2] | Brady B, Elbel J, Mack M, et al. Cracking rock: progress in fracture treatment design. Oilfield Review , 1992, 4(4): 8-11. |
| [3] | 张山, 刘清林, 赵群, 等. 微地震监测技术在油田开发中的应用. 石油物探 , 2002, 41(2): 226–231. Zhang S, Liu Q L, Zhao Q, et al. Application of microseismic monitoring technology in development of oil field. Geophysical Prospecting for Petroleum (in Chinese) , 2002, 41(2): 226-231. (in Chinese) |
| [4] | Drew J D, Leslie D, Armstrong P, et al. Automated microseismic event detection and location by continuous spatial mapping. SPE 95113 , 2005. |
| [5] | Maxwell S C, Rutledge J, Jones R, et al. Petroleum reservoir characterization using downhole microseismic monitoring. Geophysics , 2010, 75(5): 75A129-75A137. DOI:10.1190/1.3477966 |
| [6] | Burch D N, Daniels J, Gilard M, et al. Live hydraulic fracture monitoring and diversion. Oilfield Review , 2009, 21(3): 18-31. |
| [7] | Khadhraoui B, Leslie D, Drew J, et al. Real-time detection and localization of microseismic events. SEG, Denver 2010 Annual Meeting , 2010. |
| [8] | Rentsch S, Buske S, Luth S, et al. Fast location of seismicity: A migration-type approach with application to hydraulic-fracturing data. Geophysics , 2007, 72(1): S33-S40. DOI:10.1190/1.2401139 |
| [9] | Ran X, Sava P. Probabilistic microearthquake location for reservoir monitoring. Geophysics , 2010, 75(3): MA9-MA26. DOI:10.1190/1.3417757 |
| [10] | Pei D H, Quirein J A, Cornish B E, et al. Velocity calibration for microseismic monitoring: applying smooth layered models with and without perforation timing measurements. SPE 115722 , 2008. |
| [11] | Warpinski N R, Sullivan R B, Uhl J E, et al. Improved microseismic fracture mapping using perforation timing measurements for velocity calibration. Society of Petroleum Engineers Journal , 2005, 10(1): 14-23. |
| [12] | 宋维琪, 王新强, 高艳可. 地面监测微地震事件等效速度反演定位方法. 石油物探 , 2012, 51(6): 606–612, 632. Song W Q, Wang X Q, Gao Y K. The inversion positioning methods of the surface microseismic with equivalent velocity. Geophysical Prospecting for Petroleum (in Chinese) , 2012, 51(6): 606-612, 632. (in Chinese) |
| [13] | Coates R T, Schoenberg M. Finite-difference modeling of faults and fractures. Geophysics , 1995, 60(5): 1514-1526. DOI:10.1190/1.1443884 |
| [14] | Vlastos S, Liu E, Main I G, et al. Dual simulations of fluid flow and seismic wave propagation in a fractured network: effects of pore pressure on seismic signature. Geophys. J. Int. , 2006, 166(2): 825-838. DOI:10.1111/gji.2006.166.issue-2 |
| [15] | Block L V, Cheng C H, Fehler M C, et al. Seismic imaging using microearthquake induced by hydraulic fracturing. Geophysics , 1994, 59(1): 102-112. DOI:10.1190/geo1992-0156 |
| [16] | 吴忠宝, 胡文瑞, 宋新民, 等. 天然微裂缝发育的低渗透油藏数值模拟. 石油学报 , 2009, 50(5): 727–730, 734. Wu Z B, Hu W R, Song X M, et al. Numerical simulation on low-permeability reservoir with abundant natural micro-fractures. Acta Petrolei Sinica (in Chinese) , 2009, 50(5): 727-730, 734. (in Chinese) |
| [17] | Daley T M, Schoenberg M A, Rutqvist J, et al. Fractured reservoirs: An analysis of coupled elastodynamic and permeability changes from pore-pressure variation. Geophysics , 2006, 71(5): 33-41. DOI:10.1190/1.2231108 |
| [18] | Hummel N, Shapiro S A. Microseismic estimates of hydraulic diffusivity in case of non-linear fluid-rock interaction. Geophys. J. Int. , 2012, 188(3): 1441-1453. DOI:10.1111/gji.2012.188.issue-3 |
| [19] | Wangen M. Finite element modeling of hydraulic fracturing on a reservoir scale in 2D. Journal of Petroleum Science and Engineering , 2011, 77(3-4): 274-285. DOI:10.1016/j.petrol.2011.04.001 |
| [20] | 韩大匡, 陈钦雷, 闫存章. 油藏数值模拟基础. 北京: 石油工业出版社, 1993 . Han D K, Chen Q L, Yan C Z. Fundamentals of Numerical Reservoir Simulation (in Chinese). Beijing: Petroleum Industry Press, 1993 . |
| [21] | Ji L J, Settari A, Sullivan R B. A novel hydraulic fracturing model fully coupled with geomechanics and reservoir simulation. Society of Petroleum Engineers Journal , 2009, 14(3): 423-430. |
| [22] | Akinson B K. Fracture Mechanics of Rock. Orlando: Academic Press, 1989 . |
| [23] | 刘建军, 冯夏庭, 裴桂红. 水力压裂三维数学模型研究. 岩石力学与工程学报 , 2003, 22(12): 2042–2046. Liu J J, Feng X T, Fei G H. Study on mathematical, model of three dimensional hydraulic fracturing. Chinese Journal of Rock Mechanics and Engineering (in Chinese) , 2003, 22(12): 2042-2046. (in Chinese) |
| [24] | 张美根, 程冰洁, 李小凡, 等. 一种最短路径射线追踪的快速算法. 地球物理学报 , 2006, 49(5): 1467–1474. Zhang M G, Cheng B J, Li X F, et al. A fast algorithm of shortest path ray tracing. Chinese J. Geophys. (in Chinese) , 2006, 49(5): 1467-1474. (in Chinese) |
| [25] | 张霖斌, 刘迎曦, 赵振峰, 等. 有限差分法射线追踪. 石油地球物理勘探 , 1993, 28(6): 673–677, 684. Zhang L B, Liu Y X, Zhao Z F, et al. Finite-difference ray tracing. Oil Geophysical Prospecting (in Chinese) , 1993, 28(6): 673-677, 684. (in Chinese) |
| [26] | Shapiro S A, Rentsch S, Rothert E. Characterization of hydraulic properties of rocks using probability of fluid-induced microearthquakes. Geophysics , 2005, 70(2): F27-F33. DOI:10.1190/1.1897030 |
| [27] | Shapiro S A, Dinske C. Fluid-induced seismicity: Pressure diffusion and hydraulic fracturing. Geophysical Prospecting , 2009, 57(2): 301-310. DOI:10.1111/gpr.2008.57.issue-2 |
| [28] | Vlastos S, Liu E, Main I G, et al. Numerical simulation of wave propagation in media with discrete distributions of fractures: effects of fracture sizes and spatial distributions. Geophys. J. Int. , 2003, 152(3): 649-668. DOI:10.1046/j.1365-246X.2003.01876.x |
 2013, Vol. 56
2013, Vol. 56