2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
与海量计算的地震波场模拟相比,计算快速的地震射线追踪广泛应用在地震定位、层析成像、偏移以及地震数据采集设计等领域中[1-4].射线追踪的理论基础是在高频近似条件下,地震波场的主要能量沿射线轨迹附近传播,波动地震学过渡到几何地震学.和程函方程数值解获得的地震走时场相比[5-7],射线追踪不仅能够获得地震波的走时信息,还能获得射线轨迹,这对于反演层析成像等领域至关重要;而且动力学追踪沿着射线轨迹通过输运方程可以计算出振幅,获取地震波的动力学信息[3, 8].传统的运动学射线追踪方法包括试射法[9-13]和弯曲法[14-23].试射法在全局搜索接收器方面效果较好,而弯曲法的计算效率较高.其他的方法包括波前法[24-25]、最短路径法[26-28]和模拟退火法[29-30]等.这三种方法在追踪全局最小走时路径方面有优势.Cerveny(2001)对射线追踪方法进行了很好的总结[3].
射线追踪方法建立在一定的模型参数化基础上,即如何描述地球介质模型.根据介质空间分布特征可以分为离散介质和连续介质两种类型.离散介质类型一般对地球介质空间进行网格划分,可以看做是对连续介质的抽样.常见的网格模型为大小相等的矩形网格(三维为立方体),在网格内部或节点上定义各自的地震波速度等属性.离散化模型适应性强,在此基础上的走时计算和射线追踪方法稳健性好是最大的优点,如基于程函方程数值解获得的地震走时[5-6]以及最短路径射线追踪方法[26, 28]等.网格结构存在两个主要的困难:首先,难以描述复杂构造的精细结构,虽然网格节点越密,近似性越高;离散的网格节点很难描述连续起伏的构造分界面,有些时候需要再单独重新定义分界面[9].其次,网格尺寸的大小通常需要满足描述最精细区域的要求,因此网格结构通常需要较大密度分布的网格节点,而网格节点上的正演计算通常至少和网格节点数目成正比[26, 28],因此计算受计算机的内存和运算速度影响很大,三维空间尤其如此.
连续介质类型在波场数值模拟中很少使用,但在基于射线理论的几何地震学中普通使用,如常梯度或有解析表达式的速度场,网格化必然造成精度的损失,用连续介质描述则有很大的优势,常见的类型为分段连续介质.层状结构是常见的分段连续介质描述方法,不同的分层界面用来描述物性间断面.它要求每一个分界面都必须从模型体的左边界贯穿到模型体的右边界.分界面按顺序由上到下依序排列,不得交叉,每层之间可以分别定义均匀或非均匀介质等.层状结构描述简单,模型基础上的正演射线追踪计算方便快捷[31-36].但层状结构在描述逆断层以及图 1所示的复杂三维地质体时会变得十分困难,而块状结构描述则容易的多.块状结构模型中,三维地质体被看做是大小不等、形状各异的地质块组成的集合体.Gjøystdal等首先提出了三维块状建模的概念,地质块采用并集、交集、余集和补集等集合运算的操作来构造,显示很不直观[37].Pereyra发展了块状模型描述的技术,块体更加直观和自然,但采用B样条曲面描述的模型界面,限制了只能构造尖灭和蘑菇云等典型地质模型[38].我们在此基础上,采用三角形面片描述模型界面,在构建复杂模型方面有了很大的提升,理论上可以构建任意复杂构造结构的地质体[13, 22-23, 39].
|
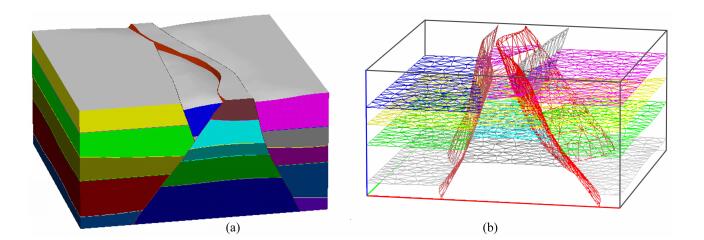
图 1 复杂堑垒构造地质体, 不同颜色代表不同的地质块(a), 模型界面由三角形面片构成(b) Fig. 1 The horst structure model, different blocks are shown in different colors (a) and separated by triangulated interfaces (b) |
块状模型上的射线追踪则复杂的多.我们已经发展了适用于常速度[22],常梯度速度分布[23]的逐段迭代射线追踪算法,以及VTI介质中的子三角形法射线追踪算法[39],并已成功应用在复杂的块状模型中.本文将模型介质扩展到任意分布的非均匀介质,并发展了与之相适应的逐段迭代追踪算法.
2 三维复杂非均匀地质模型参数化 2.1 三维块状模型实际地质结构经过挤压、隆升等地质运动后,由水平地层变成了十分复杂的结构,用层状结构描述比较困难,应用块状结构模型描述则很自然、容易.块状结构模型中,地质体被看做由大小不等、形状各异地质块组成的集合体,每个地质块有自己的地质属性,如地震波速度、密度等物性结构,并与其他的地质块存在相邻的边界[13, 22].我们对二维区域剖面采用“域→面→边→点”的描述方式[23, 40].不同的地质面元为封闭的,被边界分隔开,边界由给定的离散点插值得到的三次样条来给定.三维地质体的描述采用“体→块→面→三角形→点”的层次结构[13, 22-23, 39].不同地质块之间的物性分界面由一系列的三角形面片拼接而成.
三维块状模型中界面的描述极为关键.和Coons、Bezier、B样条等曲面相比,三角形面片有如下的优势:第一,描述界面离散的控制点不需要定义在矩形网格区域,可以是任意数量及空间分布;第二,三角形面片的拼接不会出现空隙,这在B样条等曲面拼接中有非常严格的要求[22];第三,修正和删除部分离散节点,并重新构建界面非常容易,对于三维建模至关重要;第四,射线(如直线段)和三角形面片的交点是解析解,而和B样条等界面的求交则是个迭代过程[10, 41],由于射线和曲面的求交在射线追踪过程中存在大量重复的计算,因此,三角形界面能够节省大量的射线追踪时间.在著名的三维建模软件GOCAD系统中,也是用三角形来构造模型的界面[42-43].
相对于C2阶连续的B样条曲面,三角形面片的缺点是界面为C0阶连续,三角形内部各点法向量是确定且惟一的,如果两个三角形面片不在一个平面上,则界面法向量在跨三角形的连接处会出现突变,因此反射和透射射线在跨连接处也会出现突变,这对于如扰动量修正射线轨迹的弯曲法射线追踪存在极大的困难.针对该问题,我们对界面上各点的法向量进行了光滑处理,重新定义界面上各点的法向量,使得法向量在整个界面内是连续变化的[13, 22-23, 39].
图 1为上述结构下的典型区域建模,此模型的设计比类伸展盆地中特征性的堑垒构造,该构造广泛出现在中国东部盆地如渤海湾盆地、苏北盆地以及松辽盆地等.该模型由18个地质块构成,6676个三角形描述模型界面,三角形则由2700个离散点来控制.
2.2 非均匀速度分布各向同性地质块内的连续速度分布可以定义为常速度、常梯度速度、指数型、二次曲线以及典型的解析表达式[44],但对于更普遍的非均匀介质,定义离散的矩形网格节点速度分布,并通过线性插值或多项式插值获得空间任意点的速度分布是普遍的做法[45].
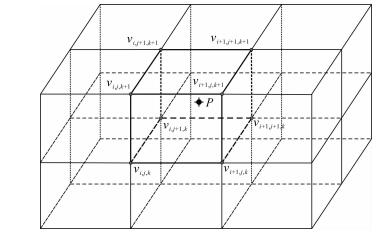
为了描述速度间断面,我们对三维地质体的每个块体内部速度场单独定义,分别建立一套独自的矩形网格节点,并在节点上定义速度值.一般来说,网格节点的范围应该覆盖该地质块.如图 2所示,对于某块体内部的任意点P(x,y,z),首先找到该点落在矩形网格中的位置,并由周围8个节点位置处的速度三线性插值获得P点的速度v(x,y,z),
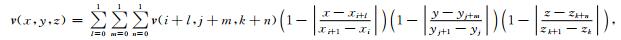
|
(1) |
|
图 2 由矩形网格定义的非均匀速度场, P点速度由该点落在的矩形网格8个节点的速度插值定义 Fig. 2 Heterogeneous velocity distribution is to define a set of discrete velocity nodes.A trilinear interpolation function is used to describe the velocity at point P within a rectangular grid of nodes |
式中,v(i+l,j+m,k+n)分别代表 8个节点的速度值;xi,yj,zk分别为矩形速度网格在x,y,z三个方向的位置坐标.上式要求P点落在网格区域内部,如果落在所有网格区域的外部,即定义速度场的网格区域未完全覆盖该地质块,则需要考虑绝对值的符号.
对于三维地质体中任意点的速度分布,首先判断该点落在哪个地质块体内,再按上述步骤,用该地质块的矩形网格节点速度来插值获得该点的速度值.
3 三维非均匀模型的射线追踪Um和Thurber提出了伪弯曲法射线追踪,用于解决连续介质中的两点射线追踪问题,但却无法适应存在强速度间断面的情况[18].我们提出了逐段迭代射线追踪算法,用来追踪存在强速度间断面模型,该算法属于弯曲法的范畴,已经在二维和三维常速度分布[22]和常梯度速度分布[23]均取得了很好的射线追踪效果.对于更普遍的非均匀介质模型,我们发展了相适应的逐段迭代射线追踪算法,结合伪弯曲法,提出了一种扰动修正方案:对落在界面上,即速度间断面上的路径点,进行逐段迭代法的扰动修正;在模型连续介质内部的路径点,用伪弯曲法来修正.
3.1 逐段迭代法修正界面路径点如图 3所示,对于任意分布的非均匀介质,假设Pk-1,Pk+1为跨过界面的射线路径起始点和终止点,Pk为落在界面上的路径点,满足界面方程
|
(2) |
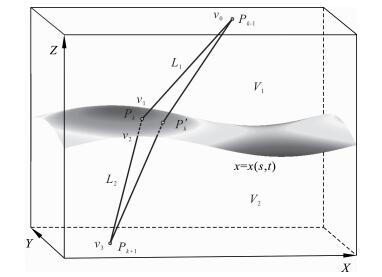
|
图 3 逐段迭代法修正落在界面上的中间点示意图 Fig. 3 Illustration of the mid-point modification of segmentally-iterative methods when the mid-point is located on an interface |
如果,Pk-1,Pk+1和Pk点距离很小,则射线轨迹可以近似看做为两段直线段Pk-1Pk和PkPk+1.固定起始点Pk-1和终止点Pk+1,则射线轨迹的走时T是中间点Pk坐标xk(ξ,η)的函数:
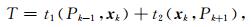
|
(3) |
可以近似写为
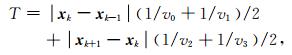
|
(4) |
其中,v0和v3为起始点Pk-1和终止点Pk+1处的速度,v1和v2为界面路径点Pk两侧的速度.
为了满足射线走时的费马原理,假设修正后的路径点位置为(ξ+Δξ,η+Δη),则有如下的偏导数方程成立,
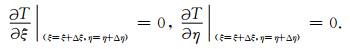
|
(5) |
对上式进行泰勒展开,并保留一阶小量,可以得到
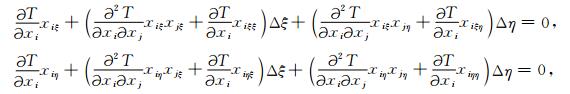
|
(6) |
其中下标i代表中间点的三个坐标,因此可以得到中间点的一阶修正公式:
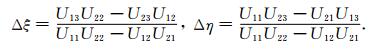
|
(7) |
其中,
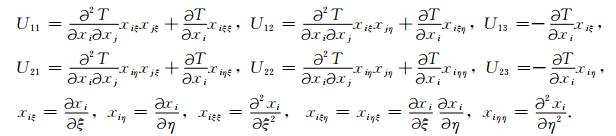
|
(8) |
上述修正过程和均匀速度场以及常梯度速度场相似,不同的是非均匀情况下射线走时表达式(3)及(4)和后两者的差异.如果定义
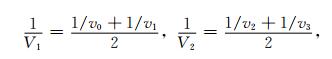
|
(9) |
即相当于界面两侧为常速度v1和v2(图 3),则上述过程和均匀介质中的修正公式[22]相似.
修正公式(7)为一阶显式增量,相对于传统的迭代方法求取中间点[46],能显著提高效率,由于中间点的修正过程在射线追踪中存在成千上万次的重复计算,因此,射线追踪高效省时.
对于层状模型,用修正后的路径点(ξ+Δξ,η+ Δη)替换初始路径点(ξ,η)即可.对于块状模型,如果修正后的路径点(ξ+Δξ,η+Δη)仍然落在初始路径点(ξ,η)所在的界面上,则直接用该修正后的路径点替代初始路径点;否则,需要判断是否需要增加新的路径点或者删除部分路径点[22],这是块状模型相对层状模型射线追踪最大的难点问题,对不同的复杂模型,需要专门的考虑.
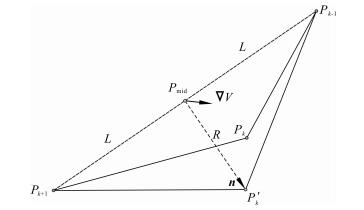
3.2 伪弯曲法修正介质内路径点我们遵照伪弯曲法来修正连续介质内部的射线路径点[18].设Pk-1,Pk,Pk+1为射线路径上连续的三点,坐标分别为xk-1,xk,xk+1(图 4).固定路径段的两端点Pk-1和Pk+1,扰动修正过程为寻找一个新的中间点P′k来替代原来的中间点Pk,使得新的射线路径段Pk-1P′kPk+1上满足走时最小.如式(10)所示,修正量包括修正后路径点的方向向量n以及修正距离R[18].
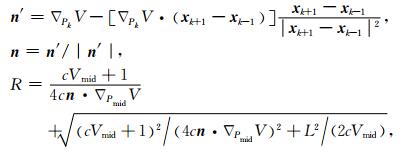
|
(10) |
|
图 4 伪弯曲法修正落在介质内部的中间点示意图 Fig. 4 Illustration of the mid-point modification of pseudo-bending methods when the mid-point is inside a medium |
其中,L=|xk+1-xmid|,c=(1/Vk+1+1/Vk-1)/2, PkV为中间点Pk处速度梯度向量,Vmid为中点Pmid(坐标xmid)处的速度值, PmidV为中点Pmid处的速度梯度向量.
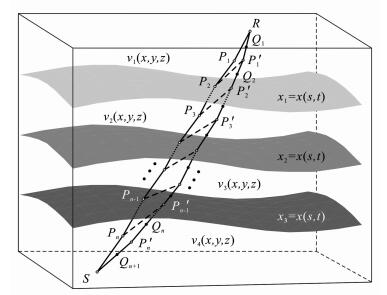
3.3 联合逐段迭代法与伪弯曲法的扰动修正方案针对存在速度间断面的非均匀介质,我们联合逐段迭代法和伪弯曲法,提出了“三点修正”射线追踪方案.以图 5中层状模型的透射波为例:首先给出炮点S和接收器R之间的初始路径RP1P2P3… Pn-1PnS,P1,P3,…,Pn为落在层状介质内部的路径点,P2,P4,…,Pn-1为落在界面上的路径点.从射线路径的某一端点R出发,顺序选取三点R、P1、P2,由于中间点P1在块体内部,用伪弯曲法修正中间点P1到新的路径点P'1;再顺序选取三点P'1、P2、P3,由于中间点落在界面上,用逐段迭代法修正中间点P2到新的路径点P'2;如此以一点的跨越作为步长,顺序地选取三点,并依次迭代修正路径点,直到另一端点S.这样,新计算出的路径点和两个端点就构成了一次迭代后的射线路径RP'1P'2P'3… P′n-1P′nS;如此迭代下去,直到新的射线路径满足一定的精度要求为止;此时,对射线路径点插值加密,如在收敛的RP'1P'2P'3…P′n-1P′nS射线路径点的中点处插入新的路径点,即R和P'1中点插入路径点Q1,P'1和P'2中点插入路径点Q2,最后形成新的射线路径RQ1P'1Q2P'2…QnP′nQn+1S;如果再迭代一次该路径,还满足精度要求,则认为射线路径满足最终要求,射线追踪过程结束;否则,重复上述过程,直到最终满足精度要求为止.
|
图 5 联合逐段迭代法与伪弯曲法扰动修正方案示意图 Fig. 5 The sketch of the ray tracing scheme of combination of segmentally iterative methods and pseudo-bending methods |
上述过程中,由于部分路径点落在模型连续介质内部,因此,即使射线路径迭代收敛,仍然需要对射线路径点加倍,再迭代一次.射线路径点加密的思路和伪弯曲法射线追踪一致[18].注意到非均匀介质中界面路径点的修正公式(7)要求界面两侧的路径段长度很小.而上述修正方案中随着迭代的深入和路径点的逐渐加密,射线路径段的长度越来越小,因此走时公式(4)逐渐满足近似要求,得到的修正公式(7)也满足近似要求.
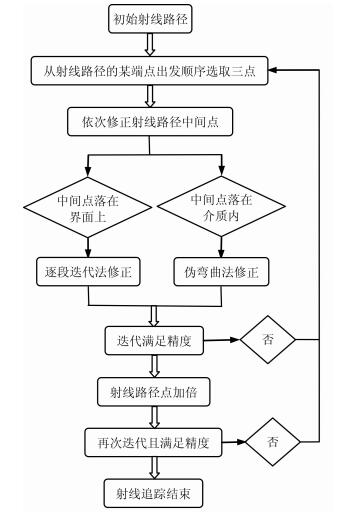
总结射线追踪的扰动修正方案,可以得到图 6所示的流程图.
|
图 6 射线追踪扰动修正方案流程图 Fig. 6 The flow chart of the three-point perturbation scheme for ray tracing |
上述射线追踪过程如果应用在层状模型中,则和Zhao等[46]的追踪过程相似,不同的是,我们采用显式修正的方式,而不是迭代的方法修正落在界面上的路径点,因此追踪过程更高效省时.上述射线追踪过程如果应用在块状模型中,射线路径点的数目在迭代进程中会根据需要自动增加或者删除[22],这是块状模型较层状模型射线追踪更复杂的表现.
4 模型试验为了检验射线追踪扰动修正方案在三维非均匀地质模型中的适用性,我们设计了两个复杂的速度模型,并进行了射线追踪试验.
4.1 地层互切模型地层互切模型(图 7a)主要是从理论角度验证在三维空间变化的地层截切、叠加的、在几何学上可能存在的复杂性,以开发并检验方法本身的有效性,适应处理各种复杂地质体.该模型包含5个地质块、3635个三角形及1681个点.模型的x,y,z轴方向分别以红、绿、蓝三种颜色直线表示(图 7a).图 7b显示了三维非均匀速度场在y=2.5km处的速度切片.直线连接起始点S和终止点R,以及和模型界面交点P,作为初始射线路径,图 7a显示了追踪过程中的部分射线路径变化及最终的射线追踪结果(蓝色曲线).
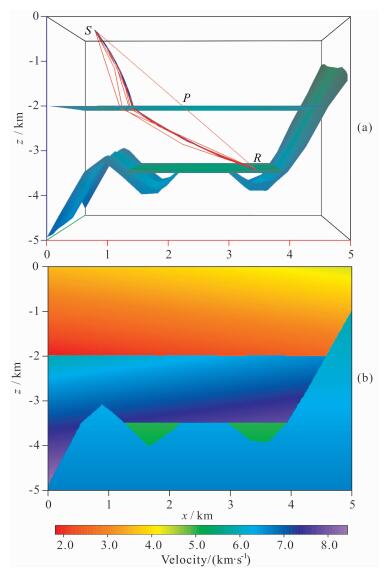
|
图 7 (a)地层互切模型中射线路径的扰动修正过程示意图, 蓝线为最终路径; (b)y=2.5km处速度切片 Fig. 7 (a) Illustrations of the sequence of ray paths as they are perturbed from a three-point initial path SPR; (b) Velocity slice at the position y=2.5 km |
三维组合模型(图 8a)是针对侵入体与围岩复杂地质、构造关系专门设计的,同时考虑到岩浆侵入体本身的分异.当岩浆侵入到上覆围岩中,往往导致围岩发生变形,形成具有伸展性质的穹窿构造.穹窿构造的发育往往伴随着断层的发育.侵入岩浆本身因分离结晶作用也会发生分异,形成具有不同组成和密度的岩相带甚至是富含金属矿床的矿带.
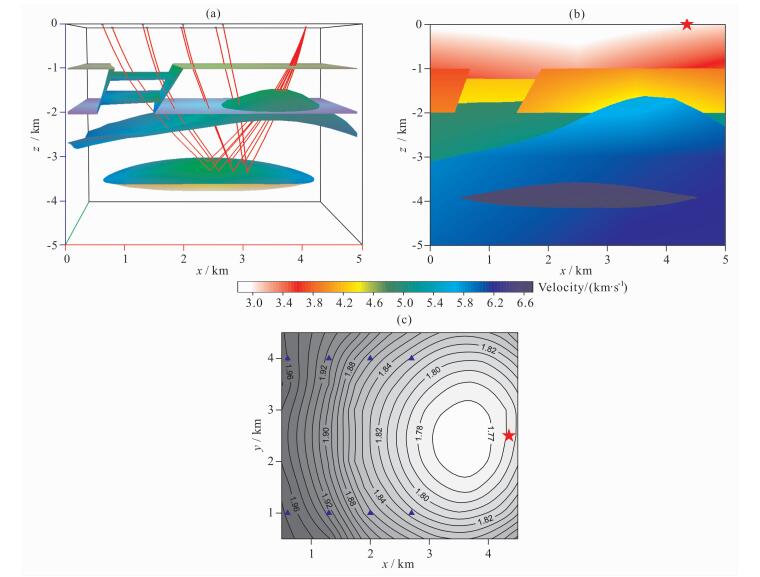
|
图 8 (a)三维组合模型射线追踪结果; (b)y=2.5km处速度切片; (c)走时等值线图, 炮点(红色五角星)和8个射线路径对应的接收器(蓝色三角形) Fig. 8 (a) 3D ray tracing results in the Combination Model with heterogeneous velocity distributions in different blocks; (b) Velocity slice at the position y=2.5 km; (c) Associated travel-time isolines |
三维组合模型(图 8a)在x,y,z轴三个方向的尺度均为5km,定义z轴向上为正.组合模型包含正断层、逆断层、侵入体和透镜体等复杂构造,由7个块、4649个三角形和2152个点组成.图 8b显示了三维非均匀速度场在y=2.5km处的速度切片.炮点(红色五角星)在地表位置为(4.35km,2.5km),207个(23×9)接收器位于地表.为了清楚显示,我们只显示了8个接收器(图 8c中蓝色三角形)在高速异常透镜体上表面的反射射线路径(图 8a)和射线走时等值线(图 8c).
射线追踪的速度影响因素很多,包括计算机的计算速度、射线追踪的精度、模型的复杂性、炮点和接收器的数目等等.在组合模型中,单个炮点和800个(40×20)接收器均放在地表,微机(Centrino-2,2.53GHz)计算结果显示,试射法追踪时间为25.59s;扰动修正方案追踪时间为13.64s,效率更高.两种方法追踪的精度要求我们均设定为0.5m;试射法的精度定义为出射点和接收器的最大距离;而扰动修正方案精度定义为整条路径最大的修正距离.
5 结论块状结构结合三角形界面可以描述复杂的三维模型,从根本上克服了层状结构描述复杂模型的困难.我们发展了非均匀介质中的逐段迭代法,并结合伪弯曲法,提出了射线追踪的扰动修正方案,可以适应非均匀介质的层状模型和块状模型等.本文主要考虑透射波和反射波的情况.地层互切模型和组合模型试验显示射线追踪的扰动修正方案的适用性;相对于试射法,追踪效率显著提高.
致谢感谢中国科学院地质与地球物理研究所张福勤研究员和苗来成副研究员有益的帮助.
| [1] | 滕吉文, 张中杰, 白武明, 等. 岩石圈物理学. 北京: 科学出版社, 2003 . Teng J W, Zhang Z J, Bai W M, et al. Lithosphere Physics (in Chinese). Beijing: Science Press, 2003 . |
| [2] | 陈运泰, 滕吉文, 张中杰. 地球物理学的回顾与展望. 地球科学进展 , 2001, 16(5): 634–642. Chen Y T, Teng J W, Zhang Z J. Geophysics: The 20th century in retrospect and the 21st century in prospect. Advance in Earth Sciences (in Chinese) , 2001, 16(5): 634-642. (in Chinese) |
| [3] | Cerveny V. Seismic Ray Theory. Cambridge: Cambridge University Press, 2001 . |
| [4] | Aki K, Richards P G. Quantitative Seismology: Theory and Methods. New York: W. H. Freeman and Co., 1980 . |
| [5] | Vidale J E. Finite-difference calculation of travel times. Bull. Seismol. Soc. Am. , 1988, 78(6): 2062-2076. |
| [6] | Vidale J E. Finite-difference calculations of traveltimes in three dimensions. Geophysics , 1990, 55(5): 521-526. DOI:10.1190/1.1442863 |
| [7] | Lan H Q, Zhang Z J. Topography-dependent eikonal equation and its solver for calculating first-arrival traveltimes with an irregular surface. Geophys. J. Int. , 2013, 193(2): 1010-1026. DOI:10.1093/gji/ggt036 |
| [8] | Cerveny V, Klimes L, Psencik I. Complete seismic-ray tracing in three-dimensional structures.//Doornbos D J. Seismological Algorithms. New York: Academic Press, 1988: 89-168. |
| [9] | Langan R T, Lerche I, Cutler R T. Tracing of rays through heterogeneous media: An accurate and efficient procedure. Geophysics , 1985, 50(9): 1456-1465. DOI:10.1190/1.1442013 |
| [10] | Virieux J, Farra V. Ray tracing in 3-D complex isotropic media: An analysis of the problem. Geophysics , 1991, 56(12): 2057-2069. DOI:10.1190/1.1443018 |
| [11] | Sun Y. Ray tracing in 3-D media by parameterized shooting. Geophys. J. Int. , 1993, 114(1): 145-155. DOI:10.1111/gji.1993.114.issue-1 |
| [12] | Sambridge M, Braun J, McQueen H. Geophysical parameterization and interpolation of irregular data using natural neighbors. Geophys. J. Int. , 1995, 122(3): 837-857. DOI:10.1111/gji.1995.122.issue-3 |
| [13] | 徐涛, 徐果明, 高尔根, 等. 三维复杂介质的块状建模和试射射线追踪. 地球物理学报 , 2004, 47(6): 1118–1126. Xu T, Xu G M, Gao E G, et al. Block modeling and shooting ray tracing in complex 3-D media. Chinese J. Geophys. (in Chinese) , 2004, 47(6): 1118-1126. (in Chinese) |
| [14] | Julian B R, Gubbins D. Three-dimensional seismic ray tracing. J. Geophys. , 1977, 43: 95-113. |
| [15] | Thurber C H, Ellsworth W L. Rapid solution of ray tracing problems in heterogeneous media. Bull. Seismol. Soc. Am. , 1980, 70(4): 1137-1148. |
| [16] | Pereyra V, Lee W H K, Keller H B. Solving two-point seismic-ray tracing problems in a heterogeneous medium.Part 1. A general adaptive finite difference method. Bull. Seismol. Soc. Am. , 1980, 70(1): 79-99. |
| [17] | Keller H B, Perozzi D J. Fast seismic ray tracing. SIAM J. Appl. Math. , 1983, 43(4): 981-992. DOI:10.1137/0143064 |
| [18] | Um J, Thurber C. A fast algorithm for two-point seismic ray tracing. Bull. Seismol. Soc. Am. , 1987, 77(3): 972-986. |
| [19] | Prothero W, Taylor W J, Eickemeyer J A. A fast two-point, three-dimensional raytracing algorithm using a simple step search method. Bull. Seismol. Soc. Am. , 1988, 78: 1190-1198. |
| [20] | Pereyra V. Two-point ray tracing in general 3-D media. Geophys. Prospect. , 1992, 40(3): 267-287. DOI:10.1111/gpr.1992.40.issue-3 |
| [21] | Mao W J, Stuart G W. Rapid multi-wave-type ray tracing in complex 2-D and 3-D isotropic media. Geophysics , 1997, 62(1): 298-308. DOI:10.1190/1.1444131 |
| [22] | Xu T, Xu G M, Gao E G, et al. Block modeling and segmentally iterative ray tracing in complex 3D media. Geophysics , 2006, 71(3): T41-T51. DOI:10.1190/1.2192948 |
| [23] | Xu T, Zhang Z J, Gao E G, et al. Segmentally iterative ray tracing in complex 2D and 3D heterogeneous Block Models. Bull. Seismol. Soc. Am. , 2010, 100(2): 841-850. DOI:10.1785/0120090155 |
| [24] | Vinje V, Iverson E, GjΦystdal H. Traveltime and amplitude estimation using wavefront construction. Geophysics , 1993, 58(8): 1157-1166. DOI:10.1190/1.1443499 |
| [25] | Vinje V, Iversen E, Astebol K, et al. Estimation of multivalued arrivals in 3D models using wavefront construction-Part Ⅱ. Geophys. Prospect. , 1996, 44(5): 819-842. DOI:10.1111/gpr.1996.44.issue-5 |
| [26] | Moser T J. Shortest path calculation of seismic rays. Geophysics , 1991, 56(1): 59-67. DOI:10.1190/1.1442958 |
| [27] | Zhang Z J, Wang G J, Teng J W, et al. CDP mapping to obtain the fine structure of the crust and upper mantle from seismic sounding data: An example for the southeastern China. Phys. Earth Planet. Inter. , 2000, 122(1-2): 133-146. DOI:10.1016/S0031-9201(00)00191-6 |
| [28] | Zhao A H, Zhang Z J, Teng J W. Minimum travel time tree algorithm for seismic ray tracing: Improvement in efficiency. J. Geophys. Eng. , 2004, 1(4): 245-251. DOI:10.1088/1742-2132/1/4/001 |
| [29] | Velis D R, Ulrych T J. Simulated annealing two-point ray tracing. Geophys. Res. Lett. , 1996, 23(2): 201-204. DOI:10.1029/95GL03690 |
| [30] | Velis D R, Ulrych T J. Simulated annealing ray tracing in complex three-dimensional media. Geophys. J. Int. , 2001, 145(2): 447-459. DOI:10.1046/j.1365-246x.2001.01401.x |
| [31] | Zhang Z, Lin G, Chen J, et al. Inversion for elliptically anisotropic velocity using VSP reflection traveltimes. Geophys. Prospect. , 2003, 51(2): 159-166. DOI:10.1046/j.1365-2478.2003.00362.x |
| [32] | Zhang Z J, Badal J, Li Y K, et al. Crust-upper mantle seismic velocity structure across Southeastern China. Tectonophysics , 2005, 395(1-2): 137-157. DOI:10.1016/j.tecto.2004.08.008 |
| [33] | Zhang Z J, Klemperer S L. West-east variation in crustal thickness in northern Lhasa block, central Tibet, from deep seismic sounding data. J. Geophys. Res. , 2005, 110: 1-14. DOI:10.1029/2004JB003139 |
| [34] | Zhang Z J, Wang Y H. Crustal structure and contact relationship revealed from deep seismic sounding data in South China. Phys. Earth Planet. Inter. , 2007, 165(1-2): 114-126. DOI:10.1016/j.pepi.2007.08.005 |
| [35] | Zhang Z J, Xu T, Zhao B, et al. Systematic variations in seismic velocity and reflection in the crust of Cathaysia: New constraints on intraplate orogeny in the South China continent. Gondwana Res. , 2013, 24(3-4): 902-917. DOI:10.1016/j.gr.2012.05.018 |
| [36] | Zelt C A, Smith R B. Seimic traveltime inversion for 2-D crustal velocity structure. Geophys. J. Int. , 1992, 108(1): 16-34. DOI:10.1111/gji.1992.108.issue-1 |
| [37] | Gj ø ystdal H, Reinhardsen J E, Åstebol K. Computer representation of complex 3-D geological structures using a new "solid modeling" technique.Geophys. Prospect. , 1985, 33(8): 1195-1211. |
| [38] | Pereyra V. Modeling, ray tracing, and block nonlinear travel-time inversion in 3-D. Pure and Applied Geophysics , 1996, 148(3-4): 345-386. DOI:10.1007/BF00874572 |
| [39] | Xu T, Zhang Z J, Zhao A H, et al. Sub-triangle shooting ray tracing in complex 3D VTI media. Journal of Seismic Exploration , 2008, 17(2-3): 131-144. |
| [40] | 徐果明, 卫山, 高尔根, 等. 二维复杂介质的块状建模及射线追踪. 石油地球物理勘探 , 2001, 36(2): 213–219. Xu G M, Wei S, Gao E G, et al. Block model-building and ray-tracing in 2-D complicated medium. Oil Geophys. Prospect. (in Chinese) , 2001, 36(2): 213-219. (in Chinese) |
| [41] | Rawlinson N G, Houseman G A, Collins C D N. Inversion of seismic refraction and wide-angle reflection traveltimes for three-dimensional layered crustal structure. Geophys. J. Int. , 2001, 145(2): 381-400. DOI:10.1046/j.1365-246x.2001.01383.x |
| [42] | Mallet J L. Discrete smooth interpolation. ACM Transactions on Graphics , 1989, 8(2): 121-144. DOI:10.1145/62054.62057 |
| [43] | Mallet J L. Discrete smooth interpolation in geometric modeling. Computer-Aided Design , 1992, 24(4): 178-193. DOI:10.1016/0010-4485(92)90054-E |
| [44] | Al-Chalabi M. Time-depth relationships for multiplayer depth conversion. Geophys. Prospect. , 1997, 45(4): 715-720. DOI:10.1046/j.1365-2478.1997.520293.x |
| [45] | Thurber C H. Earthquake locations and three-dimensional crustal structure in the Coyote Lake area, central California. J. Geophys. Res. , 1983, 88(B10): 8226-8236. DOI:10.1029/JB088iB10p08226 |
| [46] | Zhao D P, Hasegawa A, Horiuchi S. Tomographic imaging of P and S wave velocity structure beneath northeastern Japan. J. Geophys. Res. , 1992, 97: 19909-19928. DOI:10.1029/92JB00603 |
 2013, Vol. 56
2013, Vol. 56


