波动方程法是地震波场数值模拟的重要方法,其本质是求解地震波动方程.有限差分法[1-2]是迄今最常用而且较成熟的波动方程正演模拟方法,其算法简单,易于实现,而且精度较高.但是有限差分方法只能使用规则网格剖分,当模拟起伏地表或地层等复杂构造的地质体时,具有很大的局限性,其精度不够理想.随着计算机计算速度的不断提高,内存存储的不断扩大,地震波动方程有限元模拟方法[3-5]也逐渐发展起来.有限元方法可以使用不规则网格剖分,克服有限差分的上述缺陷,保证了模拟的逼真性.但是该方法在每个时间步上都需要求解大型的线性常微分方程组,造成其计算和存储量巨大、效率相对较低.这些缺点对于模型数据巨大、效率要求较高的地震波场模拟问题来说,尤其不能接受.如果能有效地改进有限元方法的效率,则有限元方法将大有可为.谱元法将有限元方法与谱方法相结合,具有高并行性和高精度的特点,但是目前该方法对网格要求较严格,通用性不好.基于以上优缺点,近年来也出现了一些将有限元和有限差分方法相结合的尝试[6-7].
间断有限元方法(Discontinuous Galerkin finite element methods,简写为DG)是将有限体积方法和有限元方法相结合形成的一类新型高精度方法,其既具有有限元方法可以模拟任何复杂介质模型的韧性,又具有极高的并行性,能够克服有限元方法计算效率低的缺点.另外,由于结合了高精度算法的斜率限制等技术[8],间断有限元方法在处理断裂、高陡等变化剧烈的地质构造时具有明显的优势.该类方法自Reed和Hill[9]提出之后,在近年来得到了迅速的发展,多种形式的间断有限元方法被提出,其中包括龙格-库塔间断有限元(简写为RKDG)方法[10-11]、局部间断有限元(简写为LDG)方法[12-13]、IP方法等,并已经成功应用于计算流体动力学、气象学、海洋学、电磁学等领域.近年来,间断有限元方法在地震勘探领域的应用也受到越来越多的关注,国内鲜有成果见于文献,但国外研究早已蓬勃开展.在弹性波动方程模拟中,Käser等人提出了ADER-DG方法[14-18],该方法是将间断有限元方法与任意高阶时间积分方法相结合形成的,可以使得时间离散达到与空间离散相同的精度.在声波方程模拟中,IP方法[19]和LDG方法[20]是主要的选用方法.相比于IP方法,LDG方法具有全局和局部能量守恒特性,有助于控制波传播过程中耗散作用.
本文选取了局部间断有限元方法对二维地震声波波动方程进行数值模拟.该方法的主要思想是将高阶微分方程分解成一组耦合的一阶微分方程系统,然后使用RKDG方法求解此系统.在空间上,采用LDG方法进行离散,进而得到一个常微分方程系统,然后选取了蛙跳格式(Leap-Frog scheme)求解此系统,从而得到了LDG数值模拟算法.最后设计了计算实例进行模拟.在算例一中,分别用本文算法和连续有限元方法模拟了lamb问题,并进行了比较,验证了本文算法在计算的规模、精度和效率等方面对连续有限元方法的明显改进效果.算例二验证了该算法对起伏高陡构造的适应性,证实了算法的优越性.
2 方法考虑二维标量声波波动方程(含震源):
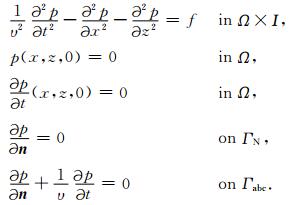
|
(1) |
其中p=p(x,z,t)表示声波波场,υ=υ(x,z)是声波速度,f=f(x,z,t)表示震源.Ω表示空间计算区域,I=[0,Ts]表示时间计算区间.边界Γ=ΓN∪Γabc,ΓN和Γabc分别表示其自由边界和吸收边界.我们使用了旁轴近似理论吸收边界条件,即用入射波方程代替全波动方程.n=(nx,nz)T为边界的外法向量,上标T表示向量的转置.
LDG方法的主要思想是先对高阶微分项进行“降阶”处理,将空间二阶微分方程分解转化成耦合一阶微分方程组,再利用间断有限元方法来求解.为此,引入新变量
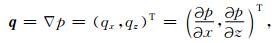
|
(2) |
则方程(1)转化为关于未知量(p,q)T的微分方程:
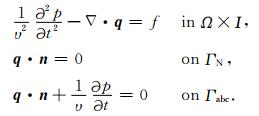
|
(3) |
另外还有一种“降阶”方法,即再引入一个变量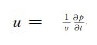

|
这两种分解方法的LDG空间离散方法是类似的,区别在于后者得到的等价形式与应力-速度方程或者弹性波方程相似,更符合物理意义,而前者可以直接求得未知量p.为了便于与连续有限元方法比较,本文中考虑由(2)和(3)组成的微分方程系统.
记网格剖分为Th,定义在其上的有限元空间记为S hm={φ|φ|K∈Pm(K),K∈Τh},Pm(K)表示剖分单元K上的最大次数不超过m的多项式的集合.h表示剖分中所有单元边长的最大值.
由于时间上采用显式格式时,算法在每个单元上的计算都是相同而且相互独立的,因此我们只在某一个单元上推导算法即可.用(·,·)k和〈·,·〉e分别表示在单元K上的面积分和在单元边界e上的线积分,将方程(3)的两端同乘以检验函数φ∈ Pm(K),然后在K上积分,
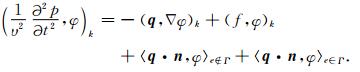
|
对于在Γ=Γabc∪ΓN上的线积分,应用(3)式中的边界条件,即对于ΓN上的积分,以0替代q·n,对于Γabc上的积分,以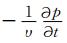
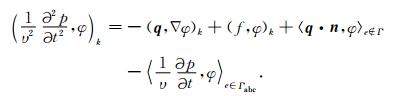
|
以离散解ph和qh分别替换p和q,由于离散解在单元边界上是间断的,因此对于边e上的积分,如果e∈Γ,则直接用q·n在边界上的值替代即可.如果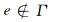
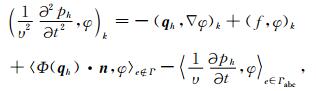
|
(4) |
其中向量Φ(qh)的定义为
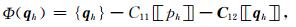
|
C12是以C12为对角线元素的二阶矩阵,C11和C12为常数.平均{·}和跳跃[[·]]的定义如下:边e为单元K和K*的公共边,nk和nk* 分别为它们的外法向量,假设v和w分别为标量和向量函数,则在边e上有
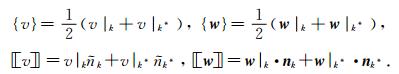
|
方程(4)等价于如下矩阵形式的常微分方程系统
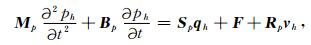
|
(5) |
其中质量矩阵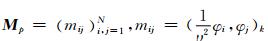
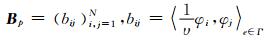
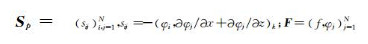
注意到常微分方程组(5)中同时含有一阶和二阶的时间导数,因此我们选用了蛙跳格式(Leap-Frog scheme)来进行时间离散.令Δt=Ts/Nt表示时间步长,Nt为时间步个数,则对于第n+1(≤Nt)步,有
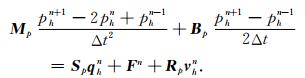
|
(6) |
类似地,在方程(2)两端同乘以ψ=(φ,φ)T∈ Pm(K)×Pm(K),并在K上积分,可得
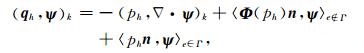
|
(7) |
其中数值通量为
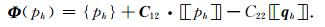
|
方程(7)的等价矩阵形式为

|
(8) |
至此,我们的算法可以描述如下:定义p
h0为方程(p
h0,φ)k=(p(x,z,0),φ)k,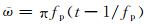
1) 并行地执行:在单元K上,计算方程组(6)求出p hn+1;
2) 并行地执行:将p hn+1代入方程(8)求出q hn+1;循环以上步骤,直至计算所有时间步.
3 计算实例在下面的算例中,均选用了定点上延迟的雷克子波,可描述为
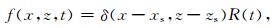
|
其中(xs,zs)为源点坐标,设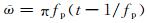
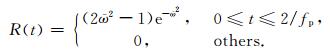
|
其中峰值频率取为fp=30Hz.时间步长Δt=0.1ms,采样间隔取为0.5ms,道间距为10m.计算时,采用了最大边长度不大于10m的三角形网格,参数选取为C11=C22=0,C12=1/h,计算设备选用了12核的工作站.
算例1
考虑lamb问题,计算区域为Ω={(x,z)|0≤x≤800,0≤z≤800},波速υ=2000m/s,震源位置(xs=400,zs=400).四条边均取吸收边界条件.计算时长T=0.4s.我们采用连续有限元方法(记为CFEM)和局部间断有限元算法分别求解该问题,对于每种算法,实验了m=0,1,2,3次的多项式作为基函数的情形.为了便于对比,所有的实验都使用了同一个三角形网格剖分.
对于LDG算法,我们实验了串行(记为LDG-Serial)和简单并行(记为LDG-Parallel)两种策略,这里的简单并行指使用多线程并行求解各个剖分单元,使用OpenMP实现线程并行,线程数设置为30.这样的并行方式是基于LDG算法各个剖分单元的计算是独立的特点之上的,CFEM不具备这样的特点,此处不考虑CFEM的并行.事实上,CFEM的并行需要借助于区域分解方法[21],算法十分复杂,此方法同样可用于LDG-Parallel策略中,即进程并行的同时,每个进程中进行多线程并行,这种方式可进一步降低存储压力和提升效率,但本文未作考虑.下面从问题规模、计算效率和计算精度三个方面进行对比.
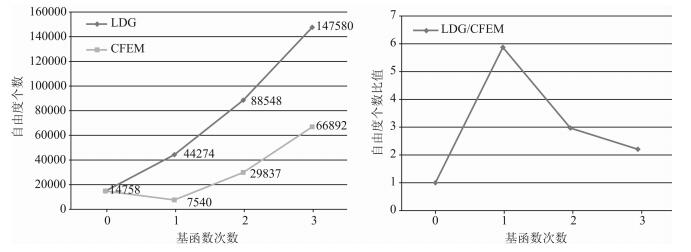
问题规模 理论上,LDG方法的未知量个数dLDG总是剖分单元个数Ne的倍数,而CFEM方法的未知量个数dCFEM一般依赖于剖分中单元顶点的个数.分析图 1可以发现,当基函数次数为0时,LDG方法与CFEM方法是等效的,dLDG和dCFEM都等于剖分单元的个数Ne.随着次数m的增加,dLDG总是大于dCFEM,但二者的比值dLDG/dCFEM在不断减小.这表明在三角形网格下,随着次数的增大,两种方法的计算和存储规模的差距在逐渐缩小.
|
图 1 未知量个数比较 Fig. 1 Comparison of number of degrees of freedom |
计算效率 图 2描述了CFEM,LDG-Serial和LDG-Parallel的单步计算时间随基函数次数的变换情况,记CFEM,LDG-Serial和LDG-Parallel方法的计算时间分别为tC,tS和tP.由于LDG方法比CFEM方法要多计算在边上的积分,所以即使在m=0时,tS仍远大于tC,但是并行之后,计算时间tP大幅度缩短至与tC相当.随着m的增大,各个时间都有不同程度的增大,其中tC的增速最快,并在m=3时超过了tS.tP增速最缓慢,tP与tC的差距逐渐拉大.因此LDG方法可获得较高的计算效率.

|
图 2 计算时间比较 Fig. 2 Comparison of time elapsed |
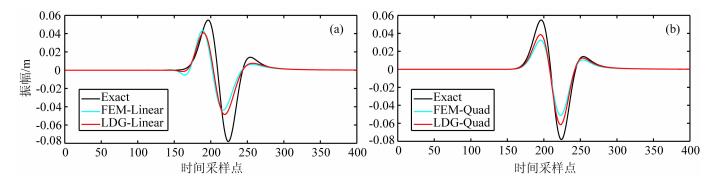
计算精度 图 3中给出了接收点在震源正上方250m处时接收到的波形.LDG、CFEM的模拟结果以及lamb问题解析解分别用红色、蓝色和黑色线条标记,图 3a和3b分别为采用一次元和二次元的结果.从图中可以发现,相比于有限元方法,间断有限元方法在模拟精度和压制频散方面具有更好的效果.
|
图 3 精度比较 Fig. 3 Comparison of accuracy |
算例2
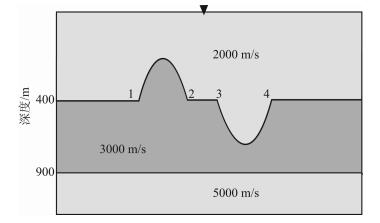
考虑如图 4所示的起伏地层模型.模型长2000m,深1000m,分为3层,第2层上边界位于400m深处,设置了背斜和向斜构造,其中顶点1和2,3和4的距离为400m,弧高300m,属于高陡构造.第3层位于900m深.自上而下速度依次为2000m/s,3000m/s和5000m/s.震源点坐标为(1000,0).地表取自由边界条件,其余边界取吸收边界条件.为了压制“假频”,基函数采用了二次多项式.
|
图 4 算例2的速度模型 Fig. 4 Velocity model of Example 2 |
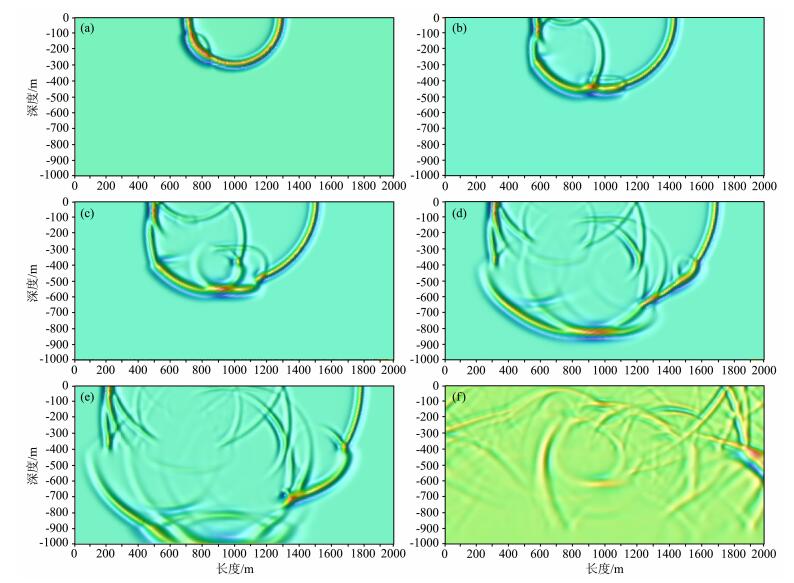
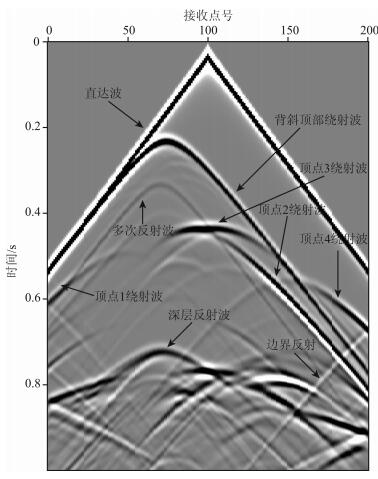
图 5中给出了0.18s,0.25s,0.29s,0.38s,0.43s和0.71s时刻的波场快照,从图中可以发现,地震波在背斜顶部以及1~4四个顶点处产生的绕射波、深水平层的反射波、以及绕射波形成的多次反射波都能清晰地捕捉到.单炮记录如图 6所示,由于使用了旁轴近似理论吸收边界条件,所以边界反射现象未能全部消除.记录中,同相轴清晰,无“假频”干扰,即使深层的反射波也得到了较好的表现.可见,本算法对此类构造具有较好的模拟效果.
|
图 5 算例2的波场快照 (a)0.18 s; (b)0.25 s; (c)0.29 s; (d)0.38 s; (e)0.43 s; (f)0.71 s Fig. 5 Wave field snapshots of Example 2 |
|
图 6 算例2的单炮记录 Fig. 6 Single shot record of Example 2 |
本文应用局部间断有限元方法离散二维声波方程,在时间上选用了显式的蛙跳格式,形成了一种新型模拟算法.该算法结合了有限差分方法和有限元方法的优点,如可以使用三角形单元,因而可以很好地模拟起伏地形;具有天然的并行性,因而计算效率比有限元方法高出很多;在单个单元内的未知量个数比有限元方法和有限差分方法都多,因而计算精度更高等等.给出的数值算例证实了这些优点.基于以上的优越性,该算法可以进一步推广到弹性波数值模拟以及偏移成像等领域.
| [1] | 董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报 , 2000, 43(3): 411–419. Dong L G, Ma Z T, Cao J Z, et al. A staggered-grid high-order difference method of one-order elastic wave equation. Chinese J. Geophys. (in Chinese) , 2000, 43(3): 411-419. (in Chinese) |
| [2] | 殷文, 印兴耀, 吴国忱, 等. 高精度频率域弹性波方程有限差分方法及波场模拟. 地球物理学报 , 2006, 49(2): 561–568. Yin W, Yin X Y, Wu G C, et al. The method of finite difference of high precision elastic wave equations in the frequency domain and wave-field simulation. Chinese J. Geophys. (in Chinese) , 2006, 49(2): 561-568. (in Chinese) |
| [3] | 薛东川, 王尚旭, 焦淑静. 起伏地表复杂介质波动方程有限元数值模拟方法. 地球物理学进展 , 2007, 22(2): 522–529. Xue D C, Wang S X, Jiao S J. Wave equation finite-element modeling including rugged topography and complicated medium. Progress in Geophysics (in Chinese) , 2007, 22(2): 522-529. (in Chinese) |
| [4] | 张美根, 王妙月, 李小凡, 等. 各向异性弹性波场的有限元数值模拟. 地球物理学进展 , 2002, 17(3): 384–389. Zhang M G, Wang M Y, Li X F, et al. Finite element forward modeling of anisotropic elastic waves. Progress in Geophysics (in Chinese) , 2002, 17(3): 384-389. (in Chinese) |
| [5] | 邓玉琼, 张之立. 弹性波的三维有限元模拟. 地球物理学报 , 1990, 33(1): 41–53. Deng Y Q, Zhang Z L. Three-dimensional finite element modeling of elastic waves. Chinese J. Geophys. (in Chinese) , 1990, 33(1): 41-53. (in Chinese) |
| [6] | Ma S. Hybrid modeling of elastic P-SV wave motion: A combined finite-element andstraggered-grid finite-difference approach. Bulletin of the Seismological Society of America , 2004, 94(4): 1557-1563. DOI:10.1785/012003087 |
| [7] | Yang J H, Liu T, Tang G Y, et al. Modeling seismic wave propagation within complex structures. Applied Geophysics , 2009, 6(1): 30-41. DOI:10.1007/s11770-009-0005-2 |
| [8] | LeVeque R J. Finite Volume Methods for Hyperbolic Problems. Cambridge: Cambridge University Press, 2002 . |
| [9] | Reed W H, Hill T R. Triangular mesh methods for the neutron transport equation, Technical Report, LA-UR-73-479, Los Alamos Scientific Laboratory, 1973. |
| [10] | Cockburn B, Shu C W. Tvb Runge-Kutta local projection discontinuous Galerkin finite element method for scalar conservation laws II: general framework. Mathematics of Computation , 1989, 52: 411-435. |
| [11] | Cockburn B, Shu C W. Runge-Kutta discontinuous Galerkin methods for convection-dominated problems. Journal of Scientific of Computing , 2001, 16(3): 173-261. DOI:10.1023/A:1012873910884 |
| [12] | Cockburn B, Shu C W. The local discontinuous Galerkin method for time-dependent convection-diffusion systems. SIAM Journal of Numerical Analysis , 1998, 35(6): 2440-2463. DOI:10.1137/S0036142997316712 |
| [13] | Arnold D N, Brezzi F, Cockburn B, et al. Unified analysis of discontinuous Galerkin methods for elliptic problems. SIAM Journal of Numerical Analysis , 2002, 39(5): 1749-1779. DOI:10.1137/S0036142901384162 |
| [14] | Käser M, Dumbser M. An arbitrary high-order discontinuous Galerkin method for elastic waves on unstructured meshes I: the two-dimensional isotropic case with external source terms. Geophys. J. Int. , 2006, 166(2): 855-877. DOI:10.1111/gji.2006.166.issue-2 |
| [15] | Dumbser M, Käser M. An arbitrary high-order discontinuous Galerkin method for elastic waves on unstructured meshes-II.The three-dimensional isotropic case. Geophys. J. Int. , 2006, 167(1): 319-336. DOI:10.1111/gji.2006.167.issue-1 |
| [16] | De la Puente J, Käser M, Dumbser M, et al. An arbitrary high-order discontinuous Galerkin method for elastic waves on unstructured meshes IV: anisotropy. Geophys. J. Int. , 2007, 169(3): 1210-1228. DOI:10.1111/gji.2007.169.issue-3 |
| [17] | De la Puente J, Dumbse M, Käser M, et al. Discontinuous Galerkin methods for wave propagation in poroelastic media. Geophysics , 2008, 73(5): T77-T97. DOI:10.1190/1.2965027 |
| [18] | Delcourte S, Fezoui L, Glinsky-Olivier N. A high-order discontinuous Galerkin method for the seismic wave propagation. ESAIM: Proceedings , 2009, 27(3): 70-89. |
| [19] | De Basabe J D, Sen M K, Wheeler M F. The interior penalty discontinuous Galerkin method for elastic wave propagation: grid dispersion. Geophys. J. Int. , 2008, 175(1): 83-93. DOI:10.1111/gji.2008.175.issue-1 |
| [20] | Ainsworth M, Monk P, Muniz W. Dispersive and dissipative properties of discontinuous Galerkin finite element methods for the second-order wave equation. Journal of Scientific Computing , 2006, 27(1-3): 5-40. DOI:10.1007/s10915-005-9044-x |
| [21] | 王月英, 孙成禹. 弹性波动方程数值解的有限元并行算法. 中国石油大学学报(自然科学版) , 2006, 30(5): 27–30. Wang Y Y, Sun C Y. Finite element parallel algorithm for numerical solution of elastic wave equation. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese) , 2006, 30(5): 27-30. (in Chinese) |
 2013, Vol. 56
2013, Vol. 56

