2. 同济大学海洋与地球科学学院波现象与反演成像研究组, 上海 200092;
3. 中国石化物探技术研究院, 南京 211103
2. Wave Phenomena and Inversion Imaging Research Group (WPI), School of Ocean & Earth Science, Tongji University, Shanghai 200092, China;
3. Sinopec Geophysical Research Institute (SGRI), Nanjing 211103, China
逆时偏移[1]最早由Whitemore(1983)等人提出,相较于Kirchhoff积分和单程波成像方法,其成像精度最高,复杂构造适应能力最强.波动方程逆时偏移没有单程波传播算子倾角的限制,可以用于复杂区域和陡倾角构造成像.虽然逆时偏移是一种计算成本非常昂贵的方法,但是,随着计算机软硬件的发展和近年来人们对复杂地区成像的浓厚兴趣,使得人们对这种方法越来越重视.
逆时偏移算法与其他偏移算法一样,可以分解为波场传播和成像条件两个步骤.波场传播是用数学的方法将波场反向延拓到成像体内部,成像条件则是在成像体内提取像的准则.有限差分方法求解波动方程是目前地震波正演和逆时偏移的主要方法,也是正演和偏移成像中计算量最大的部分.成像条件方面,Claerbout提出的相关成像条件[2]是被广泛采用的逆时偏移成像条件,它的本质是将震源波场和检波点波场在同一时刻进行相关,提取成像值.
由于逆时偏移震源波场与检波器波场延拓方向不同(震源波场从零时刻向最大时刻延拓,检波器波场从最大时刻向零时刻延拓),相关成像条件需要对波场在同一时刻进行互相关,直接的实现是在震源波场延拓过程中将其记录下来,检波器波场反向延拓时读取并进行互相关成像.这种实现方案需要大量的波场存储,大规模三维数据成像时对计算机存储提出了很大的挑战,通常需要采取合适的实现策略,以达到计算量和存储量的平衡.在实现策略方面,Symes(2007)提出CheckPointing方法[3],在增加50%计算量的基础上减少了波场的存储,在计算量和存储量之间做了一个较好的折中.Robert(2009)提出用随机边界条件[4]代替吸收边界条件,通过增加一次波场反传重建波场的方式来实现相关成像条件,可以完全消除波场存储问题,在高性能计算平台上具有很大的吸引力.在实际应用过程中,随机边界条件通常在剖面中带来一些随机干扰,影响成像质量.Feng(2011)提出一种新的波场重建策略,通过成像体四周波场反传重建整个成像空间的波场[5].利用该策略实现逆时偏移,边界条件仍然使用常规的吸收边界,计算量、存储量以及成像效果均基本满足要求.Liu等(2013)进一步发展了这种波场重建机制,并与随机边界条件进行了结合,进一步提高了波场重建的实用性[6].
GPU是图形处理器(Graphic Processing Unit)的简称,是NVIDIA、AMD、Intel等芯片公司推出的计算机显示设备.GPU由于其设计目的与CPU不同,它包含更多的计算模块,近年来其计算能力已经远远超过了CPU.这样,利用GPU进行通用计算的想法也就应运而生.GPGPU(General Purpose GPU)是通用图形处理器的简称,最早概念由ATI公司提出,由于其编程较为复杂,没有得到广泛应用.直到2006年NVIDIA公司发布了其统一计算架构平台CUDA(Compute Unified Device Architecture),对C语言进行了扩展,使得开发GPGPU程序门槛大为降低,带来了CPU/GPU异构平台计算的快速发展[7].
利用GPU的强大计算能力进行逆时偏移成像,国内外众多学者已经进行了大量的研究探索.如Micikevicius(2008)研究了基于CUDA平台的有限差分实现问题,给出了快速实现有限差分实现算法[8].Sypek等(2009)对比讨论了利用GPU加快时间域有限差分运算的几种实现策略[9].Foltinek等(2009)讨论了生产规模数据的逆时偏移在GPU上实现的挑战,讨论了区域分解进行的必要性[10]. Michea和Komatitsch(2010)研究了利用GPU卡进行三维弹性波有限差分正演模拟,分析了不同情况下的加速比[11].Sun和Suh(2011)讨论了TTI介质逆时偏移对GPU的挑战[12].国内研究人员也对逆时偏移的GPU实现进行了大量研究,刘红伟等(2010)进行了二维高阶差分GPU逆时偏移[13],赵磊等(2010)进行了三维逆时偏移的GPU实现[14],李博等(2010)对比分析了基于CPU/GPU平台的逆时偏移实现策略[15],Liu等(2012)比较系统地阐述了GPU逆时偏移的相关问题[16],他们都是以随机边界条件为基础设计逆时偏移的实现策略.数值试验表明随机边界条件容易降低偏移剖面的信噪比,本文基于NearlyPML边界条件设计逆时偏移的实现策略,结合GPU运算特点和大规模数据处理的需求,分析了在CPU/GPU异构机群上实现逆时偏移需要解决的相关问题.数值试验证明了本文方法的有效性.
2 理论基础逆时偏移由双程波动方程逆时波场外推和成像条件两个步骤构成.常规的实现方法是对震源波场利用双程波方程进行正向外推,并保存外推波场.然后对接收波场根据双程波方程进行反向外推,并在外推过程中读取记录的震源波场应用成像条件提取成像值,所有时间步求和得到单炮成像数据体.最后,所有炮集的成像值叠加即可得到最终叠前深度偏移结果.
三维常密度声波介质双程波动方程为
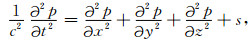
|
(1) |
式中,p=p(x,y,z,t)为介质中的压力场,c=c(x,y,z)为介质速度,s=s(x,y,z,t)为震源项.要实现波动方程的正向、反向传播,需要构造合适的波场传播算子,在逆时偏移中传播算子一般采用有限差分法来构造.有限差分法的基本原理是通过对(1)式中的二阶偏导数进行差分离散,以差分代替微分,从而实现波场逐层外推.Dablain(1986)详细地讨论了三维双程波动方程的高阶有限差分解法[17].此处仅仅列出反向外推的基本计算公式,截断误差为O(ΔxM,ΔyM,ΔzM,Δt2)的统一的时间二阶空间M阶三维波场外推差分方程为

|
(2) |
其中,ω0,ωm为差分系数,i,j,k,n分别表示x,y,z和时间t方向离散.对波场进行高效外推,人工边界条件的处理至关重要.逆时偏移常用的边界条件有吸收边界条件、随机边界条件等.采用不同的边界条件对应不同的逆时偏移实现策略,如采用吸收边界条件时通常采取checkpointing技术[3]或者边界波场重建技术[5],采用随机边界条件[4]则可以完全不需要进行波场存储,通过增加一次波场传播实现逆时偏移成像.
通常,逆时偏移采用零延迟互相关成像条件,即

|
(3) |
式中,tmax是最大记录时间,ps(x,y,z,t)为正向外推的震源波场,pr(x,y,z,t)为反向外推的记录波场,I(x,y,z)为点(x,y,z)的成像结果.
3 GPU及其特点GPU与CPU设计的目的不同,前者用于处理大规模图像的渲染(流数据处理),后者则需要处理各种复杂问题.因此,GPU更多的晶体管用于数值运算,而CPU则更多地考虑数据的控制和缓存[7].随着近年来计算机技术的发展,GPU比CPU具有更多的计算核心和更高的数据传输带宽,计算速度和传输速度均已远超CPU.同时,由于设计目的不同,GPU缓存较小,流控核心少,其分支判断能力、逻辑控制能力较CPU弱.因此,GPU非常适合处理那些能够表示为数据并行计算(同一程序在多个数据上并行执行)的问题,数据并行计算的算术计算密度(算术操作和存储器操作的比例)非常高.而数据输入输出、数据控制等相对计算量较小,判断逻辑较为复杂的运算则适合在CPU上执行.
CPU与GPU之间通过PCIE接口进行通讯,GPU访问内存(在主板上,通过PCIE访问)的速度要远小于访问其显存(在显卡上)的速度.在GPU和显卡上,又划分为不同的存储器级别:全局存储器(在显卡上,但不在GPU上)、共享存储器、纹理存储器、常量存储器等,不同的存储器存取时间差异较大,存储器容量差异也较大.为了充分挖掘GPU的计算能力,在GPU上进行运算通常按照如下方式进行:首先将计算数据导入GPU全局存储器,然后取全局存储器中的一部分数据导入共享存储器并进行运算,最后将运算结果返回给全局存储器,逐个网格循环直到全部数据计算完成.
对于大规模数据处理,通常需要较大的计算机内存(显存).当前主流CPU机群内存通常达到数十GB甚至更大,而GPU产品目前最大显存只有不足6GB或者更小,进行大规模数据处理需要一些特殊考虑.
4 三维逆时偏移GPU实现逆时偏移是典型的大规模数据处理问题,需要解决大计算量和大存储量问题.李博等[15]分析了在GPU上实现逆时偏移的几种解决方案,指出利用随机边界条件实现逆时偏移的可行性.笔者数值试验表明,采用随机边界条件通常无法使边界反射波场完全随机,从而影响最终成像结果的质量.我们的实现方案是根据Feng等[5]提出的边界波场重建策略,利用边界波场进行波场重建,在保证成像质量的前提下,折中逆时偏移的计算量和存储量.根据GPU计算能力、存储带宽等特点,实现逆时偏移波场传播仍旧需要解决一些特有问题,主要表现在两个方面:大规模计算显存不足问题和高效人工边界条件处理问题.
4.1 解决大规模数据成像的区域分解法根据公式(2)的差分格式,Micikevicius(2008)给出了在GPU上进行有限差分计算编程实例[8].以空间10阶时间2阶差分为例,计算t+1层某个点的值需要t-1层对应点和图 1所示第t层31个点的值.在GPU计算中,一组线程构成一个线程块进行运算(一个线程块内的各个线程公用共享存储器).理想的情况是将一个线程块所需的数据一次调入共享存储器,GPU计算核心从共享存储器取数据进行运算.对于三维高阶差分运算,需要导入共享存储器的数据已经远远超过GPU的共享存储器大小.Micikevicius(2008)提出只把两维数组放入共享存储器,另外一维利用每个线程的寄存器存储,从而解决了共享存储器不足问题,大大提高了三维有限差分的效率.
|
图 1 十阶空间差分网格点分布 Fig. 1 Grid distributions of ten order finite difference stencil |
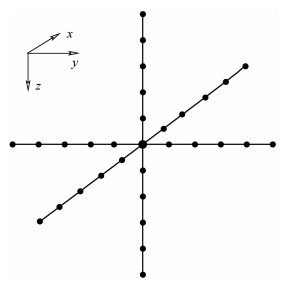
对于大规模数据逆时偏移,进行三维差分运算所需显存空间通常大于GPU卡实际显存大小,通过对差分数据体进行区域分解,将整个数据体划分为多块,每块在一个GPU上进行计算.利用区域分解进行差分运算,需要解决的核心问题是如何隐藏掉卡与卡之间的数据交换,提高计算效率.如图 2所示为区域分解示意图,我们将整个三维差分空间沿着某个方向切割到不同的GPU卡上进行差分计算.为了保证差分结果的正确性,卡与卡之间交界处的一定区域,在每步差分运算中需要进行数据交换.下面以两块卡为例介绍区域分解方法.
|
图 2 区域分解示意图 Fig. 2 Sketch map of domain decomposition |
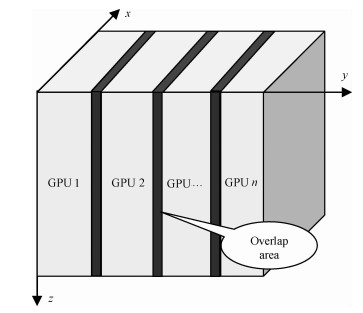
如图 3所示,左右分别为区域分解的两块卡各自的计算区域,每块卡的计算区域都可以划分为三部分(图中分别用A、B和C表示),其中,C为两块卡中重叠的区域,用于与相邻卡的交换数据,其厚度与所用的差分格式有关,在10阶差分的情况下其厚度为5个网格宽度,对于图 2所示的沿y方向进行的区域分解,假设差分数据体x,y和z三个方向的维度分别为NX,NY和NZ,则B和C的大小分别为NX×NZ×5.如图 1所示,由于t+1时刻高阶差分运算需要t时刻空间31个点的参与,正确计算t+1时刻区域B的值需要t时刻C区域的值,C区域由于靠近差分计算边界无法计算,因此需要从相邻卡的B区域获得.即每步计算需要将本卡B区域计算结果发送到相邻卡的C区域,因此图中区域B与区域C厚度相同.区域A是可以每块卡独立计算的区域,不需要进行卡与卡之间数据交换.为了隐藏B和C之间的数据交换,我们将计算过程分解为两个步骤:
|
图 3 区域分解数据交换示意图 Fig. 3 Sketch map of data exchange in domain decomposition |
第一步,每块卡计算区域B的波场;
第二步,每块卡计算各自的区域A,同时将区域B的计算结果发送到相邻卡的区域C.
这种做法在区域A较大,B和C之间数据传输较快的情况下,可以完全将数据通信隐藏在区域A的计算过程中,可以达到线性的加速比.
对于Nvidia计算能力低于2.0的GPU卡,由于其本身没有卡与卡之间直接的数据交换机制,区域B和C之间的数据交换需要通过内存中转,对于这种计算平台,我们设计方案为:每个进程控制一块GPU卡,将参与计算的进程进行分组,一个进程组处理一炮地震数据.在波场延拓过程中,进程组内的不同卡之间需要进行数据交换.由于卡与卡之间无法直接交换数据,每块卡每个时间步计算完成后需要首先将数据复制到内存,然后利用MPI进行进程组内非阻塞数据交换,最后将交换后的数据复制到显存相应的位置.整个实现流程如图 4所示.这个流程也可以适用于计算能力大于2.0的GPU卡区域分解计算,是一种通用的计算区域分解作业分配方式.
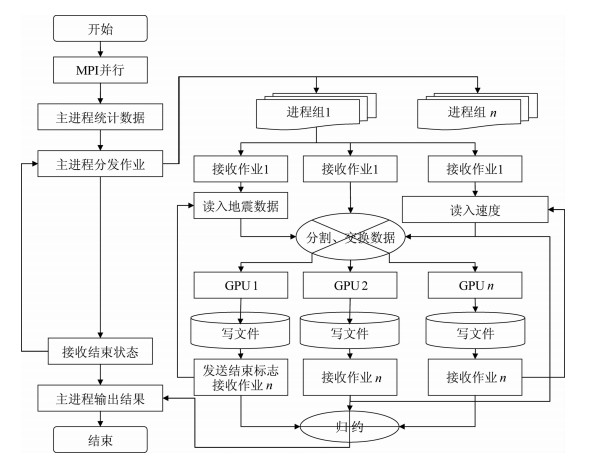
|
图 4 通用GPU卡区域分解计算流程图 Fig. 4 Computation workflow of universal GPU domain decomposition |
Nvidia计算能力高于2.0的GPU卡提供了卡与卡之间直接进行数据交换的接口,其通讯效率比通过CPU中转更高,编程复杂度也大为降低.对于这类计算平台,我们的设计方案如下:一个进程控制多块GPU卡处理一炮地震数据,每个时间步需要进行卡与卡之间直接数据交换.整个实现流程如图 5所示.
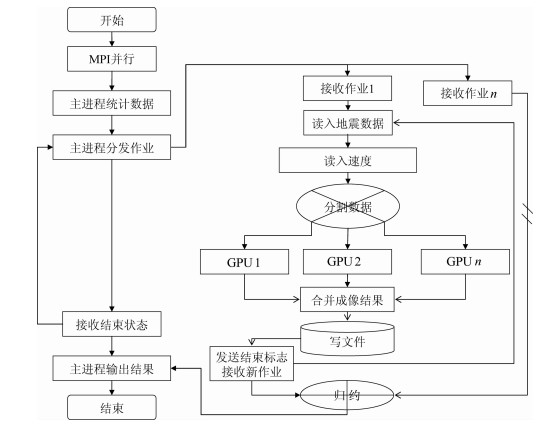
|
图 5 计算能力2.0及以上GPU区域分解计算流程图 Fig. 5 Computation workflow of GPU domain decomposition with computing capacity≥2.0 |
人工边界条件处理好坏,直接影响波场传播的效率和精度,对于波场模拟和偏移成像具有重要意义.随机边界条件[4]在差分计算边界区域设置随机变化的速度场,将传播到该区域的波场打乱成“随机”噪音,多炮叠加将噪音消除得到偏移剖面.实现策略上首先将震源波场传播到最大时间,然后震源与检波器波场同步反向传播并提取成像值,这种做法完全解决了逆时偏移对波场的存储问题.并且,该边界条件内部区域和边界区域控制方程完全一致,不需要任何的辅助方程和变量,从而也不需要增加额外存储和计算,计算上特别适合在GPU上实现.但是,数值试验表明该边界条件无法得到真正随机的波场,从而会影响逆时偏移成像质量.为了提高随机边界的效果,Fletcher和Robertsson(2011)提出了时变随机边界[18],Shen和Clapp(2011)则提出块状随机边界[19]来应对随机边界对低频信号效果较差的问题.
与随机边界相比,吸收边界条件是更为成熟的边界条件,尤其是PML(最佳匹配层)边界条件,是目前应用最为广泛的吸收边界条件.PML边界条件通过引入复坐标变换(对坐标进行拉伸),使得波动方程的平面波解在新的坐标系下传播振幅不断衰减.传统的分裂格式的PML条件存在吸收边界的控制方程与计算区域控制方程差异较大的问题,破坏了差分格式的计算模式,并且需要较大的辅助变量保存边界波场[19-20],这导致在多核CPU/GPU机群上实现效率较低.与坐标拉伸的PML不同,Cummer(2003)将PML方程对坐标的拉伸量转移到对波场进行拉伸,在电磁介质模拟中首先提出了NPML(NearlyPML)边界条件[20-21].这种边界条件具有内部计算区域与PML区域差分格式一致的优点,仅仅需要增加几个辅助方程,计算上具有明显的优势.Hu和Cummer(2004)证明了NPML边界与常规PML方程的等价性[21-22].Hu等(2007)将NPML边界条件引人到一阶声波方程模拟[22-23]中,McGarry(2009)在此基础上推导了二阶方程的NPML边界[23-24].与传统的分裂格式PML相比,NPML具有控制方程简单、需要辅助波场较少的优点,更加适用于GPU计算.
对于一阶微分方程,非常容易推导其PML边界条件.对于二阶微分方程,PML边界条件的推导要复杂的多.对于压力-速度表示的一阶声波方程,有
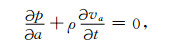
|
(4) |
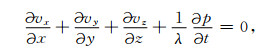
|
(5) |
其中,p表示声波压力,a为x、y或者z,va表示质点速度的a分量,t为时间,ρ为介质密度,λ=ρc2为拉梅常数.其对应的NPML方程为[22-23]
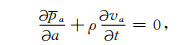
|
(6) |
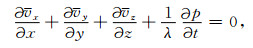
|
(7) |
式中,
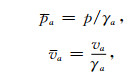
|
(8) |
其中复拉伸因子γa在频率域满足
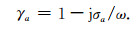
|
(9) |
根据式(9),式(8)可表示为
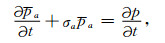
|
(10) |
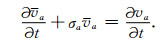
|
(11) |
根据方程(6)、(7)和(10)、(11)就可以进行一阶声波方程NPML区域的计算.方程(6)、(7)与内部计算区域(4)、(5)控制方程完全一致,边界区域只需要增加方程(10)、(11)两个辅助方程,编程实现较为简单.
方程(7)对时间取微分,结合方程(11),有
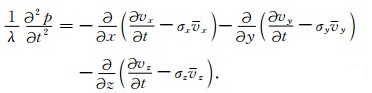
|
(12) |
方程(6)代入方程(12),假设为常密度介质,并结合关系式λ=ρc2,有
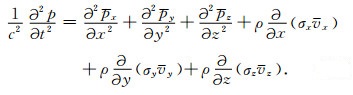
|
(13) |
我们定义
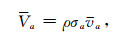
|
(14) |
从而,方程(13)变为

|
(15) |
根据方程(6)、(11)、(14),有
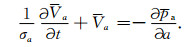
|
(16) |
方程(10、15、16)即为NPML方程的吸收边界条件公式.可以看到,对于二阶声波方程,NPML方程(15)二阶微分部分与内部区域一致,方程(15)另外增加了几个一阶速度校正项.直接解方程(15)需要判断差分的边界区域与角点区域,仍旧会给差分格式实现增加不少分支运算.方程(15)可以进一步修改为
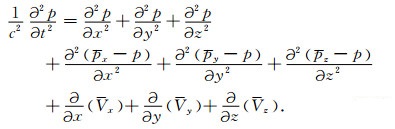
|
(17) |
根据公式(10)、(16)、(17),高阶差分波场外推单步计算流程见图 6.

|
图 6 NPML边界条件GPU实现策略 Fig. 6 Implementation strategy of GPU NPML boundary conditions |
图 6所示NPML计算策略对整个差分空间采用相同的差分格式,差分计算过程中不需要边界进行边界区域判断,NPML区域辅助波场的计算和边界区域波场的修正均可以通过独立的核函数实现,最大程度地避免了实现PML吸收边界条件的分支选择,在GPU上实现效率非常高.
5 数值试验下面我们用SEG/EAGE3D岩丘模型进行算法成像测试.该数据的观测参数为:总炮数:4781炮,50束线,炮线间距160 m.炮间距80 m,线间距40 m,道间距40 m.每束线96炮,每炮65道;记录长度5 s,时间采样率8 ms.
图 7和图 8分别展示了岩丘模型逆时偏移成像剖面和成像切片.图 7(a)为速度模型剖面,(b)为对应该速度剖面的偏移成像结果.图 8与图 7类似,左右分别为速度模型深度切片和对应该深度的成像体切片.对比速度模型和成像结果,可以看出本文基于GPU的逆时偏移实现方案能够很好地对岩丘模型成像,模型中高陡倾角构造能够得到很好的成像,成像剖面信噪比较高.

|
图 7 岩丘模型速度剖面及逆时偏移剖面 Fig. 7 Velocity model and RTM profiles of SEG 3D salt model |
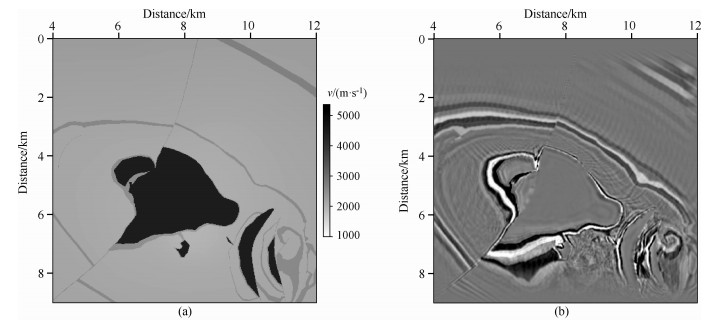
|
图 8 岩丘模型速度切片及逆时偏移切片 Fig. 8 Velocity model and RTM depth sections of SEG 3D salt model |
下面我们用含岩丘的实际资料测试GPU逆时偏移算法.该资料共5080炮,每炮2400道.偏移深度3500 m,深度间隔10 m.该区域地下岩丘发育丰富,岩丘边界存在超过90°地层,横向变速较大,对成像算法的精度要求较高.为了对高陡倾角构造成像,单炮成像孔径较大,从而需要较大的GPU显存.单炮逆时偏移显存需求量超过单块Nvidia Tesla M2090卡的最大显存量,需要将两块卡绑定实现每炮偏移计算.图 9为该实际资料inline方向成像剖面,可以看出,该GPU逆时偏移算法对岩丘边界能够较好成像,岩丘侧翼高陡倾角构造能够较好分辨,成像效果较好.

|
图 9 实际资料逆时偏移剖面 Fig. 9 RTM profile of real field data |
叠前逆时偏移作为当前最精确的成像算法对计算平台和处理策略提出了很高的要求.随着计算机工业的发展,GPU在计算速度和存储带宽方面已经远远超过了CPU,利用GPU进行叠前逆时偏移成像具有很好的应用前景.由于GPU设计上的特殊性,开展基于GPU的逆时偏移成像需要解决单卡显存较小问题和人工边界条件的施加对计算速度的影响等问题.
针对大规模数据逆时偏移GPU显存不足问题,区域分解技术将多块GPU卡绑定,进行一炮数据成像,很好地解决了逆时偏移的大显存需求问题.对于计算能力低于2.0的NvidiaGPU卡,没有GPU与GPU之间直接通讯机制,我们设计将计算进程分为不同进程组,每个进程组处理一炮地震数据,进程组内各个进程通过MPI相互通讯协作完成整个三维体的波场传播和成像运算.该方法也适用于在计算能力大于2.0的NvidiaGPU卡,理论上可以实现任意大规模地震数据的逆时偏移成像处理.计算能力大于2.0的NvidiaGPU卡提供了GPU与GPU之间直接通讯机制,通讯效率更高,区域分解实施起来也更为简单.我们利用一个进程控制多块GPU卡进行一炮逆时偏移成像运算,可以处理较大规模的三维数据逆时偏移成像.
随机边界能够解决逆时偏移波场存储问题,计算量也很小,但容易给成像剖面带来噪音干扰. PML吸收边界具有最好的吸收效果,常规PML由于控制方程与内部计算区域差异较大,影响了整个高阶差分运算的并行性,影响GPU实现的效率.二阶方程NPML边界条件能够保证边界区域和内部区域控制方程基本一致,结合合适的实现策略,可以避免实现PML边界条件需要过多分支判断的问题.并且,NPML边界条件需要保存较少的辅助波场,对GPU显存压力较小,利用GPU实现NPML边界条件具有较高的加速比.
区域分解解决了利用GPU进行大规模数据有限差分运算问题,NPML边界条件能够保证良好的吸收效果和在GPU上较高的计算效率.基于此两项关键技术,采用边界波场重建策略进行波场重建实现逆时偏移成像,使得基于GPU集群平台的大规模三维数据逆时偏移可以达到实用化的程度.
| [1] | Whitemore N D. Iterative depth migration by backward time propagation. SEG Expanded Abstracts , 1983(1): 382-385. |
| [2] | Claerbout J F. Toward a unified theory of reflector mapping. Geophysics , 1971, 36(3): 467-481. DOI:10.1190/1.1440185 |
| [3] | Symes W W. Reverse time migration with optimal checkpointing. Geophysics , 2007, 72(5): SM213-SM221. DOI:10.1190/1.2742686 |
| [4] | Clapp R G. Reverse-time migration with random boundaries. SEG Expanded Abstracts , 2009: 2809-2813. |
| [5] | Feng B, Wang H Z, Tian L X, et al. A strategy for source wavefield reconstruction in reverse time migration. SEG Expanded Abstracts , 2011: 3164-3168. |
| [6] | Liu H W, Ding R W, Liu L, et al. Wavefield reconstruction methods for reverse time migration. J. Geophys. Eng. , 2013, 10(1): 15004-15009. DOI:10.1088/1742-2132/10/1/015004 |
| [7] | NVIDIA. NVIDIA CUDA Programming Guide, Version 4.0. Santa Clara: NVIDIA, 2011. |
| [8] | Micikevicius P. 3D finite difference computation on GPUs using CUDA.//Proceedings of 2nd Workshop on General Purpose Processing on Graphics Processing Units, Expanded Abstracts, 2008: 79-84. http://www.oalib.com/references/18992114 |
| [9] | Sypek P, Dziekonski A, Mrozowski M. How to render FDTD computations more effective using a graphics accelerator. IEEE Transactions on Magnetics , 2009, 45(3): 1324-1327. DOI:10.1109/TMAG.2009.2012614 |
| [10] | Foltinek D, Eation D, Mahovsky J, et al. Industrial-scale reverse time migration on GPU hardware. SEG Expanded Abstracts , 2009: 2789-2793. |
| [11] | Michéa D, Komatitsch D. Accelerating a 3D finite-difference wave propagation code using GPU graphics cards. Geophys. J. Int. , 2010, 182(1): 389-402. |
| [12] | Sun X Y, Suh S. Maximizing throughput for high performance TTI-RTM: From CPU-RTM to GPU-RTM. SEG Expanded Abstracts , 2011: 3179-3183. |
| [13] | 刘红伟, 李博, 刘洪, 等. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报 , 2010, 53(7): 1725–1733. Liu H W, Li B, Liu H, et al. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation. Chinese J. Geophys (in Chinese) , 2010, 53(7): 1725-1733. (in Chinese) |
| [14] | 赵磊, 王华忠, 刘守伟, 等. 逆时深度偏移成像方法及其在CPU/GPU异构平台上的实现. 岩性油气藏 , 2010, 7: 36–41. Zhao L, Wang H Z, Liu S W, et al. Reverse-time depth migration and its application at CPU/GPU platform. Lithologic Reservoirs (in Chinese) , 2010, 7: 36-41. (in Chinese) |
| [15] | 李博, 刘红伟, 刘国峰, 等. 地震叠前逆时偏移算法的CPU/GPU实施对策. 地球物理学报 , 2010, 53(12): 2938–2943. Li B, Liu H W, Liu G F, et al. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU. Chinese J. Geophys (in Chinese) , 2010, 53(12): 2938-2943. (in Chinese) |
| [16] | Liu H W, Li B, Liu H, et al. The issues of prestack reverse time migration and solutions with Graphic Processing Unit implementation. Geophysical Prospecting , 2011, 60(5): 906-918. |
| [17] | Dablain M A. The application of high-order differencing to the scalar wave equation. Geophysics , 1986, 51(1): 54-66. DOI:10.1190/1.1442040 |
| [18] | Fletcher R P, Robertsson J O A. Time-varying boundary conditions in simulation of seismic wave propagation. Geophysics , 2011, 76(1): A1-A6. DOI:10.1190/1.3511526 |
| [19] | Shen X K, Clapp R G. Random boundary condition for low-frequency wave propagation. SEG Expanded Abstracts , 2011: 2962-2965. |
| [20] | Komatitsch D, Tromp J. A perfectly matched layer absorbing boundary condition for the second-order seismic wave equation. Geophysical Journal International , 2003, 154(1): 146-153. DOI:10.1046/j.1365-246X.2003.01950.x |
| [21] | Cummer S A. A simple, nearly perfectly matched layer for general electromagnetic media. IEEE Microwave and Wireless Components Letters , 2003, 13(3): 128-130. DOI:10.1109/LMWC.2003.810124 |
| [22] | Hu W Y, Cummer S A. The nearly perfectly matched layer is a perfectly matched layer. IEEE Antennas and Wireless Propagation Letters , 2004, 3(1): 137-140. DOI:10.1109/LAWP.2004.831077 |
| [23] | Hu W Y, Abubakar A, Habashy T M. Application of the nearly perfectly matched layer in acoustic wave modeling. Geophysics , 2007, 72(5): SM169-SM175. DOI:10.1190/1.2738553 |
| [24] | McGarry R, Moghaddam P. NPML boundary conditions for second-order wave equations. SEG Expanded Abstract , 2009: 3590-3594. |
 2013, Vol. 56
2013, Vol. 56

