2. Geological Survey of Japan, AIST, Tsukuba 305-8567, Japan;
3. 中国科学院云南天文台, 昆明 650011
2. Geological Survey of Japan, AIST, Tsukuba 305-8567, Japan;
3. Yunnan Observatory, Chinese Academy of Sciences, Kunming 650011, China
地震的发生受起潮力的影响已有不少报道[1-17].检验地震与起潮力是否相关的常用方法是统计地震发生时间对潮汐相位的选择性,即首先计算月日对地球的起潮力随时间的变化曲线,然后对发震时间落入不同潮汐相位区间的地震事件进行统计,若地震数目在某一潮汐相位附近较其它相位占优势,即存在一个优势潮汐相位,则认为地震的发生受到潮汐触发作用的影响或存在潮汐相关性,如果发震时间是随机分布的,结论则相反.多数研究结果[18-29]显示,一些地区的地震发生时间在某些时段相对集中于某一潮汐相位附近,认为地震和潮汐之间存在一定的相关性,且这种相关性是弱相关.国内在探索起潮力与地震活动性及地震预测检验方面有所尝试,特别是固体潮的加卸载响应比理论[30]以及更能突出震前异常信息的权重加卸载响应比方法[31-32]充分考虑了短周期半日潮对地震活动的调制作用.有研究采用小波分析方法对中国大陆及华北地区地震的0.1年积累本尼奥夫应变进行分析,得到了各种层次的地震活跃期和平静期[33].这些活跃期和平静期的交替出现也许包含着除构造应力之外的与固体潮周期相关的因素.
前人的绝大多数研究存在以下共同点:①研究范围多为曾发生过大地震的局部区域;②研究时段为大地震发生前后几个月或几年;③地震事件多为与大地震前震和余震相关的地震序列;④起潮力时间变化曲线的计算均选择短周期的潮汐波.还有一些在统计研究中遇到的问题仍然无法得到解决,例如,引发争论的关于地震触发相关潮汐周期以及潮汐触发优势相位等问题[34-37].由于在长时间段(例如几十年或上百年)和大范围内计算长周期起潮力来检验相位选择性是不易实现的,长期以来,地震与潮汐相关性的研究大都不超出潮汐短周期和地区局域性的限制.
起潮力含有复杂的周期成分,并具有不断重复作用的特点,也许正是起潮力的这种周期振荡性质而不完全是其振幅,在地震的潮汐触发中起更重要的作用[10, 22].本文试图以不同于以往研究的角度和方法来避免一些局限性,从目前记载相对远久和完善的USGS全球地震资料出发,首先构建全球地震能量释放的时间变化序列,采用能够从大量离散时变信号序列中提取其隐含的不同层次周期的小波变换方法,对全球地震能量时间变化序列进行分析,提取地震能量序列中可能存在的潮汐影响周期,探讨全球地震能量释放与潮汐周期的关系及其相关物理背景.
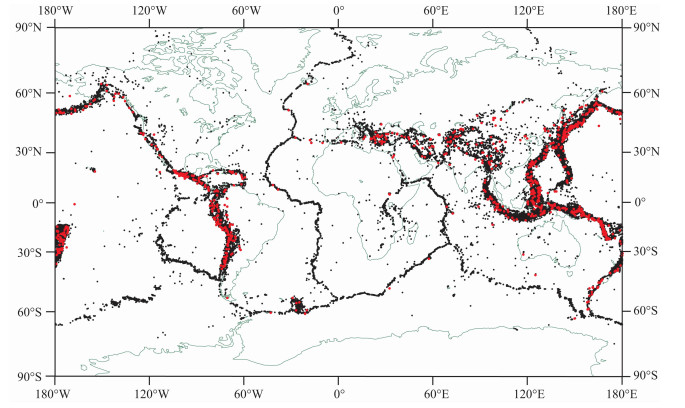
2 地震数据 2.1 地震目录本文采用的地震数据来源于USGS网站1)公布的1850年1月1日-2012年5月5日期间的全球地震目录,取5级以上(M≥5.0)的地震事件,共计64441个地震,这些地震的震中位置分布见图 1.
|
图 1 全球M≥5.0地震(1850-2012年)震中位置分布图红色和黑色小点分别表示M≥7.0和5.0≤M<7.0的地震震中位置. Fig. 1 Epicenters of global M≥5.0 earthquake during the period from 1850 to 2012 Red dots indicate the earthquakes with magnitudes larger than 7.0, and black dots show the earthquakes with magnitudes between 5.0 and 7.0. |
1) http://earthquake.usgs.gov/earthquakes/eqarchives/epic/epic_global.php
2.2 地震能量时间序列构建全球地震能量时间序列是进行小波变换和分析的基础,利用Gutenberg地震震级和能量的转换关系[38]

|
(1) |
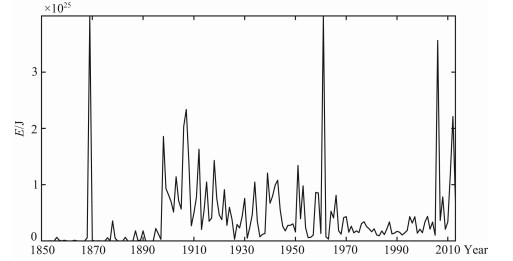
将地震目录中的每一个地震的震级转换为地震能量.式中,Mi为第i个地震的震级,Ei是第i个地震释放的能量.由此可以得到全球地震能量-时间序列.图 2是以1年为地震能量计算窗长所构建的全球M≥5.0地震能量-时间序列曲线.
|
图 2 全球M≥5.0地震能量-时间序列曲线 Fig. 2 The time series of global M≥5.0 seismic energy |
在构成全球地震能量-时间序列的计算窗长选取时,考虑到下列因素,如果地震活动受不同周期的起潮力影响,地震能量释放则可能表现出相关的准周期性,为了合理提取和研究这些可能存在于地震能量时间序列中的准周期,对长周期例如数年或数十年,地震能量的计算窗长宜选为1年;对短周期例如数天或十几天,地震能量的计算窗长宜选为1天.
3 小波变换方法原理本文采用小波变换方法对全球地震能量-时间序列信号进行周期分析.地震能量-时间序列属于非线性、非稳态的时间信号,小波变换方法是分析这类时间信号的有效方法.小波变换将时间信号分解成一系列小波函数的叠加,这些小波函数都是由一个母小波(mother wavelet)函数经过平移与尺度伸缩得来的.小波变换与传统的傅里叶变换相比较,具有多分辨率分析的特点,在时频两域均具有表征信号局部特征的能力,是一种时间窗和频率窗都可以改变的时频局部化分析方法[39].
设xn为离散时间序列,其小波变换可定义为
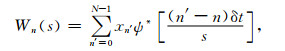
|
(2) |
式中,N为时间序列的数据总数,xn′为时间序列,ψ*表示小波函数ψ的共轭复数,s为小波尺度,δt是时间间隔,n和n′是时间指数[40].
小波函数ψ(t)是一个具有零均值且可以在频率域与时间域内进行局部化的数学函数.本文使用Morlet母小波:
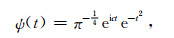
|
(3) |
其中c为无量纲频率,对于Morlet小波,取c=6较为合适,此时小波尺度s与傅里叶周期基本相等.一旦小波函数选定,需要选择一系列尺度sj进行小波变换.尺度可以用2的分数幂来表达[40]:
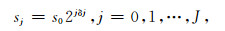
|
(4) |
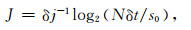
|
(5) |
式中,s0为可分辨的最小尺度,J为确定的最大尺度.δj是尺度的调节系数,δj取值越小,越能给出较好的更具细微特征的变换结果.本文取δj=0.125.通过转换小波尺度,沿着时间指数n进行局部化,可获得时间序列在某一尺度上的波动特征及其随时间变化的小波功率谱,同时可得到小波变换系数实部等值线分布图,简称小波变换图.
4 结果对地震能量-时间序列进行小波变换,得到小波变换图和相关的准周期分析图,目的是提取全球地震能量-时间序列所反映的可能与潮汐作用相关的准周期.图 3和图 4分别是不同起始震级和不同震源深度的计算窗长为1年的地震能量-时间序列的小波变换图及其准周期分析图;图 5是计算窗长为1天的地震能量-时间序列的小波变换图.
|
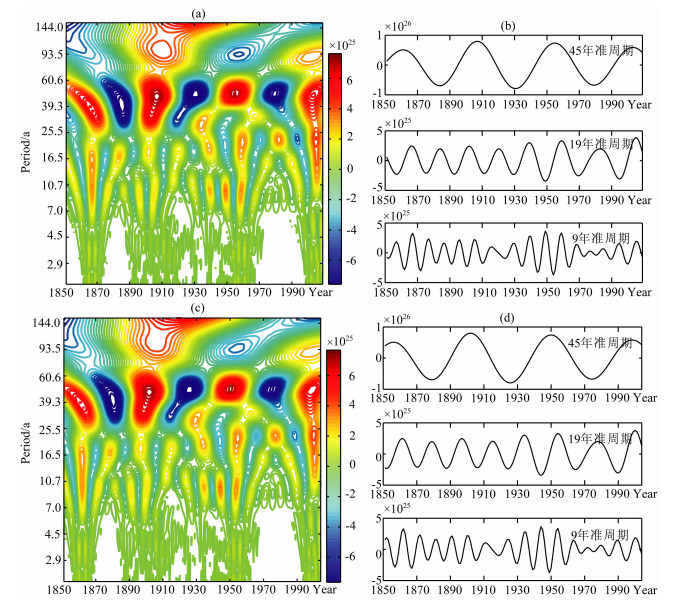
图 3 (a,b)1850-2012年全球5级以上地震能量-时间序列小波变换图及其准周期分析图;(c,d)1850-2012年全球7级以上地震能量-时间序列小波变换图及其准周期分析图 Fig. 3 (a, b) Maps of wavelet transform and corresponding quasi-periodic analyses for the time series of global M≥5.0 seismic energy from 1850 to 2012;(c, d) Maps of wavelet transform and corresponding quasi-periodic analyses for the time series of global M≥7.0 seismic energy from 1850 to 2012 |
|
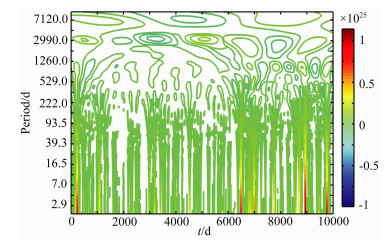
图 4 1973年1月1日起10000天时段内全球5级以上地震能量-时间序列小波变换图 Fig. 4 Map of wavelet transform for the time series of global M≥5.0 seismic energy in 10000 days since Jan 1, 1973 |
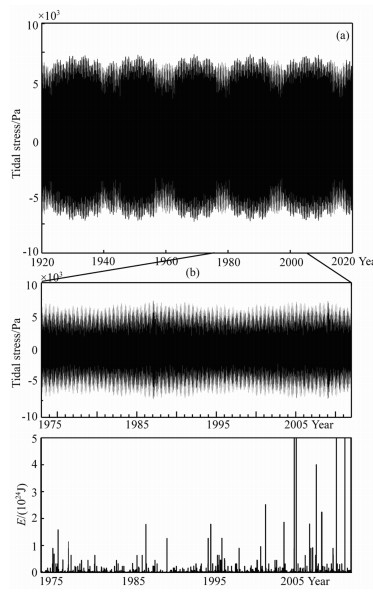
|
图 5 (a)固体潮汐应力时间变化曲线;(b)固体潮汐应力曲线与地震活动能量序列(以天为单位统计) 图(b)中2005、2010和2011年附近的4条巨震能量柱高度已超出刻度范围,其量级已达1025J,但为了不压低其它大多数地震能量柱的高度以保证视图效果,图中截断了上述4条巨震能量柱的高度,将其限制在1024J范围内. Fig. 5 (a) Curve of solid tidal stress varying with time; (b) Map of solid tidal stress and seismic energy series (Day is used to be the statistical unit) Amplitudes of energy bars for four strong earthquakes occurred in 2005, 2010, and 2011 exceed the scale range in Fig.(b), and reach to be 1025J.In order to show a clearer map of the energy bars for most of earthquakes, the amplitudes of these four earthquakes are cut off and limited in the range of 1024J. |
以图 3为例对小波变换图及其准周期分析图进行以下说明.
图 3a是地震能量-时间序列的小波变换系数实部等值线分布图,简称小波变换图.图中,横坐标为时间,纵坐标为周期,等值线色标的不同颜色代表小波谱信号的强弱,也即意味着地震能量的强弱.红色斑块代表峰值,蓝色代表谷值.每个斑块的焦点位置同时反映出地震能量的小波谱强度中心及其所对应的周期和时间.红蓝斑块交替出现显示出小波谱信号的周期性变化.
图 3b是根据图 3a中小波谱焦点位置对应的准周期而提取的小波变换系数实部值随时间变化曲线.例如,图 3b中自下而上的第一条曲线对应图 3a中7.0与10.7年之间显示出的准周期,该准周期的值可以通过对一系列焦点中心相应的周期取平均值而得,为9.05年;第二条曲线对应图 3a中在16.5与25.5年之间显示出的准周期,为18.72年;第三条曲线对应图 3a中在39.3与60.6年之间显示出的准周期,为45.13年.用准周期值对应的不同时间的小波变换系数实部值,绘出小波系数随时间变化曲线,简称准周期分析图.
4.1 不同起始震级地震能量序列的长周期提取结果在考察长周期特征时,需要时间长度尽可能长的地震能量序列,以利于长周期的提取.取1850年1月1日-2012年5月5日的地震目录构成地震能量-时间序列.同时选取两种不同起始震级(M≥5.0和M≥7.0)的地震能量-时间序列进行小波变换.图 3a、3b和图 3c、3d分别为震级M≥5.0和M≥7.0的全球地震能量-时间序列的小波变换图及其准周期分析图.
4.2 短周期提取结果在考察短周期特征时,地震能量序列的时间跨度不需要特别长,可以取1973年以来(有数字地震仪记录以来)的地震目录以1天为计算窗长构成地震能量-时间序列.图 4为1973年1月1日起10000天(约30年)时段内全球5级以上地震能量-时间序列小波变换图.图中没有显示出强弱相间的短周期焦点斑块,但在图上部的长周期部分仍出现了不十分明显的环状斑块,其对应着3200天左右(约9年)的准周期.通过图 4和图 3对日采样与年采样构成的地震能量序列的小波变换结果进行对比,可以发现年采样更能突显长周期成分,而日采样虽然也能呈现长周期成分,但不够突出,日采样有利于短周期成分提取.
5 讨论与结论 5.1 全球地震能量释放存在与长周期潮汐有关的3个准周期由图 3看出,M≥5.0和M≥7.0地震能量-时间序列小波变换图及其准周期分析图有基本相同的特征,均显示出3个准周期,分别约为9年、19年和45年,且以45年的准周期为最突出.我们首先计算了固体潮应力曲线(图 5a),该曲线显示出明显的18.6年周期,在18.6年周期中又叠加有8.85年、4.43年和嵌套于其中的各种更短周期.图 5b为固体潮应力曲线与地震活动能量序列比较,显示出地震活动幕的起落大致与固体潮应力的上述周期轮廓对应.
对上述3个准周期现象的潮汐物理机制讨论如下.
9年准周期 9年准周期现象可能的物理机制是月球近地点东移运动8.85年周期对起潮力的影响.由于月球运动椭圆轨道面的方向不是固定的,这种轨道进动造成月球二拱点即近地点和远地点之间的连线也在不停地运动,其运动方向向东,运动一圈需要8.85年,称为月球近地点东移周期.月球近地点东移运动8.85年周期对起潮力的主要影响是,每隔8.85年,太阳与二拱点连线(近地点远地点连线)成一线,同时月球经过近地点,在这个时间附近的几年会经历较大的潮汐起潮力[41],其量值可达到6.8 kPa.
19年准周期 19年准周期现象可能与月球轨道18.6年升交点西移周期对起潮力的影响有关.由于月球运动轨道(即白道)相对于地球运动轨道(即黄道)有一个5°9′的夹角,而黄道相对于赤道有一个23°27′的夹角.白道与黄道有两个交点,当月球在白道上运行由南向北通过黄道时,白道与黄道的交点称为升交点.由于太阳引力的扰动,月球的轨道平面反向进动,同时升交点西退,称为月球升交点西退运动.当月球升交点的平黄经为0°时,月球的赤纬达到最大:23°27′+5°9′=28°36′;当升交点的平黄经为180°时,月球的赤纬最小:23°27′-5°9′=18°18′.月球升交点西退运动周期为18.61[41-42],18.6年周期的固体潮应力量值可达到7.3 kPa.由于月球赤纬的这种周期性变化,将对潮汐在地球内产生的起潮力有着较大的影响,全球地震能量释放的19年准周期现象正是这种影响的体现.
45年准周期 45年准周期相对其它两个准周期显得尤为突出,但是,在月日轨道运动中目前还找不到一个直接相关的潮汐周期.本文对地震能量释放所表现出的45年准周期作如下尝试性的探讨.假如存在一种潮汐组合周期(例如8.85年的倍周期或18.6年和8.85年的组合周期),这种潮汐组合周期可能满足全球大多数断层孕育地震所需要的时间尺度,造成全球地震能量释放45年准周期的凸显.
比较图 3b和3d看出,M≥5.0和M≥7.0地震能量-时间序列的准周期分析图基本相同,但存在细微差别,表现在M≥5.0和M≥7.0的地震能量-时间序列的小波系数时间变化曲线存在一个相位差,M≥5.0地震能量序列的小波系数时间变化相位落后于M≥7.0的地震能量序列,其原因可能归结于M≥5.0地震序列中含有大量5~6级的地震,而它们多为大地震的余震.
5.2 全球地震活动能量释放没有发现与短周期潮汐相关的准周期图 4计算窗长为1天的地震能量-时间序列的小波变换图出乎意料地没有显示任何与短周期潮汐相关准周期,例如与朔望潮或双周潮相关的14天准周期.这种现象的原因可能在于短周期起潮力周期远远小于断层对于5级以上地震的孕震时间长度.
全球地震活动能量释放没有发现朔望潮准周期,这似乎与人们对大潮(朔、望)起潮力可能触发地震的认识相矛盾.事实上,全球地震能量释放不存在朔望潮准周期,并不能说明朔望潮起潮力对地震活动没有影响.朔望潮起潮力的影响实际上是包含在长周期潮的影响中,长周期潮汐的影响可能通过对短周期潮汐的调制而实现,例如,18.6年升交点西移周期的调制作用使得在一定的时期内朔望潮的振幅比平时更大,从而实现对地震活动的影响.反过来说,短周期潮汐通过被长周期潮汐的调制而起到对地震影响的作用.对一个局部地区的前震或余震序列来讲,短周期潮汐对其影响的可能性增大.作为例子,我们分别考查了云南2011年盈江5.9级地震和2012年彝良5.7级地震的余震序列,对这两个余震序列进行小波变换和活动准周期提取.盈江地震余震序列的小波变换提取到了较明显的14天准周期(图 6),而彝良地震余震序列的小波变换却没有提取到此准周期(图 7).
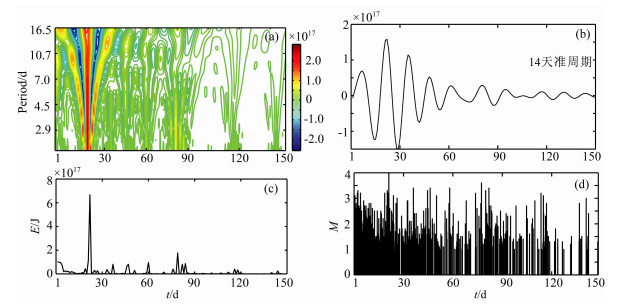
|
图 6 2011年云南盈江5.9级地震的余震序列(150天时段内M≥1.0) (a)地震能量序列小波变换图;(b)准周期分析图;(c)地震能量-时间序列图;(d)地震序列M-t图. Fig. 6 Map of 2011 Yingjiang M5.9 aftershock series in Yunnan province (aftershocks with M≥1.0 in 150 days) (a) Map of wavelet transform; (b) Map of quasi-periodic analyses; (c) Map of the time series of seismic energy; (d)M-t Map. |
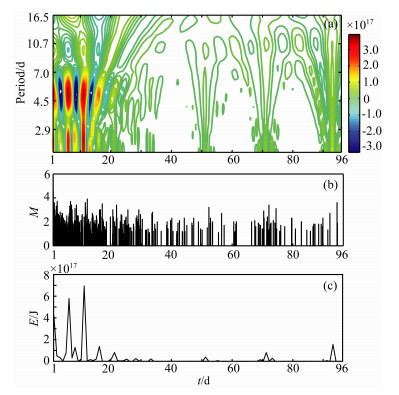
|
图 7 2012年云南彝良5.7级地震的余震序列(96天时段内M≥1.0) (a)地震能量序列小波变换图;(b)地震序列M-t图;(c)地震能量-时间序列图. Fig. 7 Map of 2012 Yiliang M5.7 aftershock series in Yunnan province (aftershocks with M≥1.0 in 96 days) (a) Map of wavelet transform; (b)M-t Map; (c) Map of the time series of seismic energy. |
上述两个例子说明短周期潮汐对局部地震序列活动有一定影响,但可能要满足某些条件这种影响才存在.所谓条件应该包含起潮力和地震断层两方面的因素,关于短周期潮汐对局部地震活动的影响及其相关条件有待大量序列震例的具体研究.
5.3 结论全球地震能量释放的时间序列存在9年、19年和45年的3个准周期,其中,45年准周期最为突出.月球近地点东移运动8.85年周期和月球轨道升交点18.6年西移周期对起潮力的影响是产生上述准周期现象的可能原因.45年的地震能量释放准周期可能与某种潮汐组合周期(例如8.85年的倍周期或18.6年和8.85年的组合周期)相关,这种潮汐组合周期可能恰好满足大于全球大多数断层孕育地震所需要的时间尺度,造成全球地震能量释放45年准周期的突出现象.关于45年的地震能量释放准周期的物理机制还有待以后深入探讨.
全球地震活动的能量释放没有发现与潮汐短周期相关的准周期.可以推论,没有发现与潮汐短周期相关的地震能量释放准周期,其原因可能主要在于短周期起潮力的周期长度远远小于断层的孕震时间长度.短周期潮汐对地震的影响主要通过长周期潮汐的调制而起作用.对一个局部地区的地震序列来讲,短周期潮汐对其影响的可能性增大.而对全球范围的地震,这种局部性的短周期特征也可能被掩盖.总之,地震的发生受起潮力影响的强弱不仅与起潮力的大小有关,同时还与起潮力的周期有关.
致谢感谢审稿专家提出的宝贵意见;感谢尹继尧博士在小波变换计算方面给予的指导和帮助.
| [1] | Heaton T H. Tidal triggering of earthquakes. Geophys. J. Int. , 1975, 43(2): 307-326. DOI:10.1111/j.1365-246X.1975.tb00637.x |
| [2] | Ding Z Y, Jia J K, Wang R. Seismic triggering effect of tidal stress. Tectonophysics , 1983, 93(2): 319-335. |
| [3] | Palumbo A. Lunar and solar tidal components in the occurrence of earthquakes in Italy. Geophys. J. Int. , 1986, 84(1): 93-99. DOI:10.1111/j.1365-246X.1986.tb04346.x |
| [4] | Tsuruoka H, Ohtake M, Sato H. Statistical test of the tidal triggering of earthquakes: Contribution of the ocean tide loading effect. Geophys. J. Int. , 1995, 122(1): 183-194. DOI:10.1111/gji.1995.122.issue-1 |
| [5] | Kasahara J. Tides, earthquakes, and volcanoes. Science , 2002, 297(5580): 348-349. DOI:10.1126/science.1074601 |
| [6] | Tanaka S, Ohtake M, Sato H. Evidence for tidal triggering of earthquakes as revealed from statistical analysis of global data. J. Geophys. Res. , 2002, 107(B10): ESE 1-1-ESE 1-11. DOI:10.1029/2001JB001577 |
| [7] | Zhao J, Han Y B, Li Z A. Relationship between the variation of lunisolar tidal force and earthquakes in Taiwan. J. Natural Disasters , 2001, 10(3): 64-67. |
| [8] | 张晶, 郗钦文, 杨林章, 等. 引潮力与潮汐应力对强震触发的研究. 地球物理学报 , 2007, 50(2): 448–454. Zhang J, Xi Q W, Yang L Z, et al. A study on tidal force/stress triggering of strong earthquakes. Chinese J. Geophys (in Chinese) , 2007, 50(2): 448-454. (in Chinese) |
| [9] | 冯向东, 魏东平. 地震活动性与日月引潮力相关性统计分析. 国际地震动态 , 2007, 341(5): 9–15. Feng X D, Wei D P. Statistical analysis of the spatial and temporal correlation between seismicity and tide-generating force by the Sun and the Moon. Recent Developments in World Seismology (in Chinese) , 2007, 341(5): 9-15. (in Chinese) |
| [10] | 杜品仁, 赵俊猛, 高祥林. 大地震的18.6年周期. 地球物理学报 , 2011, 54(9): 2256–2262. Du P R, Zhao J M, Gao X L. The 18.6-year periodicity of great earthquakes. Chinese J. Geophys (in Chinese) , 2011, 54(9): 2256-2262. (in Chinese) |
| [11] | 杨学祥, 韩延本, 陈震, 等. 强潮汐激发地震火山活动的新证据. 地球物理学报 , 2004, 47(4): 616–621. Yang X X, Han Y B, Chen Z, et al. New evidence of earthquake and volcano triggering by strong tides. Chinese J. Geophys. (in Chinese) , 2004, 47(4): 616-621. (in Chinese) |
| [12] | 韩延本, 李志安, 田静. 日月引潮力变化与某些地区地震发生时间的相关研究. 地球物理学进展 , 1996, 11(2): 114–122. Han Y B, Li Z A, Tian J. The researching of the relation of occurrence time of earthquakes and the solar-lunar tidal force in some areas of China. Progress in Geophys (in Chinese) , 1996, 11(2): 114-122. (in Chinese) |
| [13] | 赵娟, 韩延本, 李志安. 日月引潮力与华北地区的地震. 地球物理学报 , 1999, 42(Suppl.1): 24–29. Zhao J, Han Y B, Li Z A. Variation of lunisolar tidal force and the earthquakes in North China. Chinese J. Geophys (in Chinese) , 1999, 42(Suppl.1): 24-29. (in Chinese) |
| [14] | 吴小平, 冒蔚, 黄雍, 等. 基于不同构造分区中国地震的潮汐应力触发效应及相关天文特征. 中国科学G辑 , 2009, 52(8): 1271–1283. Wu X P, Mao W, Huang Y, et al. Tidal stress triggering effects of earthquakes based on various tectonic regions in China and related astronomical characteristics. Science in China Series G (in Chinese) , 2009, 52(8): 1271-1283. DOI:10.1007/s11433-009-0148-4 (in Chinese) |
| [15] | 吴小平, 黄雍, 冒蔚, 等. 云南地震的潮汐应力触发机制及相关天体位置图像. 地球物理学报 , 2005, 48(3): 574–583. Wu X P, Huang Y, Mao W, et al. Tidal stress triggering mechanism of earthquakes in Yun'nan and related patterns of celestial body positions. Chinese J. Geophys (in Chinese) , 2005, 48(3): 574-583. DOI:10.1002/cjg2.690 (in Chinese) |
| [16] | 许亚吉, 吴小平, 阎春恒, 等. 不同类型地震断层上的固体潮汐库仑破裂应力特征. 地球物理学报 , 2011, 54(3): 756–763. Xu Y J, Wu X P, Yan C H, et al. The features of tidal Coulomb failure stresses on various kinds of seismic fault. Chinese J. Geophys (in Chinese) , 2011, 54(3): 756-763. (in Chinese) |
| [17] | Li J, Jiang H K. A review on tidal triggering of earthquakes. Earthquake Research in China , 2012, 26(1): 128-141. |
| [18] | Wilcock W S D. Tidal triggering of earthquakes in the Northeast Pacific Ocean. Geophys. J. Int. , 2009, 179(2): 1055-1070. DOI:10.1111/gji.2009.179.issue-2 |
| [19] | Tanaka S. Tidal triggering of earthquakes precursory to the recent Sumatra megathrust earthquakes of 26 December 2004 (Mw90), 28 March 2005(Mw8.6), and 12 September 2007 (Mw8.5). Geophys. Res. Lett. , 2010, 37(2): L02301. DOI:10.1029/2009GL041581 |
| [20] | Métivier L, de Viron O, Conrad C P, et al. Evidence of earthquake triggering by the solid earth tides. Earth and Planetary Science Letters , 2009, 278(3-4): 370-375. DOI:10.1016/j.epsl.2008.12.024 |
| [21] | Stroup D F, Tolstoy M, Crone T J, et al. Systematic along-axis tidal triggering of microearthquakes observed at 9°50'N East Pacific Rise. Geophys. Res. Lett. , 2009, 36: L18302. DOI:10.1029/2009GL039493 |
| [22] | Stroup D F, Bohnenstiehl D R, Tolstoy M, et al. Pulse of the seafloor: Tidal triggering of microearthquakes at 9°50'N East Pacific Rise. Geophys. Res. Lett. , 2007, 34: L15301. DOI:10.1029/2007GL030088 |
| [23] | Cadicheanu N, van Ruymbeke M V, Zhu P. Tidal triggering evidence of intermediate depth earthquakes in the Vrancea zone (Romania). Natural Hazards and Earth System Science , 2007, 7(6): 733-740. DOI:10.5194/nhess-7-733-2007 |
| [24] | Tanaka S, Sato H, Matsumura S, et al. Tidal triggering of earthquakes in the subducting Philippine Sea plate beneath the locked zone of the plate interface in the Tokai region, Japan. Tectonophysics , 2006, 417(1-2): 69-80. DOI:10.1016/j.tecto.2005.09.013 |
| [25] | Tanaka S, Ohtake M, Sato H. Tidal triggering of earthquakes in Japan related to the regional tectonic stress. Earth Planets Space , 2004, 56(5): 511-515. DOI:10.1186/BF03352510 |
| [26] | Cochran E S, Vidale J E, Tanaka S. Earth tides can trigger shallow thrust fault earthquakes. Science , 2004, 306(5699): 1164-1166. DOI:10.1126/science.1103961 |
| [27] | Tanaka S, Ohtake M, Sato H. Spatio-temporal variation of the tidal triggering effect on earthquake occurrence associated with the 1982 South Tonga earthquake of Mw7.5. Geophys. Res. Lett. , 2002, 29(16). DOI:10.1029/2002GL015386 |
| [28] | Wilcock W S D. Tidal triggering of microearthquakes on the Juan de Fuca Ridge. Geophys. Res. Lett. , 2001, 28(20): 3999-4002. DOI:10.1029/2001GL013370 |
| [29] | Tolstoy M, Vernon F L, Orcutt J A, et al. Breathing of the seafloor: Tidal correlations of seismicity at Axial volcano. Geology , 2002, 30(6): 503-506. DOI:10.1130/0091-7613(2002)030<0503:BOTSTC>2.0.CO;2 |
| [30] | 尹祥础, 尹灿. 非线性系统失稳的前兆与地震预报--响应比理论及其应用. 中国科学B辑 , 1991, 21(5): 512–518. Yin X C, Yin C. The precursor of instability for nonlinear systems and its application to earthquake prediction-The load-unload response ratio theory. Science in China Series B (in Chinese) , 1991, 21(5): 512-518. (in Chinese) |
| [31] | 万永革. 权重加卸载响应比及其震例检验. 内陆地震 , 2008, 22(2): 97–103. Wan Y G. The weighted load/unload response ratio and its case verification. Inland Earthquake (in Chinese) , 2008, 22(2): 97-103. (in Chinese) |
| [32] | 万永革. 关于加卸载响应比理论运用于地震预测的几点思考. 西北地震学报 , 2004, 26(2): 178–182. Wan Y G. Some considerations on theory of load and unload response ratio and its application in earthquake prediction. Northwestern Seismological Journal (in Chinese) , 2004, 26(2): 178-182. (in Chinese) |
| [33] | 万永革, 齐福荣, 孟晓春, 等. 中国大陆及华北地区地震资料的小波分析. 大地测量与地球动力学 , 2003, 23(4): 28–33. Wan Y G, Qi F R, Meng X C, et al. Wavelet analysis of seismic data in Chinese mainland and north China. Journal of Geodesy and Geodynamics (in Chinese) , 2003, 23(4): 28-33. (in Chinese) |
| [34] | Crockett R G M, Gillmore G K, Phillips P S, et al. Tidal synchronicity of the 26 December 2004 Sumatran earthquake and its aftershocks. Geophys. Res. Lett. , 2006, 33(19). DOI:10.1029/2006GL027074 |
| [35] | Cochran E S, Vidale J E. Comment on "Tidal synchronicity of the 26 December 2004 Sumatran earthquake and its aftershocks" by R.G. M. Crockett et al. Geophys. Res. Lett. , 2007, 34(3). DOI:10.1029/2006GL028639 |
| [36] | Crockett R G M, Gillmore G K, Phillips P S, et al. Reply to comment by Elizabeth S. Cochran and John E. Vidale on "Tidal synchronicity of the 26 December 2004 Sumatran earthquake and its aftershocks". Geophys. Res. Lett. , 2007, 34(4). DOI:10.1029/2006GL028925 |
| [37] | Stein R S. Tidal triggering caught in the act. Science , 2004, 305(5688): 1248-1249. DOI:10.1126/science.1100726 |
| [38] | 傅淑芳, 刘宝诚. 地震学教程. 北京: 地震出版社, 1991 . Fu S F, Liu B C. An Introduction to Seismology (in Chinese). Beijing: Seismological Press, 1991 . |
| [39] | Daubechies I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory , 1990, 36(5): 961-1005. DOI:10.1109/18.57199 |
| [40] | Torrence C, Compo G P. A practical guide to wavelet analysis. Bulletin of the American Meteorological Society , 1998, 79(1): 61-78. DOI:10.1175/1520-0477(1998)079<0061:APGTWA>2.0.CO;2 |
| [41] | Haigh I, Eliot M, Pattiaratchi C. Global influences of the 18.61 year nodal cycle and 8.85 year cycle of lunar perigee on high tidal levels. J. Geophys. Res. , 2011, 116: C06025. DOI:10.1029/2010JC006645 |
| [42] | Cùrrie R G. Luni-solar 18.6-year signal in tree-rings from Argentina and Chile. Pure and Applied Geophysics , 1991, 137(3): 281-300. DOI:10.1007/BF00876993 |
 2013, Vol. 56
2013, Vol. 56


