2. 中国地震局地震预测研究所, 北京 100036
2. Institute of Earthquake Science, China Earthquake Administration, Beijing 100036, China
地震预警作为一种能够有效减轻地震灾害的手段已经被世界上越来越多的国家和地区所研究,并在实际应用中取得了显著的减灾实效.我国作为世界上地震活动最强烈的国家之一,也迫切需要研发一套地震预警系统用于切实减轻地震所造成的灾害损失[1],但是如何从一个正在发生的地震事件中估算出震级大小,是研发地震预警系统中需要解决的关键难题之一.许多研究学者都对该问题进行了深入的研究,如Nakamura[2]提出使用P波震相前几秒携带的信息来估算地震震级.经过多年的发展,目前已经出现了一些非常规的、稳定可靠的实时震级计算方法并应用到了各国的地震预警系统中,这些方法大致可以分为三大类[3-4]:与周期/频率相关的算法[2, 5-7]、与幅值相关的算法[8-10]以及与辐射能量强度相关的算法[11-12].
在本文里,我们将使用中国四川地区2008年发生的汶川大地震[13-14]及其余震强震观测数据来研究预警参数与最终震级大小之间的相关性.两个原因促使我们进行了这次研究.一个原因是因为南北地震带是世界上最活跃的地震带之一,历史上曾经发生过多次特大地震,为此,在该地区投入精力实现地震预警系统就具有十分重要的意义.另一个原因是在汶川地震发生后,中国地震局布设了一批流动观测台站,与原有的强震台站一起记录到了大量的余震事件,是国内首次获取到如此全面的强震观测资料,为该次研究提供了很好的数据基础.通过这次研究,我们可以为汶川地区建立地震预警系统提供参考.另外,本文的研究结果还可以用于检验不同的作者使用不同的数据集获取到的结果.
2 待估算参数本文分别从实时震级计算方法的三大类中选取了4个预警参数来研究与震级之间的相关性:P波卓越周期和特征周期属于与周期/频率相关的算法;位移幅值属于与幅值相关的算法;速度平方积分属于与辐射能量强度相关的算法.下面将分别对这4个预警参数进行介绍.
2.1 P波卓越周期和特征周期P波卓越周期由Nakamura[2]提出,后来Allen等[5],Kanamori[15],Olson等[16]采用该方法进行了一系列相关研究,其计算公式如下:
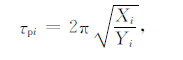
|
(1) |
式中,Xi=αXi-1+x2 i是平滑后垂直向地面运动速度的平方值,Yi=αYi-1+(dx/dt)2 i是平滑后地面运动速度导数的平方值,τpi为is时测定的卓越周期,xi是记录的地面运动速度值,α为平滑系数,决定了平滑的速度,一般取为0.999.Allen等[5]和Olson等[16]发现P波3~4s的窗内的最大τp值与震级之间存在着一种线性关系.他们使用了来自南加州、阿拉斯加、中国台湾和日本的强震事件记录(Mw3.0~Mw8.0)统计出了该关系.
Wu等[17]提出了另外一种基于P波频率分量的特征周期计算方法:
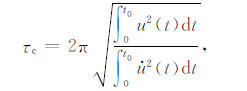
|
(2) |
式中,τc的单位为s,u(t)代表高通滤波后垂直分向地震动位移值,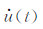
τp、τc与震级的相关性引起了科学界对地震规模确定性的一场争论.Olson等[16]认为最终地震震级大小取决于初始破裂,即使对于大震这个结论也是成立的.而Rydelek等[19]随后对其研究结果表示质疑,因为他们通过对日本震级大于6级的地震进行研究,发现这些参数与震级之间并不存在着明显的相关性.最近,Wolfe[20]、Yamada等[21]的研究结果表明,P波卓越周期与强震(Mw>6)之间的线性关系不仅与震源参数有关,还与衰减关系、场地效应和滤波效应有关.
2.2 位移幅值Pd另外一个用于实时震级估算的预警参数是由Wu等[8]和Zollo等[9]提出的经过高通Butterworth滤波器(低频截止频率为0.075 Hz)滤波的位移幅值Pd.其基本思想是统计事件记录前几秒的峰值位移(Pd),震源距(R)和事件震级(M)之间的关系:
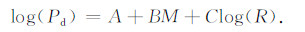
|
(3) |
Wu等[8]与Zollo等[9]在具体进行计算时使用的方法有一些区别.例如,Wu等[8]使用宽频带地震计记录到的地震事件的垂直向数据来获取Pd值,而Zollo等[9]使用的是强震记录数据三个方向的合成来获取Pd值.另外,Zollo等[9]还在S波上读取Pd值.随后,Lancieri等[22]讨论了在区域预警系统中使用S波信息的可能性.本文将采用Zollo等[9]的方法获取Pd值.
Pd与地震震级之间的相关性已经在欧洲-地中海和日本的一定震级范围内的强震数据集(欧洲-地中海:4≤Mw≤7.4,日本:4≤Mw≤7.1)上进行了探讨[8, 10].通过使用捡拾到P波后4s时间窗内的P波初始位移的最大值和捡拾到S波后2s时间窗内的S波初始位移的最大值进行统计分析,结果都表明Pd与震级之间存在着一个良好的关系,直到Mw达到7级都没有出现震级饱和现象.而使用捡拾到P波后2s时间窗内的P波初始位移的最大值统计则会出现震级饱和现象.目前,使用Pd估算震级的方法已经被意大利的PRESTo预警系统所采用[22-25].另外,Nielsen[26]、Murphy等[27]还采用动力学和运动学参数研究Pd与震级之间的相关性以及出现的震级饱和现象.
2.3 速度平分积分IV2Festa等[12]提出了一种用于实时震级估计的积分关系式:
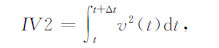
|
(4) |
式中,积分在待研究震相到来后的窗长为Δt的时间域上进行计算,v2是三个分向地面运动速度记录平方的合成.这个参数非常有趣,因为它直接与地震发生时前几秒释放的能量有关[28],其对应的关系式为:
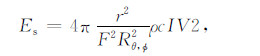
|
(5) |
式中,ρ表示介质密度,F(≈2)表示自由表面系数,c表示波速,Rθ,Φ2表示平均辐射模式,r表示震源距.
这个参数首次被Festa等[12]用于地震预警研究中.他们使用同样的用于统计Pd与震级相关性的日本数据集进行研究,结果表明,在使用捡拾到P波后4s和S波后2s的时间窗上进行估计时,会在Mw6.5出现震级饱和现象.
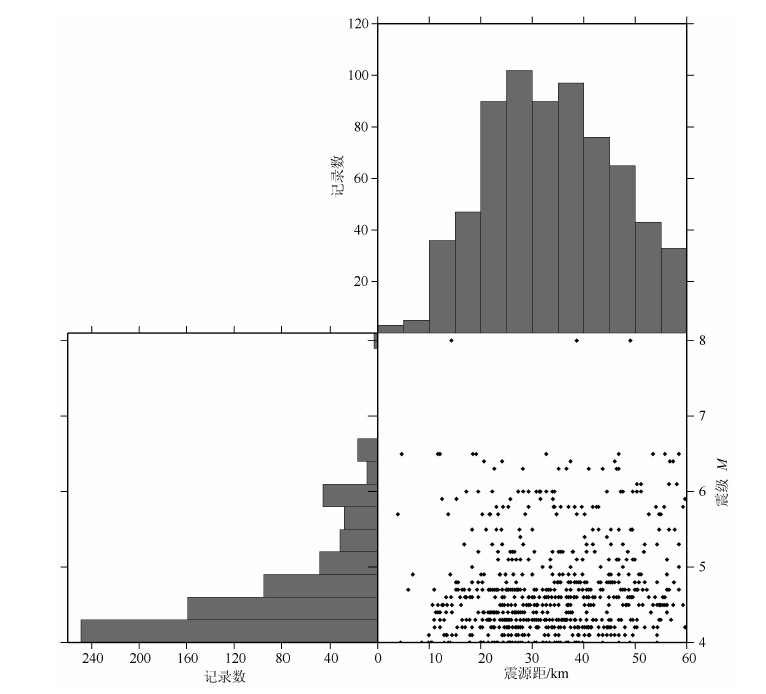
3 研究所用震例及记录挑选本研究中使用的地震事件数据全部来源于国家强震动台网中心,时间跨度从2008年5月12日至2008年10月4日,共计687条三分向地震事件记录,218个汶川地震事件(M:4.0~8.0).在进行统计分析时,只有震源距小于60km的事件记录才被采用,主要是因为从地壳地震破裂处释放的高频、直接实体波幅度在近源范围内占主导地位(如震源距与地震破裂长度可比时[29]).另外,本研究忽略不同震级标度间的区别,统称为M.最终所用记录相对于震级和震源距的分布情况如图 1所示.对强震记录进行基线校正等基本处理后,采用人工识别方法对各台的记录进行P波和S波到时捡拾.
|
图 1 记录相对于震级和震源距的分布情况 (a)记录数相对于震源距的分布直方图,每个小区间范围为5km;(b)记录数相对于震级的分布直方图,每个小区间范围为0.3级;(c)所用记录(菱形)的震源距-震级分布情况. Fig. 1 Records distribution vs magnitude and epicentral distance (a) Histogram of the number of selected strong motion records with distance.An interval of 5 km is used for each distance bin; (b) Histogram of the number of selected strong motion records with magnitude.An interval of 0.3 is used for each magnitude bin; (c) Distribution of records (diamonds) vs distance and magnitude. |
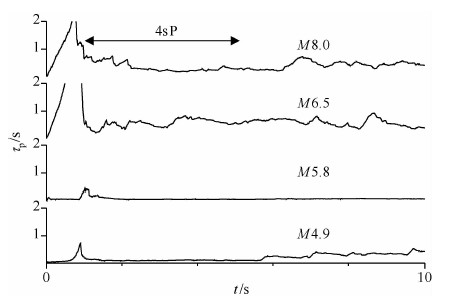
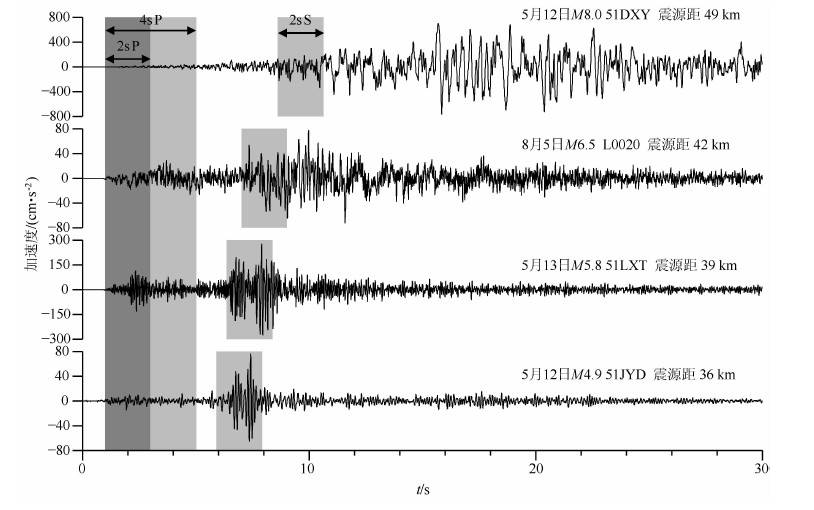
图 2中显示了跨越所研究震级范围的4条地震事件NS分向的加速度记录波形,震源距范围从36km到49km,其中包括主震(M8.0)、最大余震(M6.5)和两个余震(M5.8和4.9).用于实时估算震级的P波和S波时间窗在图中以灰色块标示.所有的事件波形都对齐到P波前一秒,幅值统一校正到“参考”震源距10km[9, 30].主震选择的是台站051DXY的记录,最大余震选择的是台站L0020的记录,其他两次余震分别选择的是台站51LXT和51JYD的记录.由于震源距不相同,所以S波震相的到时也各不相同.
|
图 2 跨越所研究震级范围的4次地震事件对应的NS分向加速度记录 Fig. 2 The north-south acceleration component for four events that span the investigated magnitude range |
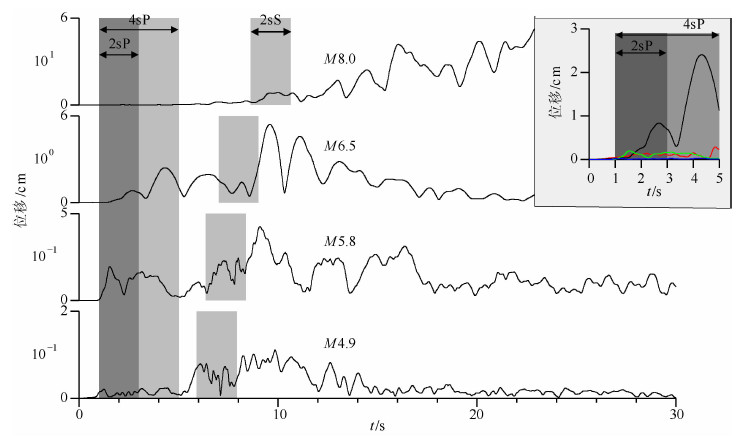
第一个待研究的预警参数是经过滤波后的幅值位移Pd.图 3显示的是图 2中的4条事件记录经过震源距统一校正到“参考场地”10km[9, 30]、两次积分和2阶带通Butterworth滤波器(频带范围为0.075~3Hz)滤波后的三个分向合成的位移模量曲线.Pd值分别取P波到后2s和4s以及S波到后2s时间窗内的最大位移幅值,在图中以灰色框标注.为了简便,下面将分别使用PdP2s、PdP4s和PdS2s进行表示.在图 3右上角的小窗口内,作者将4条事件记录P波到后4s的位移变化曲线按照同等的比例进行了重新绘制.从图中可以看出,除了M4.9级记录的位移模量曲线无法看见外,其他3条事件记录的位移模量曲线都清晰可见,而且还存在着一个现象:M6.5记录的幅值远远大于M8.0和M5.8记录的幅值,相差大概10倍左右,使用另外两个满足震源距条件的台站51WCW和51PXZ记录到的主震位移幅值也得到相同的结果.这个现象说明,使用Pd值是无法判定一个地震事件是否大于等于8级的.
|
图 3 图 2中4条事件记录对应的三分向合成位移模量曲线 插图:红线表示M8.0,黑线表示M6.5,绿线表示M5.8,蓝线表示M4.9. Fig. 3 Vector composition of three components of displacement for the events displayed in Figure 2 at the same stations Inset:The red line represents M8.0;The black line represents M6.5;The green line represents M5.8;The blue line represents M4.9. |
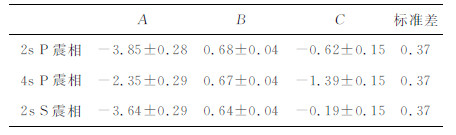
根据公式(3)进行最小二乘拟合,得到的各项系数如表 1所示.表 1中的最后一列为使用不同的震相进行拟合获取到的标准差.标准差和各项系数的偏差代表了公式(3)中没有考虑到的其他因素对结果的影响,如介质衰减、场地效应和震源辐射花样等.
|
|
表 1 Pd、震源距R与震级相关性(0.075~3 Hz) Table 1 The correlation between Pd、epicentral distance and magnitude (0.075~3 Hz) |
为了只研究震级M与早期P震相和S震相峰值幅度的关系,我们根据公式(3)对震源距进行修正,将其统一校正到“参考”震源距10km[9, 30],可以得出如下公式:
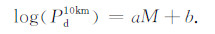
|
(6) |
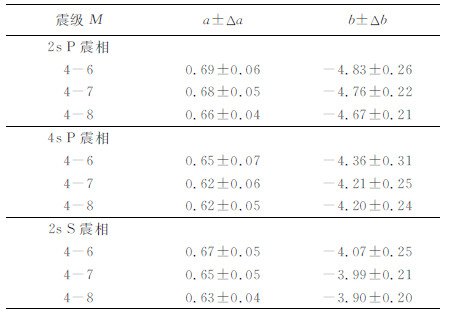
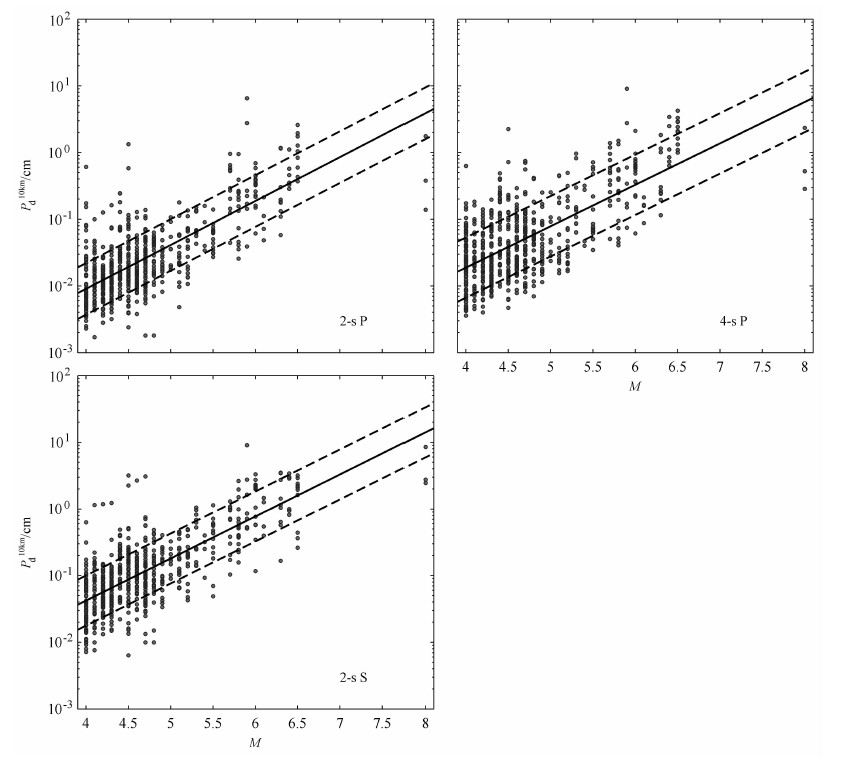
根据公式(6)统计获取到的Pd与震级之间的相关性结果显示在图 4中,所有的位移幅值都经过了2阶带通Butterworth滤波器(频带范围为0.075~3Hz)的滤波处理[6, 10, 31].从图 4中可以看出,PdP 2s、PdP4s和PdS2s在震级小于等于6.5级时,都没有出现震级饱和现象,但是对于主震却出现了非常明显的震级饱和,尤其是PdP 2s和PdP4s,饱和现象更为严重.同时,我们注意到在M6级附近,拟合直线斜率出现了变化.为此,我们又根据不同的震级范围对数据重新进行拟合,以探讨拟合直线斜率与震级范围之间的关系.表 2中列出了线性拟合参数a和b相对于不同震级范围的值及其偏差.与预先估计的一致,随着震级范围的扩大,拟合直线的斜率会逐渐变小.这就意味着震级越大,Pd值的预估效果就越差.另外,我们还注意到,参数a和b与中国台湾和加利福尼亚地区统计获取的参数[8-10]之间有着比较大的差距,他们获取到的斜率a在1附近,而我们获取到的斜率a都小于0.7.之所以会出现这种差距,主要是由于他们在进行数据统计时同时使用了宽频带地震计记录和强震数据记录,而我们只是使用了强震数据记录,这样就会使得低频噪声在通过加速度记录两次积分后的位移信号中起支配作用,大大影响了P波震相的幅度.
|
图 4 Pd与震级相关性(滤波频带:0.075~3 Hz) 圆点表示每条台站记录校正到“参考”震源距10km的Pd值,黑色实线表示线性拟合曲线(震级范围:4-8级),黑色虚线表示一倍标准方差. Fig. 4 Correlation between Pd and magnitude (0.075~3 Hz) Circles represent the Pd values of each record normalized to a common reference distance of 10 km.The black solid lines are the best fit curves evaluated through a linear regression on the magnitude range of 4-8, plotted along with one standard deviation (black dashed lines). |
|
|
表 2 Pd与震级相关性(0.075~3 Hz) Table 2 The correlation between Pd and magnitude (0.075~3 Hz) |
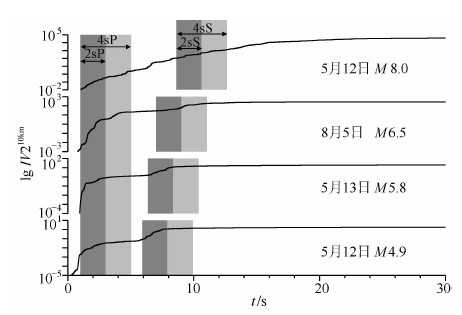
下一待研究的预警参数是速度平方积分(IV2). 图 5显示了图 2中的4条事件记录经过震源距校正到“参考场地”10 km[12]、一次积分和2阶带通Butterworth滤波器(频带范围为0.075~10 Hz)滤波的三个分向速度平方合成后的积分曲线.我们分别使用P波和S波到后2s和4s时间窗内的数据来计算IV2,表示为IV2 phasetime,其中time表示时间窗长度,phase表示震相.从图 5中可以发现,4条事件记录对应的IV2曲线变化情况都不相同:主震的IV2曲线上升的非常缓慢,最大余震和M5.8的IV2曲线在P波震相开始时上升非常剧烈,而M4.9的IV2曲线则在S波震相开始时有非常明显的上升过程,这与具体台站所在地区的品质因子Q有关.
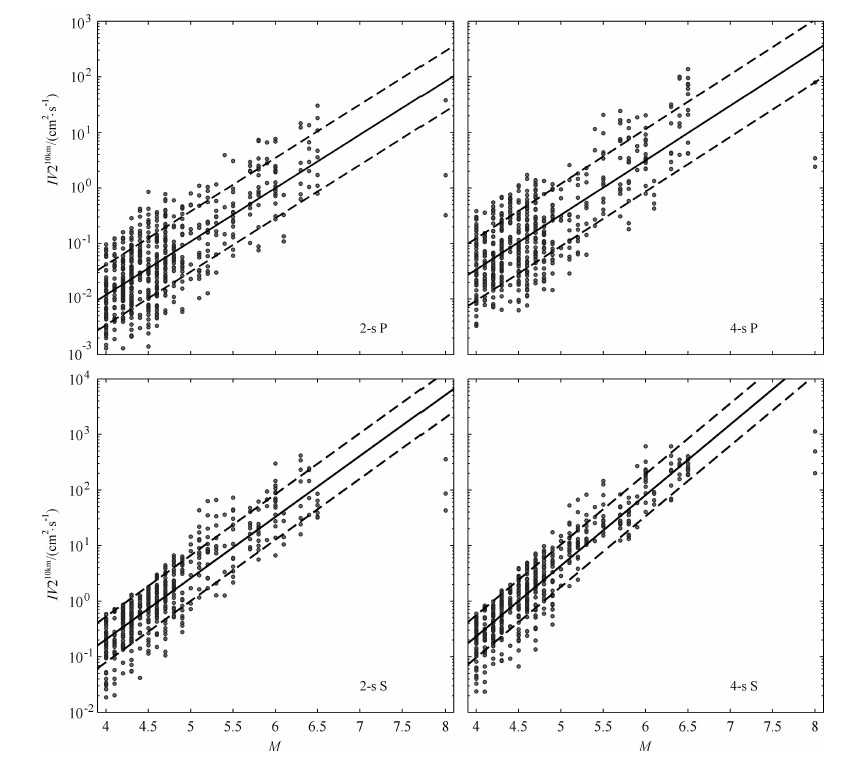
IV2与震级的相关性统计结果显示在图 6中,参与统计的事件记录都预先经过了2阶带通Butterworth滤波器(频带范围为0.075~10 Hz)的滤波处理,并统一校正到“参考场地”10km[12].
|
图 6 IV2与震级相关性(滤波频带:0.075~10 Hz) 圆点表示每条台站记录校正到“参考”震源距10km处的IV2峰值,黑色实线表示线性拟合曲线(震级范围:4~8级),黑色虚线表示一倍标准方差. Fig. 6 Correlation between IV2 and magnitude (0.075~10 Hz) Circles represent the IV2 peak values of each record referred to a common distance of 10 km.The black solid lines are the best fit curves evaluated through a linear regression on the magnitude range of 4~8, plotted along with one standard deviation (black dashed lines) |
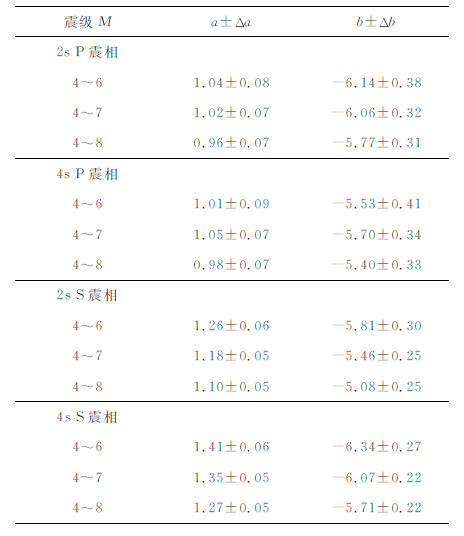
显然,IV2phasetime在震级小于等于6.5级时,都没有出现震级饱和现象,但是对于主震却存在着一个完全低估的现象,这点与上一小节Pd参数获取到的结果相同.同样,我们又对不同的震级范围重新进行线性拟合,以便于查看拟合直线斜率与震级范围之间的关系(见表 3).
|
|
表 3 IV2与震级相关性(0.075~10 Hz) Table 3 The correlation between IV2 and magnitude (0.075~10 Hz) |
从表 3中可以看出,对于同一震相和同一时间窗,随着震级范围的增大,斜率和截距都随之减小,这主要是由于小地震在较短时间内就能释放其绝大部分累积的能量,而大地震则需要较长的时间才能够释放其累积的能量,尤其是对于汶川主震来说,其前期释放的能量非常少,因此在一个较短的时间窗内,小地震的IV2值就相对比大地震的IV2值要大.另外,随着震相从P变化到S,时间窗长度从2s变化到4s,斜率呈现逐渐增大的趋势,并最终达到最大值1.41±0.06(震级范围:4~6),该值与预期的值1.5非常接近[32],同时两个拟合参数的偏差也在逐渐缩小,这点与地震波在传播过程中能量释放的强度有关,因为相对P波来说,S波包含更多的能量信息,随着时间窗的增长,包含的能量信息也随之增加,从而使得统计结果越来越接近理论值.
4.3 τp和τc与震级相关性最后待讨论的预警参数是P波卓越周期和特征周期.图 7显示的是图 2中的4条事件记录使用公式(1)计算获取到的τp值变化曲线,所有的曲线都使用相同大小的幅值比例进行绘制.在具体统计时,我们使用的是P波到后4s时间窗内的τp最大值与震级进行相关性统计的,在图中以箭头进行标示.从图中可以看出,M5.8和M4.9的τp曲线明显小于其他两次事件,尤其是M5.8的曲线更是趋近于零值,而另外两次事件对应的τp曲线幅度相差无几,并不存在M8.0明显大于M6.5的情况.由于特征周期τc只是一个单独的值,所以无法显示出与图 7类似的变化曲线.
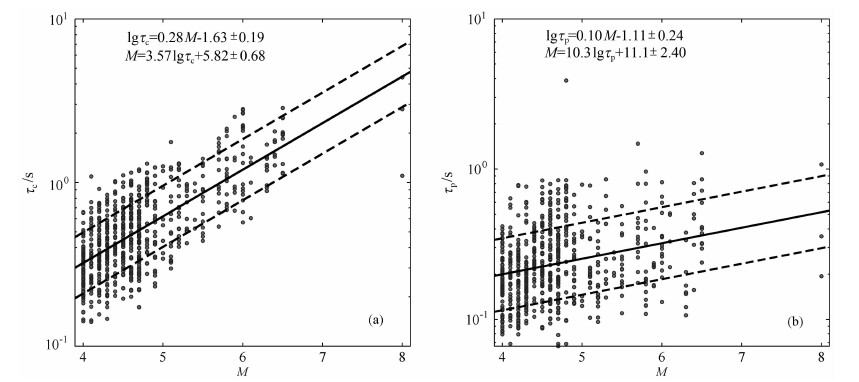
特征周期与地震震级之间的相关性显示在图 8a中,我们这里使用P波到后4s时间窗内的记录数据来计算τc值.在进行具体计算前,积分后的速度数据和位移数据都分别通过截止频率为0.075 Hz的高通滤波器进行滤波预处理,以消除由于积分效应引入的低频频率的影响.从图 8a的统计结果可以看出,特征周期τc能够较好地反映地震规模,由参数τc计算地震震级的方差为0.68个震级单位.但是,对于主震来说,却存在着一个比较明显的震级“饱和”现象.此时,如果再用该值来计算震级,就会明显地低估震级.另外,本文获取到的τc参数与震级之间的相关性与Wu等[8, 33]利用中国台湾地区、日本和南加州的数据集获取到的结果差别不大,说明该参数受到地区性的影响较小,是一个稳定可靠的参数.
|
图 8 参数τ与震级相关性 (a)τc与震级;(b)τp与震级;圆点表示每条台站记录的τ值,黑色实线表示线性拟合曲线,黑色虚线表示一倍标准方差. Fig. 8 Correlation between τ parameters and event magnitude (a)τc vs.magnitude; (b)τp vs.magnitude.Circles represent the τ values of each record.The black solid lines are the best fit curves evaluated through a linear regression, plotted along with one standard deviation (black dashed lines). |
相反,利用卓越周期τp获取到的统计结果(图 8b)虽然看上去能够较好地反映地震规模,甚至在对主震进行估计时,也没有明显地出现震级“饱和”现象,但是它却存在着以下三个问题:(1)计算地震震级的方差明显过大,达到了2.4个震级单位,而且个别记录的计算结果发散性很大,即使是同一次地震,由不同台站计算得到的τp值之间也存在着一些差异性;(2)统计结果曲线的斜率很小,只有0.10±0.03,该结果与Allen等[5]利用南加州地区数据获取到的结果以及Lancieri等[30]利用智利7.8级主余震事件数据获取到的结果相差非常大;(3)与τc参数的统计结果也不具有可比性,这种差别与τp计算时使用P波触发前面数据的噪声大小有关[18],由于所使用的数据部分来自于流动台站,所以其信噪比普遍偏低,导致记录到的数据噪声较大.
5 讨论本文的研究结果为汶川地区建立地震预警系统提供了参考,相关统计结果将运用到我们正在研发的区域预警系统中.该系统在进行实时估算地震动水平时,首先假定震源是一个“点源”模型,并采用各向同性波振幅衰减模式.这些假设可能不够充分,从而会导致预警时间估算(在破坏性波动到来前能够获取到的用于采取地震减灾措施的时间)和对感兴趣台站的地震动峰值预估出现严重的偏差[25].在汶川地震中,仅仅使用震源距衰减关系并不能够充分地对各项预警参数进行一个十分有效的估算.实际上,还应该考虑场地条件、仪器响应等方面对预警参数估计的影响.另外,震源深度对各项预警参数也具有较大的影响,为此,提供一个精确的、实时地震震源深度估计就显得非常重要.众所周知,在进行震源深度定位时,使用S波震相可以大大提高其估算的精度,但是,目前还没有用于预警应用的实时S震相拾取器,未来在该方面还需要开展大量的研究.
一个替代的方案就是使用布设在目标区域附近的由一台单独的地震设备或者台阵组成的现地(Onsite)地震预警系统,通过测量初始P波的幅值和特征周期来预估在同一区域的最大地震动幅值[6].在这种方法中,预警时间由相应台站S波到时与P波到时的差值来给定.但是,本文统计获取到的卓越周期与震级之间的相关性为汶川地区布设现地地震预警系统的可行性给出了一个负面的结果.为此,需要研究一些其他的现地预警参数之间的相关性来替代现有的卓越周期统计结果,如Pd或IV2与PGA或其他一些与结构破坏相关的参数之间的相关性[17, 24].
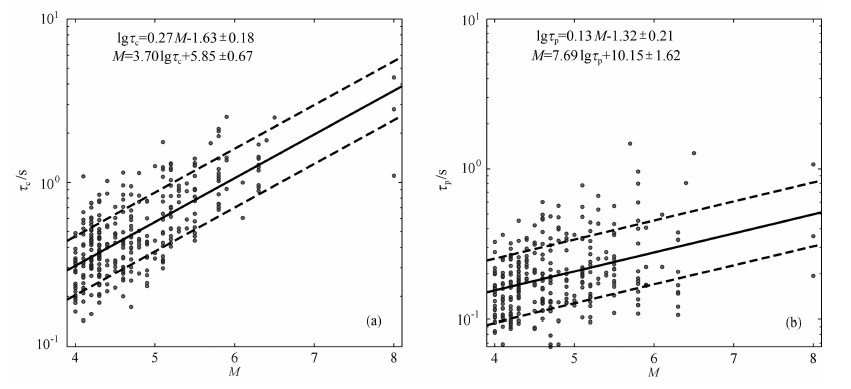
在对本文的数据进行处理时,我们还对采用或不采用流动观测数据进行了分析,如图 9所示,结果表明,不管是否使用流动观测台站记录到的数据,各个预警参数的拟合结果都没有出现太大的变化,整体趋势保持不变.之所以会出现这样的情况,是因为现有固定台站和流动观测台站所使用的强震记录仪器的分辨率绝大多数都只有16位或者18位,从而记录到的数据的信噪比不高,使得固定台站和流动观测台站记录到的数据质量没有太大的区别.
|
图 9 参数τ与震级相关性(只使用固定台站记录数据) (a)τc与震级;(b)τp与震级.圆点表示每条台站记录的τ值,黑色实线表示线性拟合曲线,黑色虚线表示一倍标准方差. Fig. 9 Correlation between τ parameters and event magnitude (Only permanent stations records are used) (a)τcvs.magnitude; (b)τpvs.magnitude.Circles represent the τ values of each record.The black solid lines are the best fit curves evaluated through a linear regression, plotted along with one standard deviation (black dashed lines). |
本文的研究结果除了可以运用到实际的应用系统中,还能为科学界对于预警参数与最终地震震级之间的相关性争论做出一定的贡献.从前面的统计结果可以看出,各项预警参数在进行汶川主震估算时都会出现一定的“饱和”现象,该点可以通过等时线理论进行解释[22, 27].所谓等时线,就是在给定的时间到达指定的台站的一系列辐射能量点的集合.在指定时间和指定台站记录到的远场辐射能量大小可以表示为在受到等时线限定的断层面积上的曲面积分值.等时线上的点并不是同时辐射能量的,断层破裂前端辐射的能量在波传播时由于受到震源与台站之间介质的影响而被延迟.本文的统计结果表明P波2s等时线包围的断层平均面积要大于或等同于较小地震(小于6.5级)最终的断层尺度,而相对大地震来说,则会由于对断层的欠采样而出现地震饱和效应.
另外一个观点[26]认为,地震破裂的发育、传播与弹性能能流密度Gc有关,初期具有较高Gc的破裂能够传播到更远的距离.因此,地震震级与初始阶段应力降水平和(或)断层初始破裂面积间有着密切的关系.这个观点将在我们下一步的工作中使用本文的数据进行验证.
6 结论我们分析了地震预警系统中用于实时震级估算的4个参数:位移幅值,速度平方积分,P波卓越周期和特征周期.这些参数与震级之间的相关性曾被不同的作者使用不同地区的数据集进行过研究[5-6, 9-10].在本文中,我们通过使用汶川主震及其余震的强震观测数据研究了这些参数的行为.之所以选择这些数据集进行本文的研究,主要是考虑到以下几个方面:①所使用的地震事件都是在相同的地质构造背景下记录到的,同时,所记录到的数据还覆盖了地震预警关注的各个梯度的地震震级;②由于在汶川主震发生后,布设了大量的流动观测台站,使得记录到的地震事件非常多,是国内首次获取到如此全面的地震观测资料;③同一次地震在指定范围内有多个台站记录到了其事件波形,能够满足开展地震预警研究所需要的条件.
本文在第一部分中根据指定条件(震源距小于60km)建立地震目录,并对所选用的强震记录进行基线校正等基本处理后,采用人工识别的方法进行P波和S波震相捡拾.然后,在第二部分中分别对Pd、IV2、τc和τp与震级之间的相关性进行了统计.统计结果表明,各项参数在震级小于等于6.5级时,都没有出现饱和现象,但是,对于汶川主震进行估算时,都会出现一定的饱和现象,尤其是IV2参数,饱和现象非常严重.为了查看Pd、IV2参数的拟合曲线相对于震级范围的斜率变化情况,本文还对这两个参数在不同的震级范围进行了统计.结果表明,随着震级范围的增大,拟合曲线的斜率会逐渐缩小,使得相应参数的预估效果逐渐变差.另外,在获取到的结果中,使用Pd参数拟合的曲线与中国台湾和加利福尼亚地区获取到的结果差别较大,主要原因是与统计时使用的具体数据类别有关.他们是同时使用宽频带地震计和强震数据记录,而我们只是使用了强震数据,这样就会出现强震记录在两次积分后,低频噪声在位移信号中占主要地位,大大影响了P波震相的幅度.还有一点需要注意的是,τp参数获取到的统计结果虽然在对主震进行估计时,没有出现明显的震级“饱和”现象,但是由于拟合结果直线的斜率很小,从而使得该参数失去了实时震级估算的意义,不适合应用到汶川地区即将布设的地震预警系统中.
需要强调的是,在进行地震震级测定时还涉及到多个方面的内容,如震源过程、场地条件、传播介质、仪器响应等,而地震预警中可用的信息十分有限,单一的周期参数或幅值参数在一定程度上能够反映地震的规模,但不可能反映地震的全部特征,这就使得在进行预警震级估计时,结果会存在着较大的离散性.因此,这些参数应该集合起来进行一个综合的判断,从而提高震级预估的精度.此外,本文中只使用了强震台站观测数据,并且数据中还有部分来自于流动观测台站,由于数据记录所用仪器的分辨率绝大部分只有16位或者18位,数据的信噪比不高,使得个别的统计结果与其他地区的研究结果有较大的差别.如果在统计时能够集合测震台站观测数据,则可以大大提高统计结果的准确性,这项研究将在我们下一步的工作中开展.
致谢感谢国家强震动台网中心为本文的研究提供的数据支持.感谢评审人提出的宝贵意见,使得本文的研究内容有了很大的充实.
| [1] | 金星, 张红才, 李军, 等. 地震预警连续定位方法研究. 地球物理学报 , 2012, 55(3): 925–936. Jin X, Zhang H C, Li J, et al. Research on continuous location method used in earthquakeearly warning system. Chinese J. Geophys. (in Chinese) , 2012, 55(3): 925-936. (in Chinese) |
| [2] | Nakamura Y. On the urgent earthquake detection and alarm system (UrEDAS). Proceedings of Ninth World Conference on Earthquake Engineering , 1988, 7(2-9): 673-678. |
| [3] | 金星, 张红才, 李军, 等. 地震预警震级确定方法研究. 地震学报 , 2012, 34(5): 593–610. Jin X, Zhang H C, Li J, et al. Research on earthquake early warning magnitude estimate. Acta Seismologica Sinica (in Chinese) , 2012, 34(5): 593-610. (in Chinese) |
| [4] | 张红才, 金星, 李军, 等. 地震预警震级计算方法研究综述. 地球物理学进展 , 2012, 27(2): 464–474. Zhang H C, Jin X, Li J, et al. Review on magnitude estimation methods applied to earthquake early warning systems. Progress in Geophys. (in Chinese) , 2012, 27(2): 464-474. (in Chinese) |
| [5] | Allen R M, Kanamori H. The potential for earthquake early warning in southern California. Science , 2003, 300(5620): 786-789. DOI:10.1126/science.1080912 |
| [6] | Wu Y M, Kanamori H. Rapid assessment of damage potential of earthquakes in Taiwan from the beginning of P waves. Bulletin of the Seismological Society of America , 2005, 95(3): 1181-1185. DOI:10.1785/0120040193 |
| [7] | Simons F J, Dando B D E, Allen R M. Automatic detection and rapid determination of earthquake magnitude by wavelet multiscale analysis of the primary arrival. Earth and Planetary Science Letters , 2006, 250(1-2): 241-223. DOI:10.1016/j.epsl.2006.07.037 |
| [8] | Wu Y M, Zhao L. Magnitude estimation using the first three seconds P-wave amplitude in earthquake early warning. Geophysical Research Letters , 2006, 33(16): L16312. DOI:10.1029/2006gl026871 |
| [9] | Zollo A, Lancieri M, Nielsen S. Earthquake magnitude estimation from peak amplitudes of very early seismic signals on strong motion records. Geophysical Research Letters , 2006, 33(23): L23312. DOI:10.1029/2006GL027795 |
| [10] | Zollo A, Lancieri M, Nielsen S. Reply to comment by P. Rydelek et al. on "Earthquake magnitude estimation from peak amplitudes of very early seismic signals on strong motion records". Geophysical Research Letters , 2007, 34(20): L20303. DOI:10.1029/2007GL030560 |
| [11] | Bose M, Wenzel F, Erdik M. Preseis: A neural network-based approach to earthquake early warning for finite faults. Bulletin of the Seismological Society of America , 2008, 98(1): 366-382. DOI:10.1785/0120070002 |
| [12] | Festa G, Zollo A, Lancieri M. Earthquake magnitude estimation from early radiated energy. Geophysical Research Letters , 2008, 35(22): L22307. DOI:10.1029/2008GL035576 |
| [13] | 杨少敏, 兰启贵, 聂兆生, 等. 用多种数据构建2008年汶川特大地震同震位移场. 地球物理学报 , 2012, 55(8): 2575–2588. Yang S M, Lan Q G, Nie Z S, et al. Coseismic displacement caused by the 2008 great Wenchuan earthquake derived from various types of geodetic data. Chinese J. Geophys. (in Chinese) , 2012, 55(8): 2575-2588. (in Chinese) |
| [14] | 万柯松, 倪四道, 曾祥方, 等. 汶川大地震中的应急地震学. 中国科学(D辑) , 2009, 39(1): 1–10. Wan K S, Ni S D, Zeng X F, et al. Real-time seismology for the 05/12/2008 Wenchuan earthquake of China: A retrospective view. Sci. China (Ser. D) (in Chinese) , 2009, 39(1): 1-10. (in Chinese) |
| [15] | Kanamori H. Real-time seismology and earthquake damage mitigation. Annual Review of Earth and Planetary Sciences , 2005, 33(1): 195-214. DOI:10.1146/annurev.earth.33.092203.122626 |
| [16] | Olson E L, Allen R M. The deterministic nature of earthquake rupture. Nature , 2005, 438(10): 212-215. |
| [17] | Wu Y M, Kanamori H. Experiment on an onsite early warning method for the Taiwan Early Warning System. Bulletin of the Seismological Society of America , 2005, 95(1): 347-353. DOI:10.1785/0120040097 |
| [18] | Shieh J T, Wu Y M, Allen R M. A comparison of τc and τpmax for magnitude estimation in earthquake early warning. Geophysical Research Letters , 2008, 35(20): L20301. DOI:10.1029/2008GL035611 |
| [19] | Rydelek P, Horiuchi S. Earth science: Is earthquake rupture deterministic?. Nature , 2006, 442(7100): 1476-4687. DOI:10.1038/nature04963 |
| [20] | Wolfe C J. On the properties of predominant-period estimators for earthquake early warning. Bulletin of the Seismological Society of America , 2006, 96(5): 1961-1965. DOI:10.1785/0120060017 |
| [21] | Yamada T, Ide S. Limitation of the predominant-period estimator for earthquake early warning and the initial rupture of earthquakes. Bulletin of the Seismological Society of America , 2008, 98(6): 2739-2745. DOI:10.1785/0120080144 |
| [22] | Lancieri M, Zollo A. A Bayesian approach to the real time estimation of magnitude from the early P-and S-wave displacement peaks. Journal of Geophysical Research , 2008, 113(B12): B12302. DOI:10.1029/2007JB005386 |
| [23] | Iannaccone G, Zollo A, Elia L, et al. A prototype system for earthquake early-warning and alert management in southern Italy. Bulletin of Earthquake Engineering , 2010, 8(5): 1105-1129. DOI:10.1007/s10518-009-9131-8 |
| [24] | Zollo A, Amoroso O, Lancieri M, et al. An integrated regional and on-site early warning approach: Off-line application to the MW6.3, 2009 central Italy (L'Aquila) earthquake. American Geophysical Union , 2009, 95(3): 1181-1185. |
| [25] | Zollo A, Iannaccone G, Lancieri M, et al. Earthquake early warning system in southern Italy: Methodologies and performance evaluation. Geophysical Research Letters , 2009, 36(5): L00B07. DOI:10.1029/2008GL036689 |
| [26] | Nielsen S. Can earthquake size be controlled by the initial seconds of rupture?//Earthquake Early Warning Systems. Berlin Heidelberg: Springer-Verlag, 2007: 9-20. |
| [27] | Murphy S, Nielsen S. Estimating earthquake magnitude with early arrivals: A test using dynamic and kinematic models. Bulletin of the Seismological Society of America , 2009, 99(1): 1-23. DOI:10.1785/0120070246 |
| [28] | Kanamori H, Mori J, Hauksson E, et al. Determination of earthquake energy release and ML using TERRAscope. Bulletin of the Seismological Society of America , 1993, 83(2): 330-346. |
| [29] | Zeng Y H, Aki K, Teng T L. Mapping of the high-frequency source radiation for the Loma Prieta earthquake, California. Journal of Geophysical Research , 1993, 98(B7): 11981-11993. DOI:10.1029/93JB00346 |
| [30] | Yamada M, Heaton T, Beck J. Real-time estimation of fault rupture extent using near-source versus far-source classification. Bulletin of the Seismological Society of America , 2007, 97(6): 1890-1910. DOI:10.1785/0120060243 |
| [31] | Scholz C H. The Mechanics of Earthquakes and Faulting. (2nd ed). Cambridge, UK: Cambridge Univ. Press, 2002 . |
| [32] | Wu Y M, Kanamori H. Development of an earthquake early warning system using real-time strong motion signals. Sensors , 2008, 8(1): 1-9. DOI:10.3390/s8010001 |
| [33] | Lancieri M, Fuenzalida A, Ruiz S, et al. Magnitude scaling of early-warning parameters for the MW 7.8 Tocopilla, Chile, earthquake and its aftershocks. Bulletin of the Seismological Society of America , 2011, 101(2): 447-463. DOI:10.1785/0120100045 |
 2013, Vol. 56
2013, Vol. 56