2. 中国科学院研究生院, 北京 100190;
3. 中国西安卫星测控中心, 西安 710043
2. Graduate University of Chinese Academy of Sciences, Beijing 100190, China;
3. China Xi'an Satellite Control Center, Xi'an 710043, China
目前在对低轨道(Low Earth Orbit,简称LEO)卫星进行定轨预报时多采用参考大气,常用的有:CIRA系列模型、Jacchia系列模型、DTM模型、MSIS系列模型等.这些大气模型都能反映高层大气密度的基本变化特征,在航天器的轨道确定和预报工作中发挥着重要的作用.但由于高层大气的复杂性以及一些未知因素、物理机制的影响,加上建立模型所用的统计资料的分布不均匀和精度限制等,已有的大气模型精度不高,均方根(RMS)误差普遍在30%左右,极端情况下可达100%甚至更高[1],尤其是在短期变化方面.目前,大气密度模型已经是低轨道航天器轨道确定和预测中最主要的误差来源之一[2],远不能满足航天测控对轨道大气密度短期预报精度越来越高的要求,迫切需要开展提高模型精度的研究工作.
NRLMSISE-00(US Naval Research Laboratory Mass Spectrometer and Incoherent Scatter Radar Extended)大气模型是MSIS系列模型的最新版本,描述了从地面到热层(0~1000km)的中性大气密度、温度等大气物理性质,是目前使用广泛的大气模型之一.它是由美国海军实验室(NRL)的Picone等[3]学者在MSISE-90模型基础上开发改进而来的全球大气经验模型,新加入了卫星加速计和卫星轨道数据反演得到的大气总质量密度数据、solar UV occultation的SMM仪器所观测到的氧分子数密度数据以及非相干散射雷达(ISR)的温度数据.但该模型在轨道大气密度短期变化方面的误差仍然较大.利用一些新的高精度探测数据对NRLMSISE-00模型结果进行修正,以提高大气密度短期预报的精度,具有非常重要的应用价值,也有利于分析一些尚未解决的科学问题.
在大气密度模型结果修正方面,我国的苗娟等[4]以中国神舟飞船探测数据为基础,提出一种基于实时大气密度观测数据的模型修正方法,通过简单计算分析实时数据与模型之间的误差特点,建立了一种平均误差修正方法,一定程度上提高了大气密度的预报精度.该方法考虑了纬度和地方时两个因素,对数据的实时性要求较高,适用于同一卫星轨道的大气密度预报.美国的Doornbos等[1]利用大量卫星星历数据建立修正模型,对CIRA-72模型和MSIS-86的密度结果进行修正,该方法可对不同卫星轨道大气密度模型结果进行修正.目前也有不少学者针对大磁暴发生期间模型的大气密度进行预报修正研究,如Zhou等[5]利用CHAMP(Challenging Mini-Satellite Payload)卫星2001-2004年9次大磁暴期间的数据结合NRLMSISE-00模型研究了大气密度与焦耳加热及与Sym-H指数的关系,用于对NRLMSISE-00模型在磁暴期间的大气密度结果进行修正.Kim等[6]利用NRLMSISE-00模型的氦密度数据对TIE-GCM模型进行修正,使得TIE-GCM模型的标准偏差提高了21%.
近年来GRACE-A/B(Gravity Recovery and Climate Experiment)双星和CHAMP卫星探测了大量高质量的大气密度数据,数据覆盖大半个太阳活动周(2002-2008年,版本V2.2)[7-9].目前我国也已有多颗卫星搭载了空间大气密度探测器,积累了一定数量的大气密度探测数据.这些新的观测数据,为提高大气密度的短期预报精度提供了一定的条件.我们拟通过将NRLMSISE-00模型与实测大气密度数据进行详细对比分析,分析模型的误差随地方时、经度、纬度、高度、F10.7指数等因素的变化特征,进而提出如何利用实测数据对NRLMSISE-00大气模型的密度结果进行修正的方法,用于对所有LEO大气密度的预报修正.
2 数据来源和说明本文主要利用GRACE-A、GRACE-B和CHAMP卫星的大气密度数据进行研究分析. CHAMP卫星和GRACE A/B卫星上均搭载了星载加速仪,通过计算反演可给出卫星所处位置上较为准确的大气密度.CHAMP卫星于2000年7月15日发射升空,初始轨道为454km的近圆极轨道,周期大约93 min,倾角约87°[7-8].GRACE双星于2002年3月17日发射升空,倾角为89°,初始轨道高度约500km[9].CHAMP卫星的大气密度数据大约需要4个月覆盖全部地方时,而GRACE卫星大约6个月覆盖全部地方时.
本文采用的数据时间范围为:CHAMP卫星的轨道大气密度从2001年5月15日至2008年12月31日,GRACE卫星的大气密度数据从2002年8月1日至2008年11月13日(版本V2.2).这三颗卫星提供的大气密度数据有较高的探测精度,长达7年的数据也覆盖了大半个太阳活动周期(其中2002、2003年为太阳活动中高年,2007、2008年为太阳活动低年),有利于开展大气密度相关研究.
3 大气密度预报修正方法在LEO,一般可认为局部大气密度与附近高度的大气密度测量值存在着指数扩散关系,定义某一时刻轨道高度为h的某观测点上的轨道大气密度真值ρ(h)与NRLMSISE-00模型大气密度输出值ρM(h)的比值为
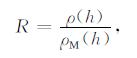
|
(1) |
R表示了模型值对真值的偏离程度.因此,在对低轨道大气密度进行短期预报时,如果能获得准确的R值,则可对NRLMSISE-00模型输出的大气密度值进行修正,从而达到利用模型提高大气密度短期预报精度的目的.(1)式也常用于对大气密度进行归一化(标准化)处理,如将大气密度归一化到400km高度[8, 10].因此,可将R视为NRLMSISE-00模型的修正因子.
倘若修正因子R是一个平均值为1的随机变量,则(1)式修正的意义不大.如果R有一些规律性的变化,代表模型存在一些系统性的偏差,则(1)式的修正可以提高模型的预报精度.我们认为,NRLMSISE00模型基于过去的数据建立,且难以考虑到一些新发现的物理因素(如非迁移潮汐),所以会与新的观测数据之间存在一些系统性的偏差.因此利用新的大气密度数据研究修正因子R的规律,建立修正因子模型,从而对NRLMSISE-00模型修正,可提高现有大气模型的预报精度.
定义NRLMSISE-00模型与实测数据的相对误差为
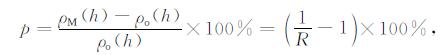
|
(2) |
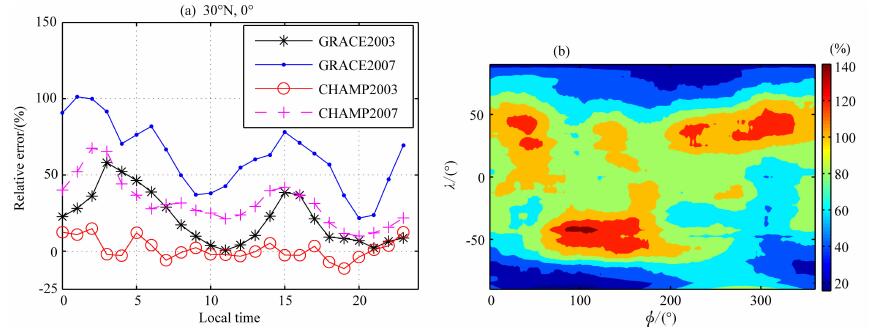
其中,ρM(h)为NRLMSISE-00模型结果,ρo(h)为密度观测值.可见R与NRLMSISE-00模型的误差直接相关.利用GRACE和CHAMP卫星多年的大气密度数据对NRLMSISE-00模型的密度结果进行误差分析,分析模型密度结果的误差与太阳活动、经纬度、高度和地方时等因素的关系,分析中将数据根据地方时、经纬度划分为1h×2.5°×2.5°的网格.为了简单化处理,在修正方法研究的过程中,以地磁当前3h的ap指数为判定标准,将地磁活动简单划分为3个状态:ap<27为地磁相对平静期,27≤ap≤80为地磁活跃期至中等强度磁暴扰动期,ap>80为大磁暴扰动期,本文主要考虑地磁相对平静期的情况(ap<27).图 1给出了误差分析的部分结果.从图中可见,模型值总体比卫星观测值偏大.在相同的经纬度上空,对于同一颗卫星而言,在太阳活动低年的2007年误差比太阳活动较为活跃的2003年大,相对误差与太阳活动强度(F10.7指数)反相关.但对于同一年份,模型大气密度在轨道高度较高的GRACE卫星轨道上误差相对更大.相对误差随地方时有明显的变化,地方时2~3点、15点前后误差较大,地方时10点和20点附近相对误差较小,如图 1a所示.从图 1b可见,对于同一颗卫星、相同地方时下,不同经纬度上空模型误差不一致,高纬度误差相对较大,误差分布存在着四波结构.
|
图 1 NRLMSISE-00大气密度相对于GRACE卫星和CHAMP卫星实测值的相对误差 (a)不同年份下相对误差随地方时的变化;(b)2007年LT2:00模型在GRACE卫星轨道上的相对误差. Fig. 1 Density relative error of NRLMSISE-00 model (a) Relative error varied with local time at GRACE orbit and CHAMP orbit; (b) Relative error at GRACE orbit in 2007. |
总之,2002-2008年间,GRACEA/B和CHAMP卫星的大气密度数据与NRLMSISE-00模型的密度值之间存在着较大的差异,模型值总体比实测值偏大,在太阳低年相对误差平均值可达75%.模型的误差与太阳活动、经纬度、地方时、高度等因素仍然有关. NRLMSISE-00模型与实测数据的差异,主要是由于该模型对一些物理因素没有纳入考虑有关,如大气非迁移潮汐、太阳辐射不同波段的变化对大气密度的影响等,导致出现系统性的偏差.
因此,在对修正因子建模时,仍然需要考虑太阳活动、高度、经纬度地方时等因素的影响.利用GRACE和CHAMP卫星的密度数据,结合NRLMSISE-00模型值可得到一系列Ri数据集合.在地磁平静期下,设某高度h0的修正因子如下:
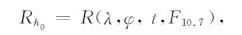
|
(3) |
其中λ表示纬度,φ表示经度,h0表示高度,t代表地方时.我们首先用二次多项式拟合Rh0与F10.7指数的关系,得到RF10.7,再减去RF10.7:
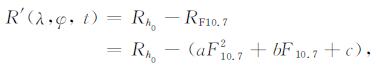
|
(4) |
a、b、c为拟合系数.此时R′仅与经纬度和地方时有关.再对R′在1h×2.5°×2.5°网格点求平均,可得到代表该地方时和经纬度条件下的修正因子R′.
利用GRACE和CHAMP卫星大气密度数据,结合NRLMSISE-00模型值,采用上述方法,最后可得到包含修正因子与F10.7指数的二次项系数(a,b,c)以及对应于1h×2.5°×2.5°网格点上的修正因子R′的数据集合.根据该数据集合,可对该高度上NRLMSISE00大气密度预报值进行修正.
采用不同轨道高度上的卫星大气密度数据,应用上述方法,可以得到一系列代表不同轨道高度的大气密度修正因子数据集合.对于其它轨道高度,可以通过分段线性插值的方法[1]得到修正因子R:
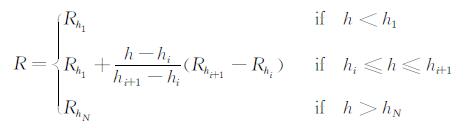
|
(5) |
其中,hi(i=1,…,N-1)代表的是已积累一定数量的大气密度探测数据的轨道高度.
对于中等强度以下的磁暴扰动期(27≤ap≤80),采取类似方法得到中等强度磁暴扰动下的修正因子R集合.而对于大磁暴扰动的情况,由于探测数据较少,对模型值不予以修正,直接采用NRLMSISE-00模型的预报结果.
4 修正方法预报结果验证为了解上述大气密度预报修正方法的效果,开展了试验一、二的预报试验.
为了便于描述,用RG表示利用GRACE A/B卫星实测数据建立的修正因子集合,代表的轨道高度约为480km;用RC表示利用CHAMP卫星的大气密度数据所建立的修正模型,其代表的轨道高度约为380km.为了评估修正后的3天短期预报效果,我们给出预报结果的相对误差、相对误差的标准偏差、均方根(RMS)误差.
4.1 试验一给出2个例子的预报结果:
(1)利用2002年8月1日-2003年10月4日之间GRACE A/B卫星的大气密度反演数据,建立修正因子集合RG,结合NRLMSISE-00模型对2003年10月5-7日(2003年第278-280天)3天的大气密度进行修正预报,将预报结果与GRACE-A卫星的探测结果、未修正的NRLMSISE-00模型计算结果进行比较.
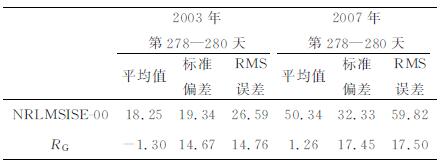
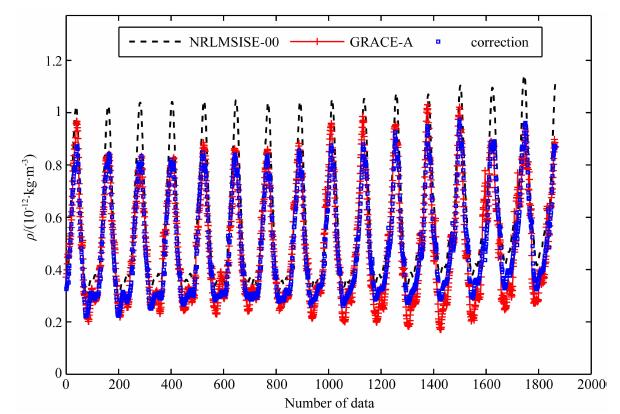
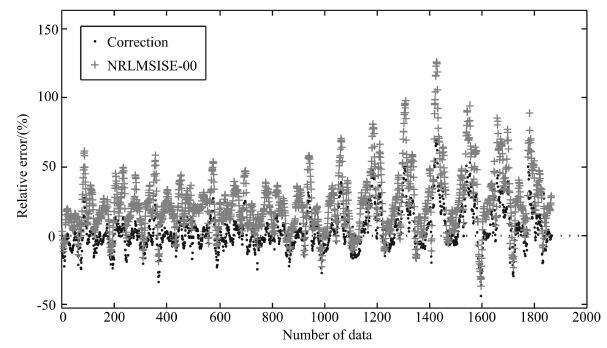
2003年第278-280天存在着短暂的地磁小扰动,总体为地磁平静期,这3天内轨道高度平均值为491km.图 2给出了RG对2003年第278天轨道上大气密度的修正预报结果、NRLMSISE-00模型的结果以及GRACE-A卫星的观测结果.图 3给出了修正后的相对误差以及NRLMSISE-00模型的相对误差(以GRACE-A卫星观测值为真值).从图 2可以看出,修正值与卫星的实测值更为接近,而模型值总体偏大.从图 3可见,RG修正值的相对误差明显小于NRLMSISE-00模型的相对误差.从表 1相对误差的统计结果可知,在此3天内,修正值的相对误差平均值为-1.30%,相对误差的标准偏差为14.67%,而NRLMSISE-00模型值的相对误差平均值为18.25%,相对误差的标准偏差为19.34%.
|
图 2 2003年第278天GRACE-A卫星轨道大气密度的修正预报结果、卫星观测值和NRLMSISE-00模型值的对比 Fig. 2 Density at GRACE-A orbit on day 278 of 2003 |
|
图 3 2003年第278天GRACE-A卫星轨道大气密度修正预报的相对误差和NRLMSISE-00模型值的相对误差 Fig. 3 Density relative error at GRACE-A orbit on day 278 of 2003 |
|
|
表 1 GRACE-A卫星轨道大气密度3天短期预报的相对误差统计结果(%) Table 1 Density relative error at GRACE-A orbit (%) |
(2)利用2006年1月1日-2007年10月4日之间GRACE A/B的大气密度数据建立修正因子RG,对2007年10月5-7日(2007年第278-280天)GRACE-A卫星轨道上的大气密度进行3天短期预报.
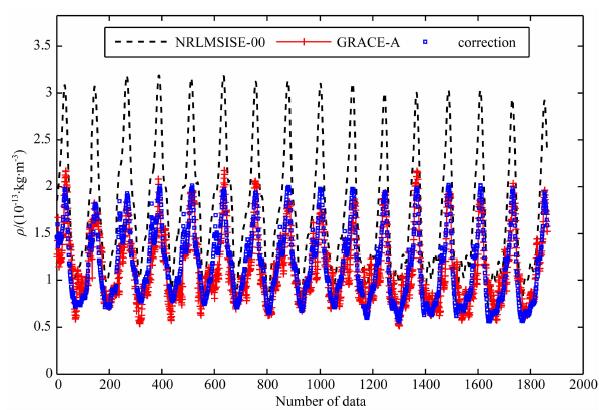
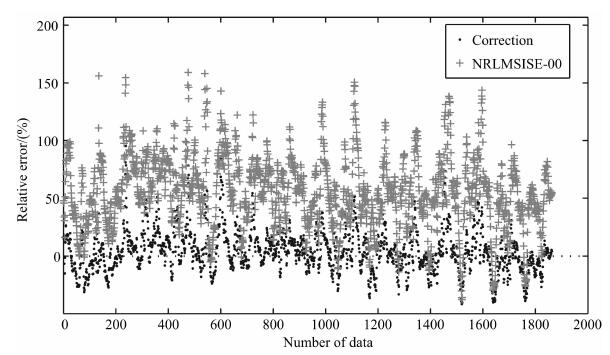
2007年第278-280天为地磁平静期,这3天内轨道高度平均值为478km.图 4、5显示了修正预报的效果和相对误差以及NRLMSISE-00模型的结果.从图 4、5可知,修正后的预报误差较之修正前显著降低,修正后的密度预报值与卫星观测结果非常接近,修正了NRLMSISE-00模型结果整体偏大的缺点.从表 1中给出的统计结果来看,修正后的3天短期预报相对误差平均值为1.26%,相对误差的标准偏差为17.45%,而NRLMSISE-00模型值的相对误差平均值为50.34%,相对误差的标准偏差为32.33%.
|
图 4 2007年第278天GRACE-A卫星轨道大气密度的修正预报结果、卫星观测值和NRLMSISE-00模型值的比较 Fig. 4 Density at GRACE-A orbit on day 278 of 2007 |
|
图 5 2007年第278天GRACE-A卫星轨道大气密度的修正预报相对误差和NRLMSISE-00模型值的相对误差 Fig. 5 Density relative error at GRACE-A orbit on day 278 of 2007 |
类似地,我们也对轨道高度较低的CHAMP卫星轨道大气密度进行3天短期预报检验,给出2个验证事例:
(1)利用RC对2007年第278-280天CHAMP卫星轨道大气密度进行短期预报,并与模型值、卫星实测值比较.
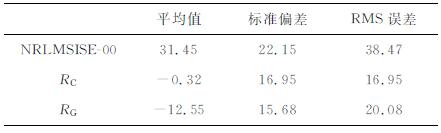
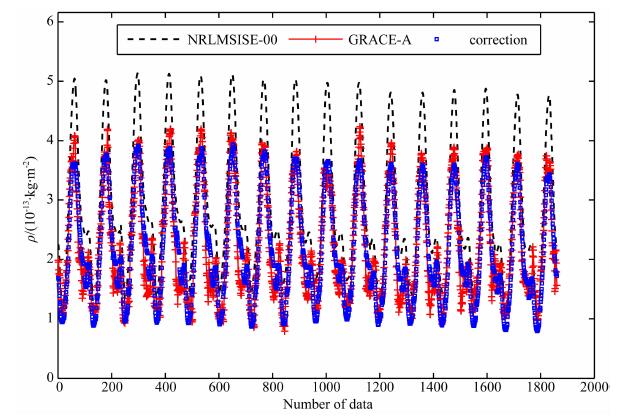
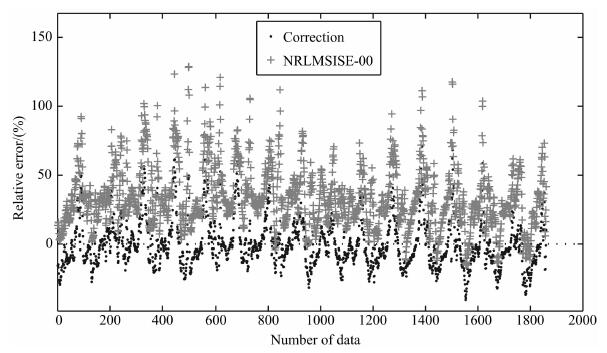
CHAMP卫星在2007年第278-280天的轨道平均高度为351km.图 6、7是2007年第278天CHAMP卫星轨道上RC修正后的大气密度预报结果、NRLMSISE-00模型值以及卫星实测值的对比图以及相应的相对误差.在2007年,NRMSISE-00模型密度输出结果明显偏大,而利用历史探测数据对模型进行修正的预报结果与卫星实测值较为接近,修正预报的大气密度精度显著提高,如图 6、7所示.表 2为相对误差的统计结果,2007年修正值的相对误差平均值为-0.32%,相对误差的标准偏差为16.95%,而NRLMSISE-00模型值的相对误差平均值为31.45%,其标准偏差为22.15%.通过修正,将模型的RMS误差从38.47%降低为16.95%.可见,该修正方法同样对CHAMP卫星轨道上的NRLMSISE-00模型结果有较好的修正效果,可显著降低轨道大气密度短期预报的误差.
|
图 6 2007年第278天CHAMP卫星轨道大气密度的修正预报结果、卫星观测值和NRLMSISE-00模型值的比较 Fig. 6 Density at CHAMP orbit on day 278 of 2007 |
|
图 7 2007年第278天CHAMP卫星轨道大气密度的修正预报相对误差和NRLMSISE-00模型值的相对误差 Fig. 7 Density relative error at CHAMP orbit on day 278 of 2007 |
|
|
表 2 2007年第278-280天CHAMP卫星轨道大气密度3天短期预报的相对误差统计结果(%) Table 2 Density relative error at CHAMP orbit (%) |
(2)利用RG对2007年第278-280天CHAMP卫星轨道大气密度进行短期预报,并与模型值、实测值比较.
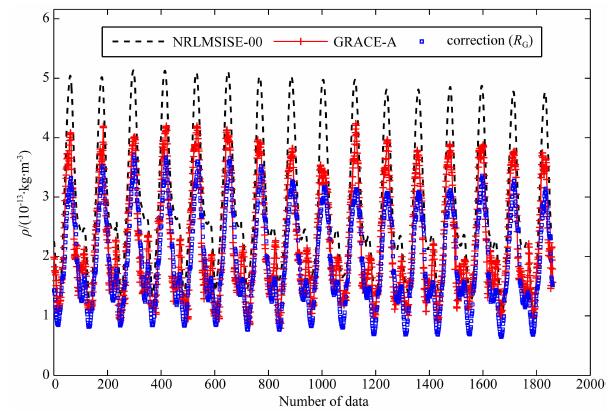
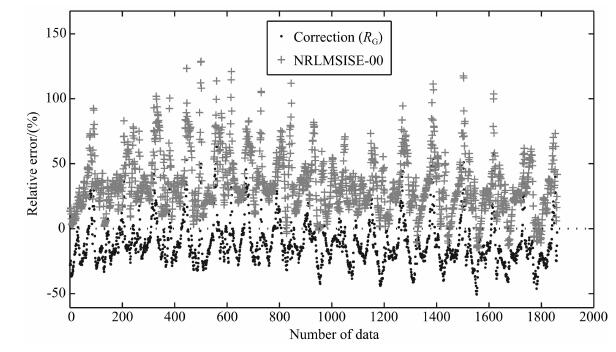
假定近期缺乏CHAMP卫星轨道上的大气密度探测数据,根据高度插值公式(5),可采用GRACE卫星探测数据建立的修正因子集合RG,对NRLMSISE-00模型在CHAMP卫星轨道上的密度结果进行修正.图 8、9和表 2给出用RG对模型在CHAMP卫星轨道上2007年第278-280天的大气密度修正结果.GRACE卫星在2006-2007年间轨道高度约为480km,而CHAMP卫星约为360km.从图 8、9中可以看出,尽管GRACE卫星轨道高度比CHAMP卫星轨道高度要高100多公里,用RG对CHAMP卫星轨道上的NRLMSISE-00模型结果进行修正,同样取得不错的修正效果,表 2中的统计结果表明,NRLMSISE-00模型在2007年278-280天的RMS误差约为38.47%,而用RG修正因子修正之后,RMS误差降为20.08%.因此,上述修正方法不但可对已经积累了一定数量大气密度数据的轨道进行密度修正,也可推广到缺乏近期大气密度数据积累的轨道,对其轨道大气密度进行短期预报.
|
图 8 2007年第278天CHAMP卫星轨道大气密度利用RG修正预报结果、卫星观测值和NRLMSISE-00模型值的比较 Fig. 8 Density of RG correction, CHAMP observation and NRLMSISE-00 model result at CHAMP orbit on day 278 of 2007 |
|
图 9 2007年第278天CHAMP卫星轨道大气密度RG修正预报的相对误差、NRLMSISE-00模型的相对误差 Fig. 9 Density relative error of RG correction and NRLMSISE-00 model at CHAMP orbit on day 278 of 2007 |
上述结果表明,利用已有的轨道大气密度实测数据对NRLMSISE-00大气模型密度结果进行修正的方法,可显著提高模型的大气密度短期预报精度.
在计算修正因子时,所采用探测数据的地方时需要满足所预报的地方时需求,因此对于准太阳同步卫星,由于地方时缓慢变化,所以采用预报期前10天的数据也可以进行修正预报.但如果探测数据积累不连续,则需要考虑覆盖全部地方时的数据长度.采用近期的密度数据进行修正,更有利于反映NRLMSISE-00模型在当前空间环境条件下与真值的偏离,有助于提高修正模型的预报精度,不宜采用时间间隔太久的数据.例如,如果用太阳活动高年的数据所获得的修正因子集合去修正太阳活动低年时NRLMSISE-00的密度输出结果,修正效果则很难达到预期目标.或者采用至少覆盖一个太阳活动周期的数据,则对探测数据的实时性要求可以降低,以避免太阳活动强度差异所带来的误差.实际上,太阳活动对大气密度的影响非常复杂,大气密度的变化与F10.7指数的前一天观测值以及81天平均值均有强相关性,NRLMSISE-00大气模型输入参量中既要求有前1天的F10.7指数,也要求输入F10.7指数的81天平均值.而目前我们对修正因子建模的过程中仅考虑了前1天的F10.7指数.并且,在NLRMSISE-00模型中用于表征太阳活动的F10.7指数未能完全反映太阳活动对大气密度的影响,Guo等[11]采用F10.7、EUV和FUV等多种太阳活动指数对CHAMP卫星的大气密度数据进行拟合,认为通过拟合可以解释71%的密度变化,比单用F10.7指数拟合效果要好.因此,在进一步工作中可以考虑选择更合适的指数表征太阳活动.
季节变化、年内变化等因素,也可能是NRLMSISE-00模型的误差来源之一,这些因素未在模型进行修正的过程中加以考虑.Guo等[12]用CHAMP卫星的数据对大气密度的年内变化作了详细的分析,认为低轨道大气密度存在着明显的年内变化,如半年变化、三分之一年、四分之一年的变化等,而NRLMSISE-00模型仅对半年变化有所体现.由于本文工作中所采用的GRACE卫星和CHAMP卫星为准太阳同步卫星,数据覆盖全部的地方时需要4-6个月,较难同时考虑地方时和季节变化对NRLMSISE-00模型误差的影响,这些因素也希望能在积累更多数据后进一步深入分析.
5 结论通过分析NRLMSISE-00大气模型与GRACE A/B和CHAMP卫星2002-2008年大气密度数据之间的误差特征,提出了一种基于实测数据和NRLMSISE-00模型的大气密度短期预报修正方法:根据已有实测数据与模型的误差,考虑地方时、经纬度、太阳活动等因素获得模型的修正因子,利用修正因子对模型输出结果进行修正,从而达到提高大气密度短期预报精度的目的.将此修正方法应用于对低轨道卫星的大气密度3天短期预报中,对NRLMSISE-00大气模型的密度值进行修正,取得了很好的预报效果,大气密度短期预报的误差显著减小,尤其是在太阳活动中低年.结果显示,修正后的预报密度的RMS误差可以降低50%以上,2008年1月份修正模型在GRACE和CHAMP卫星轨道上大气密度的RMS误差从59.21%降低到27.85%以及从50.70%降低到21.51%.该方法可在积累一定量大气密度实测数据时建立涵盖多个轨道高度的三维修正因子模型,从而广泛应用到轨道上的大气密度短期预报业务中.
今后可在建立修正模型的过程中,考虑采用多个太阳活动指数以更全面表征太阳活动对低轨道大气密度的影响,考虑大气密度的季节变化等因素,尝试采用覆盖一个太阳活动周的大气密度数据等进一步的方案,以完善建立修正因子模型的方法.
致谢感谢http://sisko.colorado.edu/sutton/data.html提供了GRACE和CHAMP卫星的大气密度数据.
| [1] | Doornbos E, Klinkrad H, Visser P. Use of two-line element data for thermosphere neutral density model calibration. Advances in Space Research , 2008, 41(7): 1115-1122. DOI:10.1016/j.asr.2006.12.025 |
| [2] | Qian L Y, Solomon S C. Thermospheric density: an overview of temporal and spatial variations. Space Science Reviews , 2012, 168(1-4): 147-173. DOI:10.1007/s11214-011-9810-z |
| [3] | Picone J M, Hedin A E, Drob D P, et al. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. Journal of Geophysical Research , 2002, 107(A12): SIA15-1-SIA15-16. DOI:10.1029/2002JA009430 |
| [4] | 苗娟, 刘四清, 李志涛, 等. 基于实时观测数据的大气密度模式修正. 空间科学学报 , 2011, 31(4): 459–466. Miao J, Liu S Q, Li Z T, et al. Atmospheric density calibration using the real-time satellite observation. Chinese Journal of Space Science (in Chinese) , 2011, 31(4): 459-466. (in Chinese) |
| [5] | Zhou Y, Maa S Y, Lührb H, et al. An empirical relation to correct storm-time thermospheric mass density modeled by NRLMSISE-00 with CHAMP satellite air drag data. Advances in Space Research , 2009, 43(5): 819-828. DOI:10.1016/j.asr.2008.06.016 |
| [6] | Kim J S, Urbinab J V, Kanec T J, et al. Improvement of TIE-GCM thermospheric density predictions via incorporation of helium data from NRLMSISE-00. Journal of Atmospheric and Solar-Terrestrial Physics , 2012, 77: 19-25. DOI:10.1016/j.jastp.2011.10.018 |
| [7] | Reigber C, Lühr H, Schwintzer X. CHAMP mission status. Advances in Space Research , 2002, 30(2): 129-134. DOI:10.1016/S0273-1177(02)00276-4 |
| [8] | Bruinsma S, Tamagnan D, Biancale R. Atmospheric densities derived from CHAMP/STAR accelerometer observations. Planetary and Space Science , 2004, 52(4): 297-312. DOI:10.1016/j.pss.2003.11.004 |
| [9] | Tapley B D, Bettadpur S, Watkins M, et al. The gravity recovery and climate experiment: Mission overview and early results. Geophysical Research Letters , 2004, 31(9): L09607. |
| [10] | Bruinsma S, Biancale R. Total densities derived from accelerometer data. Journal of Spacecraft and Rrockets , 2003, 40(2): 230-236. DOI:10.2514/2.3937 |
| [11] | Guo J P, Wan W X, Forbes J M, et al. Effects of solar variability on thermosphere density from CHAMP accelerometer data. Journal of Geophysical Research , 2007, 112(A10). DOI:10.1029/2007JA012409 |
| [12] | Guo J, Wan W X, Forbes J M, et al. Interannual and latitudinal variability of the thermosphere density annual harmonics. J. Geophys. Res , 2008, 113(A8): A08301. |
 2013, Vol. 56
2013, Vol. 56