地球物理学报  2013, Vol. 56 Issue (1): 348-353   PDF    
引用本文
郑鑫, 陶夏新, 王福彤 等. 去除交通环境振动观测记录中本底振动的自互功率谱法. 地球物理学报, 2013, 56(1): 348-353, doi: 10.6038/cjg20130136.  
ZHENG X, TAO X X, Wang F T, et al. An auto-cross PSD method to remove background vibration from observational records of traffic environment vibration. Chinese J. Geophys. (in Chinese), 2013, 56(1): 348-353, doi: 10.6038/cjg20130136.  
去除交通环境振动观测记录中本底振动的自互功率谱法
郑鑫1,2,3 , 陶夏新2,3 , 王福彤3,4 , 解恒燕1     
1. 黑龙江八一农垦大学工程学院, 黑龙江 大庆 163319;
2. 哈尔滨工业大学土木工程学院, 哈尔滨 150090;
3. 中国地震局工程力学研究所, 哈尔滨 150080;
4. 黑龙江大学建筑工程学院, 哈尔滨 150001
收稿日期 2011-12-12, 2012-10-28 收修定稿
基金项目: 国家自然科学基金重点项目(50538030);黑龙江省教育厅科学技术研究面上项目"轨道交通引起的季冻区冬夏两季饱和土场地环境振动衰减关系研究"资助
作者简介: 郑鑫, 男, 博士, 副教授, 1974年生, 2012年毕业于哈尔滨工业大学, 主要从事岩土地震工程的研究工作.E-mail:zx07@yahoo.cn
摘要: 去除环境振动观测记录中的本底振动是提高信噪比、揭示交通环境振动特征的一个重要环节.本文在分析现有从交通环境振动观测记录中去除本底振动方法不足的基础上, 从考虑本底振动与观测振动互相关性出发, 提出了采用自互功率谱法去除本底振动的新方法, 推导了计算公式, 并通过实际算例论证了方法的可靠性.分析结果表明, 本文提出的自互功率谱法能够更有效地去除观测数据中的本底干扰, 获得更贴近实际的交通环境振动的功率谱、时程、振动级以及加权振级.在本底振动占优势的低频段, 本文提出的方法较现有方法计算精度有明显的提高.
关键词: 交通环境振动      本底振动      自互功率谱法      振动级     
An auto-cross PSD method to remove background vibration from observational records of traffic environment vibration
ZHENG Xin1,2,3, TAO Xia-Xin2,3, WANG Fu-Tong3,4, XIE Heng-Yan1     
1. Department of Engineering, Heilongjiang Bayi Agricultural University, Daqing Heilongjiang 163319, China;
2. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China;
3. Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, China;
4. School of Civil Engineering and Architecture, Heilongjiang University, Harbin 150001, China
Abstract: Removing background vibration from the observational records of traffic environment vibration is an important step in increasing the signal to noise ratio and demonstrating the characteristics of traffic environment vibration. In this work, the shortcomings of existing methods to resolve this task are analyzed. Then, an idea of removing the background vibration from the auto-cross spectrum was put forward, in which the cross-relativity between the background vibration and the observed vibration is considered. The calculation formula is derived and the reliability of this method is demonstrated through an example. The results show that using the auto-cross spectrum method, the background vibration in observation data can be removed more effectively, and the power spectrum, time history, vibration level and weighted level of the traffic environment vibration that are close to the real ones are obtained. In the low-frequency band dominated by background vibration, the method presented in this paper is superior to the other current methods in accuracy..
Key words: Traffic environment vibration      Background vibration      Auto-cross PSD method      Vibration level     
1 引言

在公路、轨道交通系统引起的环境振动问题的研究中, 现场实测是不可缺少的有效手段.然而, 观测获得的数据不仅包含车辆运行引起的环境振动, 还含有附近工厂机器设备产生的振动、建筑施工现场产生的振动、地脉动以及由观测设备、观测方法产生的观测误差, 此类干扰振动或误差通常称为本底振动[1-2].在现场观测数据的处理过程中, 人们总是希望把周围环境的影响降到最低, 从而突出交通运输工具运行对环境造成的影响.在距离交通线路非常近的区域本底振动的影响可以忽略, 而在距离线路较远区域必须考虑本底振动的影响[3].为了考查场地土层速度结构等因素对环境振动的影响, 必须保证若干测点与线路有一定距离, 本底振动必然对观测数据产生干扰.只有有效地清除这些干扰因素, 对实测数据进行修正, 才能对交通系统诱发的环境振动问题进行准确和客观的分析[4].

在以往的文献中, 主要有三种方法去除观测数据中本底振动的影响.文献[1]对振动级修正法[5-7]及Fourier谱幅值修正法[8]进行了文献综述, 指出了两种去除观测数据中本底振动方法的优点和不足, 进而假设交通系统引起的环境振动与其他因素引起的本底振动为相互独立的随机过程, 通过对观测功率谱密度的修正去除本底振动, 本文称之为自功率谱法.实际上, 在同一测点获得的这两部分振动不可能完全独立, 相同的场地条件会使两者具有一定程度的相关性, 导致自功率谱法在去除本底振动时会有不足.本文在此基础上, 提出一个可以考虑本底振动与观测记录之间相关性的本底振动去除的修正方法, 探讨减少本底振动带来的误差, 尤其是低频部分振动级计算偏差的可能性.

2 自互功率谱法的计算公式

观测得到的环境振动由交通的环境振动和本底振动两部分组成, 可以表达为

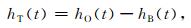
(1)

式中, hT(t)为交通系统引起的环境振动时程, hO(t)为观测记录总时程, hB(t)为本底时程. hO(t)是观测得到的, hB(t)也可以通过观测没有车辆通过时测点的振动获得.然而, 问题在于观测不是在同一时段进行的, 两个时程的时间坐标不能一一对应, hT(t)并不能通过式(1)从两者的直接相减获得.比较两个时程的功率谱之差, 并不需要时间坐标的对应, 是一个解决方案.

本底振动可视为各态历经的过程, 交通环境振动显然不是各态历经的, 本文下面的推导中不得不有所简化.

对(1)式两边做Fourier变换, 得

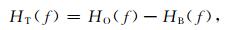
(2)

其中, H(f)表示h(t)的Fourier谱.对(2)式两边求幅值的平方, 有

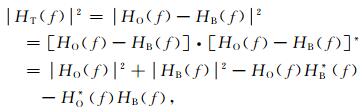
(3)

式中[·]*表示共轭, 由于HO(f)HB* (f)与HO* (f)HB(f)互为共轭, 则HO(f)HB* (f)+HO* (f)HB(f)可表示为2Re[HO(f)HB* (f)].

据此, (3)式可写成

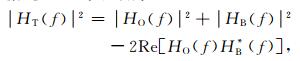
(4)

对(4)式求期望, 有

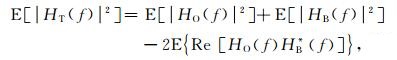
(5)

上式两边除以振动持时T得

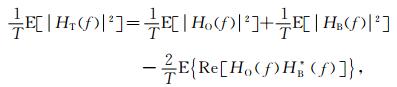
(6)

据定义, 可以写成

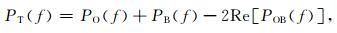
(7)

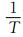
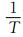
式中, P* (f)≈ E [|H* (f)|2]分别为三条时程的自功率谱密度函数, POB(f)≈ E[| HO(f)HB* (f)]为本底振动与观测振动的互功率谱密度函数. (7)式表明, 交通环境振动的功率谱可以通过观测振动的功率谱加上本底振动的功率谱, 再减去观测振动与本底振动的互功率谱实部的2倍获得.因此, 这一修正法简称为自互功率谱法[9-10].

3 方法可靠性的验证及对比分析 3.1 验证方法与算例

为了考察本文方法的可靠性, 首先取一条北京地铁13号线现场实测的加速度时程并计算其功率谱和振动级, 作为真实振动的设定曲线.另取一条同一测点在无车辆运行期间获得的加速度时程曲线作为本底振动, 两者叠加到一起生成"观测"振动数据.为了方便叙述, 三者分别简称为环境振动、本底振动和观测振动.分别计算本底振动和观测振动的功率谱和振动级, 代人(7)式, 根据自互功率谱法得到的环境振动的功率谱、时程及振动级曲线, 比较结果振动级曲线与原来计算得到作为验证依据的曲线, 可以判断本文方法的可靠性, 进一步与自功率谱法的相应结果比较, 可见两种方法修正精度的差别.

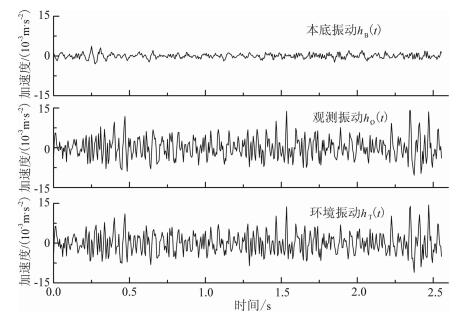
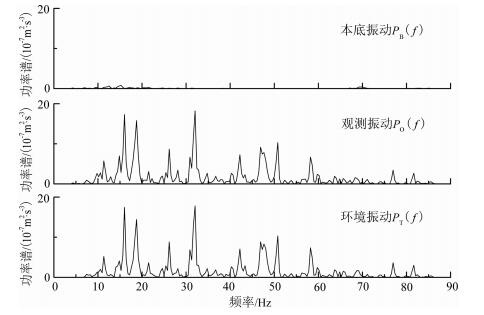
图 1展示了作为算例的加速度时程曲线, 分别为本底加速度时程hB(t), 选定的环境振动时程h′T(t)(此处加"′"是为了与去除本底振动得到的环境振动相区别), 以及两者叠加生成的观测振动时程hO (t); 图 2为相应的功率谱密度P′T(f)、PB(f)和PO(f); 图 3为本底振动与观测振动的互功率谱密度实部的曲线.

图 1 算例的时程曲线 Fig. 1 The time histories selected for back ground, observed and rail traffic caused vibrations
图 2 相应的功率谱密度曲线 Fig. 2 PSDs of the background, observed and rail traffic caused vibrations
图 3 算例中本底振动与观测振动的互功率谱密度曲线实部 Fig. 3 Setting cross-PSD of background vibration and observation vibration for calculating example

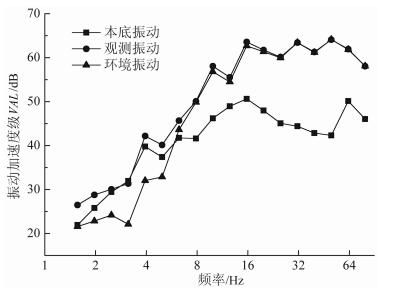
图 4为1/3倍频程中心频率处振动加速度级VAL曲线.正常人能感觉到的竖向振动为10-3m/s2, 对应的VLz是60dB, 不可忍耐的加速度是0. 5m/s2, 对应的VLz是114dB.选定时程经ISO2631/1-1985竖向计权因子处理后的振级VLz分别等于50. 63dB (本底振动)、64. 15dB(观测振动)及64. 09dB(环境振动).上述计算结果说明, 所选本底振动不会对人们的正常生活产生影响, 所选的环境振动人们能够明显感觉得到, 但尚可以忍受.

图 4 三种振动的三分之一倍频程中心频率处振动加速度级VAL Fig. 4 Vibration acceleration levels VAL of the three vibrations
3.2 计算结果与讨论 3.2.1 功率谱的比较

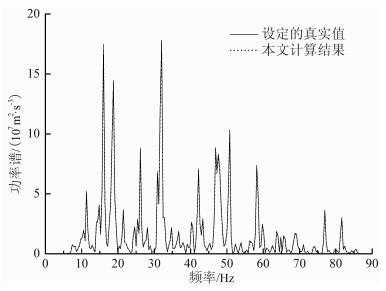
按照(7)式计算得到真实振动功率谱计算曲线PT(f)绘于图 5, 图中同时展示了图 2所示原环境振动的功率谱曲线.从中可见, PT(f)与原来的P′T(f)基本符合, 表明本文自互功率谱法去除本底振动是可靠的.

图 5 功率谱的计算曲线与设定曲线的比较 Fig. 5 Comparison of calculated PSD with its setting value

为了比较, 亦用自功率谱法计算了上述算例的环境振动功率谱.定义功率谱的绝对误差为

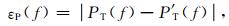
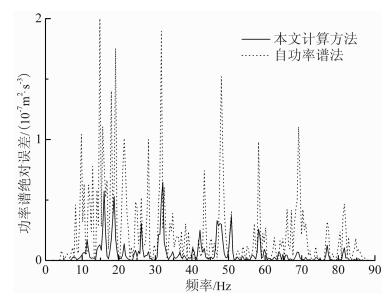
两种方法去除本底振动的结果的绝对误差如图 6所示.从图中可见, 自互功率谱法的误差明显低于自功率谱法的误差, 说明本文提出的自互功率谱法具有更好的精度.

图 6 两种方法的功率谱绝对误差 Fig. 6 The absolute errors of PSDs from the two procedures
3.2.2 时程的比较

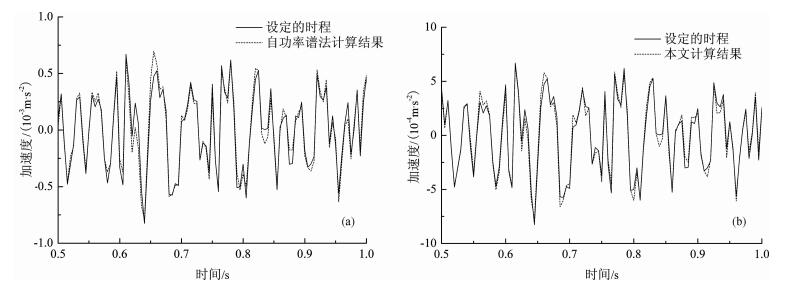
从功率谱到时程的计算需要补充相位信息.目前人们比较认同的计算时程的做法是把观测振动的相频曲线当做真实振动的相频曲线, 这对于去除交通荷载引发的环境振动记录中的本底振动来说是可行的.本文采用该方式获取相位信息. 图 7分别给出了自功率谱法与自互功率谱法计算的加速度时程, 可见两种方法的计算曲线hT(t)与设定曲线h′T(t)都很接近, 自互功率谱法的结果更靠近设定曲线.定义加速度时程的绝对误差为

图 7 两种方法得到的环境振动加速度时程 (a) 自功率谱法计算的时程结果; (b) 自互功率谱法计算的时程结果. Fig. 7 The acceleration time histories from the PSDs by the two procedures (a) Calculated by auto power spectrum approach; (b) Calculated by auto-cross power spectrum approach.

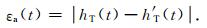
两种方法的绝对误差展示在图 8中.从中可见在大多数时间点上, 自互功率谱法的误差均显著低于自功率谱法的误差.

图 8 加速度时程计算曲线的绝对误差 Fig. 8 Time history calculating errors of PSD revising approach and auto-cross PSD revising approach
3.2.3 振动级的比较

分别根据功率谱修正法和自互功率谱法得到的功率谱计算了1/3倍频程中心频率处的振动加速度级VAL. 图 9给出了两种方法的计算结果并与振动级设定曲线进行对比. 图 9可见, 在8 Hz以上的高频部分, 三条曲线符合得非常好, 没有明显的差别, 在低频部分, 自功率谱法的误差较大, 本文自互功率谱法的结果与原来所选振动时程的振动级曲线符合得很好.

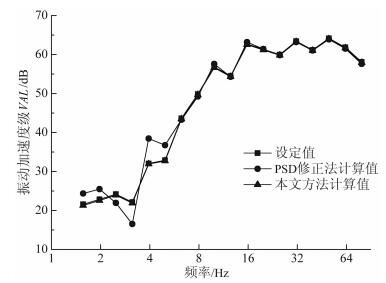
图 9 两种方法计算的振动级 Fig. 9 The calculated VALs with the present one

自功率谱法经竖向计权因子处理后的振级VLz等于63. 89dB, 本文的自互功率谱法得到的加权振级VLz等于63. 98dB, 与原值64. 09dB相比, 本文方法的计算结果显然优于自功率谱法.

4 结论

本文在自功率谱法的基础上进一步提出自互功率谱法去除交通系统引发环境振动观测数据中的本底振动, 推导了全套计算公式.将选定的车辆达到前足够长的观测记录样本和车辆通过时的观测记录样本组合为交通"环境振动"、"本底振动"和"观测记录", 论证了本文方法的可靠性.结果表明:

(1) 自互功率谱法能够有效地去除观测数据中的本底干扰, 获得真实振动的功率谱和时程曲线, 从而也能够有效地得到1/3倍频程中心频率处振动级VAL以及加权振级VLz.

(2) 由于考虑了本底振动与观测信号的相关性, 在估计实际信号的功率谱密度, 进而计算加速度振动级的计算中, 克服了功率谱修正法的不足, 尤其在本底振动占优势的低频部分可得到令人满意的结果.

参考文献
[1] 王福彤, 陶夏新, 郑鑫, 等. 交通环境振动观测中本底振动去除的功率谱修正法. 振动与冲击 , 2011, 30(4): 124–126. Wang F T, Tao X X, Zheng X, et al. PSD correction method for removing background vibration from traffic environmental vibration observation. J. Vib. Shock (in Chinese) , 2011, 30(4): 124-126.
[2] 师黎静, 陶夏新, 赵纪生, 等. 近地表速度结构的地脉动探测方法国际盲比检验. 地球物理学报 , 2009, 52(4): 1004–1013. Shi L J, Tao X X, Zhao J S, et al. International blind test of microtremors method for near-surface velocity structure exploration. Chinese J. Geophys. (in Chinese) , 2009, 52(4): 1004-1013.
[3] 谢伟平, 赵伟, 陈无平. 关于《环境影响评价技术导则:城市轨道交通》中若干问题的探讨. 华中科技大学学报(城市科学版) , 2007, 24(4): 1–4. Xie W P, Zhao W, Chen W P. Discussion of some questions in technical guidelines for environment impact assessment of urban rail transit. J. Huazhong Univ. Sci. Tech. (Urban Sci. Ed.) (in Chinese) , 2007, 24(4): 1-4.
[4] 闫维明, 聂晗, 任珉, 等. 地铁交通引起地面振动的实测与分析. 铁道科学与工程学报 , 2004, 3(2): 1–5. Yan W M, Nie H, Ren M, et al. In situ experiment and analysis of ground surface vibration induced by urban subway transit. J. Rail. Sci. Engin. (in Chinese) , 2004, 3(2): 1-5.
[5] 张昕.高架轨道交通引起环境振动的实测和理论分析研究[博士论文].上海:同济大学, 2002. Zhang X. Practical and theoretical research on the environmental vibration caused by elevated railroad traffic[Doctor's thesis](in Chinese). Shanghai:Tongji University, 2002. (in Chinese)
[6] 邱俊杰.高架轨道交通引起环境振动的实测与评价方法研究[硕士论文].武汉:武汉理工大学, 2005. Qiu J J. Practical and evaluation research on the environmental vibration caused by elevated railroad traffic[Master's thesis](in Chinese). Wuhan:Wuhan University of Technology, 2005. (in Chinese)
[7] 崔高航, 陶夏新, 陈宪麦. 城轨交通地面线路产生环境振动频域分析. 沈阳建筑大学学报(自然科学版) , 2008, 24(2): 239–243. Cui G H, Tao X X, Chen X M. Analysis of environmental vibration induced by urban rail transit on ground in frequency domain. J. Shenyang Jianzhu Univ. (Nat, Sci.) (in Chinese) , 2008, 24(2): 239-243.
[8] 张向东, 闫维明, 任珉, 等. 交通环境振动测试中的本底振动分析. 振动与冲击 , 2009, 28(4): 177–179. Zhang X D, Yan W M, Ren M, et al. Background vibration analysis for traffic environmental vibration testing. J. Vib. Shock (in Chinese) , 2009, 28(4): 177-179.
[9] 赵冲久, 韩阳. 基于自互功率谱法的高桩码头物理模型模态参数识别研究. 水道港口 , 2011, 32(5): 356–360. Zhao C J, Han Y. Structural modal parameter identification of high-piled wharf physical model based on auto-cross spectrum density method. J. Waterway Harbor (in Chinese) , 2011, 32(5): 356-360.
[10] 程兆刚, 韩保红, 张淑琴, 等. 基于环境激励下对某型运输车辆模态参数识别的研究. 煤矿机械 , 2011, 32(7): 49–51. Cheng Z G, Han B H, Zhang S Q, et al. Excitation based on certain type of environment transport vehicles identification of modal parameters. Coal Mine Machinery (in Chinese) , 2011, 32(7): 49-51.