2. 复旦大学数学科学学院, 上海 200433
2. School of Mathematical Sciences, Fudan University, Shanghai 200433, China
采用弹性动力学中的波动方程来描述地震波在地下介质中的传播过程, 具有能够利用完全的波场信息的优势, 因此一直都是地震勘探中的研究热点.如在定位地下分布的油气资源时, 一般的做法是在地面上人工激发地震波.由于介质的非均匀性, 当地震波在地层介质中向各方向传播时会产生反射、衍射、散射和透射等现象, 部分地震波返回到地面就构成了所接收的地震观测数据.地震勘探的主要工作就是基于波动方程, 从这些观测数据中, 反演出地层剖面及介质的物性参数, 进而确定地下构造, 以此作为油气勘探或工程物探的基础.从位移响应的理论合成数据应与实际测量数据相吻合的观点出发, 应用中把波动方程速度反演问题转化为非线性函数的极小值问题.
近些年, 从线性[1-2]到非线性[3-4], 从时域[5]到频域[6-7]及Laplace域[8], 从叠后反演到叠前反演[9-10], 波形反演获得了广泛研究.在实际应用中, 相比较线性地震波反演, 非线性地震波形反演更接近实际情况, 并且Mora也证明了在正常的勘探条件下, 只有采用完全非线性地震波形反演方法才能观测到地震速度波场的所有波长分量. Tarantola[3]、Mora[4]等对完全非线性波形反演进行了详细研究, 力求通过迭代下降方法, 寻求使得目标函数最小的速度模型.随后, 各类优化算法, 如最速下降法, 牛顿法, 共轭梯度法等得以应用.由于波形反演的非线性性, 使得目标函数存在大量的局部极小值, 反演结果对初值依赖较强.为了克服局部极值问题, 各类方法被讨论, 其中包括模拟退火法[11]与遗传算法[12]等统计学方法, 将多尺度思想、同伦思想与各类优化算法相结合的多种方法[13-15], 以及小波变换的多尺度方法[16]等.
由于波形反演是不适定的, 即数值结果对数据比较敏感, 而观测数据不可避免地存在噪声, 所以必须采用正则化方法求其近似解, 解决这一问题首选方法是Tikhonov正则化方法.传统的Tikhonov正则化方法选取二次罚项, 其作用在于减弱原不适定问题近似解的震荡性, 使得近似解具有一定的光滑性, 从而给出稳定的近似解.但同时也会导致解的过度光滑, 而偏离实际.然而, 在实际应用中, 常常会遇到解为不连续函数或含尖点的函数, 此时经典的正则化方法因其过度光滑的特点已不再适用, 而TV正则化[17](Totalvariationregularization)与稀疏正则化方法(Regularizationwithsparsityconstraints) (又称lp约束正则化方法(1≤p < 2))则能很好地反演出跳跃性较大的参数部分.为了更好地刻画参数的性态, 本文引入稀疏约束正则化方法.
2 稀疏约束正则化方法稀疏约束正则化方法可以看作是选取罚项为加权的lp范数, 适用于求解反演参数且具有稀疏性的反问题.所谓的"稀疏性"是指解序列大部分为零(近似为零)或者解在正交基或框架下具有稀疏表示, 即大部分系数为零(近似为零).稀疏性成为刻画解的一种方式, 特别是在压缩感知中, 应用l1约束正则化方法, 可以有效地减少采样数据, 节省存储空间, 并且通过少量的信号实现信号的准确或近似重构, 因此稀疏正则化方法在信号处理及图像去噪中获得了广泛应用[18-19], 同时在地震层析反演[20-21], 地震波阻抗反演[22]中体现了明显的优势.
2004年Daubechies等[23]给出了稀疏正则化方法与迭代伸缩算法的理论分析, 指出其用于求解反演参数且具有稀疏性的线性反问题的有效性.随后, Ramlau等[24]将稀疏约束正则化方法推广到非线性问题.对非线性不适定算子方程F(x)=y, F: X→Y, 若X, Y为序列空间(X=lp, Y=l2), 相应的稀疏约束泛函可表示为
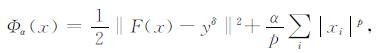
|
(1) |
当p=2时即为经典的Tikhonov正则化方法.若X为Hilbert空间, 适当地引入框架理论, 任意x∈X存在序列{φi}使x=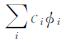
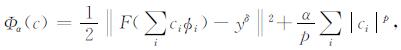
|
(2) |
其中α > 0为正则参数.同时在数值算例中指出, 随着p的减少, 近似解呈现更加稀疏的性态; 但从优化的角度考虑, 当0 < p≤1时, 罚项部分失去了凸性与零点的可微性, 因此本文的讨论限定在1 < p < 2上.
易知, 泛函(1)的极小点满足
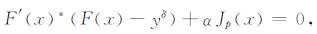
|
(3) |
其中Jp(x):=sgn(x)|x|p-1(sgn(x)为符号函数).求解方程(3)首选方法是梯度型方法, 但Wang [22]分析到普通的梯度型方法会导致混沌现象(Chaoticnature), 因此需要引入适当的投影算子.类似地, Ramlau[24]指出, 迭代伸缩算法亦可看作是一种投影算法.另一想法是, 考虑到在Banach空间(序列空间lp)中将求解梯度型方法推广为
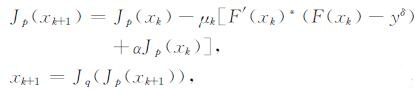
|
(4) |
这里p, q > 1为满足1/p+1/q=1的对偶对, μk为尺度参数.上式可看作是对普通的最速下降法(p=2) (又称之为Landweber方法)的推广.文献[25]对这一方法的收敛性进行了详细分析.本文将应用对偶方法(4) 求解稀疏约束泛函(1) 的极小点, 类似地, 为求解稀疏化后的约束泛函(2) , 迭代公式(3) 可写为
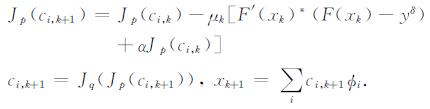
|
本文基于二维声波方程波形反演问题探讨稀疏约束正则化方法的可行性和有效性.描述地震波传播的二维声波方程的模型是
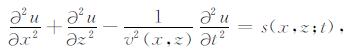
|
(5) |
其中, x, z分别是水平方向和垂直方向, z=0为地表. u(x, z, t)为质点的位移函数. s(x, z, t)为震源函数, 并且s(x, z, t)=0, t < 0. v(x, z)为介质在(x, z)处的速度.
波动方程的边界条件为
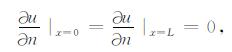
|
(6) |
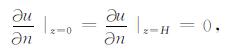
|
(7) |
初始条件为
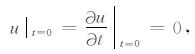
|
(8) |
这样, (5)-(8)就构成了一个声波方程的正演模型.如果加上地表的测量数据
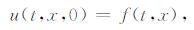
|
(9) |
就构成了确定速度v的声波方程反演问题.首先对(5)式进行数值差分离散, 即有
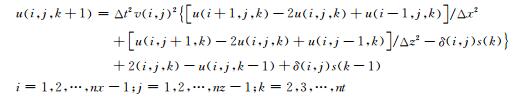
|
相应的边界条件(6), (7)式与初始条件(8)式可写为u(0, j, k)=u(1, j, k), u(nx, j, k)=u(nx-1, j, k),
j=1, 2, …, nz-1; k=2, 3, …, nt
u(i, 0, k)=u(i, 1, k), u(i, nz, k)=u(i, nz-1, k),
i=1, 2, …, nx-1; k=2, 3, …, nt
u(i, j, 0)=u(i, j, 1)=0, i=1, 2, …, nx;
j=1, 2, …, nz
其中nx, nz分别为矩形剖分在x, z方向的网格个数, nt为时间间隔个数, Δx, Δz, Δt分别为空间、时间网格上的剖分步长, 
记v=v(i, j), 为待反演的速度模型, y=u(i, 1, k) (i=1, 2, …, nx-1, k=2, 3, …, nt)为观测数据, 用F表示模型空间到数据空间的映射, 即离散正演算子, 则通常的地震勘探反演问题可描述为有限维非线性算子方程:
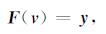
|
(9) |
本节将考虑孔洞和分层两类不同模型, 应用对偶方法进行数值模拟, 以验证稀疏约束正则化方法的有效性.算例1与算例2记录了当模型本身为稀疏时稀疏约束正则化方法的反演结果; 当模型为不稀疏时, 先应用小波变换对其进行稀疏化处理, 再应用稀疏约束正则化方法反演, 如算例3、4与5.
在数值模拟中, 选取空间范围为800m×800m, 空间间隔Δ x=Δz=40 m, 时间采样间隔为Δt=0. 004s, 震源子波选取最常用的雷克(Ricker)子波.其数学表达式为
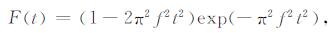
|
其中, f=60Hz为子波主频.
为了测试稀疏正则化方法的抗噪能力, 分别对模型1-3添加1%的随机噪声, 对模型4与模型5添加25%的随机噪声.在求解稀疏约束的优化问题中, 应用对偶方法(4)式, 选取背景值v0=2800作为反演的初值, 正则参数为
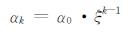
|
其中, ξ∈ (0, 1), α0=10-3.选取迭代的停止准则为广义偏差原则, 即
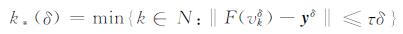
|
其中, k*为迭代步数, τ >1, 具体值可依靠经验选取.本文在算例1、2中选取τ=1. 3, 算例3~5中选取τ=3.
为了比较算法精度, 定义相对误差为
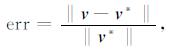
|
这里v为反演结果, v*为真实值, 其中范数皆为l2范数.
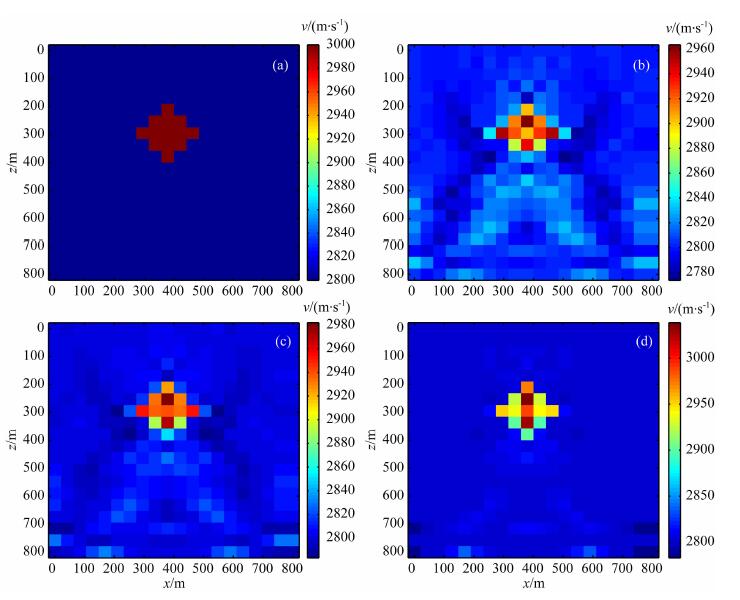
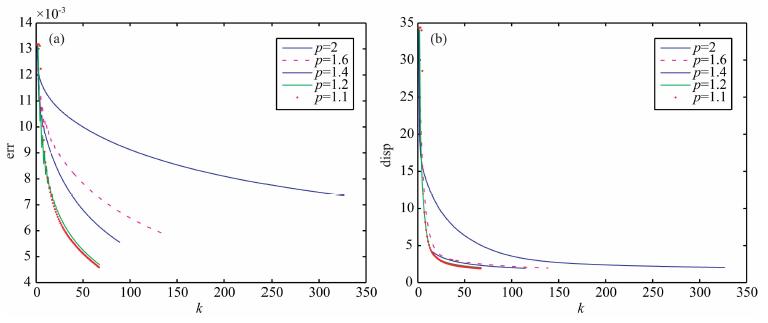
4.1 孔洞模型反演结果算例1:真实模型如图 1a所示, 在对偶方法中, 选取不同的p值(2, 1. 6, 1. 2), 得到的反演结果分别如图 1(b, c, d)所示.结果表明, 随着p的减少, 稀疏约束正则化方法可以获得更稀疏的解, 这与稀疏约束正则化方法的预期是一致的. 表 1记录了不同p相应的迭代步数k*, CPU运行时间T(s)及近似解与真解的相对误差err的计算结果; 具体的相对误差(err)及偏差(disp=‖F(vkδ)-yδ‖)的变化情况可见图 2(a, b), 不难看到随着p的减少, 在迭代误差与计算效率上, 稀疏约束正则化方法都呈现一定的优势.
|
图 1 算例1 (a) 真实模型速度; (b) Landweber方法(p=2)的反演结果; (c) p=1. 6对偶方法的反演结果(d) p=1. 2的对偶方法的反演结果. Fig. 1 Model 1 (a)Velocity of the real model; (b)Inversion result of Landweber method (p=2); (c) Inversion result of dual method with p=1.6; (d) Inversion result of dual method with p=1.2. |
|
|
表 1 算例1的数值结果 Table 1 The numerical results of model 1 |
|
图 2 算例1的相对误差(a)与偏差(b) Fig. 2 The relative error (a) and the discrepancy (b) of Model 1 |
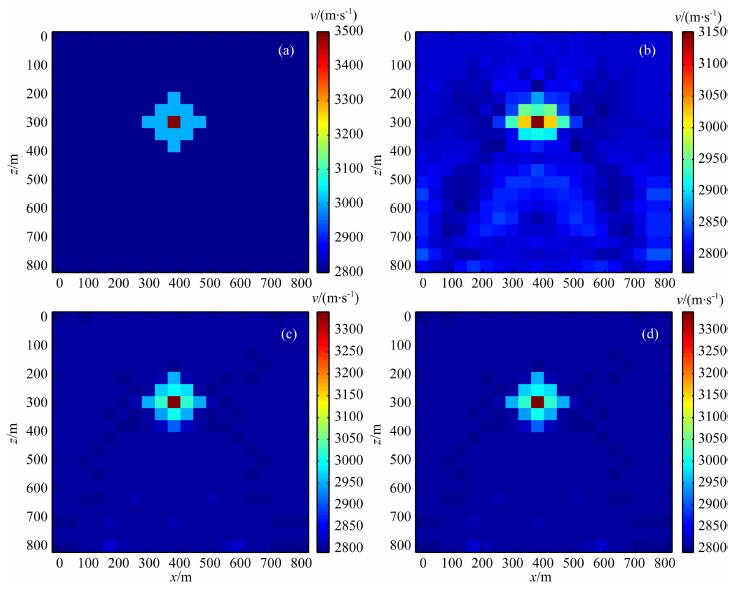
算例2:考虑更复杂的介质, 真实模型如图 3a所示, 在对偶方法中, 选取不同的p值(2, 1. 2, 1. 1), 得到的结果如图 3(b, c, d)所示.结果表明, 对比经典方法, 稀疏约束正则化方法反演效果要好的多.
|
图 3 算例2 (a) 真实模型速度; (b) Landweber方法(p=2)的反演结果; (c) p=1. 2对偶方法的反演结果; (d) p=1. 1的对偶方法的反演结果. Fig. 3 Model 2 (a) Velocity of the real model; (b) Inversion result of Landweber method (p=2); (c) Inversion result of dual method with p=1. 2; (d) Inversion result of dual method with p=1. 1. |
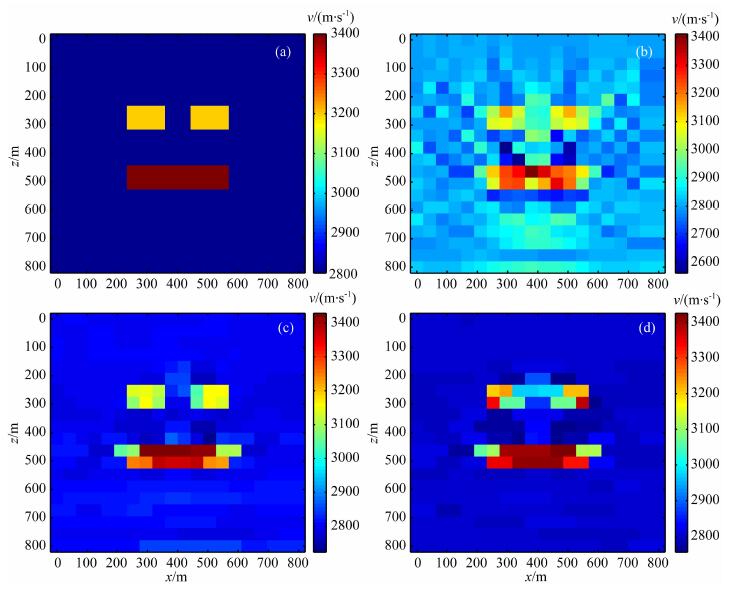
算例3:选取真实模型如图 4a所示, 应用尺度为4的Haar小波对其进行稀疏化, 再利用对偶方法, 选取不同的p值(2, 1. 2, 1. 1)进行求解, 结果如图 4(b, c, d)所示.结果表明, 对比经典方法, 稀疏约束正则化方法反演效果要清晰得多.但是可以注意到, 当p减少到一定程度时, 反演结果会过度稀疏化, 即出现能量集中的现象, 导致某些网格点反演值偏高.因此导致了p=1. 1时的计算结果反不如p=1.2好.为此, 记录选取不同的p值相应的小波系数重构情况, 如图 5所示, 其中横坐标代表小波系数指标i, 纵坐标表示小波系数值.首先可以看到, 应用小波分解获得的小波系数的确是稀疏的; 其次对比真实模型的小波系数值(实线)与近似解的小波系数值(星号), 随着p的减少, 重构系数确实呈现更稀疏的性态; 特别注意的是的当p=1.1时, 重构的小波系数确实更稀疏了, 但是真实模型的小波系数却没那么稀疏, 即称为过度稀疏的现象, 因此参数p需适当选取; 从另一角度, 也可以认为经小波变换后的小波系数不够稀疏, 因此为了获得更稀疏系数, 如何选择适当的框架或基底, 也是我们进一步考虑的问题.
|
图 4 算例3 (a) 真实模型速度; (b) Landweber方法(p=2)的反演结果; (c) p=1. 2对偶方法的反演结果; (d) p=1. 1的对偶方法的反演结果. Fig. 4 Model 3 (a) Velocity of the real model; (b) Inversion result of Landweber method (p=2); (c) Inversion result of dual method withp=1.2; (d) Inversion result of dual method with p=1. 1. |

|
图 5 算例3的小波系数结果 (a) p=2的反演系数结果; (b) p=1. 3的反演系数结果; (c) p=1. 2的反演系数结果; (d) p=1. 1的反演系数结果. Fig. 5 The wavelet coefficient of Model 3 (a) The wavelet coefficient of inversion with p=2; (b) The wavelet coefficient of inversion with p=1.3; (c) The wavelet coefficient of inversion with p=1.2; (d) The wavelet coefficient of inversion with p=1. 1. |
考虑分层模型, 真实模型如图 6a, 7a所示, 此时模型不稀疏, 为了稀疏化本文应用小波变换对其进行稀疏化处理, 选取尺度为4的Haar小波.

|
图 6 算例4 (a)真实模型速度; (b)Landweber方法(p=2)的反演结果; (c)p=1. 4对偶方法的反演结果; (d)p=1. 2对偶方法的反演结果. Fig. 6 Model 4 (a) Velocity of the real model; (b) Inversion result of Landweber method (p=2); (c) Inversion result of dual method withp=1. 4; (d) Inversion result of dual method with p=1. |
|
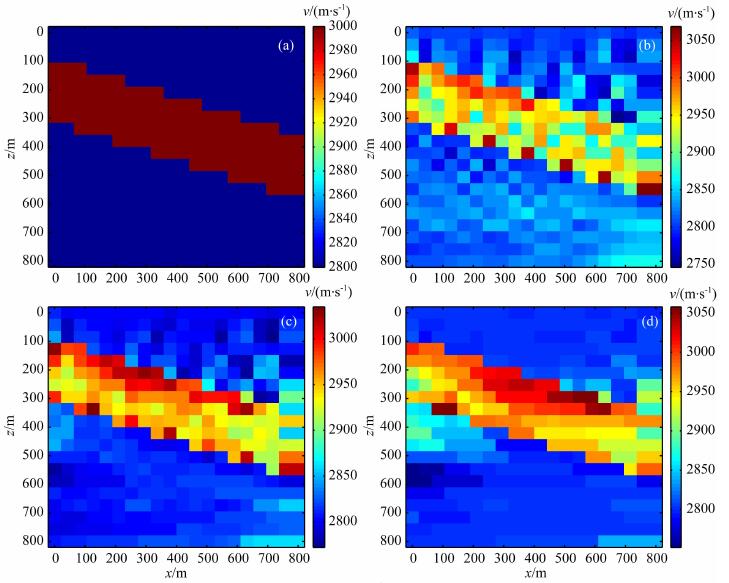
图 7 算例5 (a) 真实模型速度; (b) Landweber方法(p=2)的反演结果; (c) p=1. 6对偶方法的反演结果; (d) p=1. 2对偶方法的反演结果. Fig. 7 Model 5 (a) Velocity of the real model; (b) Inversion result of Landweber method (p=2); (c) Inversion result of dual method with p=1.6; (d) Inversion result of dual method with p=1.2. |
算例4:在对偶方法中, 选取不同的p值(2, 1. 4, 1. 2), 结果如图 6(b, c, d)所示.
算例5:在对偶方法中, 选取不同的p值(2, 1. 6, 1. 2), 结果如图 7(b, c, d)所示.
综合图 4与图 5的反演结果, 可见对比经典Landweber方法, 随着p的减少, 对偶方法对不连续介质模型的边缘具有良好的识别能力.
5 结语完全的地震波形反演问题本质上是非线性的, 在反演过程中经常会遇到介质不规则或不连续的情况, 而应用传统的Tikhonov正则化方法又会出现解过度光滑现象, 从而使反演结果失效.为此, 本文引入了非线性稀疏约束正则化方法, 将其应用于二维声波方程波形反演问题.数值结果表明, 在稀疏约束正则化方法中, 随着p的减少, 反演结果会呈现更稀疏的性态, 且对非连续介质模型的边缘具有更好的识别能力.这项试验无疑是有实际意义的, 下一步我们将尝试将这一理论应用到更复杂的地震波形反演问题中.同时, 从稀疏约束泛函来看, 当p逐渐减少时, 罚项部分凸性变弱, 我们有理由怀疑此时对偶方法的收敛域变小, 因此如何克服局部极小值问题, 仍需进一步探讨.
| [1] | Tarantola A. Linearized inversion of seismic reflection data. Geophysical Prosp. , 1984, 32(6): 998-1015. DOI:10.1111/gpr.1984.32.issue-6 |
| [2] | Berkhout A J. Multidimensional linearized inversion and seismic migration. Geophysics , 1984, 49(11): 1881-1895. DOI:10.1190/1.1441601 |
| [3] | Tarantola A. A strategy for nonlinear elastic inversion of seismic reflection data. Geophysics , 1986, 51(10): 1983-1903. |
| [4] | Mora P. Nonlinear two-dimensional elastic inversion of multioffset seismic data. Geophysics , 1987, 52(9): 1211-1228. DOI:10.1190/1.1442384 |
| [5] | Zhou C X, Cai W Y, Luo Y, et al. Acoustic wave equation traveltime and waveform inversion of cross hole seismic data. Geophysics , 1995, 60(3): 765-773. DOI:10.1190/1.1443815 |
| [6] | Pratt R G, Shin C, Hicks G J. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion. Geophysical Journal International , 1998, 133(2): 341-362. DOI:10.1046/j.1365-246X.1998.00498.x |
| [7] | Shin C, Min D J. Waveform inversion using a logarithmic wavefield. Geophysics , 2006, 71(3): R31-R42. DOI:10.1190/1.2194523 |
| [8] | Shin C, Cha Y H. Waveform inversion in the Laplace domain. Geophysical Journal International , 2008, 173(3): 922-931. DOI:10.1111/gji.2008.173.issue-3 |
| [9] | Xu T, McMechan G A, Sun R. 3-D prestack full-wavefield inversion. Geophysics , 1995, 60(6): 1805-1818. DOI:10.1190/1.1443913 |
| [10] | 苑书金. 叠前地震反演技术的进展及其在岩性油气藏勘探中的应用. 地球物理学进展 , 2007, 22(3): 879–886. Yuan S J. Progress of pre-stack inversion and application in exploration of the lithological reservoirs. Progress in Geophysics (in Chinese) , 2007, 22(3): 879-886. |
| [11] | Sen M K, Stoffa P L. Nonlinear one-dimensional seismic waveform inversion using simulated annealing. Geophysics , 1991, 56(10): 1624-1638. DOI:10.1190/1.1442973 |
| [12] | Stoffa P L, Sen M K. Nonlinear multi-parameter optimization using genetic algorithms inversion of plane-wave seismograms. Geophysics , 1991, 56(11): 1794-1810. DOI:10.1190/1.1442992 |
| [13] | Bunks C, Saleck F M, Zaleski S, et al. Multiscale seismic waveform inversion. Geophysics , 1995, 60(5): 1457-1473. DOI:10.1190/1.1443880 |
| [14] | 傅红笋, 韩波. 二维波动方程速度的正则化-同伦-测井约束反演. 地球物理学报 , 2005, 48(6): 1441–1448. Fu H S, Han B. A regularization homotopy method for the inverse problem of 2-D wave equation and well log constraint inversion. Chinese J. Geophys (in Chinese) , 2005, 48(6): 1441-1448. |
| [15] | Han B, Fu H S, Liu H. A homotopy method for well-log constraint waveform inversion. Geophysics , 2007, 72(2): R1-R7. |
| [16] | 孟鸿鹰, 刘贵忠. 小波变换多尺度地震波形反演. 地球物理学报 , 1999, 42(2): 241–248. Meng H Y, Liu G Z. Multiscale seismic waveform inversion by wavelet transform. Chinese J. Geophys (in Chinese) , 1999, 42(2): 241-248. |
| [17] | 陈勇, 韩波, 肖龙, 等. 多尺度全变分法及其在时移地震中的应用. 地球物理学报 , 2010, 53(8): 1883–1892. Chen Y, Han B, Xiao L, et al. Multiscale total variation method and its application on time-lapse seismic. Chinese J. Geophys (in Chinese) , 2010, 53(8): 1883-1892. |
| [18] | Donoho D L. Superresolution via sparsity constraints. SIAM J. Math. Anal. , 1992, 23(5): 1309-1331. DOI:10.1137/0523074 |
| [19] | Candes E, Romberg J, Tao T. Stable signal recovery from incomplete and inaccurate measurements. Comm. Pure Appl. Math. , 2006, 59(8): 1207-1223. DOI:10.1002/(ISSN)1097-0312 |
| [20] | Loris I, Douma H, Nolet G, et al. Nonlinear regularization techniques for seismic tomography. J. Comput. Physics. , 2010, 229(3): 890-905. DOI:10.1016/j.jcp.2009.10.020 |
| [21] | Jafarpour B, Goyal V K, Laughlin D B, et al. Transform-domain sparsity regularization for inverse problems in geosciences. Geophysics , 2009, 74(5): R69-R83. DOI:10.1190/1.3157250 |
| [22] | Wang Y F. Seismic impedance inversion using l1 norm regularization and gradient descent methods. J. Inv. Ill-Posed Problems , 2011, 18: 823-838. |
| [23] | Daubechies I, Defrise M, Mol C D. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Comm. Pure Appl. Math. , 2004, 57(11): 1413-1457. DOI:10.1002/(ISSN)1097-0312 |
| [24] | Ramlau R, Teschke G. A projection iteration for nonlinear operator equations with sparsity constraints. Numer. Math. , 2006, 104(2): 177-203. DOI:10.1007/s00211-006-0016-3 |
| [25] | Kaltenbacher B, Schopfer F, Schuster T. Iterative methods for nonlinear ill-posed problems in Banach spaces:convergence and applications to parameter identification problems. Inverse Problems , 2009, 25(6): 065003. DOI:10.1088/0266-5611/25/6/065003 |
 2013, Vol. 56
2013, Vol. 56


