地球物理学报  2013, Vol. 56 Issue (1): 280-288   PDF    
引用本文
朱生旺, 李佩, 宁俊瑞. 局部倾角滤波和预测反演联合分离绕射波. 地球物理学报, 2013, 56(1): 280-288, doi: 10.6038/cjg20130129.  
Zhu S W, Li P, Ning J R. Reflection/diffraction separation with a hybrid method of local dip filter and prediction inversion. Chinese J. Geophys. (in Chinese), 2013, 56(1): 280-288, doi: 10.6038/cjg20130129.  
局部倾角滤波和预测反演联合分离绕射波
朱生旺 , 李佩 , 宁俊瑞     
中国石油化工股份有限公司石油勘探开发研究院, 北京 100083
收稿日期 2011-10-24, 2012-11-26 收修定稿
基金项目: 国家重点基础研究发展计划(973)课题"碳酸盐岩缝洞型油藏缝洞单元地球物理表征研究"(2011CB201002)及重大专项课题"缝洞储集体识别与描述技术研究"(2011ZX05014-001)联合资助
作者简介: 朱生旺, 男, 1962年生, 教授级高级工程师, 现从事油气地球物理科研工作.E-mail:zhusw.syky@sinopec.com; zhusw@pepris.com
摘要: 地震绕射波源于介质非连续性, 从地震记录中将绕射波分离出来并进行成像, 其结果对研究诸如碳酸盐岩缝洞储层这类复杂非均质储层具有重要意义.对炮集记录进行平面波分解, 在地层倾角不大的假设下, 反射波和绕射波同相轴在平面波分解剖面上存在较大的倾角差异.基于此, 我们提出分步进行绕射波分离的方法:(1)利用局部倾角滤波方法将绕射波的较大倾角信息成分分离出来, 此时, 余下的部分包含有反射波和残留的低倾角绕射波信息; (2)利用频率-空间域预测反演方法从上述含有反射波和残留的低倾角绕射波信息中分离出残留绕射波成分; (3)将两次分离的绕射波信息相加得到最终的绕射波估计.用该方法能够得到相对完整的绕射波信息, 有效地克服了靠单一的倾角差异进行绕射波分离时明显损失低倾角信息, 从而影响绕射波成像结果横向分辨率这一问题.理论与实际资料试算验证了该方法的有效性.
关键词: 绕射波分离      倾角滤波      预测反演      分辨率     
Reflection/diffraction separation with a hybrid method of local dip filter and prediction inversion
ZHU Sheng-Wang, LI Pei, NING Jun-Rui     
Petroleum Exploration and Production Research Institute, SINOPEC, Beijing 100083, China
Abstract: It is of great significance to separate seismic diffractions from seismic data and apply the imaged results of these separated diffractions to the research of some complicated reservoirs, the karst reservoir for example. On the planar decomposition section, the dip difference between specular reflection events and diffraction events is remarkable in the case that the dips of reflection interfaces are small. Based on the above facts, we propose a hybrid method for diffraction separation: (1) We divide each planar decomposition section into two portions by local dip filtering: the portion d1 mainly containing diffraction information with high dip and the portion containing the specular reflection r and residual diffraction information with low-dip (d2); (2) The separation of specular reflection r and residual diffraction information d2 from obtained in step (1) is conducted by prediction inversion in F-X domain; (3) d2 added to d1 makes the estimation of diffractions. This separation method can get relatively complete diffraction information, which effectively avoids the problem appearing in the general filter methods based only on dip attribute that low dip portion of diffraction is lost and thus narrowing the spatial bandwidth of the diffraction which will damage the lateral resolution. The feasibility of the proposed method is proven by both theoretical and real data tests..
Key words: Diffraction separation      Dip filter      Prediction inversion      Resolution     
1 引言

在反射地震数据中, 绕射波是反映地下介质非连续性的重要信息, 对于断裂和地质异常体的解释, 特别是针对碳酸盐岩缝洞储层这类复杂非均质储层的认识, 要求地震资料处理中保护绕射波信息并使其精确成像是十分重要的.

如何有效利用绕射波信息来反映地下介质的横向变化, 前人已做过很多研究和尝试, 如:Landa等[1]根据绕射波运动学特性, 提出通过相关来增强绕射点位置的地震信号振幅, 以探测局部非均质异常体的方法; Pozdnyakov[2]提出的估计散射强度属性的聚焦变换法; Khaidukov[3]提出的聚焦-去焦(focusing-defocusing)绕射成像方法, 等等.在实际中反映局部地质异常或储层的绕射波信息通常淹没在强反射信息中, 因此人们又提出直接从叠前数据中分离出绕射波并单独对其进行偏移成像, 目的是使成像结果能够凸显非均质地质体的边界和形体, 从而帮助更准确地预测与认识储层.如Nowak等[4]尝试了从地震记录中分离绕射波的方法, 即利用炮集记录中反射波与绕射波同相轴轨迹的几何差别, 通过双曲线Radon变换, 将绕射波从地震记录中分离出来.

实际上, 绕射与反射没有明确的界限, 因此很难从反射记录中严格地将绕射波分离出来.进行绕射波分离只能是加强源于横向非连续性的反射信息, 而压制连续反射界面的反射信号.提取绕射波信息的方法基本上是传统的信号分离方法, 假设反射界面倾角不大, 这样在一定的道集(如共偏移距道集)或某些变换结果(如平面波分解结果)上绕射波与反射波同相轴存在较大的倾角差异, 依此实现反射与绕射主要信息的分离.Reeshidev[5]总结了增强绕射波的几种方法, 包括分别在炮点和检波点域压制正向散射能量的双滤波、共偏移距道集上的倾角滤波、特征向量滤波、Harlan信噪分离[6]等方法, 这些方法有各自的优势和局限性; Sergey [7]给出了平面波去反射滤波, 也就是利用倾角差异压制反射波的局部倾角滤波方法, 该方法的最大优点是局部适应性好, 但要求输入数据要有较高信噪比, 因此适合在平面波分解结果上应用; M.Turhan Taner[8]利用Sergey的方法给出了绕射波分离的理论算例.

分离出的绕射波信息的完整性直接影响绕射波成像结果的质量.即使假设反射波是来自接近水平的低倾角界面, 我们仍不能通过单一的倾角滤波方法分离出相对完整的绕射波信息, 这是由于在低倾角附近, 绕射波与反射波不能由同相轴倾角区分.因此, 基于倾角差异的分解方法都普遍存在低倾角绕射波信息失真或缺失问题.低倾角信息缺损使空间有效带宽变窄, 这将导致绕射波成像结果横向分辨率降低.为了弥补绕射波分离结果的带宽损失, 我们提出局部倾角滤波和频率-空间域预测反演联合的绕射波分离方法, 其实现步骤是:(1)对单炮记录进行平面波分解, 并经过数据重排得到对应不同斜率参数的剖面; (2)对每一个共斜率剖面用平面波滤波方法实现局部倾角滤波, 提取绕射波高倾角信息成分, 并对剔除高倾角成分后的数据通过预测反演得到绕射波的低倾角信息成分; (3)将提取的绕射波高、低倾角信息相加得到最终绕射波估计; (4)进行平面波合成和数据重排得到绕射波炮集数据.理论试算结果表明, 这种绕射波分离方法能比较有效地克服靠单一的倾角差异进行绕射波分离时损失低倾角信息这一问题, 所得到的绕射信息相对完整, 从而使绕射波成像结果有较高的横向分辨率.

在塔河碳酸盐岩缝洞发育区, 孔洞结构与分布复杂, 孔洞尺度不一、填充物多样性、几何形状不规则、空间变化剧烈, 其大小、充填、形态同绕射波特征有着密切的联系[9], 将地震波场中的绕射波分离出来单独成像, 有利于提高缝洞的识别精度, 将本文提出的绕射波分离方法应用在塔河地区, 压制了风化壳的强反射能量, 突出了缝洞的串珠信息, 其成像结果能够更好地识别缝洞.

2 方法原理

绕射波与反射波的一个显著差异是时距曲线的不同, 地面地震记录中的绕射时距曲线由双平方根方程描述, 而反射时距曲线为双曲线.这种时距关系上的差异反映在平面波域是, 在平面波分解(τ-p)域的共斜率(p)剖面上, 绕射波同相轴能量大部分包含在高倾角信息成分中[8].因此, 假设反射界面倾角较小, 则在τ-p域的共p剖面上, 反射波与绕射波同相轴存在较大的倾角差异, 二者具有较好的可分离性.

将地震炮记录变换到τ-p域, 用sp(x, τ)表示斜率为p的共p剖面, 这里x为炮点地面坐标.设sp(x, τ)中反射波同相轴的时间倾角(相邻道时差)在(-σm, σm)范围内, 则通过局部倾角滤波可将sp(x, τ)分解为两部分, 即

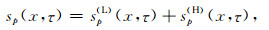
(1)

这里, sp(H)(x, τ)表示滤除时间倾角在(-σm, σm)范围之内的同相轴后的信息, 由于假设反射波同相轴的时间倾角在(-σm, σm)范围内, 故sp(H)(x, τ)可作为绕射波的高倾角(时间倾角在(-σm, σm)之外)信息成分dp(H)(x, τ)的估计, 即

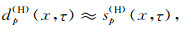
(2)

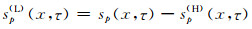
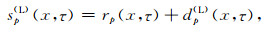
而则包含反射波rp(x, τ)以及绕射波的低倾角(时间倾角在(-σm, σm)范围内)信息成分dp(L)(x, τ), 即

(3)

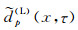
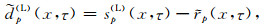
sp(L)(x, τ)中的反射波rp(x, τ)在空间上应具有较好的连续性, 而dp(L)(x, τ)可视为振幅异常.换言之, 在频率-空间域, rp(x, τ)具有近似线性预测关系, 而dp(L)(x, τ)则表现为不可预测的噪声.因此, 利用频率-空间域的线性预测关系可以由sp(L)(x, τ)得到rp(x, τ)的估计珘rp(x, τ), 进而得到dp(L)(x, τ)的估计结果, 即

(4)

最后, 由

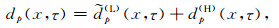
(5)

给出共p剖面上的绕射波分离结果.

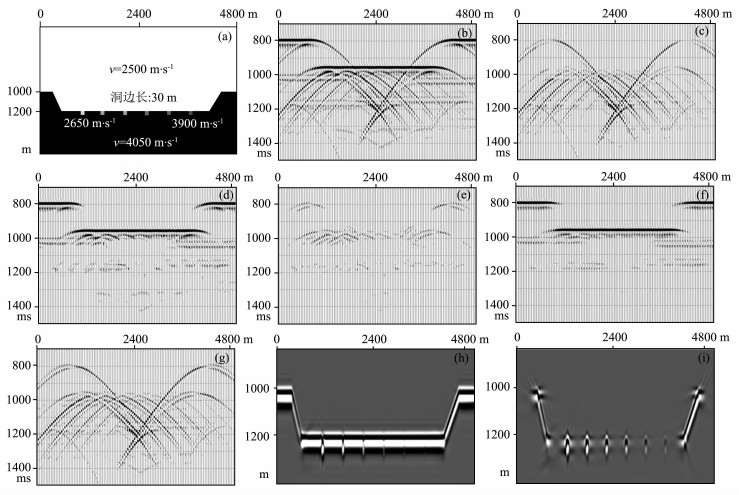
现用理论模型数据来说明上述方法的实现过程.在图 1中, (a)为生成基于声波方程的数值模拟数据的速度模型; (b)为平面波分解的共倾角剖面; (c)为从(b)中分离出的绕射波高倾角成分, 即dp(H)(x, τ); (d)为(b)与(c)相减的结果, 即sp(L)(x, τ); (e)为从(d)中分离出的绕射波低倾角成分, 即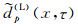; (f)为(d)与(e)相减的结果, 即反射波估计; (g)为(c)与(e)相加得到的最终绕射波分离结果dp(x, τ); (h)为原始数据的深度偏移剖面; (i)为分离出的绕射波的深度偏移剖面.从该模型数据处理结果可以看到, 分离出的绕射波信息相对完整, 与原始数据成像剖面比较, 在分离出的绕射波成像剖面上, 连续界面的反射波得到压制后, 洞的反射变得清晰.

图 1 绕射波分离过程与结果 (a)速度模型; (b)平面波分解的共倾角剖面; (c)用倾角滤波方法从(b)中分离出的绕射波高倾角成分; (d)(b)与(c)相减的结果; (e)用预测反演方法从(d)中分离出的绕射波低倾角成分; (f)(d)与(e)相减的结果; (g)(c)与(e)相加得到的最终绕射波分离结果; (h)原始数据的深度偏移剖面; (i)分离出的绕射波的深度偏移剖面. Fig. 1 A theoretical model example of diffraction separation (a)Velocity model; (b)Planar decomposition section; (c)High-dip diffraction data separated from(b)by local dip filtering; (d)Result of subtracting (c) from (b); (e)Low-dip diffraction data using prediction inversing; (f)Result of subtracting (e) from (d); (g)Result of adding (e) to (c); (h)PSDM result of original data; (i)PSDM result of diffraction data.

下面给出绕射波高、低倾角成分提取的具体方法.

2.1 局部倾角滤波及绕射波高倾角信息提取

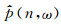
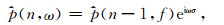
采用去平面波滤波方法实现局部倾角滤波, 进行绕射波高倾角信息提取.在频率-空间域, 相邻道间时差为σ的二维平面波信号满足关系

(6)

式中, n为道序下标, ω为角频率.Sergey(2002)给出了时移算子eiωσ的时间域近似TSσ(Zt)如下:

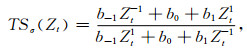
(7)

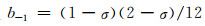
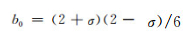
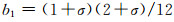
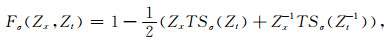
这里, , , .显然, 利用(7)式进行时移运算可采用计算效率很高的追赶法.由式(6)、(7)可构建时空域局部倾角滤波的二维滤波器

(8)

滤波器Fσ(Zx, Zt)可用于消除输入数据中时间倾角为σ的信息成分.

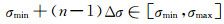
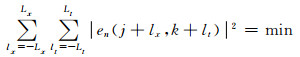
进行局部倾角滤波, 首先要给出倾角值, 信号倾角σ由倾角扫描得到.记sp(x, τ)的离散形式为sp(j, k), 这里k、j分别为时间和空间离散采样下标.设信号倾角σmin≤σ≤σmax, 给定倾角扫描增量Δσ和时、空方向上的扫描时窗长度Lt、Lx.取σn=, en(j, k)为用Fσn (Zx, Zt)对sp(j, k)作滤波的结果, 则由使

(9)

成立的n确定sp(j, k)的局部倾角σn(j, k).

式(9)是单倾角扫描方法, 可扩展到双倾角扫描, 以估计可能存在的两个不同的信号倾角.设enm(j, k)为用Fσn (Zx, Zt)Fσm (Zx, Zt)对sp(j, k)作滤波的结果, 则由使

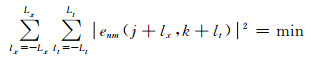
(10)

成立的n、m确定sp(j, k)的两个局部倾角σn(j, k)和σm(j, k).双倾角扫描计算量较大, 为提高计算效率, 可由单倾角扫描得到双倾角中主信号倾角的估计值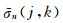, 然后以为中心, 缩小主倾角扫描范围.

有了sp(j, k)的局部倾角参数σ(j, k), 则在反射波同相轴的时间倾角限于(-σm, σm)范围内的假设下, 由

(11)

即得到绕射波的高倾角信息成分的估计, 这里Fσ是由(8)式给出的局部倾角滤波器.

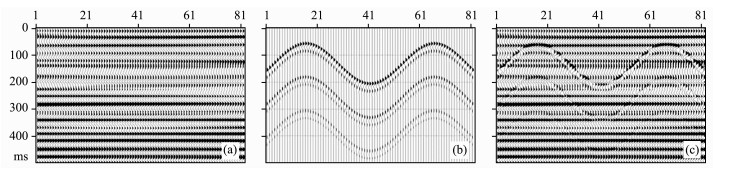
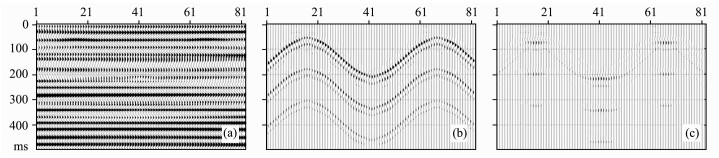
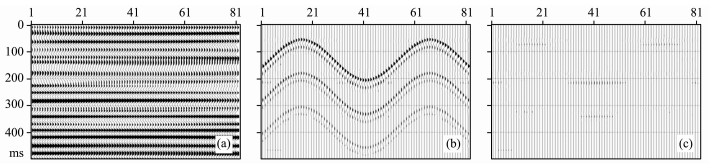
滤波器(8)用于分离不同时间倾角的信号具有良好的效果, 现给出一个用上述方法进行倾角分离的理论数据算例.图 2是一理论数据, 其中(a)为振幅在空间上渐变的一组水平同相轴, (b)为振幅不变的三组正弦波形状的弯曲同相轴, (c)是(a)与(b)叠加的结果.用上述的局部倾角滤波方法对(c)进行水平同相轴和弯曲同相轴分离, 其结果如图 3所示. 图 3a是分离出的水平同相轴信息, 图 3b是分离出的弯曲同相轴信息, 图 3c是图 3b与图 2b之差, 即分离误差.从结果可看到, 水平与弯曲同相轴的大部分能量都得到了较好的分离, 特别是在两组同相轴倾角差较大时, 分离精度较高.

图 2 含水平和弯曲同相轴的合成记录 (a)水平同相轴成分; (b)弯曲同相轴成分; (c)(a)与(b)叠加的结果. Fig. 2 Synthetic seismogram containing aclinal and flexural events (a) Aclinal events; (b) Flexural events; (c) Result of adding (b) to (a).
图 3 采用局部倾角滤波方法的水平和弯曲同相轴分离结果 (a)分离出的水平同相轴成分; (b)分离出的弯曲同相轴成分; (c)分离出的弯曲同相轴成分与真实结果(图 2b)之差. Fig. 3 Results of local dip filtering (a) Aclinal events; (b) Flexural events; (c) Difference between Fig.3 band Fig.2b.
2.2 预测反演及绕射波低倾角信息提取

即使是假设反射界面倾角较小, 依靠局部倾角滤波也仅能获得绕射波同相轴高倾角部分信息, 而绕射波同相轴顶点附近的低倾角能量不能由反射波与绕射波同相轴的倾角差异进行分离.在共p剖面上, 剔出高倾角信息成分后的绕射波的残留低倾角信息dp(L)(x, τ)以孤立的振幅异常与反射波叠加在一起, 在频率-空间域, 利用反射波的线性可预测性可以把这种残留的绕射波低倾角信息提取出来, 将其加入到通过局部倾角滤波得到的绕射波高倾角信息成分中, 就能够得到相对完整的绕射波信息估计.

根据傅里叶理论我们知道, 时空域的任何信号都能由该域上的有限个数(N个)的平面波信号叠加来逼近, 这里需要的N越大, 则反映信号在空间上的变化越剧烈.N个平面波的叠加结果在频率空间域上具有线性预测关系, 且预测算子长为N.频率空间域的预测算子长度和预测滤波误差反映信号在空间上的复杂程度, 因此, 信号的连续性可用线性可预测性来反映.在频率空间域, 反射波一般具有较强的线性可预测性, 不可预测的成分可认为是非反射的局部异常信息.

将(3)式变换到频率空间域, 得

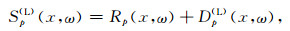
(12)

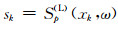
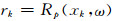
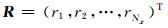
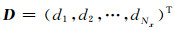
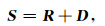
对给定的频率ω, 记, S=(s1, s2, …, sNx)T, , , dk=D (L) p(xk, ω), , 这里Nx为一个计算窗在空间方向上的道数.则有

(13)

设pl(l=1, …, L)为S的线性预测算子, 其由极小化目标函数

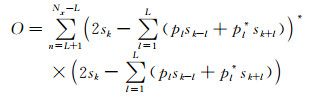
(14)

得到, 这里*表示复共轭.用算子pl(l=1, …, L)对S作滤波可得到R的估计, 再由D=S-R即得到局部异常信息D的估计, 这就是通常的异常信息估计的预测滤波方法.预测滤波方法最大的缺陷是局部异常能量向邻近道泄漏, 使得异常信息估计精度不高, 鉴于此, 我们提出一种更有效的反演方法.

记Nx×Nx矩阵

对于待求的反射波R, 一方面要求其要尽可能满足线性预测关系, 另一方面又要与输入S接近, 因此, 取目标函数

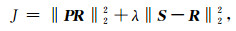
(15)

极小化上述目标函数, 可得到方程

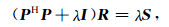
(16)

这里PH为P的共轭转置, I为单位矩阵, λ是权衡R的可预测性和R与S的背离程度的参数, λ越小, 则越强调待求信号R的线性预测关系的满足程度, 相反, λ越大则越强调缩小R与输入S之间的差异.求解(16)式便可得到反射信号R的一个估计.有了R, 则由D=S-R即得到D, 最终将得到绕射波的低倾角信息成分Dp(L)(x, ω)的估计.

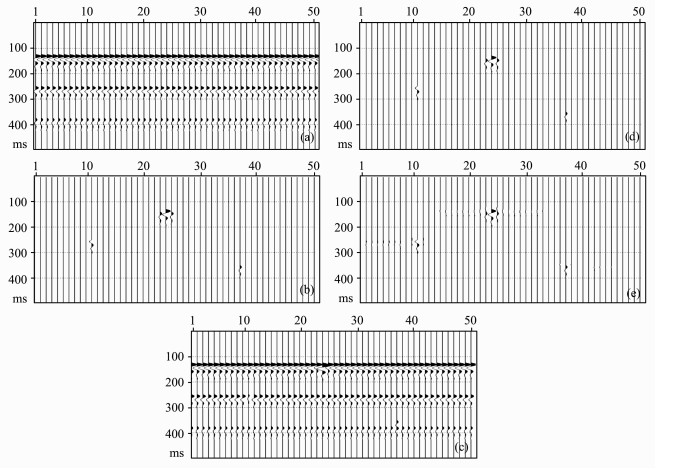
图 4是通过理论数据测试预测反演方法有效性的结果.从图上可以看到, 较传统的预测滤波比, 预测反演方法提取的局部异常具有较高横向分辨率, 更接近真实结果.

图 4 反演与滤波提取局部异常信息的效果对比 (a)连续同相轴; (b)局部异常; (c)(a)与(b)相加的结果; (d)用预测反演方法从(c)中提取的局部异常; (e)用预测滤波方法从(c)中提取的局部异常. Fig. 4 Comparison of local anomalies from inversion and filtering (a) Continuous events; (b) Abnormal signal; (c) Result of adding (b) to (a); (d) Separated signal using inversion method; (e) Separated signal using filtering method

在图 2给出的水平同相轴与弯曲同相轴分离测试中, 如果对其中分离出的水平同相轴再用预测反演方法做局部异常提取, 并将提取的局部异常加到图 2b的结果上, 则得到用局部倾角滤波与预测反演联合方法分离水平和弯曲同相轴的结果, 如图 5所示.显然, 联合方法得到的分解结果的精度有了显著提高, 预测反演方法的应用使弯曲同相轴的零倾角位置的能量损失得到了有效补偿.

图 5 采用局部倾角滤波与预测反演联合方法得到的水平和弯曲同相轴分离结果 (a)分离出的水平同相轴成分; (b)分离出的弯曲同相轴成分; (c)分离出的弯曲同相轴成分与真实结果(图 2b)之差. Fig. 5 Results of separation combining local dip filtering and prediction inversion (a) Aclinal events; (b) Flexural events; (c) Difference between Fig.5b and Fig.2b.
3 方法试算

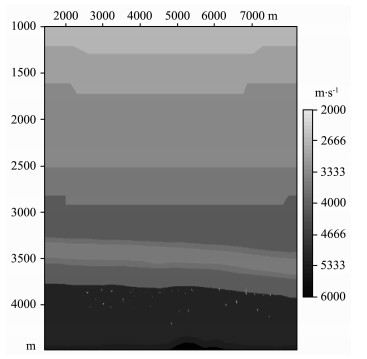
图 6是根据塔里木盆地某探区实际解释的地质模型而建立的一个二维速度模型.模型中3700m深度附近的界面代表奥陶系风化面, 其下部随机分布了一些尺度、形状不同的溶洞.溶洞的横向尺度在5~100m, 高度在10~200m范围内变化, 填充速度为3200~3900m/s, 围岩的速度为4400 m/s.对该模型进行数值模拟计算得到模拟叠前地震数据, 再对模拟数据进行绕射波分离和叠前深度偏移处理.

图 6 速度模型 Fig. 6 Velocity model

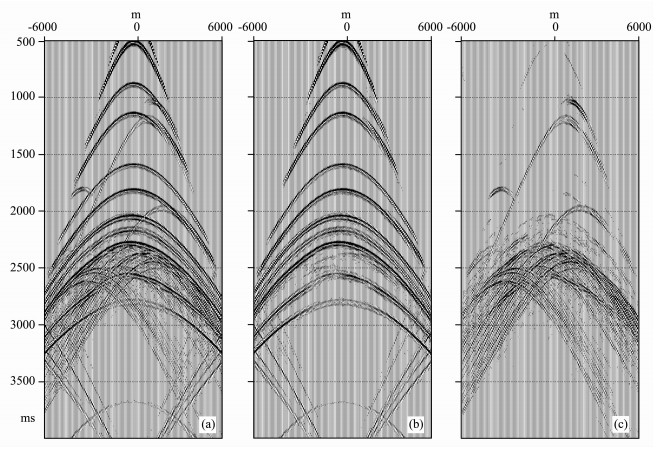
图 7给出的是一个炮集记录结果.从分离结果看, 绕射波与反射波的绝大部分能量得到了正确的分离.

图 7 原始及绕射波分离后的炮记录 (a)原始炮记录; (b)分离出的反射波炮记录; (c)分离出的绕射波炮记录. Fig. 7 Shot gathers before and after separating (a) Original shot gather; (b) Reflection gather; (c) Diffraction gather.

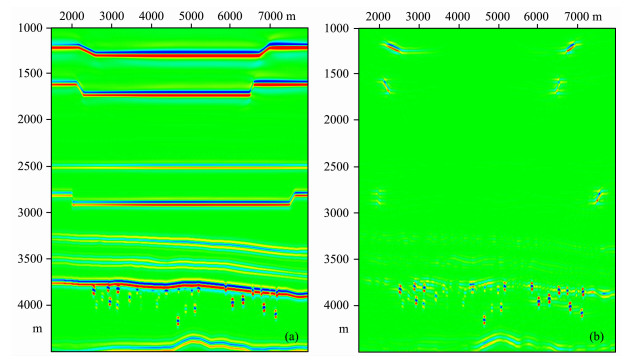
图 8是对该模型数据及分离出的绕射波进行叠前深度偏移的结果.从原始数据的成像结果可以看到, 部分靠近强反射面, 且绕射能量较弱的洞体成像后淹没在强反射同相轴中, 难以识别.在分离出的绕射波成像结果上, 连续反射波能量得到了压制, 而断点和孤立的洞体反射能量保留下来, 显然, 该结果有助于对缝洞等地质异常体的识别.

图 8 反射波与绕射波成像结果对比 (a)未做绕射波分离的叠前深度偏移剖面; (b)分离出的绕射波的叠前深度偏移剖面. Fig. 8 Comparison of PSDM results (a)PSDM result of the original data; (b) PSDM result of the diffraction data.

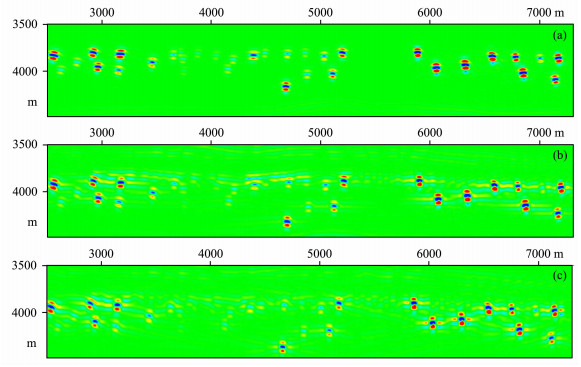
对溶洞分布区域, 图 9给出了本文方法与Harlan信噪分离方法的结果对比.从结果可看到, 在用Harlan信噪分离方法得到的绕射波成像结果上, 与溶洞对应的“串珠”状反射在横向上出现较强的旁瓣, 这说明所提取的绕射波的空间带宽(即低倾角信息)损失较大, 而采用本文方法得到的绕射波成像结果与精确的绕射波成像结果更为接近.

图 9 两种绕射波分离方法效果对比 (a)精确绕射波成像结果; (b)本文方法分离的绕射波成像结果; (c)Harlan信噪分离方法分离的绕射波成像结果. Fig. 9 Comparison of two diffraction wave separations (a) Theoretical diffraction data; (b) Separation by the method proposed in this paper; (c) Separation by Harlan signal/noise separation method.

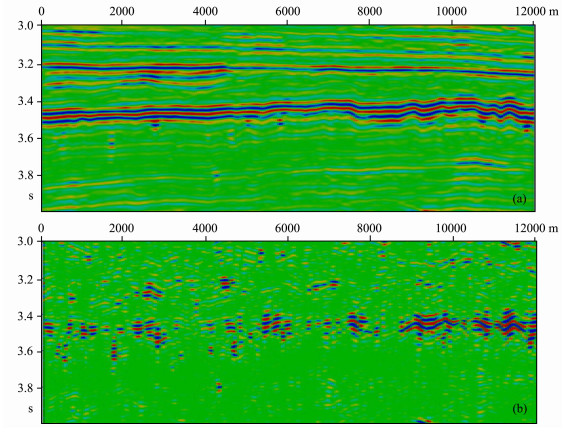
图 10给出的是三维应用实例, 图中(a)、(b)两剖面分别取自原始数据和提取的绕射波信息的三维叠前时间偏移数据体, 这里仅显示了反映奥陶系风化面反射(3.5s附近)的一段数据.显然, 在绕射波成像剖面上, 来自连续反射面的反射信号得到了压制, 保留的反射信息与断层、反射界面形态突变、溶洞等地质现象相关, 尤其是使疑似来自溶洞的孤立“串珠”状反射更被突显出来.显然, 这种绕射波成像结果可用于更好地进行缝洞储集体的识别.

图 10 实际资料处理结果 (a)未做绕射波分离的叠前时间偏移剖面; (b)分离出的绕射波的叠前时间偏移剖面. Fig. 10 Processing results of real data (a) PSTM result of original field data; (b) PSTM result of diffraction data.
4 结语

将绕射波从原始地震数据中分离出来单独成像, 其结果有助于提高碳酸盐岩缝洞型储层这类复杂非均质储层的识别能力.实现绕射波的有效分离是得到可靠的反映非均质体特征的成像结果的关键, 在地下反射界面倾角较小的前提下, 局部倾角滤波和预测反演相结合是在平面波域提取绕射波信息的有效方法.仅依赖倾角差异分离绕射波会严重损失低倾角信息, 配合以预测反演方法则可得到相对完整的绕射波信息, 减少绕射波空间带宽的损失, 从而更好地保证绕射波成像结果的横向分辨率.

参考文献
[1] Landa E, Keydar S. Seismic monitoring of diffraction images for detection of local heterogeneities. Geophysics , 1998, 63(3): 1093-1100. DOI:10.1190/1.1444387
[2] Tcheverda V, Pozdnyakov V A. 3D focusing transformation: reliable tool for imaging of scattering objects. // Abstracts of SEG/New Orleans 2006 Annual Meeting, 2006: 2564-2568. http://www.oalib.com/references/19001680
[3] Khaidukov V. Diffraction imaging by a focusing-defocusing approach. // Expanded Abstracts of 73rd Annual Internat SEG Mtg, 2003: 26-31. http://www.oalib.com/references/19001672
[4] Nowak E J, Imhof M G, Tech V. Diffractor localization via weighted Radon translations. // Expanded Abstracts of 74th Annual Internat SEG Mtg, 2004: 10-15. http://www.oalib.com/references/19001673
[5] Bansal R, Imhof M G. Diffraction enhancement in prestack seismic data. Geophysics , 2005, 70(3): V73-V75. DOI:10.1190/1.1926577
[6] Harlan W S, Claerbout J F, Rocca F. Signal/noise separation and velocity estimation. Geophysics , 1984, 49(11): 1869-1880. DOI:10.1190/1.1441600
[7] Fomel S. Applications of plane-wave destruction filters. Geophysics , 2002, 67(6): 1946-1960. DOI:10.1190/1.1527095
[8] Turhan Taner M. Separation and imaging of seismic diffractions using plane-wave decomposition. // Abstracts of SEG/New Orleans 2006 Annual Meeting, 2006: 2401-2405. http://www.oalib.com/references/19001677
[9] 曲寿利, 朱生旺, 赵群, 等. 碳酸盐岩孔洞型储集体地震反射特征分析. 地球物理学报 , 2012, 55(6): 2053–2061. Qu S L, Zhu S W, Zhao Q, et al. Analysis of seismic reflection characters for carbonate Karst reservoir. Chinese J. Geophys (in Chinese) , 2012, 55(6): 2053-2061.