2. 中国科学院地质与地球物理研究所, 北京 100029;
3. 浙江省第九地质大队, 浙江湖州 313000
2. Institute of Geology & Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
3. No.9 Geological Exploration Unit of Zhejiang, Zhejiang Huzhou 313000, China
拾取有效速度谱是速度分析中一个很重要的工作.这项工作可通过手工拾取或者由计算机自动拾取来实现.比起计算机算法, 手工拾取往往更具灵活性, 这是因为人的眼睛对聚焦性不是很高的速度谱具有较强的识别能力.但是, 在估算速度谱参数方面, 手工拾取存在一定的不足, 主要表现为效率低下、成本高昂且精确度不高.因此, 当所要处理的地震剖面长, 即包含的速度谱信息更加丰富时, 应将自动技术融合到速度拾取过程中.
自动技术运用的好, 不仅能解决因只做部分拾取致使丢失有效地质信息所带来的经济损失, 还能提高计算效率.为此, 人们一直在寻求自动拾取的算法或方法.Toldi[1]的不做拾取的速度分析、Zhang和Claerbout[2]非线行优化自动拾取及陈志德等[3]的蒙特卡洛自动层速度拾取, 在获取相对简单地质体的速度时已经取得了一定的效果, 但对于解决复杂地质体的速度分析都同样存在难于获得精确解的问题.
Viterbi算子是一种具有自动搜寻目标函数的算子该算子因被Viterbi于1967年首用于解码问题而得名.由于该算子的方便易用性和灵活性, 被广泛地应用于与解码问题相关联的不同领域中. McEliece[4]、Yoshua[5]及Luz[6]等相继对该算法在解码等问题中的应用做了详尽的论述.Zhang [7]将其引入并用于解决地震质料处理中关于拾取的一些问题, 林年添等[8]将其应用到复杂地质体速度自动拾取, 均取得了良好的效果.
自动拾取常常通过优化来实现, 它包括两个步骤:定义目标函数和优化拾取.上述所引入的自动搜寻算法-Viterbi算子便是用于第二步骤中优化拾取.但为自动搜寻算法提供的数据源(目标函数), 有时往往由于其曲面光顺程度低, 直接影响到搜寻解的准确性.对于速度拾取而言, 速度谱的聚焦性差, 自动拾取得到的速度将可能是不准确的, 所得的动校正等结果也会是不可靠的.因此, 有必要对上述的数据源进行先期的光顺处理.
光顺处理在汽车、飞机、船舶等设计制造业中起着重要作用, 这是由于在曲面设计造型中常常通过光顺处理来提高目标体表曲面顺滑程度[9-12], 以达到工程设计要求.针对不同设计目的和精度的要求等[13], 在相关领域已经涌现或派生了多种多样有关光顺处理的算法并不同程度地取得了良好效果[14-18].
借鉴曲面设计造型中光顺处理原理, 本文将光顺处理技术引入到速度谱曲面的光顺处理中, 以解决上述速度谱曲面可能存在的不光滑问题.即对速度谱曲面进行加权均值滤波处理(目标函数的再定义), 以获取顺滑程度高的速度谱曲面[12].如此, 再应用约束优化搜寻算子进行叠加速度的拾取, 就可以获得精度更高的速度[19].
综上所述, 通过优化来实现自动拾取的两个步骤修改为:①定义与再定义目标函数; ②优化拾取.
2 速度谱的光顺处理表示
若有一个共中心点CMP道集数据u(i, j), 则根据Taner等[20]的相似度准则可获得速度谱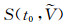

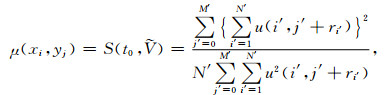
|
(1) |
式中, i'=(1, 2, …, N')为地震道号; j'=(0, 1, 2, …, M')为道内采样点号; 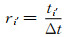
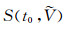
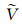
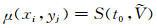
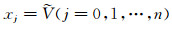
式(1)即为由相似度准则得到的速度谱(定义目标函数), 但由于所得速度谱曲面可能存在不光顺情况, 不利于约束优化拾取.为此, 需要对速度谱曲面进行光顺处理(再定义目标函数).
现引入另一个量w(xi, yj), 它与μ(xi, yj)之间的关系如下:
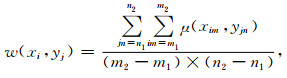
|
(2) |
式中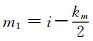
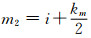
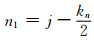
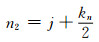
式(2)即为利用均值滤波函数对目标函数进行再定义(速度谱的光顺处理)的结果, w(xi, yj)即为新的速度谱.
不难看出, 函数w(xi, yj)是以点(xi, yj)为中心坐标, 在(m2 -m1)× (n2 -n1)窗口内对原速度谱μ(xi, yj)求平均而得到的新函数, 窗口大小可根据需要进行选择.窗口的每次移动, 就意味着产生一个新的w(xi, yj)[19].对于点(xi, yj)上的速度谱函数(未经再定义的函数)而言, 函数w(xi, yj)赋予了其一个具有新意义的值[19].它的意义在于:上述所构造的函数w(xi, yj)是(m2 -m1)× (n2 -n1)窗口内各点的速度谱μ(xi, yj)作为变量共同贡献的结果.新构造的w(xi, yj)其各点彼此间更具内在的联系, 因为(xi, yj)上的μ(xi, yj)对w(xi, yj)做了贡献, 对于点(xi-1, yj-1)上的w(xi-1, yj-1)或对于点(xi+1, yj+1)上的w(xi+1, yj+1)也都做了贡献. w(xi, yj)将做为下述Viterbi算法搜寻最大“能量团”的数据源.为区别于速度谱函数μ(xi, yj), 称w(xi, yj)为视速度谱函数[19].
3 Viterbi算法及速度优化拾取Viterbi算法是一种具有寻找最短路径的最优化搜寻算法.它在电信领域中被广泛应用于译解卷积码等问题.该算法的基本原理出自这样的观察[19]:即, 如果点A与点C间存在一条最短路径, 而该最短路径中存在一个中间点B, 那么, 点A与点B间的这段路径也是该路径段间最短的.Viterbi算法涵盖两个基本步骤:一是向前做最短路径的累积计算; 二是向后做递减跟踪, 寻找最优解.本文, 将此算法应用到速度的自动拾取中, 则可描述为:向前做速度谱最大“能量团”的累积计算及向后递减跟踪, 寻找最佳速度.
假设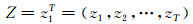

|
(3) |
式中, P(z1)为初始观测序列概率, 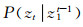
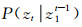
如果在t时刻的状态qt是{1, …, M}内一个有限的数, 并且假设只是从0到T的处理时间, 而且已知初始状态和最终状态.那么, 状态序列可以用有限的矢量来表示, 即
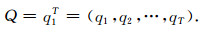
|
一阶的Markov过程就是用

|
或表示为
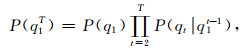
|
(4) |
式中, P(q1)为初始状态概率, 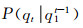
根据Bayes规则, 前述的观察序列z1T与状态序列q1T之间的关系可表示如下:
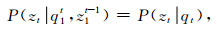
|
(5) |
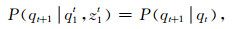
|
(6) |
式(5)中, P(zt|qt)为发射概率, 即两种序列联合条件分布概率, P(z1t-1)为先验概率, 联合分布条件分布概率P(zt|q1t)为后验概率; 式(6)中, P(qt+1|qt)为传递概率, 即状态序列条件分布概率, P(z1t)为先验概率, 状态序列条件分布概率P(qt+1|q1t)为后验概率.式(5)、(6)中, t=1, 2, …, T.
简言之, 当要预测观察序列或下一个状态时, 状态变量qk包含了过去所有相关的状态变量和观察序列的值, 也就是这些值的和.依据条件独立概率分布的假设, 观察序列和状态变量联合概率分布的关系还可以简化为
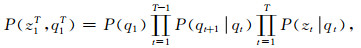
|
(7) |
式中, p(q1)为初始状态概率, P(zt|qt)为发射概率, P(qt+1|qt)为传递概率, t=1, 2, …, T.
那么, 如果给定一个观察序列z1T, 从而推断与之相对应的最可能的状态序列q1T , 这个可以利用下面的最大化算法得到.
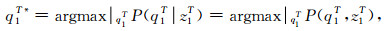
|
(8) |
式中q1T*为条件分布概率P(q1T|z1T)或联合概率分布P(q1T, z1T)的最大值.
Viterbi算法能有效地递归求解上述的最大值.首先定义
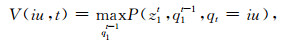
|
(9) |
式中iu=qt(t=1, 2, …, T), V(iu, t)即为联合概率分布P(z1t, q1t-1)的最大取值, 实际上就是观测序列P(z1t)的最大取值, 但它依赖于先验概率, 即状态序列分布概率P(q1t-1).
然后由下式递归计算得到

|
(10) |
式中, iu=qt, jv=qt-1, t=1, 2, …, T.P(zt|qt=iv)表示t时刻的观测序列和状态序列的联合概率分布, P(qt=iu|qt-1=jv)为状态序列条件分布概率, 或称传递概率, 主要起到递归计算作用, 而V(jv, t-1)表示传递序列变量qt-1=jv携带了zt-1之前所有信息.
V(iu, t)的初始化值为V(iu, 1)=P(z1|q1)P(q1).因此我们获得最后的序列.
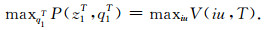
|
如果上述递归式的最大增量jv* (iu, t)得以确定, 那么最佳的q1T*就可以通过一个向后递归计算得到, 即利用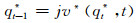
如果我们把按照上述方法构造得到的视速度谱w(xi, yj)看做一个观察序列z1T, 而把对应于上述状态序列q1T的用于记录路径的传递变量记为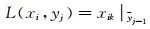
最大速度谱“能量团”向前累积(积分)过程可表示为
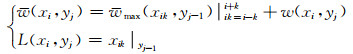
|
(11) |
式(11)等同于式(5)和式(6).其中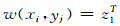
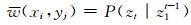
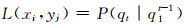
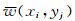

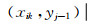

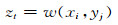
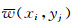

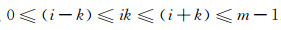
当上述的累积达到yj=yn-1时, 即可搜寻最大值
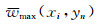
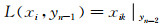
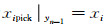

|
(12) |
式中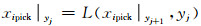
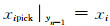
本文所述的速度自动拾取步骤为:首先, 输入的数据要求为共中心点CMP道集u(i, j); 第二步, 利用相似度系数判别准则制作速度谱(式(1)); 第三步, 利用均值滤波函数(式(2))对相似度速度谱μ(xi, yj)再定义(速度谱光顺处理)得到视速度谱函数w(xi, yj), 此外, 在这一步骤中通常会根据不同来源的数据, 选择适当大小的窗口以获取最佳光顺处理效果; 第四步, 则是利用第三步得到的视速度谱通过Viterbi算法-方程式(10)拾取所需的叠加速度; 第五步, 是利用式(13)做动校正NMO处理:

|
(13) |
式中, t0为零炮检距的双程反射时间; vNMO为动校正速度; t(x)为炮检距x上的反射时间.
第六步, 做水平叠加处理并输出结果.
上述步骤中, 步骤一到步骤四为速度优化自动拾取的核心步骤, 第五、第六步骤主要用于直观评估所拾取速度实际效果.
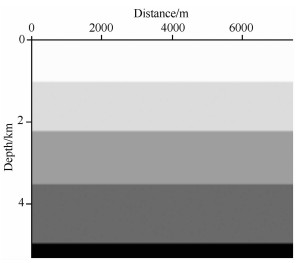
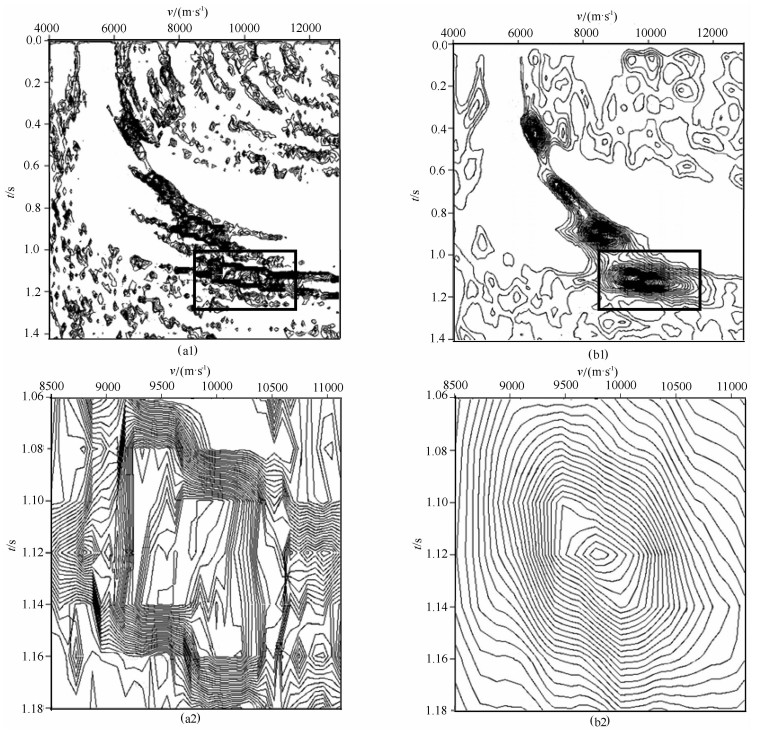
图 1为一个水平层模型, 图 2(a1)为由图 1得到的相似度速度谱, 而图 2(b1)则为图 2(a1)经光顺处理得到的速度谱.后者相比于前者, 其“能量团”更集中, 且非主流“能量团”得到了压制.图 2(a2)和图 2(b2)所示分别为图 2(a1)和图 2(b1)中局部(图中小方框部分)的“能量团”, 前者的等值线不光滑, 且不规则, 主“能量团”边上存在异常小峰值, 这不论对于人工拾取还是对于计算机自动拾取都存在困难, 即很难判定“能量团”最大值准确位置.而后者则一目了然, 使上述问题很容易得到解决.
|
图 1 一个水平层地质模型 Fig. 1 A horizontal geological model |
|
图 2 由图 1水平层地质模型得到的相似度速度谱(CMP3500)光顺处理前后比较图 (a1)常规相似度速度谱; (b1)经过光顺处理的速度谱; (a2)和(b2)分别为(a1)和(b1)中局部(小方框内)的速度谱. Fig. 2 Comparison on the semblance velocity spectrum(CMP3500), before and after fairing, acquired from the horizontal geological model(Fig.1). (a1) Shows the source semblance velocity spectrum; (b1) Shows the one filtered by weighted mean from (a1); (a2) and (b2) Show the local velocity spectrum correspondent to the smaller block diagram. |
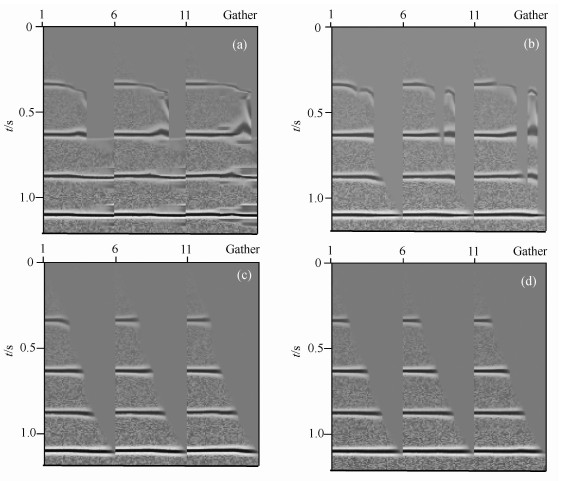
根据均值滤波原理, 通过建立不同大小模块(待处理像素其周围邻近像素的不同)可获得表面光顺程度不同的新图像, 即速度谱.图 3就是一个选择不同大小模块对拾取产生不同效果的应用实例, 其地质模型如图 1所示.图 3a为未进行光顺处理就直接用Viterbi算法拾取速度并做动校正处理的结果, 很明显这是一个动校正明显不足的结果.图 3b和图 3c为选取不同大小模块光顺处理的结果, 从中不难看出, 模块的大小直接影响最终结果.因此选择适当大小的模块对于获取更好的图像(准确的速度)非常重要.图 3c相对于图 3b, 其结果更接近于实际的速度值(见图 3d).图 3d为用已知准确速度动校正的结果.
|
图 3 地震数据CMP道集所制作速度谱经光顺处理和利用Viterbi算法自动拾取速度并做动校正的结果 (a)未进行光顺处理的结果; (b, c)选取不同大小时窗进行光顺处理的结果; (d)则为用已知准确速度动校正和叠加的结果. Fig. 3 Normal moveout correction from the staking velocity auto-picked by the Viterbi algorithm with the surface fairing data (a) Shows a staking profile from the unsmoothed velocity spectrum; (b, c) Show the result from the smoothed one with different time windows; (d) Shows the one from known and correct stacking velocity. |
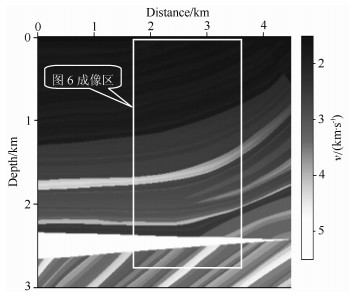
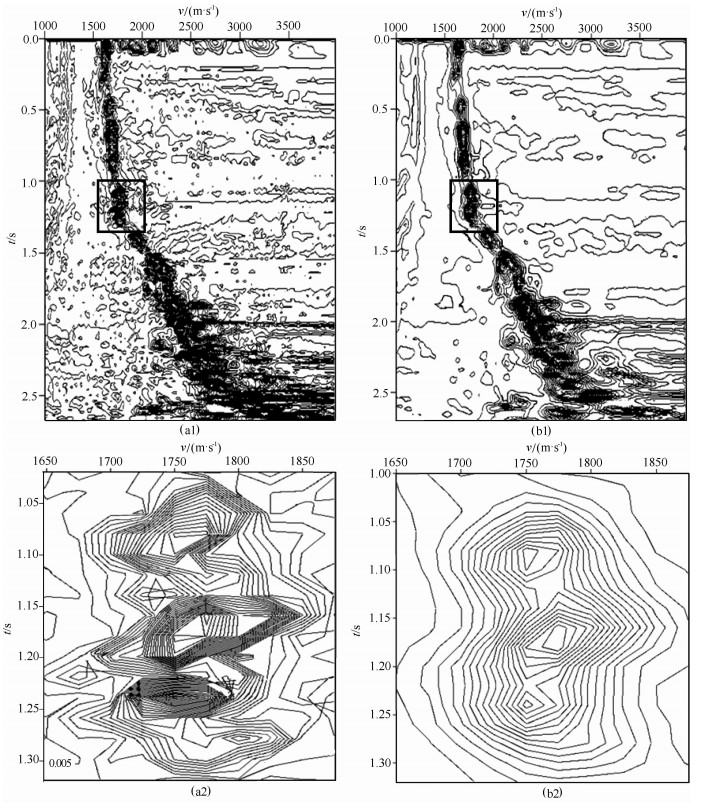
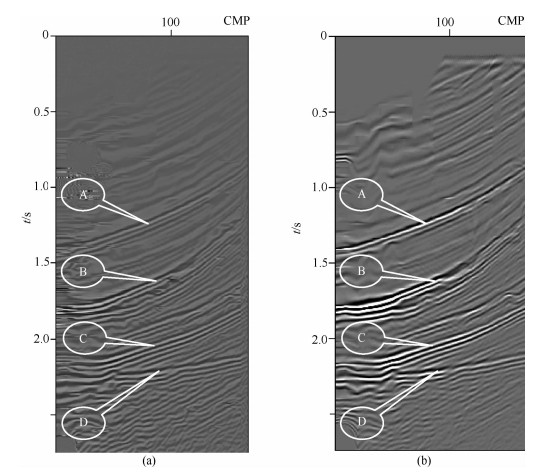
图 4是另一个速度模型(Marmosi模型的局部), 由其所得CMP100的速度谱如图 5.该速度谱曲面光顺处理前后的情形如同图 2.图 5(b1)为图 5 (a1)经光顺处理得到的速度谱, 图 5(a2)和图 5(b2)所示分别为图 5(a1)和图 5(b1)中的局部(图中小方框部分), 光顺处理后的速度谱(图 5b)精度明显优于未进行光顺的(图 5a).利用Viterbi算法分别对两种不同的速度进行优化自动拾取, 并将所拾取速度用于动校正及水平叠加叠加结果如图 6(图 4中的局部成像), 图 6a为未进行光顺处理就直接用Viterbi算法拾取速度并做动校正叠加的结果, 图 6b为对速度谱进行光顺处理后再利用Viterbi算法拾取速度并做动校正叠加的结果.不难看出, 相比于图 6a, 图 6b中A、B、C、D所指示的同相轴明显得到了很好的增强.这个例子所得到的结果再次说明光顺处理对于常规速度分析中速度的自动拾取起到了良好的作用.
|
图 4 速度模型(Marmousi模型局部) Fig. 4 Velocity model(part of Marmousi model) |
|
图 5 由图 4速度模型得到的相似度速度谱(CMP100)光顺处理前后比较图 (a1)常规相似度速度谱; (b1)经过光顺处理的速度谱; (a2和b2)分别为(a1)和(b1)中局部(小方框内)的速度谱. Fig. 5 Comparison on the semblance velocity spectrum(CMP100), before and after fairing, acquired from the velocity model(Fig.4) (a1) Shows a regular semblance velocity spectrum; (b1) Shows the one filtered by weighted mean from (a1); (a2) and (b2) show the local velocity spectrum correspondent to the smaller block diagram. |
|
图 6 利用Viterbi算法自动拾取图 5中不同速度并做水平叠加的剖面图比较 (a)未进行光顺处理所拾取速度叠加的结果; (b)光顺处理后所拾取速度叠加的结果. Fig. 6 Comparison on the profile stacking from the different velocity, in figure 5, auto-picked by the Viterbi algorithm (a) Shows a staking profile from the unsmoothed velocity spectrum; (b) Shows the result from the smoothed one. |
自动拾取除了希望获得优质的成像外, 还有一个促使我们实现自动拾取的原因, 那就是降低处理成本的问题, 亦即提高处理效率.对于用图 1或图 4的速度模型进行光顺处理和优化自动拾取并最终得到如图 3c或图 6b的结果, 在所有CMP点都参与分析的情况下也仅需几秒钟, 这个对于手工拾取而言是远远达不到的.
5 结论从文中的讨论看, 我们不难得出:若不对原始速度谱(所定义函数)进行光顺处理(函数的再定义), 就有可能得不到好的源数据(高分辨率速度谱), 也就可能得不到可靠的速度信息; 而若没有具有快速搜寻最优解功能的Viterbi算法的参与, 就不能实现速度的自动拾取.因此说, 光顺处理技术与路径积分优化法的有机结合才形成了一个有效的具有获取高精确解的速度自动拾取功能的方法.
实现速度的自动拾取, 意味着速度分析效率的提高, 也就意味着我们在进行地震数据处理时可做更多、更有效、更充分的分析工作.亦即在速度分析中, 我们就可以进行更多点(CMP), 甚至进行全部点的速度分析以更多地获取速度信息, 这对于减少可能的经济损失(由于高昂的计算代价而在速度分析中可能仅做部分速度信息的拾取致使丢失有效地质信息所带来的经济损失), 降低勘探成本, 提高生产效率, 具有积极的意义.
本文讨论了将自动拾取方法应用于简单或较简单模型试算结果, 得到了较好的结果, 为进一步开展复杂地体相关研究奠定了基础.但如何应用于解决复杂地质体的速度拾取, 相关研究有待于进一步的深入.此外, 本文为了说明光顺处理对于改善速度谱质量的作用, 仅应用了加权均值滤波法, 若应用其它相关算法做光顺处理会获得不同, 或许是更好的效果, 相关研究有待深入探讨.
| [1] | Toldi J. Velocity analysis without picking. Stanford: Stanford University, 1985. http://www.oalib.com/references/19001154 |
| [2] | Zhang L, Claerbout J. Automatic dip-picking by non-linear optimization. SEP(67) , 1990: 123-138. |
| [3] | 陈志德, 刘振宽, 李成斌. 三维叠前深度偏移速度分析及蒙特卡洛自动层速度拾取. 地球物理学报 , 2002, 45(2): 246–254. Chen Z D, Liu Z K, Li C B. 3-D Pre-stack depth migration velocity analysis and automatic monte carlo velocity picking in depth. Chinese J. Geophys (in Chinese) , 2002, 45(2): 246-254. |
| [4] | McEliece R J. The Theory of Information and Coding. Massachusetts: Addison-Wesley Publishing Company, 1977 . |
| [5] | Yoshua B. Markovian Models for Sequential Data. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.40.5337. 1996-10-22. http://www.oalib.com/references/19001156 |
| [6] | Méndez L A T. Viterbi Algorithm in Text Recognition: Term project for course: 308-644B. Montreal: McGill University, 1998. http://www.oalib.com/references/19001157 |
| [7] | Zhang L. Automatic picking and its applications. SEP(70) , 1990: 275-292. |
| [8] | 林年添, 刘洪, 李建勇. 基于Viterbi算法的复杂地质体速度约束化自动拾取. 地球物理学进展 , 2004, 19(2): 311–316. Lin N T, Liu H, Li J Y. Automatic picking velocity by the viterbi algorithm for the complex geological case. Progress in Geophysics (in Chinese) , 2004, 19(2): 311-316. |
| [9] | Pérez-Arribas F, Suárez-Suárez J A, Fernández-Jambrina L. Automatic surface modelling of a ship hull. Computer Aided Design , 2006, 38(6): 584-594. DOI:10.1016/j.cad.2006.01.013 |
| [10] | 李学艺, 姜虹, 陈松, 等. 基于马尔可夫随机场的曲面光顺算法. 西安交通大学学报 , 2003, 37(3): 241–244. Li X Y, Jiang H, Chen S, et al. Surface fairing algorithm based on Markov random fields. Journal of Xi'an Jiaotong University (in Chinese) , 2003, 37(3): 241-244. |
| [11] | Sariöz E. An optimization approach for fairing of ship hull forms. Ocean Engineering , 2006, 33(16): 2105-2118. DOI:10.1016/j.oceaneng.2005.11.014 |
| [12] | 林年添, 柴慧婵, 魏立杰, 等. 速度谱曲面的光顺处理及其作用. 地球物理学进展 , 2011, 26(3): 311–316. Lin N T, Chai H C, Wei L J, et al. Surface fairing with its action on the Velocity Spectrum. Progress in Geophysics (in Chinese) , 2011, 26(3): 311-316. |
| [13] | 杨长春, 倪彤光. 一种高效的混合曲面光顺算法. 计算机应用 , 2005, 25(11): 2609–2611. Yang C C, Ni T G. Efficient hybrid algorithm for mesh smoothing of surfaces. Journal of Computer Applications (in Chinese) , 2005, 25(11): 2609-2611. |
| [14] | Luo X N, Liu N, Gao C Y. Fairing geometric modeling based on 4-point interpolatory subdivision scheme. Journal of Computational and Applied Mathematics , 2004, 163(1): 189-197. DOI:10.1016/j.cam.2003.08.064 |
| [15] | Zhang C N, Zhang P F, Cheng F H. Fairing spline curves and surfaces by minimizing energy. Computer-Aided Design , 2001, 33(13): 913-923. DOI:10.1016/S0010-4485(00)00114-7 |
| [16] | 甘屹, 齐从谦, 陈亚洲. 基于遗传算法的曲线曲面光顺. 同济大学学报(自然科学版) , 2002, 30(3): 322–325. Gan Y, Qi C Q, Chen Y Z. Smoothing of curves and surfaces based on genetic algorithm. Journal of Tongji University (Natural Science) (in Chinese) , 2002, 30(3): 322-325. |
| [17] | Renka J R. Constructing fair curves and surfaces with a Sobolev gradient method. Computer Aided Geometric Design , 2004, 21(2): 137-149. DOI:10.1016/j.cagd.2003.07.006 |
| [18] | Xu G L. Surface fairing and featuring by mean curvature motions. Journal of Computational and Applied Mathematics , 2004, 163(1): 295-309. DOI:10.1016/j.cam.2003.08.075 |
| [19] | 林年添.保重心脉冲压缩滤波及其在速度自动拾取中的应用.北京:中国科学院研究生院, 2004. Lin N T. Automatic Picking Velocity by Gravity Center Preserved Pulse Compressed Filter and the Viterbi Algorithm (in Chinese). Beijing: Chinese Academy of Sciences, 2004. (in Chinese) |
| [20] | Taner M T, Koehler F, Sheriff R E. Complex seismic trace analysis. Geophysics , 1979, 44(6): 1041-1063. DOI:10.1190/1.1440994 |
 2013, Vol. 56
2013, Vol. 56

