作为多波地震勘探数据处理的主要组成部分, 转换波数据处理受到广泛的关注, 其中转换波的静校正问题是决定转换波数据处理效果好坏的关键环节之一.转换波的静校正量可分解为炮点的纵波静校正量和检波点的横波静校正量.前者可以通过常规纵波静校正得到解决, 而后者则要困难许多.由于横波的传播不受孔隙流体的影响, 其近地表层通常在潜水面以下, 加之横波波速小于纵波波速, 使得检波点的横波静校正量很大且与炮点纵波静校正量不相关[1].因此采用常规纵波的线性静校正方法处理转换波静校正问题很难得到满意的效果.
剩余静校正本质上是非线性问题, 适合采用非线性全局最优化方法, 这点在求取大剩余静校正量问题上尤为明显.Rothman于1986年提出将模拟退火方法应用于求解大的剩余静校正量的问题[2], 之后的很多国内外学者在这方面提出了自己的见解和方法[3-4].转换波的静校正问题是典型的大静校正量问题, 因此采用非线性全局最优化方法求取转换波静校正量是可行的[5-6].
Ronen和Claerbout于1985年提出最大能量法[7], 将叠加剖面能量作为目标函数, 采用迭代的方法求取静校正量.这种方法处理小静校正量、高信噪比的地震资料时有收敛速度快、误差较小的优点; 但是当资料信噪比较低且存在大的静校正量时, 该方法很容易陷入局部最优解[8].
粒子群算法(Particle Swarm Optimization Algorithm, 简称PSO)是一种群体智能(Swarm Intelligence)算法.它是由Eberhart和Kennedy于1995年提出的[9], 其思想是基于对鸟群和鱼群的模拟.其优点是算法简单, 收敛速度快, 适于并行计算; 缺点是易收敛于全局最优解, “早熟”现象显著.
本文提出了一种新的粒子群算法:团体粒子群算法, 改善了粒子群算法易“早熟”的缺点.并将团体粒子群算法与最大能量法进行了串行融合, 将其应用于求取转换波检波点横波剩余静校正量, 理论模拟证明了本方法有较好的效果.
2 基本原理 2.1 原始粒子群算法PSO是一种群智能算法.粒子群中的每个粒子都有两个属性:位置和速度.位置代表所求问题的可能解, 速度控制粒子在解空间里的移动的方向和距离.此外还有由具体问题总结出来的目标函数, 将粒子的位置代入目标函数求取粒子对应的适应度值.整个优化过程就是粒子追随适应度值最优的粒子进行搜索.
第n次迭代时, 第i个粒子, 第m维的速度vim和位置xim的更新方程如下[10]:
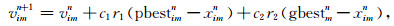
|
(1) |
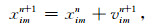
|
(2) |
式中, pbestim为第i个粒子、第m维的历史最优位置; gbestm为所有粒子、第m维的全局最优位置; c1、c2称为学习因子, 分别调节粒子向着个体历史最优位置和全局历史最优位置的运动, 合适的c1、c2会在保证算法不陷入局部极值的前提下加快收敛速度, 通常令c1=c2=2;r1、r2为两个取值在[0, 1]之间的随机数.
2.2 标准粒子群算法原始的粒子群算法其局部搜索能力较强, 而全局收敛能力相对较弱, 为了改善这一缺陷, Shi和Eberhart将惯性权重引入了速度进化方程中[11]:
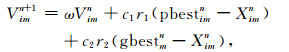
|
(3) |
式中ω称为惯性权重, 它控制着粒子前一次迭代时的速度对当前速度的影响, 研究证明, 较大的ω利于算法的全局搜索, 而较小的ω则能加强算法局部搜索的能力.惯性权重的引入一定程度上增加了PSO的全局搜索能力.
PSO采用多点并行的方式进行搜索, 在算法进行过程中粒子之间互相交流信息, 使得收敛速度很快, 且原理简单、易于实现、调用参数较少, 适合工程等方向实际应用.但是标准粒子群算法也有很明显的缺点, 那就是“早熟”现象比较严重.由于粒子群的更新是跟随者当前全局最优解和邻域最优解, 在应用粒子群算法解决复杂的多峰值问题搜索时, 如果当前最优解不是全局最优解而是局部最优解的话, 一旦粒子群体靠近这个区域, 由于其搜索机制的限制将很难跳出这个局部最优解.即使增大粒子数目也不能从根本上克服这个问题.学者们对粒子群的主要改进思路也是主要围绕着避免算法早熟、增加种群多样性进行的.
2.3 最大能量法最大能量法是求取剩余静校正量的一种常用方法, 它是由Ronen和Claerbout于1985年提出的.最大能量法基于一个基本思想, 即应用正确的静校正量后地震剖面的叠加能量应该达到极大, 这样就可以把求取静校正量转变为一个最优化问题[7-8]:
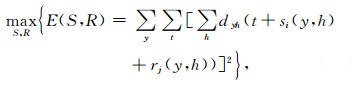
|
(4) |
式中:E为叠加剖面的能量; S={si}, R={rj}分别为炮点和检波点的剩余静校正量; dyh(t)表示共中心点道集y中, 偏移距为h的动校正后的地震道.最大能量法计算过程可以描述为:将叠加剖面的能量作为目标函数, 依次扫描所有的炮点和检波点的静校正量, 全部扫描完一次即完成一次迭代.在扫描一个炮点或检波点时, 其余点固定, 计算该炮点或检波点的可能静校正量对应的叠加剖面的能量, 取最大能量对应的静校正量为该炮点或检波点的静校正量并进行校正.
最大能量法对高信噪比、小静校正量地震资料具有收敛速度快、成像效果好的优点.但处理存在大静校正量、信噪比较低的资料时往往容易收敛于局部极值, 产生“周波跳跃”现象.可以说, 最大能量法静校正的效果很大程度上依赖于初始模型的好坏.
3 团体粒子群算法及其与最大能量法的串行融合算法 3.1 团体粒子群算法在标准粒子群算法中, 粒子通过追随全部粒子的最优解和自身的历史最优解进行运动, 并很快聚集.这种搜索方法虽然效率很高, 但是缺点是粒子聚集太快, 极容易陷入局部极值.为了防止这种粒子的聚集导致的过早收敛, 本文引入了一类新的特殊粒子:团体粒子.将这种包含团体粒子的粒子群算法称为团体粒子群算法.
以寻找目标函数Y=f(X)的最小值问题为例, 将团体粒子群算法计算过程描述如下:
(1)随机初始化一个群体.
假设解空间为M维, 群体有I个粒子, 其中含J个团体粒子, 则第i个粒子的速度和位置表示为Vi=(vi1, vi2, …, vim)和Xi=(xi1, xi2, …, xim), 其中i=1, 2, …, I, 按下面两个公式初始化群体:
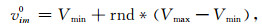
|
(5) |
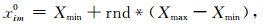
|
(6) |
式中rnd为一个0~1之间的随机数; Xmax和Xmin分别表示粒子的最大位置和最小位置; Vmax和Vmin分别表示粒子的最大速度和最小速度; 通常令Vmax=kXmax, Vmin=kXmin, 其中0.1≤k≤1.0.对第i个粒子第m维的位置和速度, 有如下公式[12]:
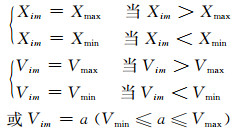
|
(7) |
(2)计算所有粒子的适应度, 更改粒子的历史最优位置和全局最优位置.
在第n次迭代时, 对第i个粒子有:
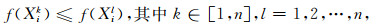
|
(8) |
则将Xik称为第i个粒子的历史最优位置, 记为Pbesti=(pbesti1, pbesti2, …, pbestiJ)
对所有粒子而言, 有:
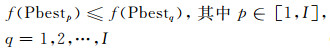
|
(9) |
则将Pbestp称为全局最优位置, 记为Gbest=(gbest1, gbest2, …, gbestJ)
(3)判断是否达到循环结束条件, 达到则结束循环并输出结果, 未达到则继续进行下面步骤.一般的判断准则有限制最大循环次数和判断两次全局最优适应度值之差的绝对值是否小于一个常数.
(4)更新位置和速度.
团体粒子群算法中所有粒子的位置更新公式是相同的, 即式(2).对于团体粒子和普通粒子, 其速度更新公式是不同的.对于普通的粒子, 其速度更新公式就是公式(3);对于团体粒子, 第n次迭代时有:

|
(10) |
则对于“团体”中的第j个粒子, 第n次迭代时、第m维的速度更新方程如下:
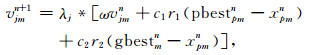
|
(11) |
式中, pbest、gbest、ω、c1、c2、r1、r2和n与公式(1)(3)中的含义相同; λj为速度扰动因子, 它是一个随机数, 其值对不同粒子是不同的, 而对每个粒子不同维度则是相同的.从式(11)可见, 对于任意一个团体粒子, 其速度变化是与第n次迭代时团体中的最优粒子的速度方向相同而大小不同的.
(5)返回(2)步继续计算.
3.2 算法测试为了验证团体粒子群算法的寻优能力优于标准粒子群算法, 采用测试函数Rastrigin进行试验, 其公式为:
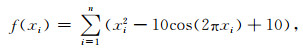
|
(12) |
式中n为自变量个数.
Rastrigin函数有一个全局极小值, 位置是x1=x2=…=xn=0, 函数值为0.Rastrigin函数有2个自变量时的图形如图 1所示.
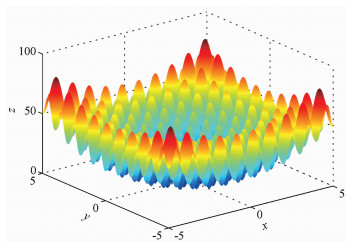
|
图 1 2个自变量的Rastrigin函数 Fig. 1 Rastrigin function of two variables |
可见Rastrigin函数是一个欺诈性很强的函数, 有很多局部极值, 极易使算法陷入局部最优解.下面对有3个自变量的Rastrigin函数分别进行标准粒子群算法和团体粒子群算法寻优操作, 为了保证测试的客观性, 设定两种算法的种群大小均为60, 其中团体粒子群算法中的团体粒子个数为40, 个体粒子数为20.每种算法的运算10次, 统计成功寻找到最小值的次数.若成功用●表示, 失败则用○表示.结果见表 1.
|
|
表 1 两种算法比较 Table 1 Comparison of two algorithms |
从表 1可见, 团体粒子群算法的寻优能力优于标准粒子群算法.这是因为在算法进行中, 团体粒子以相同的运动方向对空间进行较均匀的搜索, 这样就减弱了标准粒子群算法中由于聚集过快导致的“早熟”现象, 有利于算法找到全局最优解.
3.3 团体粒子群算法和最大能量法的串行融合算法静校正问题是一个多维多极值的复杂问题, 单纯应用一种算法依然很难取得好的效果.为了综合团体粒子群算法的全局寻优能力和最大能量法较强的局部寻优能力, 将两个算法进行了串行融合, 再将串行融合后的算法应用于求取转换波的检波点横波静校正量问题上, 取得了较好的效果.
串行融合算法的计算过程可以描述为:
(1)确定目标函数
对比式(4), 由于进行转换波静校正时纵波静校正已做完, 因此无需计算炮点静校正量.目标函数可以设计为:
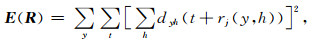
|
(13) |
则静校正对应的问题即为寻找令E最大的一组R.
(2)进行N1次团体粒子群算法
以式(13)作为目标函数, 用团体粒子群算法公式中的位置X代表式(13)中所有的检波点横波静校正量R, 即X每个维度的值xm为各个检波点的横波静校正量rj.根据式(5)-(11)进行N1次团体粒子群算法.其中N1人为给定, 用以控制团体粒子群算法的迭代次数.
(3)进行N2次最大能量法
根据先验信息和经验设定检波点静校正量的可能取值范围为[τmin, τmax], 且τmax=τmin +GΔτ, Δτ为时间采样间隔, G为一正整数.假设第n2次迭代时, 第j个检波点的静校正量为rjn2, 此点前n2-1次迭代求得的静校正量之和为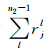
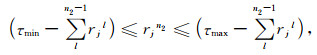
|
(14) |
令
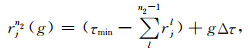
|
(15) |
其中g=0, 1, …, G.将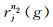
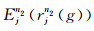
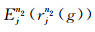
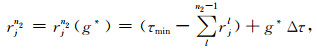
|
(16) |
对与该检波点相关的地震道用静校正量rjn2进行静校正.对每个检波点都进行如上的计算和静校正, 就完成了一次迭代, 直至迭代次数达到N2次停止最大能量法.则最大能量法求得的第j道的静校正量为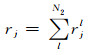
(4)判断是否达到算法终止条件
终止条件可设计为算法进行N次迭代或者两次迭代的叠加剖面能量之差的绝对值小于某个常数.若满足终止条件, 则停止计算, 输出叠加剖面和求得的静校正量; 若为满足终止条件, 则返回步骤(2)继续运算.
在串行融合算法运行中, 团体粒子群算法较强的全局搜索能力可以给最大能量法提供较好的初值; 最大能量法较强的局部搜索能力可以在团体粒子群算法提供的初值基础上进行局部快速搜索.二者循环进行, 最终搜索到最优解.
4 模型试算 4.1 团体粒子群与最大能量串行融合算法的应用利用上述方法对理论模型数据进行了试算.建立一个含一个反射界面的二维地质模型并合成地震记录.界面深度为120m, 纵波速度为2000 m/s, 横波速度为1000 m/s, 单边放炮, 20道接收, 共放69炮, 地震波主频为25Hz.在合成的地震记录中加入[-60ms, 60ms]之间的随机数作为检波点横波静校正量.图 2为含有检波点横波静校正量的叠加剖面, 这个剖面是经过动校正和炮点静校正后的叠加剖面, 图 3为加入的检波点静校正量.可见叠加剖面由于检波点静校正量的存在导致同相轴断续明显, 毫无规律.
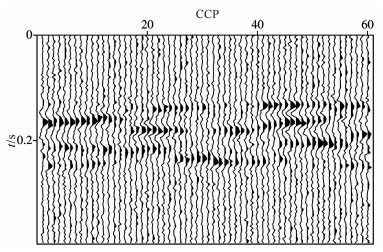
|
图 2 加入静校正量的叠加剖面 Fig. 2 Stack section without static correction |
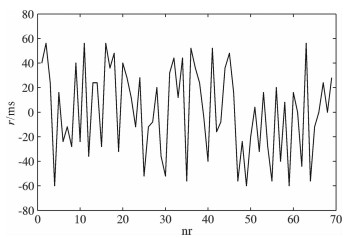
|
图 3 加入的检波点静校正量(nr代表检波点号, r为剩余静校正量) Fig. 3 Receiver statics(nrrepresents the serial number of receivers) |
图 4为串行融合算法静校正后的叠加剖面图和求得的静校正量与理论值之差.从图 4a中可见一条连续性很好的同相轴, 且其位置和形态与模型中反射界面的位置符合, 可以客观准确地反应底下界面情况; 图 4b也说明串行融合算法求取的静校正量很准确.这说明串行融合算法很好地消除了静校正量对叠加剖面的影响, 是一种全局寻优能力很强的最优化算法.
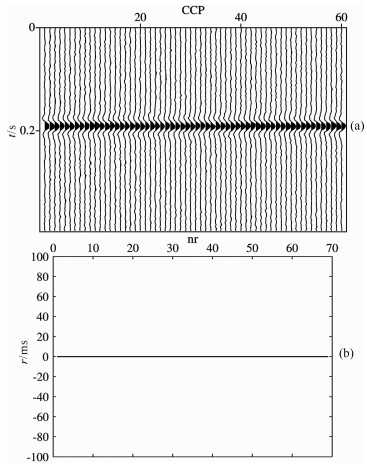
|
图 4 串行融合算法静校正结果 (a)静校正后叠加剖面; (b)求得的静校正量与理论值之差. Fig. 4 Results of serial fusion algorithm in this paper (a) Stack section after statics correction; (b) Difference between the estimated staticsandthetruestatics. |
在上面的串行融合算法静校正中, 团体粒子群算法的种群大小取20, 其中团体粒子个数为10;每次循环中团体粒子群算法迭代次数(即N1)为10次.为了验证不同的N1对本文方法求取静校正量效果的影响, 设计并进行了如下实验:取N1为2~20次, 种群大小等其它参数不变, 对上述模型分别采用本文方法进行静校正, 并计算N1不同时求得的静校正量的平均绝对误差(Mean Absolute Error, 简称MAE), MAE的求取公式如下:
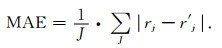
|
(17) |
式中, J为总检波点数, r'j为第j个检波点横波静校正量的理论值, rj为本文方法求取的第j个检波点横波静校正量.
图 5为求得的静校正量平均绝对误差随N1变化图, 可见当N1取值较小时, 误差较大; 随着N1的增大, 误差逐渐减小; 当N1取值大于等于5后, 误差达到最小且随着N1的增加不再变化.这是因为当N1过小也即是团体粒子群算法迭代次数过少时, 团体粒子群算法搜索区域有限, 无法为最大能量法提供较好的初值; 而随着N1的增加, 团体粒子群算法的搜索区域也随之增加, 从而可以为最大能量法搜索到较好的初值, 两种方法交替进行进而搜索到最优解.但是N1过大会导致计算的时间显著增加, 因而实际计算中N1的取值应随目标问题的复杂度而定.
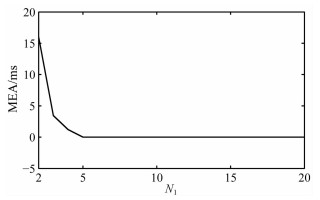
|
图 5 求得的静校正量平均绝对误差随N1变化图 Fig. 5 MAE variation of estimated statics due to N1 |
我们分别用标准粒子群算法和最大能量法对合成的地震数据求取静校正量.图 6为采用标准粒子群算法静校正后的叠加剖面图和求得的静校正量与理论值之差.从图 6a中可见, 标准粒子群算法静校正后的叠加剖面比未做静校正的叠加剖面同相轴连续性略有提高但仍断续明显, 说明这种方法并未很好地消除静校正量的影响; 图 6b也反映了标准粒子群算法求得的静校正量的误差很大, 最大的误差绝对值高达80 ms, 已经大于了加入的静校正量的最大值.产生这样的结果是由于标准粒子群算法“早熟”的缺陷, 使算法陷入了局部极小值, 可见标准粒子群算法转换波静校正效果不好.图 7为采用最大能量法静校正后的叠加剖面图和求得的静校正量与理论值之差.从图 7a中可见最大能量法静校正后的叠加剖面相对于未作静校正的叠加剖面和标准粒子群算法静校正后的叠加剖面而言, 其同相轴连续性有很大的提高, 同相轴不再是杂乱无章, 而是有两条很明显的同相轴, 两条同相轴中间包含一个错断.可以解释为其对应的模型含有一个断层, 这显然是不正确的.所以最大能量法也没有得到正确的静校正量; 图 7b也反映出最大能量法求取的静校正量误差虽然相对标准粒子群算法要小很多, 但是其最大误差的绝对值仍接近30ms.由此可见, 标准粒子群算法和最大能量法均无法得到准确的静校正量, 无法应用于转换波静校正.
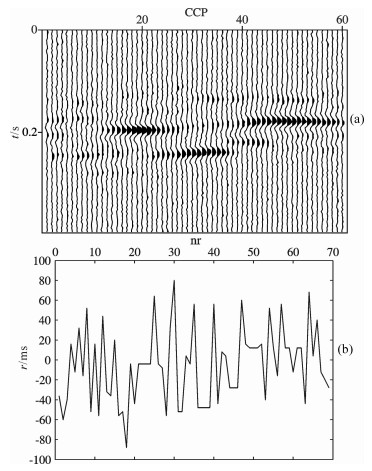
|
图 6 标准粒子群算法静校正结果 (a)静校正后叠加剖面; (b)求得的静校正量与理论值之差. Fig. 6 Results of standard PSO statics (a) Stack section after statics correction; (b) Difference between the estimated statics and the true statics. |
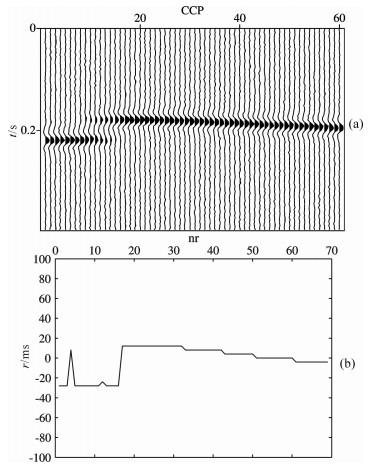
|
图 7 最大能量法静校正结果 (a)静校正后叠加剖面; (b)求得的静校正量与理论值之差. Fig. 7 Results of maximum energy method statics (a) Stack section after statics correction; (b) Difference between the estimated statics and the true statics. |
(1) 转换波静校正问题是一个复杂的、多维度多参数的、非线性问题.利用标准粒子群算法和最大能量法均无法得到很好的效果.
(2) 对Rastrigin函数的寻优实验证明, 团体粒子群算法的全局寻优能力优于标准粒子群算法的.
(3) 团体粒子群算法和最大能量法的串行融合算法综合了前者较强的全局寻优能力和后者较好的局部收敛能力, 是一种有效的估算转换波静校正量的方法.通过串行融合算法和标准粒子群算法、最大能量法对模型进行静校正的结果比较, 证实了该方法可以很好地求取大的转换波检波点静校正量, 静校正后的剖面连续性好.
串行融合算法虽然对于求取转换波静校正量问题取得了较好的效果, 但是对于大静校正量的纵波剩余静校正问题, 由于其问题复杂度更高, 本方法很难取得较好效果, 这也是下一步的研究目标.
| [1] | Cary P W, Eaton D W S. A simple method for resolving large converted-wave (P-SV) statics. Geophysics , 1993, 58(3): 429-433. DOI:10.1190/1.1443426 |
| [2] | Rothman D H. Automatic estimation of large residual statics corrections. Geophysics , 1986, 51(2): 332-346. DOI:10.1190/1.1442092 |
| [3] | 林依华, 张忠杰, 尹成, 等. 复杂地形条件下静校正的综合寻优. 地球物理学报 , 2003, 46(1): 101–106. Lin Y H, Zhang Z J, Yin C, et al. Hybrid optimization of static estimation in complex topography. Chinese J. Geophys (in Chinese) , 2003, 46(1): 101-106. |
| [4] | 刘鹏程, 纪晨. 改进的模拟退火-单纯形综合反演方法. 地球物理学报 , 1995, 38(2): 199–205. Liu P C, Ji C. An improved simulated annealing-downhill simplex hybrid global inverse algorithm. Chinese J. Geophys (in Chinese) , 1995, 38(2): 199-205. |
| [5] | Eaton D W S, Cary P W, Schafer A W. Estimation of P-SV residual statics using stack power optimization. The CREWES Research Report: University of Calgary, 3. 1991. |
| [6] | Armin W Schafer. Converted-wave statics methods comparison. in The CREWES Research Report: University of Calgary. 1991. http://www.oalib.com/references/19001612 |
| [7] | Ronen J, Claerbout J F. Surface-consistent residual statics estimation by stack-power maximization. Geophysics , 1985, 50(12): 2759-2767. DOI:10.1190/1.1441896 |
| [8] | 吴波, 尹成, 潘树林, 等. 最大能量法剩余静校正的改进. 石油地球物理勘探 , 2010, 4(3): 350–354. Wu B, Yin C, Pan S L, et al. The improvements on maximum energy method residual static correction. Oil Geophysical Prospecting (in Chinese) , 2010, 4(3): 350-354. |
| [9] | Kennedy J, Eberhart R C. Particle swarm optimization. // Proc. IEEE Conf. on Neural Networks, IV. Piscataway, NJ, 1995, 1942-1948. |
| [10] | Eberhart R, Kennedy J. A new optimizer using Particle Swarm theory. // Proceedings of the sixth international symposium on Micro Machine and Human Science. Nagoya Japan, 1995: 39-43. |
| [11] | Shi Y H, Eberhart R. A modified particle swarm optimizer. IEEE International Conference of Evolutionary Computation, Anchorage, Alaska, May 1998. |
| [12] | 杨维, 李歧强. 粒子群优化算法综述. 中国工程科学 , 2004, 6(5): 87–94. Yang W, Li Q Q. Survey on particle swarm optimization algorithm. Engineering Science (in Chinese) , 2004, 6(5): 87-94. |
 2013, Vol. 56
2013, Vol. 56


