无线电探测是最重要的地球物理探测方式之一,在遥感遥测、地下流体探测和海洋环境监测方面有其它探测方式难以企及的优势[1].高频无线电海洋探测是在高频电波海面回波观测与分析基础上发展起来的一种海洋探测模式,它利用垂直极化的高频电波沿海面传播衰减小、能绕射的特点实现对海面的超视距探测[2-3].相比传统探测仪器的点、线式探测数据,高频地波雷达可以提供覆盖面积大、实时性强的探测数据,而且不受台风、海啸等恶劣天气的限制.因此,世界各国都开展了高频地波雷达海洋探测研究,具有代表的商业化成品雷达主要有美国Codar公司的SeaSonde系统,德国汉堡大学的WERA系统和中国武汉大学研制的OSMAR系列雷达等[4-6].
高频地波雷达主流的海洋探测要素为海面风场、浪场和表面流场.经过近40年的发展,表面流场的探测已经达到业务化运行阶段,而风场和浪场的反演技术处于发展阶段[7-15].风、浪探测的主要困难在于揭示高频地波雷达回波谱与海浪方向谱的模型为非线性积分方程,而且该方程的解存在模糊性,此外,实测回波数据中包含很多不确定因素.目前,高频地波雷达海浪方向谱反演方法主要包括两类[9-16]:一类是进行线性化近似的求解方法,包括Barrick法[9]、Lipa法[10-11]、Howell法[12]和Green法[13]等,其中Bamck法直接将二阶散射能量看成频率谱的加权,适合于工程上的海浪频率谱和波高信息的提取,Lpa法将海面方向谱看成方向函数与频率谱函数的乘积,根据不同的线性化条件将回波多普勒谱按不同区间近似求解,过分依赖于谱模型;Howell和Green均选取线性化后的积分方程进行不同基函数展开后求解海浪方向谱;另一类是非线性求解方法,主要包括Wyatt[14]、Hisaki[15]、Hashimoto等[16]的求解方法,其中Wyatt提出的第一种方法是根据风浪谱模型进行参数拟合,第二种方法是借鉴大气遥感领域的非线性迭代算法;Hisaki先后提出了完全的非线性迭代算法和结合海洋波浪模式的非线性迭代算法,Hashimoto提出了基于Bayesian统计的迭代算法,这些方法对资源的要求高,且计算时间长,不适合工程应用的实时性要求.本文借鉴地球物理学反问题研究成果[17-19],提出一种基于正则化策略的高频地波雷达海浪方向谱线性反演方法:先将非线性积分方程进行线性化直接接转化为关于海浪方向谱的线性方程,然后求解该大规模矩阵方程的方法.该方程为大型病态不适定方程,通过引人正则化罚函数,使得该问题变为适定问题,从而得到该方程的正则化逼近解.
2 反演模型基本原理与方法 2.1 Barrick基本方程Barrick在1972年推导了高频雷达与海面波浪相互作用的方程,奠定了高频雷达电波与海浪相互作用的理论基础.该理论指出:海洋回波一阶谱是由波长为雷达电波波长一半的海浪与雷达电波相互作用所产生的后向散射形成的,属于Bragg散射; 海洋回波二阶谱由雷达电波波矢k0。与波矢分别为k和k'的两列海浪共同作用而形成的,其中k0、k与k'之间满足k +k'=-2k0[20]. Barrick给出的方程为
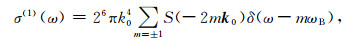
|
(1) |
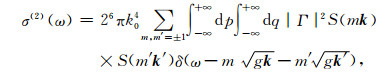
|
(2) |
其中σ(1)和σ(2)分别表示电波与海面波浪相互作用的一阶和二阶雷达散射截面(RCS),ω表示归一化角频率,k0为电波波数,表明电波波矢量的大小,ωB为Bragg散射频率,S(k)为海浪方向谱,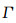
Hasselmann指出,在一阶峰附近的二阶谱的散射波矢k≈-2k0,相应的海浪处于短海浪波长,其浪高谱随波矢k'成k'-4变化[21].这种短海浪波长的海浪经风吹很容易形成并达到饱和状态,且方向大致相同.
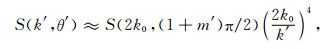
|
(3) |
利用一阶谱能量Rm'=26πk04S(2k0,(1 +m')π/2)对二阶谱进行归一化,从而消除路径衰减等乘性因子的影响,则(2)式可以写成:
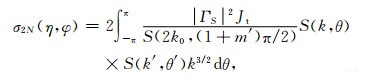
|
(4) |
其中,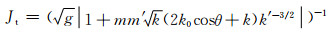
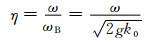
将海浪方向谱近似表达式(3)代入(4)式,则有:
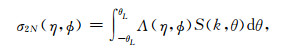
|
(5) |
其中,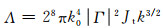
由上述二阶散射方程可知,二阶散射截面是沿着等频线η的积分值,因此将海浪方向谱S(k,θ)=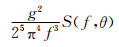
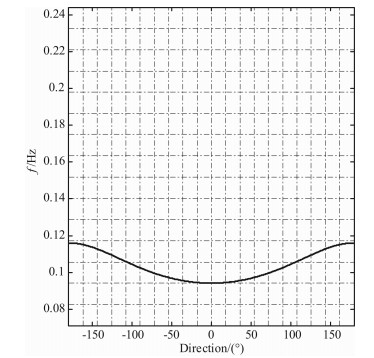
如图 1所示,将空间方位离散为M个方位,将可以反演的有效海浪频率离散为N个频点,则平面上共有M×N个格点的谱值,每个方格内的谱值看做是定值,则二阶散射截面可以表示为曲线经过格子处的加权累加,每个格子内的谱值可以当做周围四个格点处谱值的加权求和.图中曲线为归一化多普勒频率为1. 2对应的等频线.设格点(i,j)处的海浪谱值x(i,j),则离散化的海浪方向谱可以表示为
|
图 1 海浪方向谱离散化示意图 Fig. 1 Diagram of discrete ocean wave directional spectra |
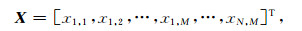
|
(6) |
那么每个方格的谱值可以表示为
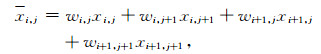
|
(7) |
从而方格的谱值组成矩阵后可以表示为
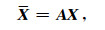
|
(8) |
其中,A为由权值w组成的权矩阵.
归一化的二阶散射截面可以表示为

|
(9) |
其中,C为每个海浪方向谱元的系数矩阵,
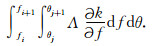
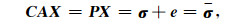
|
(10) |
其中,P=CA为该方程的系数矩阵,e表示观测噪声,σ为包含噪声的归一化二阶散射截面.
3 正则化反演方法 3.1 正则化模型对于(10)式这类大型矩阵方程,具有不适定性,数学上适定性问题满足三个条件:(1)解的存在性;(2)解的唯一性;(3)解的稳定性.不满足这三个条件中的任何一项即可以定义为不适定问题.不适定问题只能在某种意义上求取近似解,这在数学物理学反问题中普遍存在[22-27]. 1977年Tikhonov提出了完整的不适定问题正则化理论,通过引入正则化项将不适定问题转化为近似的适定问题来求解.本文基于Tikhonov正则化思想将问题(10)转化为求代价函数最小的优化问题,其代价函数可以表示为
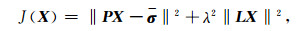
|
(11) |
其中,L为正则化算子,λ为正则化参数,控制着问题的解对P和σ的敏感程度.
上述优化问题(1)的代价函数中第二项代表了正则化项,由于该项的存在,使得不适定问题解的唯一性和稳定性得到保证.通常正则化项中包含了模型的某些先验知识,因此,能够在反演中帮助去除奇值,提高算法的收敛速率.在选择正则化算子时,往往希望既易于实现,又能较好的保持细节信息.一般有Tikhonov单位算子、Laplace算子、总变差正则化算子、双边滤波正则化算子等,这些与具体问题的先验信息相关.由于海浪方向谱具有光滑特性,在此选取Tikhonov单位算子,即海浪方向谱的二范数最小,从而将代价函数改写为

|
(12) |
对(12)式求导,可以得到
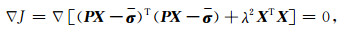
|
(13) |
从而得到正规方程组
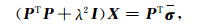
|
(14) |
则问题的解为
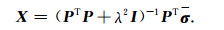
|
(15) |
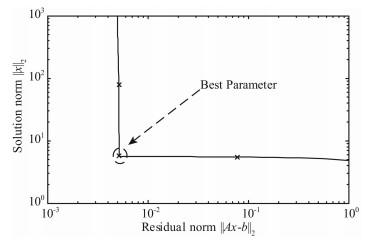
利用(15)式求得的正则化解包括两方面的误差,一方面来自矩阵方程右端的观测数据误差项e,另一方面是引入正则化项带来的误差.对于最小目标函数,正则化参数对反演结果起着重要的作用,它控制着正则化项误差和观测数据误差项在目标函数中所占的比例.一个好的正则化参数能合理的平衡这两种误差.从物理意义上来看,观测数据误差项反映了反演结果的失真程度,而正则化误差项则是反演结果的平滑程度度量.如果正则化参数选取的小,则意味着正则化误差项在代价函数中所占的比例少,对反演结果平滑程度的影响也小,此时,噪声得不到很好的抑制,反演结果中噪声将会很大;相反,如果正则化参数选取的大,则意味着正则化误差项在代价函数中所占的比例大,观测数据误差项比例小,此时,反演结果过于平滑,细节不易突出,但是噪声将会得到很好的抑制.通常的正则化参数选取方法有偏差原理(Discrepancy Principle),L曲线法(L-Curve)和广义交叉验证(GCV)方法等.实际中由于无法得知右端观测数据误差的大小,因此通常采用L曲线法来确定正则化参数[28]. Hansen[28-29]从理论上给出了L曲线特征的完全分析,并用多个实例证明了采用L曲线选择的参数等价于偏差原理和广义交叉验证法,并且L曲线法具有其它两种方法不具备的优点.图 2给出了L曲线确定正则化参数的示意图,其中横坐标表示正则化解残差的范数,纵坐标表示正则化解的范数.从(24)式可以看出,当正则化参数变大,则解的范数具有较大的权,从而解的范数变小,残差的范数变大,对应于图 2中水平部分; 反之,则对应于图 2中垂直部分.
|
图 2 利用L曲线确定正则化参数示意图 Fig. 2 Diagram of regularization parameter determination by L-curve method |
对于(15)式中矩阵的逆求解比较复杂,本文采用奇异值分解法来求解(14)式正规方程.首先,对P进行奇异值分解,可以表示为
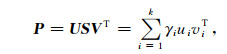
|
(16) |
式中,U为m×n阶正交矩阵,U=[u1,u2,…,um],V为n×n阶正交矩阵,V=[v1,v2,…,vn],S为对角阵,S=diag(γ1,γ2,…,γk), k=min{m,n},γ1 ≥ γ2≥ … ≥γk>0.
将上式代入到正规方程中,并分别左乘VT,(SST)-1,V后得到
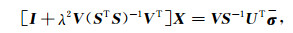
|
(17) |
(17)式的左边可以写成
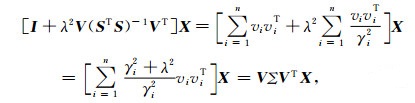
|
(18) |
其中,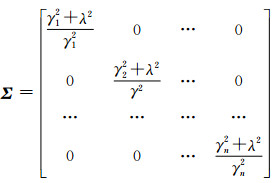
将上式代入(17)式便可得到
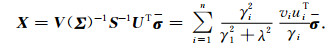
|
(19) |
(19)式即为问题的Tikhonov正则解.
由矩阵条件数计算可知,矩阵P的最小奇异值越小,其病态越严重,加入一个正则化因子对解施加了一个弱的平滑度约束,使得正规方程组的病态状况有很大改善,从而也滤掉了较小奇异值的解.
4 反演算法数值模拟为了验证本文提出的海浪方向谱反演算法的有效性,设计了数值模拟试验.先利用方程(1)和方程(2)进行正演运算,得到给定条件下的归一化海面回波多普勒谱数据σtrue由于观测值不可避免的带有各种噪声,假定该噪声为可加性高斯白噪声,则模拟的观测数值可以表示为
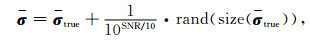
|
(20) |
其中,SNR为信噪比,mnd(size(σtrue))为与σtrue维数一致的高斯噪声矩阵.数值模拟中,采用的海浪方向谱为二维频率谱与方向因子的乘积,其中二维频率谱为Pierson-Moscowitz谱,方向因子Longuet-Higgins方向函数.
4.1 单部雷达反演数值模拟对于单部雷达,由于探测原理固有的模糊性,不能分辨出跟雷达波束方向夹角相同的两列频率相同的海浪,因此,只能反演出频率谱.对于单站情况进行了3次仿真实验(图 3-5):
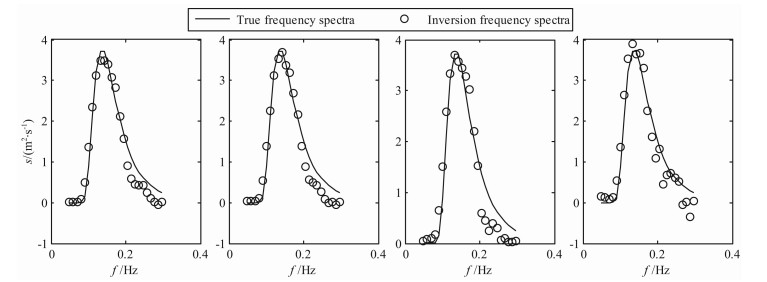
|
图 3 单部雷达仿真实验1条件下反演的频率谱 Fig. 3 Frequency spectra inversion by single radar at simulation experiment 1 |
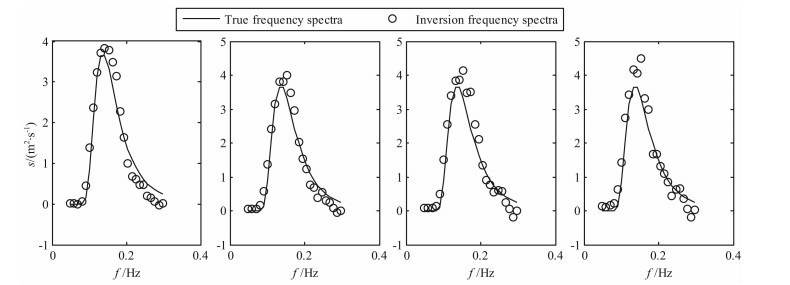
|
图 4 单部雷达仿真实验2条件下反演的频率谱 Fig. 4 Frequency spectra inversion by single radar at simulation experiment 2 |
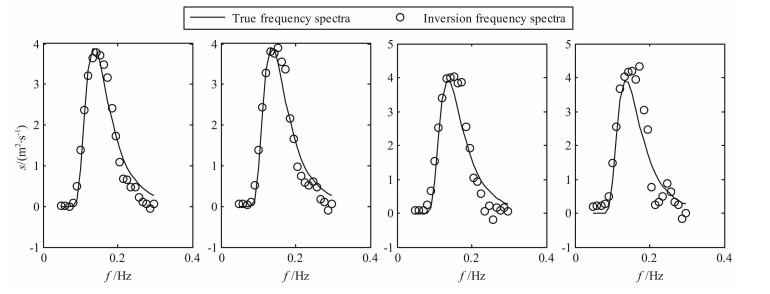
|
图 5 单部雷达仿真实验3条件下反演的频率谱 Fig. 5 Frequency spectra inversion by single radar at simulation experiment 3 |
仿真实验1:雷达工作频率f0=25. 4 MHz, 风速u=10 m/s,风向φw=90°,风向扩展因子s=4, 雷达波束方位φr1=0°,SNR=15、10、8、5 dB.
仿真实验2 :雷达工作频率f0=25. 4 MHz, 风速u=10 m/s,风向φw=45°,风向扩展因子s=4, 雷达波束万位φr1=0°,SNR=15、10、8、5 dB.
仿真实验3 :雷达工作频率f0=25. 4 MHz, 风速u=10 m/s,风向φw=135°, 风向扩展因子s=4, 雷达波束方位φr1=0°,SNR=15、10、8、5 dB.
4.2 双部雷达反演数值模拟对于双部雷达,可以消除与雷达波束方向夹角相同的两列海浪的模糊性,从而能反演出海浪方向谱.对于双部雷达情况进行了三次仿真实验:
仿真实验4 (图 6-8)雷达工作频率f0=25.4 MHz,风速u=10 m/s,风向φw=90。,风向扩展因子s=4, 雷达1波束方位φr1=0°,雷达2波束方位φr2=60°.
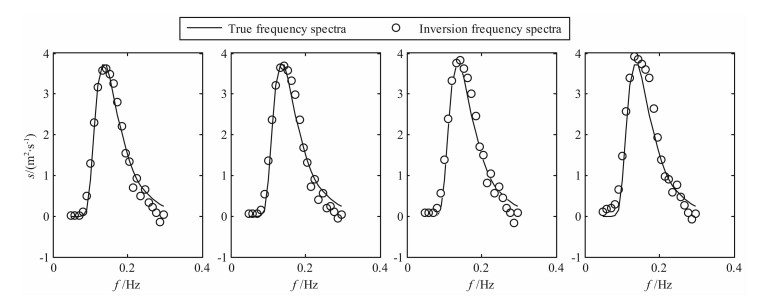
|
图 6 双部雷达仿真实验4条件下反演的频率谱 Fig. 6 Frequency spectra inversion by two radars at simulation experiment 4 |
|
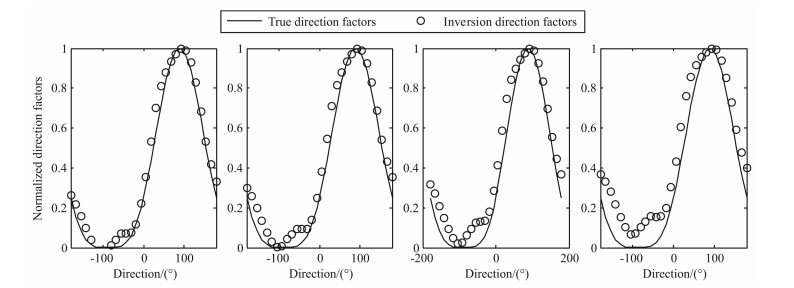
图 7 双部雷达仿真实验4条件下反演的方向因子 Fig. 7 Direction factors inversion by two radars at simulation experiment 4 |
|
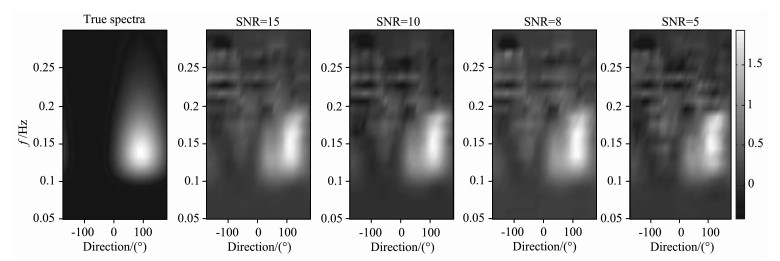
图 8 双部雷达仿真实验4条件下反演的方向谱 Fig. 8 Ocean wave directional spectra inversion by two radars at simulation experiment 4 |
仿真实验5(图 9-11):雷达工作频率f0=25.4 MHz,风速u=10 m/s,风向φw=135°,风向扩展因子s=4,雷达1波束方位φr1=0°,雷达2波束方位φr2=60 °.
|
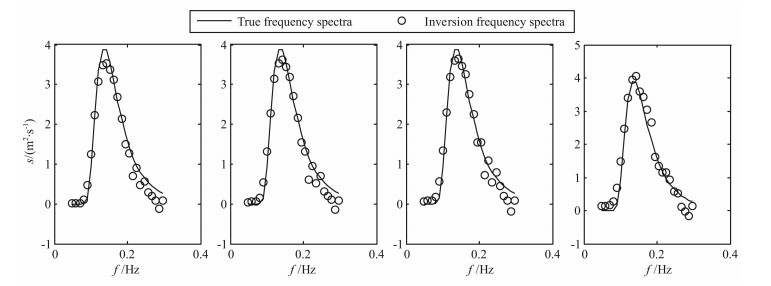
图 9 双部雷达仿真实验5条件下反演的频率谱 Fig. 9 Frequency spectra inversion by two radars at simulation experiment 5 |
|
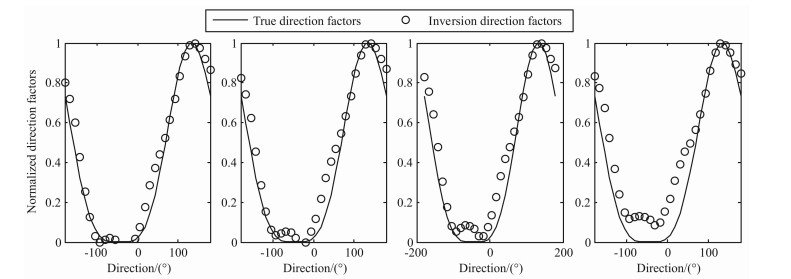
图 10 双部雷达仿真实验5条件下反演的方向因子 Fig. 10 Direction factors inversion by two radars at simulation experiment 5 |

|
图 11 双部雷达仿真实验5条件下反演的方向谱 Fig. 11 Ocean wave directional spectra inversion by two radars at simulation experiment 5 |
仿真实验6(图 12-14):雷达工作频率f0=25.4 MHz,风速u=10 m / s,风向φw=45°,风向扩展因子s=4,雷达1波束方位φr1=0 °,雷达2波束方位φr2=120°.
|
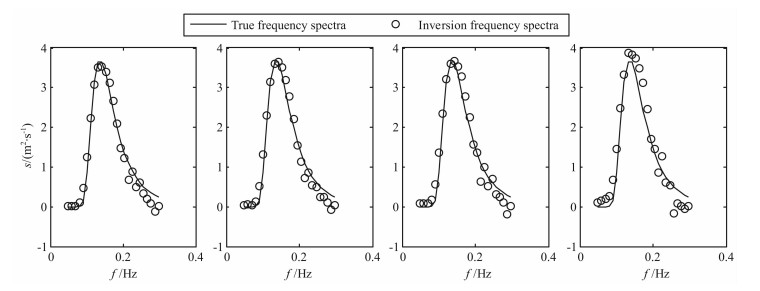
图 12 双部雷达仿真实验6条件下反演的频率谱 Fig. 12 Frequency spectra inversion by two radars at simulation experiment 6 |
|
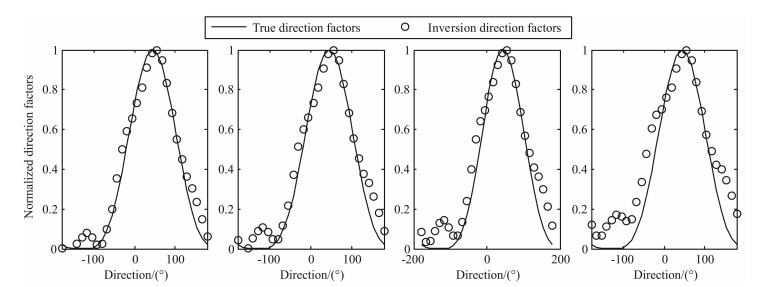
图 13 双部雷达仿真实验6条件下反演的方向因子 Fig. 13 Direction factors inversion by two radars at simulation experiment 6 |
|
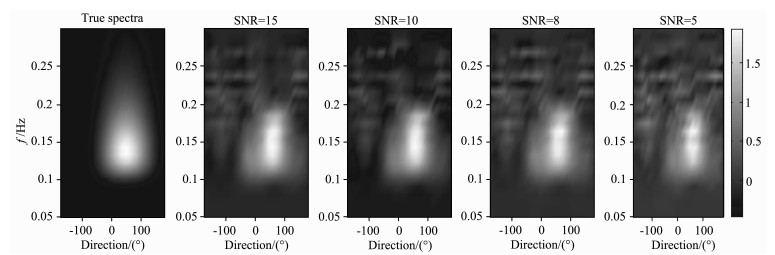
图 14 双部雷达仿真实验6条件下反演的方向谱 Fig. 14 Ocean wave directional spectra inversion by two radars at simulation experiment 6 |
通过上述6个仿真实验结果可以看出,利用本文提出的基于正则化方法的海浪谱反演方法能够得到较为准确的海浪谱.从图 3-5中可以看出,在单站雷达模式下得到的频率谱与仿真给定的频率谱符合得较好,峰值频率吻合程度高;从图 8、图 11和图 14中可以看出,利用两部雷达能够得到较为准确的海浪方向谱,在反演的谱图上能够明显的反映海浪能量随方向和频率的分布,利用海浪频率谱、方向因子和方向谱之间的关系,可以由方向谱得到频率谱和方向因子,图 6、图 9和图 12是相应的频率谱,与给定的频率谱吻合程度高;图 7、图 10和图 13是相应的归一化方向因子,与给定的方向因子吻合程度高,信噪比越高,符合程度越好.从反演得到的频率谱中可以看出在海浪频率较高部分会出现谱值抖动性较大的现象,这种现象在反演的海浪谱图中的表现是频率较高部分谱图的某些方向上会出现一些局部谱值,这是由于图 1所示的等频线在海浪频率较高部分未能完全覆盖,这样会造成雷达回波中未包含较高频率海浪部分方向的信息,从而导致反演结果的抖动性,从现有的反演方法看,这种现象是合理的,今后需要结合谱的分布模型来对这些区域进行反演.
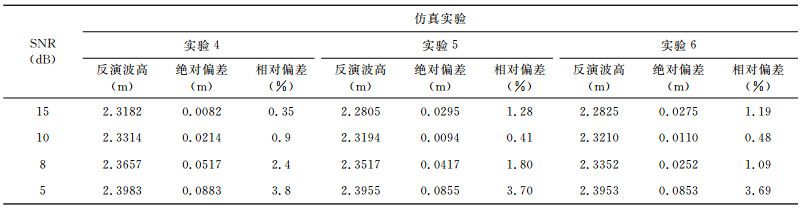
表 1和表 2利用海浪谱与海面有效波高之间的关系计算了由本文反演算法反演的海浪谱得到的有效波高,并给出了相对偏差和绝对偏差,单站模式下,绝对偏差在0.15 m以内,相对偏差在6.5%以内.双部雷达模式,绝对偏差在0.1 m内,相对偏差在4%以内.从整体来看,呈现出信噪比越高,有效波高符合程度越高,这从信息论角度来说是合理的; 但是也存在信噪比低,反演的结果符合程度好的现象,这是由于反演方程在线性化过程中会带来一定的误差,正则化过程也会带来一些误差,这些误差从某种程度上也可以看成噪声,也会影响反演结果.总的来说,对于不同的信噪比,本文提出的方法具有一定的普适性.
|
|
表 1 单部雷达反演数值模拟反演有效波高表 Table 1 Significant wave height inversion simulation by single radar |
|
|
表 2 双部雷达反演数值模拟反演有效波高表 Table 2 Significant wave height inversion simulation by two radars |
利用上述方法对位于福建龙海的中程高频地波雷达OSMAR071观测数据进行分析.高频地波雷达OSMAR071是武汉大学电波传播实验室研制的阵列式OSMAR系列高频地波雷达的定型产品,回波信号质量较OSMAR工程样机有较大的改善[30].该雷达是采用FMICW波形的宽波束地波雷达,波束范围可达150°,扫频带宽为30 kHz,距离分辨率为5 km,接收阵列为8元非线性阵列,采用基于海洋回波的无源校准方法进行通道幅度和相位一致性校准后,利用超分辨算法进行MUSIC(Multiple Signal Classification)算法对海流测向精度可达1.5°该雷达每0.6528×1024 s可以得到一场多普勒谱数据.
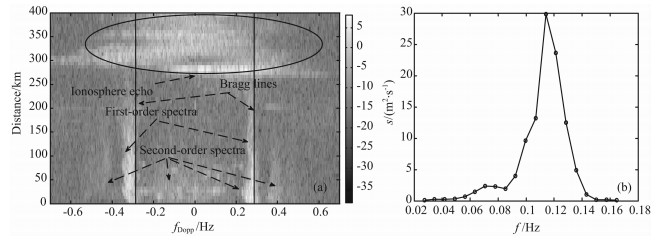
分析的数据时间为2009年6月22日15 :00“莲花”台风期间的数据,当时雷达工作频率为7.90 MHz. 图 15a给出了探测的回波距离-多普勒谱,从图上可以明显看到三维多普勒谱特征:在正、负Bmgg频率附近有两个较强的一阶谱区,距离可达250 km,一阶谱区周围有连续的二阶谱区,距离能达到100 km左右,在270 km附近和300 km附近有覆盖较宽多普勒频率的强回波,这是由于天线辐射部分能量到电离层,电离层回波引起的,通常称为电离层干扰.图中的两条竖线是深水条件下的Brngg频率线,通过一阶谱区谱点偏离Bagg线的频偏量可以得到海流信息.通过二阶谱可以反演海浪相关信息,单部雷达可以反演海浪频率谱信息,图 15b为利用本文提出的方法得到的海浪频率谱,该分析的距离30 km,与正北夹角160°方向,可以反演的海浪频率范围为0.0274-0. 1720 Hz算法实施过程中将0.0274 Hz到0. 1720 Hz的频率范围等分划分为20段,方位划分为30段,从而未知数个数为600,有效的观测频点个数为160,正则化参数为0.05.从图 15b可以看出反演的频率谱具有单峰特征,主效海浪频率为0.1141 Hz,由此频率谱计算得到的有效波高为3.51 m,符合于台风期间海况相对较高的实际情况.
|
图 15 OSMAR071探测到的回波多普勒谱和反演的海浪频率谱(2009年6月22日15:00) (a)回波多普勒谱;(b)海浪频率谱. Fig. 15 Doppler Spectrum detected by HFSWR OSMAR071 and inverted wave frequency spectra (2009-06-22 15:00) |
本文提出了一种从高频地波雷达海洋回波谱中反演海浪方向谱的方法.先将海浪方向谱直接离散化,使得线性化后的归一化高频地波雷达海面回波二阶散射截面积分方程离散化为矩阵方程,然后矩阵方程转化为Tikhonov正则化条件下的优化问题.通过引入二范数最小正则化条件,得到了海浪方向谱的近似解.通过模拟仿真试验,表明该方法能够在一定程度上抑制观测噪声,反演出海浪方向谱; 实测数据的初步应用中,得到了海浪频率谱,表明了该算法的有效性.这对于实际应用提供了有希望的前景.由于实测数据存在着很多不确定性,在该算法进行工程性应用前还需对以下问题进行明确:(1)与实测海浪方向谱的比对工作;(2)实测二阶谱的净化工作.这些都是下一步要研究的内容.此外,对线性化条件进行改进,或者直接发展一种非线性反演方法能进一步提高反演精度,也值得研究.
致谢感谢审稿人对本文的评阅.
| [1] | Wang Y F, Stepanova I E, Strakhov V N, et al. Inverse Problems in Geophysics and Solution Methods. Beijing: Higher Education Press, 2011 . |
| [2] | Crombie D D. Doppler spectrum of sea echo at 13.56Mc/s. Nature , 1955, 174(4459): 681-682. |
| [3] | Barnes L. HF Radar: The Key to Efficient Wide Area Maritime Surveillance. (Edition 3). London: ICG Publishing LTD, 1998 : 115 -118. |
| [4] | Barrick D E. 30 Years of CMTC and CODAR. Proceedings of the IEEE/OES/CMTC 9th Working Conference on Current Measurement Technology, 2008: 131-136. |
| [5] | Gurgel K W, Antonischski G, Essen H H, et al. Wellen radar(WERA): a new ground wave HF radar for ocean remote sensing. Coastal Engineering , 1999, 37(3-4): 219-234. DOI:10.1016/S0378-3839(99)00027-7 |
| [6] | 侯杰昌, 吴世才, 杨子杰, 等. 海洋表面流的高频地波雷达遥感. 地球物理学报 , 1997, 40(1): 18–26. Hou J C, Wu S C, Yang Z J, et al. Remote sensing of ocean surface currents by HF radar. Chinese J. Geophys (in Chinese) , 1997, 40(1): 18-26. |
| [7] | 吴雄斌, 杨绍麟, 程丰, 等. 高频地波雷达东海海洋表面矢量流探测试验. 地球物理学报 , 2003, 46(3): 340–346. Wu X B, Yang S L, Cheng F, et al. Ocean surface currents detection at the eastern China sea by HF surface wave radar. Chinese J. Geophys (in Chinese) , 2003, 46(3): 340-346. |
| [8] | Yan S H, Wu X B, Chen Z Z. Remote sensing with TDMF radar: some preliminary results. Progress in Electromagnetics Research Letters , 2010, 14: 79-90. |
| [9] | Barrick D E. Extraction of wave parameters from measured HF radar sea-echo doppler spectra. Radio Science , 1977, 12(3): 415-424. DOI:10.1029/RS012i003p00415 |
| [10] | Lipa B J, Barrick D E. Extraction of sea state from HF radar sea echo: mathematical theory and modeling. Radio Science , 1986, 21(1): 81-100. DOI:10.1029/RS021i001p00081 |
| [11] | Lipa B J, Barrick D E, Meresca J W, et al. HF radar measurements of long ocean waves. J. Geophys. Res. , 1981, 86(C5): 4089-4102. DOI:10.1029/JC086iC05p04089 |
| [12] | Howell R, Walsh J. Measurement of ocean wave spectra using narrow-beam HF radar. IEEE Journal of Oceanic Engineering , 1993, 18(2): 296-305. |
| [13] | Green J J, Wyatt L R. Row-action inversion of the barrick-weber equations. Journal of Atmospheric and Oceanic Technology , 2006, 23(3): 501-510. DOI:10.1175/JTECH1854.1 |
| [14] | Wyatt L R. The measurement of the ocean wave directional spectrum from HF radar doppler spectra. Radio Science , 1986, 21(3): 473-485. DOI:10.1029/RS021i003p00473 |
| [15] | Hisaki Y. Nonlinear inversion of the integral equation to estimate ocean wave spectra from HF radar. Radio Science , 1996, 31(1): 25-39. DOI:10.1029/95RS02439 |
| [16] | Hashimoto N, Tokuda M. A bayesian approach for estimation of directional wave spectra with HF radar. Coastal Engineering Journal , 1999, 41(2): 137-149. DOI:10.1142/S0578563499000097 |
| [17] | Jardani A, Revil A, Boleve A, et al. Three-dimensional inversion of self-potential data used to constrain the pattern of groundwater flow in geothermal fields. J. Geophys. Res. , 2008, 113: B09204. |
| [18] | Wang Y F. Regularization for inverse models in remote sensing. Progress in Physical Geography , 2012, 36(1): 38-59. DOI:10.1177/0309133311420320 |
| [19] | 韩波, 窦以鑫, 丁亮. 电阻率成像的混合正则化反演算法. 地球物理学报 , 2012, 55(3): 970–980. Han B, Dou Y X, Ding L. Electrical resistivity tomography by using a hybrid regularization. Chinese J. Geophys (in Chinese) , 2012, 55(3): 970-980. |
| [20] | Barrick D E. Remote Sensing of Sea State by Radar. // Derr V E, ed. Washington D. C.: U. S. Government Printing Office: Remote Sensing of the Troposphere, 1977. |
| [21] | Hasselmann K. Determination of ocean-wave spectra from Doppler radio return from the sea surface. Nature , 1971, 299: 16-17. |
| [22] | 杨文采. 非线性地球物理反演方法:回顾与展望. 地球物理学进展 , 2002, 17(2): 255–261. Yang W C. Non-linear geophysical inversion methods: review and perspective. Progress in Geography (in Chinese) , 2002, 17(2): 255-261. |
| [23] | 王文娟, 潘克家, 曹俊兴, 等. 基于Tikhonov正则化的双频电磁波电导率成像反演. 地球物理学报 , 2009, 52(3): 750–757. Wang W J, Pan K J, Cao J X, et al. Electrical conductivity imaging using dual-frequency EM data based on Tikhonov regularization. Chinese J. Geophys (in Chinese) , 2009, 52(3): 750-757. |
| [24] | 王彦飞, 杨长春, 段秋梁. 地震偏移反演成像的迭代正则化方法研究. 地球物理学报 , 2009, 52(6): 1615–1624. Wang Y F, Yang C C, Duan Q L. On iterative regularization methods for migration deconvolution and inversion in scismic imaging. Chinese J. Geophys (in Chinese) , 2009, 52(6): 1615-1624. |
| [25] | Tikhonov A N, Arsenin V Y. Solutions of Ill-posed Problems. New York: John Wiley and Sons, 1977 . |
| [26] | 崔岩, 王彦飞, 杨长春. 带先验知识的波阻抗反演正则化方法研究. 地球物理学报 , 2009, 52(8): 2135–2141. Cui Y, Wang Y F, Yang C C. Regularizing method with a priori knowledge for seismic impedance inversion. Chinese J. Geophys (in Chinese) , 2009, 52(8): 2135-2141. |
| [27] | 曹静杰, 王彦飞, 杨长春. 地震数据压缩重构的正则化与0范数稀疏最优化方法. 地球物理学报 , 2012, 55(2): 596–607. Cao J J, Wang Y F, Yang C C. Seismic data restoration based on compressive sensing using the regularization and zero-norm sparse optimization. Chinese J. Geophys (in Chinese) , 2012, 55(2): 596-607. |
| [28] | Hansen P C. Analysis of discrete Ill-posed problems by means of the L-curve. SIAM Review , 1992, 34(4): 561-580. DOI:10.1137/1034115 |
| [29] | Hansen P C, O'Leary D P. The use of the l-curve in the regularization of discrete Ill-posed problems. SIAM J. Science Compute , 1993, 14(6): 1487-1503. DOI:10.1137/0914086 |
| [30] | Wu X B, Li L, Shao Y X, et al. Experimental Determination of Significant Waveheight by OSMAR071: Comparison with Results from Buoy. Journal of Wuhan University Nature Science , 2009, 14(6): 499-504. DOI:10.1007/s11859-009-0608-8 |
 2013, Vol. 56
2013, Vol. 56