地球物理学报  2013, Vol. 56 Issue (1): 47-52   PDF    
引用本文
孙中苗, 翟振和, 肖云 等. 航空重力测量的系统误差补偿. 地球物理学报, 2013, 56(1): 47-52, doi: 10.6038/cjg20130105.  
Sun Z M, Zhai Z H, Xiao Y, et al. Systematic error compensation for airborne gravimetry. Chinese J. Geophys. (in Chinese), 2013, 56(1): 47-52, doi: 10.6038/cjg20130105.  
航空重力测量的系统误差补偿
孙中苗1,2 , 翟振和1,2 , 肖云1,2 , 李迎春1,2     
1. 西安测绘研究所, 西安 710054;
2. 地理信息工程国家重点实验室, 西安 710054
收稿日期 2012-03-21, 2012-06-23 收修定稿
基金项目: 国家自然科学基金项目(41174017)资助
作者简介: 孙中苗, 男, 1968年生, 研究员, 博士, 博导.现从事航空重力测量理论与方法的研究.E-mail:sun_szm@sina.com
摘要: 基于航空重力测量的基本数学模型, 详细分析了航空重力测量的系统误差来源.大致可将系统误差分为三类, 即停机坪重力基准值、比力初值的观测误差, 格值、交叉耦合系数、摆杆尺度因子的标定误差和水平加速度改正的模型化误差等.然后, 对每类系统误差的量级及其补偿方法进行了研究, 指出水平加速度改正是引起系统误差的主要因素之一.大同、哈尔滨和渤海湾航空重力测量的实测数据分析均表明, 在各项系统误差尤其是水平加速度改正得到有效补偿后, 航空重力与地面(或船测)参考值的系统误差将小于1×10-5m·s-2.
关键词: 航空重力测量      交叉耦合改正      摆杆尺度因子      水平加速度改正      系统误差     
Systematic error compensation for airborne gravimetry
SUN Zhong-Miao1,2, ZHAI Zhen-He1,2, XIAO Yun1,2, LI Ying-Chun1,2     
1. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China
Abstract: Sources of systematic errors in airborne gravity measurements are analyzed in detail using the basic mathematical model. They can be classed into three types. One is the observation error in the apron gravity and the base reading of the airborne gravimeter, the second is the calibration error of cross-coupling correction, beam scale factor and the scale value, and the third is the modeling error for the horizontal acceleration correction. The magnitudes of the various systematic errors are discussed and the related compensation methods are proposed. It is indicated that the modeling error of the horizontal acceleration correction is one of the largest errors. Analysis of real data demonstrates that after compensating the various systematic errors especially the modeling error of the horizontal acceleration correction, the systematic bias between airborne gravity and the ground (or sea) reference value in the Datong and Harbin areas and Bohai Bay are all less than 1×10-5m·s-2..
Key words: Airborne gravimetry      Cross-coupling correction      Beam scale factor      Horizontal acceleration correction      Systematic error     
1 引言

航空重力测量主要用于快速获取地面重力测量难以到达地区的地球重力场信息.早期的航空重力测量由于当时所用导航设备的精度限制, 仅取得一些低精度的试验性成果[1-2]; 1990年前后, 高精度动态差分GPS技术在航空重力测量中得到广泛应用, 获得了大量有意义的航空重力测量成果[3-4].目前可实用的航空重力测量系统主要有平台式和捷联式两类.平台式是将航空重力仪(如LCR、Bell重力仪)安装在二轴或三轴阻尼平台上进行测量, 半波长分辨率为5~10km时的精度为(2~8)×10-5m·s-2[5-10]; 捷联式是捷联式惯性导航和GPS组合的重力测量系统, 其与平台式系统对于中等分辨率具有相当精度[11-13].我国于2003年投入使用的航空重力测量系统(CHAGS)采用了LCR航空重力仪, 属平台式系统, 迄今已经完成了近40万平方公里的测量, 5′×5′格网平均重力异常的标准差为(2~5)×10-5m·s-2[14-16].

CHAGS采用相对重力测量原理, 即航空重力仪在飞机起飞前、降落后需在停机坪作静态观测, 以将航空重力观测值与地面重力基准值相联系.此过程在得到航空重力仪初始观测值的同时, 实现了航空重力与地面重力的基准统一.统一基准后, 理论上航空重力和地面重力之间不应存在明显的系统偏差.但实测数据计算结果表明, 如果对航空重力测量潜在的系统误差未能进行有效地补偿, 两者之间将存在(3~4)×10-5m·s-2的系统偏差[14], 当然这其中也包含了地面重力测量可能存在的系统误差.

本文将从航空重力测量的基本数学模型出发, 全面分析CHAGS的系统误差成因并进行分类, 然后按类探讨各项系统误差的补偿方法, 最后以实测数据分析补偿效果.

2 基本数学模型及系统误差分类

航空重力标量测量的基本数学模型为[11, 14]:

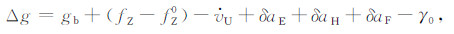
(1)

式中, Δg为测线(空中)重力异常; gb为停机坪处的重力基准值; fZ、fZ0分别为比力及其初值; 、δaE分别为垂直加速度、厄特弗斯改正和水平加速度改正; δaE表示空间改正; γ0为正常重力.

比力fZ的计算公式为:

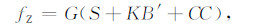
(2)

式中, G为重力仪的格值, 用于将计数单位转换成mGal; S为弹簧张力; K为重力仪的摆杆尺度因子, 也称K因子; B′为摆杆的速度; CC为交叉耦合改正.

LCR航空重力仪的CC改正可用其五个监视项表示为如下线性关系[14]:

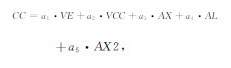
(3)

式中, ai(i=1, …, 5)为CC系数; VE、VCC、AX、AL、AX2分别是五个CC监视项的名称, 在航空重力仪中均有直接输出.

将(2)、(3)式代入(1)式, 整理可得:

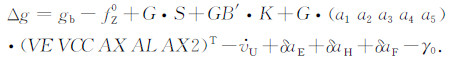
(4)

严格而言, (4)式右端的每一项都有可能产生系统误差.按成因划分, 大致可分为三类.一是观测误差, 包括停机坪重力基准值gb的联测误差、比力初值fZ0的观测误差; 二是标定误差, 主要是格值G、CC系数、K因子的标定误差; 三是δaH、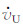、δaE等改正项的模型化误差.

3 系统误差补偿方法 3.1 观测误差的补偿

停机坪处的重力基准值通常是用陆地重力仪从重力基准点(如2000国家重力基本网的基本点或其引点)联测得到.一般按二等重力点精度联测, 故因联测引起的系统误差可忽略不计.但航空重力仪安装在机舱内, 重力传感器中心离停机坪有一定高度, 需将停机坪的重力基准值归算至重力传感器中心.对于常用的航测飞机, 向上归算高度为2~3 m.若不进行此项归算, 将产生约1×10-5 m·s-2的系统误差.

比力初值fZ0是航空重力仪在停机坪处的静态观测值.飞机起飞前和降落后一般均要求观测20min以上.若航空重力仪的零点漂移不大, 一个飞行架次(5~6h)的闭合差一般小于0.5×10-5m·s-2; 取初始观测和闭合观测之均值作为fZ0, 系统误差可小于0.25×10-5m·s-2.若零点漂移较大, 则需进行零点漂移改正[17].

3.2 标定误差的补偿

格值G、CC系数、K因子等常数都是由厂家标定获得的.随着仪器使用年限的增加, 这些常数显然发生着变化.若不及时作出新的标定, 它们将成为引起系统误差的主要因素.这类系统误差的补偿, 主要在于建立合适的标定模型.

3.2.1 格值G的标定

厂家给出的格值是在一个重力段差约为240× 10-5m·s-2的野外基线场上测得的.实际测量时, 由于空中相对于地面的重力段差往往比上述重力段差大得多, 因此需采用重力段差较大的长基线对格值进行重新标定, 以降低仪器的系统误差进而提高航空重力测量的精度.通常, 航空重力测量作业区域距离驻地较远, 驻地机场和作业区机场就可构成重力段差满足要求的长基线.若两者间的基线长度不够或重力段差太小不能满足要求, 基线的一端可选择其它机场.标定时, 重力段差采用高精度的陆地相对重力仪或绝对重力仪同步测得.

设A和B分别为重力长基线的两个端点, A点和B点的重力段差为Δg0.若在A点作两次观测(即进行闭合测量), 弹簧张力的观测值依次为SA1、SA2, 相应的潮汐改正为TA1、TA1, 两次观测的平均时间间隔为Δt0.进一步设重力仪在B点的弹簧张力观测值为SB, 潮汐改正为TB, 距A点的第一次观测的平均时间间隔为ΔtB, 则可得格值G的计算公式为

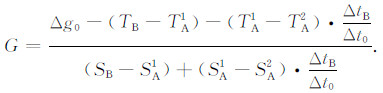
(5)

文献[18]研究表明, 按式(5)标定的新格值较旧格值约大1/1000, 由于重力仪从地面到飞行高度(离地大于1500 m)的段差平均为850CU(计数单位), 最大达2800CU, 与地面参考数据相比较, 系统性误差约为1×10-5m·s-2.

3.2.2 CC系数的标定

分为外部标定法和内部标定法.外部标定法需要利用航空重力测量区域内已有的高精度地面重力测量数据.假设由地面重力测量数据采用向上延拓算法获得的采样点Pi的空中重力异常参考值为ΔgPi, 则由(4)式可得:

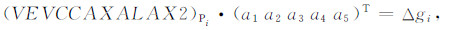
(6)

式中,

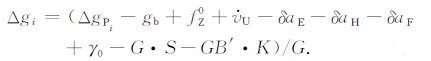
(7)

将多个采样点按(6)式组成观测方程, 通过最小二乘方法即可解出交叉耦合改正的五个系数a1~a5.

若在航空重力测量区域没有或只有少量地面重力测量数据, 可以采用基于交叉点不符值的内部标定法.假设测线i与测线j相交于P点, 则P点的空中重力异常不符值Vij可表示为:

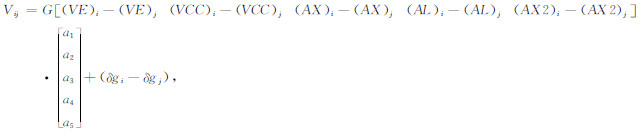
(8)

式中, δg=gb-fZ0-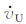+ δaE + δaH +δaF -γ0 + GS +GB'·K.由多个交叉点按(8)式组成观测方程组, 利用最小二乘方法即可解得CC改正的五个系数a1~a5.

3.2.3 K因子的标定

与CC系数的标定类似, 可分为外部标定法和内部标定法.对于外部标定法, 有:

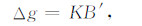
(9)

式中, Δg=(ΔgP-gb+fZ0+ -δaE-δaH -δaF+ γ0 -G·S-G·CC)/G.

可见, 只要绘制出Δg相对于B′的变化图, 通过曲线拟合方法即可标定K因子.

对于内部标定法, 有:

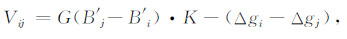
(10)

式中, Δg=gb-fZ0-+δaE +δaH +δaF -γ0 + GS+G·CC.

由多个测线交叉点不符值, 按最小二乘原理即可求出K因子.

此外, CC系数和K因子可同时进行标定, 标定模型与(9)式·(10)式类似, 此处不再详述.

文献[14]研究表明, 利用新标定的CC系数和K因子计算的空中重力异常与地面参考值的系统偏差可得到显著减小.

3.3 模型误差的补偿

(1)式中, 垂直扰动加速度、厄特弗斯改正、空间改正、正常重力以及水平加速度改正均需要按照相应的数学模型进行计算.其中前四项的输入信息是飞机的位置和速度, 目前利用GPS确定的位置和速度的精度分别可优于10cm、1cm/s, 由此引起的系统误差均小于0.5×10-5m·s-2, 故一般不予顾及.此处重点讨论水平加速度改正的模型化误差.

假设利用GPS确定的水平加速度的东、北分量分别为aE、aN, 相应于aE、aN的平台倾角为α、β, 则水平加速度改正δaH为:

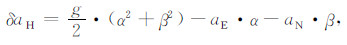
(11)

其中, α、β可用如下公式计算:

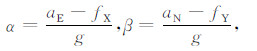
(12)

式中, fX、fY分别为平台横轴(横向水平加速度计)和纵轴(纵向水平加速度计)敏感到的水平加速度.

将(12)式代入(11)式化简得

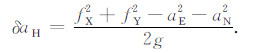
(13)

显然, (11)式和(13)式是完全等价的.但(11)式是水平加速度的线性组合, 即如果水平加速度属于零均值噪声, 由此产生的水平加速度改正误差也是零均值的, 从而在后续的重力估算中不会由此引入系统偏差.而(13)式是非线性形式, 零均值噪声取平方后变成正值噪声, 因fX或fY和aE或aN可能表现为不同的噪声特性, 减法运算难以抵消平方项中的噪声, 从而有可能由此带入系统偏差.对fX、fY、aE和aN作预滤波处理可以减弱这种影响, 但实用中预滤波尺度的选择存在不确定性(见表 1分析).

表 1 水平加速度改正方法比较（单位：l0-5m·s-2) Table 1 Comparison of horizontal acceleration corrections by different methods (unit: 10-5m·s-2)

文献[19]研究表明, 阻尼式平台的倾角α、β在0.01Hz以上的频段基本没有信息, 因此可用与平台运动周期相当的60~100s的低通滤波器先对α、β作滤波处理, 再按(11)式计算水平加速度改正, 以此来降低系统偏差的影响.表 1对上述两种处理方法进行了对比(以大同航空重力测量中的南北测线NS026和东西测线WE002为例).

从表 1可以看出, 当(13)式的输入量以及(11)式的倾角均未经滤波时, 两种方法的结果相同, 因为它们本身就是等价的.但应用滤波器后, 均值产生了很大变化, 如对于WE002测线, 5s的预滤波使均值从4.68×10-5m·s-2变化至-2.23×10-5m·s-2.可见水平加速度改正可以引入显著的系统偏差.虽然对于(13)式, 随着预滤波尺度的增加, 均值变化不大, 但究竟多大的尺度为最优无法得知, 且最优滤波长度随着测量环境的不同也是变化的.对于(11)式, 采用不同的平台滤波器, 均值有些许变化, 但大致变化稳定.由于平台的运动特性是已知的, 平台滤波器的尺度容易确定, 因此这种方法相对合理.

4 实验结果与分析

实验数据分别源自2002年、2003年以及2008-2010年完成的大同、哈尔滨和渤海湾航空重力测量.三个测区内都有精度较高的地面(或船测)重力数据, 将其向上延拓到测线高度, 可以作为航空重力测量的外部参考(以下简称为参考值), 参考值的精度优于2.0×10-5m·s-2 [20].

大同实验区范围为1°40′×2°00′.测区东部属中等山区, 地形起伏较大, 最高海拔2800m, 西北部为丘陵区, 平均海拔1000 m.飞行高度上的重力异常为(-50~80)×10-5m·s-2.测线总计30条, 平均高度3400 m, 相邻测线间距5′.测量期间的平均飞行速度为360km/h.测区内设有5个地面GPS基准站, 飞机上装有2个GPS动态天线.测量于每天的7:00-12:00进行, 期间正值当地风季, 飞行条件较差.

哈尔滨测区范围1°20′×1°30′, 属平原地区, 地形最大起伏为170 m.飞行高度约1200 m, 平均飞行速度为230km/h, 共计飞行4架次, 24条测线, 其中南北、东西各12条, 相邻测线间距为5′.地面设置了3个GPS基准站, 机载GPS接收机2套.飞行测量于8:00-15:00进行, 气流相对平稳.

渤海湾测区范围包含16个1°×1°, 属陆海交界区域, 相邻测线的间距为5′, 飞行高度约2500m, 飞行速度平均约280km/h, 测量条件属中等湍流, 初步处理结果参见文献[21].

大同和哈尔滨测区可以分别构成165个和144个5′×5′空中格网平均重力异常, 渤海湾测区不失一般性选择了2个具有较高船测重力数据的1°×1°区域(共288个5′×5′空中格网平均重力异常), 它们与相应参考值之差统计于表 2.

表 2 航空和地面5'×5'格网平均重力异常之差统计（单位：l0-5m·s-2)reference values (unit：10-5m·s-2) Table 2 Differences of5 X5r mean gravity anomalies between airborne gravity survey and ground reference values (unit:10-5m·s-2)

从表 2可见, 对各类系统误差进行有效补偿后, 航空重力与地面(或船测)重力之间的系统偏差均小于1×10-5m·s-2, 远低于未作良好补偿之前的(3~4)×10-5m·s-2 [14, 21].其中, 尤以水平加速度改正的补偿效果最为明显(可参见表 1).

5 结语

航空重力测量的系统误差受诸多因素的影响, 本文将其分为观测误差、标定误差和模型化误差三类, 并对系统误差成因及其补偿方法进行了详细研究, 得出如下初步结论:

(1)停机坪重力基准值、航空重力仪比力初值可引入一定量的系统误差, 但航空重力与地面重力基准统一后, 这类观测误差通常很小, 可不予顾及.

(2)随着航空重力仪使用年限的增加, 厂家提供的格值、交叉耦合系数、摆杆尺度因子等仪器常数产生了变化, 它们是引起系统误差的主要因素之一, 采用外部和内部标定法重新标定的常数进行计算, 可极大地降低系统误差的影响.

(3)水平加速度改正是系统误差的主要来源, 利用本文给出的线性模型和基于运动平台特性设计的低通滤波器, 可以显著地减弱该项系统误差.

(4)对于大同、哈尔滨和渤海湾航空重力测量, 各类系统误差得到有效补偿后, 其与地面(或船测)参考值的系统偏差不到1×10-5m·s-2.

参考文献
[1] Thompson L G D, LaCoste L J B. Aerial gravity measurements. Journal of Geophysical Research , 1960, 65(1): 305-322. DOI:10.1029/JZ065i001p00305
[2] Nettleon L L, LaCoste L J B, Harrison J C. Tests of an airborne gravity meter. Geophysics , 1960, 25(1): 181-202. DOI:10.1190/1.1438685
[3] Brozena J M, Mader G L, Peters M F. Interferometric global positioning system:Three-dimensional positioning source for airborne gravimetry. Journal of Geophysical Research , 1989, 94(B9): 12153-12162. DOI:10.1029/JB094iB09p12153
[4] Hehl K. Bestimmung von Beschleunigungen auf einem bewegten Träger durch GPS und Digitale Filterung. München:Universität der Bundeswehr München, Heft 43, 1992.
[5] Brozena J, Childers V A. The NRL airborne geophysics program.//International Association of Geodesy Symposia, Geodesy Beyond 2000-The Challenges of the First Decade. Heidelburg:Springer Verlag, 2000:126-130.
[6] Forsberg R, Olesen A V, Keller K, et al. Airborne gravity and geoid surveys in the Arctic and Baltic seas.//Proceedings of IAG International Symposium on Gravity, Geoid and Geodynamics 2001. Banff, Canada, 2001:586-592.
[7] Harrison J C, MacQueen J D, Rauhut A C, Cruz J Y. The LCT Airborne Gravity System.//Proceedings IAG Symposium G4 Airborne Gravity Field Determination, XXI General Assembly of the IUGG. Boulder, Colorado, 1995:163-168.
[8] Klingelé E E, Cocard M, Halliday M E, et al. The Airborne Gravimetric Survey of Switzerland. Contribution to the Geology of Switzerland Series, Swiss Geophysical Commission, Report No. 31. 1995.
[9] 郭志宏, 罗锋, 王明, 等. 航空重力数据无限脉冲响应低通数字滤波器设计与试验研究. 地球物理学报 , 2011, 54(8): 2148–2153. Guo Z H, Luo F, Wang M, et al. The design and experiment of Ⅱ R lowpass digital filters for airborne gravity data. Chinese Journal of Geophysics (in Chinese) , 2011, 54(8): 2148-2153.
[10] 郭志宏, 熊盛青, 周坚鑫, 等. 航空重力重复线测试数据质量评价方法研究. 地球物理学报 , 2008, 51(5): 1538–1543. Guo Z H, Xiong S Q, Zhou J X, et al. The research on quality evaluation method of test repeat lines in airborne gravity survey. Chinese Journal of Geophysics (in Chinese) , 2008, 51(5): 1538-1543.
[11] Bruton A M. Improving the accuracy and resolution of SINS/GPS airborne gravimetry. Calgary:University of Calgary, 2001.
[12] Ferguson S, Hammada Y. Experiences with AIRGrav:Results from a New Airborne Gravimeter.//Proceedings of IAG International Symposium on Gravity, Geoid and Geodynamics 2000. Banff, Canada, 2000.
[13] Glennie C L, Schwarz K P, Bruton A M, et al. A comparison of stable platform and strapdown Airborne Gravity. Journal of Geodesy , 2000, 74(5): 383-389. DOI:10.1007/s001900000082
[14] 孙中苗.航空重力测量理论、方法及应用研究.郑州:信息工程大学, 2004. Sun Z M. Theory, methods and applications of airborne gravimetry (in Chinese). Zhengzhou:Information Engineering University, 2004. (in Chinese)
[15] 孙中苗, 夏哲仁, 石磐, 等. 航空重力测量数据的滤波与处理. 地球物理学进展 , 2004, 19(1): 119–124. Sun Z M, Xia Z R, Shi P, et al. Filtering and processing for the airborne gravimetry data. Progress in Geophysics (in Chinese) , 2004, 19(1): 119-124.
[16] 夏哲仁, 石磐, 孙中苗. 航空重力测量系统CHAGS. 测绘学报 , 2004, 33(3): 216–220. Xia Z R, Shi P, Sun Z M, et al. Chinese airborne gravimetry system CHAGS. Acta Geodaetica et Cartographica Sinica (in Chinese) , 2004, 33(3): 216-220.
[17] 孙中苗, 李迎春, 翟振和. LaCoste & Romberg航空重力仪的零点漂移. 测绘通报 , 2009(11): 24–26. Sun Z M, Li Y C, Zhai Z H. Zero drift of the LaCoste & Romberg airborne gravimeter. Bulletin of Surveying and Mapping (in Chinese) , 2009(11): 24-26.
[18] 孙中苗, 李迎春, 张松堂, 等. LaCoste & Romberg航空重力仪的格值标定. 大地测量与地球动力学 , 2008, 28(2): 132–135. Sun Z M, Li Y C, Zhang S T, et al. Calibration of scale value for Lacoste & Romberg airborne gravimeter. Journal of Geodesy and Geodynamics (in Chinese) , 2008, 28(2): 132-135.
[19] Olesen A V. Improved airborne scalar gravimetry for regional gravity field mapping and geoid determination. Copenhagen: University of Copenhagen, 2002 .
[20] 王兴涛, 夏哲仁, 石磐, 等. 航空重力测量数据向下延拓方法比较. 地球物理学报 , 2004, 47(6): 1017–1022. Wang X T, Xia Z R, Shi P, et al. A comparison of different downward continuation methods for airborne gravity data. Chinese Journal of Geophysics (in Chinese) , 2004, 47(6): 1017-1022.
[21] 张松堂, 孙中苗, 翟振和. 海岸带航空重力测量的初步结果及分析. 测绘科学与工程 , 2009, 29(1): 6–9. Zhang S T, Sun Z M, Zhai Z H. Initial results of airborne gravimetry in coast area. Geomatic Science and Engineering (in Chinese) , 2009, 29(1): 6-9.