2. 大庆钻探工程公司测井公司,大庆 163412
2. Wireline Logging Company, Daqing Drilling Engineering Company, Daqing 163412, China
多分量感应测井仪器是新一代的电测井仪器,由三轴发射(Tx,Ty,Tz)与三轴接收(Rx,Ry,Rz)线圈系组成,在每个深度点上能够同时测量出磁场的九个分量(Hxx,Hxy,Hxz,Hyx,Hyy,Hyz,Hzx,Hzy,Hzz)[1],能够提供地层纵横向电阻率、层边界位置和井眼倾角等多种信息[2-3],对砂泥岩薄交互层等电各向异性[4]地层评价将发挥积极作用.为了对多分量感应资料进行合理解释并建立有效的反演算法,需要研究考察各种复杂地层条件下仪器的响应特征.然而,共面线圈系电磁场不再具有轴对称性,多分量感应响应研究本质上涉及到非均质各向异性地层中电磁场的三维数值模拟技术.由于解析法[5-6]、模式匹配算法[7-9]等快速算法只能应用于相对简单的一维和二维地层模型中多分量感应特征的考察,对于倾斜井眼或裂缝储层等复杂地层模型,仍然需要借助三维数值模拟技术确定多分量感应测井响应,例如,三维有限差分(FD)[10-17],三维有限元(FE)[18]以及三维积分方程(IE)[19]等.然而在低频范围(小于1 MHz)和电阻率大反差地层中,传统三维数值方法往往会产生低感应数(LIN)问题[15],导致离散方程的收敛速度下降、效率降低等问题.目前解决这一问题主要通过两种途径:静态散度校正方法和低感应数预处理.静态散度校正首先由Smith[20]提出,通过在迭代运算过程中对离散电场添加一个标量梯度因子,使得校正后的电场Ec 满足如下关系:在导电介质中∇·σEc =0,在不导电介质中∇·Ec =0,使迭代速度提高2~4倍.Weiss和Newman提出了低感应数预处理方法[15],直接把电场分解为一个无源场和一个无旋场的叠加,目的是释放算子( ∇×∇×)的零空间,改善离散方程的条件数,在低频范围内可使迭代速度提高10~100倍.有限体积法作为一种广义有限差分方法具有非常好的守恒性,其基本思路是将研究区域分解成一系列不重复的控制体积,利用微分方程在控制体积上积分实现对该方程的离散.Haber[21]利用基于耦合势的有限体积方法考察了各向同性地层中的大地电磁问题.
本文旨在利用基于耦合势的有限体积算法研究非均匀各向异性地层中多分量感应测井仪器的三维响应.文中采用基于耦合势的交错网格[21],推导出非均匀各向异性介质中离散化的maxwell方程,其重点是对旋度算子作用下磁流源的离散.并应用不完全LU 分解预处理的稳定双共轭梯度法快速求解大型稀疏线性代数方程组.在数值模拟试验中,通过与解析和模式匹配方法计算结果的对比,检验该算法的有效性,并进一步研究考察仪器偏心、倾斜井、垂直裂缝等复杂条件下的测井响应.
2 方法与理论 2.1 Maxwell方程的分解设σ 是非均质各向异性地层中的电导率张量,电磁场随时间变化关系为eiωt,ω = 2πf是圆频率.非均匀各向异性介质中多分量感应测井的响应正演模拟就是求解如下的maxwell方程:
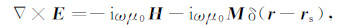
|
(1) |
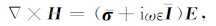
|
(2) |
其中μ0 =4π×10-7H/m 是真空磁导率,ε代表介电常数,I是单位张量,Mδ(r-rs)表示rs处的磁偶极子.将(2)代入(1),得到关于电场E的Helmholtz方程:

|
(3) |
其中,σ* 是复电导率张量,定义为
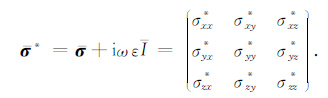
|
为克服低感应数问题,引入矢势A并满足库仑规范条件∇·A=0,以及标势φ,即将电场分解无散场和无旋场之和[21]:
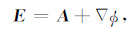
|
(4) |
于是,磁场可改写成:H=i ∇×A/ωμ0.将(4)代入到(3)中,并利用∇×∇×A=-∇2A,得到关于矢势和标势的Helmholtz方程:
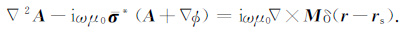
|
(5) |
(5) 式在x,y,z三个方向上的分量可分别表示为
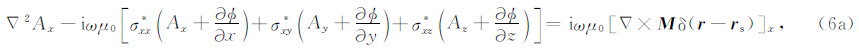
|
(6a) |
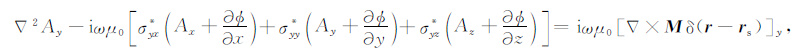
|
(6b) |
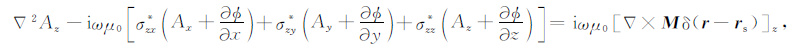
|
(6c) |
其中
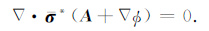
|
(7) |
(6a-6c)和(7)式联立就是完整的耦合势Helmholtz方程组,由于实际数值计算只能在有限大小的六面体区域Ω 内进行,所以在区域外边界∂Ω 上往往需添加截断边界条件n×E|∂Ω =0,由此,得到矢势、标势的截断边界条件[16]:
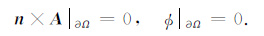
|
(8) |
为了求解式(6a-6c)和(7)在边界条件(8)式下的数值解,需要对其进行离散处理.为此,首先规定x、y和z三个方向上的网格剖分规则,在x方向上一共剖分Nx个网格,其Nx+1 个整数网格节点记为{xi|x0 <x1 <x2 < … <xi < … <xNx,i=0,1,2…,Nx},在整数网格的中点处标有Nx个半整数节点记为{xi|x1/2 <x3/2 <x5/2 < … <xi-1/2 < … <xNx-1/2,i=1,2…,Nx},这样就形成Nx-1个半整数网格.于是网格的整数间距和半整数间距可以统一表示为
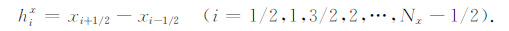
|
(9) |
y和z方向网格剖分方法与x方向完全相同.根据体积元中心在网格节点中的位置不同,计算区域Ω 可剖分成四种类型控制体积单元,每种控制体积单元对应的区域和体积为
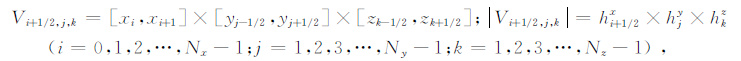
|
(10a) |
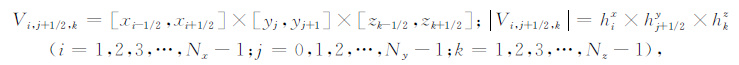
|
(10b) |
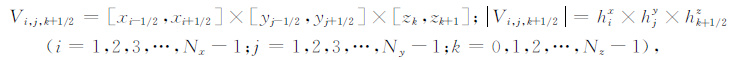
|
(10c) |

|
(10d) |
这四种控制体积元的个数与离散后未知量的个数相同且分别为:Nx× (Ny-1)× (Nz-1),(Nx-1)×Ny× (Nz-1),(Nx-1)× (Ny-1)×Nz,(Nx-1)× (Ny-1)× (Nz-1).
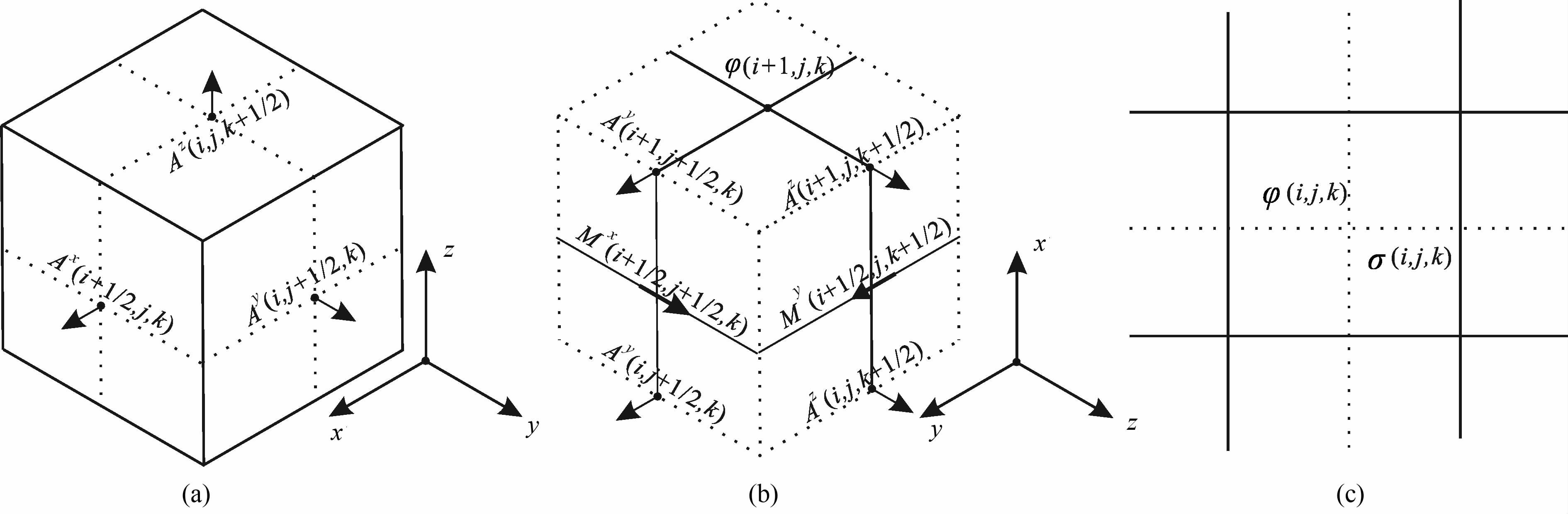
作为对传统交错网格进行扩展[22],下面以体积元Vi,j,k(i,j,k均为整数)为基础,给出基于耦合势的交错网格格式.离散矢势和电流密度矢量J的分量被定义在体积元Vi,j,k的面中心节点处,磁偶极子源定义在Vi,j,k棱的中点上,标势被定义在Vi,j,k的体中心处(如图 1a和1c所示).且假定Vi,j,k内部电导率为常数,而在相邻体积单元之间的边界上电导率是不连续的,甚至可能反差很大.与传统交错网格相比,基于耦合势交错网格的优势是:既不会出现由于网格间电导率不连续产生的离散电场的“双值"问题,同时又保证了电流密度矢量J的连续性.
|
图 1 离散化的矢势、标势在交错网格上的分布 (a)控制体积元Vi,j,k;(b)控制体积元Vi+1/2,j,k;(c)Vi,j,k的剖面图. Fig. 1 Distribution of discrete vector-scalar potentials in staggered grid (a) Control volume cell Vij,k;(b) Control volume cell Vi+1/2j,k;(c) Cross-section of Vi,j,k. |
由于(6b)和(6c)的离散过程与(6a)完全类似,为简洁起见,下面仅给出(6a)的离散过程与结果.根据图 1b,首先对式(6a)在控制体积元Vi+1/2,j,k上做体积分,得到
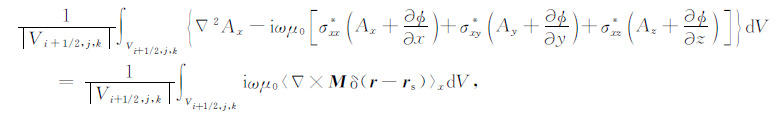
|
(11) |
由高斯散度定理,式(11)左边的第一个体积分可转化为如下的面积分:
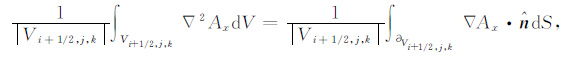
|
(12a) |
利用基于体积元上六个面的中值积分公式和一阶差分公式,将(12a)式右端离散为
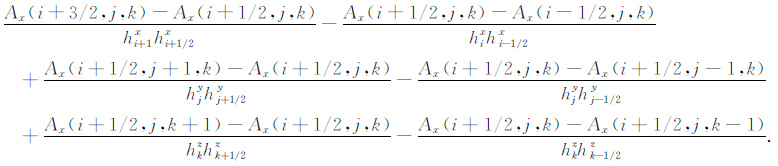
|
(12b) |
对(11)式左边的第二个体积分进行直接离散,得
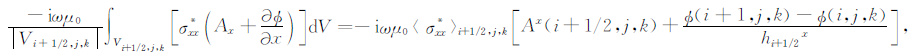
|
(13) |
其中
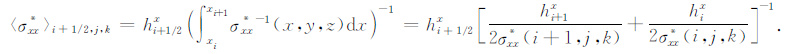
|
(14) |
由于地层各向异性将导致电流方向与电场方向不同,因此(11)式的左侧出现了第三、四项积分,借助有限体积平均技术分别得到如下离散结果:
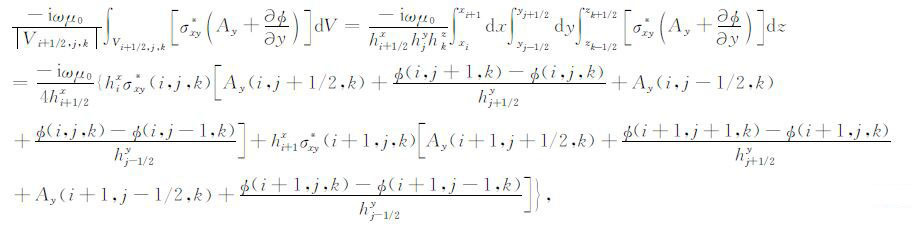
|
(15) |
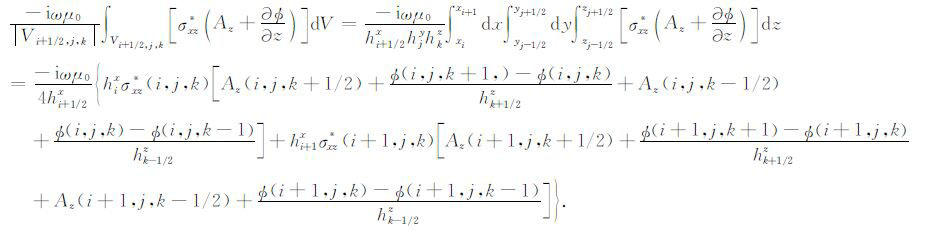
|
(16) |
而(11)式右端的积分可转化为如下的面积分:
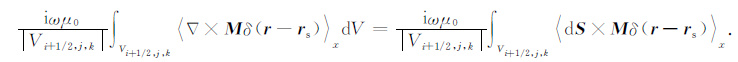
|
(17) |
磁流极子M在三个坐标系方向上的分量为Mx、My和Mz,利用δ 函数的积分性质,(17)式右端可近似表示为
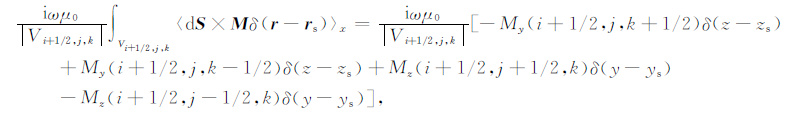
|
(18) |
当网格剖分足够小时可以近似认为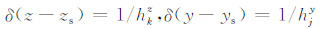
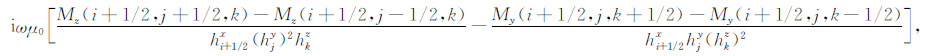
|
(19) |
为了离散方程(7),对其在控制体积元Vijk上积分,并根据高斯散度定理,得
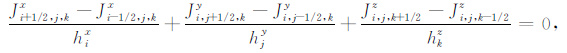
|
(20) |
其中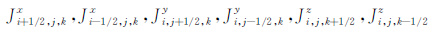
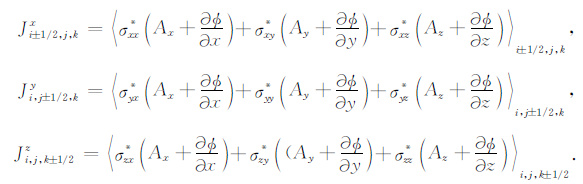
|
(21) |
对(21)式右端的离散化处理,可采用与(13)、(15)和(16)式类似的离散过程.于是,成功完成了对式(6a-6c)和(7)的离散.
2.3 离散化线性方程组及其快速迭代算法将上面对式(6)和(7)的离散结果进行整理,得到关于矢势A和标势φ的离散化线性代数方程组FX=b,该方程等价于
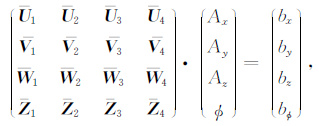
|
(22) |
其中F 是由16个块状子矩阵组成的非对称的大型稀疏复矩阵,通过对矩阵F 的研究发现,子矩阵U1、V2、W3和Z4是对称矩阵,并且V1和U2、U3和W1、V3和W2互为转置.此外,子矩阵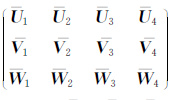

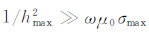
本节将通过解析法(AM)[5]和模式匹配算法(NMM)[8-9]所得结果的对比,检验耦合势有限体积法的有效性与计算精度.然后,考察仪器偏心、倾斜井、垂直裂缝等复杂条件对测井响应的影响.在数值计算中,网格数Nx×Ny×Nz为40×40×92,为了能够用尽可能少的网格节点模拟出足够精确的数值结果、减少计算时间,网格剖分原则是:以计算区域Ω 中心为原点沿z轴上下1m 范围内采用网格间距为hz=0.05 m 的均匀网格,以及在x和y方向上0.2m范围内采用hx=hy=0.025 m 的均匀网格,从均匀网格的最后节点到截断边界这段距离采用网格间距逐渐增加的对数网格.为了减小截断边界对发射和接收线圈附近电磁场的影响,令计算区域大小为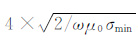
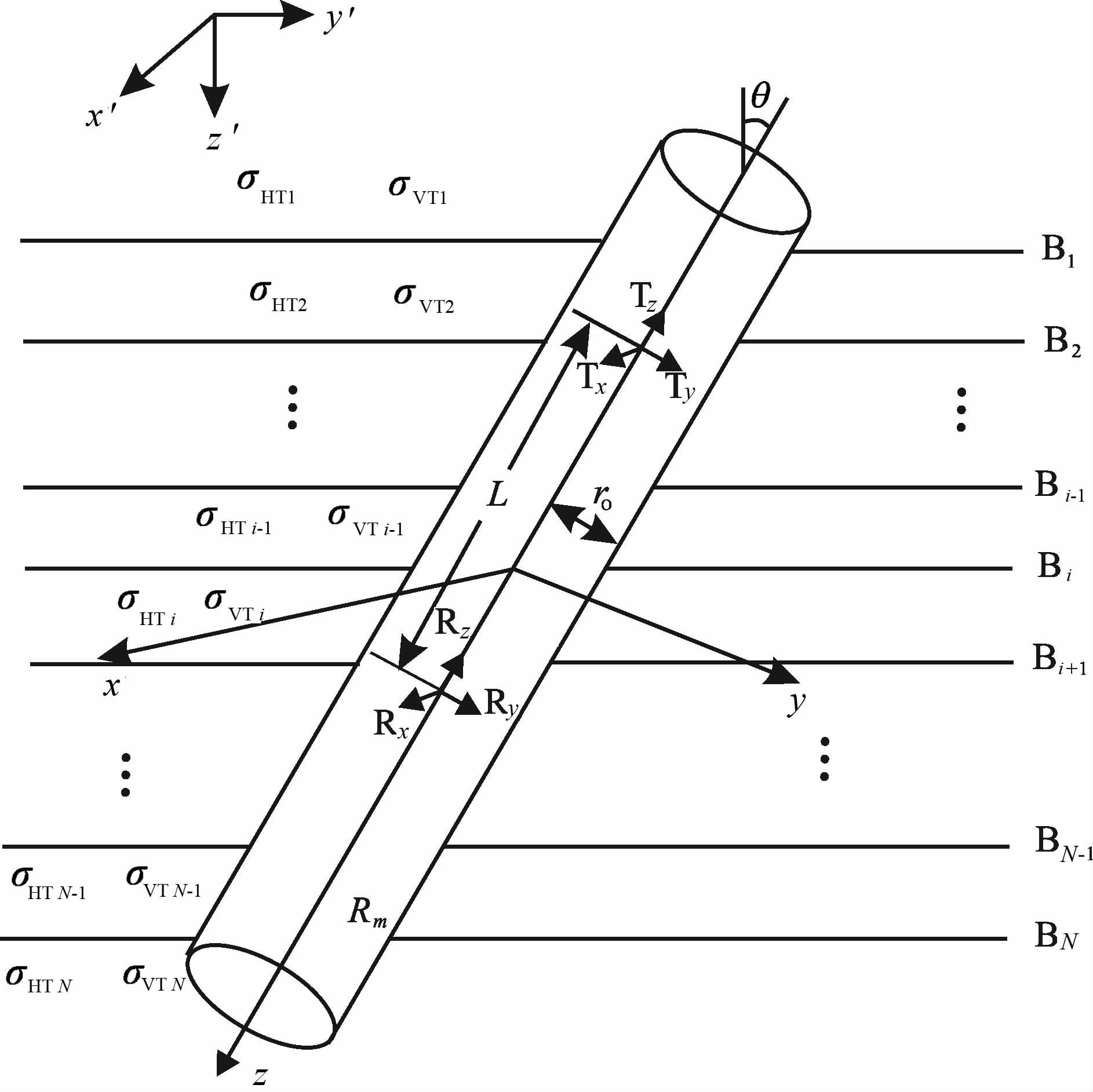
图 2是含有倾斜井眼的水平层状地层模型和仪器结构示意图,地层总数为N,地层i的原状横向与纵向电导率分别为σHTi、σVTi(i=1,2,…,N),井眼半径和井眼泥浆电导率分别为ro 和σm.图中同时给出了仪器坐标系xyz和地层坐标系x′y′z′,z轴与井轴一致,而z′ 轴与地层面垂直,且假定y轴与y′轴重合,井眼倾角为θ°.发射线圈和接收线圈分别用(Tx,Ty,Tz)和(Rx,Ry,Rz)表示,仪器源距为L.利用接收线圈上磁场强度张量的各个分量,利用如下公式计算视电导率张量[25]:
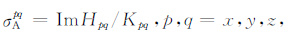
|
(23) |
|
图 2 含倾斜井眼地层模型和多分量感应仪器示意图 Fig. 2 Schematic diagram of formation model with dippingborehole and structure of multi-component induction logging tool |
其中,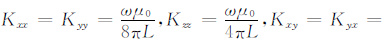
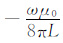
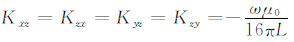
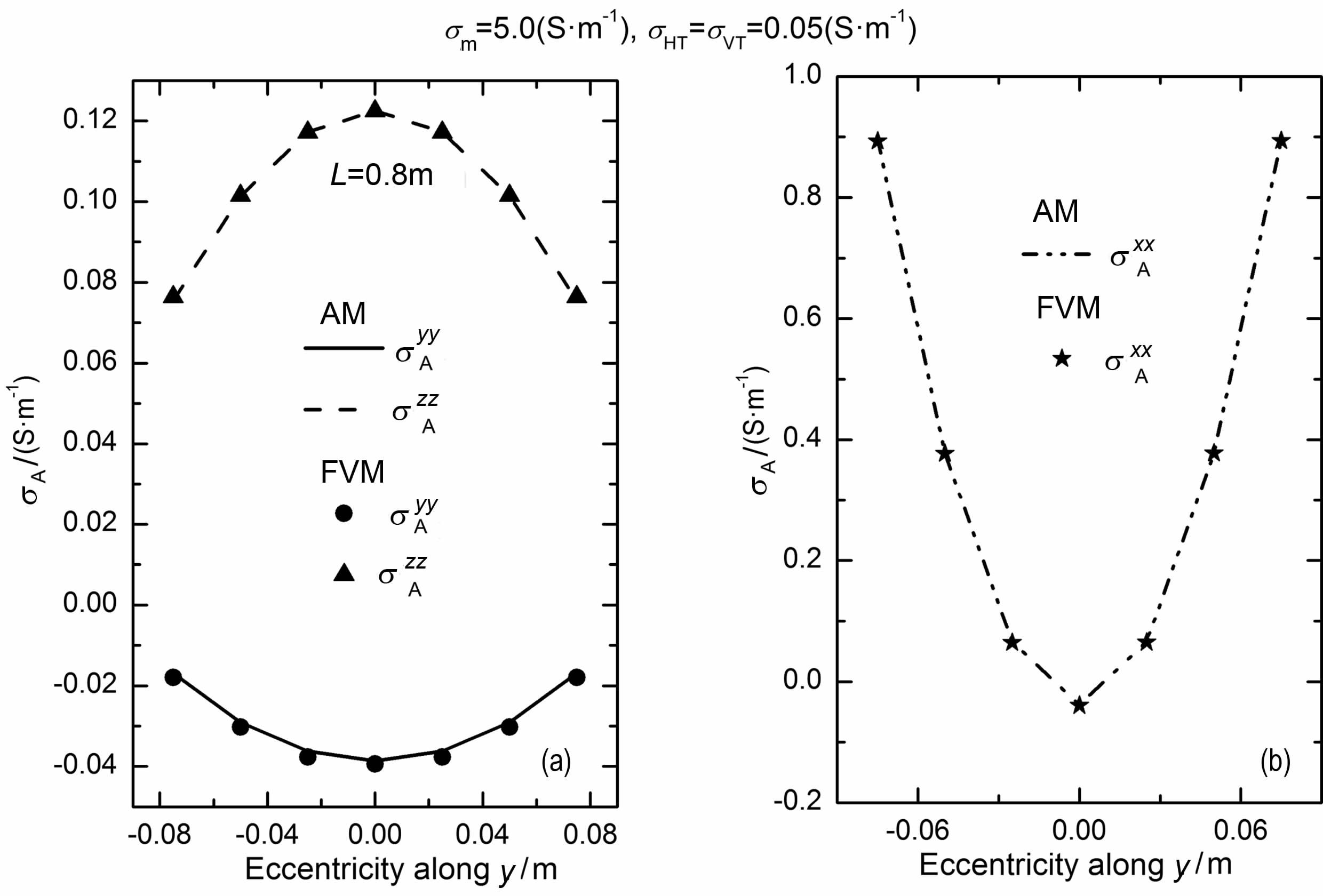
为对耦合势有限体积法进行检验并考察多分量感应的偏心效应,首先假定模型为不含水平界面的两层柱状模型,且外层为原状地层,其电阻率为σHT =σVT =0.05(S·m-1),内层是井眼,泥浆电导率σm=5.0(S·m-1),井眼半径ro=0.108m, 源距L=0.8 m, 发射线圈工作频率为25kHz.图 3是仪器沿y方向偏心时,有限体积法(FVM)与解析法(AM)得到三个主分量σAxx 、σAyy 和σAzz 随偏心距变化曲线的对比.结果显示两者吻合得非常好,说明该算法能很好地模拟出含井眼的多分量感应响应.此外,从图不难看出,仪器偏心对三个主分量响应均有明显影响,但影响方向和变化幅度不同,σAxx 和σAyy 随偏心距的增加而增加,而σAzz 随偏心距的增加而减小.值得注意的是,σAxx 的变化幅度明显要比σAyy 和σAzz 大很多,说明当共面线圈系沿着垂直于发射方向偏心时受到的偏心影响最强.原因是:当线圈Tx沿y偏心时,井眼中存在较强的且与井轴平行的电场,从而产生很强的井眼电流,正是由于井眼电流对接收线圈的作用,使得偏心影响变得异常明显.在同样的偏心情况下,发射线圈Ty和Tz在井中也产生与井轴平行的电场,但其场强比Tx线圈的电场小得多,所以导致σAyy 和σAzz 受偏心的影响也相对较小[26].
|
图 3 在低电阻泥浆井眼中仪器沿y轴方向偏心时由有限体积法和解析法计算结果的对比 (a)偏心对σAyy 和σAzz 的影响;(b)偏心对σAxx 的影响. Fig. 3 Comparison of finite volume method solution with the analytical solution whentool is eccentered in y-direction in the conductive borehole (a) Eccentricity effect on σAyy and σAzz; (b) : Eccentricity effect on σAxx. |
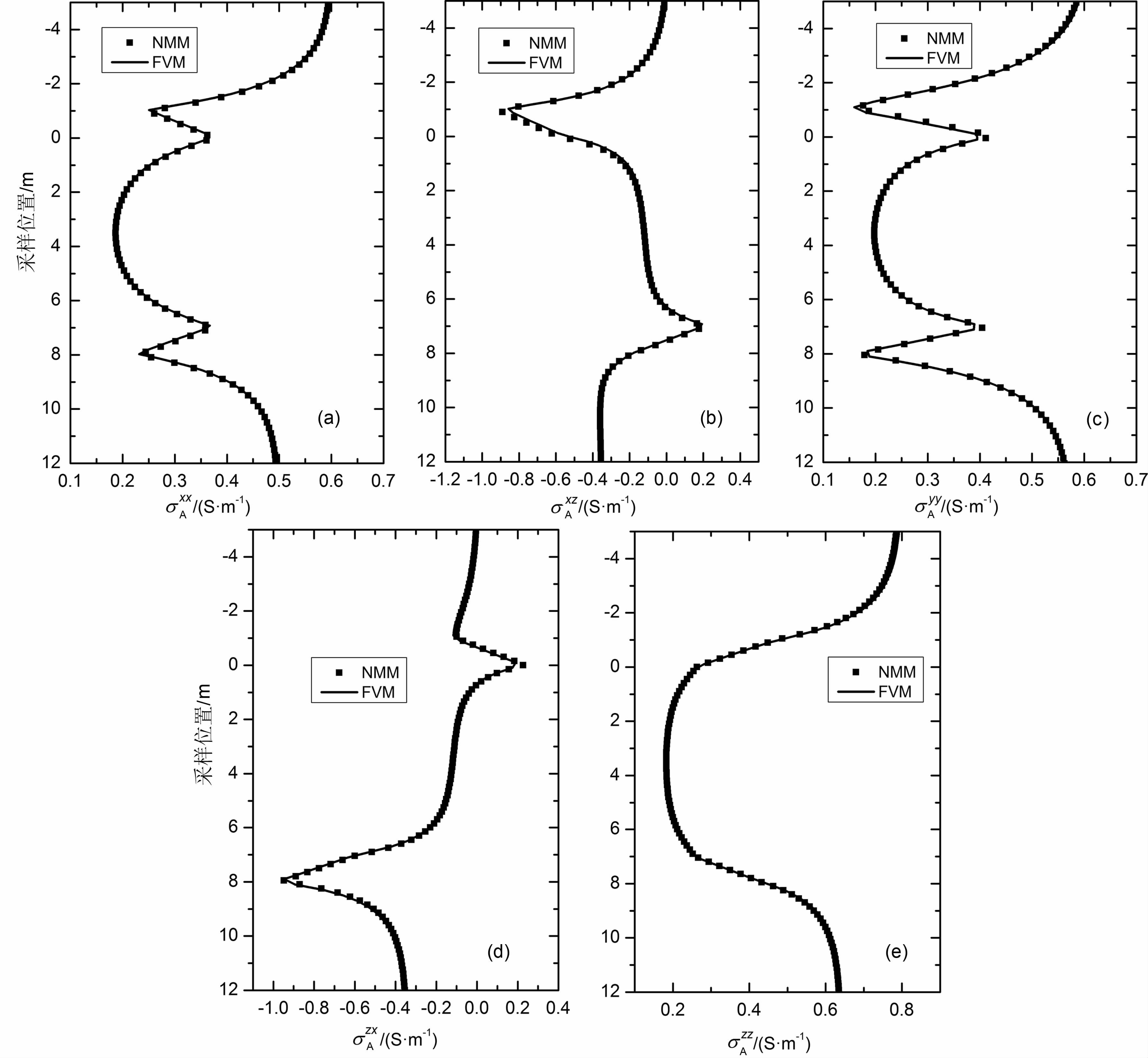
为进一步对倾斜井眼中数值结果进行检验,假定地层为三层各向异性模型,地层横向与纵向电阻率分别为1/σHT = (1.0,4.0,1.0)(Ωm)和1/σVT =(1.0,10.0,2.0)(Ωm),中间层厚度为4 m, 井眼倾角θ=60°,仪器长度L=1.0m, 工作频率25kHz.图 4是在忽略井眼泥浆影响的情况下,由FVM 和NMM 计算得到的多分量感应测井响应的正演结果对比,两种不同方法所得结果吻合很好,其相对误差低于1%.从图可以看出,视电导率的两个共面主分量σAxx 和σAyy 曲线形状相似,在层边界附近存在由积累电荷产生的“犄角";而共轴主分量σAzz 曲线特征相对简单,受积累面电荷的影响明显较小.由于井眼倾斜,出现两个非零的交叉分量σxzA 和σzxA ,在层边界附近同样出现“犄角",但是两个“犄角"方向相反,“犄角"的方向与发射线圈和接收线圈的相对位置以及仪器的移动方向有关.在整个数值计算过程中,采样点个数为110个,采样方向是沿井轴方向,采样间距为0.075/cos(θ=60°)m.在CPU 主频为3.4GHz, 内存为4G 的微机中用有限体积法计算该模型中每组数据所需时间仅为2.2h, 说明算法具有较高的实用性.
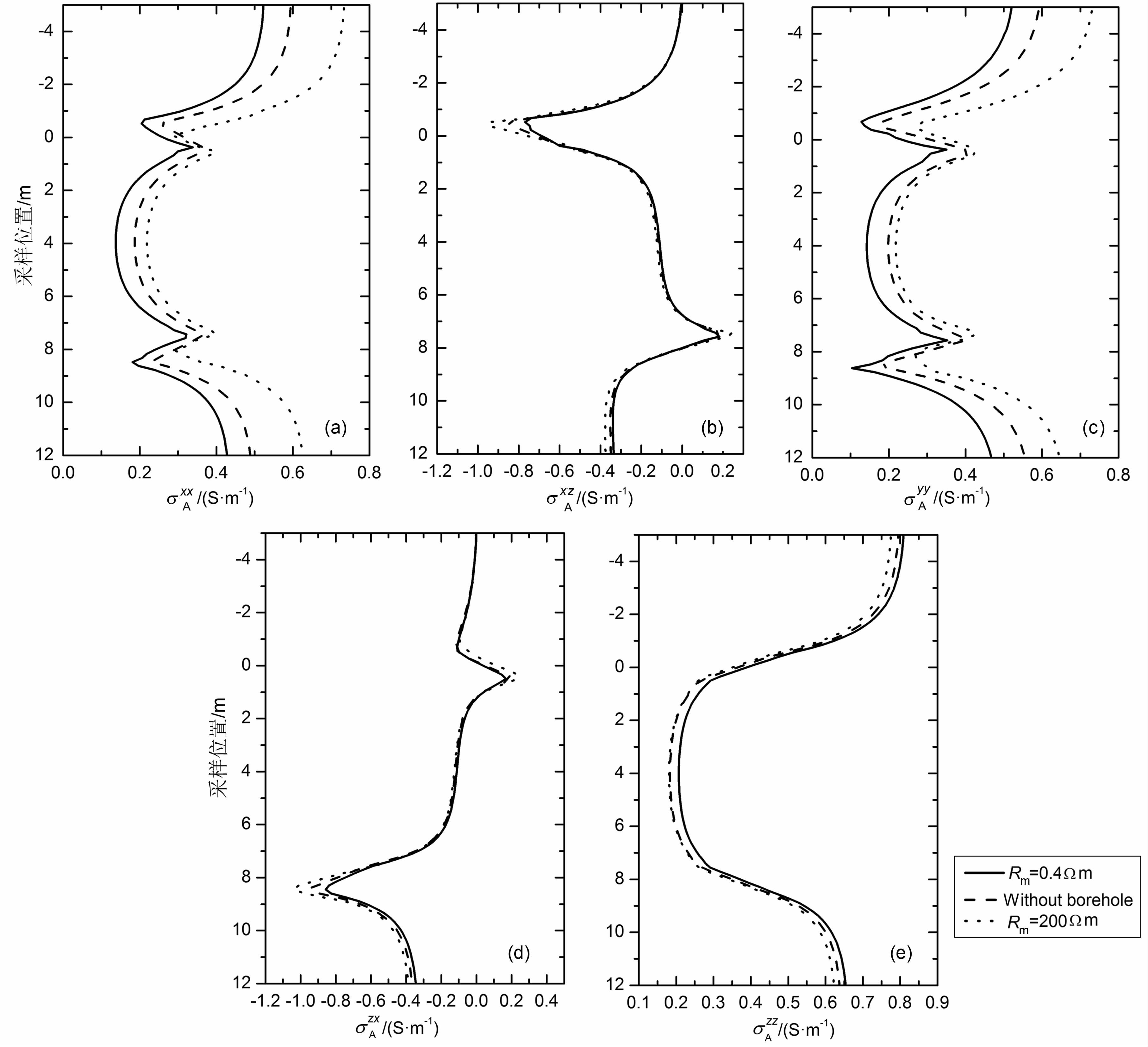
3.2 不同泥浆电阻率对多分量感应的影响为考察井眼以及泥浆电阻率变化对多分量感应测井响应的影响,仍然采用图 4 中的地层模型和仪器参数,利用FVM 分别计算井眼泥浆电阻率1/σm分别为0.4和200.0Ωm、井眼半径ro=0.108m时多分量感应的响应,并与无井眼情况下测井响应进行对比.图 5是多分量感应的5 个非零视电导率分量在三种不同情况下数值模拟结果的对比,结果显示井眼泥浆电导率的变化对两个共面主分量σAxx和σAyy 的影响很大,而对共轴主分量σAzz 的影响相对较小,对两个非零的交叉分量σxzA 和σzxA 只在层边界附近才显示出泥浆电阻率变化的影响.此外,从数值结果中还可以看到,泥浆电阻率增加导致共面主分量σAxx 和σAyy 的值增大以及共轴主分量σAzz 的减小,说明泥浆电导率的变化对不同分量视电导率的影响是不同的,给多分量感应资料的处理和解释增加了难度.
|
图 4 仪器倾斜60°,三层层状各向异性模型中由FVM 与NMM 计算多分量感应测井响应的正演结果对比 Fig. 4 Comparison of forward results of MCIL responses with 60° dip angle by FVM with that by NMM method in the 3-layed anisotropic model |
|
图 5 高阻泥浆、低阻泥浆以及无井眼条件下,多分量感应测井响应的对比 Fig. 5 Comparison of MCIL responses between in high resistivity mud, low resistivity mud and without borehole |
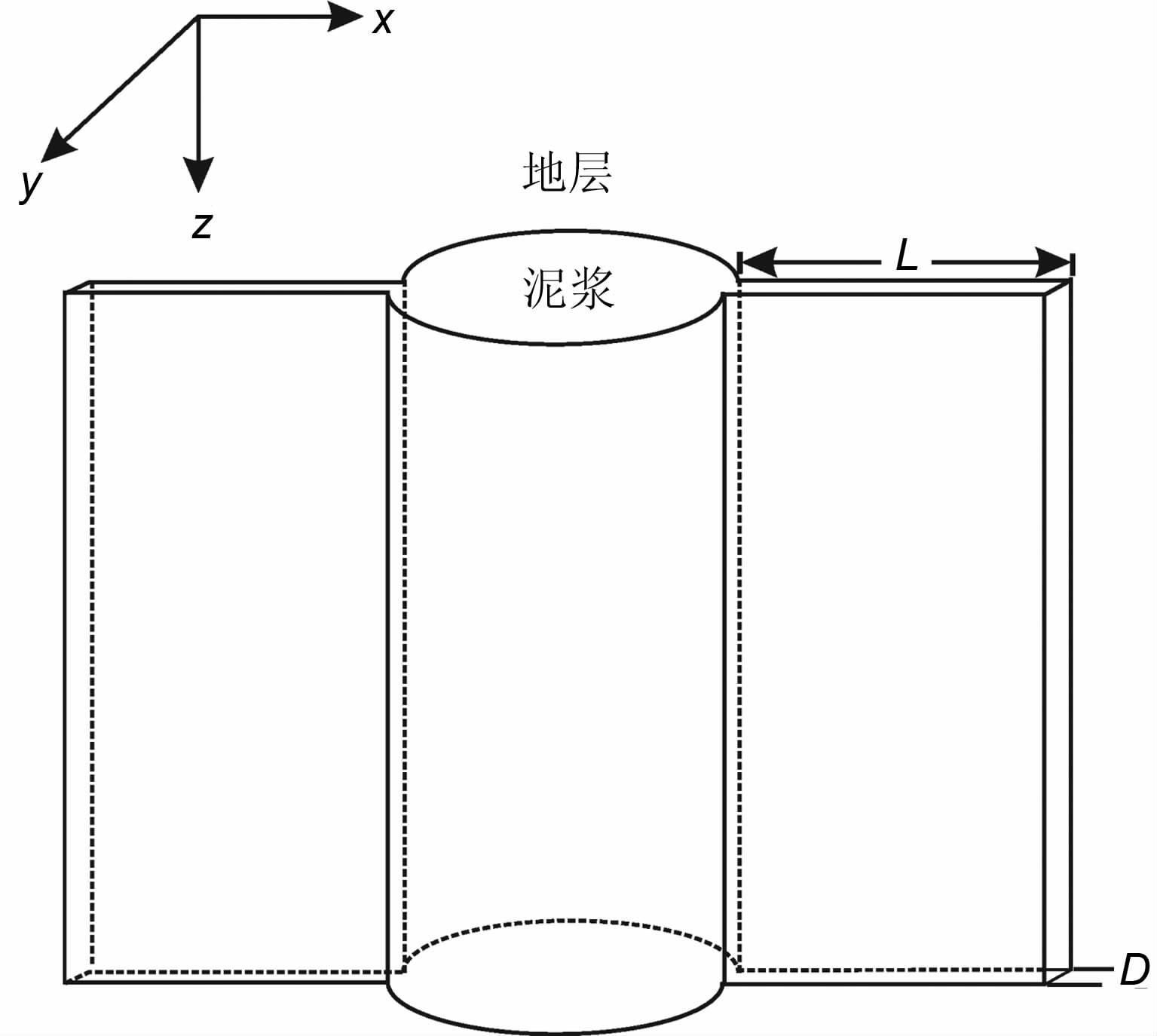
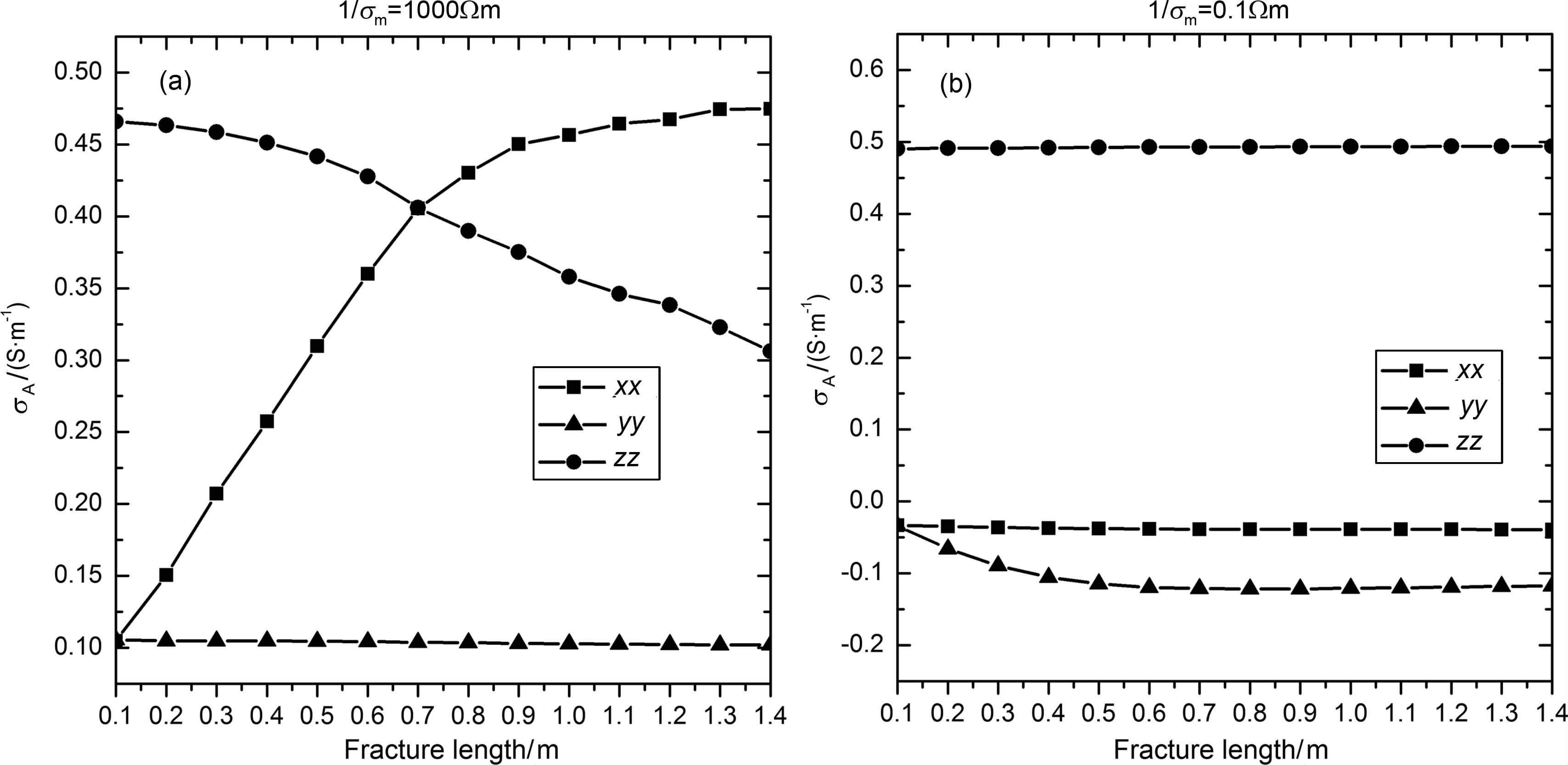
多分量感应测井对井眼周围的裂缝有较强的探测能力,研究考察裂缝变化多分量感应响应影响对于测井资料处理和解释具有重要研究意义[27-28].图 6是井眼周围简单垂直裂缝的示意图,由于水力压裂作用,在井壁两侧出现对称翼状裂缝,假设裂缝长度为L,宽度D=0.025 m.此外,井眼半径ro =0.108m、仪器源距为1.8 m、工作频率为62kHz, 原状地层电阻率为1/σHT =1/σVT =1.0Ωm.首先,给出在高阻泥浆情况下,裂缝长度变化对多分量响应的影响,图 7a是泥浆和裂缝流体的电阻率假定为1/σm=1000.0Ωm, 裂缝长度从0逐渐增加到1.3m, 多分量感应的三个主分量变化曲线,从图 7可以看出,视电导率σAxx 在浅层裂缝区域线性增加,当裂缝长度接近0.9 m 时,视电导率趋于一个常值,而σAzz对浅层裂缝变化不明显,当裂缝长度大于0.4 m后,视电导率随裂缝长度线性减小,此外,σAyy 对于裂缝长度变化不敏感.因此,可以利用σAxx 分量探测浅层裂缝,而用σAzz 分量探测深层裂缝.作为对比,7b是低阻泥浆情况下的数值结果,泥浆和裂缝流体的电阻率为1/σm=0.1Ωm, 结果显示:σAzz 和σAxx 都对裂缝长度变化不敏感,而σAyy 出现负响应并随裂缝长度的增加其绝对值增大,当裂缝长度接近0.4m 时电导率趋于一个常值.
|
图 6 垂直井眼中垂直裂缝示意图 Fig. 6 Schematic diagram of vertical fracturein a vertical well |
|
图 7 不同泥浆条件下,裂缝长度与视电导率的关系曲线 (a)高阻泥浆;(b)低阻泥浆. Fig. 7 Relation curve between apparent conductivity and fracture length in different mud resistivity (a) High resistivity mud; (b) Low resistivity mud. |
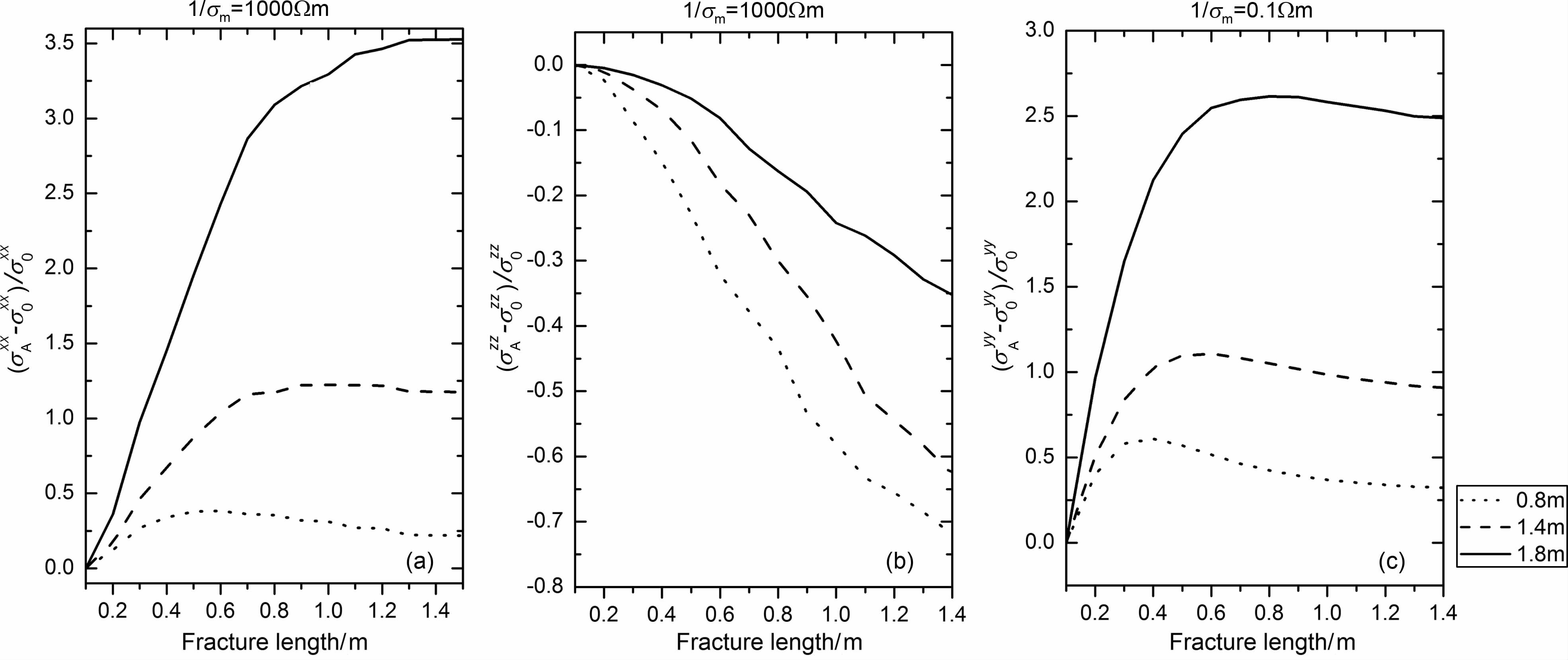
为进一步考察多分量感应测井对裂缝储层的探测能力,下面给出图 7 中的同一模型在不同源距情况下视电导率的变化特征.设多分量感应仪器的源距分别为0.8m、1.4m 和1.8m, σ0xx 、σ0yy 和σ0zz 是不含裂缝地层的视电导率值,而σAxx 、σAyy 和σAzz 是包含垂直裂缝地层的视电导率值,定义变量(σAαα -σ0αα )/σ0αα(其中α=x,y,z)用来表示视电导率随裂缝长度增加的变化率,其物理意义是视电导率对裂缝的敏感程度.图 8a和图 8b分别是高阻泥浆和裂缝流体情况下,三个不同源距的主分量σAxx 和σAzz 随裂缝长度增加的变化率曲线,因主分量σAyy 对高阻泥浆和高阻裂缝的反应不敏感,故没有给出其数值结果.从图可以看出,不同源距的视电导率对裂缝的敏感程度是不同的,对于共面线圈系的主响应σAxx ,源距越大,视电导率对裂缝的敏感程度也越大,并且能够探测更深的垂直裂缝;共面线圈系的主响应σAzz ,源距增加时,视电导率对裂缝的敏感程度反而变小.利用不同源距多分量感应响应对裂缝的敏感程度上的差异,为裂缝深度的反演提供了理论基础.最后,为比较并考察低阻泥浆和裂缝流体情况下视电导率对裂缝的敏感程度,图 8c给出了在三个不同源距主分量σAyy 随裂缝长度增加的变化率曲线,同样可以看到,源距越大,视电导率对裂缝的敏感程度也越大.
|
图 8 不同源距下视电导率变化率与裂缝长度的关系曲线 (a)高阻泥浆σAxx 变化率;(b)高阻泥浆σAzz 变化率;(c)低阻泥浆σAyy 变化率. Fig. 8 Relation curve between change rate of apparent conductivity and fracture length in different tool's spacing (a) Change rate of σAxx in high resistivity mud; (b) Change rate of σAzz in high resistivity mud; (c) Change rate of σAyy in low resistivity mud. |
本文建立了一套基于电场矢势和标势的电磁场三维有限体积算法,用于研究非均质各向异性地层中多分量感应测井响应.利用电场的矢势和标势将maxwell方程转化为耦合势Helmholtz方程,并通过有限体积离散技术与交错网格对磁偶极子向量的旋度以及耦合势Helmholtz方程进行离散,得到一个对角占优的大型代数方程,利用不完全LU 分解预处理和稳定双共轭梯度迭代法可以快速求解该方程.
数值结果表明:当仪器偏心时,测井响应的三个主分量的值均发生改变,但是只有当共面线圈垂直于线圈发射方向偏心时受到的偏心影响最强,导致偏心效应的主要原因是偏心会在井眼中产生净电流,净电流越大偏心效应越明显.在倾斜井模型中,视电导率的共面分量和交叉分量曲线比共轴分量复杂,在层边界处存在由积累面电荷产生的“犄角",共面分量受井眼影响很大,共轴分量受井眼影响相对较小,而井眼对交叉分量影响最小.此外,井眼泥浆电阻率的变化对不同分量视电阻率的影响是不同的.根据泥浆及裂缝流体电阻率的不同,可以配合使用长源距的zz线圈系和短源距的xx线圈系探测深层和浅层的高阻裂缝,而利用短源距的yy线圈系探测低阻浅层裂缝.
| [1] | Kennedy D, Peksen E, Zhdanov S. Foundations of tensor mduction well-logging. Petrophysics , 2001, 42(6): 588-610. |
| [2] | Wang H N, Tao H G, Yao J J, et al. Fast multiparameter reconstruction of multicomponent induction well-logging datum in a deviated well in a horizontally stratified anisotropic formation. IEEE Transactions on Geoscience and Remote Sensing , 2008, 46(5): 1525-1534. DOI:10.1109/TGRS.2008.916080 |
| [3] | Wang H N. Adaptive Regularization Iterative Inversion of Array Multicomponent Induction Well Logging Datum in a Horizontally Stratified Inhomogeneous TI Formation. IEEE TransacLions on Geoscience and Remote Sensing , 2011, 49(11): 4483-4491. DOI:10.1109/TGRS.2011.2142187 |
| [4] | Moran J H, Gianzero S. Effects of formation anisotropy on resistivity-logging measurements. Geophysics , 1979, 44(7): 1266-1286. DOI:10.1190/1.1441006 |
| [5] | Wang H N, So P, Yang S W, et al. Numerical modeling of multicomponent induction well-logging tools in the cylindrically stratified anisotropic media. IEEE Transactions on Geoscience Remote Sensing , 2008, 46(4): 1134-1147. DOI:10.1109/TGRS.2008.915748 |
| [6] | 姚东华, 汪宏年, 杨守文, 等. 用传播矩阵法研究层状正交各向异性地层中多分量感应测井响应. 地球物理学报 , 2010, 53(12): 3026–3037. Yao D H, Wang H N, Yang S W, et al. Study on the responses of multi-component induction logging tool in layered orthorhombic anisotropy formations by using propagator matrix method. Chinese J. Geophys. (in Chinese) , 2010, 53(12): 3026-3037. |
| [7] | Wang G L, Torres-Verdin C, Gianzero S. Fast simulation of triaxial borehole induction measurements acquired in axialy symmetrical and transversely isotropic media. Geophysics , 2009, 74(6): E233-E249. DOI:10.1190/1.3261745 |
| [8] | 汪宏年, 陶宏根, 姚敬金, 等. 用模式匹配算法研究层状各向异性倾斜地层中多分量感应测井响应. 地球物理学报 , 2008, 51(5): 1591–1599. Wang H N, Tao H G, Yao J J, et al. Study on the response of a multicomponent induction logging tool in deviated and layered anisotropic formations by using numerical mode matching method. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1591-1599. |
| [9] | 汪宏年, 胡平, 陶宏根.水平层状非均质横向同性地层中阵列多分量感应测井响应的快速计算.地球物理学报(已接受). Wang H N, Hu P, Tao H G. Fast algorithm of response of an array multi-component induction logging tool in horizontally stratified inhomogeneous anisotropic medium. Chinese J. Geophys. (Accepted). http://manu39.magtech.com.cn/Geophy/CN/abstract/abstract8449.shtml |
| [10] | Davydycheva S, Druskin V, Habashy T. An efficient finite- difference scheme for electromagnetic logging in 3D anisotropic inhomogeneous media. Geophysics , 2003, 68(5): 1525-1535. DOI:10.1190/1.1620626 |
| [11] | 沈金松. 用交错网格有限差分法计算三维频率域电磁响应. 地球物理学报 , 2003, 46(2): 281–289. Shen J S. Modeling of 3-D electromagnetic responses in frequency domain by using staggered-grid finite difference method. Chinese J. Geophys. (in Chinese) , 2003, 46(2): 281-289. |
| [12] | Newman G A, Alumbaugh D L. Three-dimensional induction logging problems, Part 2: A finite-difference solution. Geophysics , 2002, 67(2): 484-491. DOI:10.1190/1.1468608 |
| [13] | 王昌学, 杨餠, 储昭坦, 等. 多分量感应测井响应的交错网格 有限差分法模拟. 石油大学学报(自然科学版) , 2005, 29(3): 35–40. Wang C X, Yang W, Chu Z T, et al. Modeling of multicomponent induction log responses by staggered-grid finite difference method. Journal of Lhe University of Petroleum (inChinese) (in Chinese) , 2005, 29(3): 35-40. |
| [14] | 杨守文, 汪宏年, 陈桂波, 等. 倾斜各向异性地层中多分量电 磁波测井响应三维时域有限差分(FDTD)算法. 地球物理学报 , 2009, 52(3): 833841–841. Yang S W, Wang I N, Chen G B, et al. The 3-D finite difference time domain (FDTD) algorithm of response of multi-component electromagnetic wel logging tool in a deviated and layered anisotropic formation. Chinese J. Geophys. (in Chinese) , 2009, 52(3): 833841-841. |
| [15] | Weiss C J, Newman G A. Electromagnetic induction in a generalized 3D anisotropic earth, Part 2: The LIN preconditioner. Geophysics , 2003, 68(3): 922-930. DOI:10.1190/1.1581044 |
| [16] | Hou J S, Malian R K, Torres-verdin C. Finite-difference simulation of borehole EM measurements in 3D anisotropic media using coupled scalar-vector potentials. Geophysics , 2006, 71(5): G225-G233. DOI:10.1190/1.2245467 |
| [17] | 沈金松. 用有限差分法计算各向异性介质中多分量感应测井 的响应. 地球物理学进展 , 2004, 19(1): 101–107. Shen J S. Modeling of the multi-component induction log in anisotropic medium by using finite difference method. Progress in Geophysics (in Chinese) , 2004, 19(1): 101-107. |
| [18] | 孙向阳, 聂在平, 赵延文, 等. 用矢量有限元方法模拟随钻测 井仪在倾斜各向异性地层中的电磁响应. 地球物理学报 , 2008, 51(5): 1600–1607. Sun X Y, Nie Z P, Zhao Y W, et al. The electromagnetic modeling of logging-while-drilling tool in tilted anisotropic formations using vector finite element method. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1600-1607. |
| [19] | Avdeev D B, Kuvshinov A V, Pankratov O V, et al. Three-dimensional induction logging problems, Part 1: An integral equation solution and model comparisons. Geophysics , 2002, 67(2): 413-426. DOI:10.1190/1.1468601 |
| [20] | Smith J T. Conservative modeling of 3-D electromagnetic fields, Part II: Biconjugate gradient solution and an accelerator. Geophysics , 1996, 61(5): 1319-1324. DOI:10.1190/1.1444055 |
| [21] | Haber E, Asher U M, Aruliah D A, et al. Fast simulation of 3D electromagnetic problems using potentials. Journal of CompuLaiional Physics , 2000, 163(1): 150-171. DOI:10.1006/jcph.2000.6545 |
| [22] | Yee K S. Numerical solution of initial boundary value problems involving Maxwell s equations in isotropic media. IEEE Trans. onAniennas and Propagate , 1966, 14(3): 302-307. DOI:10.1109/TAP.1966.1138693 |
| [23] | Saad Y. Iterative Method for Sparse Linear Systems. Boston: PWS Publishing, 1996 . |
| [24] | Van der Vorst H A. Iterative Krylov Methods for Large Linear Systems. Cambridge: Cambridge University Press, 2003 . |
| [25] | 洪德成.三轴感应测井资料处理方法研究.长春: 吉林大学 物理学院, 2009. HongDC. Study on the Data Processing Method of Tri-axial Induction Logging . Changchun: College of Physics Jilin Univ., 2009. |
| [26] | Wang H M, Baber T, Morris C, et al. Determining anisotropic formation resistivity at any relative dip using a multiarray triaxial induction tool. SPE 103113 presented at the 2006 SPE Annual Technical Conference and Exhibition: San Antonio, Texas, U.S.A., 2007 : 24-27. |
| [27] | Wang T L, Tang X M, Yu L M, et al. Characterizing fractures with multicomponent induction measurements. Petrophysics , 2005, 46(1): 42-51. |
| [28] | 沈金松, 苏本玉, 郭乃川. 裂缝性储层的电各向异性响应特 征研究. 地球物理学报 , 2009, 52(11): 2904–2912. ShenJS, Su B Y, Guo N C. Study on the anisotropic characteristics of the electric response to fractured reservoir. Chinese J. Geophys. (in Chinese) , 2009, 52(11): 2904-2912. |
 2012, Vol. 55
2012, Vol. 55


