2. 中国科学院地质与地球物理研究所, 北京 100029;
3. 北京市大兴区果林研究所, 北京 102600
2. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
3. Institute of Orchard and Forestry, Daxing District, Beijing 102600, China
近年来,由城市垃圾填埋引发的地下环境污染已受到普遍重视,研究人员相继使用地球物理物理方法对由城市垃圾填埋引发的地下环境污染进行研究.Texkan[1]利用瞬变电磁法和音频大地电磁法圈定科隆垃圾填埋场的范围,Benson[2]采用甚低频电磁法和直流电法开展地下水污染填图作业,Park[3]利用电阻率法监测地下水污染的扩散,Ogily 等[4]应用3D 电阻率层析成像法对垃圾填埋场进行探测,Beselli[5]通过电磁法和多道直流电法对地下水污染进行监测,闫永利等[6]采用大地电磁测深法对北京阿苏卫垃圾填埋场进行检测研究.但从目前国内外解释与推断垃圾填埋地下环境污染状况的方法技术看,大多是通过人为确定的电阻率值,如10Ωm(Texkan1996),对地下环境污染区域进行粗略的划分,很难真实地反映出垃圾填埋场地下环境污染的程度.
EIS(Electrical imaging survey, 电阻率成像观测)是20世纪末发展起来的一项新的观测技术,采用的是阵列式观测方式,信息量大、分辨率高;特别是使用直流激发源,有效地抗人文电磁噪声干扰,成为工程地质、地下水污染勘查的强有力的手段[7-12].模糊数学理论是由Zadel[13]提出,目前已广泛用于天气预报、农林业规划及地震危险性分析和矿产评估等领域,成为定量解释客观事物差异中界限标志“不分明性"的有效方法[14-17].本文将EIS 观测技术与模糊数学理论有机结合,通过对通州某垃圾填埋场的面积性EIS测量,获取了垃圾填埋场地下介质的视电阻率分布;应用模糊数学隶属函数的理论,给出了分辩地下环境污染的量化指标,并对填埋场地下环境污染状况进行了分区划分.实际钻孔资料表明,分区结果与填埋场地下环境污染的分布状况吻合较好.
2 垃圾填埋场概况和EIS现场观测结果垃圾填埋场位于北京市通州区,占地约11000m2,为非正规简易垃圾填埋场.该填埋场西边是荒地,北边是果园,东边为耕地,南边是林地.整个区域地形平坦,适合EIS 观测.填埋场周边表层为第四纪泥土,厚度不足1 m, 底下是泥沙层,厚度大约13 m, 其下为粘土层,地下水位大约10m.填埋场从2007年开始填埋,填埋物主要是生活垃圾与建筑垃圾.
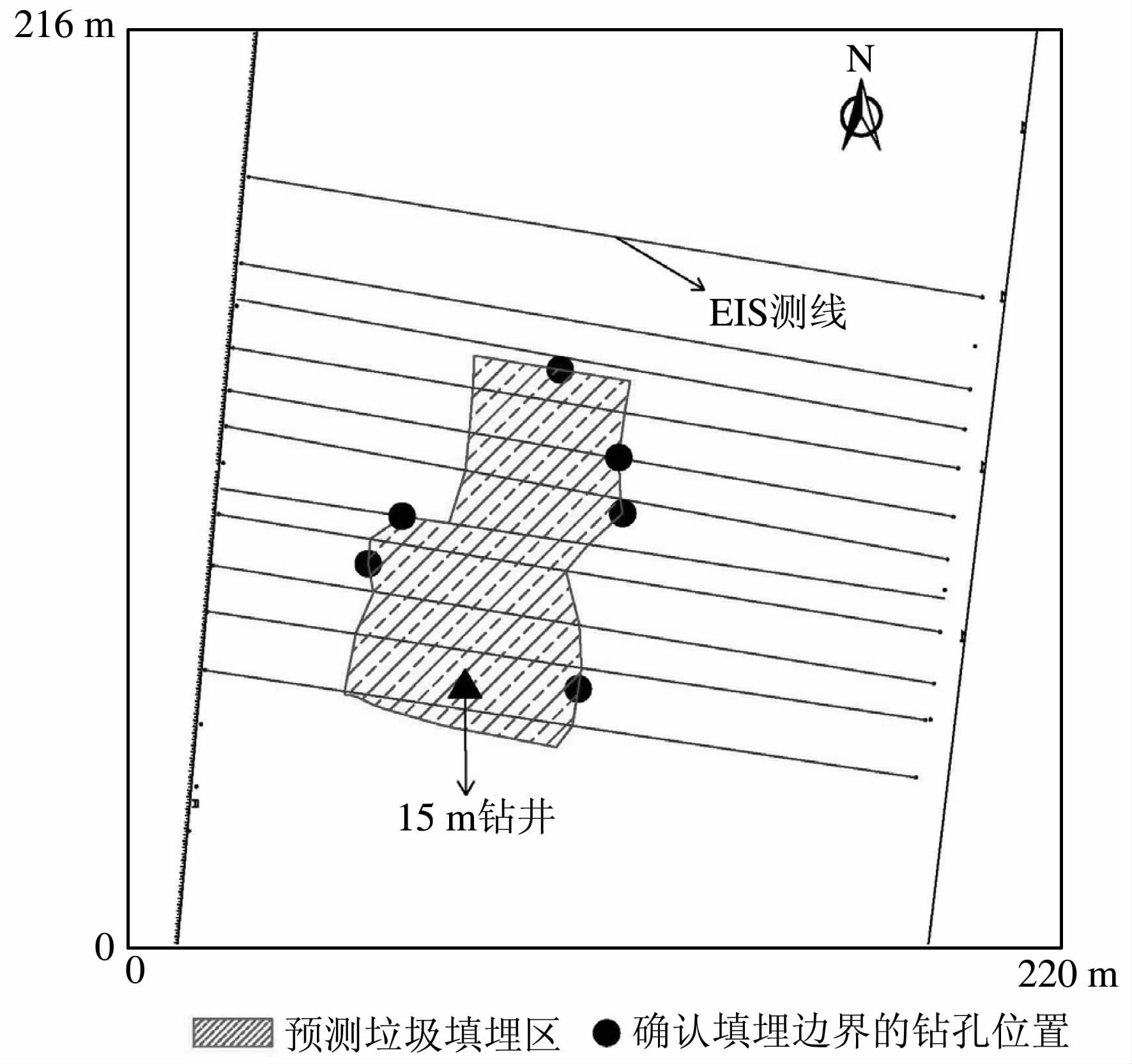
本次野外观测使用GeoPen公司生产的EIS观测仪.在整个填埋场沿东西方向布设了11条EIS测线,由北向南编号1-11号.其中,1-3号线位于填埋区之外,4-9 号线为混合垃圾(生活垃圾与建筑垃圾)填埋区,10-11为生活垃圾填埋区.野外观测采用Wenner装置,电极距为3 m, EIS 测线布设见图 1.其中阴影区域是通过EIS观测结合钻孔资料共同确定的垃圾填埋的平面范围.
|
图 1 垃圾填埋场EIS测线布设图 Fig. 1 EIS designed profiles on the Landfill |
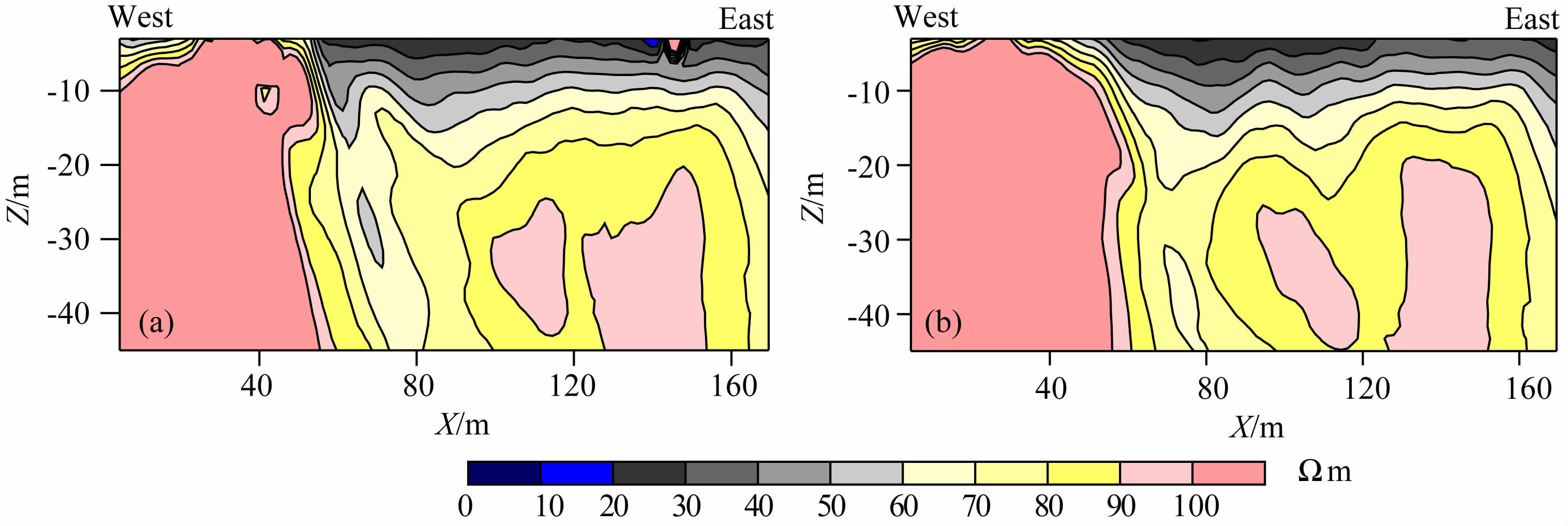
根据EIS观测结果,填埋区与非填埋区的电性结构存在较为明显的差异.图 2(a, b)分别是位于非填埋区1号测线和3 号测线的视电阻率断面.从图 2可以看出,整个剖面以大约60 m 处为界,可分为东、西两段.西段视电阻率较高,普遍介于100~200Ωm之间;而东段视电阻率相对较低,大约在20~100Ωm的范围.除在东、西两段交界的、大约60~80m地带外,地下介质的分层性较好.对比图 2a和2b电阻率变化不难看出,3号测线虽较1号测线距离垃圾填埋区更近,但未发现明显的低阻异常,这说明垃圾渗滤液的污染以纵向迁移扩散为主,横向的迁移扩散区域很小.
|
图 2 非填埋区EIS视电阻率断面(1号(a)和3号(b)EIS测线) Fig. 2 The EIS cross-section of apparent resistivity in area without refuse filled (1 (a) and 3 (b) EIS) |
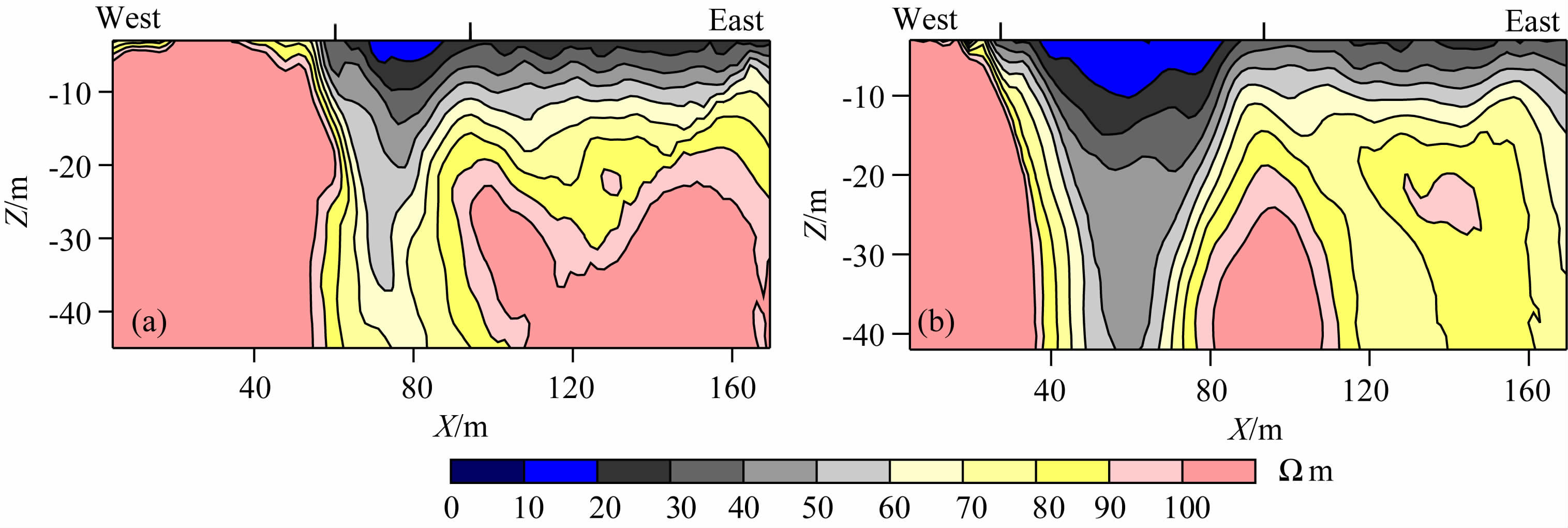
混合垃圾填埋区5 号测线视电阻率断面如图 3a所示,存在1个10~20Ωm 的低阻异常.异常的横向范围大约在70~90 m, 深度范围约为5 m.在剖面的西段0~60 m 的地带,视电阻率较高,普遍在100~200 Ωm 之间.而在东段90~170 m 的地带,随着深度的变化,视电阻率逐渐增大,从近地表的大约20~30 Ωm, 逐渐增大到超过100 Ωm.符号︱是钻孔确定的填埋场边界.
|
图 3 混合垃圾(a)和生活垃圾填埋区(b)EIST 视电阻率断面 Fig. 3 The EIS cross-section of apparent resistivity in area withmixed refuse filled (a) and domestic refuse filled (b) |
生活垃圾填埋区EIS 探测结果非常明显,如图 3b所示.在40~80m 的地带,存在一个非常明显的10~20Ωm 的低阻异常,其深度大约为10m.
从EIS观测结果分析,整个测区0~40 m 深度上,视电阻率分布具有西边高、东边低,深部高、浅部低的特点.填埋场周边的砂土分布较为均匀.影响地下介质电阻率变化的因素除了垃圾填埋物外,主要是近地表土壤的疏松度与潮湿度.西段因缺乏耕种,土壤的疏松度与潮湿度较低,电阻率较高;而东段连年耕种浇灌,土壤的疏松度与潮湿度较高,电阻率较低.
3 地下环境污染程度的划分与钻探结果该填埋场EIS 观测到的结果表明,测区东、西两侧的视电阻率表现出较大的差异.西侧视电阻率较高,普遍超过100Ωm, 远高于填埋区10~40Ωm的视电阻率;东侧则不同,在0~10 m 的深度范围内,视电阻率大致介于20~40Ωm 之间,与填埋区视电阻率的变化范围区别不大.而10m 深度以下,视电阻率高阻特征表现较为明显,普遍超过70Ωm.针对这种情况,提出了直接采用EIS 观测到的视电阻率结果计算隶属函数的方法.
采用Zadeh(1965)表示法,将地下单元ei的视电阻率值ρi视为分辩地下环境污染程度的模糊集合A的元素:
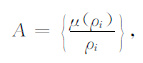
|
(1) |
式中μ(ρi)是ρi的隶属函数.
则戒上型隶属函数计算公式为
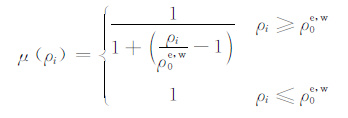
|
(2) |
其中ρ0e=20Ωm;ρ0w =40Ωm.
这里ρ0e、ρ0w 分别是东、西两侧戒上型隶属函数截断视电阻率值,μ(ρi)表征地电单元ei隶属污染区的程度.
根据钻孔资料确定的填埋场的边界,我们针对填埋区及邻近区域进行了地下环境污染程度的计算和成像,图 4(a, b)分别为5 号剖面和10 号剖面的成像结果.

|
图 4 混合垃圾填埋区隶属函数结果 Fig. 4 The result of membership function with mixed refuse filled (a) and domestic refuse filled (b) |
根据闫永利(2007)划分标准,该填埋场地下环境严重污染区(μ(ρ)≥0.75 )的深度范围大约在10~13m(混合垃圾区深度大约10 m;生活垃圾区深度约为13 m),轻度污染区的深度范围大致为10~20m.整体上污染区的深度变化为南深北浅.
为对EIS观测结果进行检验,我们对勘探现场进行了打井验证.采用2 台冲击式打井机,共完成18个钻孔.其中15m 勘探井1个,8m 井3个,6m井14个,采集样品22个.为了解调查场地土壤污染物背景水平,我们在紧邻垃圾填埋场的南侧采集背景样品2个,根据检测结果,调查场地未受垃圾渗滤液污染的土壤氨氮背景值均为“未检出".
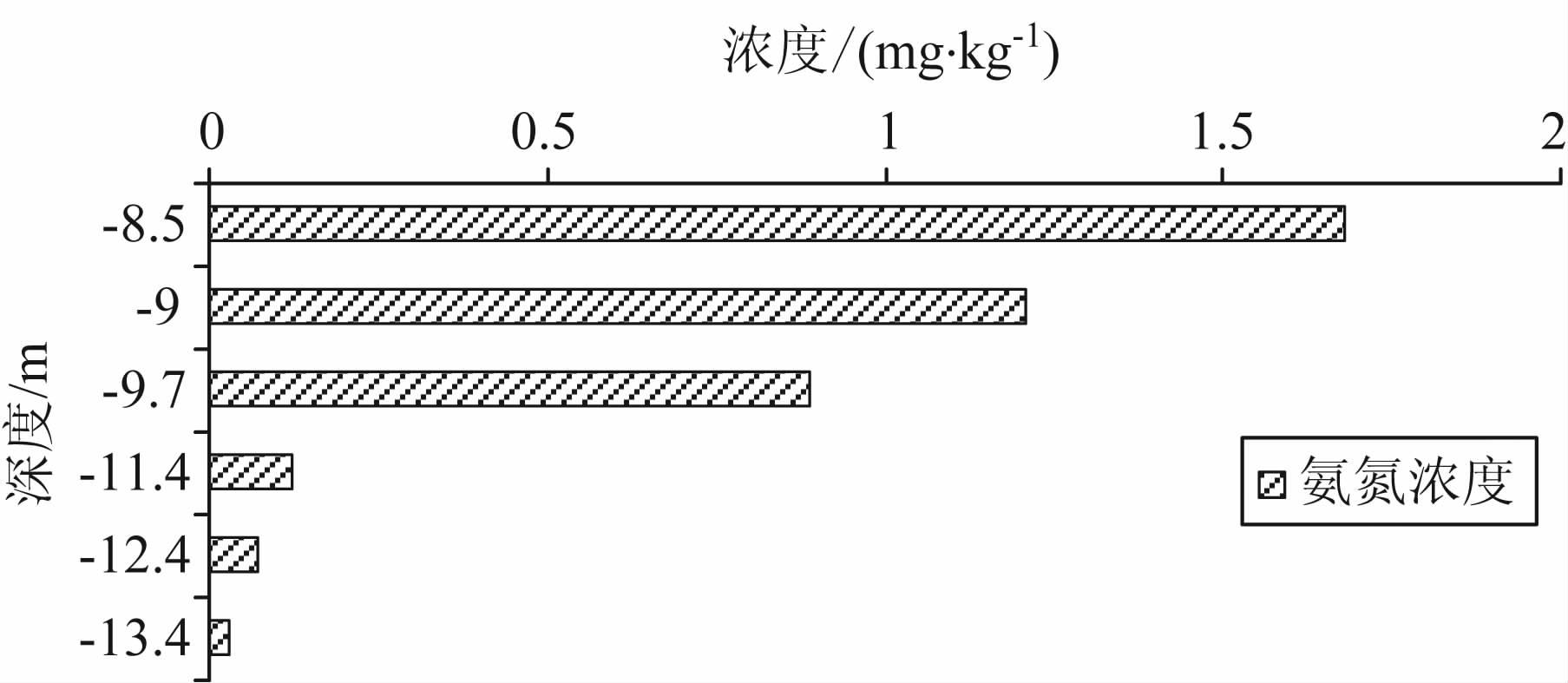
图 5给出的是10号剖面以北15m 深井(垃圾物8m)之下8.5~13.4m 的氨氮检测结果.该钻孔介于混合垃圾填埋区与生活垃圾填埋区之间.从图 5可以直观地看出,在深度9.7~11.5 m 范围氨氮含量快速衰减.表明该深度范围存在划分地下环境污染程度轻、重的合理界面.这与EIS 资料隶属函数给出的严重污染区深度(混合垃圾区10 m;生活垃圾区13m)相吻合.
|
图 5 氨氮浓度检测结果 Fig. 5 The inspecting result of ammonia-nitrogen concentration |
通过对北京通州某垃圾填埋场EIS 观测,获取了垃圾填埋场及邻近区域地下视电阻率断面,给出了不同类型(混合、生活)垃圾填埋的电性异常特征.针对该填埋场复杂背景电性结构特征,提出了新的利用EIS视电阻率直接计算隶属函数的方法,并对探测区地下环境污染程度进行了分区划分,得到了严重污染区、轻度污染区的范围.钻孔资料表明,隶属函数的分区结果较为真实地反映了地下环境污染的状况.
| [1] | Texkan B. A joint application of radiomagnetotellurics and Transient electromagnetics to the investigation of waste Deposit in Cologne. J. Appl. Geophys. , 1996, 34(3): 199-212. DOI:10.1016/0926-9851(95)00016-X |
| [2] | Benson A K. Mapping groundwater contamination using DC resistivity and VLF geophysical methods-A case study. Geophysics , 1997, 62(1): 80-86. DOI:10.1190/1.1444148 |
| [3] | Park S. Fluid migration in the vadose zone from 3D inversion of resistivity monitoring data. Geophysics , 1998, 63(1): 41-51. DOI:10.1190/1.1444326 |
| [4] | Ogilvy R D, Meldrum P I, Chambers J E. Imaging of industrial waste deposits and burred quarry geometry by 3D resistivity tomography. Eur. J. Environ. Eng. Geophys. , 1999, 3: 103-113. |
| [5] | Buselli G. Groundwater contamination monitoring with multichannel electrical and electromagnetic methods. J. Appl. Geophys. , 2001, 48(1): 11-23. DOI:10.1016/S0926-9851(01)00055-6 |
| [6] | 闫永利, 马晓冰, 袁国平, 等. 大地电磁法在阿苏卫填埋场地下水污染检测的应用研究. 地球物理学报 , 2007, 50(6): 1863–1868. Yan Y L, Ma X B, Yuan G P, et al. Application of magnetotelluric method in groundwater pollution detection on Asuwei refuse sanitary landfill. Chinese J. Geophys. (in Chinese) , 2007, 50(6): 1863-1868. |
| [7] | Alaia R, Patella D, Mauriello P. Application of geophysical 3D probability tomography in a test-site of the archaeological park of Pompei. J. Geophys. Eng. , 2008, 5: 67-76. DOI:10.1088/1742-2132/5/1/007 |
| [8] | Daily W, Ramirez A, LaBrecque D, et al. Electrical resistance tomography experiments at the Oregon Graduate Institute. J. Appl. Geophys. , 1995, 33(4): 227-237. DOI:10.1016/0926-9851(95)90043-8 |
| [9] | Friedel S, Thielen A, Springman S M. Investigation of a slope endangered by rainfall-induced landslides using 3D resistivity tomography and geotechnical testing. J. Appl. Geophys. , 2006, 60(2): 100-114. DOI:10.1016/j.jappgeo.2006.01.001 |
| [10] | Hauck C, Vonder Mühll D, Maure H. Using DC resistivity tomography to detect and characterize mountain permafrost. Geophysical Prospecting , 2003, 51(4): 273-284. DOI:10.1046/j.1365-2478.2003.00375.x |
| [11] | Lapenna V, Lorenzo P, Perrone A. 2D electrical resistivity imaging of some complex landslides in the Lucanian Apennine chain, Southern Italy. Geophysics , 2005, 70(3): B11-B18. DOI:10.1190/1.1926571 |
| [12] | Mauriello P, Monna D, Patella D. 3D geoelectric tomography and archaeological applications. Geophysical Prospecting , 1998, 46(5): 543-570. DOI:10.1046/j.1365-2478.1998.00102.x |
| [13] | Zadeh L A. Fuzzy set. Information and Control , 1965, 8(3): 338-353. DOI:10.1016/S0019-9958(65)90241-X |
| [14] | 贺仲雄. 模糊数学及其应用. 天津: 天津科学技术出版社, 1983 . He Z X. Fuzzy Mathematics and Its Application (in Chinese). Tianjin: Tianjin Science and Technology Press, 1983 . |
| [15] | 王时标, 王光远. 未确知信息的模糊处理方法在地震危险性分析中的应用. 地球物理学报 , 1994, 37(S2): 185–191. Wang S B, Wang G Y. The application in seismic risk analysis of fuzzy mathematical methods with unascertain information. Chinese J. Geophys. (in Chinese) , 1994, 37(S2): 185-191. |
| [16] | 江为为. 模糊逻辑理论在矿区勘探与解释中的应用. 地球物理进展 , 1998, 13(1): 115–119. Jiang W W. Application of fuzzy logic set theory in mineral exploration and interpretation. Progress in Geophysics (in Chinese) , 1998, 13(1): 115-119. |
| [17] | 张晓常. 模糊综合评判在地球化学异常评价中的应用. 物探与化探 , 2003, 27(2): 106–109. Zhang X C. The application of fuzzy synthetic judgement to the appraisal of geological anomalies. Geophysical and Geochemical Exploration (in Chinese) , 2003, 27(2): 106-109. |
 2012, Vol. 55
2012, Vol. 55


