2. 中国科学院研究生院, 北京 100049
2. Graduate University of Chinese Academy of Sciences, Beijing 100049, China
20世纪50年代提出的大地电磁测深法(MT)[1-2]具有探测深度大、成本低、应用范围广等优点,得到了广泛应用.然而MT 法使用天然场源,随机性较大,信号微弱,易受到其它电磁干扰,包括工业文明的电磁干扰的影响.为了采集到可靠的信号,要求迭加次数很多,采集时间很长,严重影响到MT 探测效率,一般只用于普查.可控源音频大地电磁法(CSAMT)[3-5]是在大地电磁法基础上发展起来的一种人工移动电性源测深法.人工电性源电磁法的电磁信号得到了增强,提高了抗电磁干扰的能力,自20世纪70年代以来,有了很大的发展,在资源、环境、工程地质探测中也得到了广泛的应用[6-15].但是它也存在一些缺点,例如电性源的发射设备比较笨重,在高山区移动发射源十分困难,探测水平距离一般小于10km, 有效探测深度范围一般小于1.5km.浅层矿产等资源已日趋枯竭,为了满足人们对资源的需求,需发展深部第二成矿带找矿探测.由于MT和CSAMT 法的上述不足,发展大功率固定源CSAMT(FBPCSAMT)方法被提出.这一方法的基本思想是采用一个固定的人工源发射极低频电磁信号(0.1~300Hz),发射功率足够大,使得可以在大范围内(大到全国范围内)同时采集大功率固定源发射的电磁信号.20世纪80年代,美国和苏联分别建立了极低频发射台,用于地球物理研究.苏联科学家利用位于科罗拉半岛的发射台,在数千公里以外的地区进行了大量的测量研究,尤其在地震观测方面的研究取得了很好的效果[16].为了实现探测地下深度10km 范围内电性细结构,以满足在深部第二成矿带找矿的需要的目标,首先需要一个功率足够大的人工固定源.现有的电磁源有两种,一种是电性源,由A、B电极向地下供电,A、B电极间的长度为L.电性源发射电磁波的功率取决于源的强度IL(其中I为供电电流,L为A、B电极间的距离)以及A、B电极的接地电阻,接地电阻越小,发射的效率越高.另一种是磁性源,由一个轴向和地面垂直的环状线圈发射电磁波,发射的功率取决于源的强度IS,S为环状线圈的面积,这种源不存在接地问题,因此不会产生因接地不好而造成的功率损失.但是无论是电性源,还是磁性源,要能在大范围内实现勘探区的电性源强度IL和磁性源强度IS,都必须足够大,在发射电流I一定的条件下,要求L很长,面积S很大.假设磁性源线圈的长度和电性源L一样长,则磁性源的面积为S=L2/4π,因此在L很长的条件下,磁性源的强度IS=IL2/4π,和电性源的强度IL比起来要大得多,此外由于前述接地电阻的问题,对于电性源,要实现高的电流相对于磁性源也更困难.单从发射源的强度一种因素考虑,似乎要想发展FBPCSAMT 方法,采用磁性源更为有利.
当采用大功率固定源发射电磁波,试图在大范围内同时观测人工源信号,用于探地目的时,对于长的收发距离上接收的电磁信号也包括了电离层的反射信号.远距离接收点上接收的电磁信号是从源直接发射的、在空气中传播的直达信号与电离层的反射信号以及地下的反射信号干涉的结果.由于电磁波在空气中的衰减远远小于固体层中的衰减,最终远距离上接收的电磁信号主要是空气中的直达波和电离层的反射波的干涉结果.这种干涉结果应该既和发射特征有关,也和电离层的电性结构有关,因此干涉结果的场特征存在不同特征的可能性.
近年来,对固定电性源考虑电离层影响后称为WEM 的大范围内的电磁波特征的许多研究[16-24]发现,对于x方向的水平电性源在考虑电离层的影响后,水平电磁场分量Ex,Hy存在波导场,即在远距离上接收Ex,Hy场的衰减要比不考虑电离层影响时慢得多.即考虑电离层后,从电离层反射回的波和空气中直达波干涉作用是一种相关干涉,干涉结果使波场得到加强.
为了研究发射特征对干涉结果场特征的影响,本文开展了长偶极源和环状电流源的波导场特征响应的对比研究.为此,计算了水平x方向的电性源激发的波导场Ex,Hy分量场的衰减特征,以及垂直方向的磁性源激发的波导场Ex,Hy分量场的衰减特征.本文是对比研究结果的一个归纳,发现在波导区电性源使波导区直达波和电离层反射波产生相长干涉,使波场的衰减缓慢,而磁性源使波导区直达波和电离层反射波产生相消干涉,使波场衰减加速.这个结果表明虽然磁性源的发射效率比电性源高,但由于电离层的影响,开展WEM 工作时在能选到高阻源区的条件下,电性源更为有利.
2 方法原理常规的地球物理电磁法勘探通常研究的是地球半空间模型,研究的尺度较小,不需要考虑电离层的影响,一般采用比较成熟的二维有限元法、有限差分法进行数值模拟和反演研究.而对于本文提到的采用大功率可控源,远距离的电磁波场的研究必须考虑电离层的影响.这是一个大尺度的全空间问题,常规的有限元法、有限差分法计算单元数量巨大,在此应用受到很大的限制.文献[18]采用从俄罗斯购买的软件,文献[23]采用美国犹他大学的软件,做过包含电离层、空气层和地球介质的一维层状介质的积分解的计算,但是没有考虑介质的横向不均匀性.作者所在课题组开展了对包含电离层、空气层和地球介质的一维水平层状介质电磁波传播的理论研究,并开发了相应的软件[25-26].
由于CSAMT 法实际上是一个三维问题,即便采用传统意义上的三维有限元法、有限差分法也存在一定的困难.20世纪90年代以来,以一维层状介质为背景的三维积分方程法以及三维积分方程和有限元法相结合的方法取得了重大的突破[27-29].三维积分方程法不仅能够考虑层状介质,而且可考虑固体介质内的横向不均匀性[30-39].而且三维积分方程法只对异常体进行剖分,极大地提高了计算效率.
在积分方程法中,可以将一个三维非磁性介质层状地电模型看成是由电导率为σn的一维层状背景介质和异常电导率为Δσ的三维异常介质组成,即介质的电导率为σ =σn+Δσ.电磁场可以表示成由背景场和异常场的和构成:
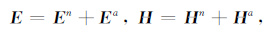
|
(1) |
En和Hn分别表示由给定源在层状背景介质中产生的背景电场和背景磁场.Ea和Ha分别表示由异常电导率Δσ的存在而产生的异常电场和异常磁场.对于背景场En和Hn可以通过层状介质积分解理论求得.对于异常场Ea或Ha,可以表示为在非均匀异常区域D上剩余电流的积分[28]:
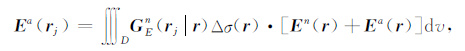
|
(2) |
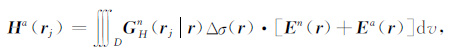
|
(3) |
其中GEn(rj|r)和GHn(rj|r)分别为均匀介质中的电场和磁场的张量格林函数.
对于电离层、空气层、固体层耦合模式已经得到了电性源格林函数的解[25-26],在此基础上自编了基于(1)、(2)、(3)式的三维积分方程正演程序.
为了开展磁性源激发的场和电性源激发的场的对比研究,需要计算磁性源电磁场的基本公式.磁性源产生的场很容易由电性源产生的场的公式得到.对于电性源的场,电性源的矢量位A,电场E,磁场H满足下述方程:
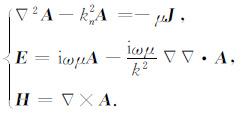
|
(4) |
对于环状电流源,引入磁性源的矢量位A* ,则A* ,E,H满足下述方程:
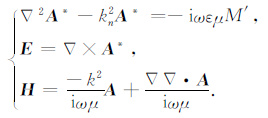
|
(5) |
式中-iωεμM′ 为磁性源,比较(4)、(5)式可知,求磁性源的电场相当于求电性源的磁场,求磁性源的磁场相当于求电性源的电场.
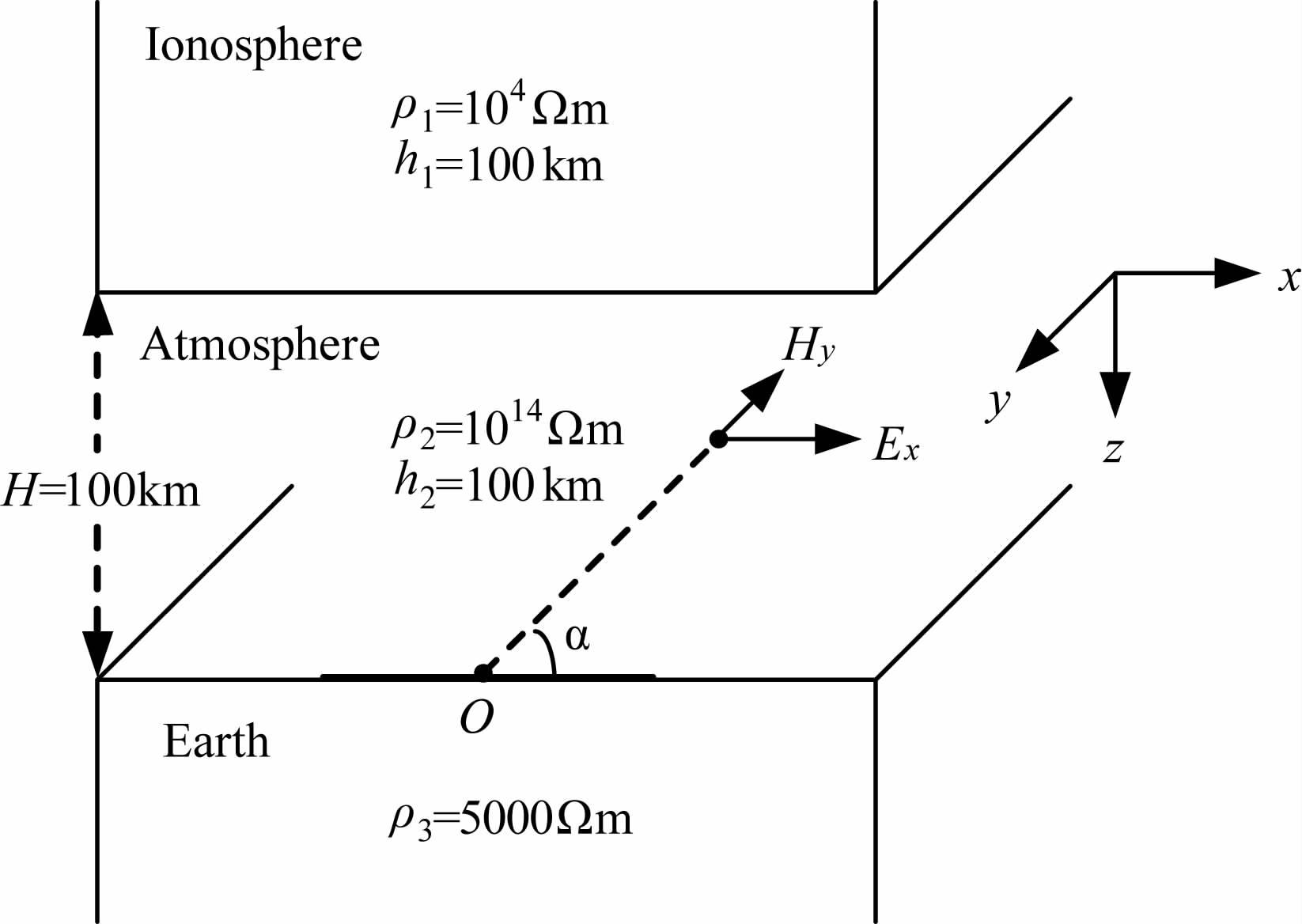
3 “地-电离层"模式三层介质线状和环状电流源场的特征 3.1 波场的频率响应特征为了认识“地-电离层"模式层状介质模型的电磁场在过渡区、波导区的波场特征,进行了图 1模型的长偶极源和环状电流源激发下,远距离在α=0°(接收点沿平行于坐标轴x方向,对于长偶极源偶极方向平行于x方向)和α=90°(接收点沿垂直于长偶极源的y方向)方向上电磁波场随频率变化的特征模拟.
|
图 1 地-电离层模式三层介质模型 Fig. 1 Three layers earth-ionosphere model |
图 1中的源分两种类型:x方向展布的长度L的线状电流源,其两端点坐标A(x,y,z)=(-25km, 0,200km)和B(x,y,z)=(25km, 0,200km);周长为L的环状电流源,中心点位于O(x,y,z)=(0,0,200km).供电电流200A.
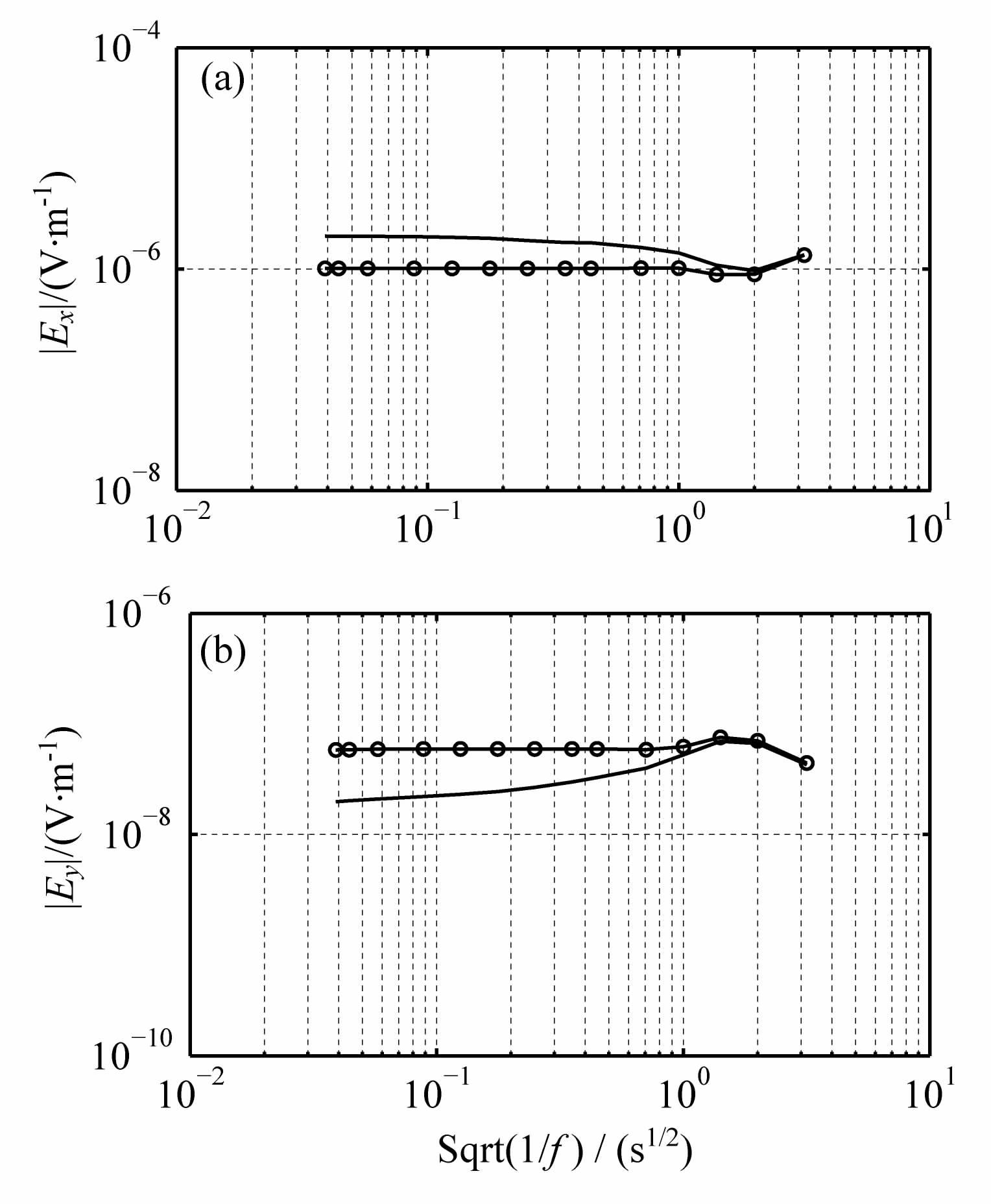
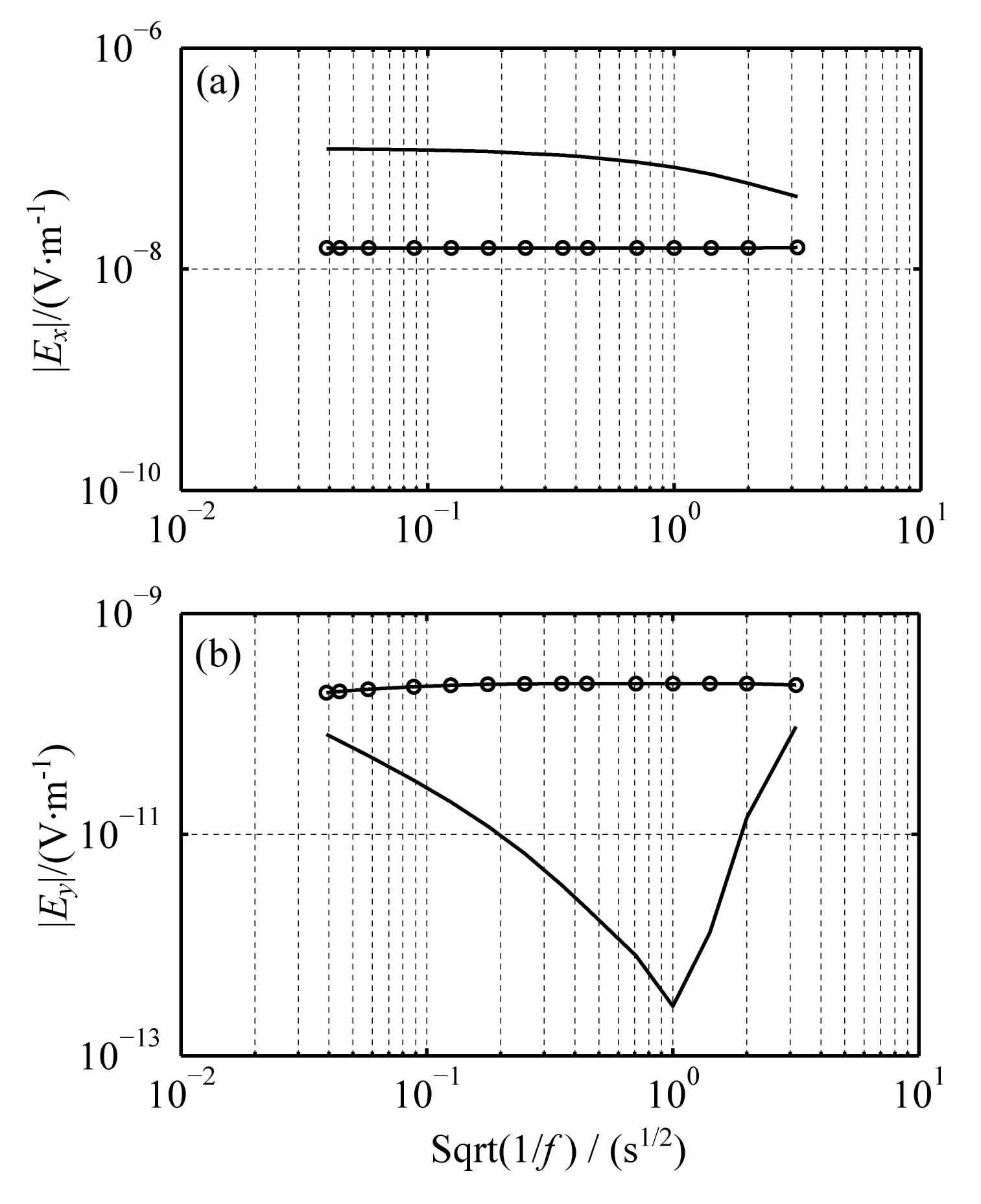
在α=0°方向上长偶极源电场分量Ex和环状电流源电场分量Ey的频率响应分别如图 2和图 3所示.图中给出了不考虑电离层影响的半空间的结果(“o"状线)和考虑电离层影响的地电离层模式的结果(实线).电场的频率响应曲线表明当接收点离开发射源一定远的距离时,考虑电离层线状源的电场幅值比不考虑电离层的电场的幅值大很多,而环状电流源电离层对高频带电场Ey起到了削弱的作用.
|
图 2 α=0°方向接收点x=200km处电场分量的频率响应 (a)线状电流源;(b)环状电流源. Fig. 2 Electric field corresponding with frequency at x=200 km (a)Linear current source;(b)Circle current source. |
|
图 3 α=0°方向接收点x=800km处电场分量的频率响应 (a)线状电流源;(b)环状电流源. Fig. 3 Electric field corresponding with frequency at x=800 km (a)Linear current source;(b)Circle current source. |
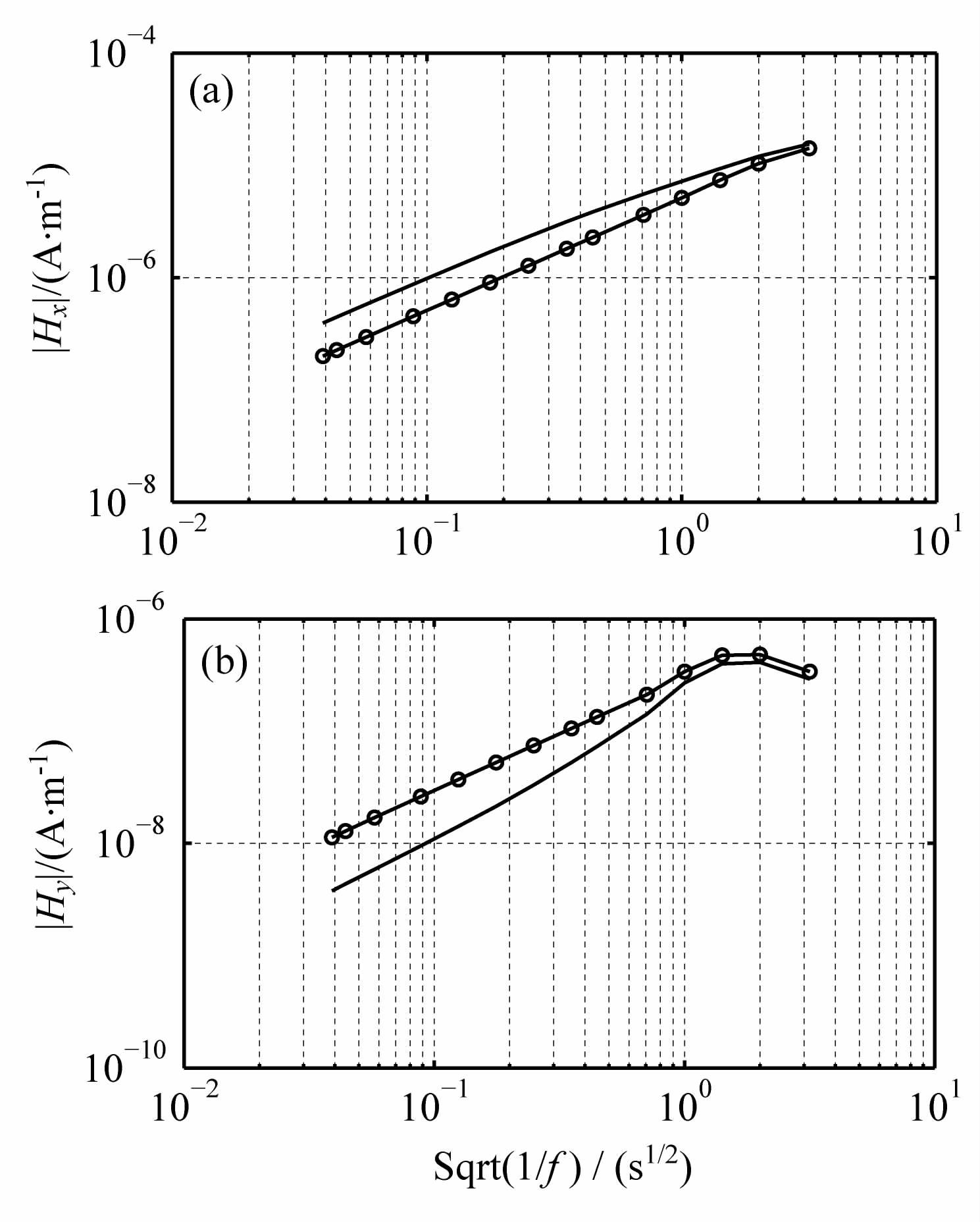
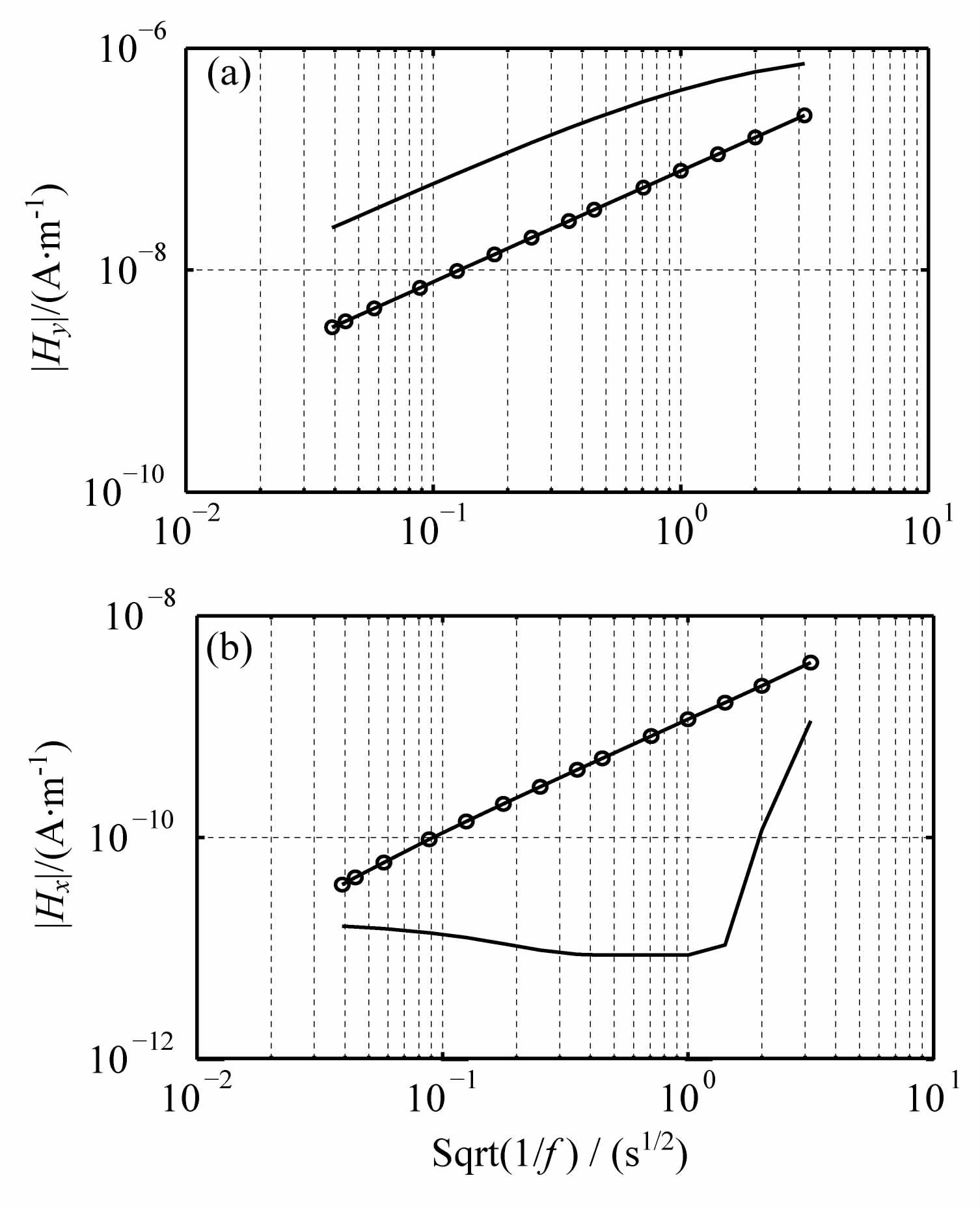
在α=0°方向上长偶极源磁场分量Hx和环状电流源磁场分量Hy的频率响应分别如图 4和图 5所示.图中给出了不考虑电离层影响的半空间的结果(“o"状线),和考虑电离层影响的地电离层模式的结果(实线).磁场的频率响应曲线同样表明当接收点离开发射源一定远的距离时,考虑电离层的线状源的磁场幅值比不考虑电离层的磁场的幅值大很多,而环状电流源电离层对高频带磁场Hx起到了削弱的作用.
|
图 4 α=0°方向接收点x=200km处磁场分量的频率响应 (a)线状电流源;(b)环状电流源. Fig. 4 Magnetic field corresponding with frequency at x=200km (a)Linear current source;(b)Circle current source. |
|
图 5 α=0°方向接收点x=800km 处磁场分量的频率响应 (a)线状电流源;(b)环状电流源. Fig. 5 Magnetic field corresponding with frequency at x = 800 km (a)Linear current source;(b)Circle current source. |
在沿α=90°方向上电磁波场随频率变化的响应特征和α=0°方向上的结果是一致的,当接收点离开发射源一定远的距离时,考虑电离层线状源的电磁场幅值比不考虑电离层的磁场幅值大很多,而环状电流源电离层对高频带电磁场起到了削弱的作用,这里不再赘述.
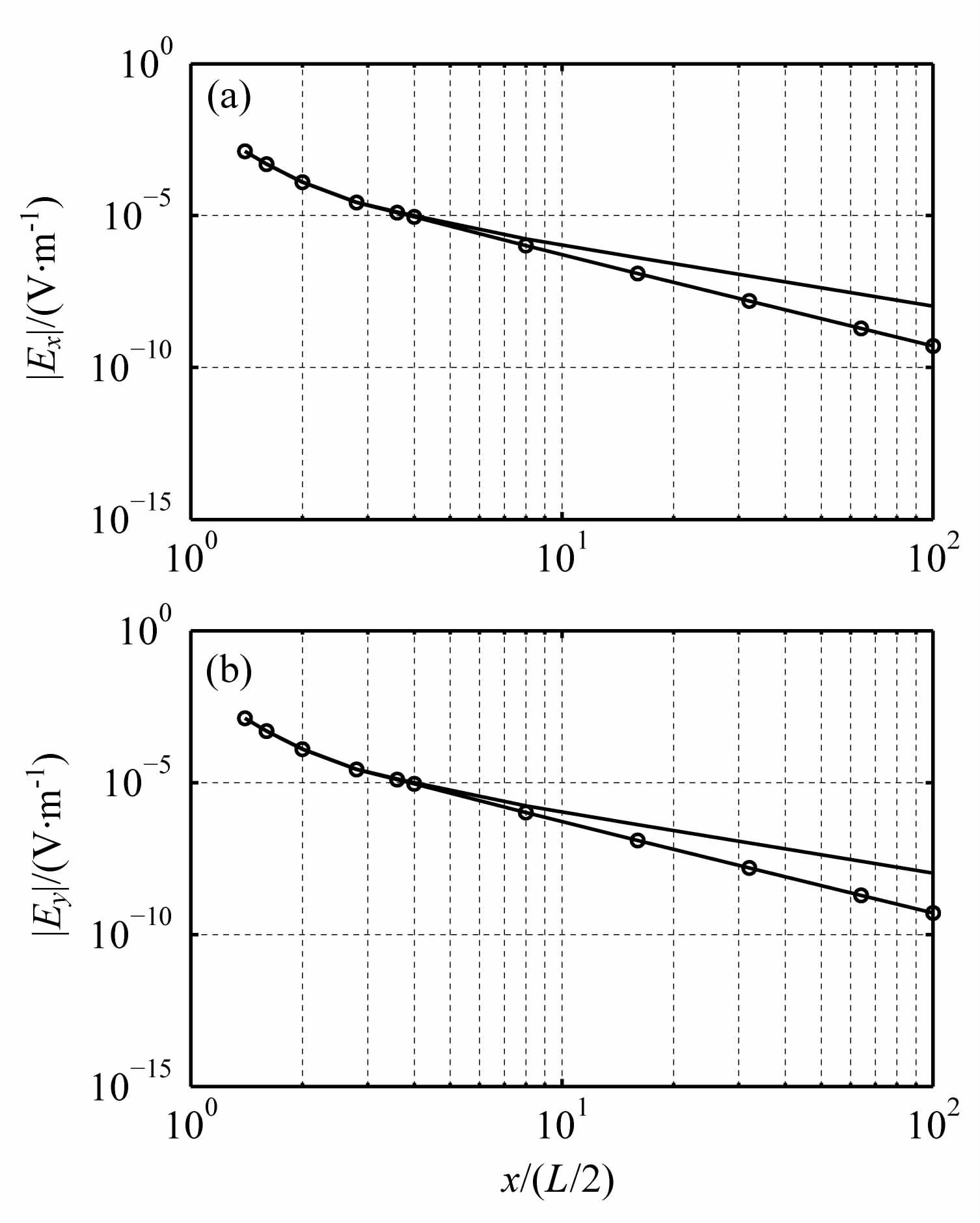
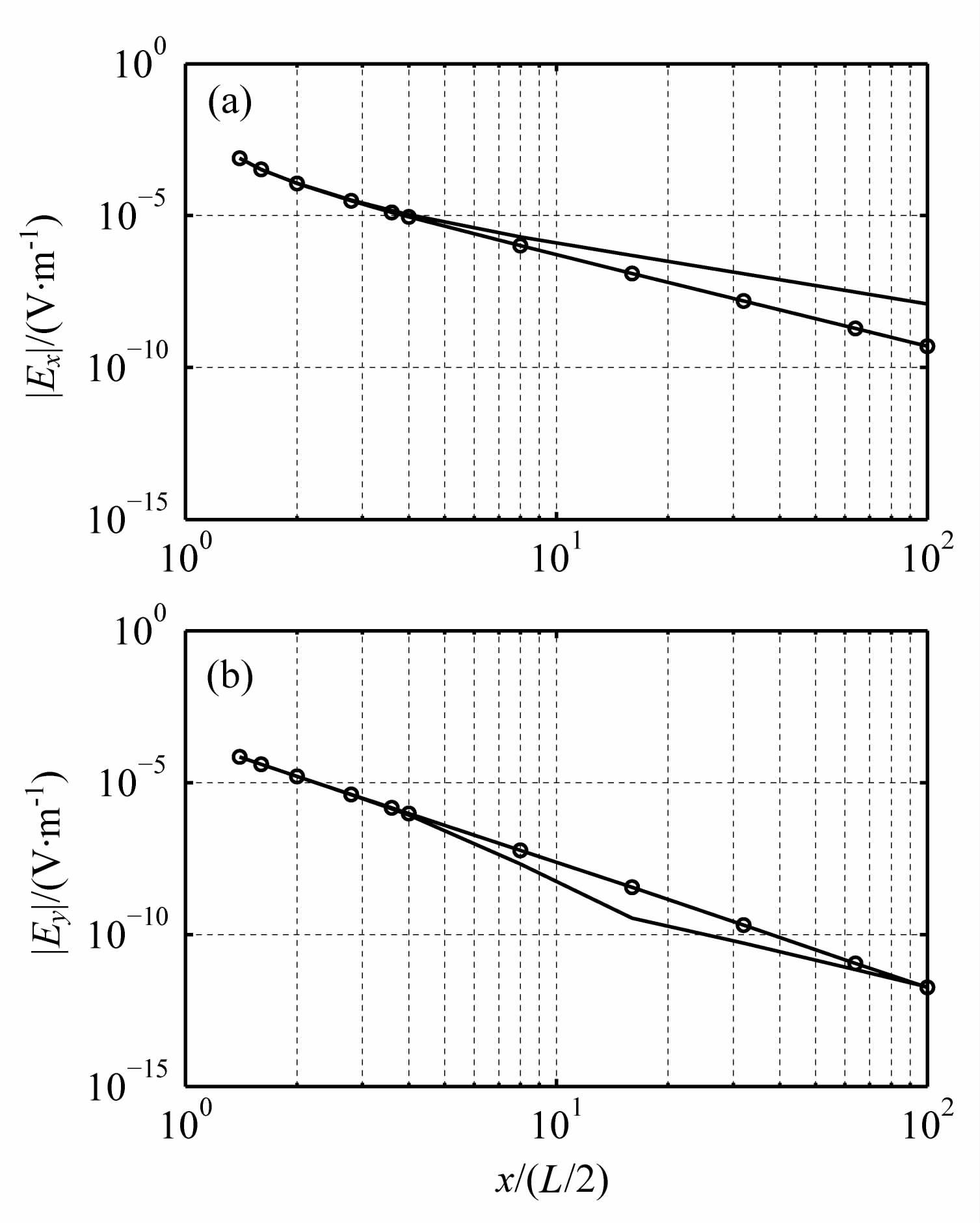
3.2 给定频率波场衰减特征在α=0°方向上电场随距离(35 km ≤x≤2500km)的衰减特征分别在图 6和图 7中给出.图中曲线表明在考虑电离层影响的“地-电离层"模式中,电离层对电性源场Ex的影响使波导区的场得到加强,而对磁性源场Ey的影响使波导区得到削弱.在小收发距离时,电离层的影响还没有,此时地面半空间模型响应与考虑电离层影响的模型响应一致.随着收发距离增加,电离层影响增大,两者频率响应分离.
|
图 6 α=0°方向接收点频率5 Hz时电场随距离变化曲线 (a)线状电流源;(b)环状电流源. Fig. 6 Electric field corresponding with distance at frequency 5 Hz (a)Linear current source;(b)Circle current source. |
|
图 7 α=0°方向接收点频率300 Hz时电场随距离变化曲线 (a)线状电流源;(b)环状电流源. Fig. 7 Electric field corresponding with distance at frequency 300 Hz (a)Linear current source;(b)Circle current source. |
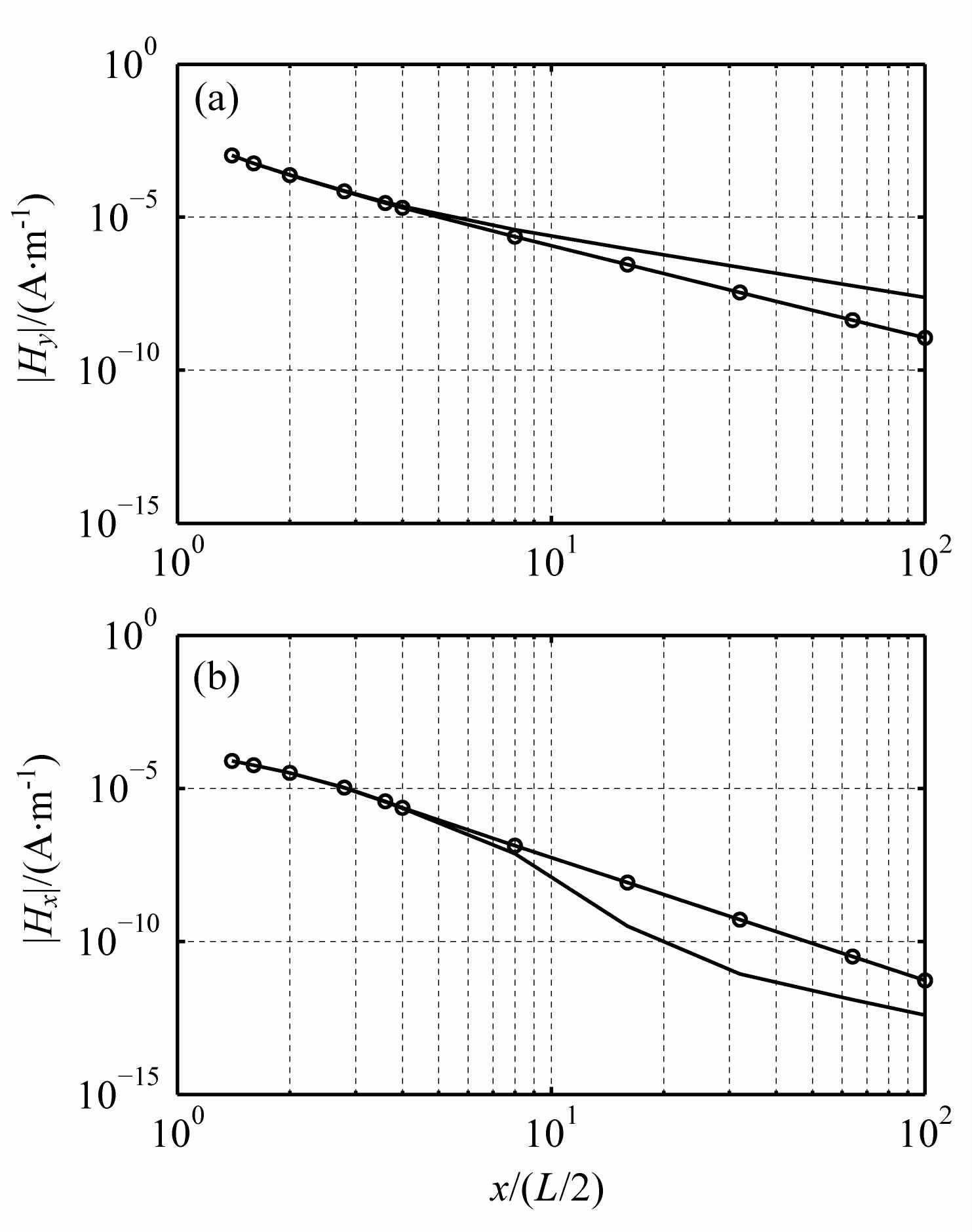
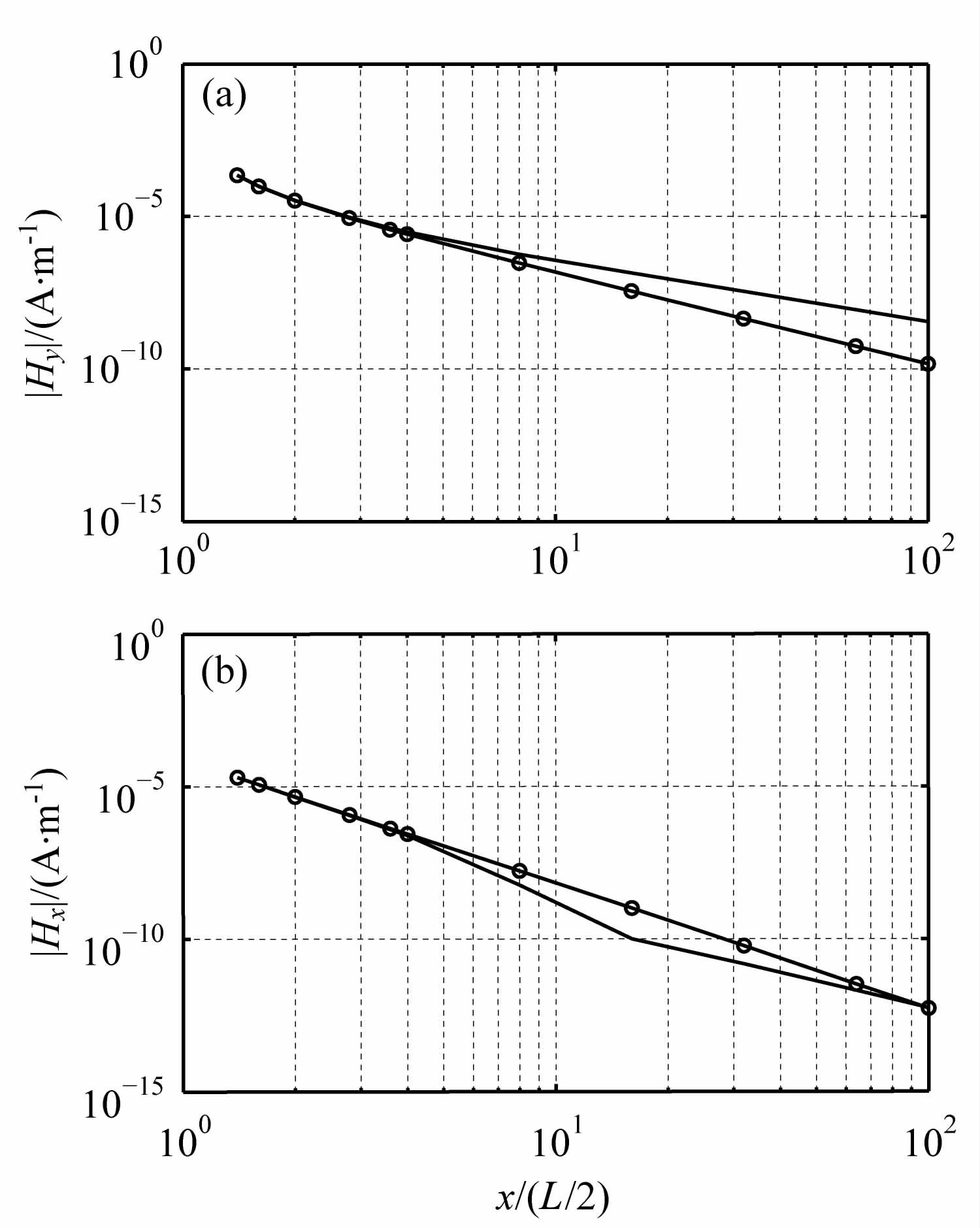
在沿α=0°方向上不同频率衰减特征分别在图 8和图 9 中给出.图中曲线表明电离层使电性源激发的磁场Hy在波导区得到加强,磁性源激发的Hx得到减弱.
|
图 8 α=0°方向接收点频率5Hz时磁场随距离变化曲线 (a)线状电流源;(b)环状电流源. Fig. 8 Magnetic field corresponding with distance at frequency 5 Hz (a)Linear current source;(b)Circle current source. |
|
图 9 α=0°方向接收点频率300 Hz时磁场随距离变化曲线 (a)线状电流源;(b)环状电流源. Fig. 9 Magnetic field corresponding with distance at frequency 300 Hz (a)Linear current source;(b)Circle current source. |
在沿α=90°方向上场的衰减特征与α=0°的类似,只是衰减的幅度要大些.
4 讨论及结论在3.1节中电性源和磁性源产生的电场和磁场分量在波导区的频率响应特征和3.2节中两种源产生的电场和磁场分量在波导区的衰减特征表明,波导区场的强度不仅由源的强度决定,而且还与电离层的影响有关.对于电性源水平x方向的源激发的电场Ex和磁场Hy,在波导区电离层的影响使它们的场值得到加强.对于磁性源垂直方向(z方向)源激发的α=0°方向上电场Ey,磁场Hx和α=90°方向上的电场Ex,磁场Hy,在波导区电离层的影响使它们的场值不但没有得到加强,反而被削弱.这是由于在波导区,接收点不仅接收到来自源的直达波,而且还接收到来自电离层的反射波(当然也接到来自固体地球层内返回的波,由于在固体层内,波被电性体吸收严重,它们的强度比空气层中的波强度小许多,这里给予忽略)两种波在接收点会产生相关或相消干涉,这取决于两种波的传播距离,也取决于激发的波的性质.在本文的情况中,电性源和磁性源激发的波在传播距离上的差异是一致的,因此主要取决于两种源产生的电场和磁场在性质上的差异.当L为数十公里时候,接收点的位置远离发射源,此时电离层的影响不可忽略,电离层的影响既可能是增强信号,也可能是削弱信号,这取决于组成线状源和面积性源的各个点状源发射的信号经电离层和空气层传播到达接收点时的相位,这些不同相位的波叠加后,可能得到增强也可能减弱.
对于电性源的结果,俄罗斯较早做了这方面的工作[18, 21],在和俄罗斯合作研究WEM 在地震预报中的应用和申请国家WEM 探地工程项目时,曾用俄罗斯的软件进行了应用研究.底青云[23-24]利用犹他大学的电性源程序的计算结果及其分析表明,在不考虑空气层的位移电流时,使用犹他大学电性源软件计算的结果和俄罗斯软件的结果是一致的.作者所在的课题组进一步自行开发了电性源软件,在不考虑空气中的位移电流时,只考虑电离层影响的波导区场的特征,所得结果与俄罗斯和美国犹他大学的软件的结果也是一致的;在考虑空气层的位移电流后自行开发的软件模拟结果有了一些新的特征,在波导区场增加的幅度更大[25].这些软件计算的结果一致性,表明对于水平方向x方向的电性源激发的Ex,Hy场分量在波导区的作用,使场得到加强的结果是可靠的.
对于垂直磁性源是否会在波导区,由于电离层的作用,会使场反而减弱,目前尚未找到有关的参考文献的结果来旁证.按照电磁场格林张量的互易关系
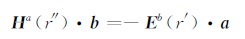
|
(6) |
表明,由r′ 处a方向电性源激发的在r″ 处产生的磁场Ha(r″)在b方向上的分量等于由r″ 处b方向磁性源激发的在r′ 处产生的电场Eb(r′)在a方向上分量的负值.这就是说可以用自行开发的电性源的软件计算水平x方向的电性源激发的z方向的磁场Hz,它的特征应该等于z方向的磁性源激发的x方向的电场Ex的特征.经计算检验,得出的结果是一致的,证明了作者的磁性源软件结果的正确性,这从另一个侧面证实本文计算的结果是可靠的.为此,认为当采用大功率固定源在波导场工作时应该采用线状电流源.
| [1] | Cagniard L. Basic theory of the magnetotelluric method of geophysical prospecting. Geophys. , 1953, 18(3): 605-635. DOI:10.1190/1.1437915 |
| [2] | Vozoff K. Magnetotelluric Methods. USA: Geophysics Reprint Series, 1986 : 1 -763. |
| [3] | 石昆法. 可控源音频大地电磁法理论与应用. 北京: 科学出版社, 1999 . Shi K F. The Theory and Applications of Control Source Audio Frequency Magnetotellurics Method (in Chinese). Beijing: Science Press, 1999 . |
| [4] | 底青云, 王若, 等. 可控源音频大地电磁数据正反演及方法应用. 北京: 科学出版社, 2008 . Di Q Y, Wang R, et al. CSAMT Forward Modeling and Inversion and Its Application (in Chinese). Beijing: Science Press, 2008 . |
| [5] | 汤井田, 何继善. 可控源音频大地电磁法理论与应用. 长沙: 中南工业大学出版社, 2005 . Tang J T, He J S. Controlled Source Electromagnetic Method and Its Applications (in Chinese). Changsha: Central South University Press, 2005 . |
| [6] | 底青云, 王妙月, 石昆法, 等. 高分辨V6系统在矿山顶板涌水隐患中的应用研究. 地球物理学报 , 2002, 45(5): 744–748. Di Q Y, Wang M Y, Shi K F, et al. An applied study on prevention of water bursting disaster in mines with the high resolution v6 system. Chinese J. Geophys. (in Chinese) , 2002, 45(5): 744-748. |
| [7] | 底青云, 王光杰, 安志国, 等. 南水北调西线千米深长隧洞围岩构造地球物理勘探. 地球物理学报 , 2006, 49(6): 1836–1842. Di Q Y, Wang G J, Gong F, et al. Geophysical exploration of a long deep tunnel on the west route of South-to-North Water Diversion Project. Chinese J. Geophys. (in Chinese) , 2006, 49(6): 1836-1842. |
| [8] | 底青云, 王妙月, 石昆法, 等. V6多功能系统及其在CSAMT勘查应用中的效果. 地球物理学进展 , 2002, 17(4): 663–670. Di Q Y, Wang M Y, Shi K F, et al. Mutifunction system-V6 and its effectiveness in CSAMT exploration. Progress in Geophysics (in Chinese) , 2002, 17(4): 663-670. |
| [9] | 底青云, 伍法权, 王光杰, 等. 地球物理综合勘探技术在南水北调西线工程深埋长隧洞勘察中的应用. 岩石力学与工程学报 , 2005, 24(20): 3631–3638. Di Q Y, Wu F Q, Wang G J, et al. Geophysical exploration over long deep tunnel for west route of South-to-North Water Transfer Project. Chinese Journal of Rock Mechanics and Engineering (in Chinese) , 2005, 24(20): 3631-3638. |
| [10] | 李帝铨, 底青云, 王光杰, 等. CSAMT探测断层在北京新区规划中的应用. 地球物理学进展 , 2008, 23(6): 1963–1969. Li D Q, Di Q Y, Wang G J, et al. Fault detection by CSAMT and its application to new district planning in Beijing. Progress in Geophysics (in Chinese) , 2008, 23(6): 1963-1969. |
| [11] | 吴璐萍, 石昆法, 李荫槐, 等. 可控源音频大地电磁法在地下水勘查中的应用研究. 地球物理学报 , 1996, 39(5): 712–717. Wu L P, Shi K F, Li Y H, et al. Applied of CSAMT to the search for groundwater. Chinese J. Geophys. (in Chinese) , 1996, 39(5): 712-717. |
| [12] | 于昌明. CSAMT方法在寻找隐伏金矿中的应用. 地球物理学报 , 1998, 41(1): 133–138. Yu C M. The application of CSAMT method in looking for hidden gold mine. Chinese J. Geophys. (in Chinese) , 1998, 41(1): 133-138. |
| [13] | 吴璐苹, 石昆法. 松山地下热水勘探及成因模式探讨. 物探与化探 , 1996, 20(4): 309–315. Wu L P, Shi K F. Exploration of underground thermal water in Songshan area and a discussion on its genetic model. Geophysical and Geochemical Exploration (in Chinese) , 1996, 20(4): 309-315. |
| [14] | 刘宏, 刘东琴, 杨轮凯, 等. CSAMT勘探方法在寻找地热中的应用. 物探装备 , 2002, 12(2): 129–131. Liu H, Liu D Q, Yang L K, et al. Application of CSAMT prospecting method in finding geotherm. Equipment for Geophysical Prospecting (in Chinese) , 2002, 12(2): 129-131. |
| [15] | 王赟, 杨德义, 石昆法. CSAMT法基本理论及在工程中的应用. 煤炭学报 , 2002, 27(4): 384–387. Wang Y, Yang D Y, Shi K F. The basic principle of CSAMT method and its application in the engineering field. Journal of China Coal Society (in Chinese) , 2002, 27(4): 384-387. |
| [16] | 赵国泽, 汤吉, 邓前辉, 等. 人工源超低频电磁波技术及其应用于首都圈地震预测的测量研究. 地学前沿 , 2003, 10(S1): 248–257. Zhao G Z. Tang J. Deng Q H, et al. Artificial SLF method and the experimental study for earthquake monitoring in Beijing area. Earth Science Frontiers (in Chinese) , 2003, 10(S1): 248-257. |
| [17] | 卓贤军. 人工超低频电磁场场强分布及测量的研究. 北京:中国地震局研究所, 2005. Zhuo X J. The Research of the Distribution and Measurement of Artificial SLF Field . Beijing: Institute of Geology, Chinese Earthquake Administration, 2005. |
| [18] | 卓贤军, 赵国泽. 一种资源探测人工源电磁技术. 石油地球物理勘探 , 2004, 39(S1): 114–117. Zhuo X J, Zhao G Z. A new electromagnetic method with artificial source in resources exploration. Oil Geophysical Prospecting (in Chinese) , 2004, 39(S1): 114-117. |
| [19] | 卓贤军, 赵国泽, 底青云, 等. 无线电磁法(WEM)在地球物理勘探中的初步应用. 地球物理学进展 , 2007, 22(6): 1921–1924. Zhuo X J, Zhao G Z, Di Q Y, et al. Preliminary application of WEM in geophysical exploration. Progress in Geophysics (in Chinese) , 2007, 22(6): 1921-1924. |
| [20] | 卓贤军, 陆建勋. "极低频探地工程"在资源探测和地震预测中的应用与展望. 舰船科学技术 , 2010, 32(6): 3–7. Zhuo X J, Lu J X. Application and prospect of WEM to resource exploration and earthquake predication. Ship Science and Technology (in Chinese) , 2010, 32(6): 3-7. |
| [21] | 卓贤军, 张佳炜. 极低频发射天线场地等效电阻率的计算. 舰船电子工程 , 2009, 29(8): 192–195. Zhuo X J, Zhang J W. A calculating method of the effective resistivity for the extremely low frequency (ELF) transmitting antenna site. Ship Electronic Engineering (in Chinese) , 2009, 29(8): 192-195. |
| [22] | 底青云, 王妙月, 王若, 等. 长偶极大功率可控源电磁波响应特征研究. 地球物理学报 , 2008, 51(6): 1917–1928. Di Q Y, Wang M Y, Wang R, et al. Study of the long bipole and large power electromagnetic field. Chinese J. Geophys. (in Chinese) , 2008, 51(6): 1917-1928. |
| [23] | 底青云, 王光杰, 王妙月, 等. 长偶极大功率可控源激励下目标体电性参数的频率响应. 地球物理学报 , 2009, 52(1): 275–280. Di Q Y, Wang G J, Wang M Y, et al. Frequency response characteristics of target electric property with long bipole large power control source. Chinese J. Geophys. (in Chinese) , 2009, 52(1): 275-280. |
| [24] | 李帝铨, 底青云, 王妙月, 等. 电离层-空气层-地球介质耦合下大尺度大功率可控源电磁波正演研究. 地球物理学报 , 2010, 53(2): 411–420. Li D Q, Di Q Y, Wang M Y, et al. Study of large scale and large power control source electromagnetic response with "Earth-ionosphere" Model. Chinese J. Geophys. (in Chinese) , 2010, 53(2): 411-420. |
| [25] | 付长民, 底青云, 王妙月. 计算层状介质中电磁场的层矩阵法. 地球物理学报 , 2010, 53(1): 177–188. Fu C M, Di Q Y, Wang M Y. Calculate electromagnetic fields in stratified medium with layer-matrix method. Chinese J. Geophys. (in Chinese) , 2010, 53(1): 177-188. DOI:10.1002/cjg2.v53.1 |
| [26] | Ward S H. Geophysical Electromagnetic Theory . Beijing: Geological Publishing House, 1978 . |
| [27] | Habashy T M, Groom R W, Spies B W. Beyond the born and rytov approximation: A nonlinear approach to electromagnetic scattering. J. Geophys. Res. , 1993, 98(B2): 1759-1775. DOI:10.1029/92JB02324 |
| [28] | Xie G Q, Li J H, Majer E L, et al. 3-D electromagnetic modeling and nonlinear inversion. Geophys. , 2000, 65(3): 804-822. DOI:10.1190/1.1444779 |
| [29] | Tseng H W, Lee K H, Becker A. 3D interpretation of electromagnetic data using a modified extended born approximation. Geophys. , 2003, 68(1): 127-137. DOI:10.1190/1.1543200 |
| [30] | Hohmann G W. Three-dimensional induced polarization and electromagnetic modeling. Geophys. , 1975, 40(2): 309-324. DOI:10.1190/1.1440527 |
| [31] | Zhdanov M S. Geophysical inversion theory and regularization problems. Amsterdam-Boston-London-New York-Oxford-Paris-Tokyo. San Diego-San Francisco-Singapore-Sydney, 2002: 231-324. |
| [32] | Nibighian M N. Electromagnetic Methods in Applied Geophysics (Volume 1): Theory. Tulsa: Society of Exploration Geophysicists, 1987 . |
| [33] | Dmitriev V I, Nesmeyanova N I. Integral equation method in three-dimensional problems of low-frequency electrodynamics. Computational Mathematics and Modeling , 1992, 3(3): 313-317. DOI:10.1007/BF01133905 |
| [34] | Raiche A P. An integral equation approach to there-dimensional modeling. Geophys. J. Roy. Astron. Soc. , 1974, 36(2): 363-376. DOI:10.1111/j.1365-246X.1974.tb03645.x |
| [35] | Weidelt P. Electromagnetic induction in there-dimensional structures. J. Geophys. , 1975, 41(1): 85-109. |
| [36] | Wannamaker P E. Advances in there-dimensional magnetotelluric modeling using integral equations. Geophysics , 1991, 56(11): 1716-1728. DOI:10.1190/1.1442984 |
| [37] | Zhdanov M S, Fang S. Quasi-linear approximation in 3D electromagnetic modeling. Geophysics , 1996, 61(3): 646-665. DOI:10.1190/1.1443994 |
| [38] | Kress R. Linear integral equations. Berlin, Heidelberg, New York, London, Paris, Tokyo: Springer-Verlag, 1999 : 365 . |
| [39] | 底青云, UnsworthM, 王妙月. 复杂介质有限元法2.5维可控源音频大地电磁法数值模拟. 地球物理学报 , 2003, 47(4): 723–730. Di Q Y, Unsworth M, Wang M Y. 2.5-D CSAMT modeling with the finite element method over 2-D comlex earth media. Chinese J. Geophys. (in Chinese) , 2003, 47(4): 723-730. |
 2012, Vol. 55
2012, Vol. 55

