2. 中国地质大学(北京)地球物理与信息技术学院, 北京 100083
2. School of Geophysics and Information Technology, China University of Geosciences, Beijing 100083, China
重磁资料的分析解释通常离不开选择多种处理转换方法进行计算与分析对比的过程,即处理转换在重磁资料解释中发挥着重要的作用.但由于一些转换计算如向下延拓、化极等有时是很不稳定的,所以,如何得到稳定有效的转换计算结果就成为重磁位场的重要研究内容之一.
重磁位场的向下延拓是典型的不稳定计算,其本质是数学物理的反问题,所以在计算时具有不稳定性.在形式上,向下延拓的不稳定性在频率域换算中表现为转换因子对数据中高频成份的放大作用,因此,一些研究就是基于频率域里附加滤波器或改造下延转换因子的手段,对造成不稳定的高频放大作用进行一定的压制,尽管该方式已经取得了良好的效果,但还难以达到高精度勘探阶段人们更高的期望.针对上述问题,近年来我国研究者对迭代法进行了深入研究,取得了一些比较深入的研究成果.迭代法首先是Strakhov等[1]在研究曲化平时提出来的,他为了实现弱地形(即场源位于起伏地形最低点之下)上异常向下延拓到最低点平面,采取并系统地建立了积分迭代法,给出了计算迭代步骤,指出了迭代的收敛性分析.只是受当时计算条件的约束,迭代法计算量相当大限制了其应用.徐世浙等[2-4]在此基础上也进行了系统的研究,并采取频率域方法提高迭代法的计算速度,充分体现了迭代法门槛低的突出优点,从而使迭代法受到普遍重视.刘东甲等[5]基于频率域从数学上证明了迭代法向下延拓的等价计算关系式,依此方式可以直接计算等效的迭代结果,避免了前人方法的实际迭代过程,因而明显提高了计算速度.另外,证明了迭代向下延拓计算随着迭代次数的增加,所得到的结果无限趋近于FFT 直接向下延拓的理论结果,依此作为迭代法下延收敛的重要依据.张辉等[6]也对迭代向下延拓的收敛性进行了类似的分析证明.曾小牛等[7]基于正则化手段压制干扰信号高频影响的实际需要,比较了迭代Tikhonov正则化法、Landweber正则化迭代法和积分迭代法,对提高迭代法下延中减弱高频干扰的效果进行了分析研究.于波等[8]也对实际资料中噪声干扰的存在对迭代下延的影响进行了分析研究.王彦国等[9]提出了泰勒级数迭代法,该方法主要是加快了迭代法计算时迭代过程的收敛速度.骆遥[10]通过对迭代下延中场分离的过程的分析,进一步对迭代过程的收敛性加以解释说明.由于迭代下延计算方法简单、易于实现,并且在很多情况下能取得相当好的效果,所以,近年来该方法在实际中得到了普遍应用(徐世浙等[11-14];杨金玉等[15];于波等[16-17];王小兵等[18];肖锋等[19];李成立等[20];余海龙等[21]).由此可见,迭代法在重磁位场下延中应用研究已受到广泛的关注和重视.
迭代法在向下延拓中的积极研究也将其影响扩展到重磁位场转换的其它方法中,比如磁异常的低纬度化极.化极转换方法也称化向地磁极(简称化极)是最基本的磁测资料处理方法之一,其主要作用是消除地磁场对场源斜磁化造成的磁异常的复杂性,与原始磁异常相比,化极计算后的磁异常在形态上更加简单,与场源的分布对应关系上也更加直接,因而成为磁异常分析解释的基础.但是,在低纬度地区测量获得的磁异常,其化极计算是不稳定的,在频率域中表现为化极转换因子具有明显的放大作用,在磁赤道附近,化极计算甚至因过分放大导致无法进行.针对低纬度化极问题的长期研究进展,这里不再一一列出,虽然取得了一些比较有效的成果,但仍然存在各种问题或不足.这里我们只对与迭代法相关的研究进展加以介绍.最早文献初步涉及到迭代法的是Keating等[22]的工作,他们尝试运用维纳滤波的化极结果反算到原斜磁化方向与原始数据进行对比,对化极结果进行修正,不过实验及分析表明,当修正次数超过3 次时,结果不会随着迭代次数的增加而改善.Li[23]运用能量平衡法将化极结果反算到斜磁化方向与原始数据对化极结果修正,相当于应用了迭代过程,但其也只进行了3 次迭代.骆遥等[24]在借鉴迭代法下延取得成果的基础上进行了赤道化极研究,其重要结论是认识到化极计算不但改变了异常的振幅而且改变了相位,所以直接通过计算值与实测值的残差进行修正的迭代法会导致结果不收敛,为此,通过技术性处理,即结合磁异常“倒相"处理方法(方迎尧等[25]),实现了迭代法磁赤道化极,取得了比较好的效果.对于重磁位场处理转换中迭代法的应用而言,针对性的“倒相"转换映射措施是对迭代法应用研究的进一步深化.
尽管迭代法应用于向下延拓及低纬度化极等转换计算已取得了一定的效果,但随着研究的逐步深入,实际上已经隐约暴露出迭代法应用于重磁位场处理转换的不足和问题.鉴于前人对迭代法的研究都是针对具体问题进行孤立分析的,通过对前人研究成果加以分析、对比,可以发现,对于不同处理转换问题,迭代法的收敛性和收敛条件是不尽相同的.所以,进一步深入研究迭代法在重磁位场计算中的收敛性以及收敛条件的一般性规律,对于更好地应用迭代法以及客观评价其特点、认识其存在的问题,具有重要意义.为此,本文对迭代法在重磁处理中的应用进行了统一的分析与研究,推导了迭代法通式,再针对具体问题推导出具体的收敛条件,并对各种因素对迭代法收敛性的影响进行了分析.我们的研究表明,向下延拓及化极等不同的重磁处理转换方法中需要选择不同的迭代计算方式,相当于是选择了不同的映射函数;在选择了合适的映射函数的情况下,如果迭代次数很大,迭代计算虽然能够收敛到理论计算结果(在频率域即FFT 理论直接计算结果),但是一些处理转换其理论计算结果本身通常是不稳定的;如果迭代次数过少,则可能对有用信息的压制过大,造成计算结果仍然存在较大的误差;频率域迭代法等效滤波计算关系式的存在证明了迭代法位场转换在本质上与改造转换因子或附加特定滤波器的作用是等效的,所以,针对向下延拓及低纬度化极这类不稳定的转换计算,迭代法并没有从根本上解决计算精度与稳定性之间的矛盾.下面我们将对此进行详细的分析.
2 方法原理重磁异常转换计算中的迭代法应用是一种通过多次的稳定计算来代替不稳定直接计算的过程,这点上明显不同于其它领域里常用的迭代方式.以向下延拓为例,就是原本直接的下延计算,转化为特定的分步迭代计算过程,每步迭代计算的主要过程是向上延拓,而不是向下延拓,这是和其它领域常规迭代法的明显区别.现有文献迭代法下延的具体迭代步骤为:首先将原始观测面上的重磁异常直接当成是待下延位置平面上的结果重磁异常,显然,这只是一个初始近似,其近似程度(即误差)是由延拓的高度差及重磁异常复杂程度共同决定的.遗憾的是其具体误差是未知的,即无法评价其近似程度.为此,第二步是为评价及修改服务的,采取的是将该延拓面上的重磁异常初始近似结果再次向上延拓到原始观测面上,这一步向上延拓是需要实际计算的.由于向上延拓是稳定转换计算,且具有很高的精度,因此这个计算过程引入的误差很小,比较而言可以忽略.这样,原始观测面上就获得了新的由上延计算得到的结果,原始数据与其对比的差异,一定程度上可以看成是下延平面上未知的理想结果与近似结果的差异的反映,基于此间接达到了对下延结果进行近似评价的目的.如果该差异(即误差)足够小,则认为下延的结果已足够逼近理想结果,否则,需要设法提高、改进.这里,迭代法的改进方式就是采取将原始数据与上延结果的差直接附加于待延拓面上的初始异常,附加修改后获得的新的近似异常,则需要重复采用上延的方法计算与评价,这样就形成了新的迭代过程.由此可见,这种迭代法下延是希望通过分步的上延计算(稳定计算)代替一步的直接下延计算(不稳定计算),其突出优点是原理清晰、步骤简单.众多研究者也都强调该计算过程的稳定性,并以最终逼近理论直接下延结果证明其收敛性.
为了客观评价迭代法在重磁位场转换中的作用,有必要进一步进行归纳分析.下面我们在频率域对迭代法的流程进行说明,以期得到一般性的迭代转换关系式.
设U0(u,v)为观测平面上原始数据u0(x,y)的Fourier变换结果,Ua(u,v)为待求的目标数据ua(x,y)的Fourier变换结果,其中x,y为空间域坐标变量,u,v为频率域频率变量,ψ(u,v)为相应转换计算的频率域转换因子,则二者在频率域转换关系可以表示为
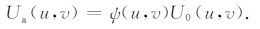
|
(1) |
对于化极、向下延拓等转换问题,(1)式中ψ(u,v)的一些值会很大甚至为无穷,直接计算是不稳定或无法计算,传统的针对性方法多数是对该转换因子进行改造,提高其计算的稳定性.对于采用迭代法计算,为了得到稳定的计算结果,首先直接将原始数据当成是目标数据的初始值(对于向下延拓)或“倒相"后作为初始值(对于赤道化极),这里我们将其作一般性推广,即定义为一个U0(u,v)到Ua(*) (u,v)的映射,Ua(*) (u,v)为目标数据频谱Ua(u,v)的近似值,其形式为
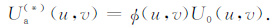
|
(2) |
在频率域里,由于我们所要解决的问题是线性的,所以映射也选择线性映射.我们称φ(u,v)为映射函数,理论上,映射函数在选择上应该是频率域转换因子的一个近似.
迭代法流程如图 1 所示.为了求解(1)式中的Ua(u,v),我们设(2)式的Ua(*) (u,v)是上述方程的近似解,但其近似程度实际上是无法评价的,为此,这里采取的措施是将其反算回去与原始数据对比,试图由此间接地评价其近似程度,显然,其前提是反运算的误差不大.设Ur(u,v)是原始数据与反运算结果的残差,则有
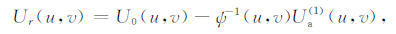
|
式中,Ua(1) (u,v)是Ua(u,v)的第一次近似,ψ-1(u,v)为ψ(u,v)的倒数即反变换因子.将残差再次带入(2)式求解修正值,可得修正值为
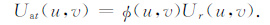
|
令
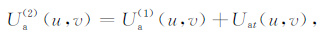
|
这里先假设通过选取合适的φ(u,v)使得结果能够收敛,具体步骤及过程在后面会详细论述,则虽然Ua(2) (u,v)仍然不是方程的精确解,但Ua(2) (u,v)是Ua(1) (u,v)的改进.可以把Ua(2) (u,v)再次反算回与原始数据对比、评价,如此,则形成迭代过程,直到误差足够小为止.
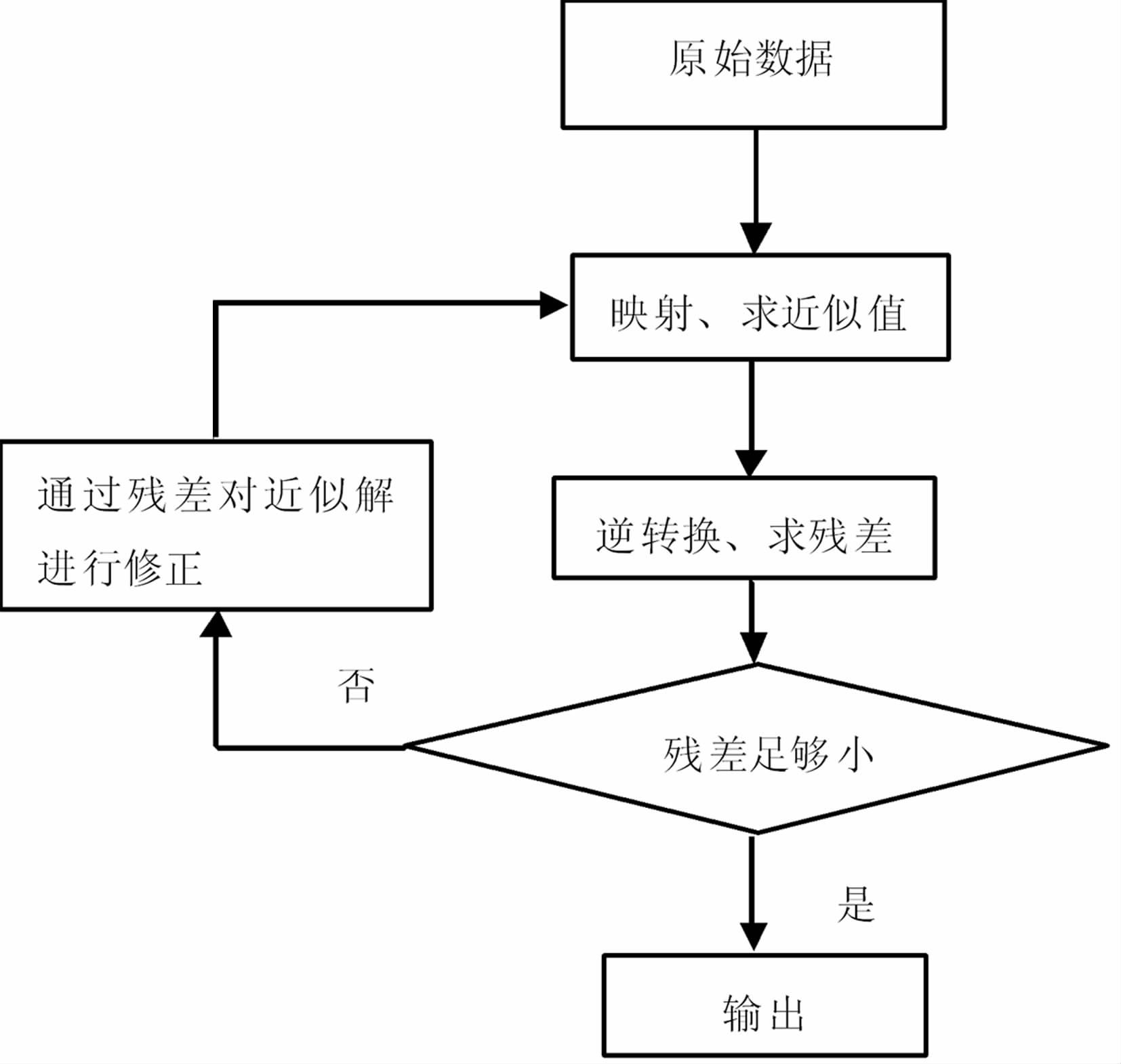
|
图 1 迭代法流程图 Fig. 1 The scheme of iteration method |
根据上面的假设,我们可以总结出迭代法的递推公式:
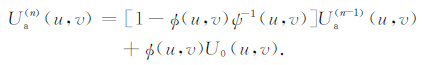
|
(3) |
下面对上述第n次的迭代结果进行归纳推导:
第一次迭代:
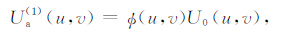
|
(4) |
第二次迭代:
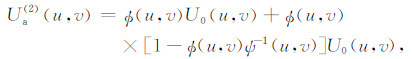
|
(5) |
根据(3)、(4)、(5)式以及数学归纳法不难得出:
第n次迭代结果为
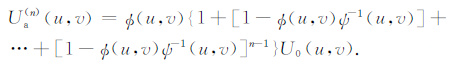
|
(6) |
根据等比数列求和公式将其化简可得

|
(7) |
从上式可以看出只要
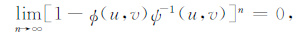
|
(8) |
即对于所有的u、v都有下式成立:
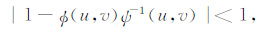
|
(9) |
迭代结果就会收敛到ψ(u,v)U0(u,v).
由此可见,映射函数φ(u,v)决定着迭代法是否收敛.在收敛的前提下,迭代无穷次的结果为FFT理论直接计算结果ψ(u,v)U0(u,v),又与我们选择的映射函数无关.而当有限次迭代时,收敛的速度受所选择的映射函数控制.下面我们将结合具体处理转换方法,分析对应的迭代计算中如何选择映射函数以及评价具体的迭代收敛特性.
3 不同处理转换问题的收敛性具体分析上面推导的迭代法通式中,映射函数如何选择及收敛性如何是关键因素,下面我们将结合不同的具体处理转换加以分析.
3.1 迭代延拓 3.1.1 迭代向下延拓在频率域,向下延拓可以表示为
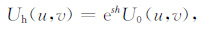
|
(10) |
其中:U0(u,v)是观测面上异常的频谱,Uh(u,v)是向下延拓结果的频谱,s为径向波数,h为下延的高度差,ψ(u,v)=esh为下延转换因子,是典型的高频放大滤波器,高度差较大时,计算受高频放大影响严重,计算结果很不稳定.
根据上面的推导可知,对于迭代向下延拓计算,其逆变换因子ψ-1(u,v)=e-sh,即为向上延拓因子,带入收敛条件式(8)可得:|1-φ(u,v)e-sh|<1,
进一步化简可得
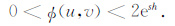
|
(11) |
式(11)即为迭代法向下延拓中,为保证迭代收敛,所选择的映射函数必须满足的条件.在满足该条件的情况下,如何选择映射函数可以基于不同的考虑,如收敛速度、计算过程简捷等.
分析前人现有的迭代法向下延拓研究成果可以发现,实际上大家均隐含着选择了最简单的常数为1的映射函数.这里为了计算简便,也不影响一般性,我们在前人基础上稍作扩展,取映射函数φ(u,v)=m,m为实常数,我们称其为迭代速度系数(后面可以看出它的这个特点),则收敛条件可以转化为
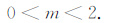
|
这里记区间S= (0,2),则S为迭代向下延拓速度系数的收敛区间.下面我们来分析速度系数m、迭代次数n以及向下延拓高度差h对滤波器的影响情况.
设Ua(n) (u,v)为第n次迭代的结果,Uh(u,v)为FFT直接向下延拓理论计算结果,则由(7)式可得迭代下延滤波器形式如下:
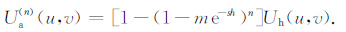
|
(12) |
由(12)式可见,迭代法下延计算等价于对直接下延转换因子乘上一个附加滤波器,所以,在本质上与传统的针对下延不稳定性而采取的通过附加稳定滤波器,从而达到改造下延转换因子、实现稳定下延的作用是一样的.
下面我们可以进一步分析评价迭代下延所附加的滤波器的频谱特征.将(12)式写成下面的形式:
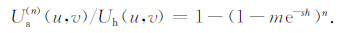
|
(13) |
针对(13)式这样的迭代下延附加滤波器,显然其特性受三个参数控制,即迭代次数n、下延高度差h和速度系数m.为简单直观起见,下面用图示方式对这三个参数的变化对滤波器的影响进行表示.
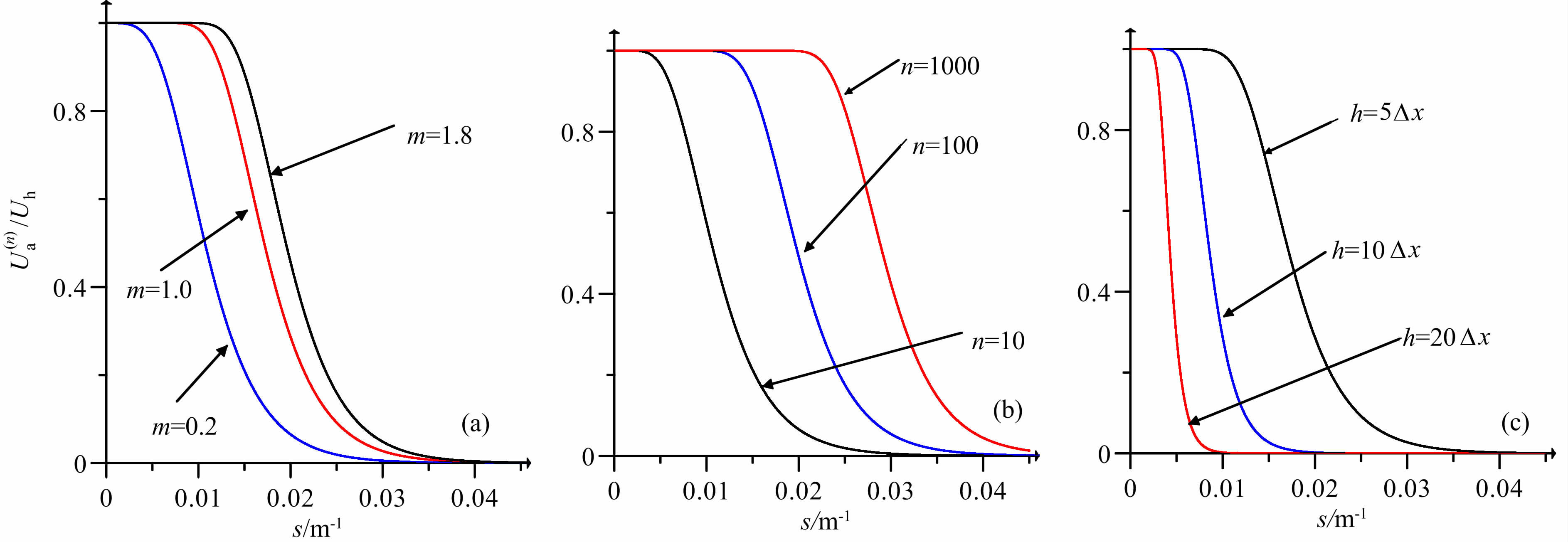
图 2分别显示了速度系数、迭代次数、下延高度对迭代向下延拓滤波器的影响,由图我们可以得到以下认识和结论:
|
图 2 迭代下延附加滤波器频谱曲线 (a)速度系数对迭代下延滤波器的影响(向下延拓高度为5倍点距,迭代100次);(b)迭代次数对迭代下延滤波器的影响(向下延拓高度为5倍点距,速度系数为1);(c)下延高度对迭代下延滤波器的影响(迭代次数为100,速度系数为1) Fig. 2 Spectrum curve of the iterative downward continuation filter (a) Effects of velocity factor on the iterative downward continuation filter (downward continuation 5 grid interval, 100 iterations) ; (b) Effects of iterativenumber on the iterative downward continuation filter (downward continuation 5 grid interval, velocity factor 1) ; (c) Effects of downward continuationheight on the iterative downward continuation filter(100 iterations, velocity factor 1). |
(1) 迭代下延附加滤波器为典型的低通滤波器,所以,迭代下延相当于在直接下延计算中附加了低通滤波作用,使得结果受高频影响减小.该滤波器只是在极限情况下即迭代次数无穷大时,其数值趋近于1,即没有任何附加滤波作用,也就是不对转换计算产生任何影响.
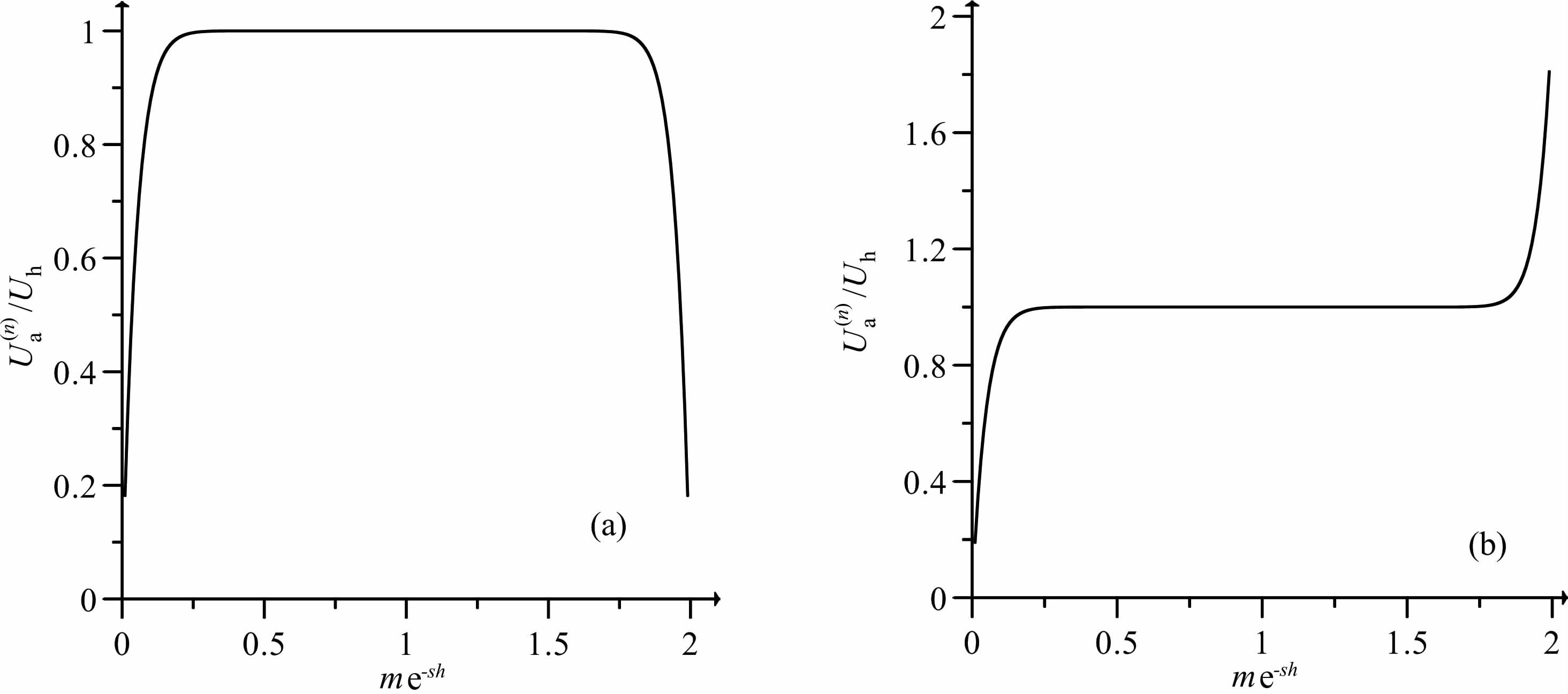
(2) 在迭代次数与下延深度不变的情况下,速度系数越大,滤波器通带范围越大(即向高频移动),其作用是速度系数越大迭代下延结果与FFT 直接下延结果越接近,故较大的系数可以使迭代下延用较少的迭代次数达到收敛,但是当速度系数过大时,会对低频数据造成一定的影响,分析如下(示意如图 3):
|
图 3 迭代次数奇偶性对滤波器的影响 (a)迭代次数为偶数(迭代次数为20);(b)迭代次数为奇数(迭代次数为21) Fig. 3 The effects of iterative number′s parity on the filter (a)Even iterative number(20); (b)Odd iterativet number(21). |
(13) 式所表示的滤波器可以认为是y=1-(1-x)n的函数,当m趋近于2时,对于低频信号而言,x=me-sh会趋近于2,若此时迭代次数n不是很大,则y会随着迭代次数选择奇数及偶数的交替变化而发生震荡现象(如图 3所示),所以此时的滤波器在压制高频信号的同时也对低频信号产生了一定的影响.将图 2(a)的低频部分局部放大,会得到如图 4所示的速度系数值对低频的具体影响.
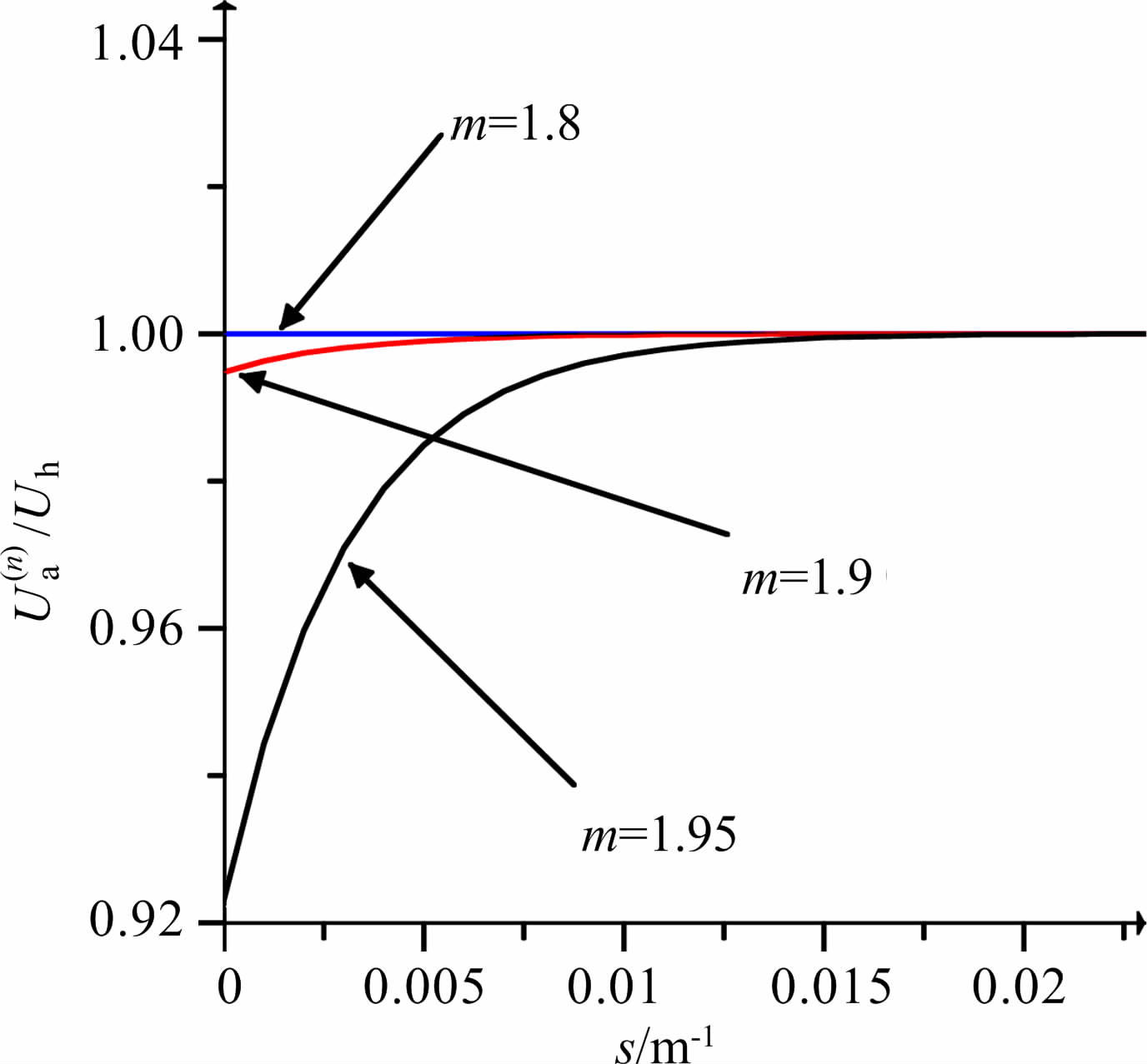
|
图 4 不同速度系数m对低频的影响 (迭代次数为50) Fig. 4 The effects of velocity factor on low-frequency(50 iterations) |
根据上面的分析可知,随着迭代次数的增加,迭代向下延拓虽然收敛到FFT 向下延拓的结果,但是当迭代次数不大时,计算结果随迭代波动,表现为误差曲线呈锯齿状震荡(后面有图例).
(3) 在下延深度与速度系数不变的情况下,迭代次数越多,滤波器通带高通范围越大,滤波器越接近“不滤波",即结果越趋近于理论下延结果.
(4) 在迭代次数与速度系数不变的情况下,下延深度小,附加滤波器通带高通范围越大,反之下延深度大,则滤波器主要表现为低通,可见下延深度越大,迭代下延需要更多的迭代次数才能与FFT 直接下延结果越接近.
由此可见,当速度系数处于稳定区间之内时,迭代次数与速度系数作用相似,均可以控制低通滤波的通带范围.
从上面的认识我们可以看出,迭代向下延拓是逼近FFT 直接向下延拓的过程,其本质上为对直接下延进行了一次低通滤波,从而压制通常会引起不稳定的高频信息,使得在较少的迭代次数下表现为良好的计算稳定性.另一方面由于其与其它压制下延因子滤波器的方法在本质上是一样的,所以,并没有从根本上彻底解决向下延拓问题中精度与稳定性的矛盾.
3.1.2 迭代向上延拓众所周知,位场向上延拓是满足Laplace方程的Dirichlet问题,属于数学物理领域中的正问题,具有稳定性,只要位场异常数据采样率足够密集,异常形态足够完整,则上延计算的精度将可达很高精度.在频率域向上延拓计算中,因上延转换因子随频率变化其值始终是稳定的,可以通过直接计算得到稳定的向上延拓结果,所以,不需要选择迭代法进行计算.这里我们仅仅为了研究迭代法的适应能力以及探索其各方面的特性,所以尝试用迭代法来解向上延拓问题,便于对迭代法在位场转换中的应用有一个更全面和深入的了解.
与迭代向下延拓类似,易得迭代向上延拓的收敛条件为
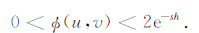
|
(14) |
如果选择映射函数为简单的实常数(即速度系数),则对应的收敛条件需满足
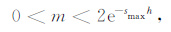
|
(15) |
上式中的smax是原始数据径向波数的最大值,h仍为高度差.
迭代上延的通式与迭代下延形式类似,其表达式为
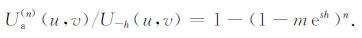
|
(16) |
上式中的U-h(u,v)为向上延拓理论结果的谱,Ua(n) (u,v)为迭代向上延拓n次结果.对(16)式进行分析表明,迭代向上延拓相当于在理论向上延拓的基础上进行一次高通滤波,所以,其计算结果理论上容易变得不稳定.并且,只有m为足够小的正实数时,迭代向上延拓才是收敛的,当迭代次数趋近于无穷大时,才能收敛到理论的向上延拓结果.
这里假设按照前人迭代下延的方法进行迭代上延计算,即进一步选择映射函数为常数1,也就是首先将原始异常数据当成为上延平面上的初次结果,因为对其无法进行直接评价,需要再将其下延到原平面进行对比评价,将评价误差再修正初始结果,采取逐步迭代修正方式进行.显然,(15)式表明m=1在大多数条件下极有可能是不收敛的(如h稍大,或smax稍大),这是迭代上延与迭代下延的明显区别,后面的理论模型计算也证明了这一点.
图 5展示的是上延高度差、迭代次数以及速度系数对迭代上延的效果影响的情况.
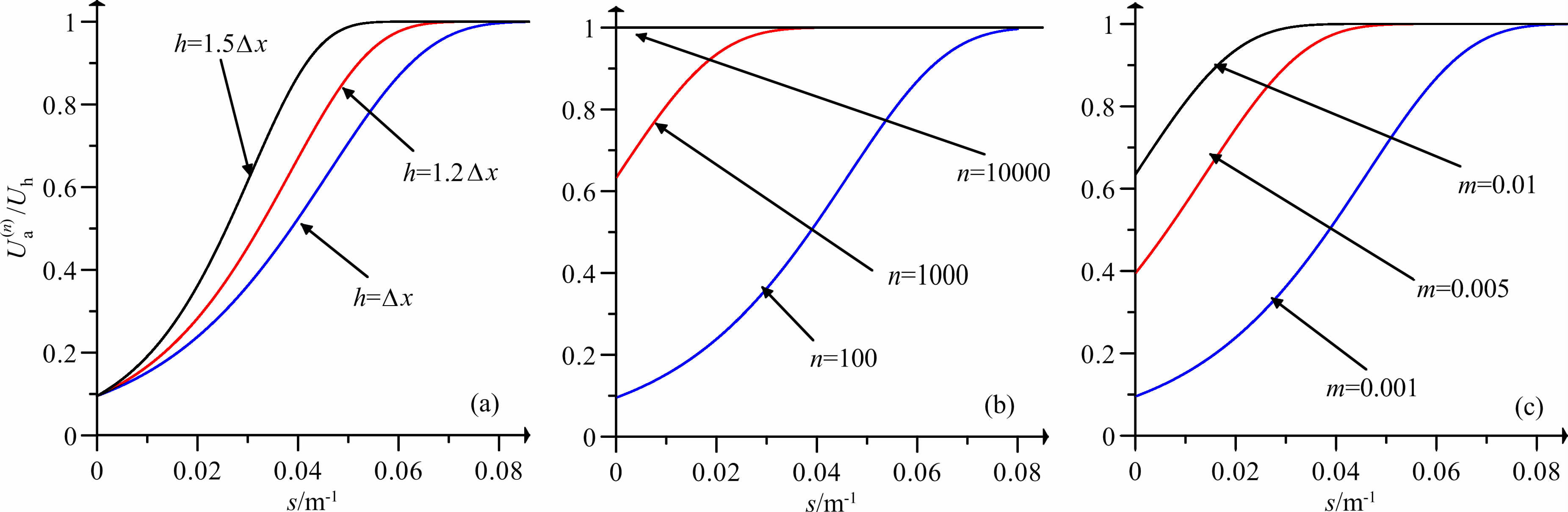
|
图 5 迭代上延附加滤波器频谱曲线 (a)上延高度对迭代上延滤波器的影响(向上延拓高度为1倍点距,迭代100次);(b)迭代次数对迭代上延滤波器的影响(向上延拓高度为1倍点距,速度系数为0.001);(c)速度系数对迭代上延滤波器的影响(迭代次数为100,速度系数为0.001). Fig. 5 Spectrum curve of the iterative upward continuation filter (a) Effects of velocity factor on the iterative upward continuation filter (upward continuation 1 grid interval, 100 iterations) ; (b) Effects ofiterative number on the iterative upward continuation filter (downward continuation 1 grid interval, velocity factor 0. 001) ; (c) Effects of upward continuation height on the herative upward continuation filter(100 derations, velocity factor 0. 001). |
从上面迭代上延可知,迭代法也可以应用于解决稳定的位场计算问题,但是如果原本稳定计算的逆运算是不稳定的,那么对映射函数的选择则要苛刻得多,否则选择迭代法就会将原本稳定计算问题转化为不稳定计算问题.
迭代下延与迭代上延的特性分析,为我们更全面地了解迭代法位场转换的性质,掌握具体的应用方法打下了理论基础.
3.1.3 迭代曲化平曲化平是将起伏观测面上获得的重磁异常转换到某一平面上等效异常的计算方法,目的是消除观测面起伏的影响.可以看出,向下延拓和向上延拓即平面之间的延拓是其特例,所以理论上同样可以运用迭代法来解决曲化平计算问题.
Strakhov等[1]及徐世浙等[4]将迭代法应用于弱地形的曲化平计算,简化了曲化平的复杂性并取得了比较好的曲化平计算结果.如果从算法角度评价该方法,通过我们上面迭代法下延及迭代法上延分析可以理解,该曲化平迭代过程相当于选择了等价的映射函数为常数1,遗憾的是由于曲化平在频率域没有直接的解析表达式,所以,无法进一步评价其等效的滤波特性了.
虽然迭代法曲化平计算过程简单并在条件较好时取得了不错的效果,但作者也指出其受地形的起伏大小、下延到地形最低点的高差等影响较大(注:迭代曲化平中间过程最重要一步是将曲面上的数据下延到地形最低点所在的平面上,所以,必须是场源较深的弱地形条件).从理论上分析其原因,可以认为是地形起伏大以及高差大,决定了未知的场源在起伏大的地形上产生的异常数据与在高差大的待转化平面上产生的异常数据比较,无论在数值大小还是异常形态上均相差比较大,如果分析其对应频谱,则曲面数据的谱可能与平面数据的谱在振幅和相位都存在明显的差异,此时仍然选取映射为1 显然是不合理的,特别是因为相位差别大的情况,这在下面化极中表现得更加明显.
由于曲化平没有简单的迭代法解析表达式,这里就不对其迭代法曲化平的映射函数的选取及收敛性等进行量化分析了.
3.2 迭代化极化极转换是最基本的磁测资料处理方法之一,所以,低纬度化极的困难一直受到重点研究.下面我们对迭代法在化极中的应用加以类似的分析研究,以期掌握其客观内在规律.
在频率域中,化极处理可以表示为
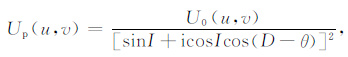
|
(17) |
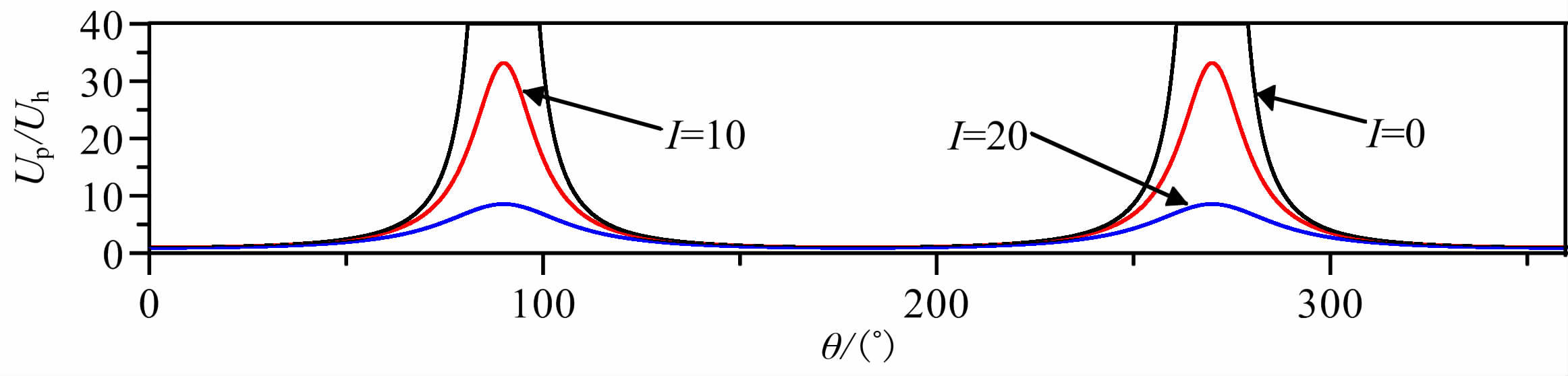
其中:U0(u,v)是斜磁化条件下异常的频谱,Up(u,v)是垂直磁化条件下磁异常垂直分量的频谱,I和D分别是地磁场的倾角和偏角且,这里我们假设磁化方向与地磁场方向一致.u、v是x、y方向上的波数,θ =arctan(u/v),i是虚数单位.图 6所示为化极因子频谱曲线,在I=0的水平磁化条件下,当θ→D±π/2时(此图中D=0°,则θ=90°和270°),频率域化极因子的幅度急速上升,频谱被无限放大,化极因子本身出现奇异,无法获得稳定的化极结果.
|
图 6 常规化极因子不同磁倾角的频谱曲线及其放大作用 Fig. 6 The effects of inclination on the RTP factor |
根据前面的推导可知,采用迭代法化极计算,化极的逆过程我们称其为“逆化极",对应的滤波器为“逆化极"因子,其形式为
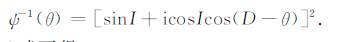
|
带入(9)式可得
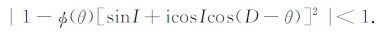
|
(18) |
在迭代法中,φ(θ)取实常数更方便(如前面的迭代延拓),也更能体现迭代法易简单实现的优点,考虑到化极计算比延拓复杂,所以这里取其为实数m(θ).则将上式展开可得
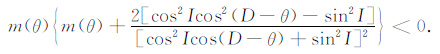
|
(19) |
我们设
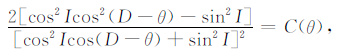
|
对(19)式求解,可得收敛条件为:
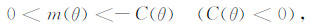
|
或者:
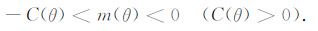
|
由于θ 是连续变化的,即cos2(D-θ)可以取到[0,1]区间内的任意值,下面我们讨论不同磁倾角情况下的收敛条件:
(1) 当I>45°时,对于所有的θ 都有:
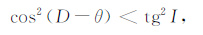
|
所以对于所有的θ 都有C(θ)<0,所以此时的收敛条件为
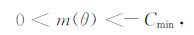
|
上式中的Cmin 为C(θ)的最小值.
(2) 当0°<I≤45°时,C(θ)不全为负值,还可能存在0值或者正值,显然当m(θ)为常数时无法满足收敛条件.如果要在此情况下保持收敛,那么m(θ)必须为一个随频率变化、需要根据具体的磁倾角和磁偏角加以针对性设计的变量了,其细节不是我们这里讨论的重点,因此,这里就不展开详细讨论了.
(3) 当I=0 时(即水平磁化环境,相当于位于磁赤道地区),C(θ)= 2,所以易得此时的收敛条件为
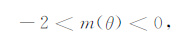
|
这种情况下,我们可以进一步令m(θ)= m为实常数,则I=0收敛条件如下:
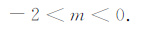
|
(20) |
通过该收敛条件可知,当取m=1时,磁赤道迭代化极是不收敛的,即直接将实测磁异常当成化极结果初始值这样逐步迭代其结果将不收敛.骆遥等(2010)在针对赤道化极研究中,注意到赤道化极前后异常相位的倒相关系,采取每次迭代都对残差“倒相"的处理,实现了迭代赤道化极,其对应的速度系数为这里的m=-1,恰好在我们的收敛区间式(20)内,所以,这里对骆遥等(2010)研究中的经验认识从理论上给予了证明.
下面我们简单分析迭代次数n以及速度系数m对滤波器的影响:设Ua(n) 为第n次迭代的结果,Up是FFT 理论直接化极结果,则迭代化极等价于在FFT 直接化极的基础上进行附加滤波,滤波器形式为
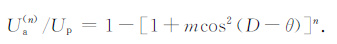
|
(21) |
图 7分别显示了速度系数、迭代次数对迭代化极滤波器的影响,经过分析,我们可以得到如下结论:
|
图 7 迭代化极附加滤波器频谱曲线 (a).速度系数对迭代化极收敛性的影响(迭代次数为50,磁倾角为0,磁偏角为0);(b).迭代次数对迭代化极收敛性的影响(磁倾角为0,速度系数为-1,磁偏角为0) Fig. 7 Spectrum curve of the terative RTP filter (a) Effects of velocity factor on the iterative RTP filter (inclination 0,declination 0,50 iterations);(b) Effects of kerative number on the kerative RTP filter (inclination 0,declination 0,velocity factor -1 ). |
(1) 在迭代次数和磁倾角不变的情况下,速度系数绝对值越大,滤波器通带范围越大,即增大速度系数的绝对值可以使结果更趋近于FFT 直接化极结果,并且增加收敛速度;但是和迭代向下延拓存在的问题类似,速度系数同样存在稳定区间,速度系数在稳定区间之外时,计算会不稳定.
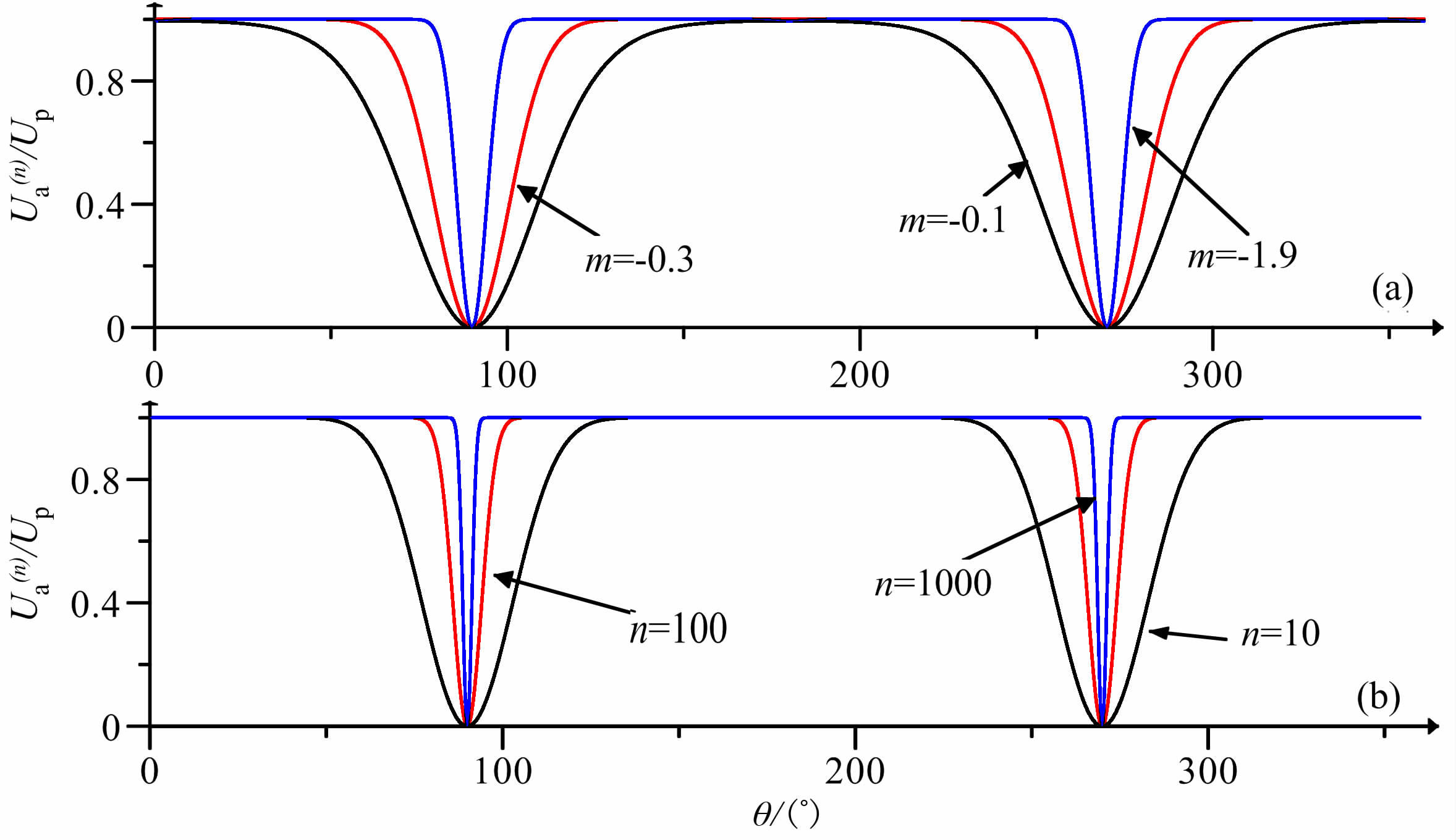
为简单起见,当取磁倾角、磁偏角均为0 时,滤波器函数记为y=1- (1+mcos2(θ))n,其中θ取0到2π,不同速度系数的滤波曲线如图 8所示.
|
图 8 速度系数迭代次数对计算稳定性的影响 (a)n=200,m=-1.9;(b)n=201,m=-1.9;(c)n=200,m=-1.999;(d)n=201,m=-1.999. Fig. 8 The effects of velocity factor and iterative number on the calculation stability |
从上面图 8中可以看出,当速度系数在稳定区间之内时(图 8(a)、图 8(b)),迭代次数的奇偶变化对滤波曲线的影响不大;而当速度系数接近收敛区域的边界,其稳定性明显降低,表现为迭代次数的奇偶变化会导致滤波曲线发生明显变化,从而将导致计算结果发生震荡(图 8(c)、图 8(d)).
(2) 在速度系数不变的情况下,迭代次数越大,滤波器通带范围越大,迭代化极结果与FFT 直接化极结果越相近,且当迭代次数趋近于无穷时,迭代化极的结果也趋近于理论化极的结果.
因此,迭代化极的本质同样是在原有化极因子的基础上加上一个带通滤波器.直接化极因子主要在相位D±π/2处具有明显的放大作用,而迭代法化极的附加滤波器恰好在这些地方予以压制,故能使得计算结果更加稳定.当速度系数处于稳定区间内时,迭代次数与速度系数的绝对值对收敛性的贡献的作用相似.
虽然我们得到了迭代法化极的关系式,并且能避免真正的迭代计算步骤,但是迭代法化极并没有从本质上解决低纬度化极因子奇异的问题,式(21)表明:迭代次数非常大时,迭代化极回归为直接化极,显然,迭代法化极是对直接化极的一种滤波近似,主要是压制化极中不稳定的频率成份,因此,和其它针对低纬度化极采取的改造化极因子或附加其它滤波器是没有本质区别的.这里还应该指出,迭代法的迭代次数是不好选择的一个参数,所以,相对于其它方法,迭代法并不具有优势.
4 数据实验分析为了对迭代法有一个更加直观的认识,我们选取迭代延拓和迭代化极方法进行模型计算实验,对迭代法的收敛性等加以分析评价,以期为合理应用迭代法打下基础.
4.1 迭代下延模型实验这里我们选取一个斜磁化球体模型的计算实验来对向下延拓计算的收敛性以及计算精度进行分析.所选球体的磁化强度为0.5 A/m, 磁倾角45°,磁偏角15°,球体中心点的x、y坐标均为0,埋深为2km, 实验矩形网格数据参数为:测线数M=301,每条测线上的测点数N=301,点距、线距均为50m.其总场磁异常ΔT等值线图见图 9 所示,图 9a为0m 平面上的磁异常,图 9b为1000m 平面上的磁异常,即位于图 9a的上方1000m 处.
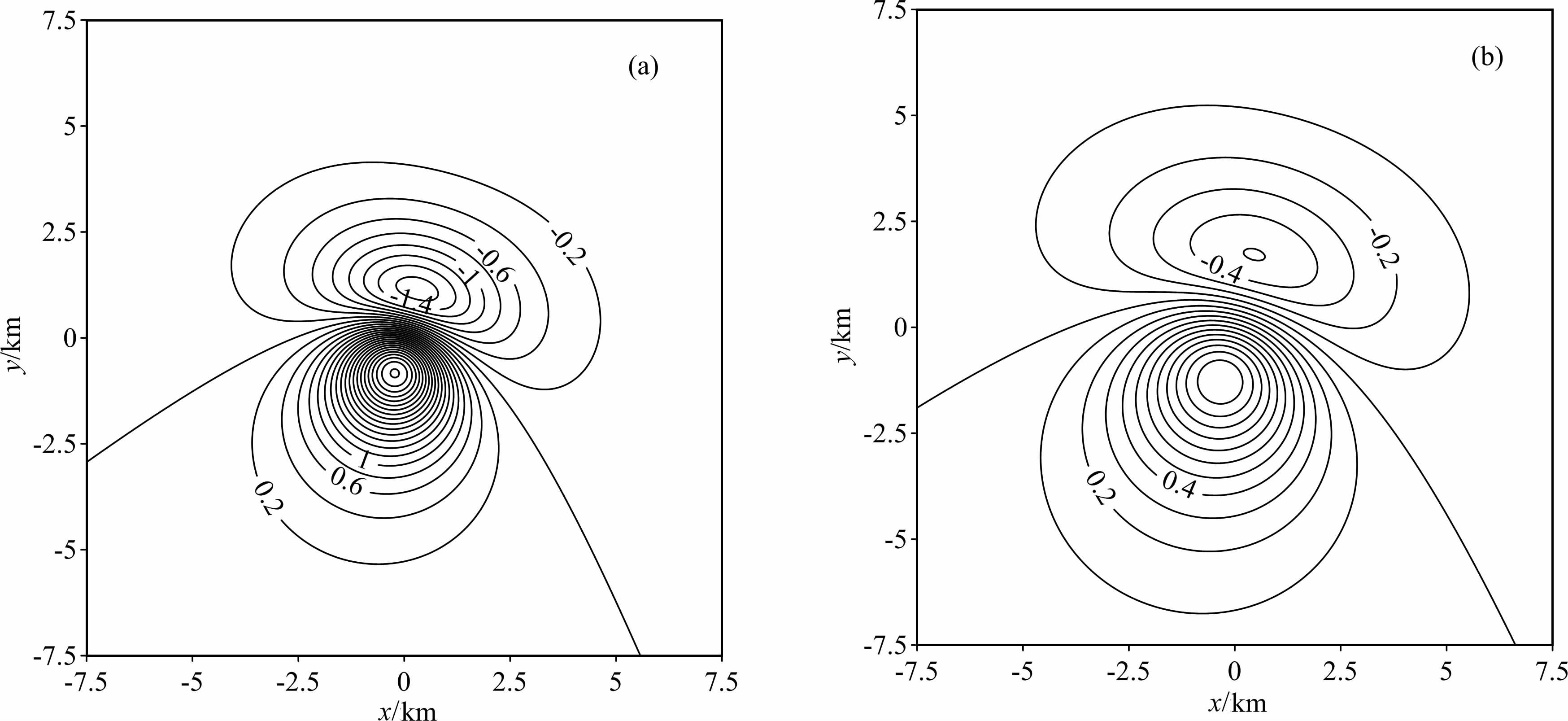
|
图 9 理论模型在不同平面上的总场异常ΔT(单位:nT) (a)0m 平面;(b)1000m 平面. Fig. 9 Theoretical magnetic anomalies on different planes (a) 0 m; (b) 1000 m. |
针对该理论模型数据,我们应用迭代法计算下延结果,其中误差大小用均方差衡量,其计算式子为:
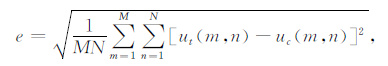
|
(22) |
上式中ut(m,n)为理论结果,uc(m,n)为迭代计算的结果.
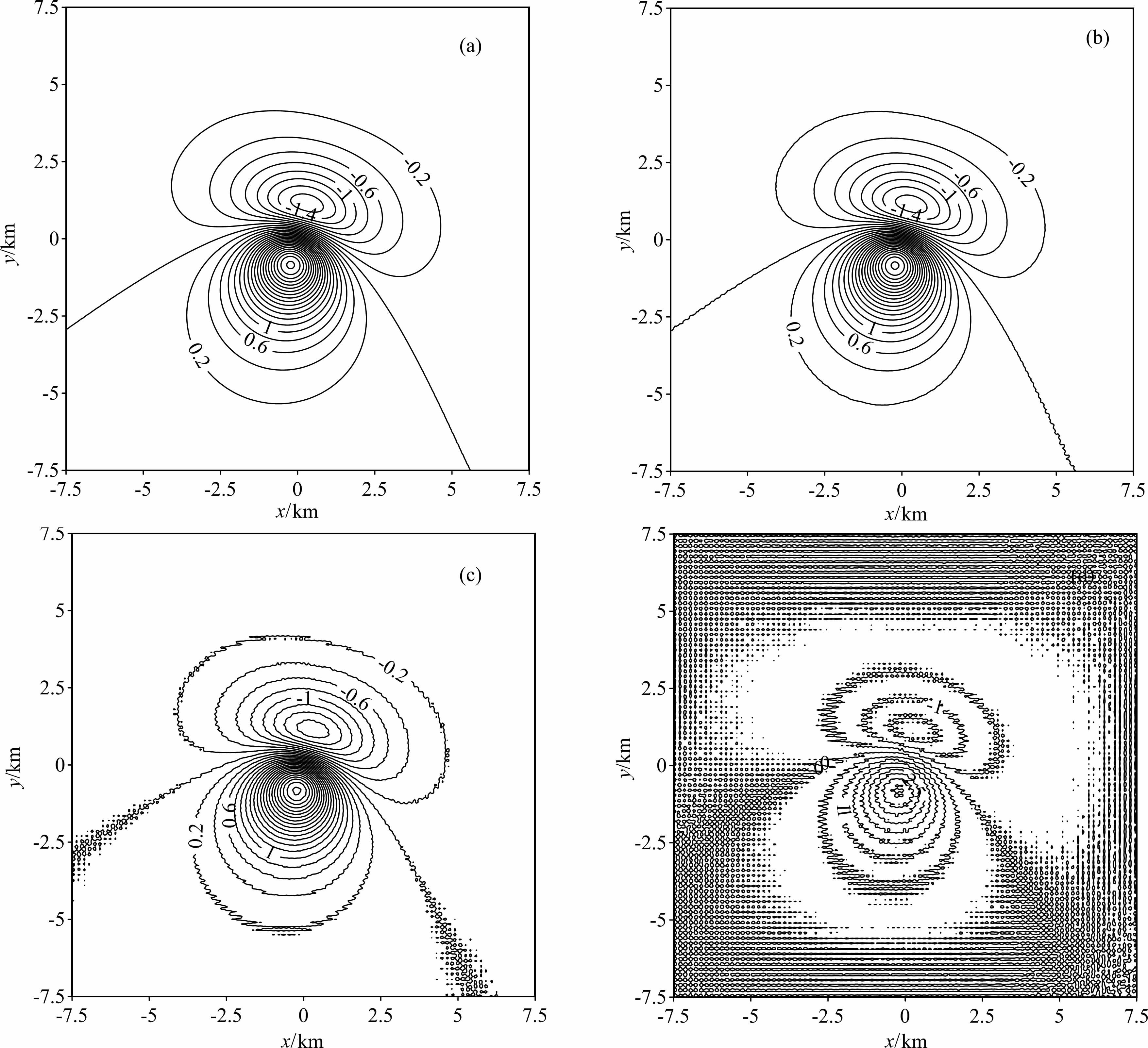
不同迭代次数计算结果如图 10所示.下延深度为20倍点距,即由高度为1000 m 的图 9b 异常数据,迭代下延得到高度为0 m 的异常数据,选择映射函数为1,即采取与前人相同的速度系数.由结果图可见,该模型迭代向下延拓计算时,在迭代次数较少时,所得的结果是稳定的;而迭代次数越大,数据的高频成分放大越明显,所得结果与FFT 理论直接下延结果越接近.
|
图 10 不同迭代次数迭代向下延拓结果 (a)迭代次数为100;(b)迭代次数为1000;(c)迭代次数为10000;(d)迭代次数为100000. Fig. 10 Iterative downward continuation results with different iterative numbers (a) 100 iterations; (b) 1000 iterations; (c) 10000 iterations; (d) 100000 iterations. |
对该例而言,分析计算时达到最小误差的迭代次数以及最小误差与速度系数、下延深度的关系,可得结论如下:
(1) 在下延深度一定且速度系数处于稳定区间的情况下,达到最小误差的迭代次数随着速度系数的增大而减小,最小误差值总体而言呈下降趋势.
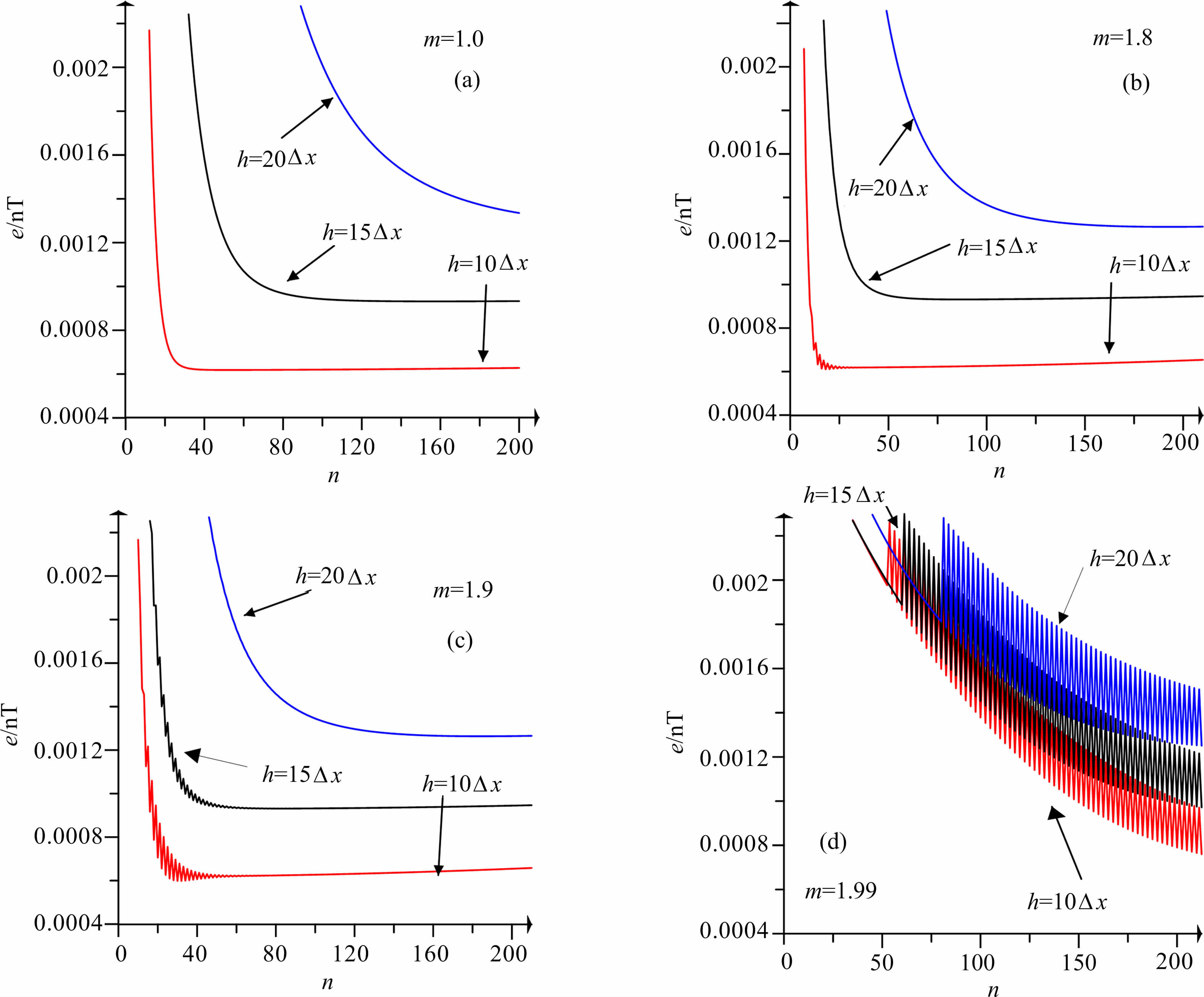
(2) 当速度系数在稳定区间之外时,迭代下延滤波器对高频压制的同时也会对低频产生影响,表现为误差曲线有明显的震荡.如图 11a所示,速度系数为1.0时,三条误差曲线都是光滑的,无震荡现象;但当速度系数达到1.99时(见图 11d),不同下延深度的误差曲线都会随着迭代的进行发生较为明显的震荡.
|
图 11 速度系数对迭代下延误差曲线的影响 (a)速度系数为1.0的误差曲线;(b)速度系数为1.8的误差曲线;(c)速度系数为1.9时的误差曲线;(d)速度系数为1.99时的误差曲线. Fig. 11 The aafected error curves by velocity factor (a) Velocity factor 1. 0; (b) Velocity factor 1.8; (c) Velocity factor 1. 9 ; (d) Velocity factor 1.99. |
(3) 在速度系数一定且处于稳定区间内的情况下,随着下延深度的增加,所需要的迭代次数增加,同时最小误差值也随之增大.
(4) 在向下延拓深度与速度系数不变的情况下,迭代下延的结果与理论结果的误差随着迭代次数的增加是先减小后又增大,相当于有最佳迭代次数(或迭代区间),但由于理论结果是未知的,实际误差无法准确获得,所以迭代法中只能间接评价误差,其可靠性降低,因此在实际迭代下延中通常难以获得最佳迭代次数.
4.2 迭代上延模型实验正如前面分析,实际中因为上延转换是稳定计算,具有很高的精度,故没有人会真正使用迭代法,那样将使原本简单问题复杂化.这里仅仅是为了评价迭代法在上延应用中如何表现,为此进行必要的尝试与特性分析.
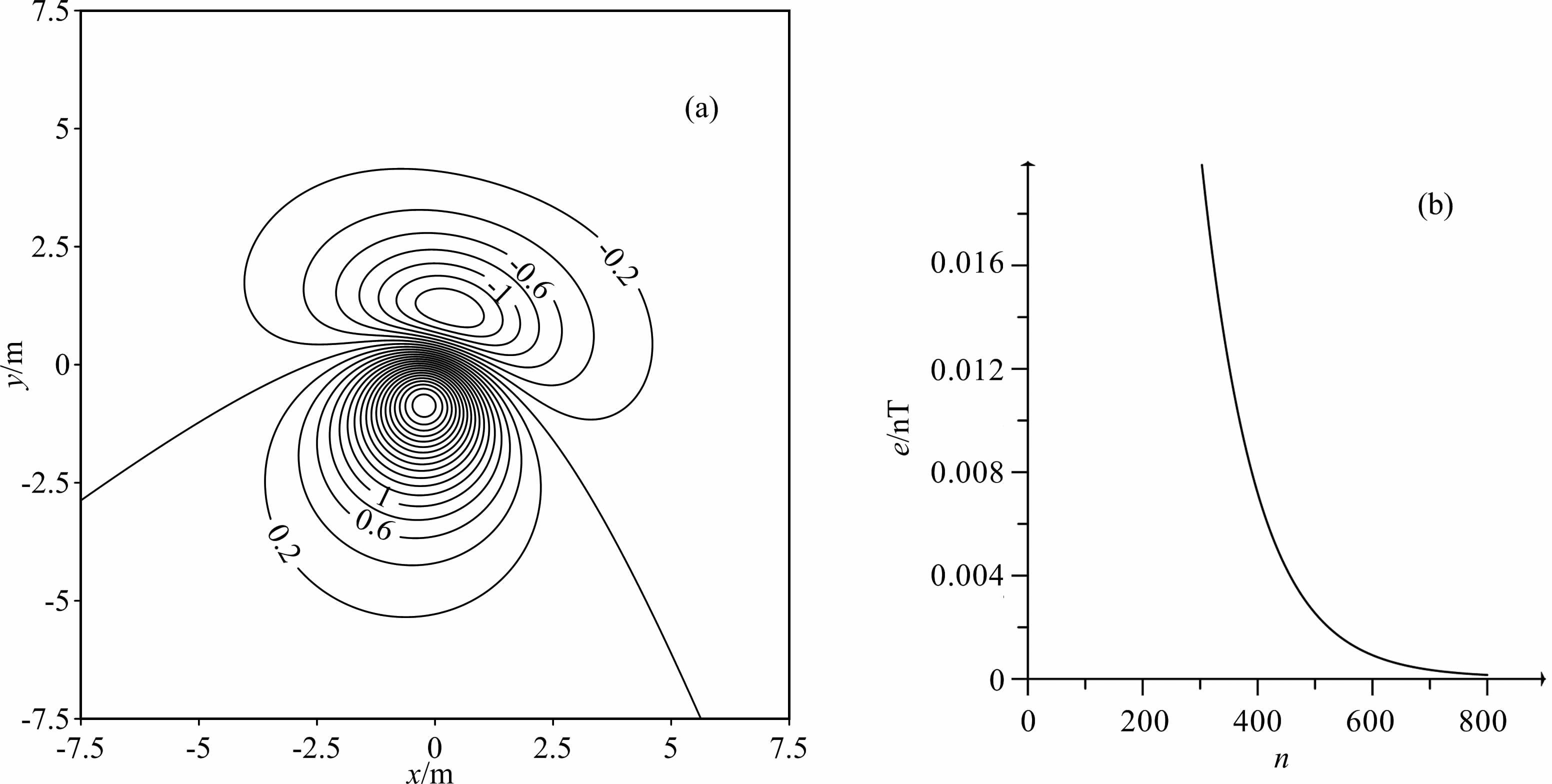
针对上面的模型数据,现在采用迭代法将图 9a中0 m 平面的数据上延到1000 m 处.首先我们拟采取与迭代下延相同的方式,根据(15)式采取常数映射,但却得不到实质结果.因为此时上延20 倍点距,即1000m, smax=0.089(m-1),速度系数取实常数值的范围为:0<m<2.1582×10-39,即非常小,造成原始数据乘以该映射值后接近于0值了,所以,迭代的变化量将极其小,需要极其巨大的迭代次数才能得到结果.所以,基于常数映射的迭代法向上延拓计算,延拓的高度差不能太大.此结论在较小延拓高度差下得到了验证,如:由0m 上延到50m, 速度系数的取实常数值的范围为:0<m<0.0117,比如取速度系数为0.01,即可得到下图的收敛结果.
图 12即是取迭代速度系数为0.01,由0 m 上延到50 m 时的计算结果,其中图 12a为迭代1000次的上延数据分布图,其结果与理论结果(图略)的误差为0.0002nT,其迭代中误差收敛情况如图 12b所示,收敛还是很快的.但是,如果取迭代速度系数为1时,由于其不在收敛条件0<m<0.0117内,实际计算也证明了其迭代是不收敛的,仅迭代5 次其结果误差已非常大了(图 13a),图 13b 的收敛曲线可以看出其是发散的.
|
图 12 理论模型迭代上延0m 到50m 结果—速度系数取0.01 (a)0m 上延到50m, 1000次迭代上延结果;(b)迭代上延误差曲线. Fig. 12 Iterative upward continuation result (velocity factor 0.01,height 50 m) and error curve (a) Iterative upward continuation result, 1000 iterations; (b) Iterative upward continuation error curve. |
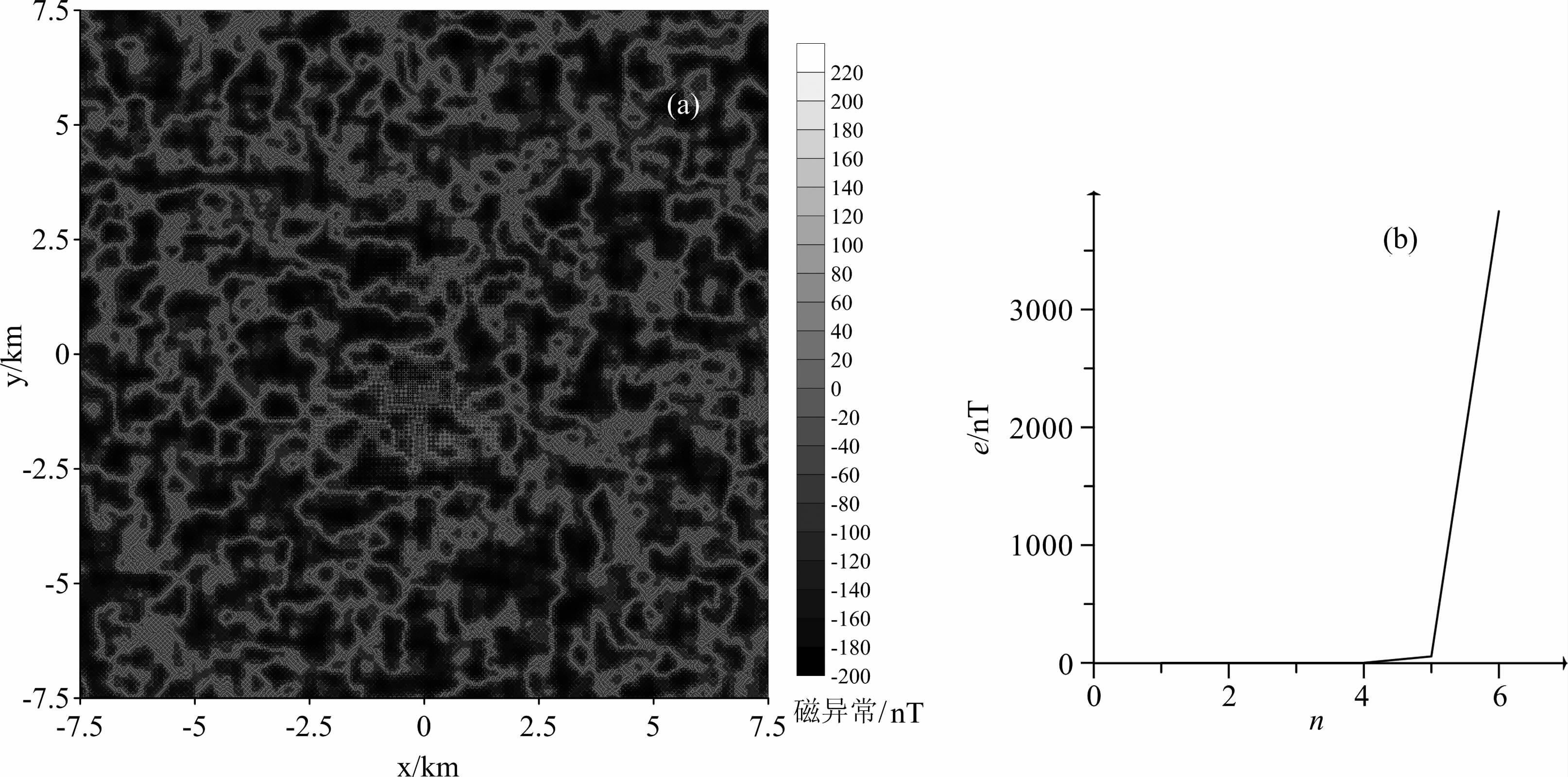
|
图 13 理论模型迭代上延0m 到50m 结果—速度系数取1.0 (a)0m 上延到50m, 5次迭代上延结果;(b)迭代上延误差曲线. Fig. 13 Iterative upward continuation result (velocity factor 1,height 50m) and error curve (a) Iterative upward continuation result, 5 iterations; (b) Iterative upward continuation error curve. |
如果由0m 平面迭代上延到250m 高度平面,实际计算的成本将大大增加.此时smax=0.089(m-1)不变,常数m的取值范围:0<m<2.1554×10-10,计算中取值1×10-10实验,最终迭代虽然收敛(见图 14),但迭代次数极大.
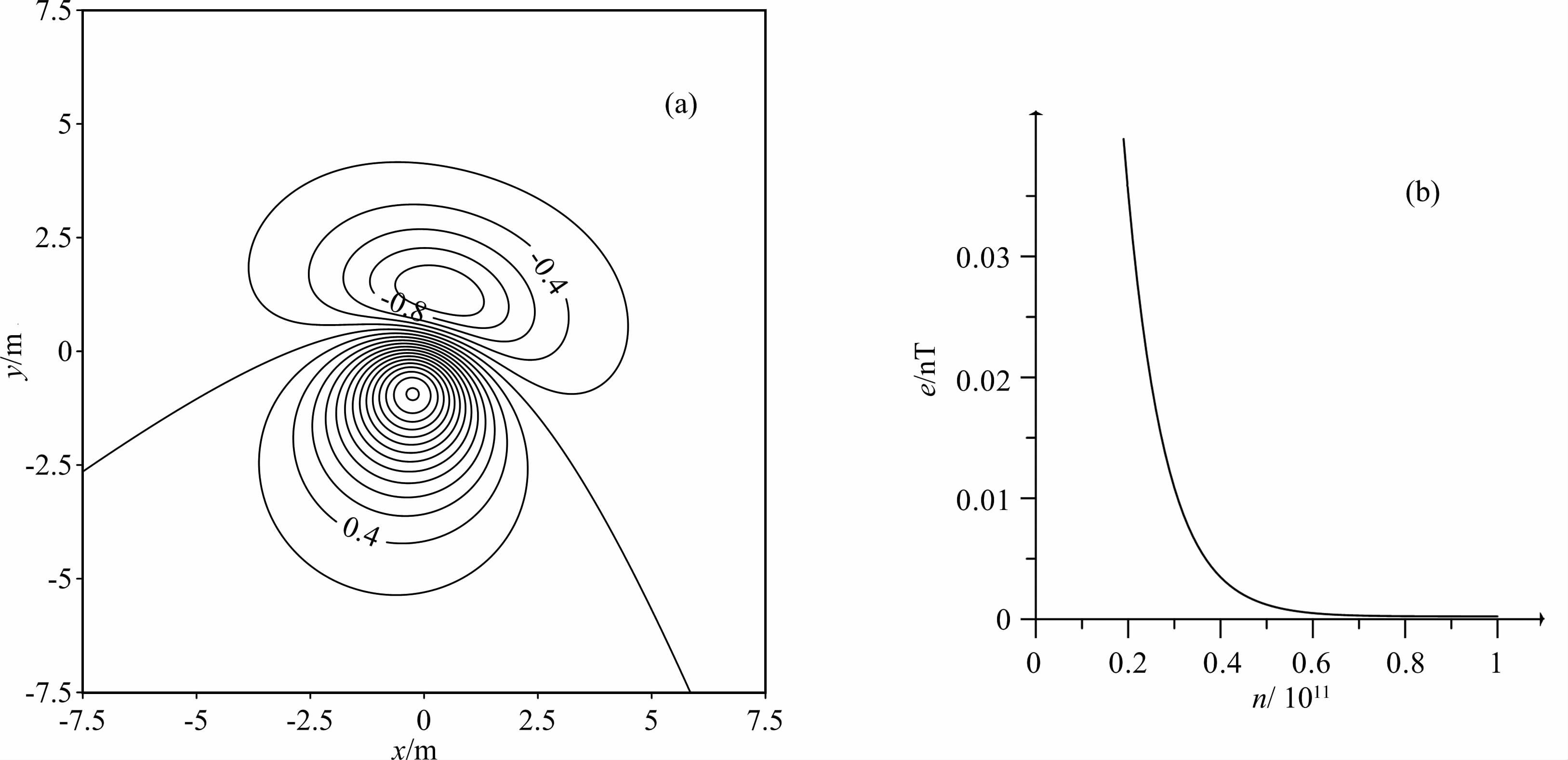
|
图 14 理论模型迭代上延0m 到250m 结果—速度系数取1.0×10-10 (a)0m 上延到250m, 1011次迭代上延结果;(b)迭代上延误差曲线. Fig. 14 Iterative upward continuation result (velocity factor 1,height 250m) and error curve (a) Iterative upward continuation result, 1011 iterations; (b) Iterative upward continuation error curve. |
正如上面指出,按照同样的方式,计算由0 m到1000m, 成本将无法承受,这是上延这样的原本稳定的直接计算,转换为迭代法后如果采取简单映射处理方式造成的后果.这时,我们就不能取简单的实常数映射了,但如果采取变量形式,应该易于解决遇到的新问题.
针对简单处理无法实现的0m 到1000m 的迭代上延,我们根据前面的(14)式的取值范围重新取值,比如取φ(u,v)=0.25e-sh,则只迭代了41次,误差即达到0.00059nT,已完全收敛到非常接近理论结果的程度了,结果见图 15所示.
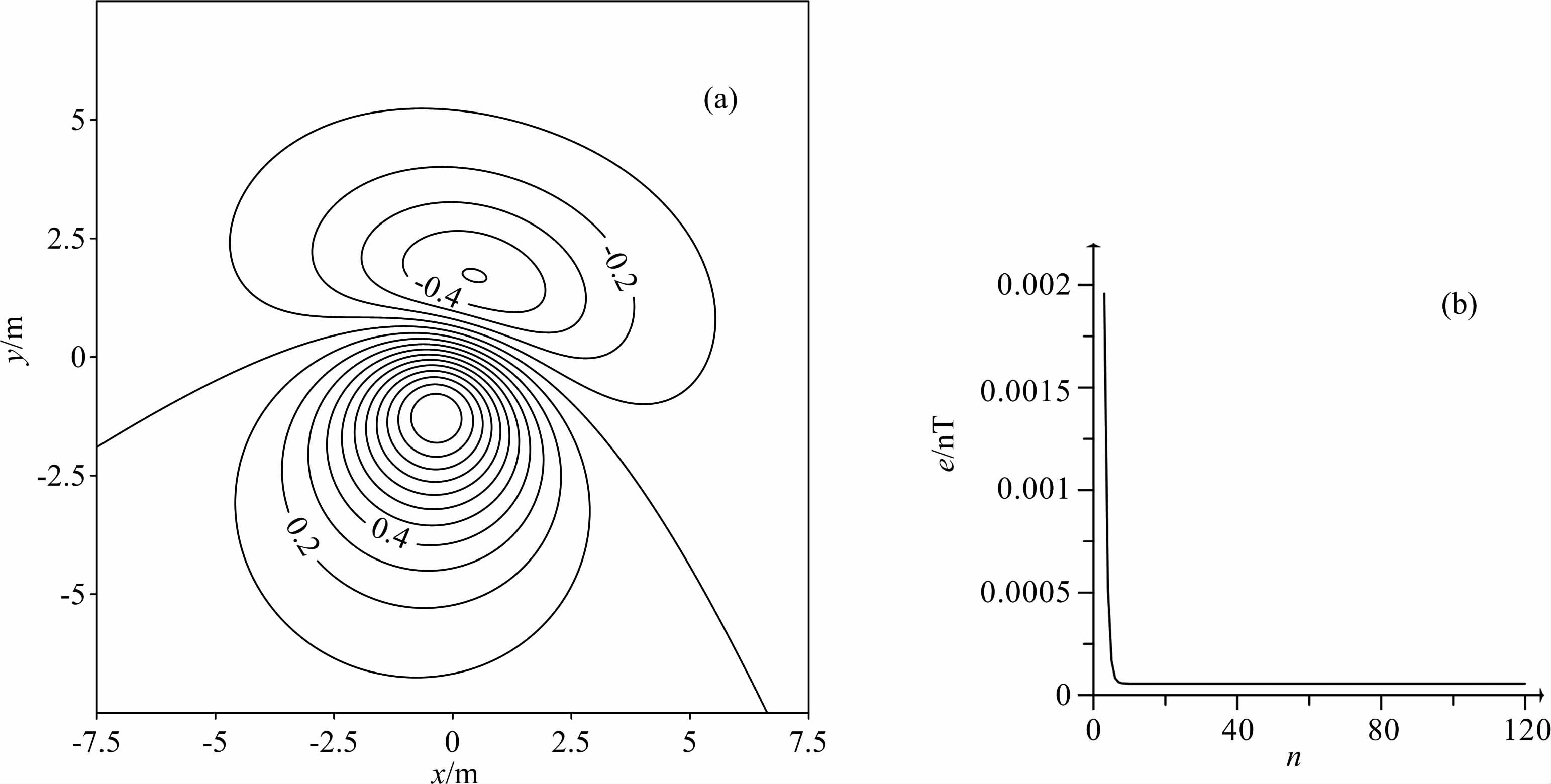
|
图 15 理论模型迭代上延0m 到1000m 结果—速度系数取φ(u,v)=0.25e-sh (a)0m 上延到1000m, 41次迭代上延结果;(b)迭代上延误差曲线. Fig. 15 Iterative upward continuation result (velocity factor 1,height 1000m) and error curve (a) Iterative upward continuation result, 41 iterations; (b) Iterative upward continuation error curve. |
通过上面迭代上延的模型计算,使我们认识到:在迭代下延中可以选择简单的常数映射,但对于迭代上延,必须采取变量映射才能有效收敛,所以,映射函数的合理选取是迭代法重磁处理转换的核心.
上述迭代上延的试验与分析,目的不是应用于实际上延计算(因为直接上延转换已足够精确),而是深化对迭代法的认识.
4.3 迭代化极数据试验为了对迭代法在化极转换中的应用效果进行评价,我们选取最困难的水平磁化条件下的化极例子进行分析.下面选择前人文献中同样的长方体模型来进行化极计算实验,模型的长和宽都是20 m, 厚2m, 上顶埋深1m, 磁化强度为1A/m.数据网格参数为:点数M=64,线数N=64,点距Δx=1 m, 线距Δy=1 m.该模型产生的理论磁异常如图 16所示.
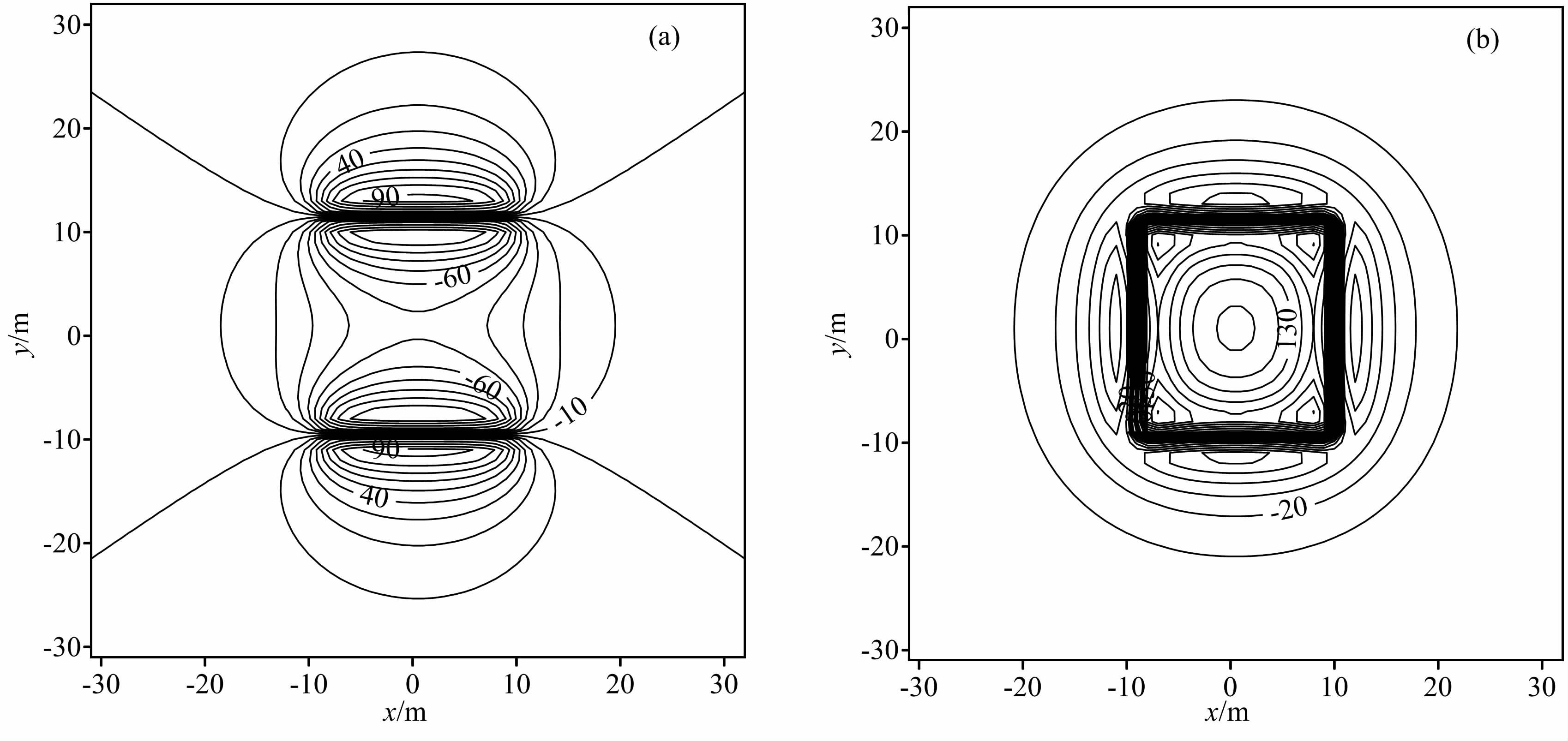
|
图 16 理论模型总场异常ΔT(单位:nT) (a)水平磁化;(b)垂直磁化. Fig. 16 Theoretical total field anomalies (a)At the equator;(b)At the pole |
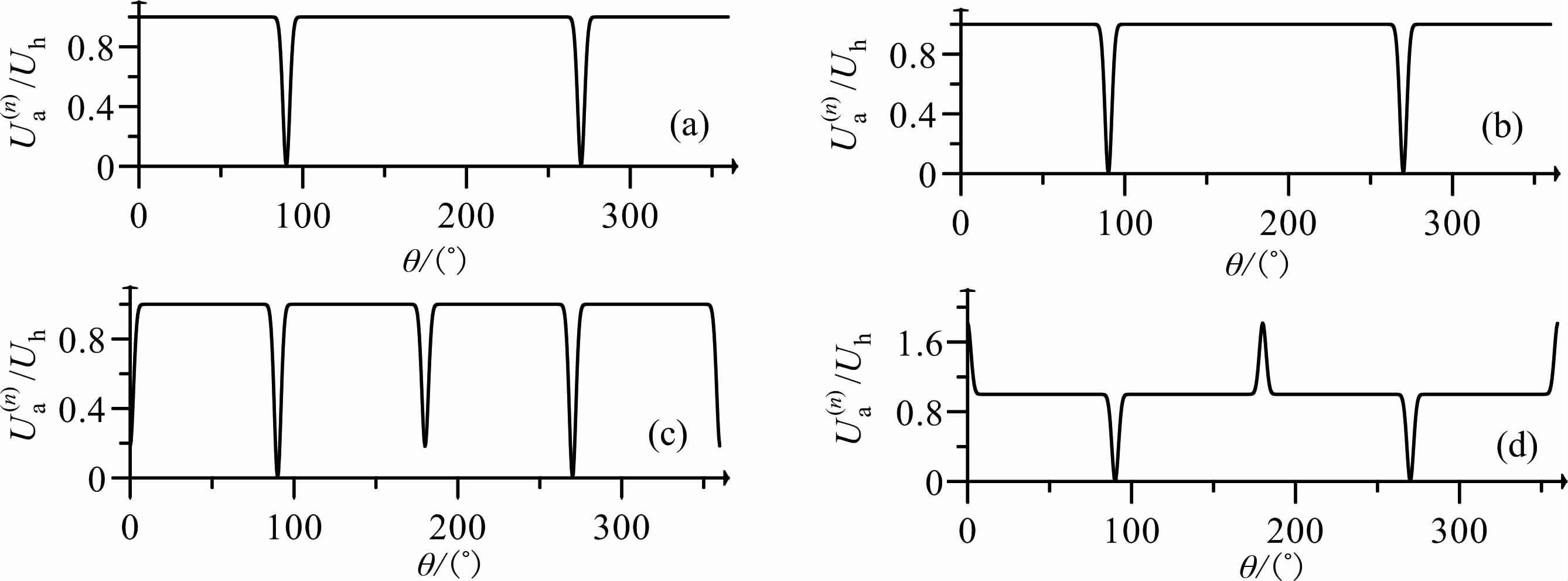
迭代化极的结果如图 17所示,计算中选择映射函数为满足收敛条件的常数-1.0(与骆遥等[24](2010)中的“倒相"对应).迭代次数及不同映射函数(即速度系数)对该模型化极误差影响见图 18.由这些结果图可以看出:化极结果随着迭代次数的增大误差先减小然后又逐渐增大,直至无穷大.实际上赤道化极的FFT 直接计算理论结果就是趋近于无穷大的,因此,迭代法赤道化极只是在较少的迭代次数时可以得到较好的化极结果,是理论结果的一个近似,而无限次迭代将使结果接近原本的直接计算,无论其原本是否稳定、是否收敛.这也是我们应用迭代法需要关注的客观因素.
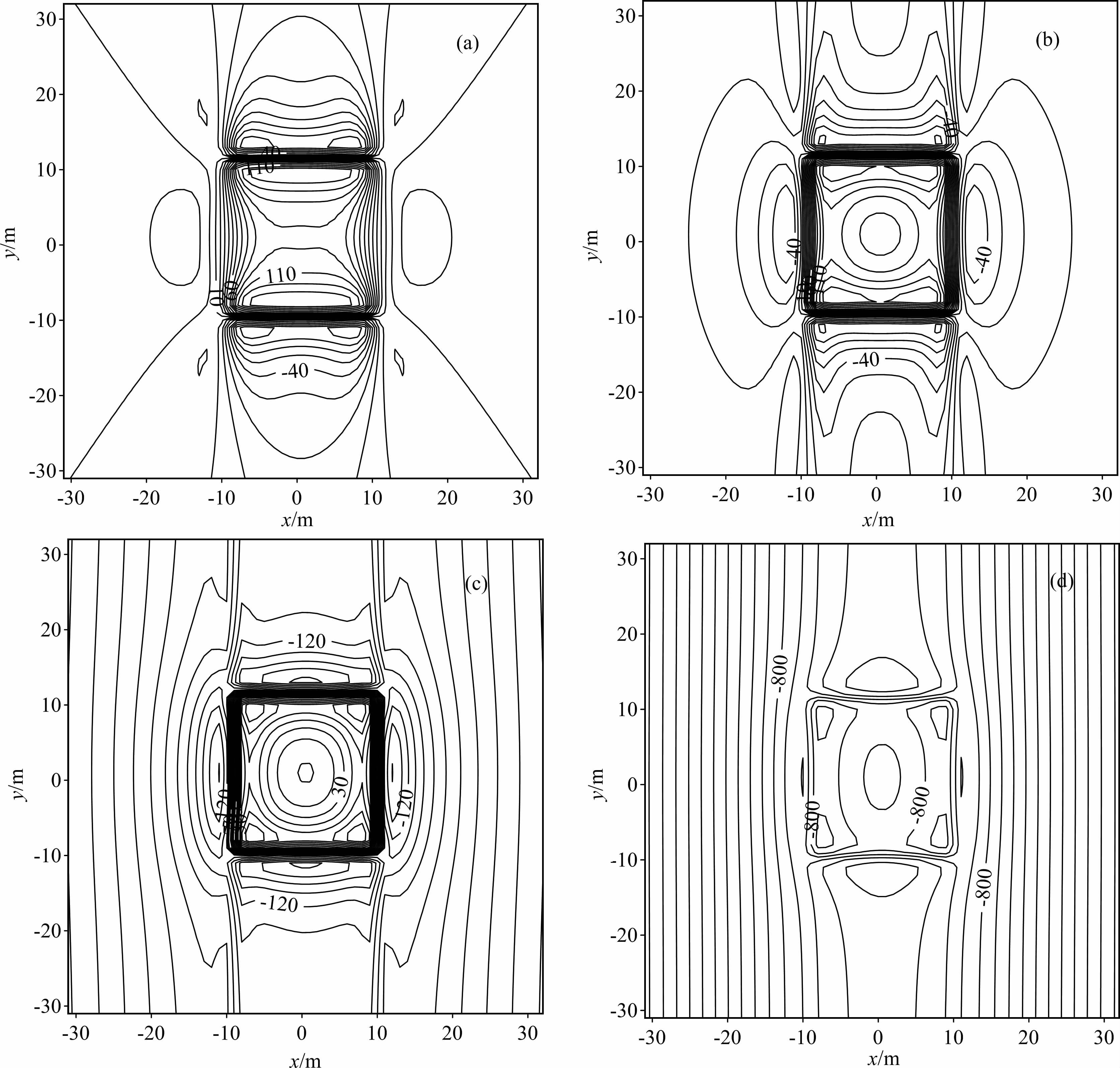
|
图 17 迭代化极结果 (a)迭代10次结果(误差:19.75nT);(b)迭代100次结果(误差:13.15nT);(c)迭代1000次结果(误差:72.89nT);(d)迭代10000次结果(误差:772.41nT) Fig. 17 Results of iterative RTP (a) 10 iterations (error: 19.7 5 nT) ; (b) 100 iterations (error: 13.15 nT) ; (c) 1000 iterations(error : 72. 89 nT) ; (d) 10000 iterations(error: 772.41 nT). |
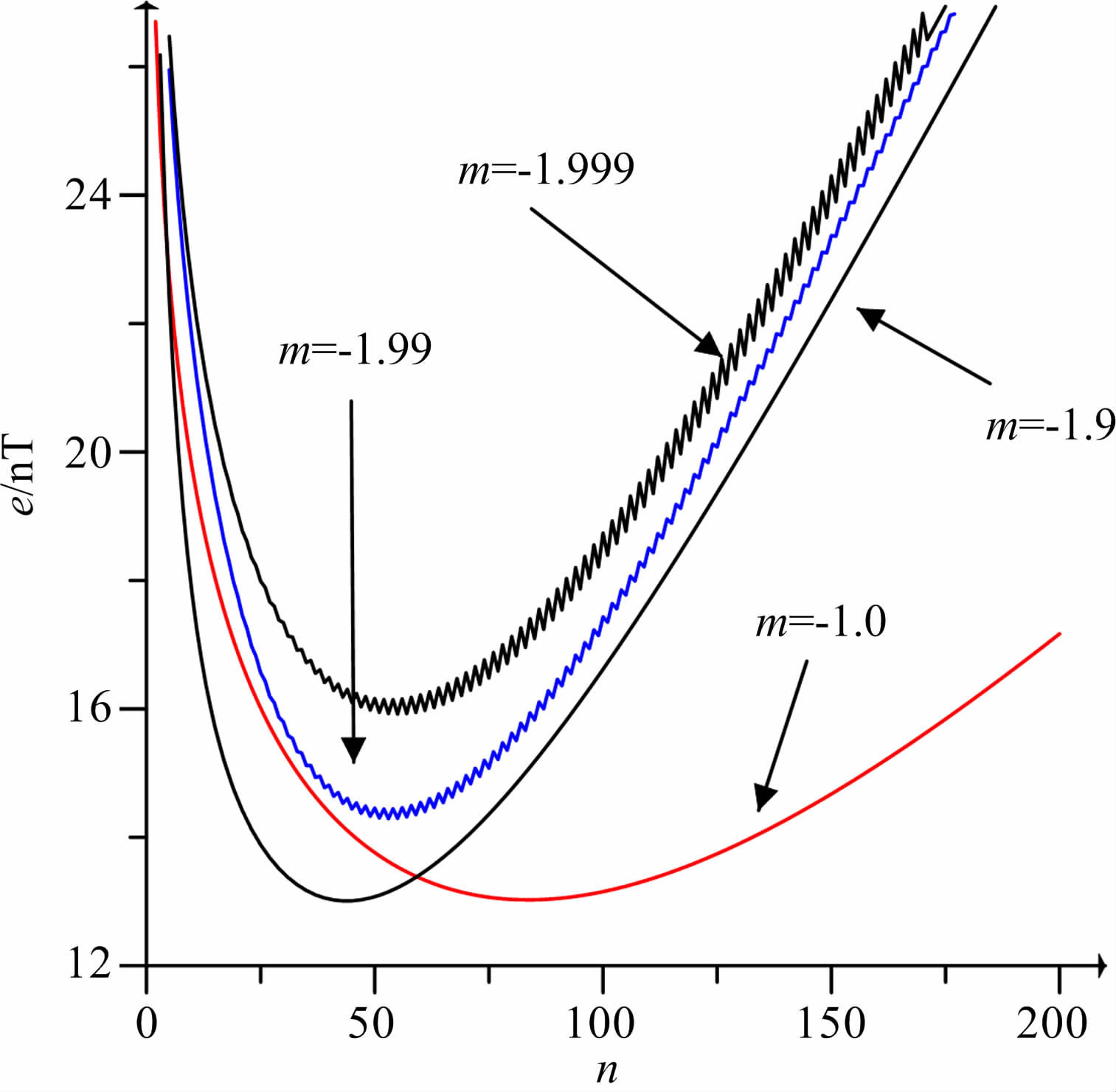
|
图 18 速度系数对迭代化极误差的影响 Fig. 18 The effects of velocity factoron the iterative RTP error |
本文主要从理论上推导了位场计算迭代法的通式,认为迭代法收敛与否取决于映射函数的选取,并给出了具体转换问题迭代法的收敛条件,分析了各种影响迭代收敛性的因素,例如:如果原本不稳定计算的逆运算是稳定的,如迭代下延和低纬度赤道化极中,可以选择简单的常数映射;但对于逆运算不稳定的情况,如向上延拓等(其逆运算为不稳定的向下延拓),那么对映射函数的选择则要苛刻得多,必须采取变量映射才能有效收敛,所以,映射函数的合理选取是迭代法重磁处理转换的核心.这就为迭代法在其他位场计算中的应用奠定了理论基础.
映射函数的选取不仅对收敛性以及收敛速度起着绝对作用,并且对计算结果的误差也有一定的影响.通常情况下,对于频谱相位不发生改变的转换,如相对高差不大的向下延拓等,映射函数的值为正值才能保证收敛;而对于低纬度化极等转换,转换前后数据频谱的振幅和相位都发生了变化,映射函数的值为负值才能保证收敛;而对于曲化平等问题,转换前后的频谱的相位是否发生变化是不确定的,所以要根据具体情况来判断,并且可能需要针对性设计变化的映射函数.
迭代法主要是用于解决一些位场计算中的不稳定问题的,但从上面的理论分析以及模型数据计算也可以看出,迭代法虽然能够通过试验不同参数获得比较好的效果,但其结果的精度并不会随着迭代次数的增加而保持增加,其本质上相当于还是一种滤波器(或其变形),其作用是对原有转换算子放大的区域予以一定的滤波压制;如果迭代次数过大,迭代法的结果将无限趋近于FFT 理论计算结果,结果依然是不稳定的;如果迭代次数过小则会压制原始数据中的有效信号,使得结果误差过大.所以针对位场处理转换中一些不稳定计算采用迭代法,并没有从根本上解决计算的精度与不稳定性之间的问题,这是我们应用迭代法时需要认识清楚的.
| [1] | CTPAXOB ΒΗ, ДEBИЦЬIH B M. О ПPИBEДEHИИ HAБ?ПОДEHHЪIX ЗHAЧEHИЙ ПОTEHЦИA?IЬHЬIX ПOJIEЙ К ОДHOMУ УPOBHIO. AKADEMIIA NAUK SSSR, IZUESTIIA, FIZIKA ZEML 1965,4: 60-72. Strakhov A V, Devitsyn V N. The reduction of observed values of a potential field to values at a constant level. Proceedings of the Academy of Sciences. Physics of the Earth (in Russian), 1965, 4: 60-72. |
| [2] | 徐世浙. 位场延拓的积分-迭代法. 地球物理学报 , 2006, 49(4): 1176–1182. Xu S Z. The integral-iteration method for continuation of potential fields. Chinese J. Geophys. (in Chinese) , 2006, 49(4): 1176-1182. |
| [3] | 徐世浙. 迭代法与FFT法位场向下延拓效果的比较. 地球物理学报 , 2007, 50(1): 285–289. Xu S Z. A comparison of effects between the iteration method and FFT for downward continuation of potential fields. Chinese J. Geophys. (in Chinese) , 2007, 50(1): 285-289. |
| [4] | 徐世浙, 余海龙. 位场曲化平的插值一迭代法. 地球物理学报 , 2007, 50(6): 1811–1815. Xu S Z, Yu H L. The interpolation—iteration method for potential field continuation from undulating surface to plane. Chinese J. Geophys. (in Chinese) , 2007, 50(6): 1811-1815. |
| [5] | 刘东甲, 洪天求, 贾志海, 等. 位场向下延拓的波数域迭代法及其收敛性. 地球物理学报 , 2009, 52(6): 1599–1605. Liu D J, Hong T Q, Jia Z H, et al. Wave number domain iteration method for downward continuation of potential fields and its convergence. Chinese J. Geophys. (in Chinese) , 2009, 52(6): 1599-1605. |
| [6] | 张辉, 陈龙伟, 任治新, 等. 位场向下延拓迭代法收敛性分析及稳健向下延拓方法研究. 地球物理学报 , 2009, 52(4): 1107–1113. Zhang H, Chen L W, Ren Z X, et al. Analysis on convergence of iteration method for potential fields downward continuation and research on robust downward continuation method. Chinese J. Geophys. (in Chinese) , 2009, 52(4): 1107-1113. |
| [7] | 曾小牛, 李夕海, 韩绍卿, 等. 位场向下延拓三种迭代方法之比较. 地球物理学进展 , 2011, 26(3): 908–915. Zeng X N, Li X H, Han S Q, et al. A comparison of three iteration methods for downward continuation of potential fields. Progress in Geophysics. (in Chinese) , 2011, 26(3): 908-915. |
| [8] | 于波, 翟国君, 刘燕春, 等. 噪声对磁场向下延拓迭代法的计算误差影响分析. 地球物理学报 , 2009, 52(8): 2182–2188. Yu B, Zhai G J, Liu Y C, et al. Analysis of noise effect on the calculation error of downward continuation with iteration method. Chinese J. Geophys. (in Chinese) , 2009, 52(8): 2182-2188. |
| [9] | 王彦国, 张凤旭, 王祝文, 等. 位场向下延拓的泰勒级数迭代法. 石油地球物理勘探 , 2011, 45(4): 657–662. Wang Y G, Zhang F X, Wang Z W, et al. Iteration method of Taylor series for downward continuation of potential fields. Oil Geophysical Prospecting (in Chinese) , 2011, 45(4): 657-662. |
| [10] | 骆遥. 位场迭代法向下延拓的地球物理含义—以可下延异常逐次分离过程为例. 地球物理学进展 , 2011, 26(4): 1197–1200. Luo Y. Geophysical implications of the iteration method for downward continuation of potential field: a case by computing regional anomaly can be continued downward. Progress in Geophysics. (in Chinese) , 2011, 26(4): 1197-1200. |
| [11] | 徐世浙, 曹洛华, 姚敬金. 重力异常三维反演-视密度成像方法技术的应用. 物探与化探 , 2007, 31(1): 25–28. Xu S Z, Cao L.H, Yao J.J. 3D inversion of gravity anomaly: an application of the apparent density magery technology. Geophysical & Geochemical Exploration (in Chinese) , 2007, 31(1): 25-28. |
| [12] | 徐世浙, 余海龙, 姚敬金, 等. 新疆色尔特能地区视密度和视磁性反演. 物探化探计算技术 , 2007, 29(S1): 12–16. Xu S Z, Yu H L. Yao J.J, et al. The inversion of apparent density and apparent susceptibility in the seerteneng area, xin jiang. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 2007, 29(S1): 12-16. |
| [13] | 徐世浙, 王瑞, 周坚鑫, 等. 从航磁资料延拓出海平面的磁场. 海洋学报 , 2007, 29(6): 53–57. Xu S Z, Wang R, Zhou J X, et al. To continue aeromagnetic data to the sea level. Acta Oceanologica Sinica (in Chinese) , 2007, 29(6): 53-57. |
| [14] | 徐世浙, 王华军, 余海龙, 等. 普光气田重力异常的视密度反演. 地球物理学报 , 2009, 52(9): 2357–2363. Xu S Z, Wang H J, Yu H L, et al. Apparent density inversion of gravity anomalies of Puguang gas field. Chinese J. Geophys. (in Chinese) , 2009, 52(9): 2357-2363. |
| [15] | 杨金玉, 徐世浙, 余海龙, 等. 视密度反演在东海及邻区重力异常解释中的应用. 地球物理学报 , 2008, 51(6): 1909–1916. Yang J Y, Xu S Z, Yu H L, et al. Application of apparent density inversion method in the East China Sea and its adjacent area. Chinese J. Geophys. (in Chinese) , 2008, 51(6): 1909-1916. |
| [16] | 于波, 刘雁春, 边刚, 等. 海洋磁力测量垂直空间改正研究. 武汉大学学报 , 2008, 33(9): 926–929. Yu B, Liu Y C. Bian G, et al. Correction of Vertical Free-Air in Marine Magnetic Surveying. Geomatics and Information (in Chinese) , 2008, 33(9): 926-929. |
| [17] | 于波, 翟国君, 刘雁春, 等. 利用航磁数据向下延拓得到海平面磁场的方法. 测绘学报 , 2009, 38(3): 202–209. Yu B, Zhai G J, Liu Y C, et al. The downward continuation method of aeromagnetic data to the sea level. Acta Geodaetica et Cartographica Sinica (in Chinese) , 2009, 38(3): 202-209. |
| [18] | 王小兵, 张金生, 乔玉坤, 等. 频率域延拓在地磁匹配中的应用研究了. 现代防御技术 , 2009, 37(6): 87–90. Wang X B, Zhang J S, Qiao Y K, et al. Application of the frequency domain continuation in the geomagnetism matching guidance system. Modern Defence Technology (in Chinese) , 2009, 37(6): 87-90. |
| [19] | 肖锋, 李海侠, 余海龙, 等. 确定水下磁性体位置的一个实例. 物探与化探 , 2009, 33(1): 105–108. Xiao F, Li H X, Yu H L, et al. The Determination of the position of an under water magnetic object: a case study. Geophysical & Geochemical Exploration (in Chinese) , 2009, 33(1): 105-108. |
| [20] | 李成立, 崔瑞华, 刘益中, 等. 盆地基底岩性的综合地球物理预测方法—以松辽盆地滨北地区基底岩性预测为例. 地球物理学报 , 2011, 54(2): 491–498. Li C L, Cun R H, Liu Y Z, et al. Comprehensive geophysical prediction method of basement lithology-Example of Binbei area, Songliao basin. Chinese J. Geophys. (in Chinese) , 2011, 54(2): 491-498. |
| [21] | 余海龙, 徐世浙, 李海侠, 等. 曲面上航磁异常与梯度分量的转换方法. 浙江大学学报(工学版) , 2011, 45(2): 397–404. Yu H L, Xu S Z, Li H X, et al. Transformation of total magnetic field anomaly and gradients on irregular surface. Journal of Zhejiang University (Engineering Science) (in Chinese) , 2011, 45(2): 397-404. |
| [22] | Keating P, Zerbo L. An improved technique for reduction to the pole at low latitudes. Geophysics , 1996, 61(1): 131-137. DOI:10.1190/1.1443933 |
| [23] | Li X. Magnetic reduction-to-the-pole at low latitudes: Observations and considerations. The Leading Edge , 2008, 27(8): 900-1002. |
| [24] | 骆遥, 薛典军. 磁赤道处化极方法. 地球物理学报 , 2010, 53(12): 2998–3004. Luo Y, Xue D J. Reduction to the pole at the geomagnetic equator. Chinese J. Geophys. (in Chinese) , 2010, 53(12): 2998-3004. |
| [25] | 方迎尧, 张培琴, 刘浩军. 低磁纬度地区ΔT异常解释的途径与方法. 物探与化探 , 2006, 30(1): 48–54. Fang Y Y, Zhang P Q, Liu H J. Approaches to the interpretation of magnetic ΔT anomalies in the low magnetic latitude area. Geophysical & Geochemical Exploration (in Chinese) , 2006, 30(1): 48-54. |
 2012, Vol. 55
2012, Vol. 55

