2. 中石化石油物探技术研究院, 南京 210014
2. SINOPEC Geophysical Research Institute, Nanjing 210014, China
在海相碳酸盐岩盆地,孔洞型油气储层是重要的储层类型,提高储层的地震识别与描述精度是该类储层勘探与开发的急需.有效的储层地震识别与描述方法必须建立在对储层地震响应特征正确认识的基础之上,碳酸盐岩孔洞储层的结构与分布复杂,孔洞的多尺度、填充物的多样性、几何形状不规则、空间变化剧烈等特征导致地震反射复杂,建立地震反射属性与储层参数之间的关系十分困难.对地震响应特征的认识不足必然影响对储层的定量描述,目前这仍是尚未很好解决的问题.
复杂储层地震响应特征是油气地球物理勘探长期研究的课题,国内外已取得的相关技术方法与研究成果很多[1-7].针对碳酸盐岩孔洞型储集体的地震响应特征,国内学者以塔河油田缝洞型储层为研究对象开展了大量的物理模拟研究[8-15]和数值模拟研究工作[16-20],取得了许多很好的研究成果,并在孔洞型油气藏的地震识别与描述中发挥了较好的指导作用.地震响应特征研究的最终目标是建立储层的几何与物理等参数与地震响应属性之间的定量关系,就碳酸盐岩孔洞型储层而言,这一目标的实现难度很大,目前所取得的主要是定性分析成果或结论.
本文基于声波方程,在不考虑洞体多次散射的近似下导出深层小尺度长方体形态的孔洞地震响应的解析关系式,利用该关系式可解释孔洞异常体大小与反射波振幅的关系,揭示不同方向上的尺度变化如何对反射振幅产生影响.同时,利用高阶交错网格有限差分弹性波数值模拟[21-24]的结果对解析分析结论进行了验证.对于较复杂的洞内充填,通过物理模型实验给出半定量与定性分析结果.通过理论分析、数值与物理模型实验,以期得到对碳酸盐岩孔洞储集体的地震预测具有指导作用的结论.
2 反射特征近似解析分析实际缝洞体的地震反射十分复杂,反射特征与缝洞体形状、大小、充填及埋深等众多因素相关.通常,大型溶洞的尺度小于或接近地震勘探子波长度,由于受分辨率限制,很难通过地震反演获得对于溶洞内部细节变化的描述,以下的数值模型正演结果表明了这一点.
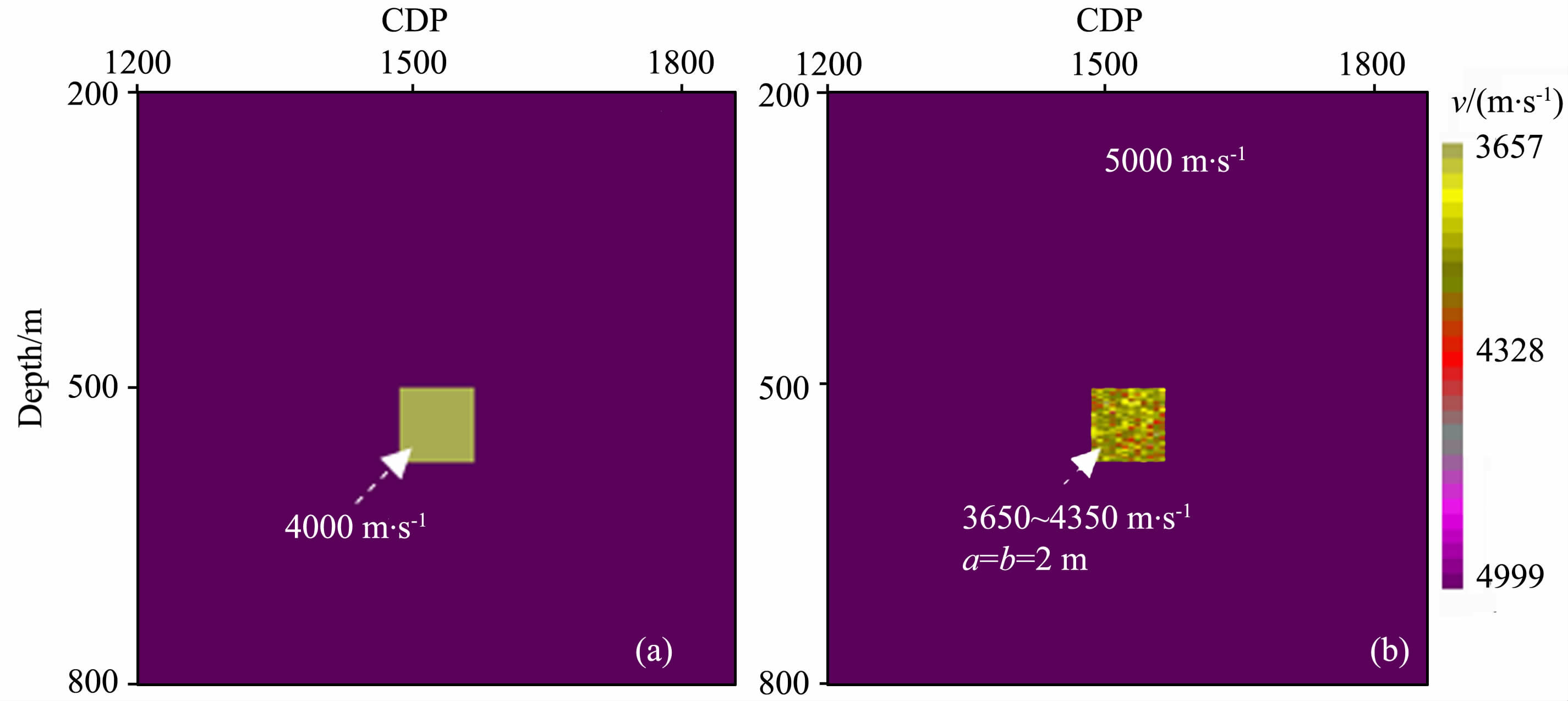
图 1是一个非常简单的模型,模型背景纵波速度为5000m·s-1,假设在模型中部500 m 深度处有一大小为75 m×75 m 的正方形洞穴,在洞穴内部分别予以纵波速度为4000 m·s-1 的均匀填充(图 1a)和纵波速度在3650~4350m·s-1范围变化的随机填充(图 1b),随机模型的自相关长度[19]为a=b=2m, 速度均值为4000 m·s-1,对所得的两个速度模型分别进行正演计算.计算中,子波主频为40Hz, 横波与纵波速度比为0.6,密度按一般经验公式由纵波速度换算得到,采用弹性波方程进行正演模拟计算[21]得到垂直分量结果.图 2是偏移剖面对比,可以看到,两个模型的正演结果非常接近,也就是说,对这样一个大小的洞穴,空间上小尺度的速度随机扰动(本例随机扰动幅度约为10%)对反射特征的影响不明显.因此,在信噪比和分辨率都有限的实际勘探中,对数千米之下溶洞只能期望得到在一定尺度上平均异常情况的认识.
|
图 1 洞内均匀填充a与随机填充(b)的速度模型 Fig. 1 Numerical cave models with uniform filling(a) and random filling(b) |

|
图 2 洞内均匀填充与随机填充的偏移剖面对比 (a)洞内均匀填充时的偏移剖面;(b)洞内随机填充时的偏移剖面;(c)(a)与(b)之差. Fig. 2 The migration results of cave models with varied fillings and the difference between each result (a)Migration result of cave model with homogeneous infilling ;(b ) Migration result of cave model with random infillings; (c)Difference between (a) and (b). |
实际中的溶洞储集体可能是由多个尺度较小(与地震子波波长相比)的溶洞通过裂缝连接而成,上面的分析说明,整体尺度不大的缝洞群只能当作一个孤立洞来认识,由地震资料给出其平均特征.对于孤立的溶洞,通过简化可给出其地震响应的近似解析关系式,该关系式可帮助对溶洞地震反射基本特征的认识.
将溶洞视为地质异常体,基于声波方程和一次散射近似,可给出在地面观测的地下异常体的散射响应:
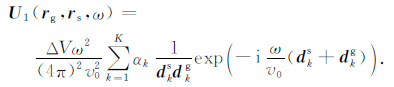
|
(1) |
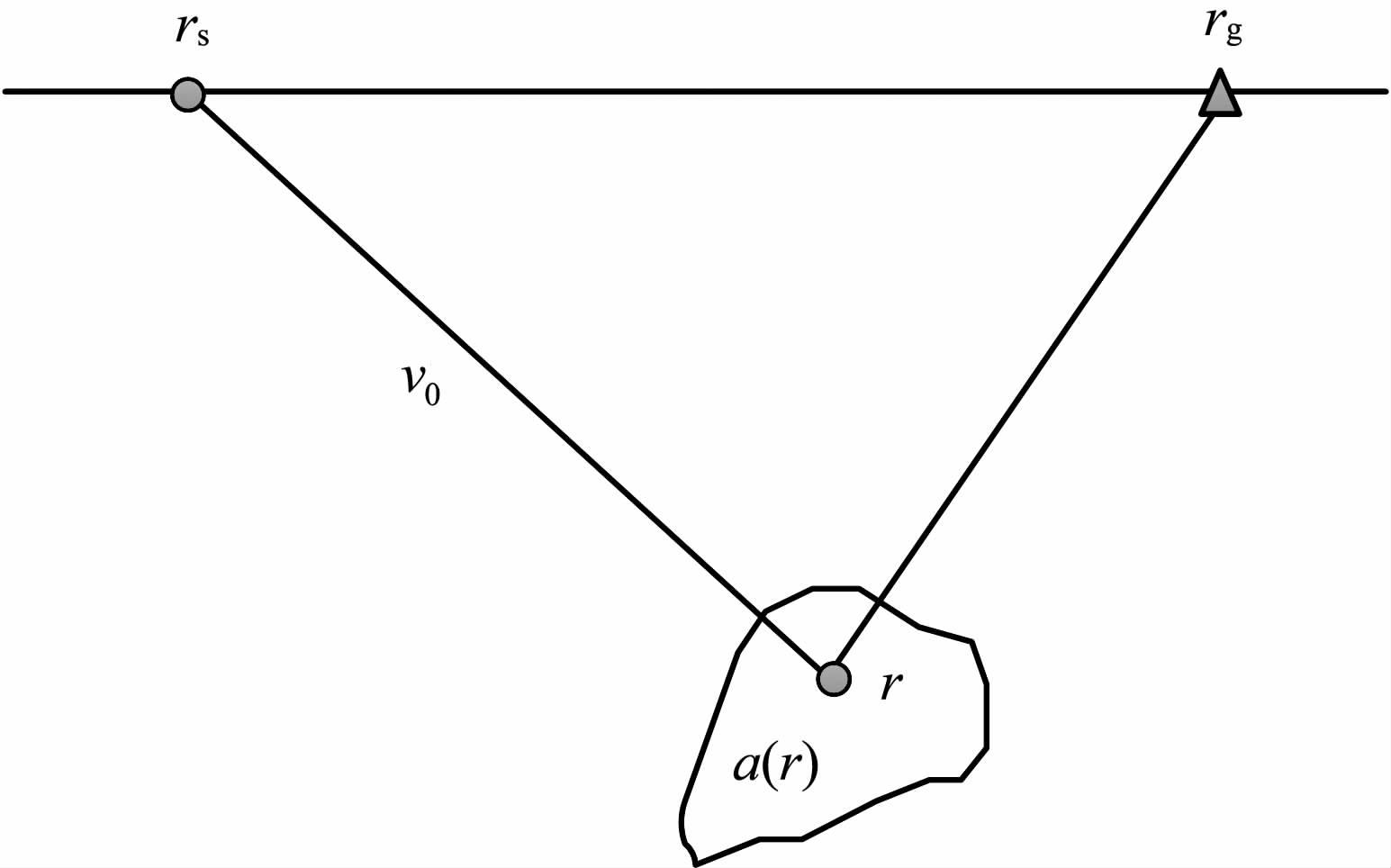
这里将地下异常体(如图 3)分为K个网格单元,单元体积为ΔV= ΔxΔyΔz,第k单元体到震源点和接受点的距离分别为dks和dkg,v0 和v(r)分别为背景速度和异常体速度,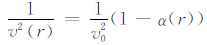
|
图 3 异常体 Fig. 3 Sketch map of diffraction object |
式(1)是在单位脉冲点震源情况和均匀速度背景下异常体反射波的计算公式,将异常体看作是一个滤波器,则式(1)就可看作是响应函数.对于埋藏于地下数千米深度的目标异常体,异常体尺度相对埋深是一个小量,对于地面地震勘探,在通过求和计算反射振幅时可认为震源点到异常体内每一点的距离以及接收点到异常体内每一点的距离为常数,这样可简化计算,便于分析.
设激发点到异常体中心距离为ds, 接收点到异常体中心的距离为dg, L为异常体内任意两点距离的最大值,即异常体的尺度,满足L$\ll $ds, L$\ll $dg, 则在(1)式中dks≈ds, dkg≈dg(k∈K),又αk=α设为常数,(1)式可简化为
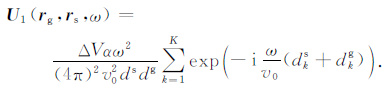
|
(2) |
分析自激自收记录,此时dg =ds =d0,记dkg=dks=d0 +Δdk,并考虑到地震波进入异常体后的传播速度为v,而非v0,(2)可写为
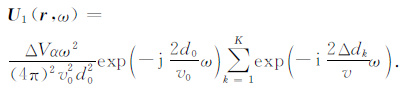
|
(3) |
当异常体的埋深和速度偏差一定时,其大小和形状通过因子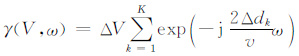
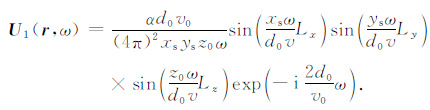
|
(4) |
式(4)给出了远场小尺度长方体形状的异常体一次反射的近似计算式,尽管是建立在声波方程近似基础上,且忽略了多次反射,但该式能够很好地反映小尺度异常体的振幅调谐特征.
|
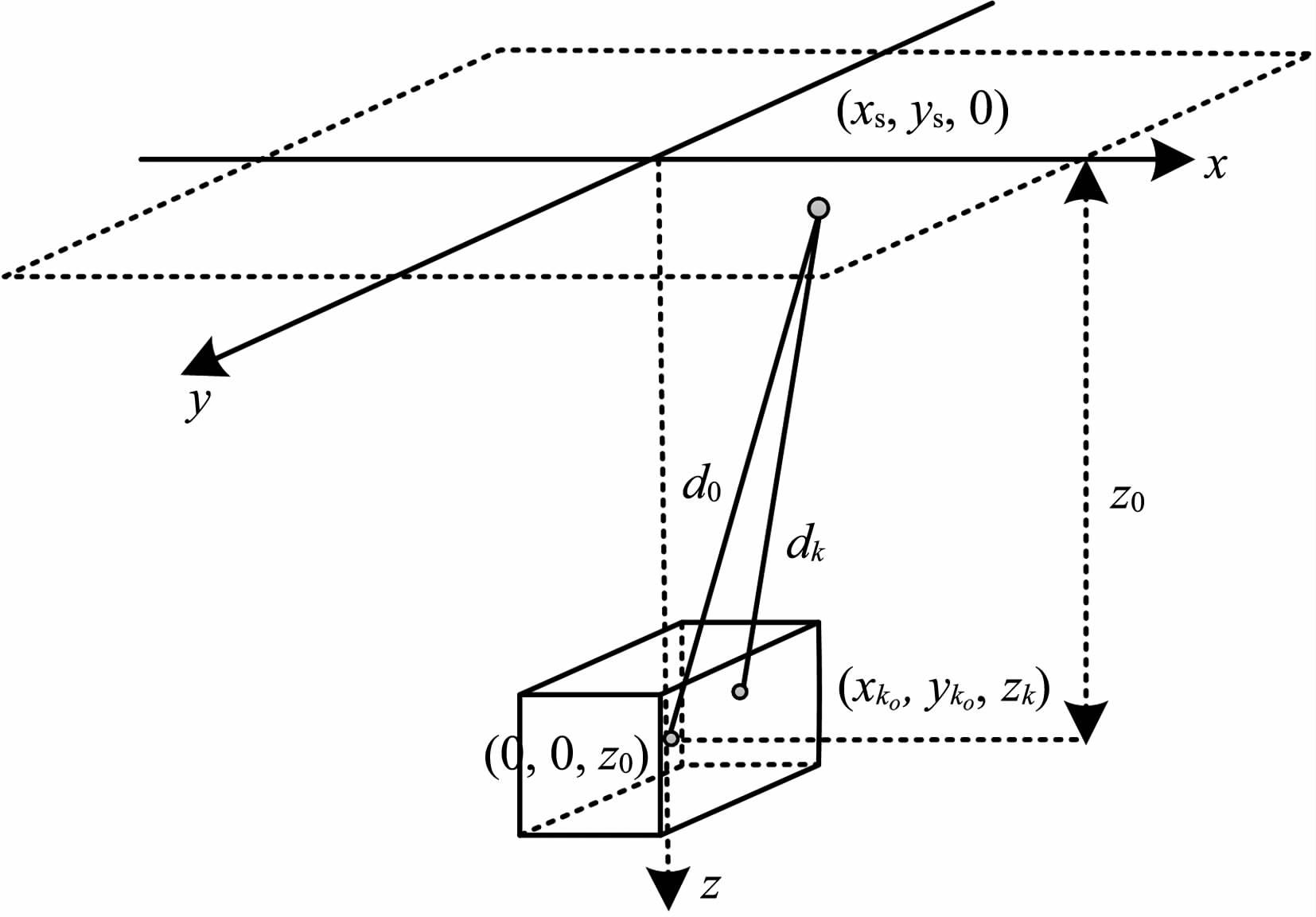
图 4 异常体位置示意图 Fig. 4 The location of diffraction object |
在层状模型下,反射振幅与薄层厚度呈近似线性关系,利用式(4)也可得到类似的结果.由sin(x)≈x(|x|$\ll $1),(4)式可简化为
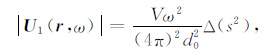
|
(5) |
这里V=LxLyLz为异常体体积,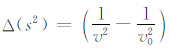
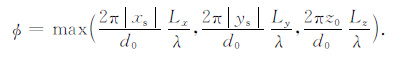
|
(6) |
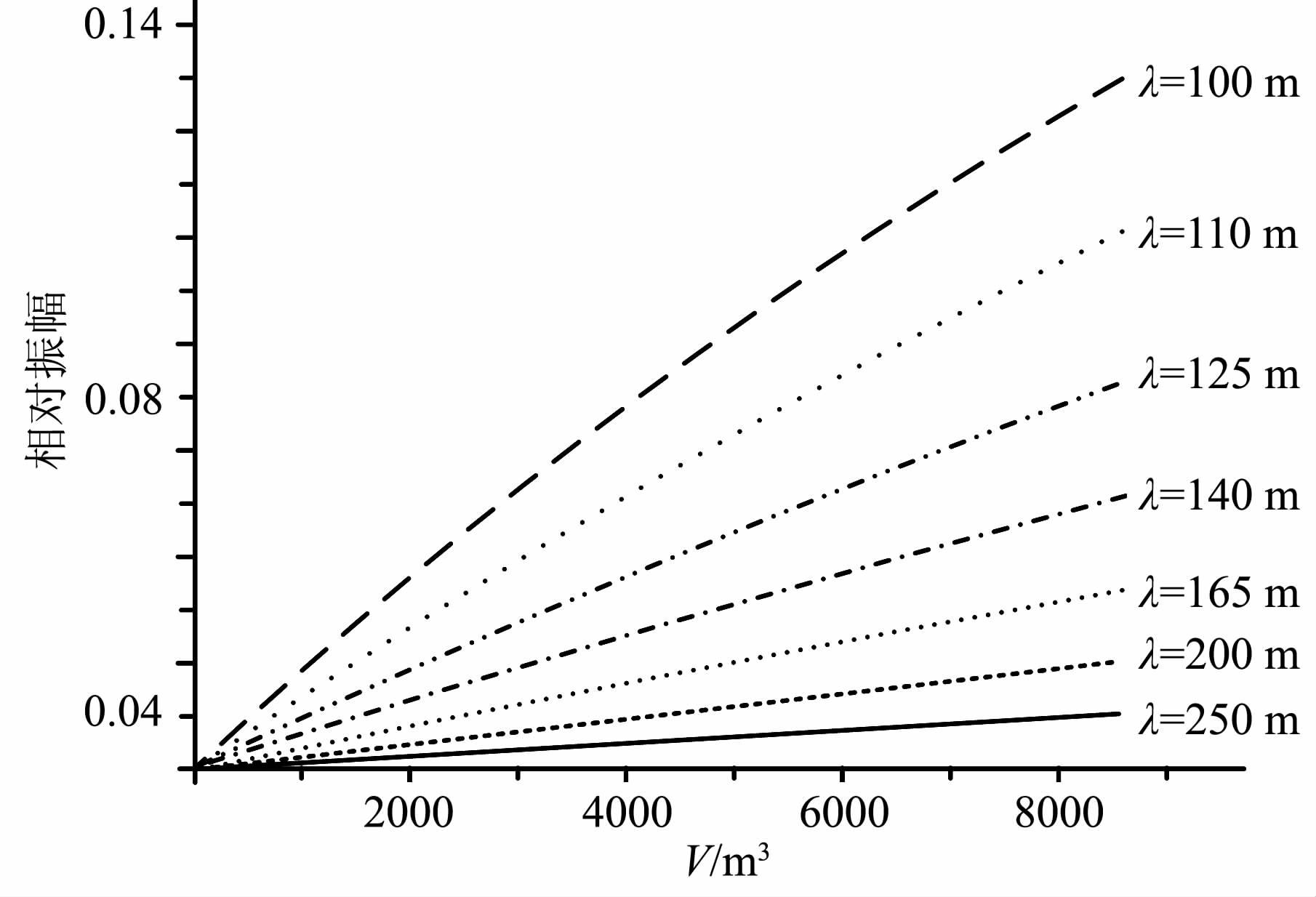
这里波长λ=2πv0/ω,当φ 足够小时,可采用式(5).从(5)式可以得到一个基本结论就是对于小尺度异常体,低频散射波振幅与异常体尺度(体积)成正比关系.简单计算可验证结论的正确性.取xs=ys=1000m, Lx=Ly=Lz=1,3m, …,20m, z0=3000m, 背景速度v0=5000m·s-1,异常体速度v=3000 m·s-1,利用式(1)计算一次散射场响应的振幅谱|U1(r,ω)| .图 5 是波长λ 分别为250,200 m, …,100m 时的响应振幅与异常体体积V=LxLyLz的关系曲线,显然,在长波长和小尺度范围内,振幅与异常体体积的关系是近似线性的,异常体尺度(体积)越大,散射振幅越强.
|
图 5 不同波长地震响应振幅与异常体体积的关系曲线 Fig. 5 Relationship between the object volume and reflectionamplitude under the condition of different wavelength |
式(4)给出的小尺度长方体异常体的振幅调谐关系可用于估算异常体的尺度,定量分析绕射波的振幅特征.由于实际缝洞体或缝洞群可视为多个小尺度异常体的叠加,因此,(4)式对于复杂缝洞体(群)的反射特征的认识仍有一定的指导意义.
对非零偏移距观测,类似可给出小尺度长方体异常体的响应表达式如下:

|
(7) |
这里的d0s、d0g 分别为激发点到异常体中心以及接收点到异常体中心的距离.
3 数值正演分析孔洞型储集体的尺度与充填程度是这类储层描述的重要参数,分析这两种参数与反射振幅之间的关系具有十分重要的意义.对于地面观测,孔洞的横向尺度与纵向尺度对反射振幅的影响不同,下面用两个数值模型分析横向和纵向尺度与反射振幅的关系.
3.1 横向尺度与反射振幅的关系
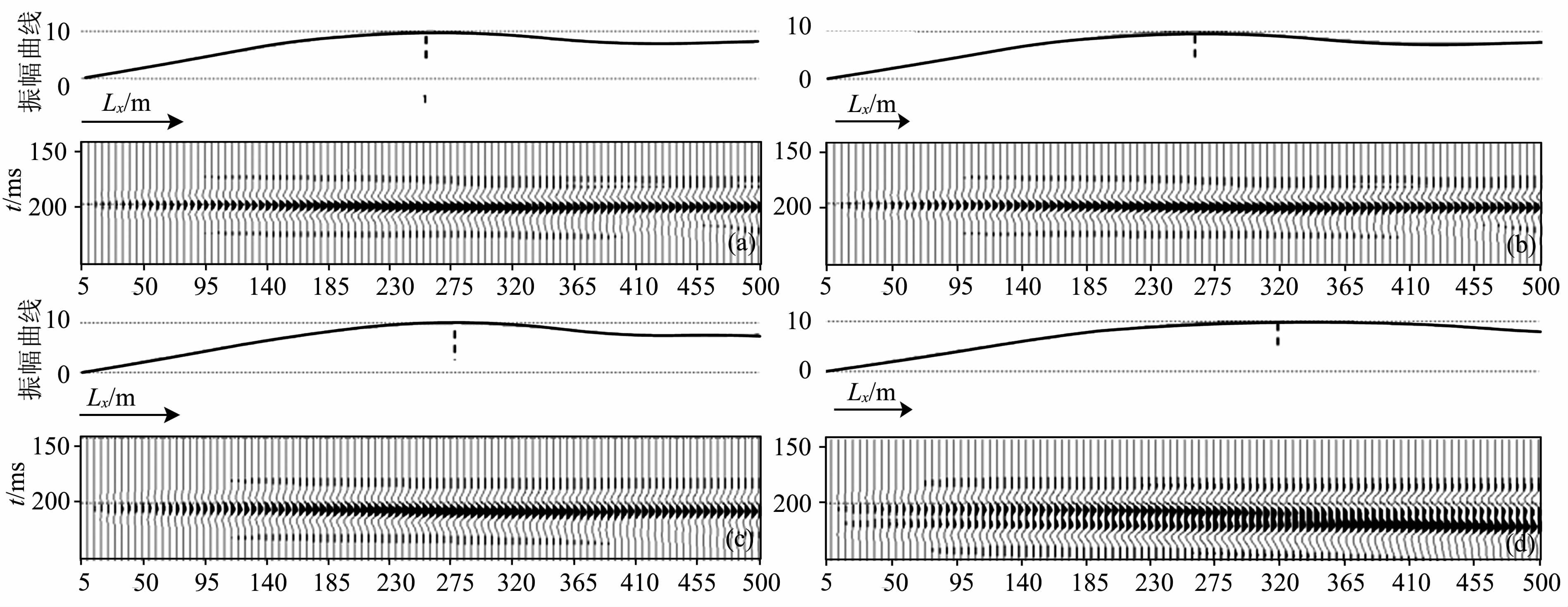
将形状为长方体的溶洞异常体置于深度500m处,取背景速度v0=5000 m·s-1,异常体速度v=4000m·s-1,子波为主频fd=40 Hz 的雷克子波.在异常体正上方的地面点激发与接收,改变异常体尺度,每次记录一道,将对不同尺度异常体观测到的反射记录显示在一起,观测振幅变化.为分析横向尺度对反射振幅的影响,固定异常体y、z两方向的尺度Ly、Lz,改变x方向尺度Lx,其结果如图 6所示,图中给出了4组不同Ly、Lz情况,分别得到不同Lx所对应的反射波记录,随Lx变化的记录的最大振幅曲线亦显示在图上.从该结果上可以看到:(1)当Lx较小时,散射波振幅有随Lx增大而增大的近似线性关系;(2)设在Lx= Lx0处散射波振幅取最大值,Lx0随Ly和/或Lz的增大而增大,当Ly、Lz较小时,Lx0约为菲涅尔半径的2倍(该例中,菲涅尔半径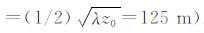
|
图 6 异常体横向尺度变化对反射振幅的影响 (a)Ly=1m, Lz=1m;(b)Ly=5m, Lz=5m;(c)Ly=20m, Lz=20m;(d)Ly=50m;Lz=50m. Fig. 6 The impacts of lateral scale variation on reflection amplitude |
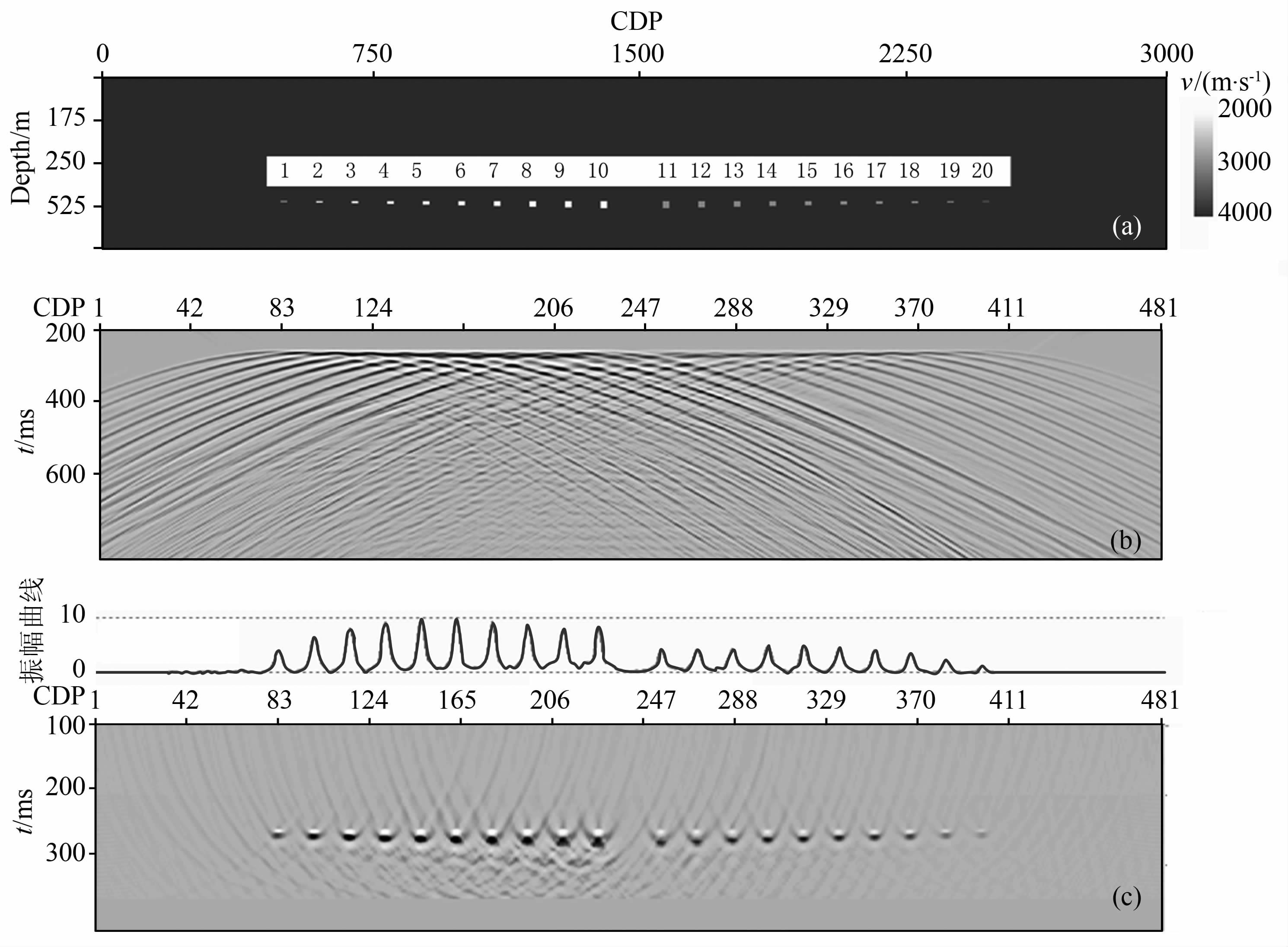
含不同尺度溶洞的速度模型如图 7所示,均匀背景纵波速度为4000 m·s-1,在500 m 深度处以模型中点垂线为对称轴向两边对称设置20 个长方形洞穴,洞间距为100m, 洞穴的宽度均为20m, 高度从最高28m 向左右两边逐渐减小到最低2m, 左半边10个洞穴的填充速度为2000m·s-1,右半边10个洞穴的填充速度为3000m·s-1.计算中,子波主频为40Hz, 模拟多次覆盖观测,炮间距6.25m, 共得到481炮记录.图 7(b, c)分别给出的是零偏移距剖面(即自激自收剖面)和相应偏移剖面.
|
图 7 速度模型及正演结果 (a)速度模型;(b)零偏移剖面;(c)偏移剖面. Fig. 7 Seismic numerical model and its modeling results (a)Velocity model;(b)Zero-offset section;(c)Migration result. |
由该模型正演结果可得出的结论是:(1)在偏移剖面上,溶洞反射波能量与溶洞大小密切相关,在溶洞高度为λ/4(按洞穴内速度计算,本例左边的洞穴λ/4为12.5m, 右边的洞穴λ/4 为18 m)时为调谐高度,反射能量达到最大值,当洞穴高度小于λ/4时,反射能量与洞穴高度成正比;(2)在偏移剖面上,溶洞反射波振幅与溶洞内部和围岩的波阻抗差成近似的比例关系,波阻抗差越大,反射振幅越强.
值得指出的是从上述两个数值模型计算结果所得到的分析结论与前面的近似解析表达式给出的结果是相吻合的.譬如,在式(4)中,当在接近溶洞体地面投影处的位置观测时,有d0≈z0,因此针对纵向尺度变化,当Lz=λ/4时,反射振幅取最大值,即调谐高度为λ/4.
4 物理模型试验充填性质与群洞组合的变化对地震反射的影响是孔洞储层地震响应特征研究的重要内容,但对于复杂的洞内充填和溶洞组合情况下的地震反射,很难对其特征作定量分析.现给出两个物理模型试验和一些有关的定性分析结论.
4.1 溶洞充填对反射振幅的影响图 8是具有不同填充物的溶洞物理模型及观测结果.图 8a表示5种填充材料不同、大小一致的溶洞,其中溶洞A 充填空气,溶洞B 充填实心体积不一小球体,溶洞C 充填同一尺度空心玻璃微珠,溶洞D 充填稠油,溶洞E 充填非均质多孔物质.除A洞外,其余的溶洞体平均速度均为1800m·s-1.按长度1∶5000,速度1∶1 的比例,洞直径4 mm, 埋深h=720mm进行观测,其代表实际溶洞直径20m, 埋深3600m, 围岩速度3000m·s-1,洞内速度1800m·s-1.图 8b为模型观测结果的叠加剖面.
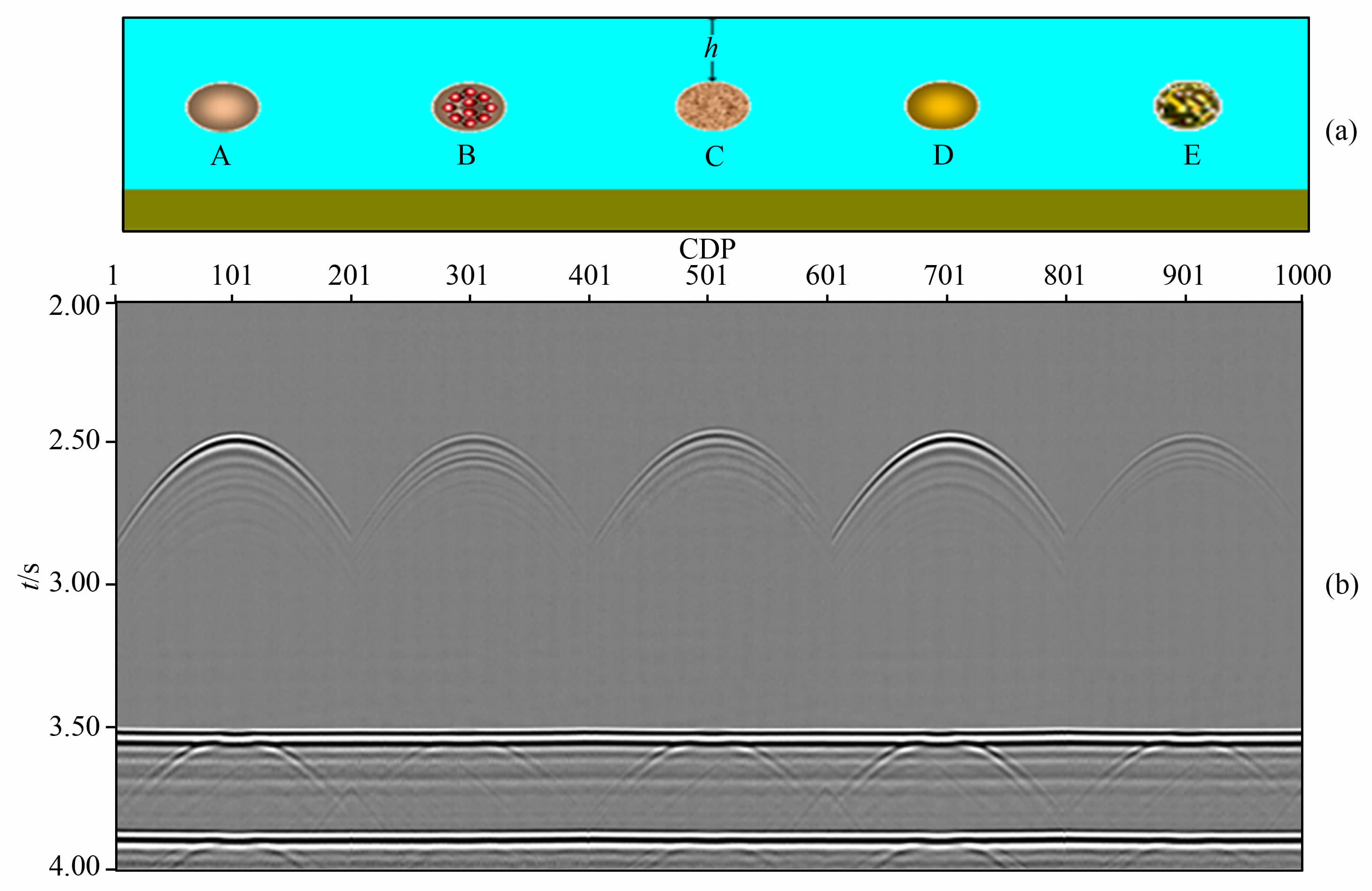
|
图 8 不同填充物溶洞模型示意图(a)及观测数据叠加剖面(b) Fig. 8 Sketch maps of caves with varied infillings and stack results of the reflection records |
图 9给出5种不同充填物溶洞的反射波最大振幅值.从图中看出相同尺度溶洞在不同物质充填时,其反射振幅大小及振幅随偏移距的衰减快慢不同.首先,反射振幅大小主要反映两个因素,即(1) 反映了洞内充填物质的波阻抗与围岩波阻抗的差异大小,故洞内充填气(A)时,反射振幅最大;(2) 反映洞内充填物的颗粒大小与均匀程度,充填颗粒越大,均匀程度越差,则散射损失越大,反射振幅越小,故洞内充填气和油(A 和D)时,反射振幅最大,充填实心体积不一的小球体(B)和充填非均质多孔物质(E)时,反射振幅最小.其次,反射振幅随偏移距增大而衰减的快慢主要与洞内充填物的性质有关,溶洞被空气和油充填时,反射振幅随偏移距增大衰减较快;溶洞被非均质固体物质充填时,反射振幅随偏移距增大衰减较为缓慢.
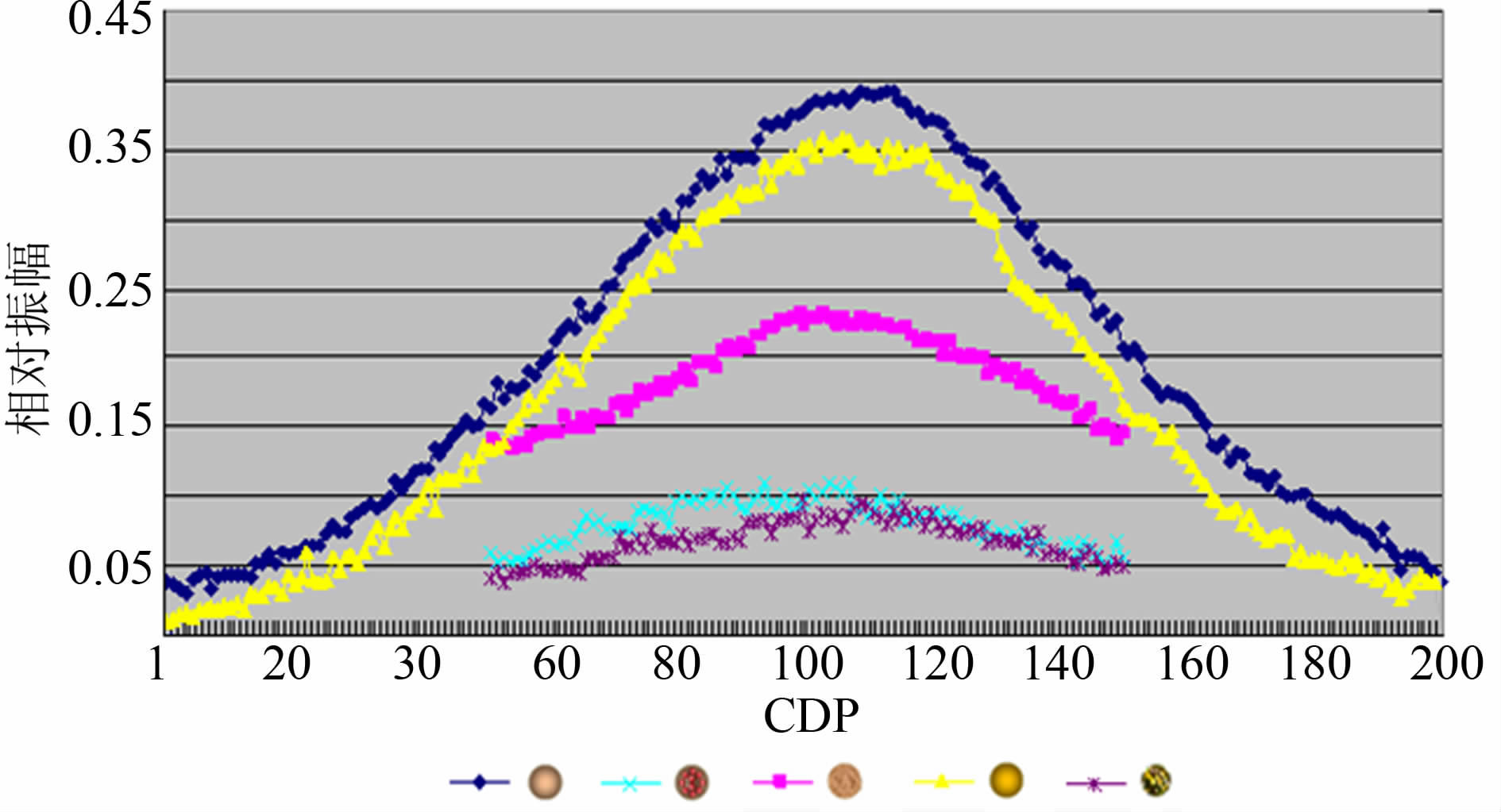
|
图 9 不同充填物溶洞的反射振幅随偏移距变化曲线 Fig. 9 AVO response for caves with varied infillings |
图 10为不同填充物溶洞反射地震偏移剖面.不难看出,充填空气与油时,成像结果的“串珠状"能量强,对称,拖尾长;非均质充填时,成像结果的“串珠状"能量强弱与充填物非均质性有关,非均质性越强,其“串珠状"形态畸变越明显,拖尾较短.图 10的下部为偏移结果的波形显示,从中可看出,空气或油充填的成像结果波形简单,而非均质充填的成像结果波形复杂.

|
图 10 不同充填物溶洞反射偏移剖面 Fig. 10 Migration results of caves with different fillings |
图 11为三种不同结构群洞物理模型、观测结果的叠加剖面及相应的偏移剖面.图 11a为单溶洞,直径20m;图 11b为三个不同大小溶洞的垂直叠置,溶洞直径分别为15、20m 及35m;图 11c为三个大小相同(直径20m)溶洞的品字形叠置;图 11d为两个相同溶洞(直径20m)和一个直径35m 溶洞的倒品字形叠置.从叠加剖面看,群洞的结构影响地震反射波场,导致反射波形及双曲线形态出现差异.在偏移剖面上,单洞反射成像收敛的“串珠状"能量强弱均匀、拖尾较短,而群洞反射成像结果随洞群结构不同,“串珠状"形态和拖尾长度发生变化.

|
图 11 单洞与不同形态群洞反射地震波记录、模型照片和偏移剖面 Fig. 11 Photos of single cave and cave group in different shapes, their reflection records, and migration results |
针对小尺度孤立洞体的假设,可给出反射响应的近似解析表示,解析分析与数值正演结果表明,小尺度单洞体的反射特征表现为:(1) 当孔洞异常体尺度较小(如小于λ/8)时,反射波振幅与异常体体积呈近似线性关系,异常体体积越大,反射振幅越强;
(2) 异常体横向(x、y方向)上尺度对反射波振幅的影响主要由菲涅耳半径控制,同时振幅随横向尺度的变化规律也与纵向尺度有关;(3) 异常体纵向(z方向)上尺度对反射振幅的影响主要表现为调谐效应,当纵向尺度等于调谐厚度(λ/4)时,反射振幅最强.
溶洞充填性质和洞群组合方式影响反射特征导致反射结构变化.充填和洞群组合方式不同,“串珠状"反射的形态不同,总的来说,洞内充填非均质性越强,群洞组合越复杂,“串珠状"反射结构也越复杂.
| [1] | 贺振华, 黄德济. 缝洞储层的地震检测和预测. 勘探地球物理进展 , 2003, 26(2): 79–83. He Z H, Huang D J. Detection and prediction of fracture-cave contained reservoir from seismic data. Progress in Exploration Geophysics (in Chinese) , 2003, 26(2): 79-83. |
| [2] | Taner M T, Koehl E R F, Sheriffle E. Complex seismic trace analysis. Geophysics , 1979, 44(6): 1041-1063. DOI:10.1190/1.1440994 |
| [3] | 刘百红, 李建华, 魏小东, 等. 随机反演在储层预测中的应用. 地球物理学进展 , 2009, 24(2): 581–589. Liu B H, Li J H, Wei X D, et al. The application of Stochastic seismic inversion in reservoir prediction. Progress in Geophys. (in Chinese) , 2009, 24(2): 581-589. |
| [4] | 龚洪林, 王振卿, 李录明, 等. 应用地震分频技术预测碳酸盐岩储层. 地球物理学进展 , 2008, 23(1): 129–135. Gong H L, Wang Z Q, Li L M, et al. Predicting carbonate reservoir by applying seismic spectral decomposition technique. Progress in Geophysics (in Chinese) , 2008, 23(1): 129-135. |
| [5] | 郭智奇, 刘财, 杨宝俊, 等. 粘弹各向异性介质中地震波场模拟与特征. 地球物理学进展 , 2007, 22(3): 804–810. Guo Z Q, Liu C, Yang B J, et al. Seismic wave fields modeling and feature in viscoelastic anisotropic media. Progress in Geophysics (in Chinese) , 2007, 22(3): 804-810. |
| [6] | 程冰洁, 李小凡, 徐天吉. 含流体裂缝介质中地震波场数值模拟. 地球物理学进展 , 2007, 22(5): 1370–1374. Cheng B J, Li X F, Xu T J. Numerical modeling of the seismic wave-field in cracked media with liquid. Progress in Geophysics (in Chinese) , 2007, 22(5): 1370-1374. |
| [7] | Wei J X. A physical model study of different crack densities. Journal of Geophysics and Engineering , 2004, 1(1): 70-76. DOI:10.1088/1742-2132/1/1/009 |
| [8] | 王立华, 魏建新, 狄帮让. 溶洞物理模型地震响应及其属性分析. 石油地球物理勘探 , 2008, 43(3): 291–296. Wang L H, Wei J X, Di B R. Seismic response of karst cave physical model and analysis of its attributes. Oil Geophysical Prospecting (in Chinese) , 2008, 43(3): 291-296. |
| [9] | 李剑峰, 赵群, 郝守玲, 等. 塔河油田碳酸盐岩储层缝洞系统的物理模拟研究. 石油物探 , 2007, 42(2): 180–185. Li J F, Zhao Q, Hao S L, et al. Physical modeling of the fracture-cave systems of carbonate reservoirs in Tahe oilfield. Geophysical Prospecting for Petrole (in Chinese) , 2007, 42(2): 180-185. |
| [10] | 贺振华, 杜正聪, 文晓涛. 碳酸盐岩喀斯特溶洞和裂缝系统的地震模拟与预测. 地球科学进展 , 2004, 19(3): 399–402. He Z H, Du Z C, Wen X T. Seismic modeling and predication of carbonate karst caves and fractures sets. Advance in Earth Science (in Chinese) , 2004, 19(3): 399-402. |
| [11] | 曹均, 贺振华, 黄德济, 等. 孔洞储层地震波特征响应的物理模型实验研究. 成都理工大学学报 (自然科学版) , 2003, 20(6): 576–582. Cao Y, He Z H, Huang D J, et al. Seismic responses to pore-hole reservoir by physical modeling. Journal of Chengdu University of Technology (Science & Technology Edition) (in Chinese) , 2003, 20(6): 576-582. |
| [12] | 季敏, 王尚旭, 陈双全. 孔洞物理模型的地震属性特征研究. 石油地球物理勘探 , 2007, 42(4): 425–428. Ji M, Wang S X, Chen S Q. Study on feature of seismic attributes in vugular physical model. Oil Geophysical Prospecting (in Chinese) , 2007, 42(4): 425-428. |
| [13] | 赵群, 曲寿利, 薛诗贵, 等. 碳酸盐岩溶洞物理模型地震响应特征研究. 石油物探 , 2010, 49(4): 351–359. Zhao Q, Qu S L, Xue S G, et al. Study on the seismic response characteristics on the physical model of carbonate cave. Geophysical Prospecting For Petrole (in Chinese) , 2010, 49(4): 351-359. |
| [14] | 李凡异, 魏建新, 狄帮让. 碳酸盐岩溶洞横向尺度变化的地震响应正演模拟. 石油物探 , 2009, 48(6): 557–562. Li F Y, Wei J X, Di B R. Forward simulation of seismic response in carbonate caverns with varied lateral scale. Geophysical Prospecting For Petrole (in Chinese) , 2009, 48(6): 557-562. |
| [15] | 吴俊峰, 姚姚, 撒利明. 碳酸盐岩特殊孔洞型构造地震响应特征分析. 石油地球物理勘探 , 2007, 42(2): 180–185. Wu J F, Yao Y, Sa L M. Analysis on seismic response of special cavernous structure of carbonate. Oil Geophysical Prospecting (in Chinese) , 2007, 42(2): 180-185. |
| [16] | 奚先, 姚姚, 顾汉明. 随机溶洞介质模型及其波场模拟. 地球物理学进展 , 2005, 20(2): 365–369. Xi X, Yao Y, Gu H M. Random cavity medium model and the wave field simulation. Progress in Geophysics (in Chinese) , 2005, 20(2): 365-369. |
| [17] | Yao Y, Xi X. Reflected wave field in random median: a review. Journal of Geophysics and Engineering , 2004, 1(2): 147-152. DOI:10.1088/1742-2132/1/2/007 |
| [18] | 撒利明, 姚逢昌, 狄帮让, 等. 缝洞型储层地震响应特征与识别方法. 岩性油气藏 , 2011, 23(1): 23–28. Sa L M, Yao F C, Di B R, et al. Seismic response characteristics and identification method of fracture-cavity reservoir. Lithologic Reservoirs (in Chinese) , 2011, 23(1): 23-28. |
| [19] | 朱生旺, 魏修成, 曲寿利, 等. 用随机介质模型方法描述孔洞型油气储层. 地质学报 , 2008, 82(3): 370–377. Zhu S W, Wei X C, Qu S L, et al. Description of the Carbonate Karst reservoir with random media model. Acta Geologica Sinica (in Chinese) , 2008, 82(3): 370-377. |
| [20] | Collion F, Tsogka C. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media. Geophysics , 2001, 66(1): 294-307. DOI:10.1190/1.1444908 |
| [21] | 朱生旺, 曲寿利, 魏修成, 等. 变网格有限差分弹性波方程数值模拟方法. 石油地球物理勘探 , 2007, 42(6): 634–639. Zhu S W, Qu S L, Wei X C, et al. Numeric simulation by grid-various finite-difference elastic wave equation. Oil Geophysical Prospecting (in Chinese) , 2007, 42(6): 634-639. |
| [22] | 董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报 , 2000, 43(3): 411–419. Dong L G, Ma Z T, Cao J Z, et al. A staggered-grid high-order difference method of one- order elastic wave equation. Chinese Journal of Geophysics (in Chinese) , 2000, 43(3): 411-419. |
| [23] | Cunha C A. Elastic modeling in discontinuous media. Geophysics , 1993, 58(12): 1840-1851. DOI:10.1190/1.1443399 |
| [24] | Jastram C, Tessmer E. Elastic modeling on a grid with vertically varying spacing. Geophys Prosp , 1994, 42(4): 357-370. DOI:10.1111/gpr.1994.42.issue-4 |
 2012, Vol. 55
2012, Vol. 55

