地层孔隙结构特征作为重要的地质学参数,影响整个石油勘探开发过程,地质工程师需要利用其对地层的储量做出准确的预测,钻井工程师需要利用其预测井壁是否会失稳、发生井下事故,油藏工程师需要利用其了解渗流机理为建立开发方案提供依据,因此,地层孔隙结构的研究对整个勘探开发过程都具有重要意义.声波在固体中传播时能携带出大量内部孔隙结构特征信息而被广泛应用于地层孔隙结构的研究.目前主要利用声波的特征属性来反演地层孔隙结构,这对常规地层具有较好的适用性.而在碳酸盐岩储层[1]的研究过程中,由于该类储层饱含裂缝和孔洞系统且空间分布上存在非规律性,在形态、大小上呈现不规则性和多尺度性,这给声波实验研究造成了很大困难,使传统的超声波实验结果不能客观反映碳酸盐岩储层的固有特征.
目前国内外通过室内实验统计、超声波测试[2-7]等方法对含缝洞孔隙结构的岩石进行了大量研究.魏建新[8]利用环氧树脂作为基质的裂缝模型,用面积相同的硅橡胶薄片模拟裂缝,再使用实验室人工灌注控制裂缝密度,研究了裂缝密度和形态对声波的影响;Husseiny等[9]研究再度证明裂缝密度的增加将导致声波速度的减小.Xu 等[10]研究表明在孔隙度一定的情况下孔洞的存在可能导致40% 的误差在纵波速度检测上;魏建新[8]、曹均[11]、季敏[12]等以超声波为实验手段,分别用人工物理模型模拟地层中的缝、孔洞结构,研究了对应的声波速度和衰减特性,结果表明,对速度的影响小于对衰减的影响,得到了振幅衰减属性对孔洞规模变化反应最敏感的结论,因此可将声波的衰减特性作为研究岩石孔隙结构的重要切入点.李琼等[13]根据物理模型相似性原理,从缝洞系统中抽取并用45钢制作了单孔洞缝物理模型,探讨单个缝洞的大小、形状与声波属性的关系;吴俊峰[14]和季敏[12]等利用物理模型进行了孔洞的声波响应特征研究,分析孔洞分布形态和孔洞规模对声波属性的影响,得知在缝洞处出现的“珠串"现象跟缝洞大小、形态和内部充填物有关.贺振华等[15]测试了不同材料和不同裂缝模型的声波特征响应,得到了振幅衰减和偏振方向和裂缝夹角之间的关系;毕权贵等[16]采用类岩石材料模型试件模拟了不同裂隙长度、裂隙厚度、裂隙倾角、非贯通裂隙对声波特性的影响.综上所述,目前国内外学者主要利用类岩石材料制作不同缝洞孔隙结构实体物理模型,通过超声波实验总结得到声波特征参数随孔隙结构变化的定性认识.由于实验条件的限制,使复杂缝洞结构的定量设置较为困难,同时,由于模型孔隙结构的多样化和研究材料的大量耗损导致无法开展大规模复杂结构的物理模型实验,使得相应的研究结果也具有一定的局限性.
针对上述问题,笔者拟以裂缝系统为研究对象,从波动理论[17-18]出发,对超声波实验过程进行数值模拟研究,计算了缝产状、孔隙度及密度变化条件下,能够反映出岩体的各向异性特征且灵敏度高、可靠性强的声波衰减系数,并对观测结果作综合分析,进而总结声波在裂缝储层中的衰减特征.
2 超声波衰减系数测试理论声波在介质中传播时存在衰减现象,而衰减系数是用来度量声波在介质中振动或波动能量的非弹性衰减率的物理量.实验室测定岩样的声波衰减系数有三种方法:
2.1 长短岩样对比法将同一种待测岩样切割成长短不同的两块,分别测量两块样品的超声波首波峰值幅度.测量过程中,保持压力、温度及耦合条件一致.按公式(1)计算岩样的声波衰减系数:
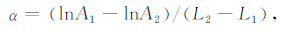
|
(1) |
式中:α 为岩样的衰减系数,dB/m;A1、A2 分别表示两块岩样的声波幅度,V;L1、L2 分别表示两块岩样的长度,m.
2.2 标准样品对比法取长度与被测岩样相同的铝块作为标准样品,分别测量并记录岩样和铝块的声波首波峰值幅度.按公式(2)计算被测岩样的声波衰减系数:
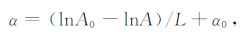
|
(2) |
式中:α0 为铝块的声波衰减系数(实际计算时可近似为0),dB/m;A0、A分别表示铝块和岩样的声波幅度,V;L表示岩样的长度,m.
2.3 信号对比法分别测量并记录岩样和探头对接时的首波峰值幅度.按公式(3)计算被测岩样的声波衰减系数:
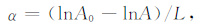
|
(3) |
式中:A0、A分别为探头对接和岩样的声波幅度,V;L表示岩样的长度,m.
本研究采用信号对比法,该方法更简洁、直观,避免了在铝块或对比岩样的声波测试过程中引入的实验误差.
3 数值模拟理论基础 3.1 波动理论用U表示某一时刻t二维空间上任一点(x,y)处的位移,二维声波方程如下:
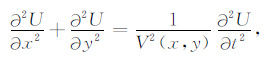
|
(4) |
这里V(x,y)表示纵波的传播速度.把函数U(x+Δx)和U(x-Δx)在U(x)处按泰勒级数展开后相加,忽略4阶及其以上的各高阶项,U对x的2阶偏微分可以近似为
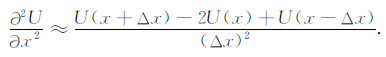
|
(5) |
同理,将展开式相减,忽略3 阶及其以上项,然后U对x的1阶偏微分可以近似为
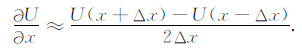
|
(6) |
通过这两个近似式可以推导出式(4)的差分表达式:
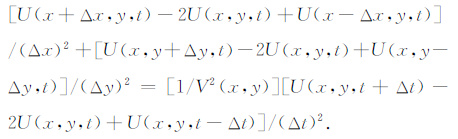
|
(7) |
在计算区域0≤x≤a,0≤y≤b内,取Δx=a/M、Δy=b/N,Δx和Δy分别表示差分网格的水平距离和垂直距离,M和N分别表示x方向和y方向的网格数的最大值.这样函数U(x,z,t)的离散化形式可表达为
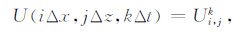
|
(8) |
其中(i=1,2,…,M;j=1,2,…,N;k=0,1,2,…,L).此外,令
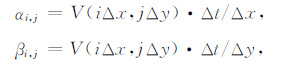
|
(9) |
这样二维声波波动方程的显式差分近似的离散化形式可表达为
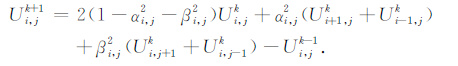
|
(10) |
当t=0时,位移速度为零.即
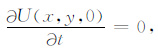
|
(11) |
离散化(11)式并代入(10)式,得到差分计算的初始公式:
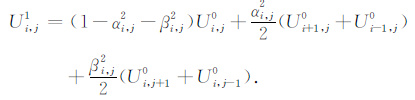
|
(12) |
在波场初始值已知的条件下,就可以通过递推公式来计算波场任何时刻的值.
3.2.2 振源条件振源的初始条件为
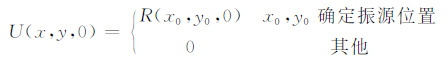
|
(13) |
假定在差分计算中,在计算区域的边界(x=0,x=a)上质点的位移为零,则边界条件可以定义为
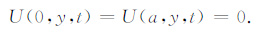
|
(14) |
在计算区域的左右边界与实际基本相符,可以按照常规反射边界处理,而上、下边界(y=0,y=b)则采用吸收边界条件[19]:
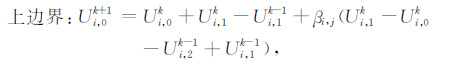
|
(15) |
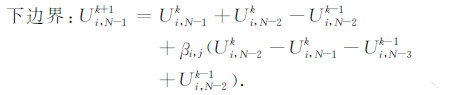
|
(16) |
当差分方程解的误差不随计算时间的推进而增加时,则该解具有稳定性.本次模拟中,对于一定的Δx,Δy,Δt来说,式(10)中的k取无限大时,要使差分方程的解保持在有意义的范围内,就需要差分方程的解趋近微分方程,即差分方程收敛于微分方程.
利用基于傅里叶展开的Von Neumann 方法,当时间步长经过k次之后,差分方程与微分方程解的误差为
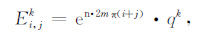
|
(17) |
式中n为虚数,m=(0,1,2,…),q表示一个时间步长上差分与微分方程的解的误差.如果|q|≤1,差分方程的解的误差将不随时间步长的增加而增加,差分方程的解将是稳定的.根据Mitchell和Griffiths[20],式(17)满足差分方程,代入式(10),得到q的解为
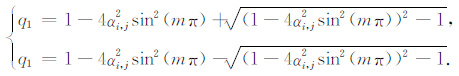
|
(18) |
如果要满足|q|≤1的要求,则得到:
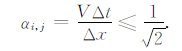
|
(19) |
当差分方程的空间和时间步长与介质速度之间满足式(19)时,差分方程的解稳定.
实验室超声波测试是采用透射法进行测量.但由于岩芯的非均质性及岩芯内裂缝分布的不确定性,给研究裂缝对声波传播特性的影响带来了较大困难.数值模拟则以被测试样的纵向剖面为模型,以探头的激发信号为振源,基于波动理论和有限差分方法用Matlab编程来实现超声波透射实验的模拟.
4 数值模拟及分析本文采用的圆柱体岩芯尺寸为66mm(长度)×25mm(直径),实体岩芯速度为6200m/s, 裂缝中空气速度为340 m/s, 提取实验室探头入射波作为初始波,保持声波传播方向不变,主频为250kHz, 将岩芯纵向剖面区域划分成330×125的网格,空间网格精度为0.2mm, 时间网格精度为20ns.通过不断调整岩芯的裂缝模型参数来实现孔隙结构的变化,对声波实验的模拟,其具体步骤如下:
首先,载入裂缝模型参数,通过数值计算画出波场快照图;
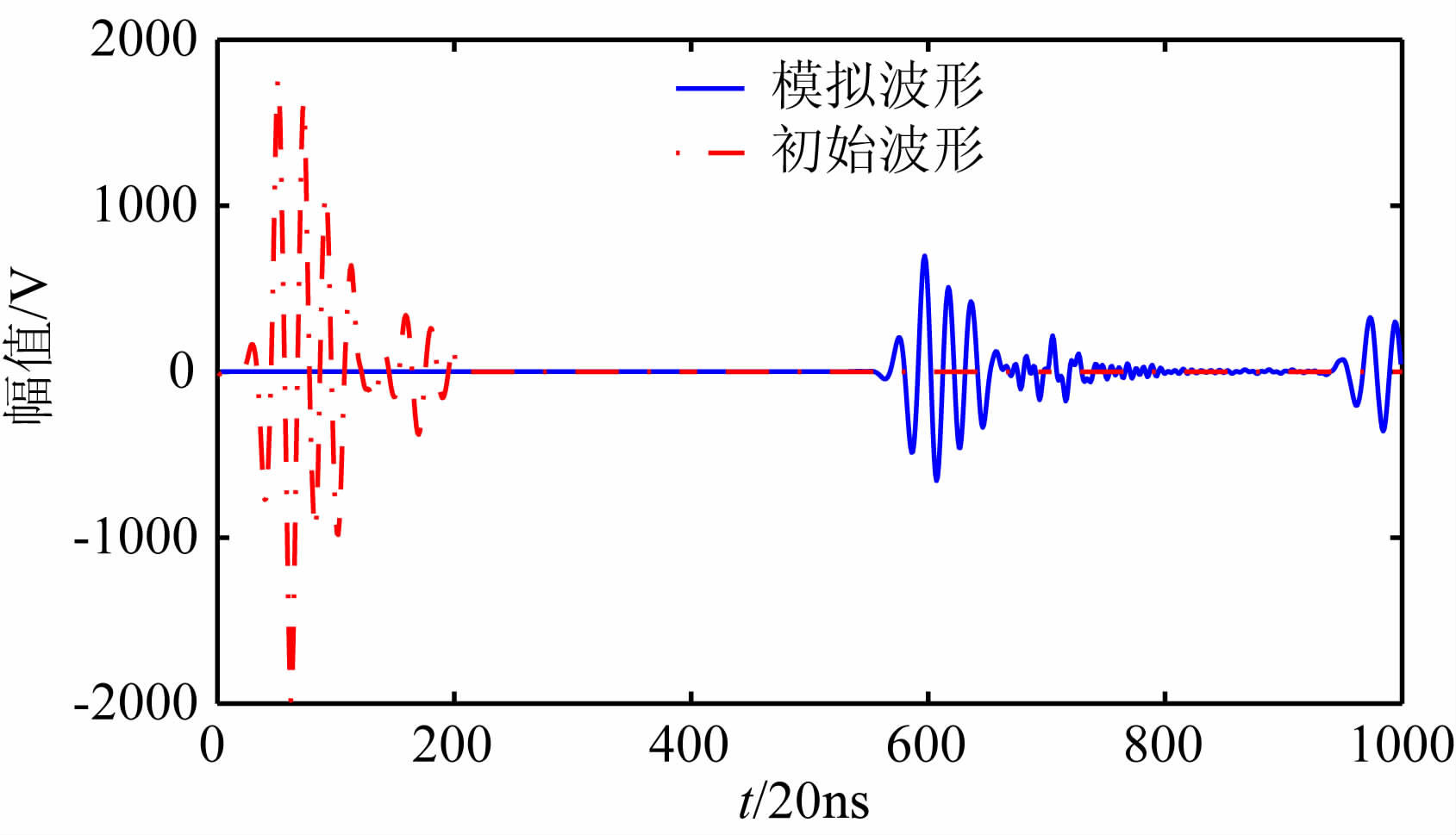
接下来,从波场模拟结果中提取出接收端波形即模拟波形(如图 1);
|
图 1 A5模拟波形与初始波形对比图 Fig. 1 The contrast diagram of simulation wave and the initial wave |
最后,处理模拟波形中的首波幅值并按照相应的公式计算出衰减系数.
4.1 裂缝孔隙度变化对声波衰减系数的影响裂缝产状一定,通过改变缝宽(张开度)、缝长、裂缝数都可以实现裂缝孔隙度的变化.
4.1.1 缝宽对声波衰减系数的影响水平缝长11mm, 缝宽分别设为0、1、5、10、15和20mm, 记为A0—A5.声波激发方向与裂缝延伸方向垂直.
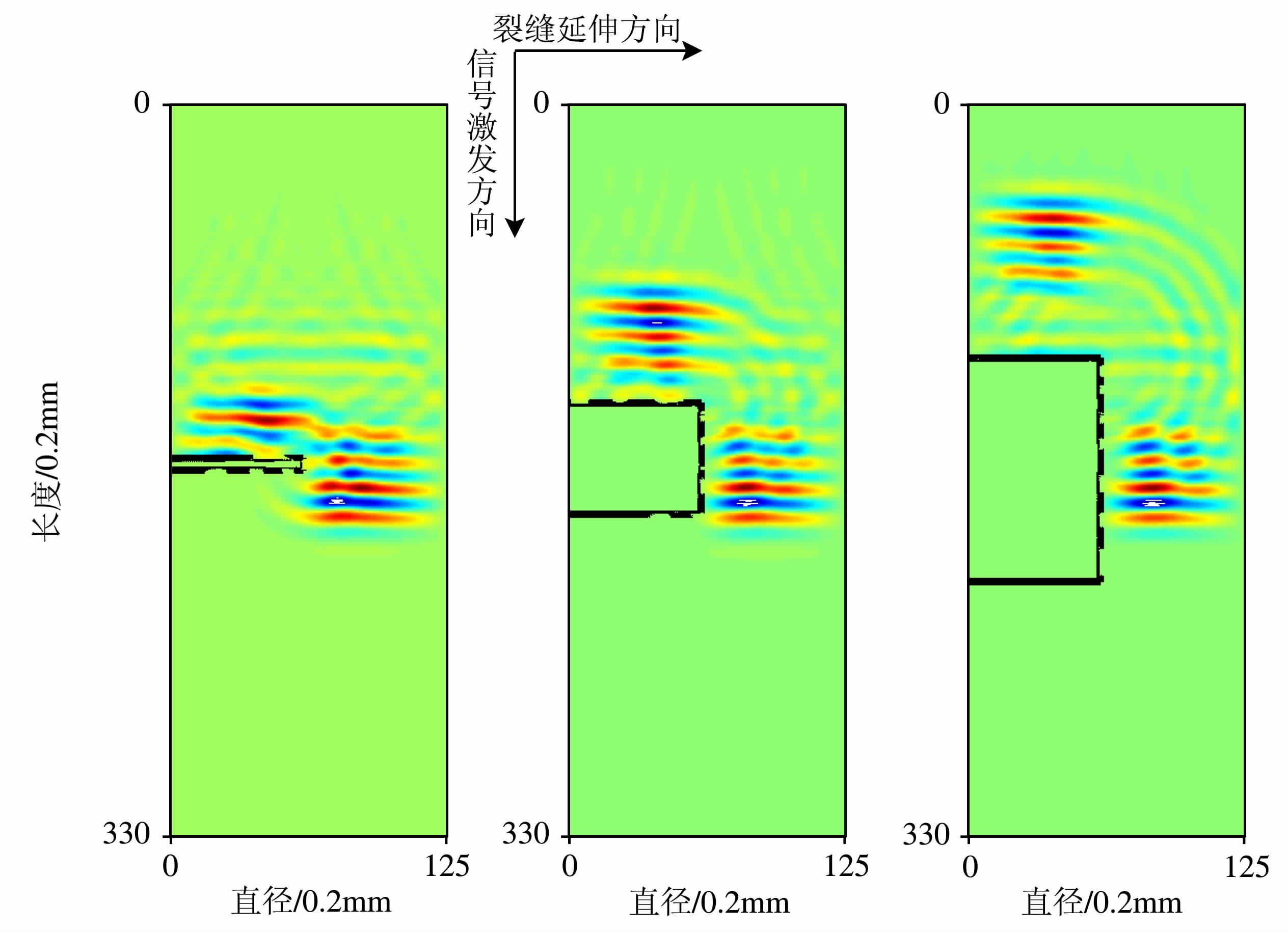
由于裂缝内空气介质和岩芯骨架的声阻抗差距大,从波场快照图 2中可以明显看出:超声波在裂缝边缘产生反射、散射,导致声波衰减.随缝宽增大,越来越多的波信号被反射回岩芯上边界,声波透射能力逐渐减弱,同时,从岩芯右壁散射到接收端的信号因裂缝右边界的反射而受到阻碍,且随缝宽变大,第二次反射的界面范围增大,信号在两界面间不断发生反射,使得声波传播的路径也变长,也导致接收端信号的能量越来越弱.
|
图 2 随缝宽增大的波场快照图(A1,A3,A5) Fig. 2 Snap shot of wavefield with increasing crack width (A1,A3,A5) |
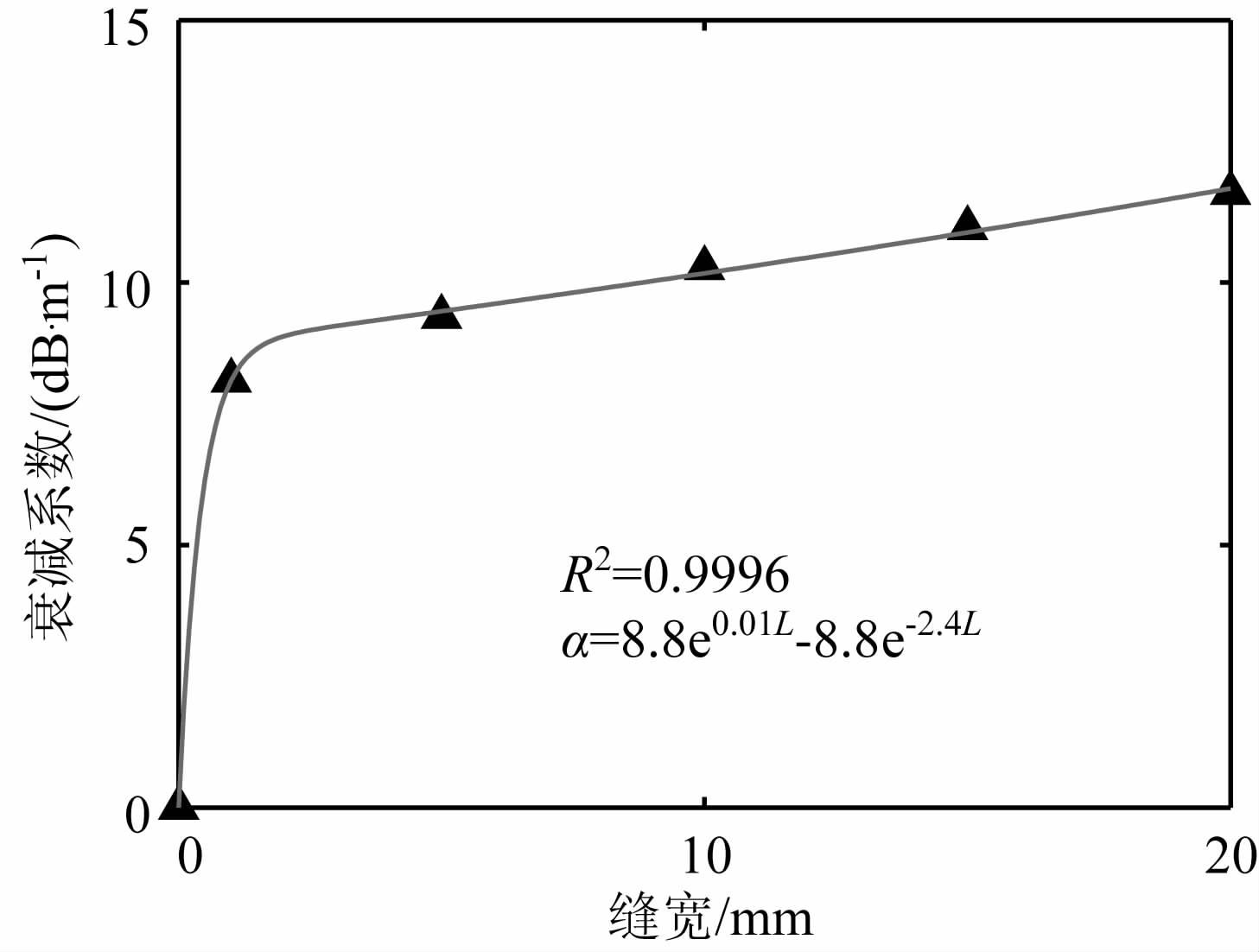
从图 3可知:当声波激发方向与裂缝延伸方向垂直时,随缝宽L增大,声波衰减系数α呈α =aebL+cedL函数规律递增,对主频为250kHz的纵波,当缝宽大于1mm, 衰减系数变化幅度逐渐减小.
|
图 3 缝宽与衰减系数关系图 Fig. 3 The relationship of crack width and attenuation coefficient |
裂缝延伸方向仍然与声波激发方向垂直,裂缝起点位置变化:
(1) 裂缝以岩芯侧面一端为起点向质心扩展.缝宽度1mm, 缝长分别设为0、1、2、4、5和10mm, 记为B0—B5.
(2) 裂缝以岩芯的质心为起点向岩芯两侧扩展.缝宽度1mm, 缝长分别设为0、1、2、4、5和10mm, 记为B10—B15.
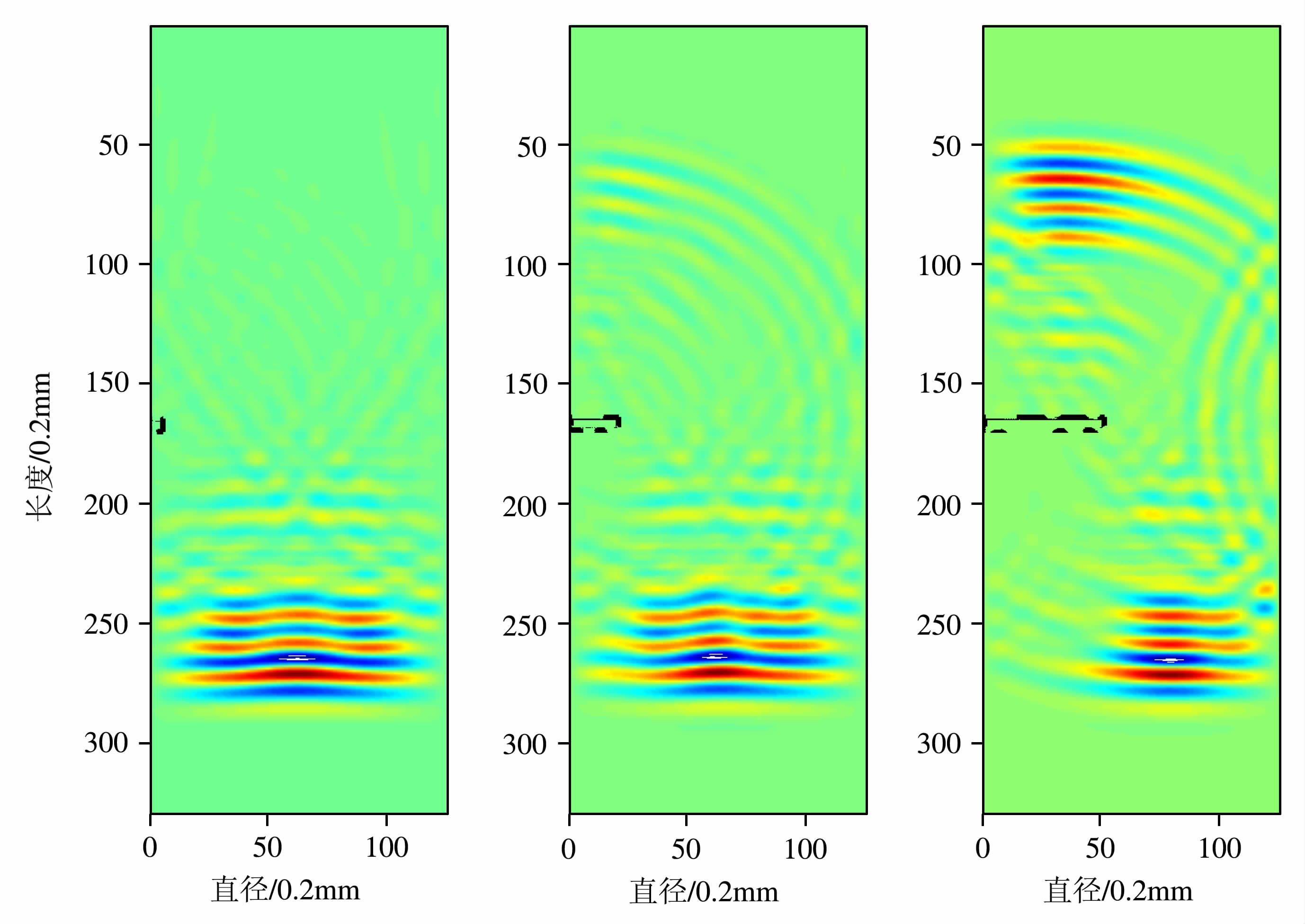
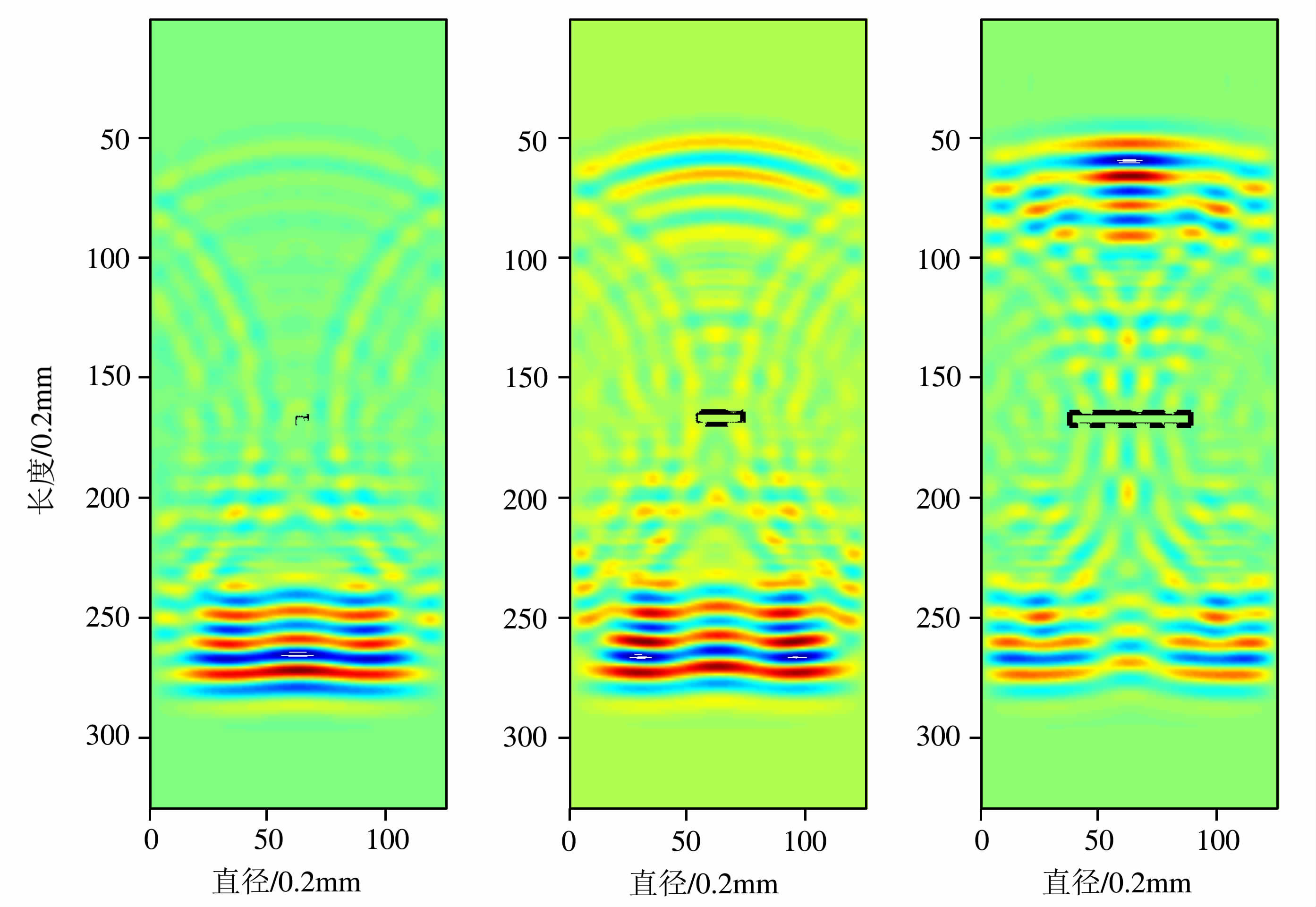
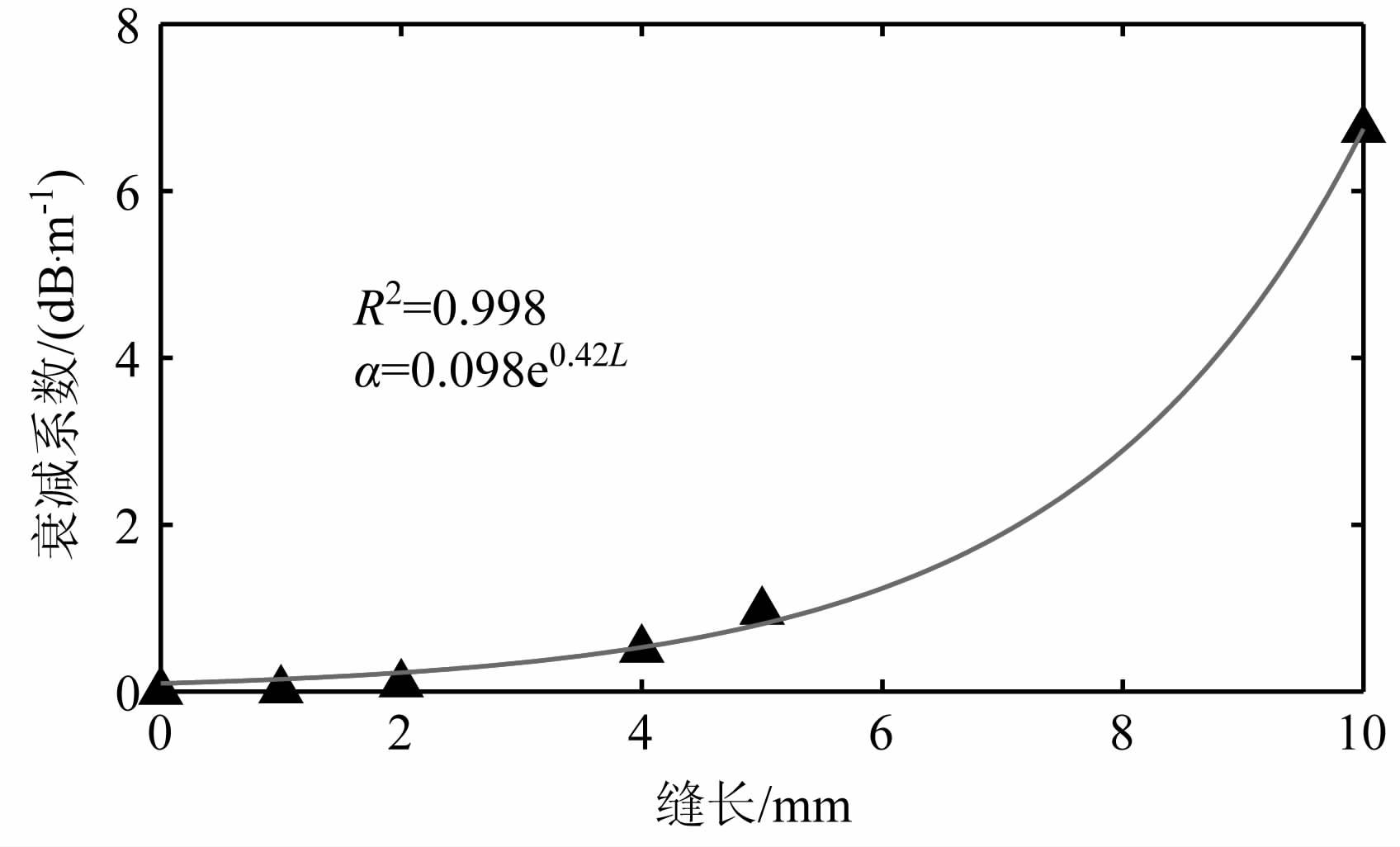
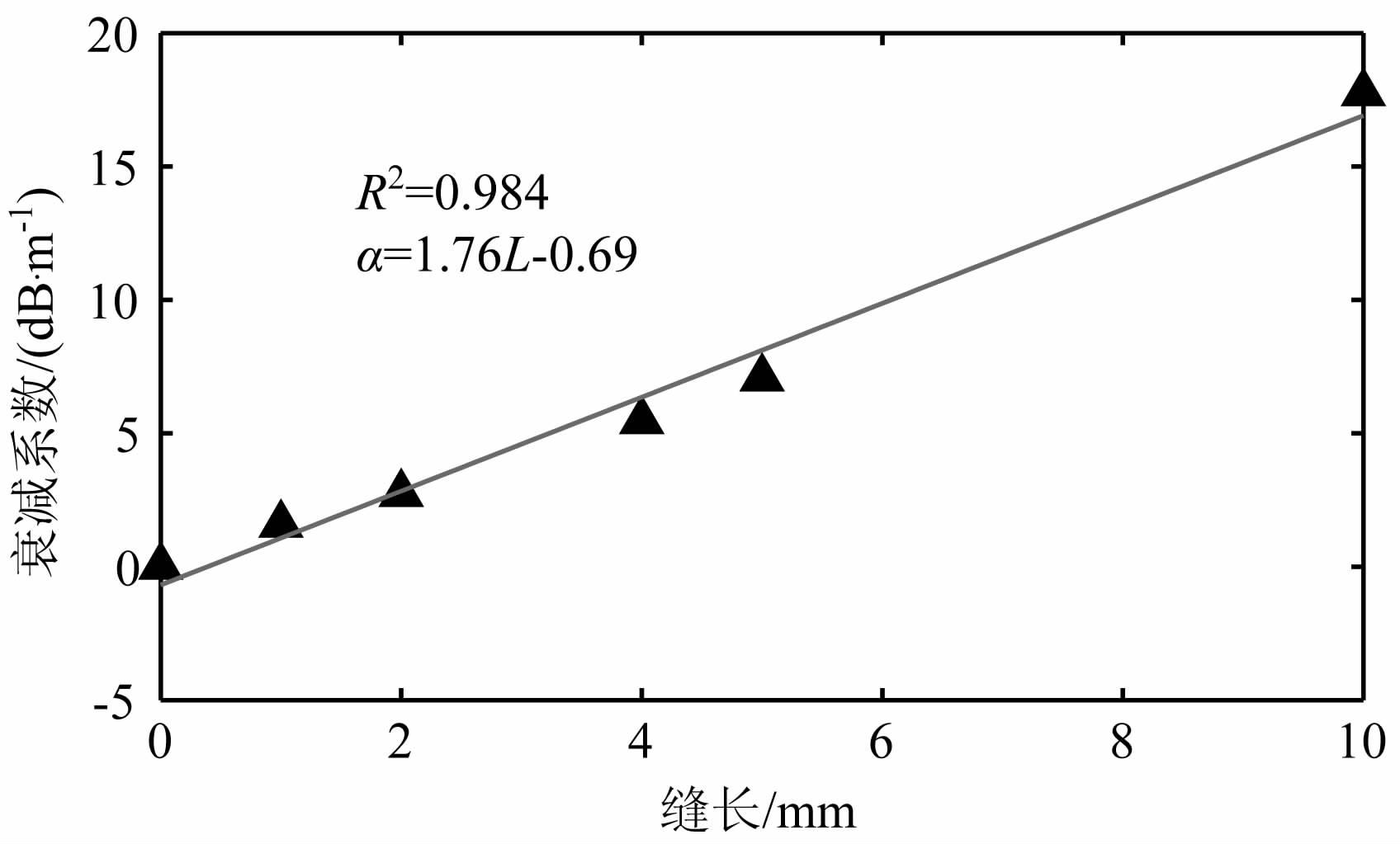
从图 6、图 7 见,在两种缝分布状态下,随缝长变大,岩芯衰减系数都呈明显的上升趋势.并且缝分布对衰减系数也有较大影响,缝在边缘时,衰减系数随缝长增加呈指数函数递增;而缝位于岩芯质心处时,衰减系数随缝长呈线性趋势增加.从波场快照(图 4、5)中可以看出:缝宽恒定时,缝长增加,阻碍传播路径的反射界面范围也越来越大,到达接收端的声波信号逐渐减少,导致了衰减系数的变大.
|
图 4 随缝长增加的波场快照图(B1,B3,B5) Fig. 4 Snap shot of wavefield with increasing crack length (B1,B3,B5) |
|
图 5 随缝长变化的波场快照图(B11,B13,B15) Fig. 5 Snap shot of wavefield with varying crack length (B11,B13,B15) |
|
图 6 缝长度与衰减系数关系图(缝在边缘) Fig. 6 The relationship of crack length and attenuation coefficient (crack tn the edge) |
|
图 7 缝长度与衰减系数关系图(缝在中间) Fig. 7 The relationship of crack length and attenuation coefficient (crack in the middle) |
缝长11mm, 缝宽1mm, 水平缝条数分别设为1、2、4、5、10、20条,记为C1—C6.
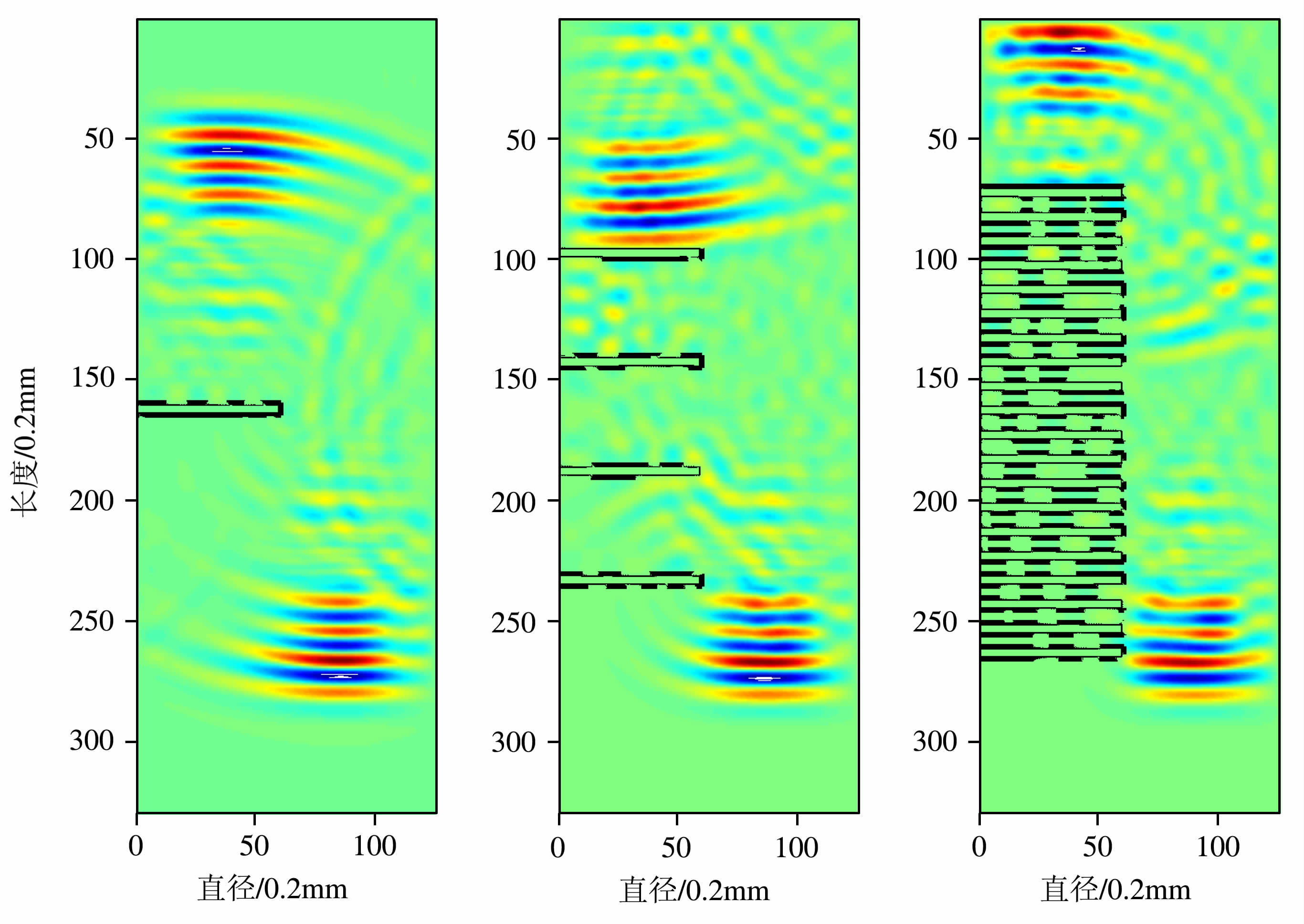
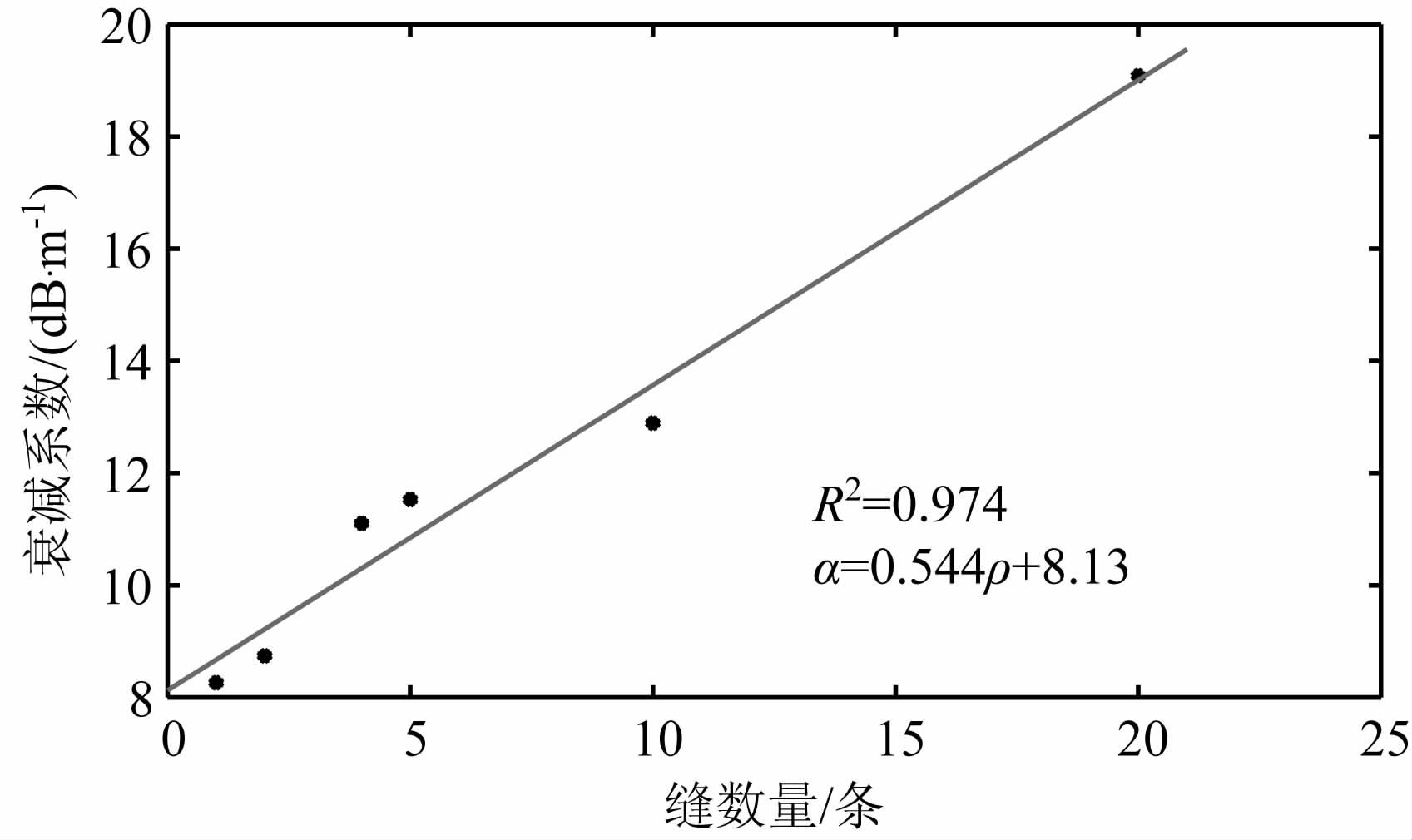
随裂缝数量增加,裂缝孔隙度变大,衰减系数线性增加(如图 9).单位长度岩芯骨架中气饱和裂缝条数增加,两相分布更不均匀,由于岩芯骨架与气相的动力模量相差很大,在骨架与气相之间产生一定的应变相位差,从而在两相界面处产生内摩擦而使机械能转化为热能,较大地消耗能量;同时,随着裂缝数量急剧增加,声波传播的路径增多(如图 8),也将导致声波衰减系数增大.
|
图 8 随缝数量增加的波场快照图(C1,C3,C6) Fig. 8 Snap shot of wavefield with crack quantity increase (C1,C3,C6) |
|
图 9 缝数量与衰减系数关系图 Fig. 9 The relationship of crack quantity and attenuation coefficient |
在孔隙度恒定的情况下,通过以下两种手段来模拟缝密度变化对衰减系数的影响:
(1) 裂缝延伸方向与声波激发方向垂直时,缝长均为12mm, 在孔隙度恒定的前提下,开度分别为20,10,5,4,2,1mm(记为D1—D6).
(2)裂缝延伸方向与声波激发方向一致时,缝长同为20mm, 在孔隙度不变的条件下,缝宽分别为12,6,4,3,2,1mm(记为D11—D16).
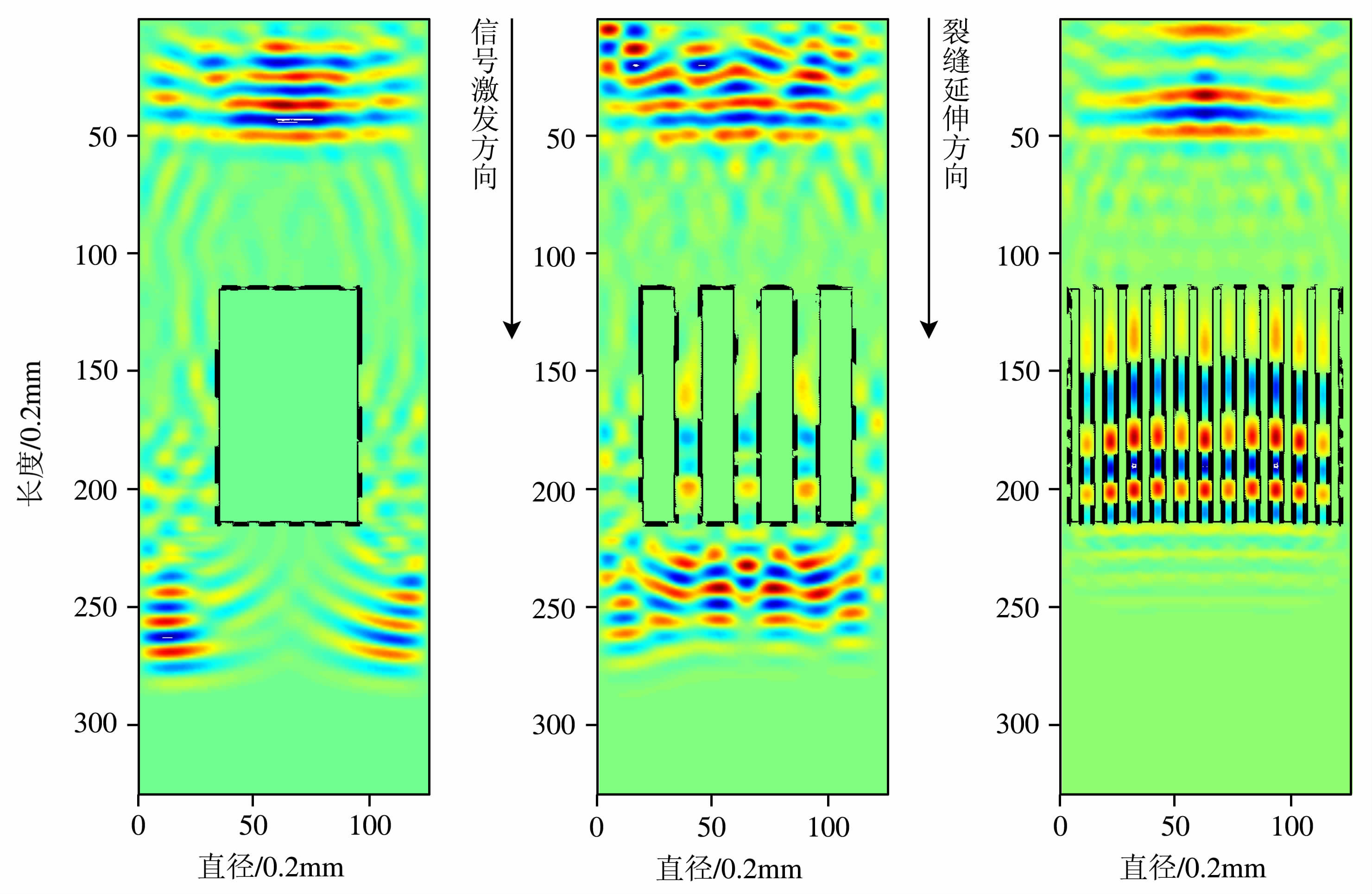
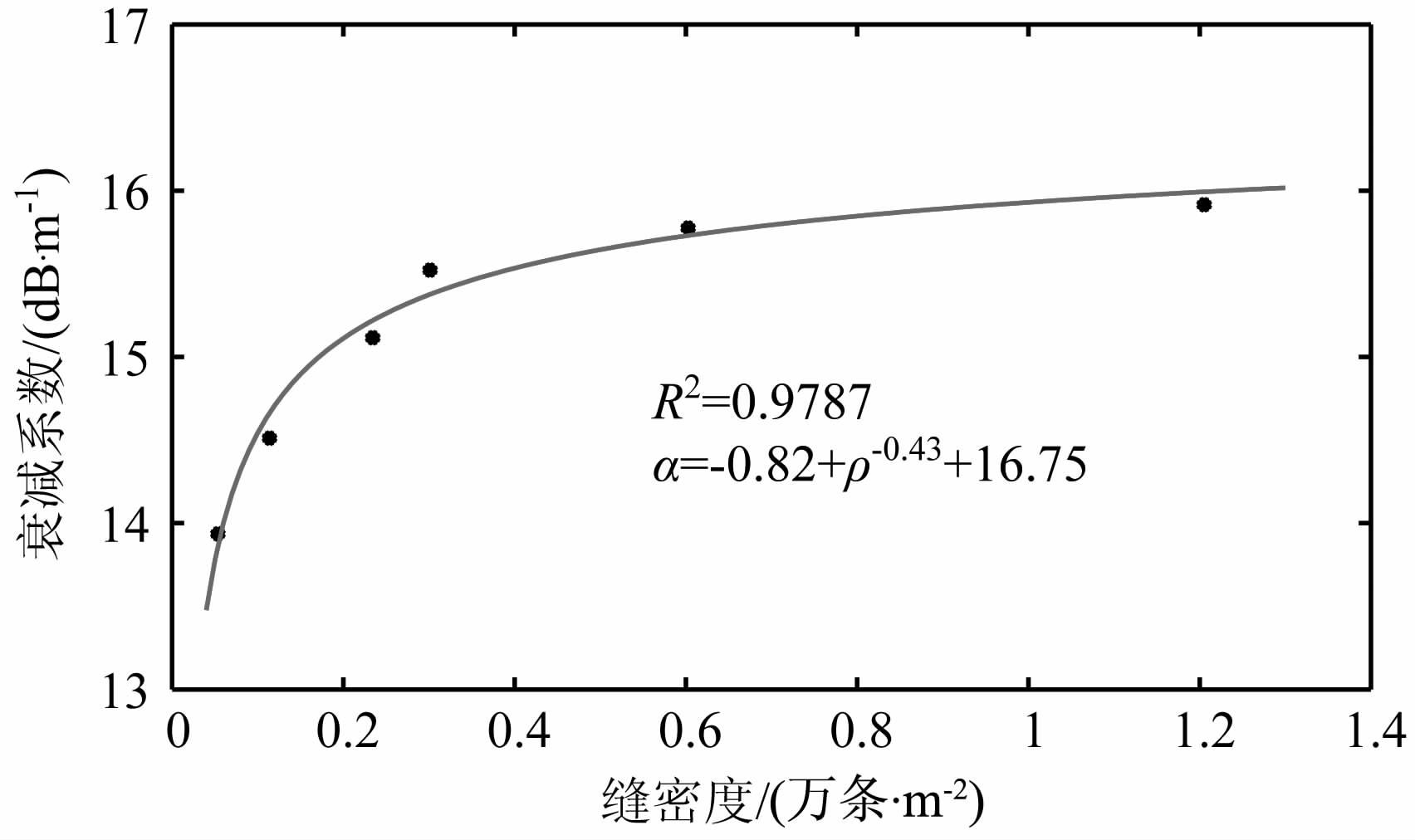
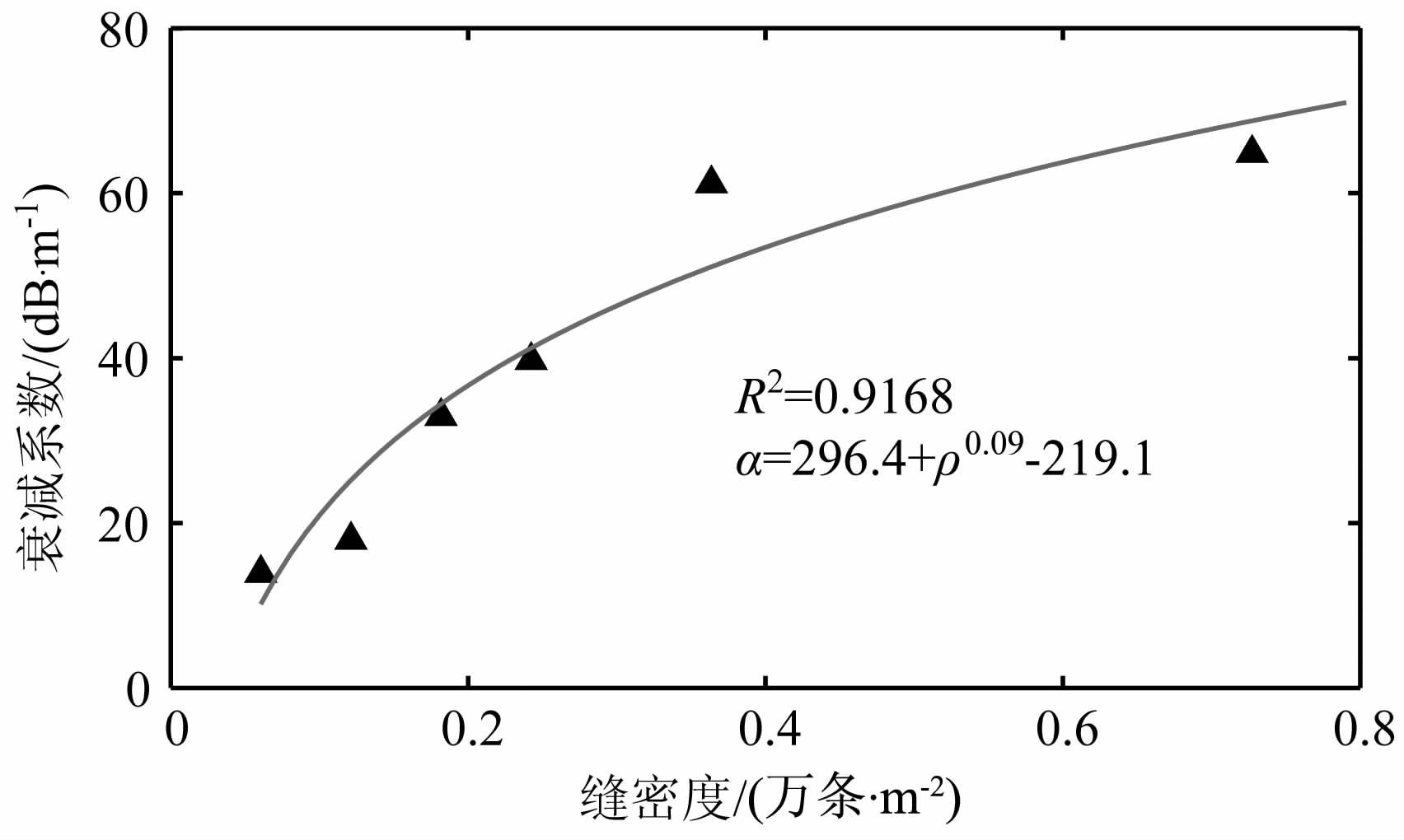
从图 12、图 13 见,在孔隙度恒定的条件下,当组成单个孔隙空间的裂缝尺寸变小时,缝数目增大,缝密度也变大,两种缝产状的岩芯衰减系数都呈明显的幂函数递增.从波场快照(图 10、11)中可以看出:当缝宽逐渐变小时,骨架与空气相之间的界面个数也相应地增加,产生更多的反射、散射,使声波穿透的能量减小,岩石声波的衰减系数增大;当开度逐渐变小时,传播路径上裂缝个数急剧增加,声波传播的路径相应地增多,而该声波传播主能量路径的宽度却越来越小,受到不同裂缝边缘之间的反射、折射干扰就会越来越明显,消耗了部分能量,导致了该衰减系数显著增大.

|
图 10 随裂缝密度增加的波场快照图(D1,D3,D5) Fig. 10 Snap shot of wavefield with increasing crack density (D1,D3,D5) |
|
图 11 随裂缝密度增加的波场快照图(D11,D13,D16) Fig. 11 Snap shot of wavefield with increasing crack density (D11,D13,D16) |
|
图 12 模型D1—D6缝密度与衰减系数关系图 Fig. 12 The relationship of crack density and attenuation |
|
图 13 模型D11—D16缝密度与衰减系数关系图 Fig. 13 The relationship of crack density and attenuation coefficient (D11-D16) |
裂缝实体模型见图 14.缝长11mm, 缝宽8mm, 裂缝与轴线之间的夹角分别为10°、20°、30°、45°、60°、90°.

|

|
图 14 模型图 Fig. 14 The model |
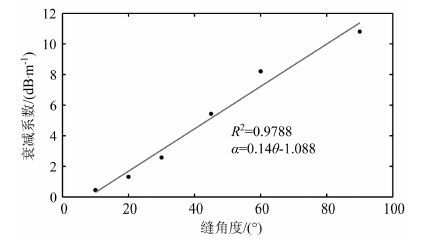
从图 15可以看出,当声波传播方向与裂缝延伸方向的夹角在10°~90°范围内时,随着裂缝角度的逐渐增大,衰减系数线性递增.由于缝角度的增加,其阻碍声波传播的裂缝横截面积增大,被反射回岩芯顶端的信号越来越强,因此,使超声波散射的能量增多,穿透的能量减小,导致了岩芯的衰减系数增大.
|
图 15 缝产状与衰减系数关系图 Fig. 15 The relationship of crack attitude and attenuation coefficient |
(1) 随孔隙度增加,衰减系数总体呈上升趋势,但孔隙度增长方式不同,衰减系数的递增函数规律亦不同.缝宽增大,声波衰减系数呈α =aebL+cedL函数规律递增;衰减系数随边缘缝长增加呈指数函数递增;衰减系数随中间缝长呈线性趋势增加;裂缝数量增加,衰减系数线性增大.
(2) 在孔隙度不变的前提下,随裂缝密度增大,衰减系数以幂函数形式递增.
(3) 当孔隙度恒定时,裂缝产状对岩芯的声波衰减系数影响很大,随着声波激发方向与裂缝延伸方向夹角角度的增大,衰减系数呈线性趋势增加.
(4) 该方法在含裂缝岩芯的超声波透射实验模拟中取得较好效果,能避免在实验操作过程中出现的人为误差,节约取芯成本,提高实验效率,为缝洞结构的岩芯声波实验研究提供了新的思路.
| [1] | Kenter J A M, Anselmetti F S, Kramer P H, et al. Acoustic properties of 'young’ carbonate rocks, ODP leg 166 and boreholes Clino and Unda, western great Bahama bank. Sedimentary Research , 2002, 72(1): 129-137. DOI:10.1306/041101720129 |
| [2] | Prasad M. Mapping impedance microstructures in rocks with acoustic microscopy. The Leading Edge , 2001, 20(2): 172-179. DOI:10.1190/1.1438902 |
| [3] | 钟锴, 徐鸣洁, 王宏, 等. 岩样中孔隙、裂缝声波特征的实验研究. 石油实验地质 , 2002, 24(2): 164–167. Zhong K, Xu M J, Wang H, et al. An experiment study on the acoustic characteristics of pores and fractures in rock samples. Experimental Petroleum Geology (in Chinese) , 2002, 24(2): 164-167. |
| [4] | Lebedev M, Julianna T S, Clennel B. Direct laboratory observation of patchy saturation and its effects on ultrasonic velocities. The Leading Edge , 2009, 28(1): 24-27. DOI:10.1190/1.3064142 |
| [5] | 刘斌, 葛宁洁, KernH, 等. 不同温压条件下蛇纹岩和角闪岩中波速与衰减的各向异性. 地球物理学报 , 1998, 41(3): 371–381. Liu B, Ge N J, Kern H, et al. Velocities and attenuation of P- and S-waves and their anisotropies in serpentinite and amphibolite under different P-T conditions. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1998, 41(3): 371-381. |
| [6] | 刘斌, KernH, PoppT. 不同围压下孔隙度不同的干燥及水饱和岩样中的纵横波速度及衰减. 地球物理学报 , 1998, 41(4): 537–546. Liu B, Kern H, Popp T. Velocities and attenuation of P- and S-waves in dry and wet rocks with different porosities under different confining pressures. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1998, 41(4): 537-546. |
| [7] | Dvorkin J P, Mavko G. Modeling attenuation in reservoir and nonreservoir rock. The Leading Edge , 2006, 25: 194-197. DOI:10.1190/1.2172312 |
| [8] | 魏建新. 不同裂缝密度的物理模型研究. 石油物探 , 2002, 41(4): 433–438. Wei J X. A physical model study of different crack densities. Geophysical Prospecting for Petroleum (in Chinese) , 2002, 41(4): 433-438. |
| [9] | Husseiny A H E, et al. Correlation of outcrop, seismic, core plus and thin sections in cretaceous carbonate rocks from Kaisa group in the U. S. E. 2010, SPE137875. |
| [10] | Xu X Y, Payne M A. Modeling elastic properties in carbonate rocks. The Leading Edge , 2009, 28(1): 66-74. DOI:10.1190/1.3064148 |
| [11] | 曹均, 贺振华, 黄德济, 等. 裂缝储层地震波特征响应的物理模型实验研究. 勘探地球物理进展 , 2003, 26(2): 88–93. Cao J, He Z H, Huang D J, et al. Seismic responses to fractured reservoirs by physical modeling. Progress in Exploration Geophysics (in Chinese) , 2003, 26(2): 88-93. |
| [12] | 季敏, 王尚旭, 陈双全. 孔洞物理模型实验及其敏感属性分析. 天然气工业 , 2007, 27(Suppl.A): 312–313. Ji M, Wang S X, Chen S Q. Cavity in the physical model experiment and sensitive attribute analysis. Natural Gas Industry (in Chinese) , 2007, 27(Suppl.A): 312-313. |
| [13] | 李琼, 贺振华, 黄德济, 等. 单孔洞缝模型超声波实验测试与分析. 石油物探 , 2007, 46(1): 101–104. Li Q, He Z H, Huang J D, et al. Ultrasonic test and analysis of single fracture-cave physical model. Geophysical Prospecting for Petroleum (in Chinese) , 2007, 46(1): 101-104. |
| [14] | 吴俊峰, 姚姚, 撒利明. 碳酸盐岩特殊孔洞型构造地震响应特征分析. 石油地球物理勘探 , 2007, 42(2): 181–185. Wu J F, Yao Y, Sa L M. Analysis on seismic response of special cavernous structure of carbonate. Oil Geophysical Prospecting (in Chinese) , 2007, 42(2): 181-185. |
| [15] | 贺振华, 李亚林, 张帆, 等. 定向裂缝对地震波速度和振幅影响的比较——实验结果分析. 物探化探计算技术 , 2001, 23(1): 2–5. He Z H, Li Y L, Zhang F, et al. Different effects of vertically oriented fracture system on seismic velocities and wave amplitude-analysis of laboratory experimental results. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 2001, 23(1): 2-5. |
| [16] | 毕贵权, 李宁, 李国玉. 非贯通裂隙介质中波传播特性试验研究. 岩石力学与工程学报 , 2009, 28(Suppl. 1): 3117–3122. Bi G Q, Li N, Li G Y. Experimental study on characteristics of wave propagation in media containing intermittent cracks. Chinese Journal of Rock Mechanics and Engineering (in Chinese) , 2009, 28(Suppl. 1): 3117-3122. |
| [17] | 郑仙种, 崔力科. 波动理论在地震勘探中的应用. 北京: 石油工业出版社, 1987 : 150 -226. Zheng X Z, Cui L K. Wave Theory in Seismic Exploration Applications (in Chinese). Beijing: Petroleum Industry Press, 1987 : 150 -226. |
| [18] | 杜世通. 地震波动力学. 北京: 石油大学出版社, 1996 : 37 -39. Du S T. Seismic Wave Dynamics (in Chinese). Beijing: Petroleum University Press, 1996 : 37 -39. |
| [19] | Reynold A C. Boundary conditions for the numerical solution of wave propagation problems. Geophysics , 1978, 43(6): 1099-1110. DOI:10.1190/1.1440881 |
| [20] | Mitchell A R, Griffiths D F. The Finite Difference Method in Partial Differential Equations. New York: John Wiley and Sons Ltd, 1980 . |
 2012, Vol. 55
2012, Vol. 55

