2. 中国石油大学(北京)理学院, 北京 102249)
2. College of Science, China University of Petroleum (Beijing), Beijing102249, China
地震波在传播过程中,由于频散和衰减,表现为高度的非平稳性[1],一般来说其频率随时间的变化而变化.时频分析技术,是将一个一维的时间信号以二维的时间-频率密度函数的形式表示.旨在揭示信号的频率成份及其随时间的变化规律[2-3].时频分析技术主要有窗口傅里叶变换[4]和小波变换[5-7].这些时频分解方法已被广泛应用于储层预测和流体识别等领域[8].然而,无论是窗口傅里叶变换还是小波变换都受不确定性原理的限制,时域分辨率和频域分辨率相互制约,无法同时取得较高的时频分析精度.
针对以上情况,人们提出了许多新的时频分析方法.Wigner-Ville变换[9]具有良好的时频聚集性.但该方法受交叉项的影响,很难取得较高的精度;Stockwell提出的S变换[10]结合了短时傅里叶变换和小波变换的优点,具有较高的时频分析精度;Liu等[11]将传统的傅里叶变换系数改造为时间的函数,提出了局部谱方法.Mallat和Zhang提出的匹配追踪算法[12-14]是一种自适应性的时频分解技术.该算法的原理如下:首先建立冗余的子波库(原子核),然后将信号自适应性地分解为一些原子的和,使得残余能量快速衰减,得到最佳匹配.信号的时频谱表示为匹配它的那些原子的频谱之和.该算法能够根据信号的特点自适应性的选择匹配原子,具有自适应性,能够取得较高的时频分析精度.但是该算法最大的缺点是计算量大,推广应用有一定的难度.Castagana应用[15]改进的匹配追踪算法得到了信号的瞬时频谱特征.Wang利用[16-17]实Morlet小波作为匹配的原子核,对信号进行了频谱分析,通过与STFT 和小波变换的特点相比较取得了好的结果.在文中作者利用四个参数来控制Morlet 子波.Morlet子波的表达式为

|
(1) |
这里μ 为位置参数,ωm 为频率,φ 为相位,σ 为尺度.当以上四个参数取不同的值时可以得到由Morlet小波生成的原子核,通过这些原子核去匹配地震记录.即:
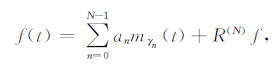
|
(2) |
这里mγn(t)表示为γn= { μn,ωn,σn,φn } 的Morlet子波;f(t)为单道地震记录;R(N)f为残差.以上四个参数通过以下等式来确定:

|
(3) |
上面提到的算法,都是建立在实信号与实小波的基础上.
本文通过复数道地震记录,利用最小二乘的原理来确定匹配原子的参数.从不同的角度阐述了匹配追踪的实现过程,通过与上文提到的方法相比较,具有收敛速度快的优势.下面来阐述本文的关于匹配追踪的实现过程.
2 算法原理下面我们分几部分阐述算法的实现过程.
2.1 相位对子波波形的影响在频率域,子波完全由信号的振幅谱与相位谱唯一确定.振幅谱表征了信号的能量在不同频率的分布情况;相位谱表征了不同频率的相位延迟.相同的振幅谱,不同的相位谱可以表示不同的子波.相位的线性变化导致子波的时移,而常相位变化改变子波的形状[18].常相位旋转可以在频率域实现,也可以在时间域实现.Arons和Yennie指出[19]在时间域常相位旋转通过以下公式实现:

|
(4) |
其中,H[x(t)]表示信号的希尔伯特变换的虚部;x(t)为地震信号;xrot(t)为相位改变后的信号.图 1表示雷克子波经不同相位旋转后的形状,从左到右相位由0°增加到360°.

|
图 1 相位对于子波形状的影响从左到右为0相位到360°相位的雷克子波 Fig. 1 The influence of phase on the shape of wavelet, from left to right is 0 degree to 360 degree |
针对于反射波地震勘探,Morlet使用复Gabor子波[20, 21]作为基本波形来分析地震记录.Morlet子波适合对地震记录作能量和频谱的定量分析.特别是该子波比较适合声波在孔隙介质中的衰减和分辨率问题的研究.复Morlet子波的表示形式为

|
(5) |
其中γj= { kj,fj,μj } 为一指标集.这里μj为子波中心;fj为峰值频率;kj尺度参数.关于相位与振幅对子波的影响,可以通过因子Aj= |Aj|exp(iφj)来实现,该因子包含了振幅与相位信息|Aj|和φj.这样Ajmγj(t)中包含有参数|Aj|,kj,μj,fj,φj,这些参数取不同值时,就得到不同的子波(原子核).以上参数在一定的范围内取值时可以建立起冗余的子波库.
利用公式(6)
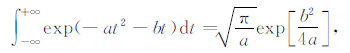
|
(6) |
可以得到中心在原点,零相位复Morlet子波傅里叶变换的解析表达式为
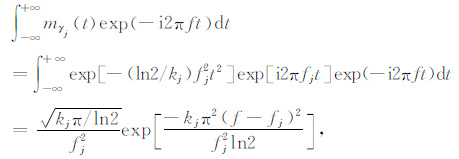
|
(7) |
这里fj≥0.可以证明Morlet子波的带宽与中心频率的比值为一常数.
2.3 基于复数道地震记录的匹配追踪原理及实现过程对于任意一道地震记录s(t),匹配追踪算法是一个迭代过程,它的目标是:通过自适应性的寻找原子核gj,使得

|
(8) |
成立.
本文通过复数道地震记录来实现匹配追踪,在算法上是对匹配追踪的补充,同时运算速度相对于前者来说有一定的优势.具体的实现过程如下:
第一步,对于给定的地震记录s(t),求取复数道地震记录S(t)=s(t)+iH(s(t)).这里H(s(t))为s(t)的希尔伯特变换.
第二步,计算S(t)的包络,首先寻找包络的最大值点的位置μj及其最大值点对应的瞬时频率fj,峰值频率包含了相对较多的信息.这一步实际上是寻找参数μj,fj的过程.然后初步给定kj=0.5,确定了μj,fj,kj就确定了mγj(t).mγj(t)的表达式见(5).
第三步,设S(t)=Ajmγj(t)+R(S).这里Aj为一个复数,Aj= |Aj|exp(iφj).Aj实际上将改变子波的振幅与相位.算法的目标是在原子库中寻找最佳的原子,使得‖R(S)‖2 取最小值.因为R(S)=S(t)-Ajmγj(t),所以这就成为一个最小二乘问题.该问题的解为

|
(9) |
这里要说明的是:Aj为一个复数,它包含了振幅和相位信息.因为使用的是复Morlet子波,子波的虚部为实部的90°相移.所以公式:

|
(10) |
以上是对子波在时域进行相移的过程,|Aj|刻画表示幅度信息,所以公式(9)实际上是寻找参数|Aj|与φj的过程.
第四步,由第三步得到的参数|Aj|,μj,fj,φj优化kj的取值,使得下式成立:

|
(11) |
这样就确定了信号Ajmγj(t).对于实的地震记录s(t),匹配原子为real[Ajmγj(t)].根据匹配信号与公式(7),计算匹配原子时频分布:

|
(12) |
第五步,令s(t)=real[R(S)],这就是从原始信号中提取出第一个匹配原子后剩余的残差.由残差判断误差大小,如果不满足精度要求,重新回到第一步开始迭代过程,直到误差小于某一阈值或者迭代次数达到一定的要求.
2.4 算法流程图(见图 2)

|
图 2 基于复数道地震记录的匹配追踪算法流程图 Fig. 2 The flow chart of match pursuit algorithm based on complex seismic traces |
如图 3所示,从图中可以看出,该算法能够较为精确的表示原始信号.

|
图 3 基于复数道地震记录的匹配追踪算法应用于一道人工合成记录 (a)蓝线为人工合成记录,(b)红线为匹配信号,(c)红线为两者的误差. Fig. 3 In the above map, the blue signal is a synthetic seismic trace, the middle red signal is the matching signal obtained from the algorithm presented above, the blow map, the red signal is the error of the two signals |
从图 4中可以看出,匹配追踪算法具有较高的精度与稳定性.

|
图 4 地震剖面图 (a)原始的二维地震剖面;(b)基于复数道地震记录的得到的匹配地震剖面;(c)原始地震剖面与匹配地震剖面的残差 Fig. 4 Seismic profile (a) The origin seismogram of an area. (b) The seismogram obtained from the algorithm presented above.(c) The seismogram obtained from the residual of the two seismograms. |
图 5为图 3中的人工合成记录的时频分布图的比较.我们选择了一个线性时频分析STFT 与一个二次时频分析Wigner-Ville变换[22]与MP 方法进行比较.图 5a表示该记录的生成过程.前四道叠加生成第五道.第一个小波形是来自单层的40 Hz雷克子波的反射波形.比较时频分布图我们可以看出,STFT 对于第一个波形的刻画中,时间分辨率降低了.这是因为STFT 对于时窗的要求十分重要,如果时间过长,时间分辨率就会降低,如果频率过长,频域分辨率就会降低.Wigner-Ville变换中交叉项的存在掩盖了小波形的信息.相对其它算法,MP 方法能够精确的刻画信号的频谱.合成记录中的第二个波形是一个40Hz的雷克子波与一个10Hz雷克子波的叠加.图中可以看出,MP 算法与STFT 相对于Wigner-Ville变换,无论在时域还是在频域都比较精确.这两种方法能够识别出波形的低,高频信息.MP算法相比STFT 有较高的精度.第三个小波形是两个相连的薄层的反射,从图中可以看出,MP方法在低、高频都能够识别薄层的位置,而其它方法没有达到这个效果.第四个小波形是两个相连的薄层的反射,其中上、下层都为一个30Hz和20Hz子波的叠加.比较时频分析方法,可看出在低频和高频,只有MP算法可以同时识别出薄层.最后一个小波形是三个相连的薄层的叠加,三个子波为30 Hz的雷克子波,其中第二道的反射系数为-1.从图中可以看出,STFT 与Wigner-Ville变换没有识别出薄层.MP算法虽然在低频没有识别出薄层,但在高频该算法能够清楚的识别出三个薄层的位置.

|
图 5 人工合成记录的时频分布图的比较 (a)人工合成记录,其中第五道为前四道的叠加;(b)STFT 时频图,时窗长度为50ms;(c)Wigner-Ville变换时频图;(d)MP方法时频图. Fig. 5 Comparisons of different time-frequency methods of a synthetic signal (a) The synthetic seismic trace; (b) The spectrum of STFT; (c) The spectrum of Wigner-Viller distribution; (d) The spectrum of MP. |
综合以上讨论可以看出,无论是孤立的单层,还是相连的薄层,无论在低频还是在高频,MP 方法相对于其它方法,都取得了较高的精度.究其原因主要是:MP方法能够自适应性的选择原子核,相对于线性时频分析STFT 与二次时频分析Wigner-Ville来说,具有较高的时间和频率分辨率,能够较为精确地表示信号的瞬时频谱特征.
3 实际资料应用谱分解理论已经被应用于地震勘探和解释等诸多领域.例如,Partyka等利用谱分解理论分析地层信息;Castagna等[23]利用谱分解理论寻找与含气储层相伴随的低频阴影现象.谱分解理论也被广泛地用于地层厚度分析,层位追踪和直接的储层预测等领域[24-25].由于地震波在传播过程中的衰减和大地吸收等诸多因素的影响,表现出高度的非平稳性.含气储层在低频剖面上显示为强的亮点,随着频率的增加会逐渐消失.利用这些特点可以用来预测含气储层.
应用实例来自于某地一口含气井.图 6a为该地的实际地震记录剖面,黄色圈定的区域为含气储集层.储集层位于3.9~4.1s 之间.图 6b 为采用STFT 得到的40Hz切片,储层得到了清楚的成像.图 7为采用基于复数道地震记录得到的不同频率切片.图 7a为30Hz切片,储层的成像不是很清楚;图 7b为40Hz切片,储层成像相对清晰;图 7c为45Hz切片,储层得到清晰成像.随着频率的增加,储层成像消失,图 7d为基于MP 方法得到的60 Hz切片,储层不能够成像,但是储层周边的区域并没有像储层那样很快消失.

|
图 6 某地的地震剖面(a)及谱分解方法为STFT 的40 Hz切片(b)圈定的区域为含气储层 Fig. 6 (a) The seismogram of somewhere, the selected area is a gas reservoir; (b) The 40 Hz slice, the method is STFT |

|
图 7 谱分解方法为MP的不同切片 (a)30Hz切片;(b)40Hz切片;(c)45Hz切片;(d)60Hz切片. Fig. 7 Iso-frequency slices of MP method (a)The 30 Hz slice;(b)The 40 Hz slice;(c)The 45 Hz slice;(d)The 60 Hz slice |
本文系统阐述了基于复数道地震记录匹配追踪算法的原理及其实现过程.通过图 4可以看出:该算法具有很好的稳定性,因为在实际地震剖面中每一道记录具有不同的波形,且实际地震剖面往往有噪声的干扰,但总体误差较小.另外,应用实例表明:该方法能够对储层位置和边界清晰成像,具有较高的时频分析精度,对于指导勘探开发与解释具有一定的意义.
现阶段,匹配追踪算法基本上都是基于雷克子波或Morlet子波生成原子库,基于多子波的匹配追踪算法从理论上将更具有应用价值,因为多子波形成的子波库具有更高的冗余,所以基于多子波的匹配追踪算法是今后的一个研究方向.
| [1] | Müller T M, Gruevich B, Levedev M. Seismic wave attenuation and dispersion resulting from wave-induced flow in porous rocks-A review. Geophysics , 2010, 75(5): 147-164. |
| [2] | Cohen L. Time-frequency distributions-A review. Proc. IEEE , 1989, 77(7): 941-981. DOI:10.1109/5.30749 |
| [3] | 武国宁, 曹思远, 刘建军. 谱图重排的谱分解理论及其在储层探测中的应用. 地球物理学进展 , 2012, 27(2): 596–602. Wu G N, Cao S Y, Liu J J. Reassigned time-frequency decomposition and its application of hydrocarbon exploration. Progress in Geophysics (in Chinese) , 2012, 27(2): 596-602. |
| [4] | 李振春, 刁瑞, 韩文功, 等. 线性时频分析方法综述. 勘探地球物理进展 , 2010, 33(4): 239–246. Li Z C, Diao R, Han W G, et al. Review on linear time frequency analysis methods. Progress in Exploration Geophysics (in Chinese) , 2010, 33(4): 239-246. |
| [5] | Chui C K. An Introduction to Wavelets. Volume 1(wavelet analysis and its applications). New York: Academic Press, 1992 : 1 -100. |
| [6] | Mallat S. A Wavelet Tour of Signal Processing. Academic Press , 1999: 1-230. |
| [7] | Mallat S G. A theory for multiresolution signal decomposition: the wavelet representation. IEEE Trans. PAMI , 1989, 11(7): 674-693. DOI:10.1109/34.192463 |
| [8] | 高静怀, 陈文超, 李幼铭, 等. 广义S变换与薄互层地震响应分析. 地球物理学报 , 2003, 46(4): 526–532. Gao J H, Chen W C, Li Y M, et al. Generalized S transform and seismic response analysis of thin interbeds. Chinese J.Geophys. (in Chinese) , 2003, 46(4): 526-532. |
| [9] | Claasen T A C M, Mecklenbrauker W F G. The Wigner distribution-a tool for time-frequency signal analysis. Part I. Continuous time signals Philips J. Res. , 1980, 35: 217-250. |
| [10] | Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum: The S transform. IEEE Transactions on Signal Processing , 1996, 44(4): 998-1001. DOI:10.1109/78.492555 |
| [11] | Liu G C, Fomel S, Chen X H. Time-frequency analysis of seismic data using local attributes. Geophysics , 2011, 76(6): 23-34. DOI:10.1190/geo2010-0185.1 |
| [12] | Sinha S, Routh P S, Anno P D, et al. Spectral decomposition of seismic data with continuous-wavelet transforms. Geophysics , 2005, 70(6): 19-25. DOI:10.1190/1.2127113 |
| [13] | Mallat S G, Zhang Z F. Matching pursuit with time-frequency dictionaries. IEEE Transactions on Signal Processing , 1993, 41(12): 3397-3415. DOI:10.1109/78.258082 |
| [14] | Qian S, Chen D. Signal representation via adaptive normalized Gaussian functions. Signal Processing , 1994, 36(1): 1-11. DOI:10.1016/0165-1684(94)90174-0 |
| [15] | Castagna J P, Sun S J. Siegfried R W. Instantaneous spectral analysis: Detection of low frequency shadows associated with hydrocarbons. The Leading Edge , 2003, 22(2): 120-127. DOI:10.1190/1.1559038 |
| [16] | Wang Y H. Seismic time-frequency spectral decomposition by matching pursuit. Geophysics , 2007, 72(1): v13-v20. DOI:10.1190/1.2387109 |
| [17] | Wang Y H. Multichannel matching pursuit for seismic trace decomposition. Geophysics , 2010, 75(4): v61-v66. DOI:10.1190/1.3462015 |
| [18] | 张繁昌, 李传辉. 基于正交时频原子的地震信号快速匹配追踪. 地球物理学报 , 2012, 55(1): 277–283. Zhang F C, Li C H. Orthogonal time-frequency atom based fast matching pursuit for seismic signal. Chinese J. Geophys. (in Chinese) , 2012, 55(1): 277-283. |
| [19] | Arons A B, Yennie D R. Phase distortion of acoustic pulses obliquely reflected from a medium with higher sound velocity. Journal of the Acoustical Society of America , 1950, 22(2): 231-327. DOI:10.1121/1.1906594 |
| [20] | Morlet J, Arens G, Fourgeau E, et al. Wave propagation and sampling theory: Part I, Complex signal and scattering in multilayered media. Geophysics , 1982, 47(2): 203-221. DOI:10.1190/1.1441328 |
| [21] | Morlet J, Arens G, Fourgeau E, et al. Wave propagation and sampling theory: Part II, Sampling theory and complex waves. Geophysics , 1982b, 47(3): 222-236. |
| [22] | Hlawatsch F, Boudreaux-Bartels G F. Linear and quadratic time-frequency signal representations. IEEE Signal Pro , 1962, 9(2): 21-67. |
| [23] | 陈学华, 贺振华, 黄德济, 等. 时频域油气储层低频阴影检测. 地球物理学报 , 2009, 52(1): 215–221. Chen X H, He Z H, Huang D J, et al. Low frequency shadow detection of gas reservoirs in time-frequency domain. Chinese J. Geophys (in Chinese) , 2009, 52(1): 215-221. |
| [24] | Partyka G J, Gridley J, Lopez J. Interpretational applications of spectral decomposition in reservoir characterization. The Leading Edge , 1999, 18(3): 353-360. DOI:10.1190/1.1438295 |
| [25] | Marfurt K J, Kirlin R L. Narrow-band spectral analysis and thin-bed tuning. Geophysics , 2001, 66(4): 1274-1283. DOI:10.1190/1.1487075 |
 2012, Vol. 55
2012, Vol. 55

