2. 大连理工大学建设工程学部工程抗震研究所, 辽宁大连 116024;
3. U. S. Geological Survey, Golden, CO 80401, USA;
4. Department of Civil, Architectural, and Environmental Engineering, Missouri University of Science and Technology, MO 65409, USA
2. Earthquake Engineering Research Division, Dalian University of Technology, Liaoning Dalian 116024, China;
3. U. S. Geological Survey, Golden, CO 80401, USA;
4. Depart of Civil, Architectural, and Environmental Engineering, Missouri University of Science and Technology, MO 65409, USA
随着地震波探测技术的高速发展,传统的层状构造地球模型正在经历一场变革,地球被证明从地壳、地幔、到地核处处都呈现出多尺度的横向非均匀性[1-2].而非均匀性往往意味着更多的地质构造运动或者矿产资源的存在.对勘探地球物理来说,这些不同尺度的横向非均匀性与油气及金属矿产的分布紧密相关[3-5].对于土木工程来说,考虑传播介质非均匀性对地震波波形的影响,可以更真实地给定结构动力分析的地震动输入波形[6-7].地球岩石层中的非均匀性在地震图上的表现是P尾波、S尾波以及Lg尾波的存在.高质量的高频数字地震资料的日益增加,使得越来越多的散射理论在地震尾波的衰减测定以及地球内部构造勘探中得到验证与应用[8-13].Aki等[14-15]首先用原生波在横向非均匀性介质中传播时的单次回返散射模型来研究区域地震尾波,这种模型适用于台站与震源距离较小的情况,二者可简化为在同一点处重合.Sato[16]推广了Aki等人的理论,给出了观测点与震源不在同一点上的单次散射模型.随着地震波传播距离的增加,多次散射逐渐占主导作用,单次散射模型不再适用.Gao[17-19]发展了Aki等人的单次散射理论,研究了多次散射对区域性地震尾波的影响.然而,在Gao[18]的多次散射公式中低估了高阶散射项(两次以及两次以上)的作用[20-21].曾健和聂用安[22-23]在Gao的多次散射理论基础上,提出了震源距不为零的多次散射模型,得到了二维、三维无限介质中地震尾波功率谱的积分表达式.在静态能量传输理论的框架内,Wu[24-25]研究了地震波的多次散射问题,并分离了固有衰减和散射衰减的影响.20世纪90年代初,Zeng等[20]在Wu的静态能量传输理论中引入时间项,推导了散射波能量基本方程,给出了高阶散射项的公式表达.与此同时,Hoshiba[21]基于能量守恒原理,采用MonteCarlo方法得到了高阶散射项的扩展系数.自此以后,在能量传输理论框架内,地震波多次散射的作用逐渐被越来越多的地震学者[26-29]所认识,并应用于地震波的尾波分析.
然而,为了数学表达上的简化,上述学者的散射模型都是基于地震波各向同性散射假定.虽然,在地震台站距离震源较近时,这种模型可以有效地模拟地震尾波能量密度包络衰减的一致性,但是不能准确模拟地震能量密度包络的展宽现象[30].为了更真实地模拟地震波的散射过程,越来越多的地震学者开始研究地震波的各向异性散射理论,Sato[31]首先提出了单次各向异性散射模型,并应用于较小震源距的地震波能量密度包络的计算.之后,基于能量传输理论,Sato[32-33]建立了二维、三维无限空间中的多次各向异性散射理论,并给出了地震波能量密度的积分方程.Hoshiba[34]基于能量传输方程,利用MonteCarlo方法求解了地震波各向异性散射的能量传输方程.Gusev和Abubakirov[35]指出利用反映强前散射过程的散射系数,通过MonteCarlo方法合成地震波的能量密度包络可以模拟地震波包络出现的展宽现象,但其结果在不同能量密度包络之间的衰减一致性的模拟上不是很理想.
为了同时模拟不同震源距S波尾波能量密度包络的衰减一致性和S 波包络的展宽现象,本文在Sato的多次各向异性散射理论框架内,通过在方向性散射系数的球谐函数展开式中引入高阶项来表征地震波不同强度的散射过程.并引入特征时间的概念来定义震源处的辐射脉冲宽度.基于此,把任意给定频率的地震波脉冲的能量谱密度引入到Sato的地震波能量密度积分方程中.然后利用离散波数方法得到了不同散射模式下的S波能量密度的包络曲线.讨论了特征时间对能量密度包络的影响,对比分析了多次前、后散射以及各向同性散射情况下的能量密度包络的差异.最后,从包络宽度与震源距的变化结果出发,研究了不同散射模式对S波能量密度包络展宽的影响.并初步探讨了能量密度包络展宽现象的形成机理.此外,以美国2008 年Wells地震的余震为例,简单讨论了多次前散射模式的有效性与实用性.
2 基本理论 2.1 Sato的各向异性散射理论Sato[33]基于能量传输理论,在三维随机无限介质内建立了表征地震波各向异性散射过程的数学模型.该模型假定传播介质中的不均匀体为随机均匀分布的散射点,散射点的随机分布,使得地震波与散射点相互作用产生非相干波场,从而使得地震波散射能量可以叠加.并假定散射模式是轴对称的各向异性散射,即散射强度仅与平面散射角ψ 相关,地震波散射的各向异性特征由方向性散射系数g(ψ)来表征,总的散射系数g0 是g(ψ)在立体角方向上积分的平均值
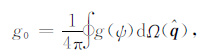
|
(1) |
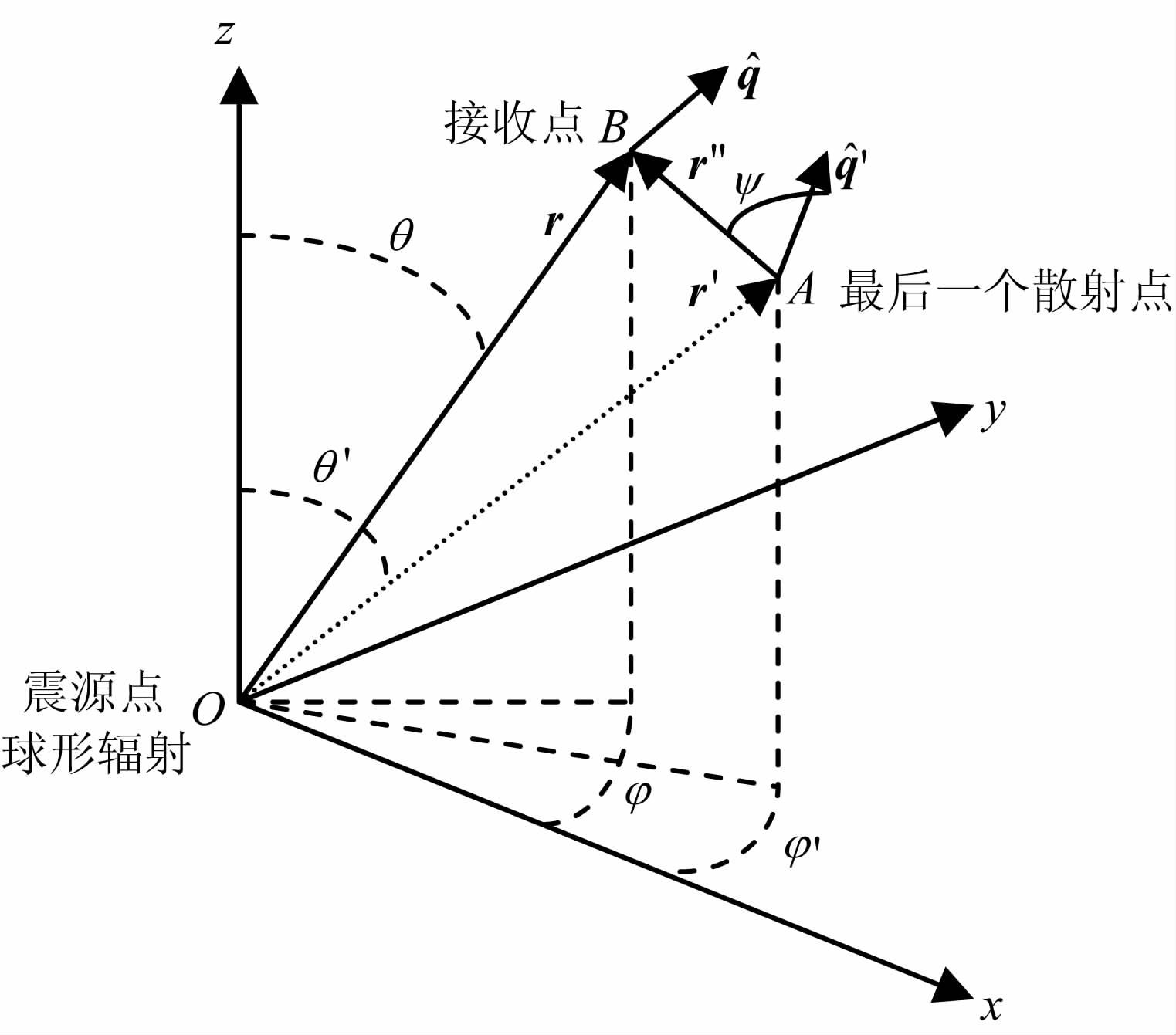
式中$\hat{q}$= (1,θ,φ)是球坐标系下的单位向量,图 1是球坐标系下多次各向异性散射过程的示意图.
|
图 1 多次各向异性散射过程示意图 O是震源点,A是最后一个散射点,B是接收点. Fig. 1 The illustration of multiple anisotropic scattering process 0 is the source, A is the last scattering point, B is the receiver. |
地球介质中随机分布的非均匀性一般用介质特征参数扰动量的自相关函数和谱密度函数来表征.例如,介质中地震波速的非均匀性可表示为
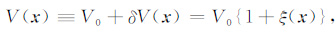
|
(2) |
式中V0 = 〈V(x)〉是介质中的平均波速,ξ(x)是x处速度的微小扰动,〈ξ(x)>= 0,〈…〉表示整体均值.ξ(x)是一个关于随机变量x的均匀的、各向同性的随机函数.这样速度扰动的自相关函数可以定义为波速扰动的均值:
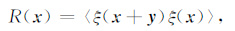
|
(3) |
自相关函数做空间傅里叶变换就可以得到速度扰动的谱密度函数.根据物理学中关于方向性散射系数的定义[2]:针对单个散射体,它是微分散射截面的函数.对于介质内随机分布的多个散射体,它是微分散射截面均值的函数,反映传播介质内的散射场的平均特性.而微分散射截面的均值是介质特征参数扰动量的谱密度函数[2, 36].因此,在统计意义上,方向性散射系数反映了介质的非均匀性质.作为方向性散射系数的特例,在均匀介质中,g(ψ)是一常数.
2.3 方向性散射系数的展开式应用各向异性散射理论求解地震波能量密度的关键是方向性散射系数的球谐函数展开式,并且展开项数的多少决定了表征地震波散射强度的完备性.本文首先从球函数的基本概念出发,重新推导了方向性散射系数的球谐函数展开式.在物理学中,球函数常常采用复数形式表达[37]:
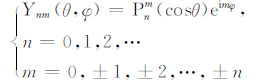
|
(4) |
式中Pnm(cosθ)是m阶伴随Legendre方程的解,球坐标0≤θ ≤ π,0≤φ ≤2π.
球函数的正交性表示为
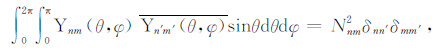
|
(5) |
式中模平方
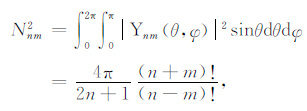
|
(6) |
则球面上任意函数f(θ,φ)的球函数展开式为
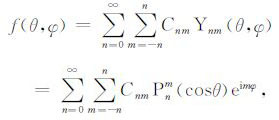
|
(7) |
展开系数:

|
(8) |
为了便于利用Sato[33]的地震波能量密度积分方程,需要对方向性散射系数做无量纲化处理:
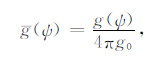
|
(9) |
针对轴对称的各向异性散射问题,定义在球坐标下的方向性散射系数g(ψ)仅与平面散射角ψ 有关,ψ =arccos($\hat{r}$″·$\hat{q}$′),这里$\hat{r}$″ = (1,θ″,φ″),$\hat{q}$′ =(1,θq′,φq′),散射角ψ 相当于(7)式中的θ ,并且g(ψ)与另外一个角度无关,所以g(ψ)球函数展开式可简化为
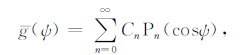
|
(10) |
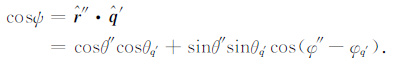
|
(11) |
根据Legendre多项式的加法定理
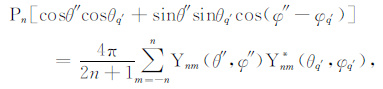
|
(12) |
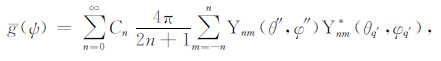
|
(13) |
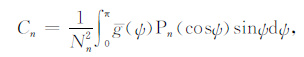
|
(14) |
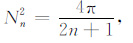
|
(15) |
(13) 式与Sato[33]的(17)式(参见附录中(A1)式)是一致的,但这里的表达较为简洁,数值求解更直观.当n=0时,g(ψ)=1,对应于各向同性散射模式,随着n的增加,g(ψ)表征的散射模式趋于完备,可以准确描述在某一方向散射较强的情况.
2.4 能量密度积分方程的修正在Sato的散射理论中,由于假定震源激发的地震波脉冲为理想脉冲,导致在计算有限频率带宽时,地震波能量密度包络往往出现Gibbs现象.而实际上震源处辐射波脉冲往往是有一定宽度的,本文利用Sato[2]在抛物线近似方法中提出的特征时间tM来表征震源处初始脉冲宽度,并基于Sato的各向异性散射模型,在地震波能量密度积分方程中引入初始地震波脉冲能量谱密度的频域表达[2]I(ω),对原有的积分方程进行修正.I(ω)中tM 的引入,可以有效地避免初始理想脉冲引起的地震波能量密度包络中Gibbs现象的出现,相关的数值验证见第4 节.修正之后的无量纲化地震波能量密度表达式如下:
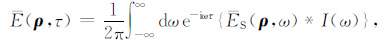
|
(16) |
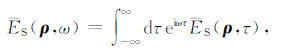
|
(17) |
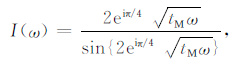
|
(18) |
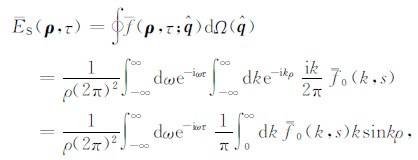
|
(19) |
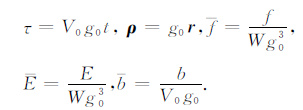
|
(20) |
ES(ρ,τ)是Sato的能量密度积分方程.式(18)中,tM 是与震源相关的常数,通过与实际台站记录的拟合计算,一般地tM =0.0~0.5.并且取值与震源距的大小无关,它表征震源处地震波能量脉冲的初始宽度.此处tM 与Sato[2]的物理含义是不同的,Sato定义的tM 是一个随震源距递增的量,表征地震波能量脉冲随着震源距的增加而逐渐展宽.(16)、(17)式中ρ = |ρ| 是无量纲化的震源距,τ 是无量纲化时间,f(ρ,τ;$\hat{q}$)是ρ 处散射点在τ 时刻沿方向$\hat{q}$的无量纲化能量密度,f0(k,s)的含义及表达式见附录中的(A2)式.无量纲化参数可以由(20)式还原,其中V0 是地震波传播的平均速度,b是固有吸收因子,W是震源处的辐射能量.
3 数值计算方法为了求解地震波能量密度积分方程,按照地震波能量的构成,我们可以把无量纲化能量密度分解为直达波、单次散射项、多次散射项(二次散射以上)三部分:
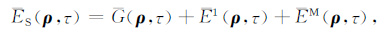
|
(21) |
式中
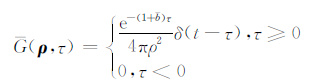
|
单次散射项E1(ρ,τ)的求解直接利用Sato[33]推导的积分方程,见附录(A6)式.
关于多次散射项EM(ρ,τ),本文采用了Zeng[38]的离散波数法对积分方程(19)式进行波数域上的离散.其中积分函数f0(k,s)可以由附录(A2)式得到.
求得ES(ρ,τ)以后,采用傅里叶变换得到其频域结果ES(ρ,ω),乘以初始地震波脉冲能量谱密度的频域表达I(ω),获得地震波修正的能量密度频域表达.然后按照(16)式做傅里叶逆变换,并通过(20)式还原到实际的地震波能量密度E(r,t).
4 数值计算实例以指数型自相关函数表征的随机介质为例,本文采用Hoshiba[34]给出的方向性散射系数表达,来讨论不同散射模式对S波能量密度包络的影响.方向性散射系数表示如下:
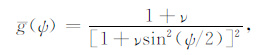
|
(22) |
式中ν>-1,当ν>0时,前散射强于后散射,称之为前散射模式;反之ν < 0 时,后散射强于前散射,称之为后散射模式,ν = 0 对应于各向同性散射模式.在图 2中分别取ν=-0.9,-0.7,0,3.0,9.0来表征不同的散射模式.在散射平面上,横轴表示g(ψ)的水平分量g(ψ)cosψ,纵轴表示g(ψ)竖向分量g(ψ)sinψ.其中针对ν= -0.9、-0.7、3.0、9.0的强散射情况,需要在g(ψ)的球函数展开式中包含高阶项,在附录(A3)式中由于高斯型超几何函数的存在,使得高阶的格林函数的计算很不稳定,本文采用了Zhang[39]给出的计算高斯型超几何函数的数值方法,并通过格林函数的递推公式进行高阶项的计算,可以将方向性散射系数的球函数展开至10阶以上.一般地,n≤8就能满足实际地震波散射强度的需要,这一点将做另文讨论.在本算例中取n=6.

|
图 2 数值算例用到的散射模式 Fig. 2 The scattering pattern used in the numerical exampl |
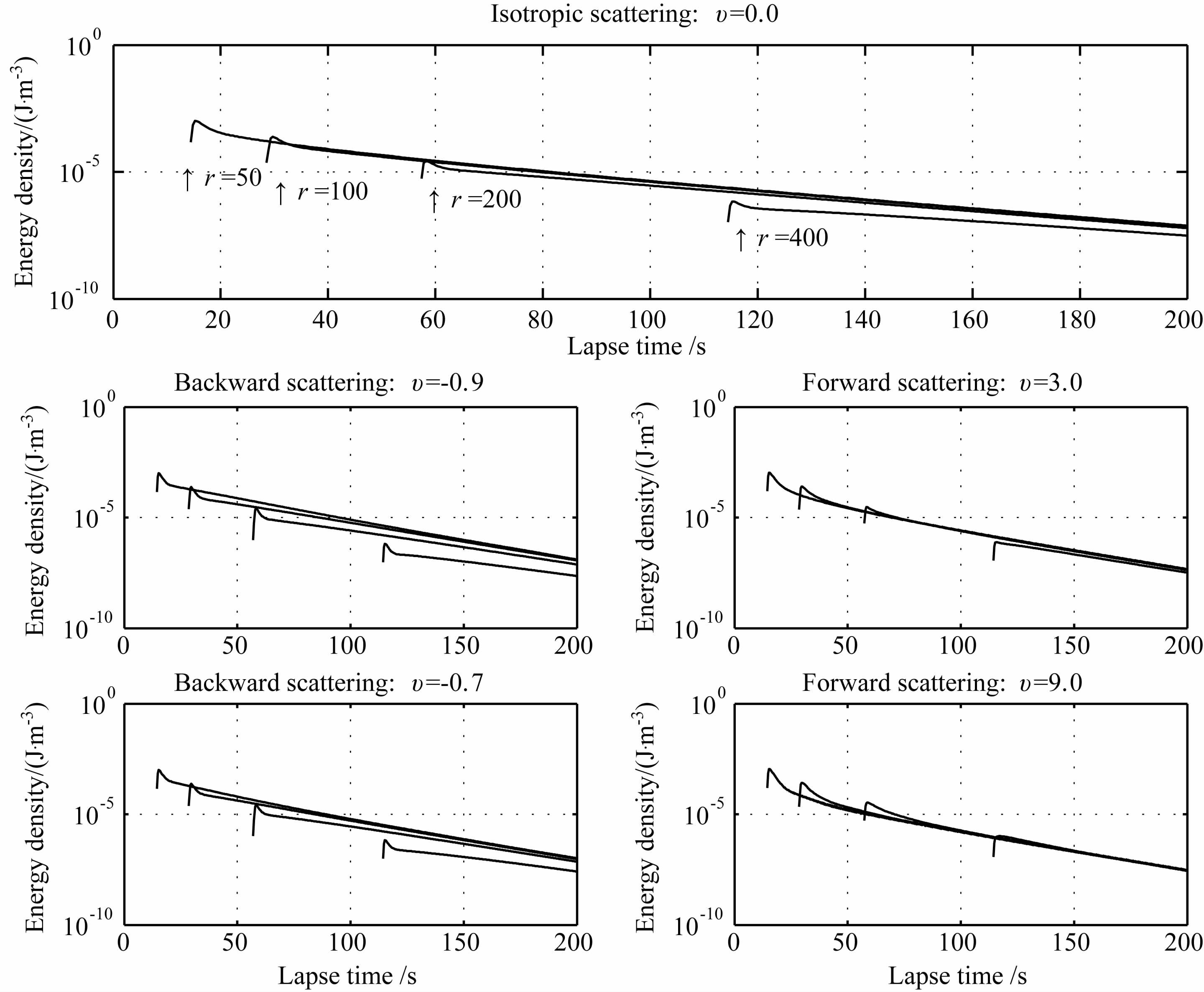
首先,取震源距r=50、100、200、400km;根据S波波速、散射系数和固有吸收系数的一般取值范围[20],地震波平均传播速度V0 取为3.5km/s;总散射系数g0 取为0.01km-1;固有吸收系数ηi取为0.01km-1,并表示为ηi=b/V0;震源辐射能量W取为1.针对图 2中给出的不同散射模式,利用修正的能量密度积分方程合成S 波的能量密度包络曲线,如图 3所示.从计算结果可以看出,当震源距较小时,无论是多次前散射模式、各向同性散射还是后散射模式都能预测到能量密度包络尾波段的同一衰减形式.然而随着震源距的增加,如r=400km 时,各向同性散射、后散射模式合成的能量密度包络尾波段衰减趋势逐渐出现偏差,而前散射模式的结果则能准确呈现不同震源距尾波段的衰减一致性.
|
图 3 不同散射模式下S波能量密度包络的衰减曲线纵坐标是对数坐标表示的能量密度. Fig. 3 Attenuation of the envelope of S wave energy density for different scattering patternsThe logarithm of energy density is denoted in vertical coordinate. |
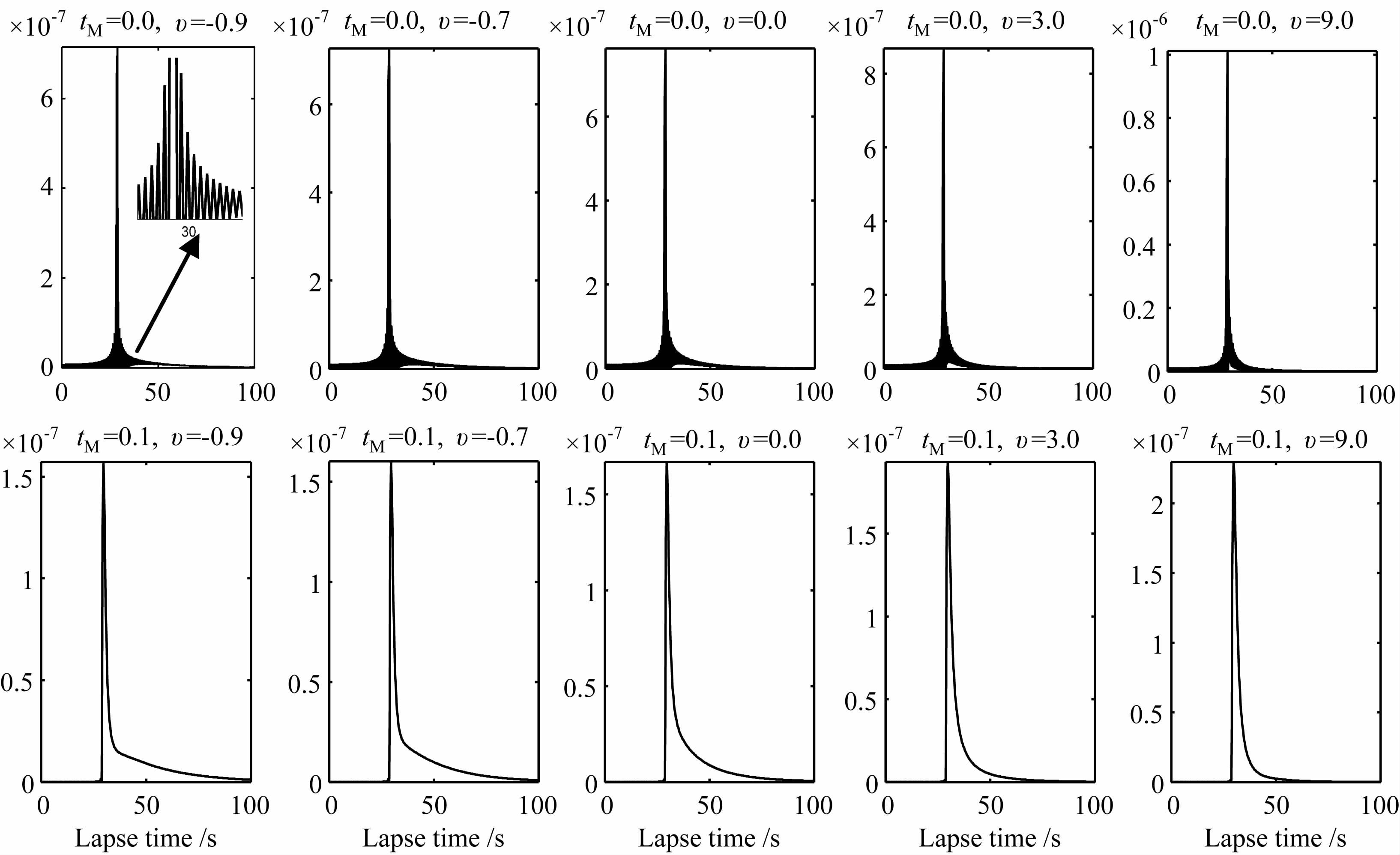
其次,基于图 2给出的散射模式,在图 4中讨论了tM 取值对S 波能量密度包络的影响.不考虑tM时,即tM =0.0,合成的地震波能量密度包络在S波到时附近出现高度的振荡现象,以致于S波能量密度包络的峰值不稳定.而当tM = 0.1 时,则能合成平滑的地震波能量密度包络.因此,在地震波能量密度积分表达中引入tM ,可以有效地消去能量密度包络的Gibbs现象.
|
图 4 tM 取值对合成的S波能量密度包络曲线的影响 Fig. 4 The effect of tM on synthesized S wave energy density envelope |
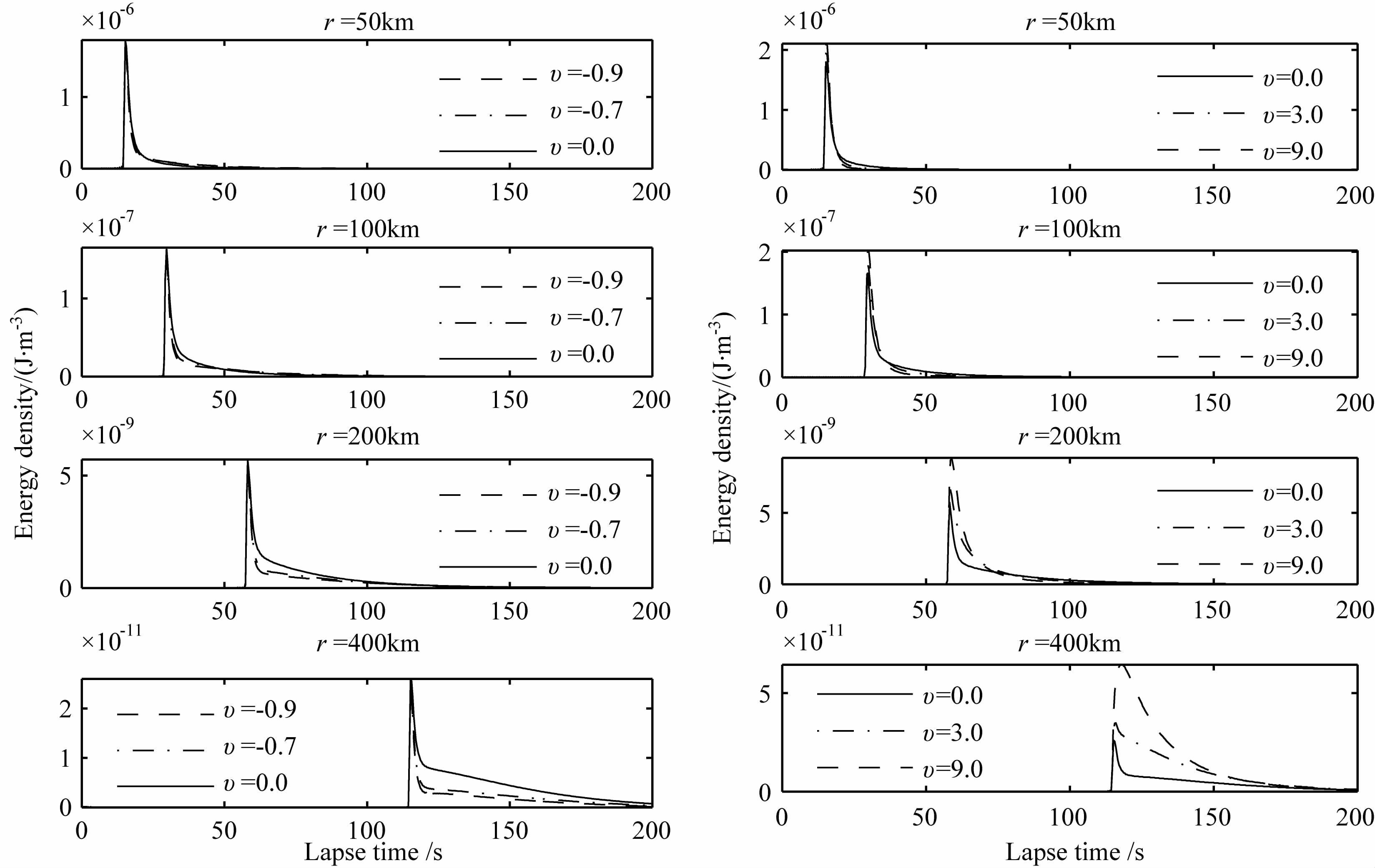
然后,使用相同的输入参数:r,V0,g0,ηi,我们还讨论了图 2所示的不同散射模式对S波能量密度包络的影响,从图 5 中给出的地震波能量密度包络曲线可以看出,当震源距较小时,比如r≤100km时,各向同性散射模式与各向异性散射模式的结果十分吻合.但随着震源距的增加,从图 5右侧部分结果可以看到,在S波到达以及到达以后的早期阶段,前散射模式合成的地震波能量密度包络与各向同性散射的结果相比较大,这点与Sato[33]的结果是一致的,并且随着前散射强度的加强,能量密度包络峰值逐渐增加.对于相同的时间段,如图 5 左侧部分所示,同样随着震源距的增加,各向同性散射模式合成的地震波能量密度与后散射模式之间结果的差别逐渐增大,并且各向同性散射的结果大于后散射的结果.因此,当震源距较大时,如r>100km 时,各向异性散射的结果与各向同性的结果会出现较大差异,尤其是强散射情况,此时,需要考虑地震波各向异性散射过程的影响.
|
图 5 不同散射模式合成的S波能量密度包络曲线 Fig. 5 The S wave energy density envelope generated by different scattering patterns |
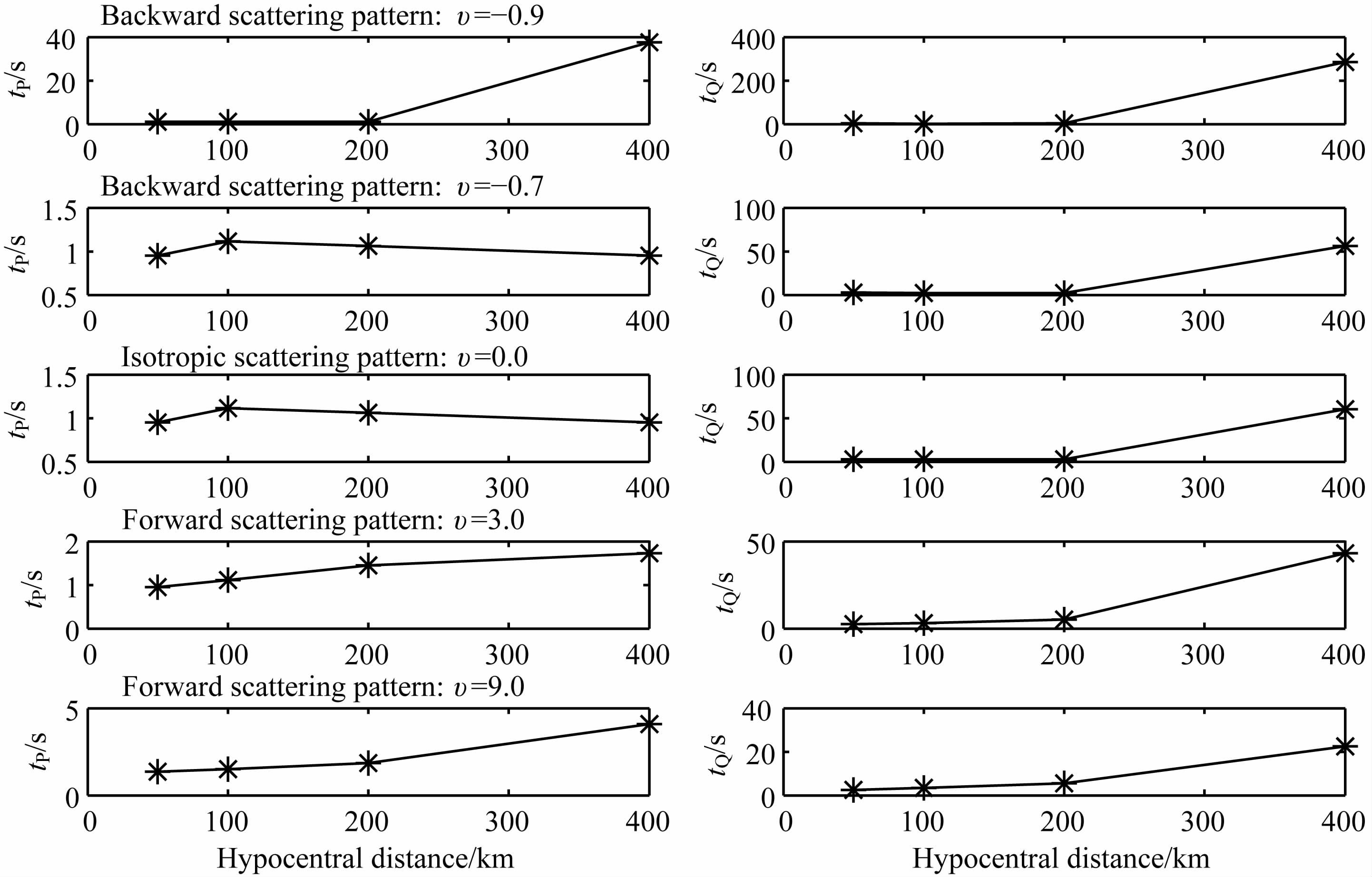
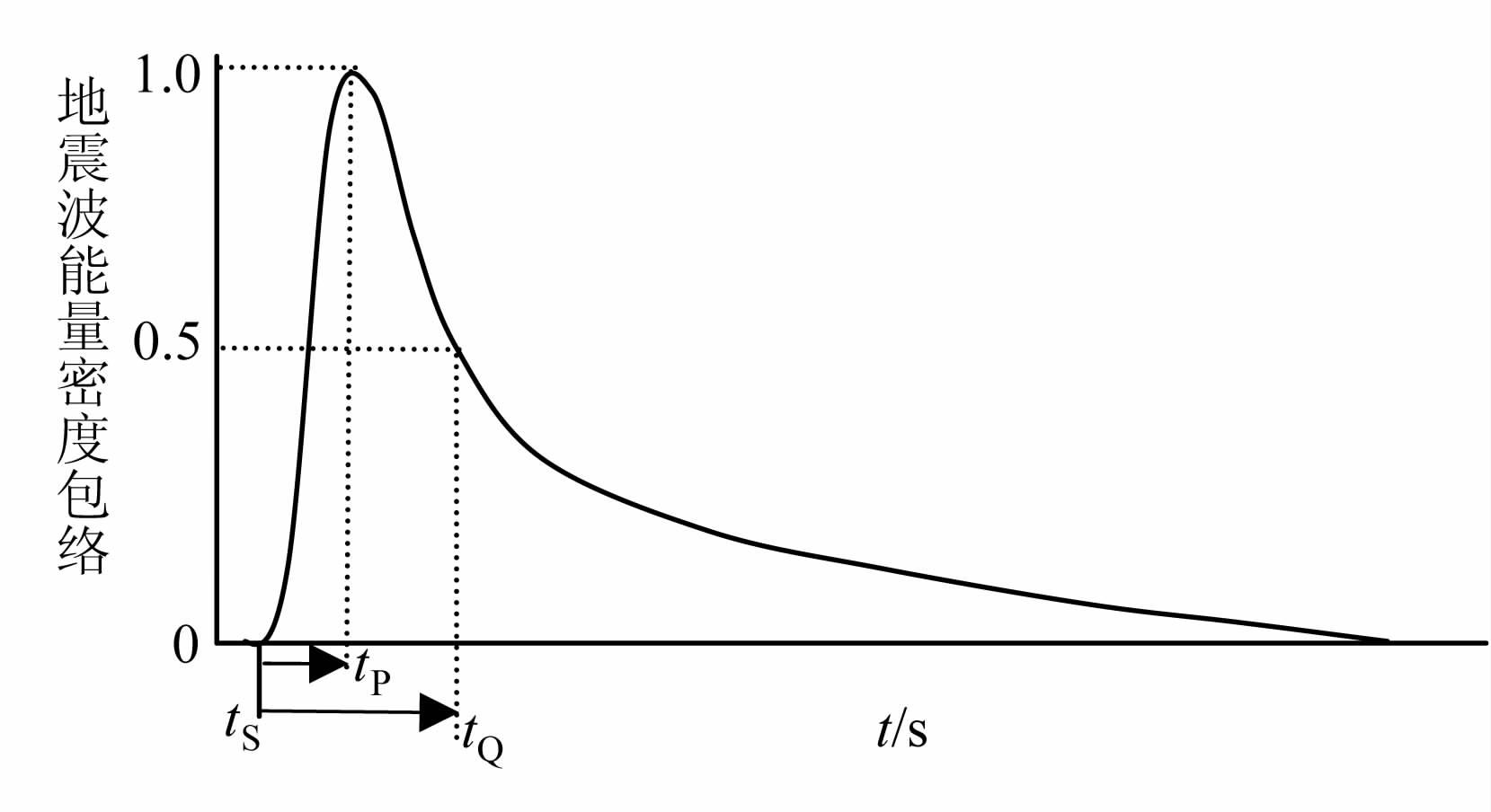
此外,在实际观测的地震图记录中,随着震源距的增加,地震波能量包络会出现逐渐展宽的现象,之前关于这方面的研究一直采用抛物线近似的方法,但该方法完全忽略了后散射模式的影响,不能准确地模拟地震波能量密度包络的尾波部分.本文的多次各向异性散射模型基于能量传输理论建立,可以同时考虑地震波的前、后散射过程,在图 6中给出了不同散射模式下S波能量密度包络的宽度tP、tQ 随震源距的变化情况,tP、tQ 的物理意义如图 7所示.从图 6的数值结果可以看出,在多次前散射模式下,能量密度脉冲宽度tP、tQ 随着震源距的增加依次递增,从而说明多次前散射模式的结果能够反映S波能量密度包络的展宽现象,而其他散射模式则不能说明这一点.由此,S波能量密度包络随震源距的增加而出现的展宽现象可解释为地震波与介质中不均匀体的多次前散射作用所引起.这点与Gusev 和Abubakirov[35]结论是一致的.
|
图 6 S波能量密度包络宽度随震源距变化曲线 Fig. 6 The variation of the envelope width of S wave energy density with hypocentral distance |
|
图 7 典型时段长度tS 表示S波到时,tP 表示从S波到时至包络峰值点的时段长度,tQ 表示从S波到时至包络1/2峰值点的时段长度. Fig. 7 Typical time lengthtS denotes S wave arrival time, tp denotes time length from S arrival to the instant ofpeak value; tQ denotes time length from S arrival to the instant of later haff peak value. |
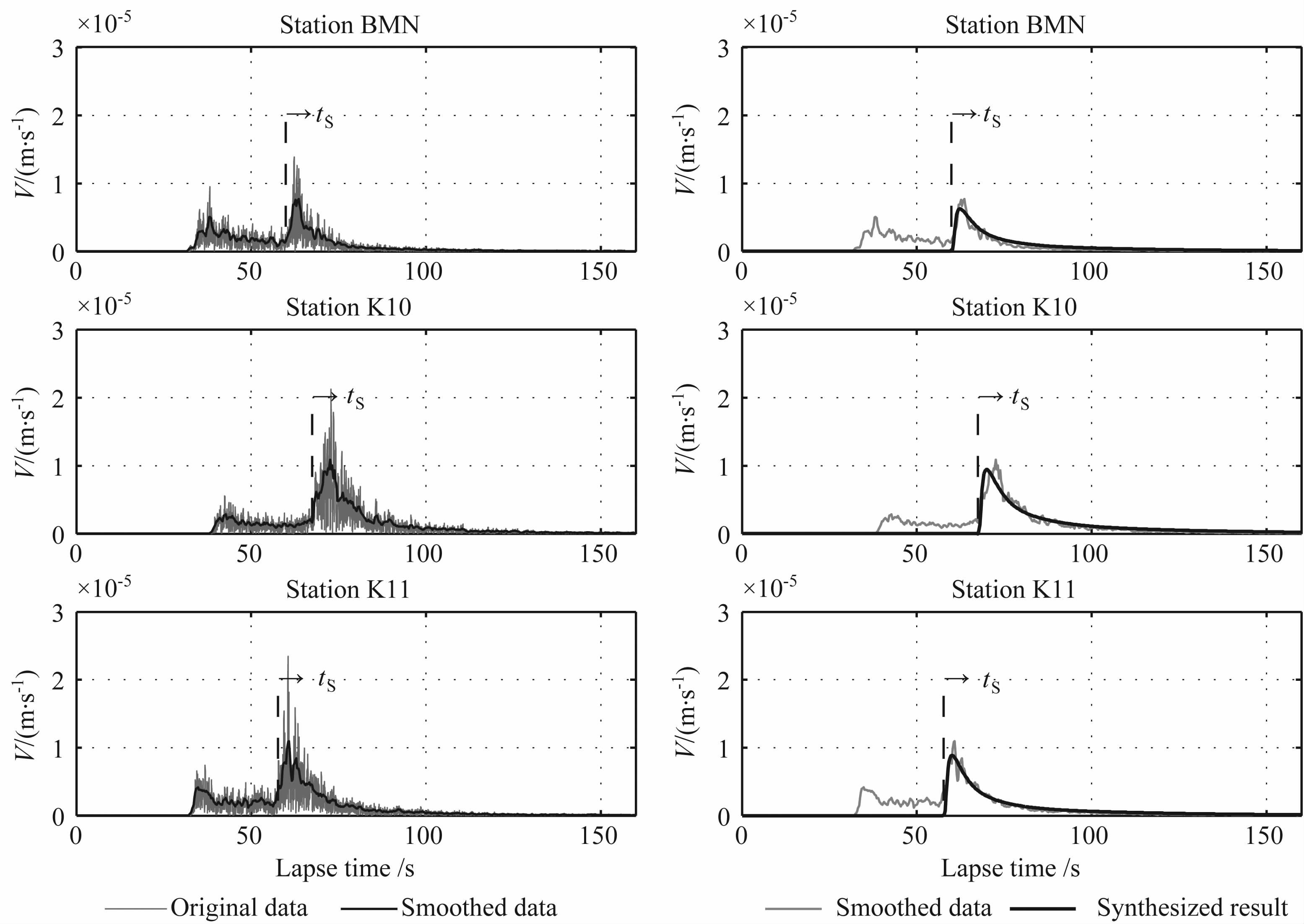
最后,以2008年美国内华达州的Wells地震的一次余震为例,该余震发生于当地时间2008年2月21日,震级4.84,震源深度10.56km.取其中三个台站BMN、K10、K11的竖向地震波速度记录,并利用地震波处理软件SAC2000 扣除记录中台站仪器响应的影响,在8~16Hz频率范围内对记录进行滤波,最后得到对应的地震波竖向速度包络曲线,如图 8中灰色线所示,其中图 8 中的黑色细实线表示灰色线的平滑处理结果.利用本文提出的修正的能量密度积分方程,基于图 2 给出的不同散射模式,由(16)式求得S波能量密度的时空分布,取能量密度的平方根拟合台站记录的速度包络.得到tM = 0.09,g0 =0.005,以及ν=9.0时的地震波前散射模式.拟合得到的S 波能量密度的平方根结果如图 8右侧的黑色粗实线所示,图中竖向虚线表示S波到时所在位置,从S波到时算起,对照实际台站记录的平滑处理结果,多次前散射模式可以得到与其一致的能量密度的平方根曲线.因此,与各向同性散射、多次后散射模式相比,多次前散射模式可以拟合高频的S波台站记录.该散射模式为观测地震图的解释提供了理论依据.
|
图 8 Wells地震余震的S波竖向速度包络曲线 Fig. 8 The S wave vertical velocity envelope of aftershock of Wells earthquake |
基于Sato的多次各向异性散射理论,本文在方向性散射系数的球谐函数展开式中引入了高阶项来表征地震波的不同散射强度,在地震波能量密度积分方程中引入表征初始地震波能量密度脉冲宽度的特征时间tM ,避免了数值求解能量密度包络时出现的Gibbs现象.针对指数型自相关函数表征的随机传播介质,利用离散波数法求解能量密度积分方程,对比分析了不同散射模式对S波能量密度包络曲线的影响,得到了以下几点结论:
(1) 在能量传输理论框架内,利用Hoshiba的方向性散射系数表达生成的前散射、各向同性散射、后散射模式,在震源距较小时,均能预测S波能量密度包络尾波段的同一衰减特性.然而,随着震源距的增加,各向同性散射、后散射模式模拟的尾波包络同一衰减逐渐出现偏差,但前散射模式的结果始终能够给出能量密度尾波段的衰减一致性.
(2) 在震源距较小(r≤100km)时,各向异性散射模式的能量密度包络与各向同性散射结果十分吻合;但随着震源距的增加,与前散射模式相比,前散射强度越强,在S波到达以及到达以后的早期阶段,能量密度包络与各向同性散射的结果相比越大.在同样的时间段,与后散射结果相比,能量密度包络与各向同性散射结果相比越小.所以当震源距较大时,应当充分考虑地震波的各向异性散射过程的影响.
(3) 与多次后散射、各向同性散射模式相比,前散射模式能够重现S波能量密度包络在传播过程中出现的展宽现象,因此,我们可以推断:S 波能量密度包络随着震源距的增加而出现的展宽现象源于地震波与介质中非均匀体的多次前散射作用.
(4) 通过与美国内华达州Wells地震余震的台站记录比较,证明了多次前散射模式可以拟合实际地震台站的记录资料.
综上所述,在能量传输理论框架内,利用修正的能量密度积分方程,基于多次前散射模式,合成的S波能量密度包络不仅能够模拟尾波段包络的衰减一致性,而且能够模拟S波能量密度包络在传播过程中出现的展宽现象.所以,多次前散射模式在实测地震图中S波的解释,以及理论地震图的合成方面,具有良好的应用价值.
附录 A Sato相关公式[2, 33]下述公式均在球坐标系下建立,参见正文图 1.无量纲化方向性散射系数的球谐函数展开式:
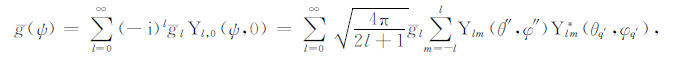
|
(A1) |
针对无量纲化能量密度函数f(ρ,τ;$\hat{q}$)做空间域上的傅里叶变换,之后做时间域上的拉普拉斯变换,然后做球函数展开.在其球函数展开式中,球函数的系数$\overline{\overline{f}}$l(k,s)可以由(A2)式得到,其中当l=0时,$\overline{\overline{f}}$0(k,s)为能量密度积分方程中的积分核函数,
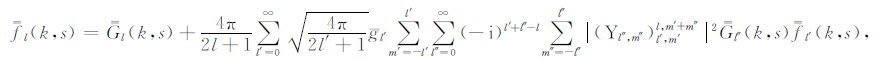
|
(A2) |
式中格林函数$\overline{\overline{G}}$l(k,s)的表达式如下:
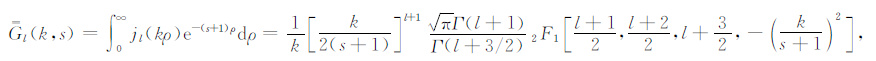
|
(A3) |
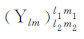
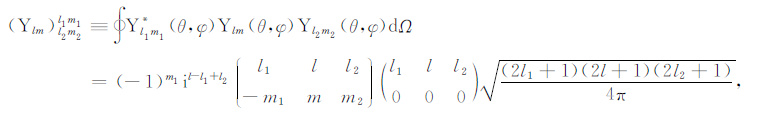
|
(A4) |
上述积分式需要满足:m1 = m+m2 和|l-l2| ≤l1 |l+l2| ,否则积分值为零.这种情况下l+l1 +l2 为偶数,(A4)式的平方值为
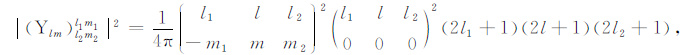
|
(A5) |
Sato的单次散射能量积分方程:
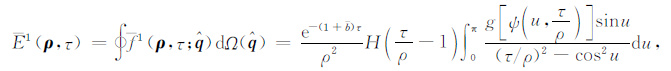
|
(A6) |
这里
本文第一作者在美国学习期间得到了国家留学基金委“建设高水平研究型大学"项目的资助,美国密苏里科技大学土木系以及USGSEarthquakeHazardsProgram 提供了学习交流的机会,两位匿名审稿专家提出了建设性意见,使得本文对问题的讨论更加清楚,作者在此表示衷心的感谢.
| [1] | 吴如山. 地震波散射: 理论与应用. 地球物理学进展 , 1989, 4(4): 1–23. Wu R S. Seismic scattering: Theory and application. Progress in Geophysics (in Chinese) , 1989, 4(4): 1-23. |
| [2] | Sato H, Fehler M. Seismic Wave Propagation and Scattering in the Heterogenous Earth. New York: AIP Press, 1998 . |
| [3] | 李灿苹. 散射波特征与非均匀地质体对应关系研究. 北京: 中国地质大学, 2006 . Li C P. A study on corresponding relationship between scattering wave characteristic and heterogeneous geologic bodies (in Chinese). Beijing: China University of Geosciences, 2006 . |
| [4] | 尹军杰. 地震散射波场特征的数值模拟研究. 北京: 中国地质大学, 2005 . Yin J J. A study on seismic scattered wave characteristics by numerical simulating (in Chinese). Beijing: China University of Geosciences, 2005 . |
| [5] | 尹军杰, 刘学伟, 李文慧. 地震波散射理论及应用研究综述. 地球物理学进展 , 2005, 20(1): 123–134. Yin J J, Liu X W, Li W H. The view of seismic wave scattering theory and its applications. Progress in Geophysics (in Chinese) , 2005, 20(1): 123-134. |
| [6] | Zeng Y H, Anderson J G, Su F. Subevent rake and random scattering effects in realistic strong ground motion simulation. Geophys. Res. Lett. , 1995, 22(1): 17-20. DOI:10.1029/94GL02798 |
| [7] | Mai P M, Imperatori W, Olsen K B. Hybrid broadband ground-motion simulations: Combining long-period deterministic synthesis with high-frequency multiple S-to-S backscattering. Bull. Seism. Soc. Am. , 2010, 100(5A): 2124-2142. DOI:10.1785/0120080194 |
| [8] | 刘建华, 刘福田, 王凤霞, 等. 单台Lg尾波 QLgC 的测量研究. 地球物理学报 , 1999, 42(3): 371–382. Liu J H, Liu F T, Wang F X, et al. A measuring study for single-trace Lg coda QLgC. Chinese J. Geophys (in Chinese) , 1999, 42(3): 371-382. |
| [9] | 胡家富, 丛连理, 苏有锦, 等. 云南及周边地区Lg尾波Q值的分布特征. 地球物理学报 , 2003, 46(6): 809–814. Hu J F, Cong L L, Su Y J, et al. Distribution characteristics of Q value of the Lg coda in Yunnan and its adjacent regions. Chinese J. Geophys. (in Chinese) , 2003, 46(6): 809-814. |
| [10] | 张天中, 马云生, 张焕生, 等. 震源谱的尾波多台多震综合求解方法. 地球物理学报 , 2004, 40(5): 702–709. Zhang T Z, Ma Y S, Zhang H S, et al. A multi-station and multi-event coda method to study seismic source spectrum. Chinese J. Geophys. (in Chinese) , 2004, 40(5): 702-709. |
| [11] | 刘建华, 刘福田, 阎晓蔚, 等. 华北地区Lg尾波衰减研究——Lg尾波Q的测量. 地球物理学报 , 2004, 47(5): 822–831. Liu J H, Liu F T, Yan X W, et al. A study of Lg coda attenuation in North China-the measurement of Lg coda Q. Chinese J. Geophys. (in Chinese) , 2004, 47(5): 822-831. |
| [12] | 刘建华, 刘福田, 阎晓蔚, 等. 华北地区Lg尾波衰减研究——Lg尾波 Q0 地震成像. 地球物理学报 , 2004, 47(6): 1044–1052. Liu J H, Liu F T, Yan X W, et al. A study of Lg coda attenuation beneath North China: seismic imaging of Lg coda Q0. Chinese J. Geophys. (in Chinese) , 2004, 47(6): 1044-1052. |
| [13] | 贾豫葛, 李小凡, 张美根, 等. 地震波散射研究的若干重要进展. 地球物理学进展 , 2005, 20(4): 939–949. Jia Y G, Li X F, Zhang M G, et al. Some important progress in research upon seismic wave scattering. Progress in Geophysics (in Chinese) , 2005, 20(4): 939-949. |
| [14] | Aki K. Analysis of the seismic coda of local earthquakes as scattered waves. J. Geophys. Res. , 1969, 74(2): 615-631. DOI:10.1029/JB074i002p00615 |
| [15] | Aki K, Chouet B. Origin of coda waves: source, attenuation, and scattering effects. J. Geophys. Res. , 1975, 80(23): 3322-3342. DOI:10.1029/JB080i023p03322 |
| [16] | Sato H. Energy propagation including scattering effects single isotropic scattering approximation. J. Phys. Earth , 1977, 25(1): 27-41. DOI:10.4294/jpe1952.25.27 |
| [17] | Gao L S, Lee L C, Biswas N N, et al. Comparison of the effects between single and multiple scattering on coda waves for local earthquakes. Bull. Seism. Soc. Am. , 1983, 73(2): 377-389. |
| [18] | Gao L S, Biswas N N, Lee L C, et al. Effects of multiple scattering on coda waves in three-dimensional medium. Pure Appl. Geophys. , 1983, 121(1): 3-15. DOI:10.1007/BF02590116 |
| [19] | 尚铁梁, 高龙生. 多次散射的传输理论及其在脉冲源的地震尾波问题上的应用. 中国科学(B辑) , 1988(1): 85–94. Shang T L, Gao L S. Multiple scattering energy transport theory and its application on seismic coda wave. Science in China (Series B) (in Chinese) , 1988(1): 85-94. |
| [20] | Zeng Y H, Su F, Aki K. Scattering wave energy propagation in a random isotropic scattering medium 1. Theory. J. Geophys. Res., , 1991, 96(B1): 607-619. DOI:10.1029/90JB02012 |
| [21] | Hoshiba M. Simulation of multiple-scattered coda wave excitation based on the energy conservation law. Phys. Earth Planet. Inter. , 1991, 67(1-2): 123-136. DOI:10.1016/0031-9201(91)90066-Q |
| [22] | 曾健, 聂永安. 单次与多次散射对地方震尾波的作用. 地震学报 , 1989, 11(1): 12–23. Zeng J, Nie Y A. The effects of single and multiple scattering on coda waves for local earthquakes. Acta Seismologica Sinica (in Chinese) , 1989, 11(1): 12-23. |
| [23] | 聂永安, 曾健, 冯德益. 三维尾波散射问题的理论研究. 地震学报 , 1995, 17(1): 68–71. Nie Y A, Zeng J, Feng D Y. The research on seismic coda wave scattering in three dimension space. Acta Seismologica Sinica (in Chinese) , 1995, 17(1): 68-71. |
| [24] | Wu R S. Seismic wave scattering and the small scale inhomogeneities in the lithosphere. Massachusetts Institute of Technology, 1984. |
| [25] | Wu R S, Aki K. Multiple scattering and energy transfer of seismic waves-Separation of scattering effect from intrinsic attenuation. II. Application of the theory to Hindu Kush region. Pure Appl. Geophys. , 1988, 128(1-2): 49-80. DOI:10.1007/BF01772590 |
| [26] | Sato H. Energy transportation in one- and two-dimensional scattering media: analytic solutions of the multiple isotropic scattering model. Geophys. J. Int. , 1993, 112(1): 141-146. DOI:10.1111/gji.1993.112.issue-1 |
| [27] | Ugalde A, Tripathi J N, Hoshiba M, et al. Intrinsic and scattering attenuation in western India from aftershocks of the 26 January, 2001 Kachchh earthquake. Tectonophysics , 2007, 429(1-2): 111-123. DOI:10.1016/j.tecto.2006.09.010 |
| [28] | Padhy S, Wegler U, Korn M. Seismogram envelope inversion using a multiple isotropic scattering model: application to aftershocks of the 2001 Bhuj earthquake. Bull. Seism. Soc. Am. , 2007, 97(1B): 222-233. DOI:10.1785/0120060035 |
| [29] | Lee W S, Yun S, Do J Y. Scattering and intrinsic attenuation of short-period S waves in the Gyeongsang Basin, South Korea, revealed from S-wave seismogram envelopes based on the radiative transfer theory. Bull. Seism. Soc. Am. , 2010, 100(2): 833-840. DOI:10.1785/0120090149 |
| [30] | Wegler U, Korn M, Przybilla J. Modeling full seismogram envelopes using radiative transfer theory with Born scattering coefficients. Pure Appl. Geophys. , 2006, 163(2-3): 503-531. DOI:10.1007/s00024-005-0027-5 |
| [31] | Sato H. Coda wave excitation due to nonisotropic scattering and nonspherical source radiation. J. Geophys. Res. , 1982, 87(B10): 8665-8674. DOI:10.1029/JB087iB10p08665 |
| [32] | Sato H. Formulation of the multiple non-isotropic scattering process in 2-D space on the basis of energy-transport theory. Geophys. J. Int. , 1994, 117(3): 727-732. DOI:10.1111/gji.1994.117.issue-3 |
| [33] | Sato H. Formulation of the multiple non-isotropic scattering process in 3-D space on the basis of energy transport theory. Geophys. J. Int. , 1995, 121(2): 523-531. DOI:10.1111/gji.1995.121.issue-2 |
| [34] | Hoshiba M. Estimation of nonisotropic scattering in western Japan using coda wave envelopes: Application of a multiple nonisotropic scattering model. J. Geophys. Res. , 1995, 100(B1): 645-657. DOI:10.1029/94JB02064 |
| [35] | Gusev A A, Abubakirov I R. Simulated envelopes of non-isotropically scattered body waves as compared to observed ones: Another manifestation of fractal heterogeneity. Geophys. J. Int. , 1996, 127(1): 49-60. DOI:10.1111/gji.1996.127.issue-1 |
| [36] | Ishimaru A. Wave Propagation and Scattering in Random Media, 2 vols. San Diego, Calif. Academic Press, 1978. |
| [37] | 季效达, 薛兴恒, 陆英. 数学物理方程. 北京: 科学出版社, 2005 . Ji X D, Xue X H, Lu Y. Equations of Mathematical Physics (in Chinese). Beijing: Science Press, 2005 . |
| [38] | Zeng Y H. Theory of scattered P- and S-wave energy in a random isotropic scattering medium. Bull. Seism. Soc. Am. , 1993, 83(4): 1264-1276. |
| [39] | Zhang S J, Jin J M. Computation of Special Functions. New York: John Wiley & Sons, 1996 . |
 2012, Vol. 55
2012, Vol. 55

