2. 中国科学院研究生院, 北京 100049;
3. 中国石油吐哈油田公司勘探公司, 哈密 839009
2. Graduate University of Chinese Academy of Sciences, Beijing 100049, China;
3. Exploration Company, Tuha Oilfield Company, PetroChina, Hami 839009, China
地震数据携带大量储层信息,针对难度越来越大的储层勘探目标,尽可能最大程度的提取更多信息进行储层描述是近几年业界的重要研究方向.基于Zopplize方程[1],利用叠前反演技术可从叠前道集振幅中提取各叠前地震参数[2],其具有各自的地质意义,可针对性的进行储层流体的解释.
前人提出了不同的流体敏感属性,Fatti等[3]定义的与纵横波反射系数有关的流体因子ΔF,Castagna等[4]提出的AVO 流体指示因子Rp-Rs, 以及Smith等[5]对其改进后的指示因子Rp-0.63Rs, Goodway等[6]提出的λ-μ-ρ 拉梅常数流体因子,Russell等[7]提出的ρf流体识别因子等,相对于常规岩石弹性属性,对岩石孔隙流体的识别在其各自特定条件下往往具有更好的敏感性.但不同特性的储层岩石,地震弹性参数对岩石孔隙流体常具有不同的敏感特征.因此,对特定储层进行流体识别时,如何选择最合适的流体敏感参数进行储层流体检测无疑是非常关键的[8-12].
本文基于岩石物理实验测量,分析了主要岩石弹性参数随流体及其饱和度的变化特征,并根据岩石物理理论建立组合流体敏感参数,期望优选最为敏感的流体属性.进一步利用统计学原理,给出流体敏感量定义,用以定量分析地震弹性参数的敏感性.从而为叠前弹性参数反演流体描述提供岩石物理基础及指导.并在X区块进行了叠前反演的应用分析.
2 岩石物理实验测量及分析 2.1 实验测量方法实验装置采用中国科学院地质与地球物理研究所岩石物性实验室的岩石原位物性测量系统[13-16],系统具有温度、围压、孔隙压、流体饱和度独立控制功能,声波测量频率主频为570kHz.系统可测量在储层温度、压力下流体饱和度变化时的纵波速度、横波速度、密度等基本参数,并通过岩石物理关系计算获得波阻抗、泊松比、拉梅常数等其它弹性参数.
压力控制包括围压控制和孔隙压力控制,分辨率为0.1 MPa, 温度加热采用高压容器内电热丝加热,精度为1 ℃.
对于流体饱和度变化测量,首先利用抽真空法使岩石完全饱含流体,并测量所饱含流体质量.实验中岩样需密封处理,两端置有封闭块,内含声波传感器和孔道,从样品一端注入流体,驱替岩石孔隙中流体,在岩石另一端控制并测量趋替出的流体量,完成流体驱替实验的不同流体饱和度点的测量.饱含流体质量及驱替出的流体量采用电子天平测量,精度为0.001g, 对于饱含10g流体的样品其饱和度测量理论误差小于0.01%(没有考虑系统误差).
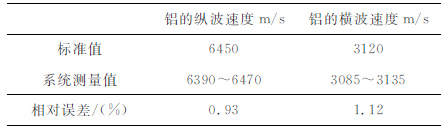
岩石样品的纵波速度、横波速度测量分别通过纵波传感器和横波传感器各自测量.纵波和横波的走时分别通过辨认接收到的波形中纵波和横波的到达时间来确定.其误差主要受样品长度测量、到时波形读取、系统基时测量三方面影响.其中样品长度采用游标卡尺测定,精度为0.01 mm, 对于长度为50mm的样品,其长度引起的相对误差小于0.02%;声波到时是通过辨认采集波形中纵波和横波的到达波形确定,其误差在1~2 数据点(一个数据点为0.02μs),50mm 长度的岩样声波通过时间至少为20μs, 则走时引起的误差小于0.2%;测量系统选用金属铝作为标准材料多次标定(见表 1),速度测量系统误差小于1.12%.因此纵、横波速度理论测量误差小于1.34%.
|
|
表 1 系统标定数据 Table 1 Calibration data of experimental system |
岩石密度测量,采用游标卡尺圆柱形样品的直径和高度,精度为0.01 mm, 采用电子天平测定样品的质量,精度为0.001g, 进而计算样品密度.对于一个重量为20g, 长度50mm, 直径25mm 的样品,其密度测量误差小于0.1%.
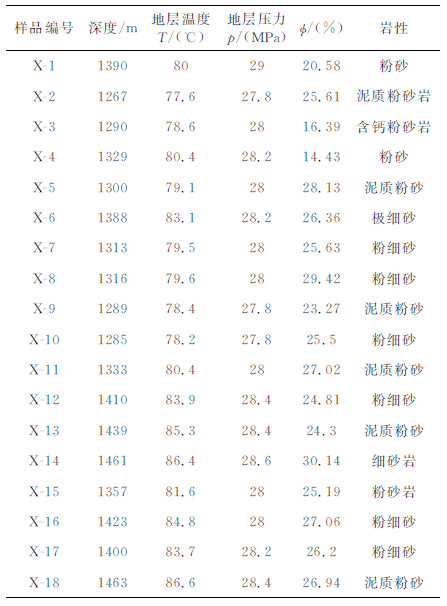
2.2 实验测量分析本文共采集了研究区18块岩心样品,加工成圆柱状(D=25mm),基本信息见表 2.
|
|
表 2 样品基本信息 Table 2 The information of samples |
下面分析了其中的典型样品X-1在不同流体饱和度下(水,气两相)主要弹性参数的响应特征.
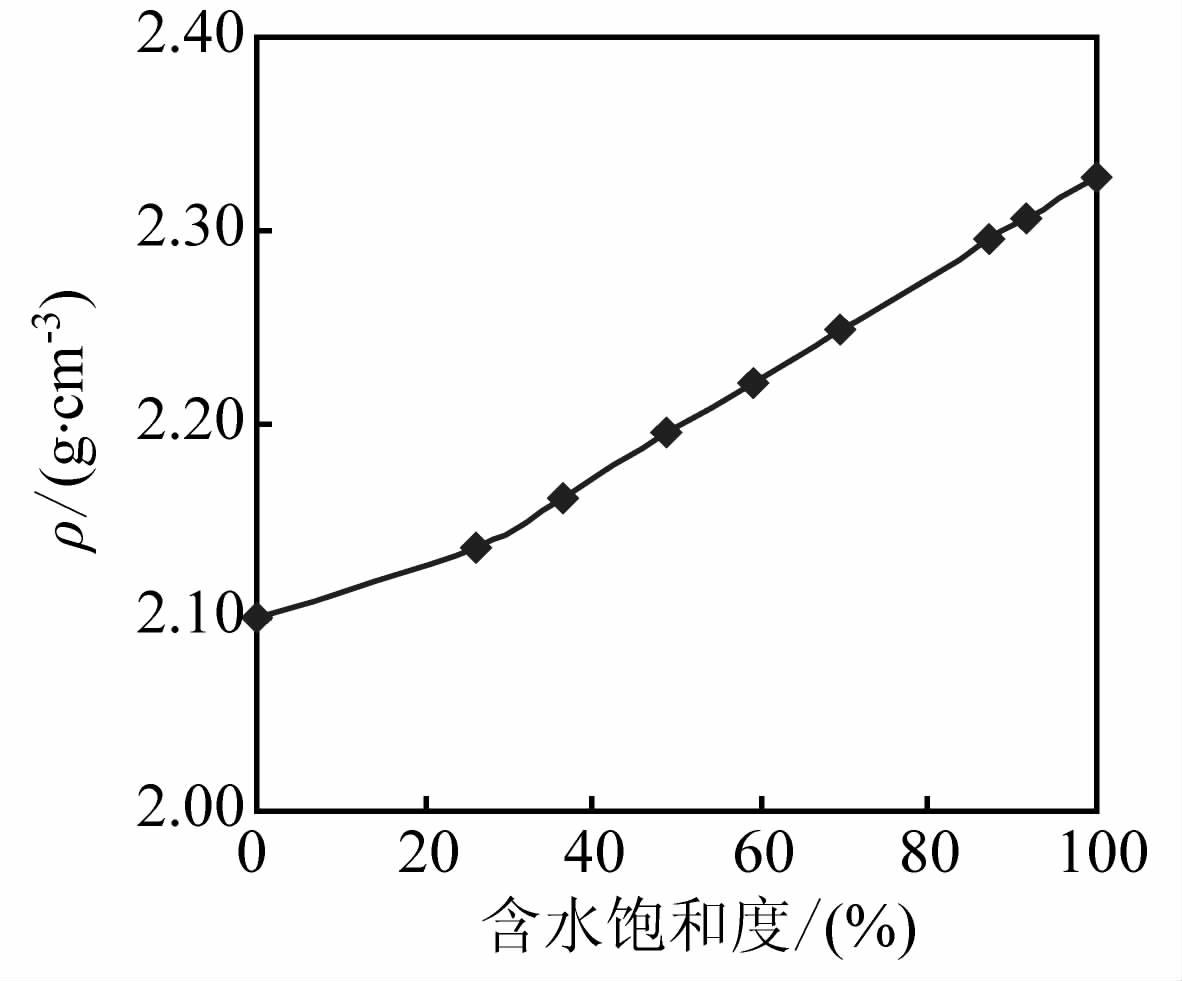
密度(ρ)变化特征(见图 1),随着含水饱和度增加,岩石密度呈近线性增加,变化幅度较小,主因岩石含水饱和度的增加而导致岩石密度的增加.
|
图 1 密度(ρ)随含水饱和度变化特征 Fig. 1 Density variation characteristics with water saturation |
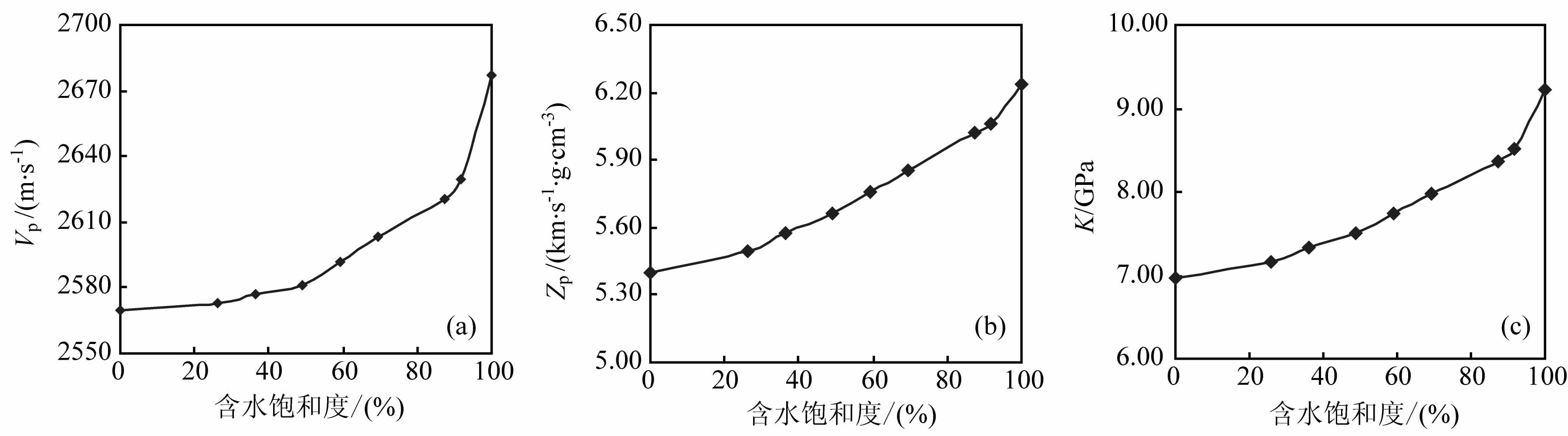
纵波速度(Vp),纵波阻抗(Zp)及体积模量(K)变化特征(见图 2(a-c)):随着含水饱和度增加,岩石的纵波速度增加,在接近饱和气段,纵波速度的变化比较缓慢,在接近饱和水段,纵波速度的变化较快,对岩石样品X-1由完全饱和气到完全饱和水其变化达110m/s.岩石纵波阻抗变化特征基本相似,纵波阻抗同时体现了纵波速度与密度的变化特征,略有差异.此外,体积模量同样随含水饱和度增加呈非线性增加,类似纵波速度及纵波阻抗,变化幅度较大.
|
图 2 纵波速度(Vp)(a)、纵波阻抗(Zp)(b)、体积模量(K)(c)随含水饱和度变化的特征 Fig. 2 P-wave variation characteristics (a),P-wave impedance variation characteristics (b) andbulk modulus variation characteristics (c) with water saturation |
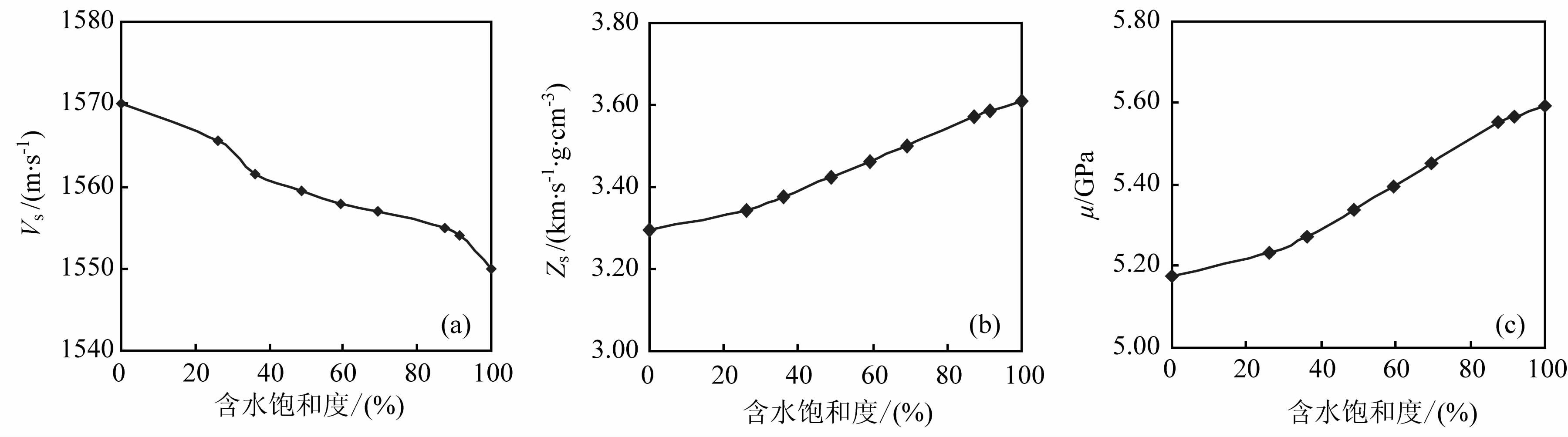
横波速度(Vs)、横波阻抗(Zs)及剪切模量(μ)变化特征(见图 3(a-c)):随着含水饱和度增加,岩石的横波速度相反减小,但变化幅度很小,样品X-1完全饱和气到完全饱和水其变化仅为20m/s, 即横波速度对含水饱和度变化极其不敏感.同样横波阻抗的变化也较小,随含水饱和度增加略有增加.此外,剪切模量测量值随含水饱和度增加略有增加,理论上流体不具备剪切能力,岩石剪切模量仅反映岩石骨架性质,随含水饱和度变化岩石剪切模量是不变的,这也反映了实验测量(密度和横波速度的测量)与理论结果存在少量的误差.此三参数实验测量结果反映了岩石剪切模量对流体不敏感,由于密度的影响而使横波速度及横波阻抗随流体饱和度变化略有波动.
|
图 3 横波速度(Vs)(a)、横波阻抗(Zs)(b)、剪切模量(μ)(c)随含水饱和度变化特征 Fig. 3 S-wave variation characteristics (a) ,S-wave impedance variation characteristics (b),shear modulus variation characteristics (c) with water saturation |
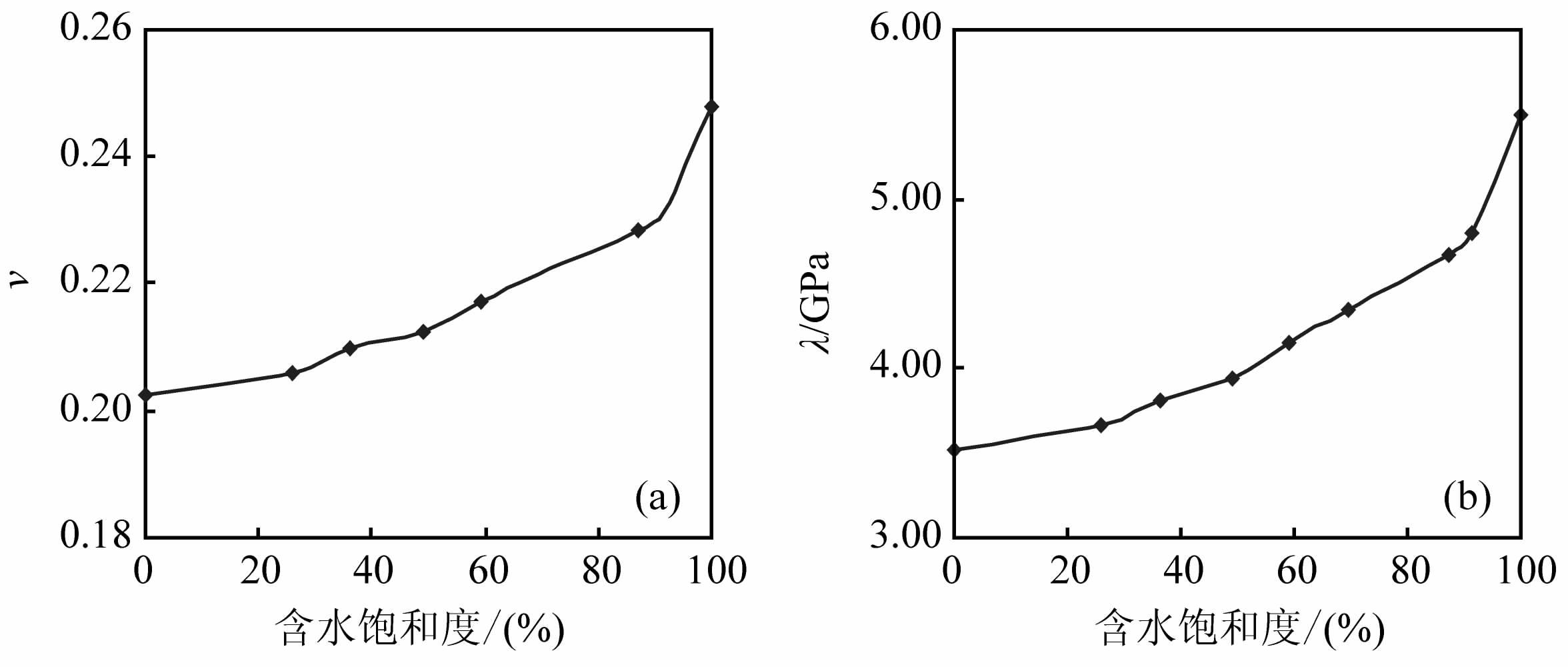
泊松比(ν)变化特征(见图 4a):由于横波对流体不敏感,因此,泊松比参数的行为主要由纵波速度来支配,即泊松比参数的行为和纵波速度的行为有所类似:随着含水饱和度增加,岩石的泊松比参数增加,在接近饱和气段,速度的变化比较缓慢,在接近饱和水段,泊松比参数变化较快.
|
图 4 泊松比(ν)(a)和拉梅系数(λ)(b)随含水饱和度变化特征 Fig. 4 8 Poisson's ratio (a) and the lame coefficient (b) variation characteristics with water saturation |
拉梅系数(λ)变化特征(见图 4b):随着含水饱和度增加,岩石的拉梅系数增加,且在接近饱和水段,拉梅参数的变化很快,可见其对流体较为敏感.
根据前述的实验数据分析结果可定性的得出,不同类型的参数对气体饱和度变化的响应不一样,Vp、Zp、K、ν、λ等对流体有明显的非线性响应,随流体饱和度变化较为敏感,而Vs、Zs、μ 随流体饱和度变化较小,对流体响应不明显.
3 岩石弹性参数分类通过叠前地震反演可获得各岩石弹性参数,各具其物理意义.为了了解岩石弹性参数对流体的响应特征,我们基于岩石物理实验测量观察及岩石物理理论的总结,从岩石弹性参数的流体敏感属性角度提出了3类岩石弹性参数的分类.
第一类是P型参数,如纵波速度Vp、纵波阻抗Zp、体积模量K、纵横波速度比Vp/Vs、ν 等,其反映了固体介质及其结构、流体的耦合.从形变的角度,这类参数对岩石的压缩性及含流体性都比较敏感.
第二类参数称为S 型参数,如横波速度Vs、横波阻抗Zs、剪切模量μ 等,从形变的角度看,这些参数主要响应于岩石的剪切特征.由于流体不传递剪应力,因此S型参数对孔隙中流体不敏感,对岩石孔隙中流体的存在与否以及含量变化都不敏感.不同岩石的剪切模量是不同的,因此,S 型参数有助于区分岩性,但对岩石中所含流体不敏感.
第三类称为组合参数,是根据储层预测目的由不同弹性参数组合构造出的参数.组合参数是多种多样的,这里我们指由P 型参数与S型参数构造而成的对流体敏感的组合参数(针对储层流体预测),如Zp2 -cZs2, λ-cμ,c为常数.试图通过岩石物理实验选取适合研究区的常数c,以达到最大限度的体现流体的性质,从而相比单参数有更高的流体识别能力.
4 构建组合型流体敏感参数在获得各岩石弹性参数的情况下,我们有条件可根据岩石物理理论来建立组合岩石弹性参数,期望获得对孔隙流体更为敏感的岩石弹性参数,提高流体识别能力.
下面说明组合流体敏感参数Zp2 -c1Zs2 和λ-c2μ 的构造方法.

|
(1) |
其中,Ksat, Kdry, K0,Kfl分别为岩石体积模量,干岩石体积模量,岩石矿物体积模量及孔隙流体体积模量;μsat, μdry分别为岩石剪切模量及干岩石剪切模量;φ 为岩石孔隙度.
Boit系数定义为:
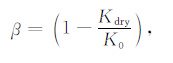
|
(2) |
并定义
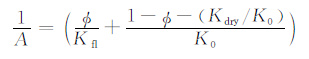
|
(3) |
则Gassmann公式可写成:
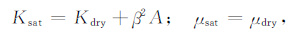
|
(4) |
从(4)式可知,Kdry反映岩石矿物组成及其结构,而岩石孔隙流体只能体现在β2A项.
纵、横波波阻抗与岩石模量关系有:
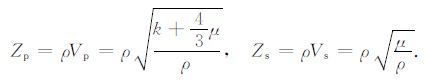
|
(5) |
其中,Zp, Zs 分别为岩石纵波阻抗及横波阻抗;Vp, Vs 分别为岩石纵波速度及横波速度;ρ 为岩石密度.
选择最佳c1 值,使表达式Zp2-c1Zs2 最大化地减少岩石矿物及结构的影响,同时最大程度地反映流体的贡献,如下式:
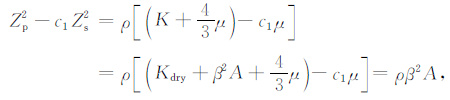
|
(6) |
其中c1 应满足:
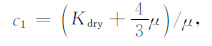
|
(7) |
岩石弹性参数间有如下关系:
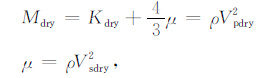
|
(8) |
其中,Vpdry, Vsdry, Mdry 分别为干岩石纵波速度,干岩石横波速度及干岩石纵波模量,则c1 满足:
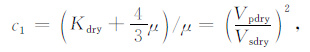
|
(9) |
组合λ-c2μ 参数.
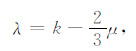
|
(10) |
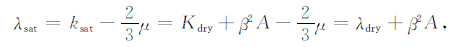
|
(11) |
其中,λsat(λ),λdry分别为岩石拉梅系数及干岩石拉梅系数.
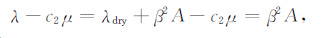
|
(12) |
C2 满足:
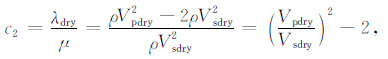
|
(13) |
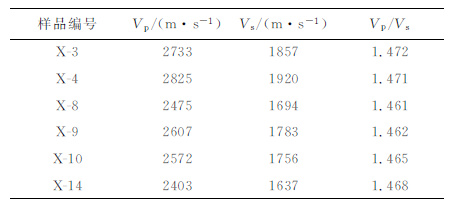
c1,c2 值可由岩石物理实验测量确定.取干岩石样品进行高温高压岩石物理实验,实验条件恢复到岩石所处地层温度和压力,实验岩石样品基本信息及测得岩石纵、横波速度见表 3.
|
|
表 3 部分干岩石样品速度测量结果 Table 3 The velocity of samples |
进一步作Vp-Vp/Vs 交汇分析(见图 5):
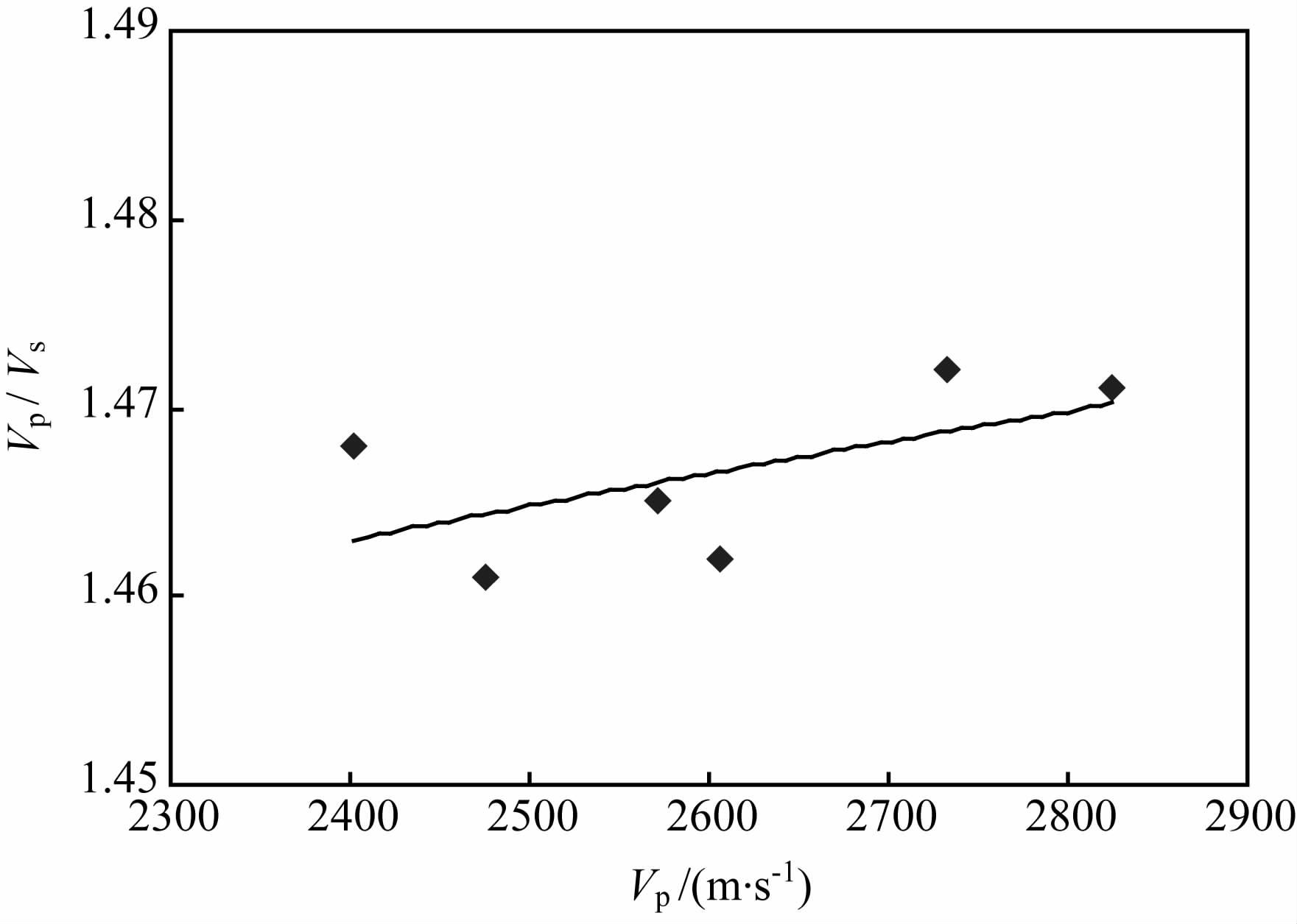
|
图 5 干岩石Vp/Vs 与Vp 交汇特征 Fig. 5 Vp/Vs and Vp intersection for dry rocks |
从实验统计结果可取Vp/Vs(干岩石)为1.466.
进而由公式(9),(13)可分别计算c1 =2.15,c2=0.15.
至此根据本研究区岩石物理性质组合了两个流体敏感弹性参数Zp2 -2.15Zs2, λ-0.15μ.
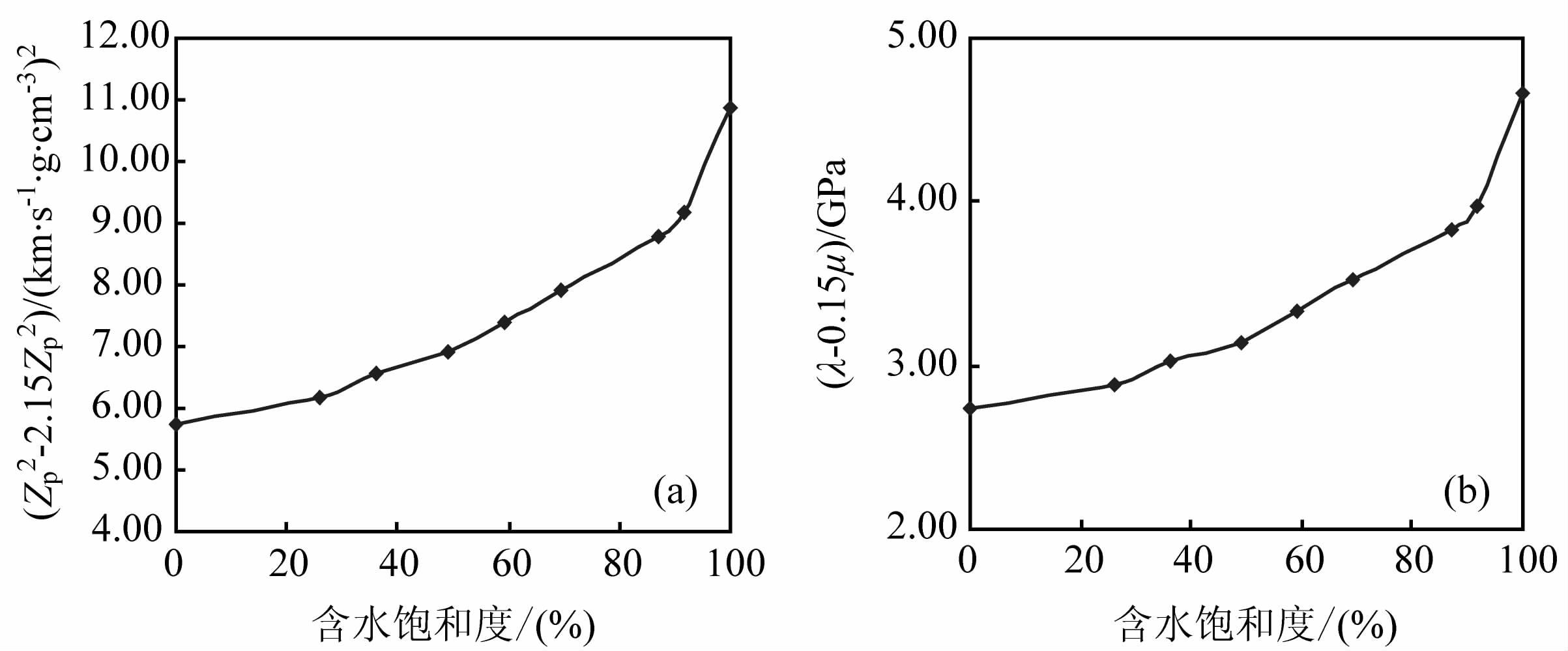
对于新构造出的这两个组合流体敏感参数Zp2-2.15Zs2 和λ-0.15μ,同样可根据岩石物理实验定性分析其随含水饱和度变化特征(见图 6),可见随含水饱和度增加,其有明显的增加趋势,对流体是极为敏感的.
|
图 6 组合参数(Zp2-2.15Zs2)(a)与组合参数(λ-0.15μ)(b)随含水饱和度变化特征 Fig. 6 Combined parameter(Zp2-2.15Zs2) (a) and combined parameter (λ-0.15μ) (b) variation characteristics with water saturation |
在定性分析岩石各弹性参数随流体饱和度变化特征基础上,为了定量描述岩石物理参数对流体的敏感性,以含水的样品为基准定义流体敏感量参数(FS):
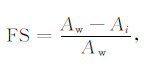
|
(14) |
式中,A为某岩石物理参数,下标w 表示饱和水,下标i表示某种流体状态.
FS值在0~1之间,显然FS越大,则表明参数A对流体就越敏感.
使用上述流体敏感性概念,对实验样品的不同岩石物理参数的流体敏感量进行了统计分析.为了便于比较,首先考虑完全饱和气和完全饱和水的两个极端的情况.即上述定义公式中i代表完全饱和气的情况.通过统计分析获得如下的结果:
从图 7看出,主要岩石弹性参数对流体的敏感量从大到小大致排列如下:

|

|
图 7 不同岩石物理参数流体敏感量比较 Fig. 7 Fluid sensitivity comparation of different rock physical parameters |
考虑各岩石物理参数的流体敏感性随流体饱和度变化特征(图 8).仍然用样品A 的数据为例,选择部分岩石物理参数,计算其在不同含水饱和度下的敏感量参数,获得如下的结果:

|
图 8 岩石物理参数流体敏感量随含水饱和度变化特征 Fig. 8 Fluid sensitivity characteristics of rock physical parameters with wate rsaturation |
从图 8的数据曲线可观察各岩石弹性参数敏感量随含水饱和度的变化情况,其敏感量从大到小仍然基本上按(Zp2-2.15Zs2)、(λ-0.15μ)、λ、ν 、Zp, ρ,Zs, μ 这一顺序.岩石弹性参数流体敏感量分析给出的建议是,如果在实际数据中能获取到合适的岩石弹性参数,就有可能最大程度的识别流体,甚至进一步给出含流体饱和度.
6 应用效果分析在对流体敏感属性岩石物理研究的基础上,应用X 区块叠前地震反演属性进行储层预测.该区块主要钻井有X1、X2、X3,目的层为辫状河沉积,储层岩性为细砂岩,泥质粉砂岩,为典型岩性含气储层.试气结果为井X1的A 段为主力产气层,但测井解释X2、X3井缺失A 段含气储层,研究目标是X1井区含气性描述.
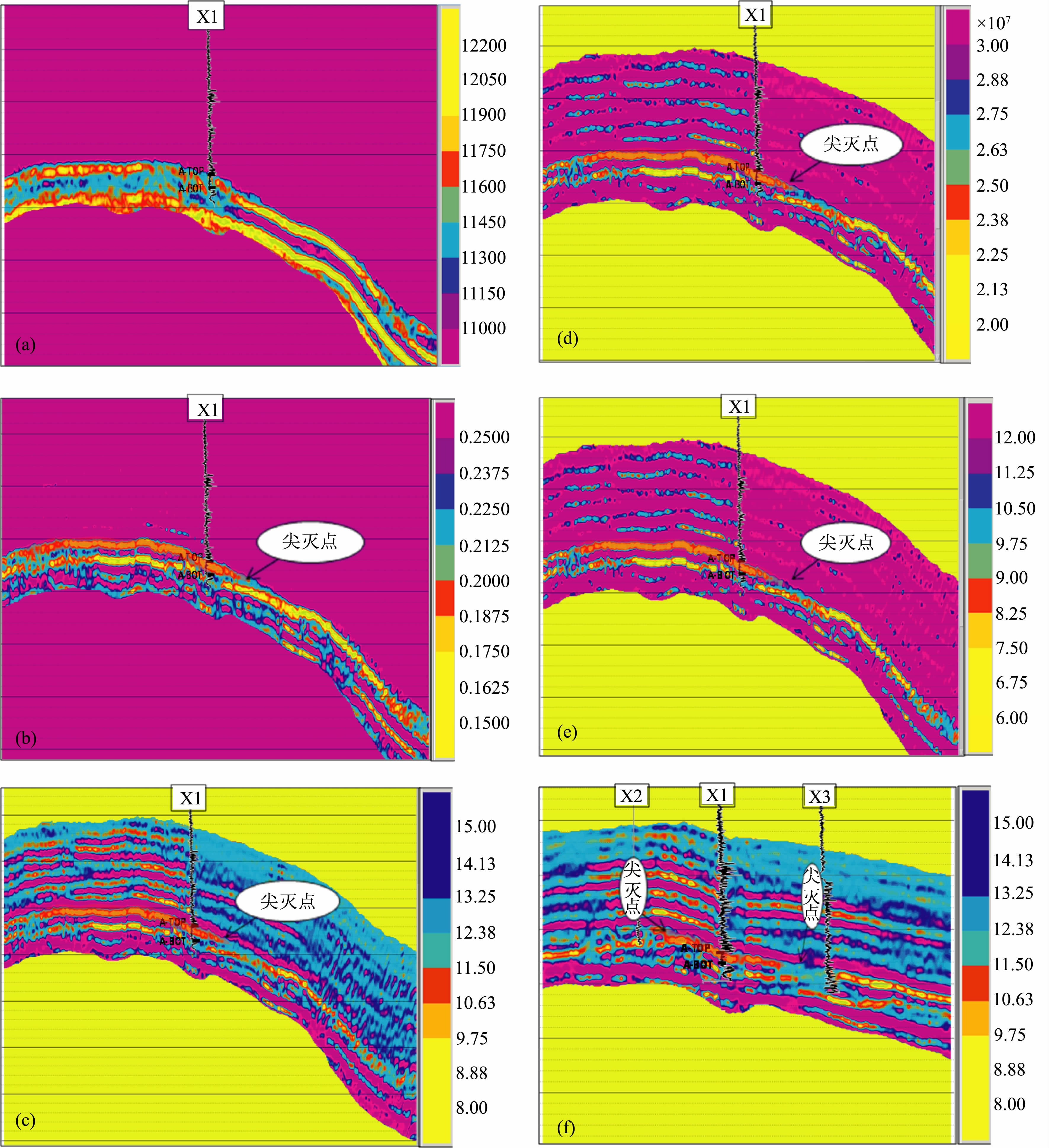
基于X 区块三维叠前地震资料及井X1进行了井控的叠前同步反演.图 9(a-e)分别为过井X1的反演属性纵波阻抗(Zp)、泊松比(ν),拉梅系数(λ)及组合属性Zp2-2.15Zs2 和λ-0.15μ.结果表明,仅用纵波阻抗(见图 9a)不能描述主要含气砂体A 段(A-TOP到A-BOT 段)的尖灭边界,整个A 段含气砂体与右边砂体几乎连为一体(黄色指示有利含气砂体),而叠前属性ν、λ 能很好地区分出含气储层及A段东向的尖灭点边界(分别见图 9b、9c),组合属性Zp2-2.15Zs2, 及λ-0.15μ 同样能非常清晰的刻画含气储层尖灭点(分别见图 9d、9e).图 9f为过X2-X1-X3连井叠前λ 属性剖面,可清晰见X1 井A 段含气砂体向X2 及X3 两方向的尖灭点,在仅用X1井约束反演的前提下,能得到与X2、X3井吻合的结果,无疑用λ 等叠前流体敏感属性预测的X1 井区含气分布将对勘探生产具有重要的指导意义.
|
图 9 纵波阻抗、泊松比、拉梅系数(a-c);组合参数Zp2-2.15Zs2(d);组合参数λ-0.15μ(e);过连井X2-X1-X3拉梅系数(f).插入曲线为GR. Fig. 9 P-impedance, Poisson′ratio, Lame coefficient (λ) (a-c); Combined parameter (Zp2-2.15Zs2) (d),combined parameter (λ-0.15μ) (e),Lame coefficient (λ) profile through X2-X1-X3 wells (f). And inserted cures are GR. |
(1) 根据岩石物理参数对流体的不同响应特征,将叠前地震属性进行了分类,有助于对叠前地震属性物理意义的理解,及其适用性分析.
(2) 依据岩石物理理论建立的组合敏感参数,尽可能的排除了流体因素之外的岩石骨架的影响,对孔隙流体更为敏感.
(3) 根据统计学原则,定量给出各弹性参数流体敏感量,进行弹性参数流体敏感性的定量分析,以评价岩石对流体的敏感量及岩石随含水饱和度变化时流体敏感量的变化特征.
(4) 岩石物理研究为叠前弹性参数反演的油气解释提供了物理依据及指导.
致谢感谢中国科学院地质与地球物理研究所岩石物性实验室提供的实验条件,同时感谢杨伟、张永工程师在岩石物理实验过程中提供的帮助.
| [1] | Mavko G, Mukerji T, Dvorkin J. Rock Physics Hankbank. Cambridge: Cambridge University Press, 1998 : 51 -55. |
| [2] | Shuey R T. A simplification of the Zoeppritz equations. Geophysics , 1985, 50(4): 609-614. DOI:10.1190/1.1441936 |
| [3] | Fatti J L, Vail P J, Smith G C, et al. Detection of gas in sandstone reservoirs using AVO analysis: a 3-D seismic case history using the Geostack technique. Geophysics , 1994, 59(9): 1362-1376. DOI:10.1190/1.1443695 |
| [4] | Castagna J P, Smith S W. Comparison of AVO indicators: A modeling study. Geophysics , 1994, 59(12): 1849-1855. DOI:10.1190/1.1443572 |
| [5] | Smith G C, Sutherland R A. The fluid factor as an AVO indicator. Geophysics , 1996, 61(5): 1425-1428. DOI:10.1190/1.1444067 |
| [6] | Goodway B, Chen T, Downton J. Improved AVO fluid detection and lithology discrimination using Lame petrophysical parameters "λρ", "μρ" & "λ/μ" from P and S inversion. SEG Expanded Abstracts , 1997, 16: 183-186. |
| [7] | Russell B H, Hedlin K, Hilterman F J, et al. Fluid -property discrimination with AVO: A Biot-Gassmann perspective. Geophysics , 2003, 68(1): 29-39. DOI:10.1190/1.1543192 |
| [8] | 邓继新, 王尚旭, 李生杰, 等. 砂岩储层地震属性参数对孔隙流体的敏感性评价. 石油学报 , 2006, 27(6): 55–59. Deng J X, Wang S X, Li S J, et al. Sensitivity evaluation of seismic attribute parameters for sandstone reservoir to pore fluid. Acta Petrolei Sinica (in Chinese) , 2006, 27(6): 55-59. |
| [9] | 尹川, 顾汉明. AVO流体指示因子的敏感性分析. 工程地球物理学报 , 2008, 5(1): 120–125. Yin C, Gu H M. The sensitivity analysis of AVO fluid factors. Chinese J. Eng. Geophys. (in Chinese) , 2008, 5(1): 120-125. |
| [10] | 李维新, 史謌, 王红, 等. 岩石物理弹性参数规律研究. 地球物理学进展 , 2007, 22(5): 1380–1385. Li W X, Shi G, Wang H, et al. The study on the relationships of elastic properties of rock physics. Progress in Geophysics (in Chinese) , 2007, 22(5): 1380-1385. |
| [11] | 王东, 张海澜, 王秀明. 部分饱和孔隙岩石中声波传播数值研究. 地球物理学报 , 2006, 49(2): 524–532. Wang D, Zhang H L, Wang X M. A numerical study of acoustic wave propagation in partially saturated poroelastic rock. Chinese J. Geophys. (in Chinese) , 2006, 49(2): 524-532. |
| [12] | 云美厚, 管志宁. 储层条件下砂岩纵波和横波速度的理论计算. 石油物探 , 2002, 41(3): 289–293. Yun M H, Guan Z N. The estimation of P and S-wave velocities in sandstone under in-situ conditions. Geophysical Prospecting for Petroleum (in Chinese) , 2002, 41(3): 289-293. |
| [13] | 伍向阳, 陈祖安, 孙德明, 等. 静水压力下砂岩孔隙度变化实验研究. 地球物理学报 , 1995, 38(S1): 275–280. Wu X X, Chen Z A, Sun D M, et al. An experimental study of changes of porosity of sandstones with pressure. Chinese J. Geophys. (in Chinese) , 1995, 38(S1): 275-280. |
| [14] | 史謌, 沈联蒂. 根据波速-压力关系评价岩石岩性、物性的实验研究. 地球物理学报 , 1990, 33(2): 212–219. Shi G, Shen L D. Evaluations of the lithological character and physical property of rocks from the relation between wave velocity and pressure- an experimental study. Chinese J. Geophys. (in Chinese) , 1990, 33(2): 212-219. |
| [15] | 王大兴, 辛可锋, 李幼铭, 等. 地层条件下砂岩含水饱和度对波速及衰减影响的实验研究. 地球物理学报 , 2006, 49(3): 908–914. Wang D X, Xin K F, Li Y M, et al. An experimental study of influence of water saturation on velocity and attenuation in sandstone under stratum conditions. Chinese J. Geophys. (in Chinese) , 2006, 49(3): 908-914. |
| [16] | 沈联蒂, 史謌. 岩性、含油气性、有效覆盖压力对纵-横波速度的影响. 地球物理学报 , 1994, 37(3): 391–399. Shen L D, Shi G. Effect of lithologic character, petroleum and effective overburden pressure on compressional wave and shear. Chinese J. Geophys. (in Chinese) , 1994, 37(3): 391-399. |
| [17] | Wood A B. A Textbook of Sound. New York: The MacMillan Co, 1995 : 360 -360. |
| [18] | Gassmann F. Uber die elastizitat poroser medien. Vier. Der Nater Gesellschaft , 1951, 96(1): 1-23. |
 2012, Vol. 55
2012, Vol. 55