2. 中国地震局地壳应力研究所, 北京 100085
2. Institute of Crustal Dynamics, China Earthquake Administration, Beijing 100085, China
众所周知,大震后通常伴随着大量的余震活动.由地震数据观测统计总结出的Omori[1]经验关系描述了余震序列随时间的发生频度:即主震后余震个数随时间推移而逐步减小的变化过程.Omori[1]经验关系对于单位时间t内大于某一震级的余震的个数n的描述满足n(t)=K/(t+c)p,其中K,p和c为常数,p值通常等于1.从统计意义上讲,尽管全球大多数地震满足该经验准则,但由于其缺乏相应的物理基础,在实际地震中,出现很多不一致的情况.位于圣安德列斯断裂上的1989 年LomaPrieta地震(MS6.9)与1811到1812年间美国中部的NewMadrid地震(MS7.0~7.4)的余震的时空分布有着明显的区别.前者余震多分布于主震后1~2a的时间内,而后者余震延续时间很长,而且大于4级的余震个数至今为止并无明显减少的趋势[2].
过去的几十年里,地震科学研究发现地震不论在近场(<2~3 个断层长度)还是远场都可以诱发(触发)余震[3-4],余震的产生机制一般可分为静态和动态触发.前者可由主震的同震位移造成主断层内部以及周边应力场变化;而动态触发机制则来源于地震波能量辐射传播造成的主断层周边断裂的失稳,动态应力波的传播也可导致远距离的地震诱发.当然,还可能有其他的因素影响了余震的时空分布的变化.针对2001年MS8.1昆仑山口西地震而言,Gomberg等[5]认为断层前缘受断层动态破裂传播方向性的影响触发了余震,特别是对于断层长度较长的地震,破裂传播方向性的影响尤其明显.Gomberg等[5]还指出,动态触发的地震活动性速率与破裂传播的方向性相一致,从而造成了余震多聚集在主震断层东部这一现象.然而,2001 年昆仑山口西地震不仅产生了400km 长的地表破裂,且动态破裂在断层上的传播速度远远大于剪切波速度3.7~3.9km/s, 经过100km 的传播之后破裂速度甚至达到5km/s[6].进一步,Bouchon和Karabulut[7]发现主震后的大多数的余震并没有发生在主断层的破裂面上,而是位于主震断层外的次生破裂上,余震的触发也可能由超剪切破裂产生的高能量地震波辐射所产生的扰动所致.2008年MS8.0汶川地震的余震绝大多数都发生在主断层带内.更为明显的差别在于昆仑山破裂是沿断层的左倾走滑型,而产生的8个较大余震中只有一个MW5.1 余震与主震的震源机制相似,为走滑型,其余余震的震源机制都表现出正断层或逆断层类型[7];而汶川地震除了青川—平武断裂周围的余震呈现走滑类型之外,主断层上余震震源机制基本都与主震相同,为逆断层[8].
然而,2001 年MS8.1 昆仑山口西地震和2008年MS8.0汶川地震发生于同一构造单元,即巴颜喀拉地块.但是,这两个大地震的余震序列无论在余震的个数、空间分布特征还是持续时间上都表现出了显著的差别.无论从触发机制的方向性的影响,还是超剪切破裂的作用,都仅仅能部分地解释昆仑山口西地震与汶川地震余震序列的时空分布的差异,不能够完全解释余震个数和持续时间上的差异.
众所周知,没有任何一个单独的触发机制能够解释所观测到的丰富的地震触发和激活过程,究其根源,其余震的发生与主震后的应力场变化可能有密不可分的关系.无论是同震位移还是动态应力波都可以造成主震破裂区域(包括断层面以外的区域)附近的应力场的变化,而该区域应力变化是触发余震的断层滑动的一个根本原因.岩石力学实验和台网观测表明,无论是静态还是瞬态的近场或远场触发的地震活动性都源于断层内部摩擦失稳模型,而该模型又基于独立自由的滑块—弹簧模型与滑动速率和状态相依赖的摩擦定律(Rate-and State-Dependent Friction Law)[9].Toda等[10]在估算汶川地区地震活动性速率时所得到的余震持续时间约为10~100a.显然,这样的时间尺度存在着一个量级的误差范围,对于下一个十年乃至三十年的地震活动性概率预报显然是过于宽泛和不准确的.
本研究从最基本的宏观库仑摩擦准则出发,基于滑动速率和状态相依赖的摩擦定律,采用不同力学模型求取断层内剪应力的加载速率,阐述了余震持续时间同应力状态之间可能存在的相互联系,在深入了解MS8.1昆仑山口西地震余震序列时间短、个数少等特征的基础上,将其与2008 年MS8.0 汶川地震序列进行了比较和对比,正确地认识了余震的持续时间对未来地震灾害评估的重要意义.
2 地震资料与地质背景2001年11月14日,在青藏高原北部巴颜喀拉与祁连—柴达木两大块体之间北西西向分界断裂——东昆仑山断裂带中西部库赛湖段发生了一次罕见的特大地震(MS8.1)——昆仑山口西地震[11].该地震的震源深度15km[12],断层的破裂长度约为400~500km[7-13],发震断层位于青藏高原北部,显现的破裂是沿着昆仑山断层呈左倾走滑.
2001年MS8.1昆仑山口西地震主震之后,余震个数较少.观测数据的处理和分析结果表明,至2010年12月31日,共发生大于M5.0的余震16个(数据来自中国地震台网中心,M5.0代表数据目录中任何类型的震级超过5.0的地震都被统计在内).最后一次大于M5.0 的余震发生于2006 年1 月6日;共发生大于M4.0的余震62个;发生大于M2.0的余震118个.图 1a显示了MS8.1 昆仑山口西地震序列和2008年MS8.0 汶川地震序列大于M2.0的所有地震发震位置.美国哈佛大学(HRV)给出了主震以及较大余震的震源机制解:主震断层面近乎直立,为走滑断层;而8 个较大余震中只有一个MW5.1余震与主震的震源机制相似,其余余震的震源机制都表现出正断层或逆断层类型[7].最大的余震是2001年11 月18 日发生的MS5.6 地震,最大余震震级比主震小2.5个震级.图 1b给出了昆仑山余震序列随时间变化规律.
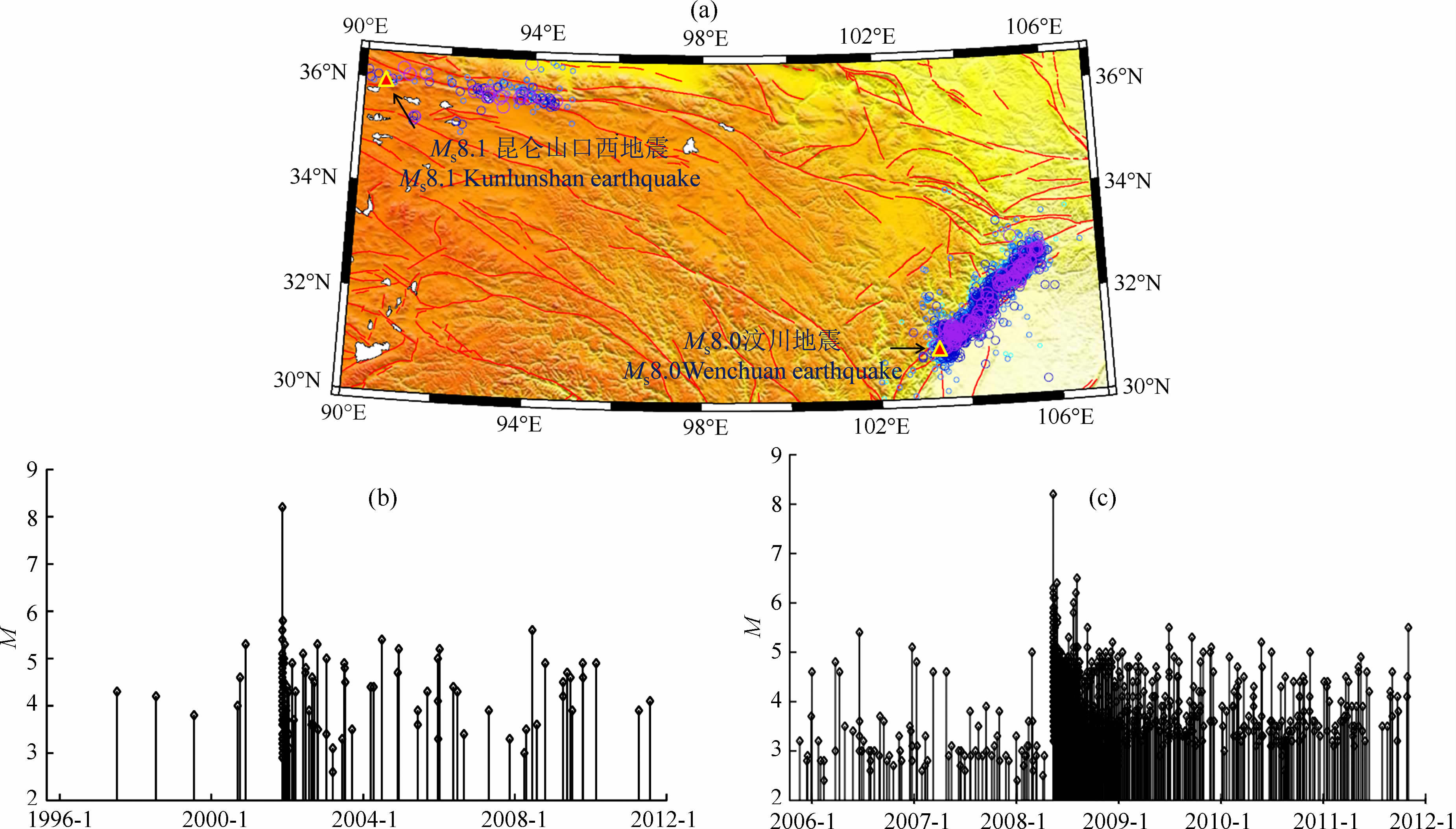
|
图 1 (a)昆仑山口西地震和汶川地震大于M2.0余震空间分布;(b, c)分别为2001年MS8.1昆仑山口西地震和2008年MS8.0汶川地震余震序列震级随时间变化规律 Fig. 1 (a)The aftershocks (M≥2. 0) spatial distribution of the Ms 8. 0 Wenchuan earthquake and Ms 8.1 Kunlunshan earthquake;(b, c) Aftershock sequences following these large earthquakes |
2008年5月12日四川省汶川县发生了MS8.0地震,震中位于龙门山断裂的中段,震源深度14km(中国地震台网中心).而汶川地震的破裂长度超过300km, 该破裂延着北东走滑、西部倾斜的龙门山逆冲断层带向前扩展.地震引起的地壳深部的岩石破裂长达300多公里[14-15].造成了及其巨大的经济损失和人员伤亡.至2010年12月31日,已有大于M5.0的余震123个,大于M4.0的余震804个,大于M2.0的余震2065个(如图 1a).最近一次M5.0的余震发生在2010年11月15日.余震的最大震级为MS6.5,且余震大多分布在主震断层带内,且与主震的震源机制基本相同[8].图 1c为汶川地震余震序列随时间变化规律.比较图 1b和1c,说明MS8.0汶川地震后余震发震的个数远远大于MS8.1 昆仑山口西地震的.
3 滑移速率和状态相依赖的摩擦定律滑移速率和状态相依赖的摩擦本构关系为我们提供了一个基本框架以对断层属性进行复杂的定量实验观测[16-19].滑移速率和状态相依赖的摩擦定律还表达了稳态滑移过程中观测到的瞬时速率与稳态速率的相关性.该模型在实验室中模拟了与时间相关的自发非稳态滑动[17, 19-25]、震后滑动[26]和沿板块边界的地震复发周期[27-28].
前人文献中讨论过一些表述滑移速率和状态相依赖的断层应力.最简单的是由Ruina[19] 基于Dieterich[17, 20]提出的.如果将其推广为多态变量[21],可以写作
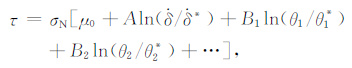
|
(1) |
其中,τ和σN 分别为剪切应力和正应力,$\dot{\delta }$ 是滑移速率,θi是状态变量;参数μ0、A和Bi为通过实验得到的系数;具有星号的项为标准化常量.Aln($\dot{\delta }$/$\dot{\delta }$* )表征了类似于小形变的不规则体或障碍体产生于滑动面的黏性阻力.Biln(θi/θ*i)表征了与接触时间成正比的两表面间的化学附着[4].实验得到,状态变量θ 与滑移速率$\dot{\delta }$ 和正应力σN 有关,有dθi=
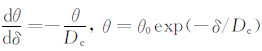
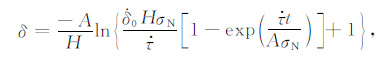
|
(2) |
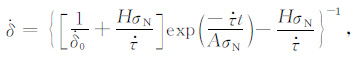
|
(3) |
其中,$\dot{\delta }$0 为初始滑动速率,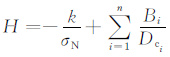
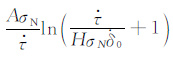

|
(4) |
|
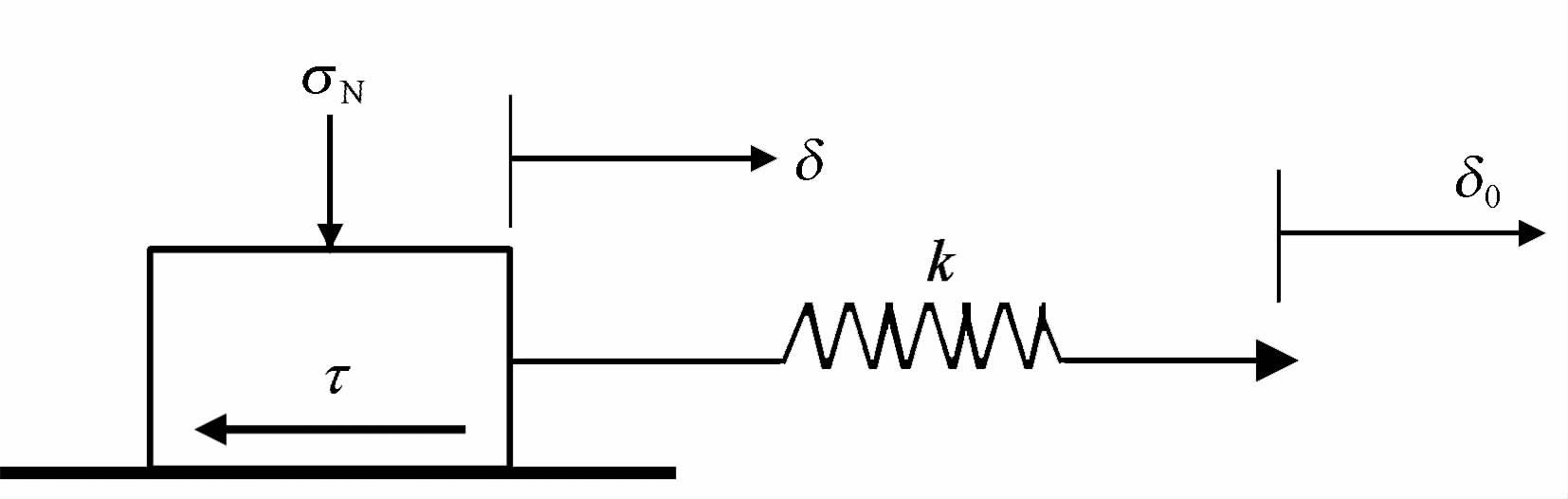
图 2 弹簧-滑块模型示意图,由此得到的滑块运动方程为τ =-k(δ-δ0) Fig. 2 Spring-Slide Block Model withkinematic equation τ =-k(δ-δ0) |
在初始时刻t0,由于主震使得周围断层突然有一个Δτ 的应力加载,那么基于弹簧-滑块模型(如图 2),有kδ0 =τ0(t<t0)和kδ0 =τ0 +Δτ(t>t0).为保证在t=t0时滑动位移和滑动速率是连续的,有δ(t=t0 -ε)=δ(t=t0 +ε)和$\dot{\delta }$(t=t0 +ε)=$\dot{\delta }$(t=t0 -ε)exp[Δτ/(AσN)],即滑动速率增加了exp[Δτ/(AσN)]倍.此时失稳时间则变为
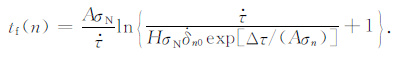
|
(5) |
将公式(4)代入公式(5)可得地震(事件)次数:
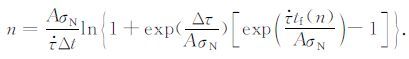
|
(6) |
此时,n和tf(n)都是离散变量.假设很多类型的地震是通过背景场活动性的扰动引起,而这个扰动又来自于之前的地震造成的应力场状态的改变,我们将瞬态地震活动性速率R定义为R=dn/dtf(n),并把n和tf(n)都看做连续函数,当参考剪切应力变化率$\dot{\tau }$r 与实际剪切应力变化率$\dot{\tau }$相等时,有
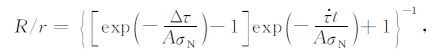
|
(7) |
其中,r是在参考场或背景场下的剪切应力变化率$\dot{\tau }$r 下的常数稳态背景活动性.Dieterich[29-30]提出余震是主震之后一次又一次的应力变化所引起,且每个余震事件是相互独立的,从而余震的成核周期被扰乱.
3.1 利用地震活动性求取剪应力变化率
余震的持续时间ta 是指对于余震地震活动性恢复到背景场的特征时间,与剪应力的加载速率相关,可定义为ta = AσN/$\dot{\tau }$.ta 在公式(7)中就是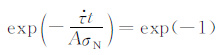
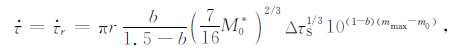
|
(8) |
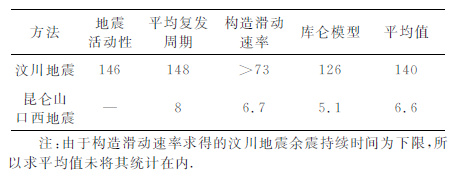
其中,b为该区域的b值,按照b= 0.43/(mave -mmin)[32] 求取,mmin、mave和mmax分别为该区域最小震级、平均震级和最大震级,m0 为起算震级,M0* 为震级为m0 的地震的地震矩,ΔτS 为静态应力降.对于汶川地震,通过输入1970年到2008年5 月之前的二级以上的地震目录,并进行半径为20km 的平滑处理,可以得到在北纬30°—34°东经102°—107°范围内的背景场地震活动性r为0.13×10-9/(a·m2),ΔτS =2.7MPa[33],mmax为汶川地震8.0级,m0 为2级,由于小震个数可能统计不完备,所以在求b值时取mmin为4级,求得b值为0.8.根据M0 =109.1+1.5mS可以求出震级为m0 的地震的地震矩M0* .由此,我们计算得到$\dot{\tau }$=6.86×10-4 MPa/a.如果取A=0.01和0.005[18],假设震前震后正应力σN 值为常数10 MPa[34],利用公式ta =AσN/$\dot{\tau }$[18]得到MS8.0汶川余震的持续时间ta 分别约为146a和73a.
对于昆仑山口西地震而言,由于该区域地震台站布设较少,而且昆仑山口西地震发生较早,得到的1970—2001 年震前的地震目录中没有二级到三级的地震记录.所以,地震目录的不完整使得我们不能够用公式(8)来计算剪应力变化率$\dot{\tau }$.
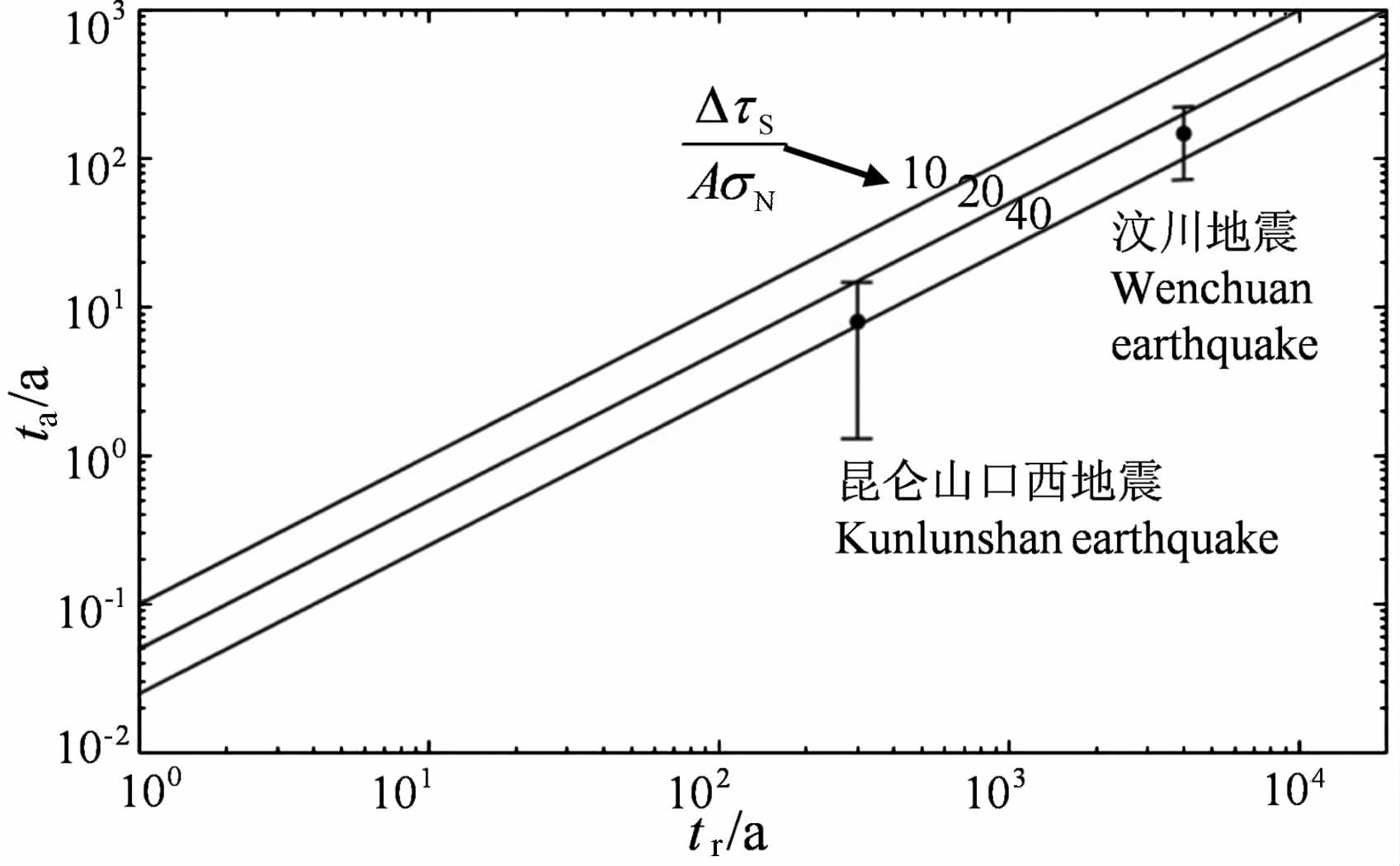
3.2 利用平均复发周期和构造滑动速率求取剪应力变化率由于剪应力加载速率$\dot{\tau }$可近似等于ΔτS/tr, 其中tr 为大震的平均复发周期,ΔτS 为主震断层的静态应力降,因此有ta =AσN/$\dot{\tau }$=trAσN/ΔτS[18].近期研究成果表明,汶川地震的平均地震复发周期为4000a[35],由此可得到$\dot{\tau }$=6.75×10-4 MPa/a.那么,采用A=0.01 和0.005,余震的持续时间ta 分别约为73a和148a, 这一结果与上面方法求得的结果基本一致.张培震等[35]指出利用地震地质考察和地震波反演求得的最大同震位移得到的汶川地震的复发周期范围为2000~6000a, 如果取A=0.01,这样所求得的余震的持续时间ta 的范围为74~222a.昆仑山口西地震近期研究成果给出,平均地震复发周期tr 为300±50a[36],如取A=0.01,正应力σN 仍取10MPa, 剪切应力降ΔτS =3.75MPa[37]求得$\dot{\tau }$=1.25×10-2 MPa/a, 余震的持续时间ta 为8a, ta 的范围为6.7~9.3a.图 3 显示了A=0.01时,按照复发周期计算得到的汶川地震和昆仑山口西地震的余震持续时间的差别,从理论上解释了昆仑山口西地震过后余震持续时间较短,而汶川地震过后两年多的时间内仍然余震频繁的原因.
|
图 3 A=0.01时,余震持续时间ta 与主震复发周期tr 预测图 Fig. 3 Predicted aftershocks duration ta against main shock recurrence time tr with A=0.01 |
然而,采用平均地震复发周期tr 估算余震持续时间ta 显然存在一定的局限性.一般来讲,地震复发周期随着地震的大小成比例变化,使得计算得到的余震活动性的持续时间也与主震的震级有着依赖关系[18, 38].由ta =trAσN/ΔτS 估算主震后的余震持续时间,隐含了余震的持续时间同震级大小成正比的变化关系.而使用$\dot{\tau }$=μ$\dot{\delta }$tect/W公式可以得到不依赖于主震震级的余震活动性持续时间.取剪切模量μ =3.0×1011dyn/cm2,A=0.01,$\dot{\delta }$tect 为构造滑动速率,W为断层的特征尺度[38].取汶川断层宽度约为22km[39],单条断层的构造滑动速率不超过1mm/a[35],可得剪应力变化率$\dot{\tau }$不超过1.36×10-3 MPa/a, 从而得到余震的持续时间不少于73a.昆仑山断层宽度约为20km[40],构造滑动速率为10mm/a[37],可得剪应力变化率$\dot{\tau }$为1.5×10-2 MPa/a, 从而得到余震的持续时间为6.7a.与前面使用地震复发周期所计算出的结果基本一致,但略小一些.从而也说明利用主震的复发周期可能会过高地估计了余震的持续时间.
3.3 利用库仑模型求取剪应力变化率除了上述方法之外,还可以通过库仑模型中应力与应变的关系求得剪应力变化率.由于$\dot{\tau }$= dτ/dt=μdε/dt=μ$\dot{\varepsilon }$,μ 为剪切模量,而ε = du/dx~u/W,其中W为断层宽度,u为平均滑动位移,应变率$\dot{\varepsilon }$ =$\dot{u}$/W=u/(T·W),T为时间.又因为应力降ΔτS =Cμu/W,C为几何系数[4].这样剪应力变化率$\dot{\tau }$= ΔτS/(C·T)只与剪切应力降和主震的复发周期T有关.对于2008年汶川地震而言,剪切应力降为2.7 MPa[33],平均复发周期约为4000a[35],由于汶川断层为逆冲兼走滑,所以C取8/(3π),得到$\dot{\tau }$=7.95×10-4 MPa/a, 略大于上面求得的$\dot{\tau }$=6.86×10-4 MPa/a.如果仍取A=0.01,这样得到的余震的持续时间ta 为126a.同样,对于2001年昆仑山口西地震来说,应力降为3.75 MPa[37],复发周期约为300a, 由于昆仑山断层为走滑断层,所以C取2/π,得到$\dot{\tau }$=1.96×10-2 MPa/a, 可以得到余震的持续时间ta 为5.1a.当取A=0.01,由上述三种方法求得剪切应力变化率和余震的持续时间如表 1和表 2所示.
|
|
表 1 汶川地震与昆仑山口西地震剪切应力变化率(MPa/a)对照表 Table 1 Shear stress rate of Wenchuan and Kunlunshan earthquakes |
|
|
表 2 汶川地震与昆仑山口西地震余震持续时间(a)对照表 Table 2 Time duration of Wenchuan and Kunlunshan aftershock sequences |
小到0.01 MPa的库仑应力扰动ΔCFS(CoulombFailureStresschange)也能够影响余震的分布[41-43].而0.01 MPa的应力扰动又仅仅是在地震过程中应力降的一小部分,这也就是库仑应力变化“加强"或“促进"了地震的发生,而不是产生一个地震的原因[44].有研究表明,汶川地震使得部分鲜水河断层、昆仑左旋断层和岷江逆冲左旋断层的应力向失稳方向逼近了0.2~0.5bar, 也就是说相当于在这些断层上经历了十年的构造应力集中[10].这也说明,汶川地震后的应力场变化可能造成了大量的小余震提前失稳,而这种现象在昆仑山口西地震后并不明显.
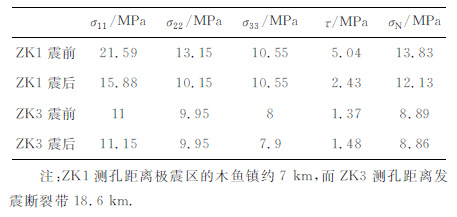
在2008年5月6日,中国地震局地壳应力研究所等单位恰好在震区北端青川断裂带内部和断裂下盘的四川盆地里完成了深度400余米的四个测孔的水压致裂绝对应力测量.ZK1深钻孔是经过震前震后两次测量、距离断层最近的钻孔,距离极震区的木鱼镇仅约7km.震前、震后的最大水平主压应力σ1分别约为21.6 MPa和15.9 MPa, 最小水平主应力σ3 不变,约为10.6 MPa[34].汶川地震主断层是一次以逆冲为主、兼具小量右旋走滑分量的断层,取主断层上平均倾角θ 为33°[39, 45].由公式τ = 1/2(σ1 -σ3)siN2θ和σN =1/2(σ1+σ3)-1/2(σ1-σ3)cos2θ可以获得倾角为33°的逆断层的剪切应力τ 和正应力σN,从而得到震前、震后剪应力变化ΔτS 为2.6 MPa, 正应力变化ΔσN 为1.7 MPa.库仑应力变化ΔCFS=ΔτS -μ″ΔσN,μ″ 为含孔隙压力变化影响的摩擦系数.哈佛大学地震目录[46]指出,在地震造成的应力变化中,使用μ″ =0.而Reasenberg和Simpson[41]在对LomaPrieta余震的研究中使用了μ″=0.2.所以,我们取其平均值μ″=0.1.这样计算出的ΔCFS =2.43MPa, 这与Toda等[10]得到的-0.5~0.5bars的库仑应力分布有较大的差别,也说明Toda等[10]低估了汶川地震主震断层内部的库仑应力状态.
正如上面所述,假如汶川地震和昆仑山口西地震的A和正应力σN 都相等,剪应力变化率$\dot{\tau }$应与余震持续时间ta 成反比.图 4a指出在不同的库仑应力变化率下,同样一个2.43MPa的应力扰动ΔCFS对于余震的活动性变化率的影响是十分显著的.对汶川地震和昆仑山口西地震而言,主震对余震的持续时间的影响也有很大的差别.从图 4b中可以明显看出,汶川地震的余震地震活动性衰减较慢,而昆仑山口西地震产生的余震序列相对衰减较快.这也说明了汶川地震余震的持续时间远长于昆仑山口西地震的.若将图 4b的曲线对时间积分,就可以半定量地比较这两个地震的余震的个数.汶川地震的曲线积分面积远远大于昆仑山口西地震的,这也说明了汶川地震后的余震个数应该远大于昆仑山口西地震的余震个数.所以,这两个地震的余震个数和持续时间之间的差别大相径庭也就不难理解了.
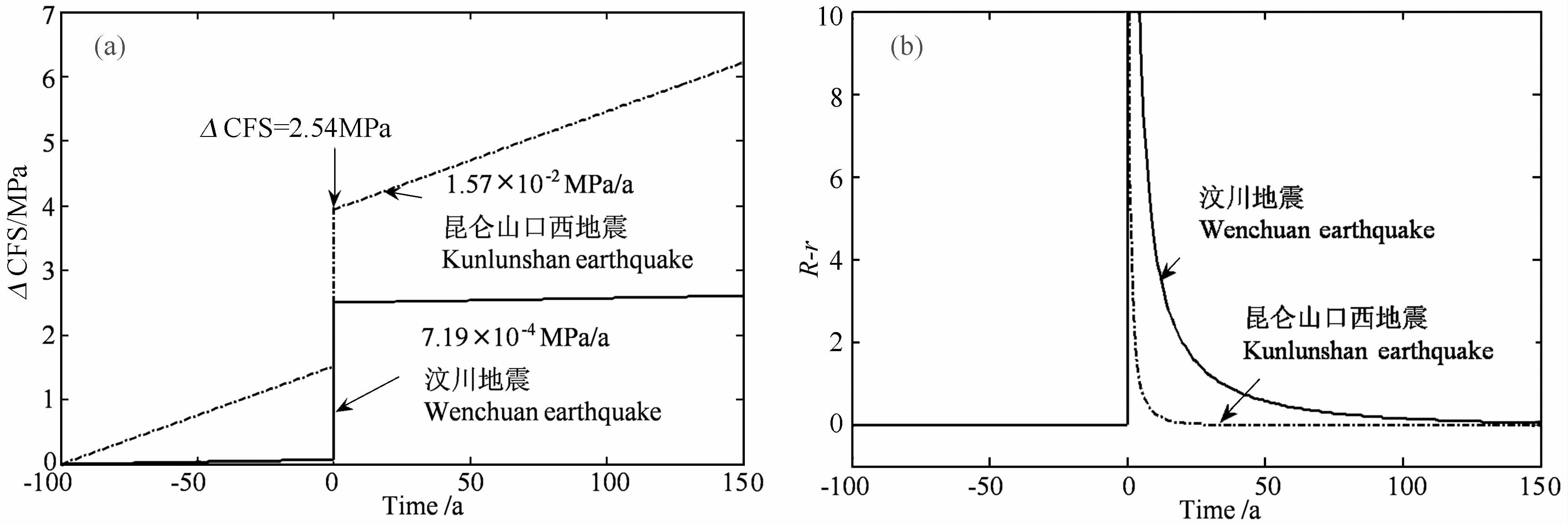
|
图 4 滑移速率和状态相依赖的摩擦定律下,汶川地震和昆仑山口西地震的库仑应力变化和利用公式(7)求得的地震活动性的变化规律 (a)在库仑应力扰动ΔCFS为2.43 MPa时汶川和昆仑山口西地震后的库仑应力变化;(b)汶川地震和昆仑山口西地震主震分别造成的余震序列活动性随时间的变化规律. Fig. 4 The Coulomb failure stress change and seismicity change based on the rate- and state-dependent friction law. (a) A sudden stress change ACFS of 2.43 MPa, causes (b) an aftershock sequences that decays inversely with time |
在实验室观测中,断层的强度依赖于断层的滑动速率和滑动时间历程.滑移速率和状态相依赖的摩擦定律不仅允许在断层失稳之前存在时间延迟,还能描述断层稳态滑动——“黏滑"过程,所以得到了广泛的应用[44].但是在使用滑移速率和状态相依赖的摩擦定律时,存在很多简化和假设.第一,在计算滑动位移δ、滑动速率$\dot{\delta }$、失稳时间tf 以及余震持续时间ta 时,假设正应力σN 为常量,而且只考虑了剪应力变化造成的应力扰动,这会为地震活动性R的求取带来很大的误差.因为,随时间变化的库仑应力变化ΔCFS不仅仅与剪应力变化ΔτS 有关,与正应力的变化ΔσN 和孔隙压力变化ΔP也有关系:ΔCFS=ΔτS-μ′(ΔσN -ΔP),其中μ′ 为摩擦系数;而且孔隙压力变化ΔP也与正应力张量变化Δσij相关.在各向同性的均匀孔状弹性介质中孔隙压力变化为ΔP=S(Δσ11+Δσ22+Δσ33)/3,其中S为斯肯普顿系数(Skempton′scoefficient)[47].特别是在近断层,正应力的变化更加明显.中国地震局地壳应力研究所等单位完成的四个测孔的水压致裂绝对应力测量中,ZK1孔和ZK3 孔进行了原地重复测量,可以求得震前震后的剪应力τ 和正应力σN (如表 3).在近断层(ZK1测孔)汶川地震前后剪应力τ 和正应力σN 变化都很明显;而在断层以外(ZK3测孔)震后剪应力τ 变化和正应力σN 变化较小.所以如果在计算中将正应力σN 看作常数,并将正应力的扰动对区域应力场的影响忽略,也会带来一定的误差.第二,在滑移速率与状态相依赖摩擦定律下,当断层滑动速率增加到不稳定的水平时,地震就发生了[18],此时断层滑动了临界滑动位移Dc.Dc 是一个断层状态的函数,是断层接触面积的平均直径,与局部的剪切应变的大小以及断层泥的厚度也有关系[48].如果地震波穿过断层或一部分断层能够引起Dc 的变化,那么断层朝失稳的方向转变的过程也会有变化[49].所以,断层的失稳时间与Dc 也有强烈的依赖关系,我们将在今后的研究中作进一步的探讨.第三,在滑动速率与状态相依赖的摩擦定律的推导过程中,存在一个假设,即震后剪切应力变化率$\dot{\tau }$与参考剪切应力变化率$\dot{\tau }$r 相等.但实际上,经历了如此大的地震,区域应力场一定有一个突变,并需要重新调整.那么震后剪切应力变化率$\dot{\tau }$与参考剪切应力变化率$\dot{\tau }$r 也必定会有所差别.这也是滑动速率与状态相依赖的摩擦定律中假设不合理的地方,我们会在将来的研究中对其进行必要的修正.第四,除了主震的动态或静态触发余震作用之外,可能有延迟余震发生的情况.当库仑应力变化ΔCFS为负数时,断层将变得更加松弛.此外,不同的求解剪切应力变化率的过程中,应力降ΔτS 的确定、b值的选取、地震复发周期tr 的确定也都带来很大的不确定因素.第五,在滑移速率和状态相依赖的摩擦定律中,A和B都是由岩石力学实验求取得到的参数,且A和B的取值一般都在0.005~0.01 的范围之内.由于余震持续时间ta =AσN/$\dot{\tau }$,A取值的不确定性也影响到了ta 的估算准确性.我们必须思考的更为关键的因素是,实验室的结果是否能够直接应用于对地壳内部断层演化过程的描述,近期有关火山地震活动性的研究也进一步强调了理论和观测现象对比[50-51].随着数据资料的增加和地震监测技术的进步,对由滑移速率和状态相依赖的摩擦定律所描述的断层内部的力学演化、成核过程以及地震活动性的时空演变规律将会得到新的认识.
|
|
表 3 汶川地震震前震后ZK1和ZK3测孔应力张量、剪应力和正应力 Table 3 Stress tensor, shear stress and normal stress of ZK1 and ZK3 before and after Wenchuan earthquake |
本文从滑移速率和状态相依赖的摩擦定律出发,利用背景场的地震活动性和大震的平均复发周期估算了2001 年MS8.1 昆仑山口西地震和2008年MS8.0 汶川地震余震可能的持续时间,分别为8a和146a.考虑到平均复发周期的不确定性误差,昆仑山口西地震余震持续时间范围为6.7~9.3a, 而汶川地震余震持续时间范围为74~222a.为了使结果不依赖于主震大小,又利用构造滑动速率和库仑定律,求得昆仑山口西地震余震持续时间分别为6.7a和5.1a, 汶川地震余震持续时间约为126a且下限为73a, 略小于滑移速率和状态相依赖的摩擦定律得到的结果.综合三种方法,得到汶川和昆仑山口西地震平均余震持续时间为140a和6.6a.昆仑山口西地震和汶川地震余震序列的个数和持续时间的差别与它们主震后的应力状态有关,也与剪切应力降ΔτS 和作用于断层上的区域正应力σN 的大小有关.两次地震的剪应力变化率$\dot{\tau }$的差别导致了在同样大的应力扰动ΔCFS之后的余震的活动性变化率的不同,从而导致了余震的持续时间和余震个数的差别.
| [1] | Omori F. Preliminary note of the Formosa earthquake of March 17, 1906. Bull. Imp. Earthq. Invest. Comm. , 1907, 1(2): 53-69. |
| [2] | Stein S, Liu M. Long aftershock sequences within continents and implications for earthquake hazard assessment. Nature , 2009, 462(7269): 87-89. DOI:10.1038/nature08502 |
| [3] | Hill D P, Pollitz F, Newhall C. Earthquake-volcano interactions. Phys. Today. , 2002, 55(11): 41-47. DOI:10.1063/1.1535006 |
| [4] | Kanamori H, Brodsky E E. The physics of earthquakes. Rep. Prog. Phys. , 2004, 67(8): 1429-1496. DOI:10.1088/0034-4885/67/8/R03 |
| [5] | Gomberg J, Bodin P, Reasenberg P A. Observing earthquakes triggered in the near field by dynamic deformations. Bull. Seismol. Soc. Am. , 2003, 93(1): 118-138. DOI:10.1785/0120020075 |
| [6] | Bouchon M, Vallee M, Huang M, et al. Observation of long supershear rupture during the magnitude 8.1 Kunlunshan earthquake. Translated World Seismology , 2004(5): 51-54. |
| [7] | Bouchon M, Karabulut H. The aftershock signature of supershear earthquakes. Science , 2008, 320(5881): 1323-1325. DOI:10.1126/science.1155030 |
| [8] | 郑勇, 马宏生, 吕坚, 等. 汶川地震强余震(MS≥5.6)的震源机制解及其与发震构造的关系. 中国科学D辑: 地球科学 , 2009, 39(4): 413–426. Deng Y, Ma H S, Lü J, et al. The relationship between focal mechanism solutions and seismogenic structure of Wenchuan earthquake aftershocks (Ms≥5.6). Science in China D: Earth Science (in Chinese) , 2009, 39(4): 413-426. |
| [9] | Gomberg J, Beeler N M, Blanpied M L, et al. Earthquake triggering by transient and static deformations. J. Geophys. Res. , 1998, 103(B10): 24411-24426. DOI:10.1029/98JB01125 |
| [10] | Toda S, Lin J, Megghraoui M, et al. 12 May 2008 M=7.9 Wenchuan, China, earthquake calculated to increase failure stress and seismicity rate on three major fault systems. Geophys. Res. Lett. , 2008, 35: L17305. DOI:10.1029/2008GL034903 |
| [11] | Xu X W, Chen W B, Ma W T, et al. Surface rupture of the Kunlun earthquake (Ms8.1), Northern Tibetan Plateau, China. Seismol. Res. Lett. , 2002, 73(6): 884-892. DOI:10.1785/gssrl.73.6.884 |
| [12] | Wesnousky S G. Displacement and geometrical characteristics of earthquake surface ruptures: Issues and implications for seismic-hazard analysis and the process of earthquake rupture. Bull. Seismol. Soc. Am. , 2008, 98(4): 1609-1632. DOI:10.1785/0120070111 |
| [13] | Klinger Y, Xu X, Tapponnier P, et al. High-resolution satellite imagery mapping of the surface rupture and slip distribution of the Mw-7.8, 14 November 2001 Kokoxili earthquake, Kunlun fault, Northern Tibet, China. Bull. Seismol. Soc. Am. , 2005, 95(5): 1970-1987. DOI:10.1785/0120040233 |
| [14] | 王卫民, 赵连峰, 李娟, 等. 四川汶川8.0级地震震源过程. 地球物理学报 , 2008, 51(5): 1403–1410. Wang W M, Zhao L F, Li J, et al. Rupture process of the M8.0 Wenchuan earthquake of Sichuan, China. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1403-1410. |
| [15] | 陈运泰. 汶川特大地震的震级和断层长度. 科技导报 , 2008, 26(10): 26–27. Chen Y T. On the magnitude and the fault length of the great Wenchuan earthquake. Science & Technology Review (in Chinese) , 2008, 26(10): 26-27. |
| [16] | Dieterich J H. Modeling of rock friction 1. Experimental results and constitutive equations. J. Geophys. Res. , 1979, 84(B5): 2161-2168. DOI:10.1029/JB084iB05p02161 |
| [17] | Dieterich J H. Constitutive properties of faults with simulated gouge. // Carter N L, Friedman M, Logan J M, et al, eds. Mechanical Behavior of Crustal Rocks. Geophys. Monogr. Ser., Washington D C: American Geophysical Union, 1981, 24: 103-120. |
| [18] | Dieterich J. A constitutive law for rate of earthquake production and its application to earthquake clustering. J. Geophys. Res. , 1994, 99(B2): 2601-2618. DOI:10.1029/93JB02581 |
| [19] | Ruina A. Slip instability and state variable friction laws. J. Geophys. Res. , 1983, 88(B12): 10359-10370. DOI:10.1029/JB088iB12p10359 |
| [20] | Dieterich J H. Modeling of rock friction 2. Simulation of preseismic slip. J. Geophys. Res. , 1979, 84(B5): 2169-2175. DOI:10.1029/JB084iB05p02169 |
| [21] | Rice J R, Gu J C. Earthquake aftereffects and triggered seismic phenomena. Pure Appl. Geophys. , 1983, 121(2): 187-219. DOI:10.1007/BF02590135 |
| [22] | Weeks J D, Tullis T E. Frictional sliding of dolomite: A variation in constitutive behavior. J. Geophys. Res. , 1985, 90(B9): 7821-7826. DOI:10.1029/JB090iB09p07821 |
| [23] | Blanpied M L, Tullis T E. The stability and behavior of a frictional system with a two state variable constitutive law. Pure Appl. Geophys. , 1986, 124(3): 415-444. DOI:10.1007/BF00877210 |
| [24] | Okubo P G, Dieterich J H. State variable fault constitutive relations for dynamic slip. //Das S, Boatwright J, Scholz C H, eds. 'Earthquake Source Mechanics. Geophys. Monogr. Set., Washington D C: American Geophysical Union, 1986, 37: 25-35. |
| [25] | Tullis T E, Weeks J D. Constitutive behavior and stability of frictional sliding of granite. Pure Appl. Geophys. , 1986, 124(3): 383-314. DOI:10.1007/BF00877209 |
| [26] | Marone C J, Scholz C H, Bilham R. On the mechanics of earthquake afterslip. J. Geophys. Res. , 1991, 96(B5): 8441-8452. DOI:10.1029/91JB00275 |
| [27] | Tse S T, Rice J R. Crustal earthquake instability in relation to the depth variation of frictional slip properties. J. Geophys. Res. , 1986, 91(B9): 9452-9472. DOI:10.1029/JB091iB09p09452 |
| [28] | Stuart W D. Forecast model for great earthquakes at the Nankai Trough subduction zone. Pure Appl. Geophys. , 1988, 126(2-4): 619-641. DOI:10.1007/BF00879012 |
| [29] | Dieterich J H. A model for the nucleation of earthquake slip. // Das S, Boatwright J, Scholz C, eds. Earthquake Source Mechanics. Geophys. Monogr. Ser., Washington D C: American Geophysical Union, 1986, 37: 37-47. |
| [30] | Dieterich J H. Earthquake nucleation on faults with rate-and state-dependent strength. Tectonophysics , 1992, 211(1-4): 115-134. DOI:10.1016/0040-1951(92)90055-B |
| [31] | Console R, Murru M, Catalli F. Physical and stochastic models of earthquake clustering. Tectonophysics , 2006, 417(1-2): 141-153. DOI:10.1016/j.tecto.2005.05.052 |
| [32] | Utsu T. A method for determining the value of b in a formula log n=a-bM showing the magnitude-frequency relation for earthquakes. Geophys. Bull. Hokkaido Univ. (in Japanese) , 1965, 13: 99-103. |
| [33] | 刘博研, 史保平. MS8.0汶川地震断层的应力状态以及对余震危险性的影响. 地球物理学报 , 2011, 54(4): 1002–1009. Liu B Y, Shi B P. The state of stress of the Ms8.0 Wenchuan earthquake faulting and its implication to the aftershock hazard. Chinese J. Geophys. (in Chinese) , 2011, 54(4): 1002-1009. |
| [34] | 郭啓良, 王成虎, 马洪生, 等. 汶川MS8.0级大震前后的水压致裂原地应力测量. 地球物理学报 , 2009, 52(5): 1395–1401. Guo Q L, Wang C H, Ma H S, et al. In-situ hydro-fracture stress measurement before and after the Wenchuan Ms8.0 earthquake of China. Chinese J. Geophys. (in Chinese) , 2009, 52(5): 1395-1401. |
| [35] | 张培震, 徐锡伟, 闻学泽, 等. 2008年汶川8.0级地震发震断裂的滑动速率、复发周期和构造成因. 地球物理学报 , 2008, 51(4): 1066–1073. Zhang P Z, Xu X W, Wen X Z, et al. Slip rates and recurrence intervals of the Longmen Shan active fault zone, and tectonic implications for the mechanism of the May 12 Wenchuan. Chinese J. Geophys. (in Chinese) , 2008, 51(4): 1066-1073. |
| [36] | Li H B, Van der Woerd J, Tapponnier P, et al. Slip rate on the Kunlun fault at Hongshui Gou, and recurrence time of great events comparable to the 14/11/2001, Mw≥7.9 Kokoxili earthquake. Earth Planet. Science Lett. , 2005, 237(1-2): 285-299. DOI:10.1016/j.epsl.2005.05.041 |
| [37] | Antolik M, Abercrombie R E, Ekstr?m G. The 14 November 2001 Kokoxili (Kunlunshan), Tibet, earthquake: rupture transfer through a large extensional step-over. Bull. Seismol. Soc. Am. , 2004, 94(4): 1173-1194. DOI:10.1785/012003180 |
| [38] | Ziv A. Does aftershock duration scale with main shock size?. Geophys. Res. Lett. , 2006, 33: L17317. DOI:10.1029/2006GL027141 |
| [39] | Ji C, Hayes G. Preliminary result of the May 12, 2008 MW7.9 eastern Sichuan, China earthquake. 2008 http://www.geol.ucsb.edu/faculty/ji/big_earthquakes/2008/05/12/ShiChuan.html. |
| [40] | Robinson D P, Brough C, Das S. The Mw7.8, 2001 Kunlunshan earthquake: Extreme rupture speed variability and effect of fault geometry. J. Geophys. Res. , 2006, 111: B08303. DOI:10.1029/2005JB004137 |
| [41] | Reasenberg P A, Simpson R W. Response of regional seismicity to the static stress change produced by the Loma Prieta earthquake. Science , 1992, 255(5052): 1687-1690. DOI:10.1126/science.255.5052.1687 |
| [42] | King G C P, Stein R S, Lin J. Static stress changes and the triggering of earthquakes. Bull. Seismol. Soc. Am. , 1994, 84(3): 935-953. |
| [43] | Hardebeck J L, Nazareth J J, Hauksson E. The static stress change triggering model: Constraints from two southern California aftershocks sequences. J. Geophys. Res. , 1998, 103(B10): 24427-24437. DOI:10.1029/98JB00573 |
| [44] | Harris R A. Introduction to special section: Stress triggers, stress shadows, and implications for seismic hazard. J. Geophys. Res. , 1998, 103(B10): 24347-24358. DOI:10.1029/98JB01576 |
| [45] | Nishimura N, Yagi Y. Rupture process for May 12, 2008 Sichuan, earthquake (preliminary result). 2008. http://www.geol.tsukuba.ac.jp/-nisimura/20080512/. |
| [46] | Kagan Y Y. Incremental stress and earthquakes. Geophys. J. Int. , 1994, 117(2): 345-364. DOI:10.1111/gji.1994.117.issue-2 |
| [47] | Kilb D, Gomberg J, Bodin P. Aftershock triggering by complete Coulomb stress changes. J. Geophys. Res. , 2002, 107: 2060. DOI:10.1029/2001JB000202 |
| [48] | Marone C J, Kilgore B. Scaling of the critical slip distance for seismic faulting with shear strain in fault zones. Nature , 1993, 362(6421): 618-621. DOI:10.1038/362618a0 |
| [49] | Parsons T. A hypothesis for delayed dynamic earthquake triggering. Geophys. Res. Lett. , 2005, 32: L04302. DOI:10.1029/2004GL021811 |
| [50] | Dieterich J, Cayol V, Okubo P. The use of earthquake rate changes as a stress meter at Kilanea volcano. Nature , 2000, 408(6811): 457-460. DOI:10.1038/35044054 |
| [51] | Toda S, Stein R S, Sagia T. Evidence from the AD 2000 Izu islands earthquake swarm that stressing rate governs seismicity. Nature , 2002, 419(6902): 58-61. DOI:10.1038/nature00997 |
 2012, Vol. 55
2012, Vol. 55