2. 中国科学院大气物理研究所大气科学和流体力学数值模拟国家重点实验室, 北京 100029
2. LASG, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China
重力波对暴雨有触发作用,并影响暴雨降水的强度和分布[1-4].郭虎等[5]对北京地区一次局地暴雨过程的分析发现,由重力波所激发的小尺度波动对强降雨的发生及其时空分布起主导作用.
对重力波的研究大多是利用简化的动力学模型估计其特征参数和传播方向,进而分析其产生机制和演变特征[1-6].大气重力波波参数特征的观测研究则主要是利用无线电探空资料揭示其地理分布和季节变化规律[7-17].例如,Allen 等[7]利用澳大利亚18个台站的温度探空资料研究了对流层(2~8km)和平流层下层(17~24km)重力波能量随季节和纬度的变化;Vincent等[8]利用温度和高空风探空资料研究Macquarie岛(55°S,159°E)上空平流层下层(12~25km)的重力波特性;卞建春等[11]利用北京观象台的高分辨率探空资料对北京上空平流层下层(17~24km)的重力波特征进行了统计分析.
利用数值模拟结果分析大气重力波演变规律也开展了较多研究[6, 18-21],但一般多采用小波分析方法[21]或根据模拟结果图像直观判断方法[6, 18]揭示重力波特征,而利用重力波频散关系从模拟结果中提取波参数的研究工作还不多见.本文利用中尺度数值模式(WRF)对2003 年7 月4—5 日淮河流域大范围暴雨过程的数值模拟结果,采用重力波参数提取方法,研究了暴雨中心区的重力波参数演变特征,并通过与模拟区域内非降水区重力波参数进行对比分析,研究了重力波和暴雨的关系.
2 数值模拟 2.1 暴雨个例和数值模拟方案设计2003年6月下旬至7月上旬,淮河流域发生了继1991年以来又一次的大范围持续性强降雨,流域内降水总量达600mm 以上,比常年同期偏多1~2倍,致使淮河洪水泛滥.其中7月4—5日的暴雨是淮河致洪的主要过程之一,强降水主要集中在安徽滁州和江苏中南部.从4日14时到5日20时,南京降水量为195 mm, 滁州降水量为380 mm, 降水强度之大十分罕见[22].
本文采用WRF(V3.1.1)模式对此次暴雨过程进行数值模拟.WRF 模式系统是由美国国家大气研究中心(NCAR)中小尺度气象处、国家环境预报中心(NCEP)环境模拟中心、预报系统实验室(FSL)的预报研究处和奥克拉荷马大学的风暴分析预报中心等四个单位共同参与开发的新一代中尺度预报模式和同化系统,由国家自然科学基金和国家海洋大气局(NOAA)共同支持[23].WRF 模式采用高度模块化和分层设计技术,可在分布式内存和共享内存两种计算机上实现加工的并行计算,并包含了高分辨率非静力应用的优先级设计、大量的物理选择以及与模式本身相协调的先进的资料同化系统[23].近年来,WRF模式已广泛应用于天气预报业务和气象研究中,并取得了良好的效果[21].
本次模拟采用三重嵌套网格,外层粗网格区域(D01)格距为36km, 网格数为100×90,区域中心位于(116.1°E,31.9°N);第二重网格区域(D02)格距为12km, 网格数为91×85,中心位于(119.1°E,32.4°N);第三重细网格区域(D03)格距为4km, 网格数为112×103,中心位于(119.3°E,32.4°N).模式垂直分为69层,模式层顶气压为50hPa, D01区域时间积分步长为180s.D01区域的微物理过程采用Lin方案[24],D02和D03区域采用Thompson方案[25];D01和D02区域的积云参数化方案采用Kain-Fritsch方案[26],D03 区域采用显式方案.模式三重区域行星边界层方案均采用YSU 方案[27],长波辐射过程采用RRTM 方案[28],短波辐射过程采用Dudhia方案[29].地图投影采用Lambert投影.模拟时间为2003年7月4日00时—5日12时(世界时,下同).模式初值和侧边界条件选用水平分辨率为1°×1°的NECP/NCAR 再分析资料.第三重嵌套细网格区域输出时间间隔为6min.
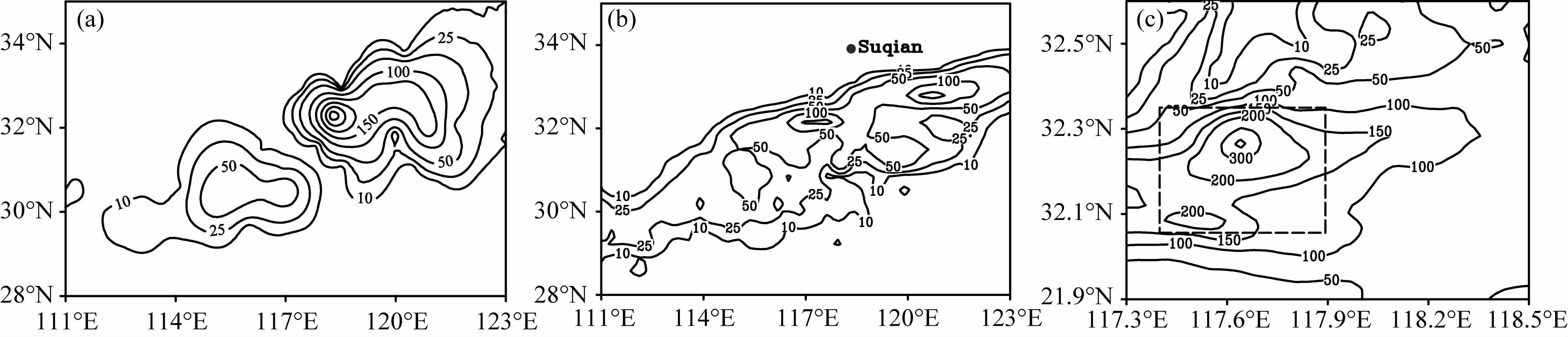
2.2 模拟结果检验由4日12时—5日12时自动站降水资料分析的累积降水量实况(图 1a)可看出,雨带呈东北—西南走向,降水主体范围在(118°E—121°E,31°N—33°N)之间,随着雨带向西南延伸降水量逐渐减小,暴雨中心位于滁州(118.3°E,32.3°N),降水量为350mm.模式对雨带整体位置模拟较好(图 1b),但降水主体范围偏小,最大降水中心位于合肥与滁州之间(117.64°E,32.26°N,第三重嵌套模拟结果,图 1c),位于实际暴雨中心的西南侧,降水量为350 mm, 与实况相同;东部沿海地区出现了一个次降水中心,降水量达200mm.从总体上来看,模式较好地模拟出了此次强降水的分布和强度.
|
图 1 2003年7月4日12时一5日12时的降水量分布(单位:mm) (a)观测;(b)粗网格区域模拟;(c)细网格区域模拟. Fig. 1 Distribution of precipitation during 1200UTC July 4—1200UTC July 5, 2003 (units: mm) (a) Observation; (b) Simulation for coarser domain; (c) Simulation for finer domain. |
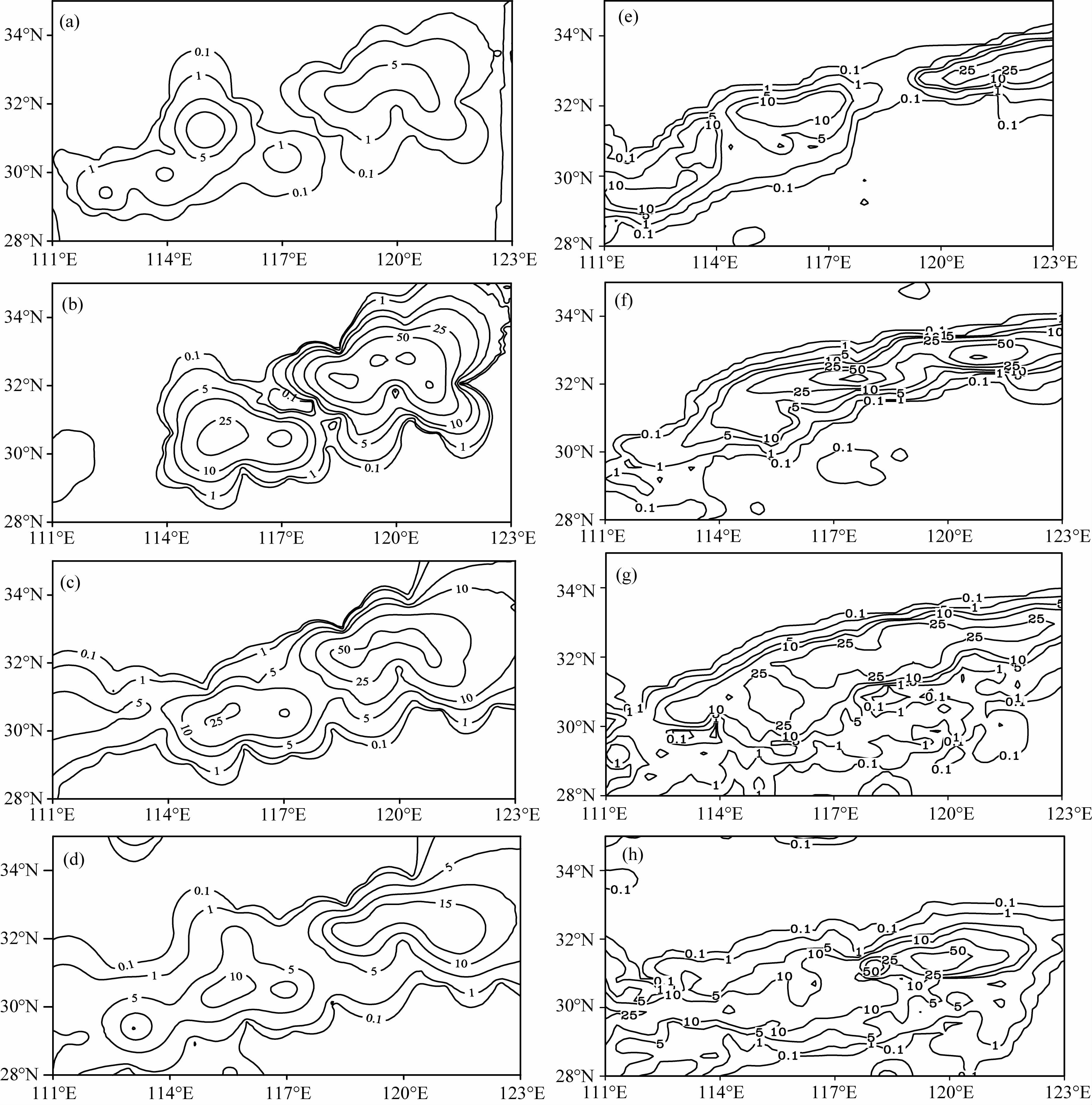
比较此次暴雨过程逐6h 累积降水量(图 2a—2d)和模拟降水量(图 2e—2h)分布可看出,模拟的降水落区与实况基本一致,降水演变趋势也与实况相近.但前两个时段(图 2e,2f),118°E 以东地区降水范围偏小,第四个时段雨区位置偏南(图 2h),而第一个时段(图 2e)和第四个时段(图 2h)模拟的雨区东部降水偏强.
|
图 2 观测(a—d)和模拟(e—h)的逐6 h累积降水量分布(单位:mm) (a, e) 4 日 12—18 时;(b, f) 4 日 18 时一5 日 00 时;(c, g) 5 日 00—06 时;(d, h) 5 日 06—12 时. Fig. 2 Observed (a—d) and simulated (e —h) cumulated precipitation in 6 h interval (units: mm) (a, e) 1200—1800UTC July 4;b, f) 1800UTC July 4—0000UTC July 5 ;(c, g) 0000—0600UTC July 5 ; (d, h) 0600—1200UTC July 5. |
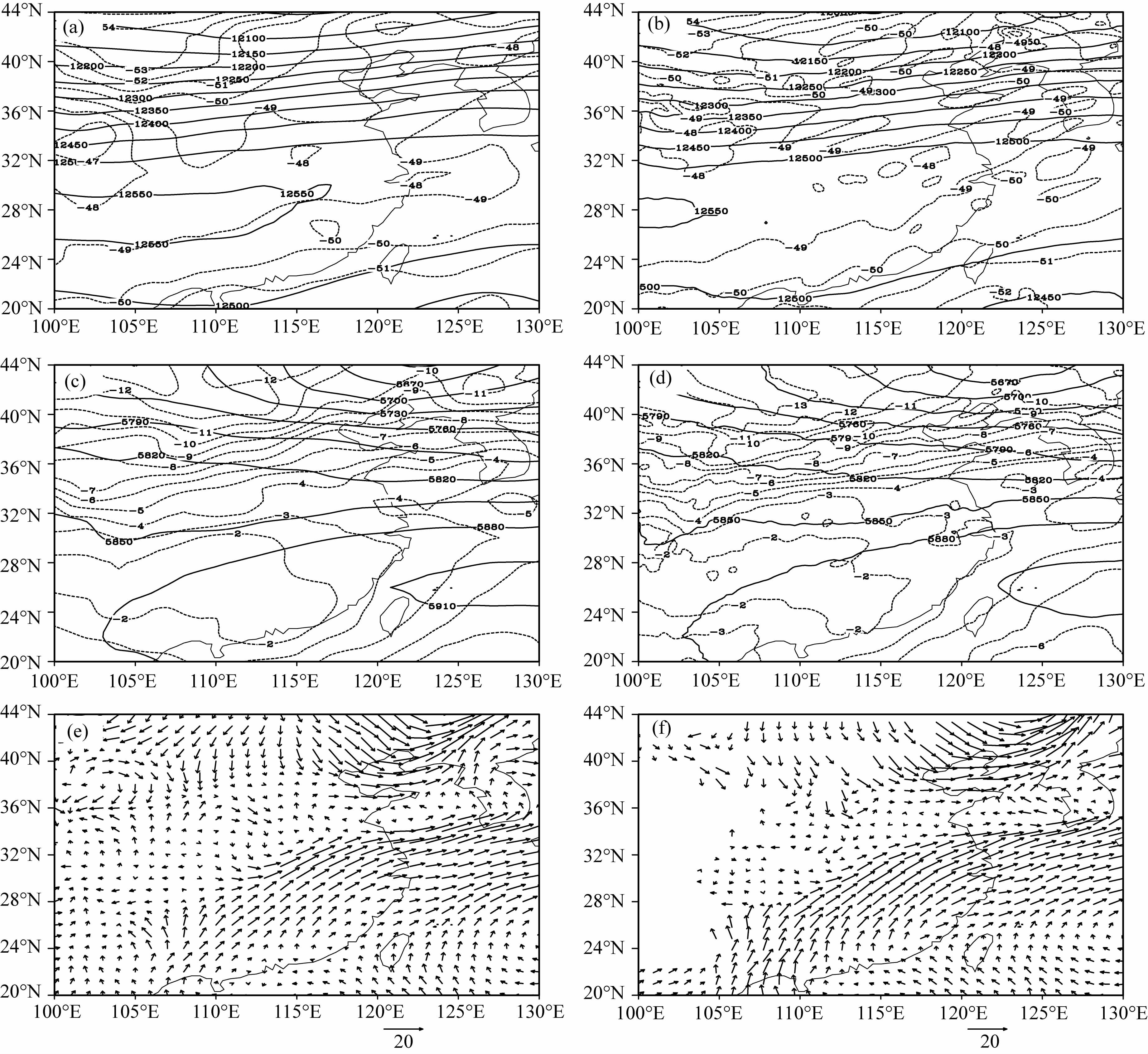
此外,模式还较好地模拟出此次暴雨过程对应的低涡、切变线和西太平洋副高等天气系统的演变.图 3是4日12时观测和模拟的位势高度场、温度场以及风场的分布.可见500hPa上(图 3d),西太副高控制我国东南部地区,脊线位于22°N 附近;850hPa上(图 3f),西南低空急流强劲,低涡位于急流左侧的河南、湖北地区,信阳—襄阳地区有东西走向的切变线.这些系统的位置与强度都与实况(图 3c 和图 3e)相吻合.
|
图 3 观测(a, c, e)和模拟的(b, d, D2003年7月4日12时位势高度(实线,单位:gpm)、温度(虚线,单位:℃)以及风场(矢量,单位:s-1) (a, b) 200 hPa;(c, d) 500 hPa;(e, f) 850 hPa. Fig. 3 Observed (a, c, e) and simulated (b, d, f) geopotential height (solid line, units: gpm), temperature (dashed line, units: C) and wind field (vector, units: m • s-1) at 1200UTC July 4, 2003 |
利用三次样条插值将第三重嵌套细网格区域模拟结果中的温度、气压和风等物理量分别插值到垂直间隔为50 m 的高度上.采用多项式拟合来建立温度和风的背景廓线:T、ub 和vb, 模拟的原始廓线减去背景廓线即得到温度扰动量(T′)和水平风速扰动量(u′、v′)的廓线.温度扰动量T′除以背景温度廓线T 得到归一化温度扰动$\hat{T}'$,即$\hat{T}'$ =T′/T.
忽略垂直速度扰动对动能的贡献,则扰动动能密度和位能密度可分别表示为
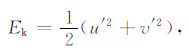
|
(1) |
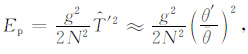
|
(2) |
其中g是重力加速度,N是Brunt-Väisälä频率,总能量密度为二者之和.
Hines[30]指出扰动风矢廓线的端点连线一般呈现为一个椭圆偏振.若重力波的水平传播方向为自北顺时针旋转角度α,则α方向即为水平风扰动矢量偏振椭圆的长轴方向[8, 11, 30].取α 方向为x轴正方向,设u′1为x方向扰动风分量,v′1垂直于u′1,且指向u′1的左侧.设背景风方向为自北顺时针旋转角度β,即β=arctan(ub/vb),则x方向背景风分量为u1 =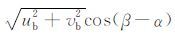
假设坐标系以u1 的速度沿x方向移动,在x-z平面上,绝热无黏条件下,取Bossinesq近似和静力平衡近似,利用标准波型法可得到重力波频散关系式为[31]

|
(3) |
其中f为地转参数,kh 为水平波数,m为垂直波数,σ 为频率,且f <|σ| $\ll $ N.偏振椭圆长短轴之比为[11]
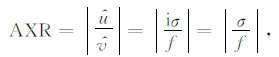
|
(4) |
其中i2 =-1,$\hat{u}$、$\hat{v}$分别为u′1、v′1的振幅.若扰动为重力惯性波,则其动能密度和位能密度之比为[11]
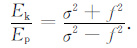
|
(5) |
从(5)式可看出,重力惯性波的动能密度总是大于位能密度,且当|σ| $\gg $ |f|即扰动为纯重力波时,动能密度和位能密度几乎相等.因此,含有少量噪声的重力波动能密度与位能密度的比值应位于1附近或大于1.许多研究表明该比值不会比1大太多,一般不超过4[8, 11].
利用Stokes参数[8, 11, 32]和主成分分析法[11],借助Hilbert变换后的归一化温度扰动和速度扰动分量之间的关系(详见文献[8]和[11]),可确定出重力波水平传播方向α、椭圆偏振度d和偏振椭圆的长短轴.
根据文献[11]和[32],假设水平风扰动垂直廓线u′(z)、v′(z)包含部分偏振波,也就是说,在一个非偏振、各向同性的背景场(方差为unoise2 +vnoise2)中存在一个振幅为(u0,v0)的单频波,即
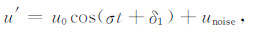
|
(6) |
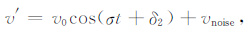
|
(7) |
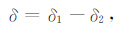
|
(8) |
则4个Stokes参数为
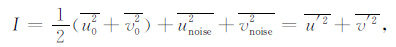
|
(9) |
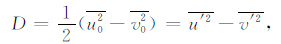
|
(10) |
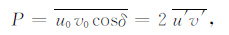
|
(11) |
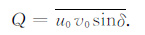
|
(12) |
(9) —(12)式中“—"表示物理量在高度上的平均,位相δ 定义为波的椭圆率.δ=0°或180°时,Q=0,为线性偏振;δ=90°或270°时,P=0,为圆偏振;中间值表示椭圆偏振.P表示同向协方差,与线性偏振有关;Q表示交叉协方差,与圆偏振有关;I为总方差,D表示各向异性.
椭圆偏振度d是指一个波动场中单频波所占的比例,可由Stokes参数表示为
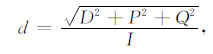
|
(13) |
其中d=1表示波动完全是单频波,d=0 表示波动为随机波[8, 11].
参照文献[8],定义正北方向为0°,顺时针旋转为方位角增加方向,间隔30°将水平面分为12个方位角,定义φi为研究时段内落入第i个方位角内的扰动能量占总能量的比例,从而可由φi判断研究时段内能量水平传播的主要方向.
利用偏振椭圆长短轴之比求出波动频率σ 和周期T(=2π/σ),利用$\hat{T}$′ 的垂直波数功率谱可以估算出波动的特征垂直波数m[8].将σ和m代入(3)式即可计算出水平波数kh.由波数与波长的关系,可得到水平波长lh(=2π/kh)和垂直波长lz(= 2π/m),因此垂直波长的计算与频率无关.
将原坐标系沿顺时针方向旋转(90°-α),则可得到水平相速为
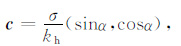
|
(14) |
水平方向群速为
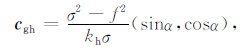
|
(15) |
考虑背景风场的水平相速为
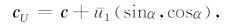
|
(16) |
考虑背景风场的水平方向群速为
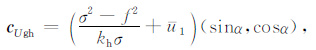
|
(17) |
当|σ| $\gg $ |f|时,则有c=cgh, cU=cUgh.
根据线性重力波理论[31],在北半球,当水平扰动风矢随高度顺时针旋转时,能量向上传播;反之,能量则向下传播.利用旋转谱技术[32]将风扰动矢量场分解为逆时针分量(AWC)和顺时针分量(CWC),则北半球重力波能量上传的部分可以认为是CWC与(CWC+AWC)的比值.以下利用上述提取重力波方法,研究暴雨中心区的重力波参数特征.
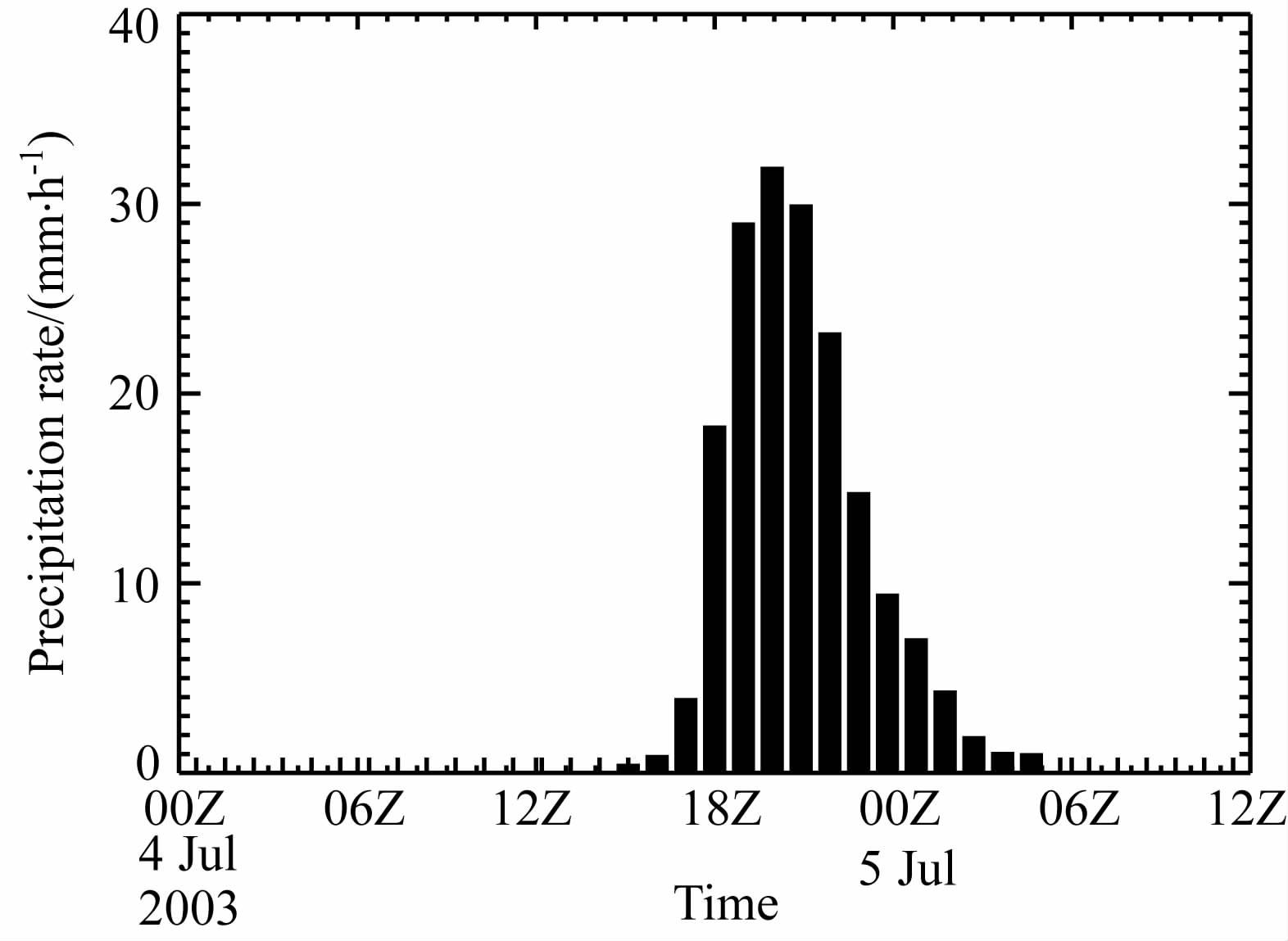
4 结果分析本文选取模式细网格区域内强降水区(图 1c中虚线框内的范围)代表暴雨中心区,从模拟的暴雨中心区平均降水强度随时间的演变(图 4)可以看出,4日18时以前,降水很少;18—20时,降水迅速增强,且降水强度在20 时达到峰值32 mm·h-1;此后,降水逐渐减弱;5 日06 时,降水停止.根据降水强度,本文取4日11—18时为暴雨前期,4日18时—5日01时为强暴雨阶段,5日01—08时为暴雨后期.
|
图 4 模拟的2003年7月4日00时-5日12时暴雨中心区平均降水强度随时间的演变(单位:mm • h-1) Fig. 4 Temporal variation of the simulated mean precipitationrate over the rainstorm area during 0000UTC July 4-1200UTC July 5, 2003 (units: mm • h-1) |
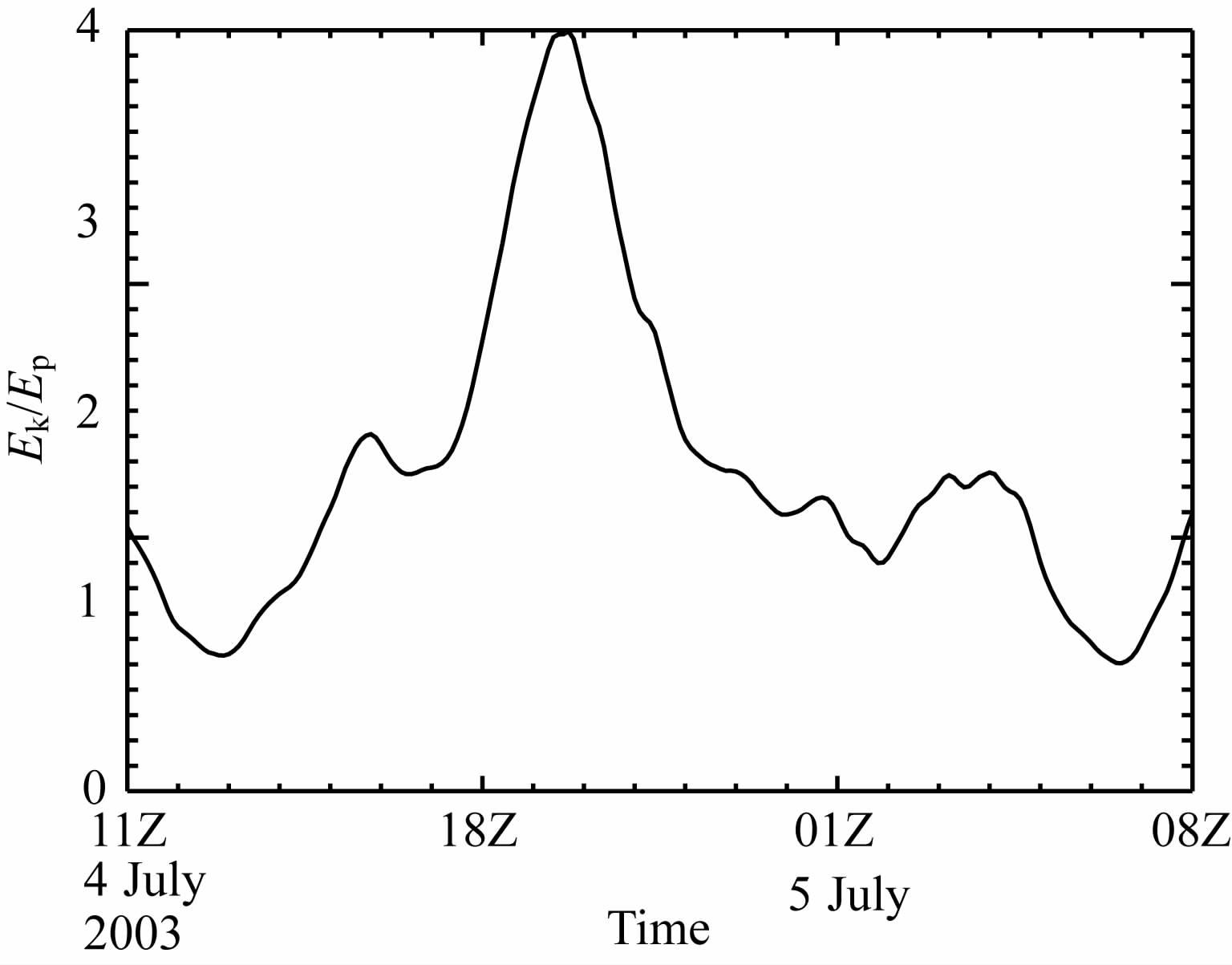
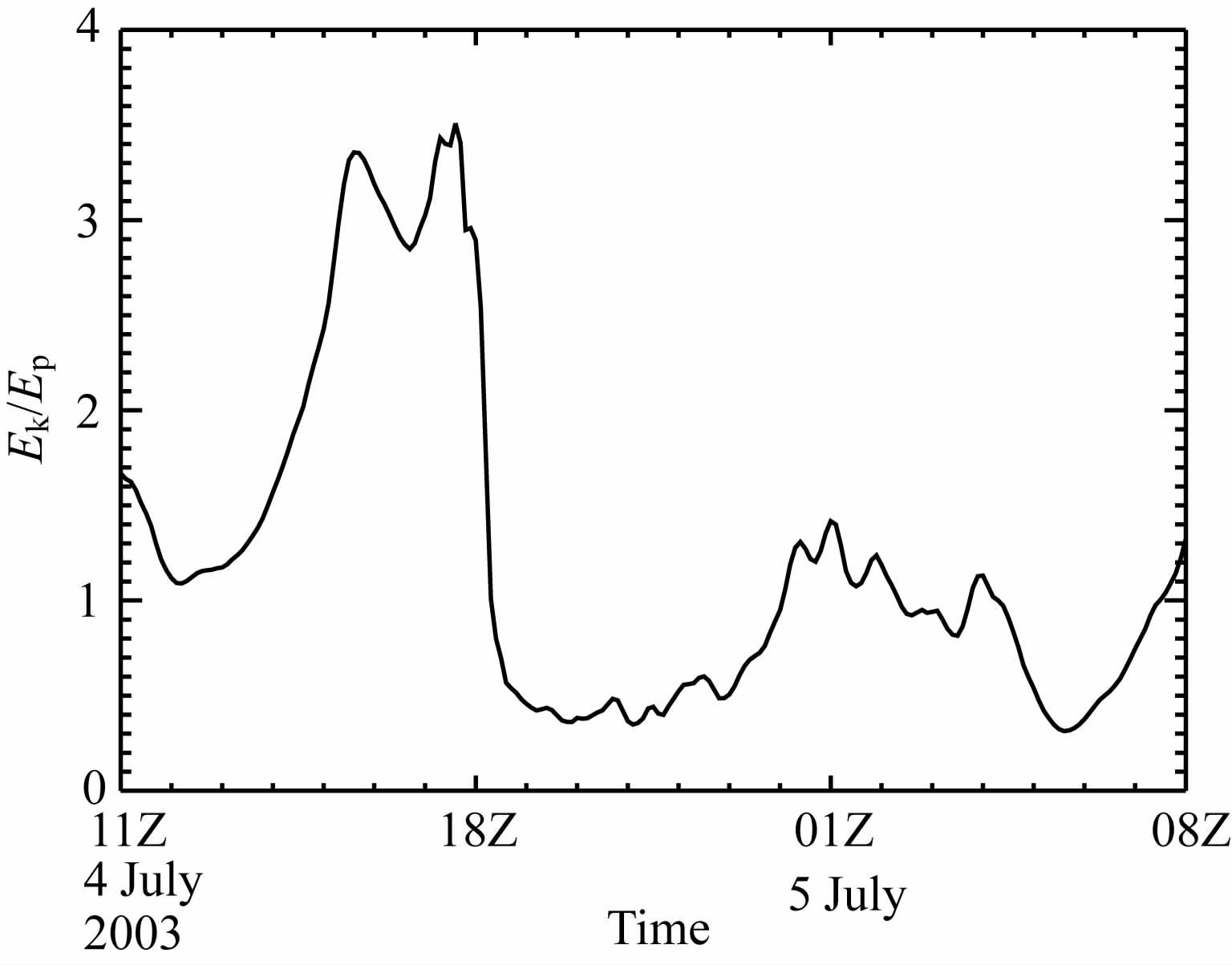
由于垂直速度扰动量级远小于水平风扰动量级,扰动动能密度和位能密度可以分别用(1)式和(2)式表示.根据前文分析可知,二者的比值应位于1附近或大于1,但一般不超过4.本文分别采用二次至六次多项式拟合方法获取暴雨中心区物理量背景场,结果发现五次多项式拟合得到的结果,除暴雨前期部分时次外,扰动动能密度和位能密度的比值均为1左右,满足利用扰动廓线计算重力波参数的要求(图 5).以下计算分析采用五次多项式拟合的结果.
|
图 5 2003年7月4日11时一5日08时暴雨中心区扰动动能密度与位能密度之比随时间的演变 Fig. 5 The temporal variation of the ratio of the perturbation kinetic energy density over the perturbation potential energy density over the rainstorm area during 1100UTC July 4一0800UTC July 5, 2003 |
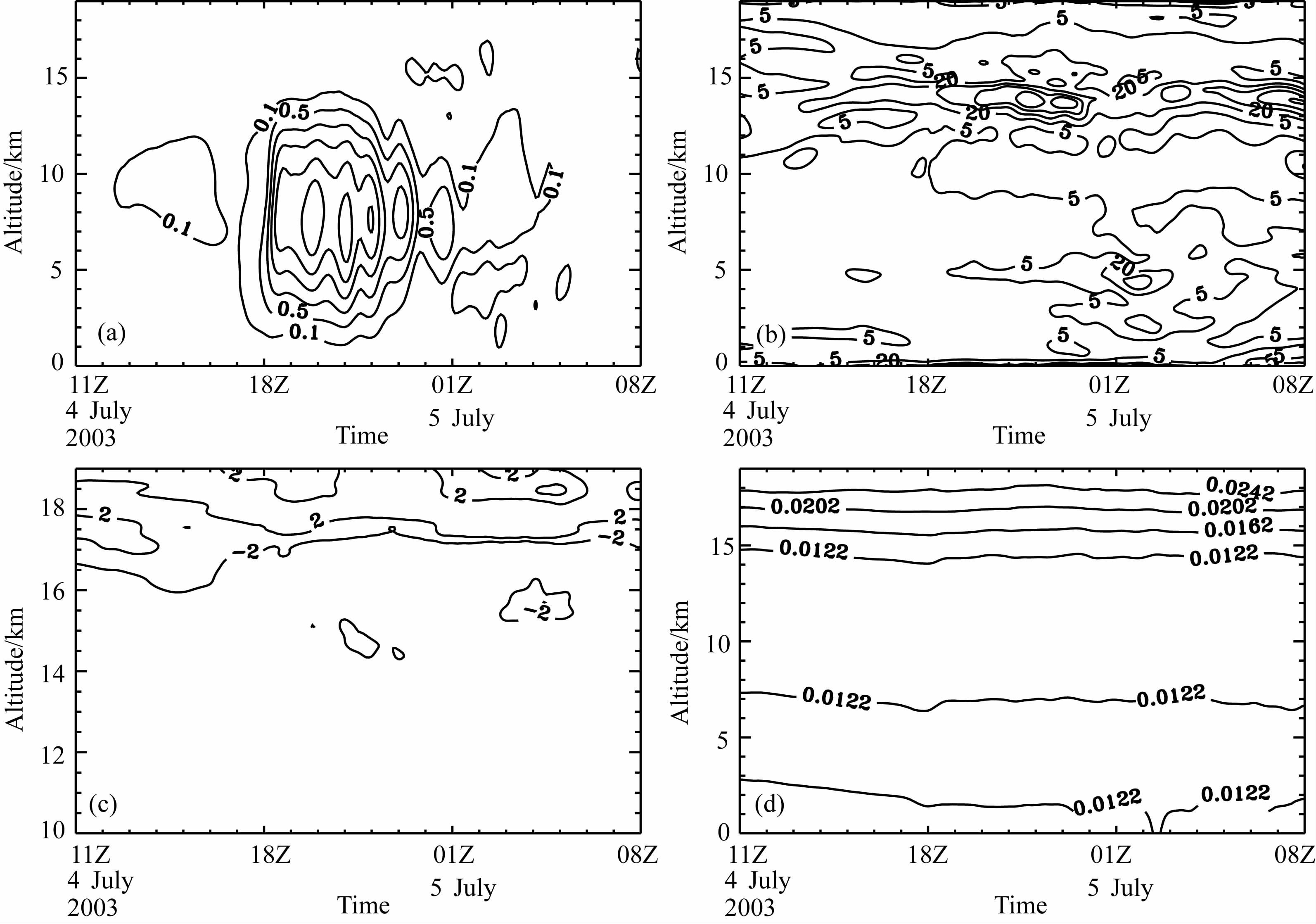
图 6给出了4日11时—5日08时暴雨中心区垂直速度、扰动能量密度、温度垂直梯度和Brunt-Väisälä频率的时间-高度演变剖面.由图 6a和图 6b可见,4日18时以前,几乎没有明显的对流活动,扰动能量较小,且主要集中在10km 以上;4日18时—5日01时,强对流迅速发展,波动振幅增大,8~15km的扰动能量显著增大;5日01时后,对流减弱,大振幅波频散,除高层少量时次外,整层能量分布趋于均匀.在研究时段内,温度垂直递减率≤2 ℃·km-1的最低高度位于16km 以上(图 6c),根据对流层顶的定义[33]可知,此次暴雨过程的对流层顶位于16km 以上.由Brunt-Väisälä频率的演变图(图 6d)可看出,8~15km 范围内Brunt-Väisälä频率几乎不随高度变化,此范围内的重力波特性差异不会很大.因此,本文主要研究8~15km 范围内的重力波参数.
|
图 6 2003年7月4日11时一5日08时暴雨中心区垂直速度(a, 单位:m • s-1,等值线间隔为0.4 m • s-1)、扰动能量密度(b, 单位:J • kg-1,等值线间隔为15 J • kg-1、温度垂直梯度(c, 单位:℃ • km-1)和Brunt-Vaisala频率(d, 单位:rad • s-1的时间-高度剖面 Fig. 6 Time-height cross-section of the vertical velocity (a, units: m • s-1, isoline space: 0.4 m • s-1) ,the perturbation energy density (b, units: J • kg-1 ,isoline space: 15 J • kg-1 ) ,the vertical temperature gradient (c, units: ℃ • km-1) and Brunt-Vaisala frequency (d, units: rad • s-1) in the center area of the rainstorm during 1100UTC July 4—0800UTC July 5,2003 |
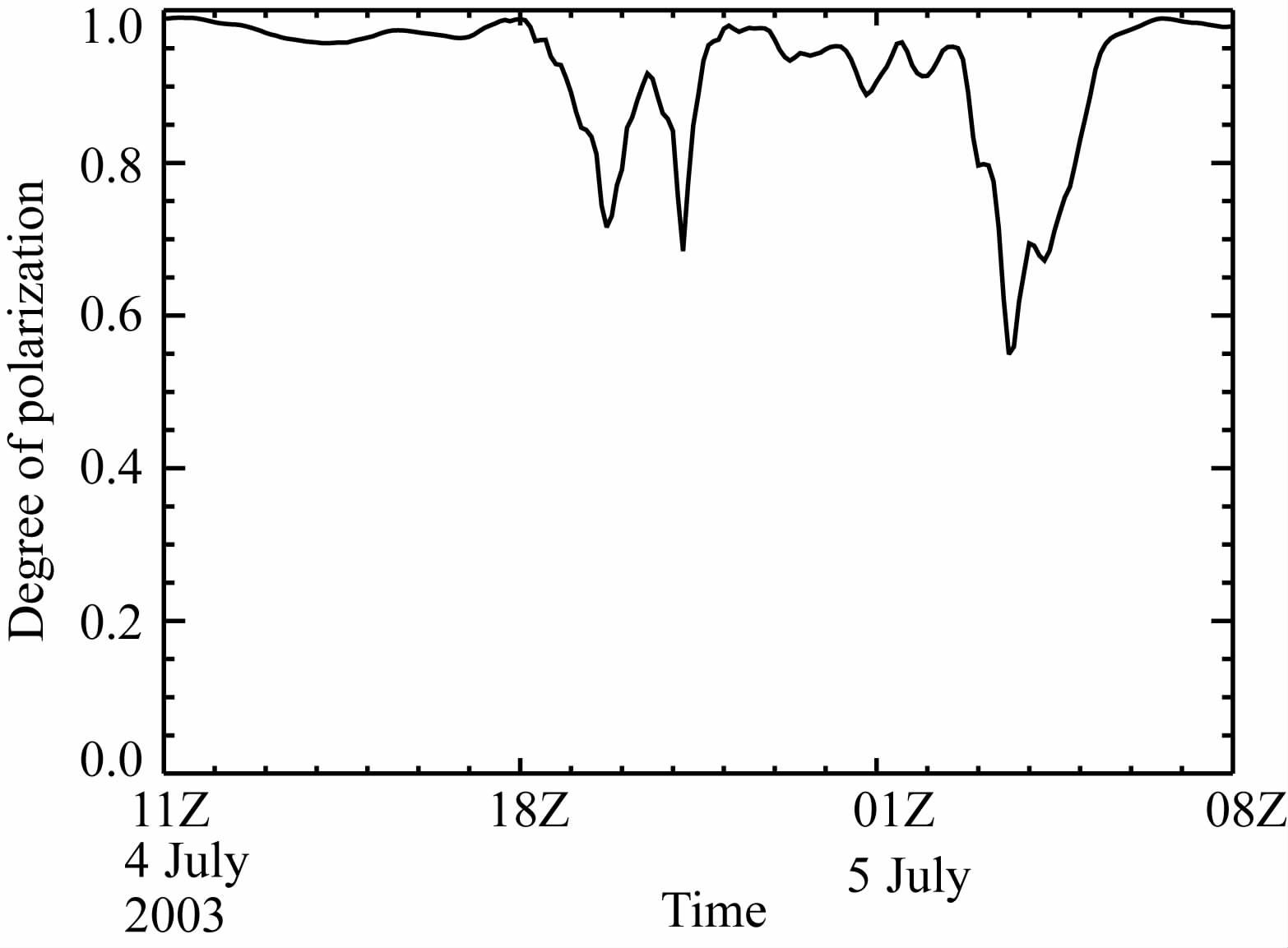
由椭圆偏振度的演变(图 7)可知,暴雨过程中椭圆偏振度均大于0.5,平均达到0.92,可以认为扰动场主要是由单频波组成.根据降水强度(图 4)和扰动能量密度(图 6b)的演变可看出,从暴雨前期到强暴雨阶段,降水强度增大,扰动能量也随之增大,表明在降水增强的过程中,重力波是增强的;暴雨后期,降水减弱,扰动能量减小,且在整个对流层分布趋于均匀,说明在降水减弱的过程中,重力波是减弱的.总之,重力波强度和暴雨强度之间存在正相关关系.
|
图 7 2003年7月4日11时—5日08时暴雨中心区椭圆偏振度随时间的演变 Fig. 7 Temporal variation of the degree of polarization over the rainstorm area during 1100UTC July 4—0800UTC July5,2003 |
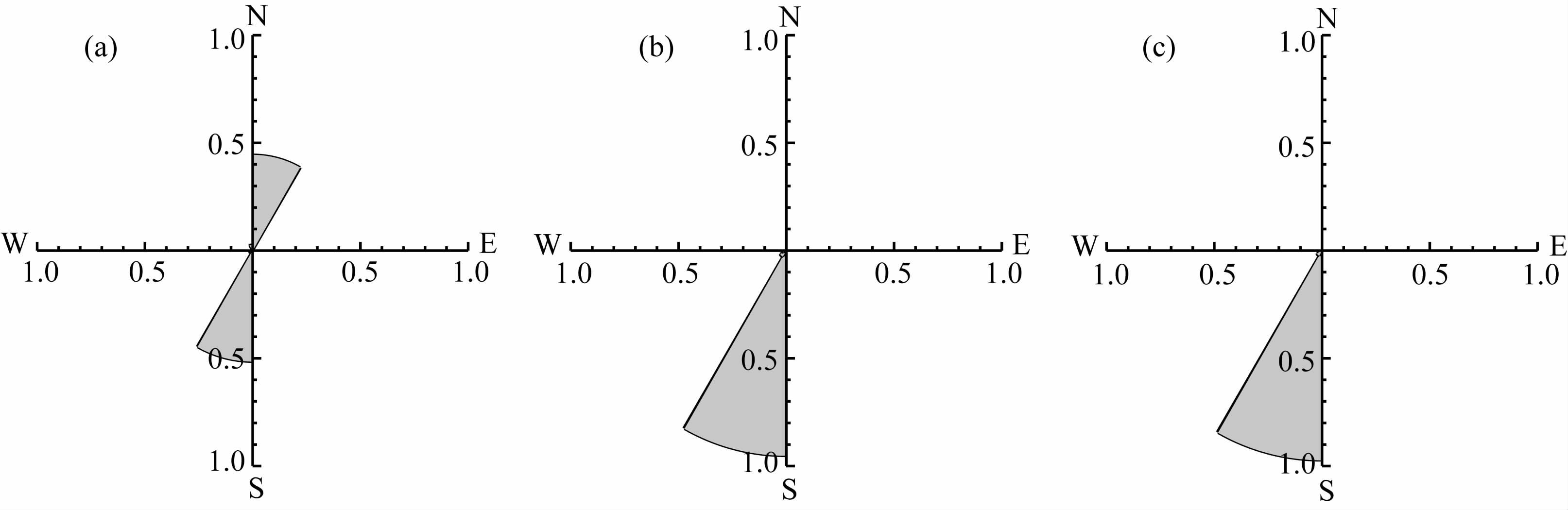
图 8是不同时段各个方位角能量占总能量的比例,可近似表示重力波水平传播方向,可见在整个暴雨过程中,重力波水平传播方向发生了很大变化:暴雨前期,重力波向北偏东和南偏西方向传播;而在强暴雨阶段和暴雨后期,重力波均向南偏西方向传播.
|
图 8 各个时段暴雨中心区重力波的水平传播方向分布 (a)4日11—18时;(b)4日18时—5日01时;(c)5日01—08时. Fig. 8 Distribution of the horizontal propagation direction over the rainstorm area for different period (a) 1100—1800UTC July 4;b) 1800UTC July 4—0100UTC July 5 ; (c) 0100—0800UTC July 5. |
刘晓等[34]认为,反向背景风场将拉伸重力波的垂直波长,加速重力波的上传;同向背景风场会延迟重力波发生不稳定的时间,缩短垂直波长,对重力波的上传有抑制作用.暴雨中心区上空8~15km 的背景风场为西南风(图略),这与后两个时段重力波水平传播方向是反向的,因而使得这两个时段的能量上传比例高于暴雨前期.三个时段重力波能量上传比例分别为48%、80%和65%.
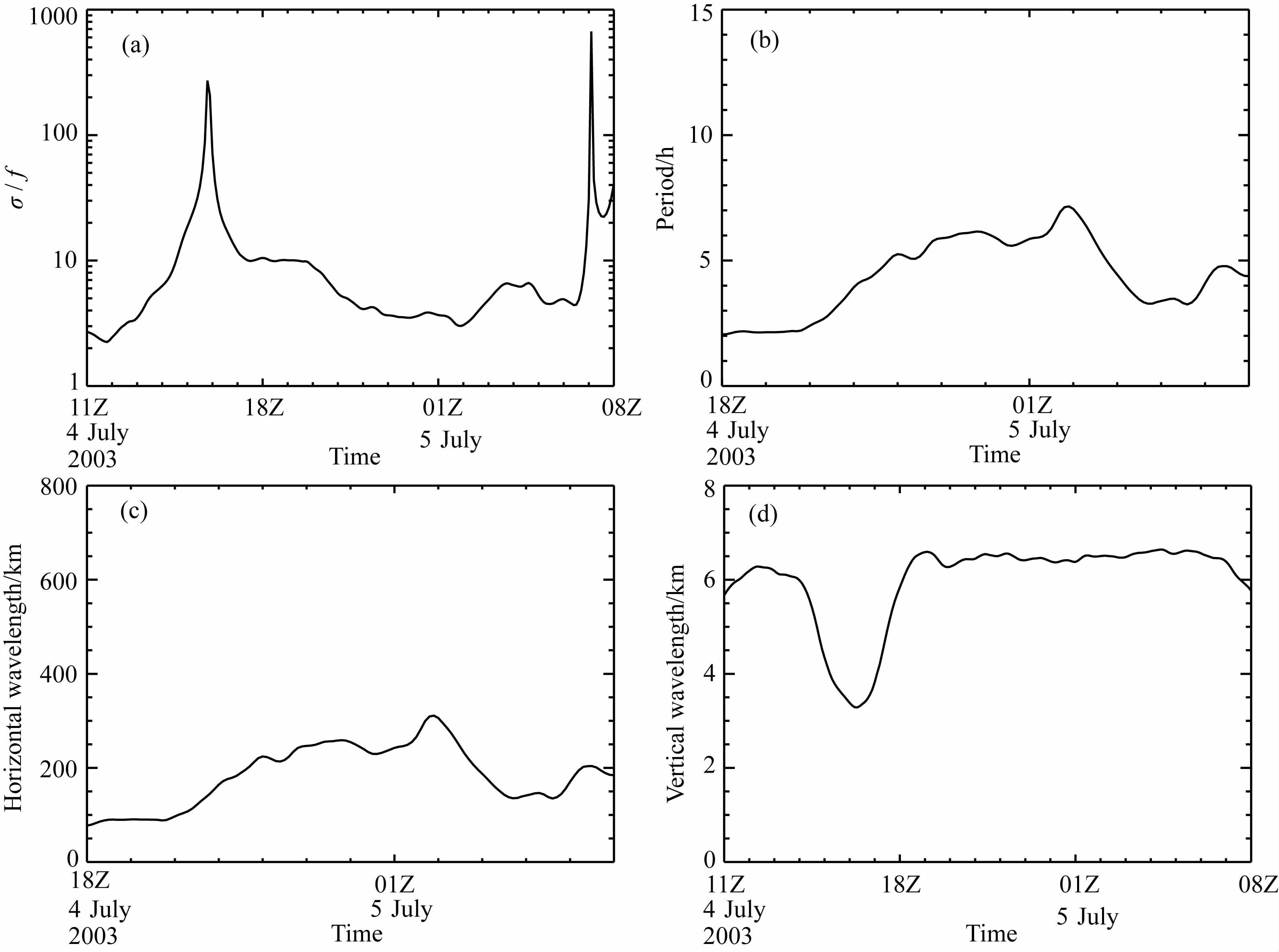
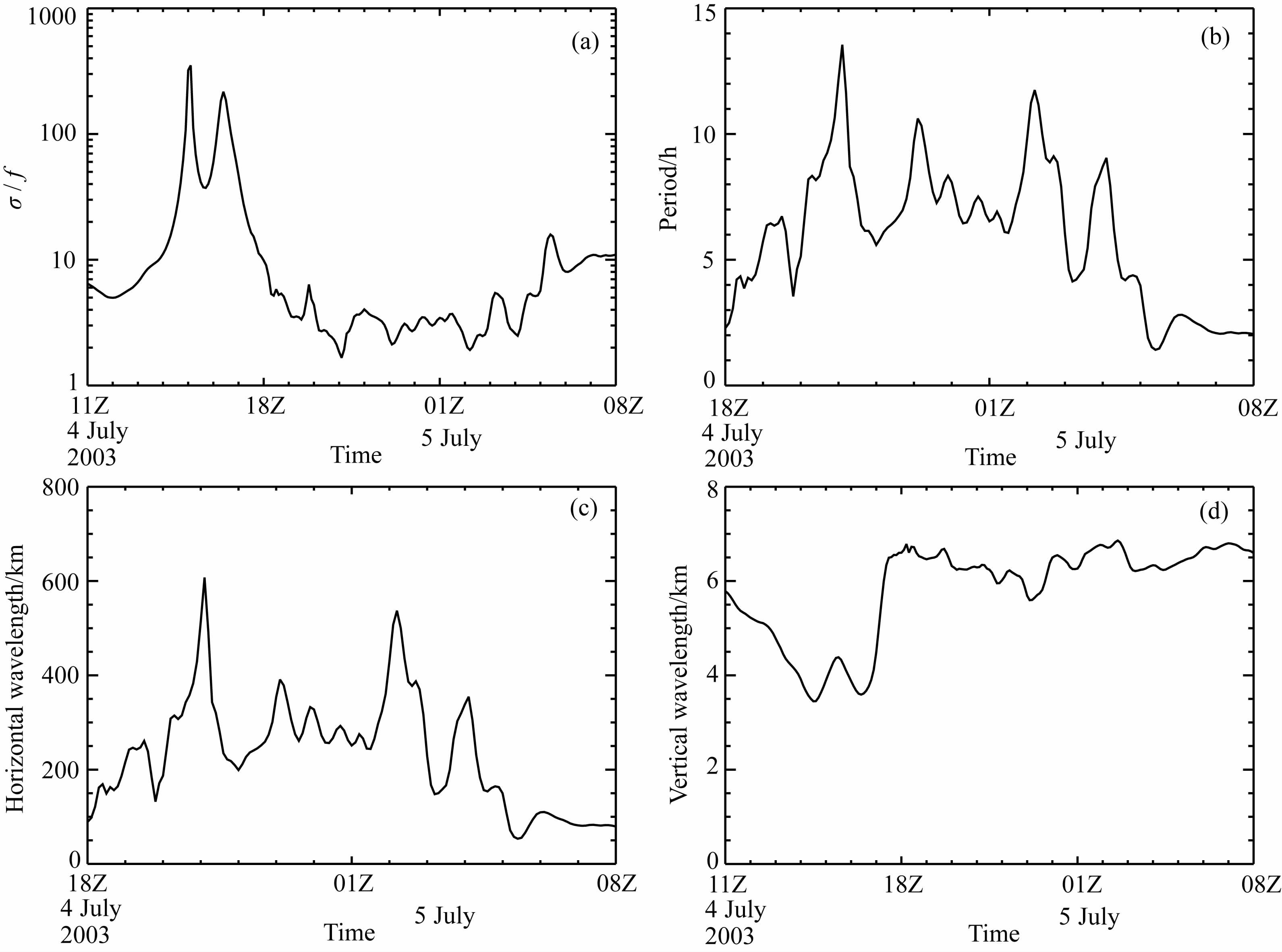
4.2 重力波参数演变特征 4.2.1 频率和周期由于暴雨过程中椭圆偏振度很高(图 7),扰动场主要由单频波组成,因此可以利用偏振椭圆长短轴之比计算频率.但偏振椭圆长短轴之比小于10时才适用,大于10时有很大不确定性,误差很大[9, 13-17].图 9a是偏振椭圆长短轴之比(即σ/f)随时间的演变,可见在暴雨前期,接近一半时次的σ/f大于10,不能据此计算重力波的频率;4 日18 时—5 日01时,σ/f介于1.66~10 之间,平均为3.61;5 日01—08时,绝大部分时次的σ/f小于10,平均为6.52.总体来看,重力波频率在暴雨后期有增大趋势.
|
图 9 暴雨中心区σ/f(a)、周期(b)、水平波长(c)和垂直波长(d)随时间的演变 Fig. 9 Temporal variation of σ/f(a), period (b), horizontal wavelength (c) and vertical wavelength (d) over the rainstorm area |
由于暴雨前期重力波频率计算误差很大,本文只分析后两个时段重力波周期的演变特征(图 9b),可见其演变趋势与频率相反,强暴雨阶段,周期介于2.5~13.5h 之间,平均为6.99h;暴雨后期,周期明显缩短,平均为4.96h.
4.2.2 波长在后两个时段,重力波的水平波长变化很大(图 9c),小到50km, 大到600km, 平均为232.95km, 其中超过200km 的时次占总数的60%,表明暴雨过程相伴的重力波属于中α 尺度波和中β 尺度波.强暴雨阶段,大部分时次水平波长大于200km, 重力波主要是中α 尺度波;暴雨后期,中α 尺度波减少,中β 尺度波增多.与周期变化趋势相似,暴雨后期重力波水平波长有显著缩短特征.比较周期和水平波长的演变趋势(图 9b 和图 9c)发现,二者呈显著正相关关系,相关系数为0.99.所以,空间尺度较大的重力波,其周期相对也长.
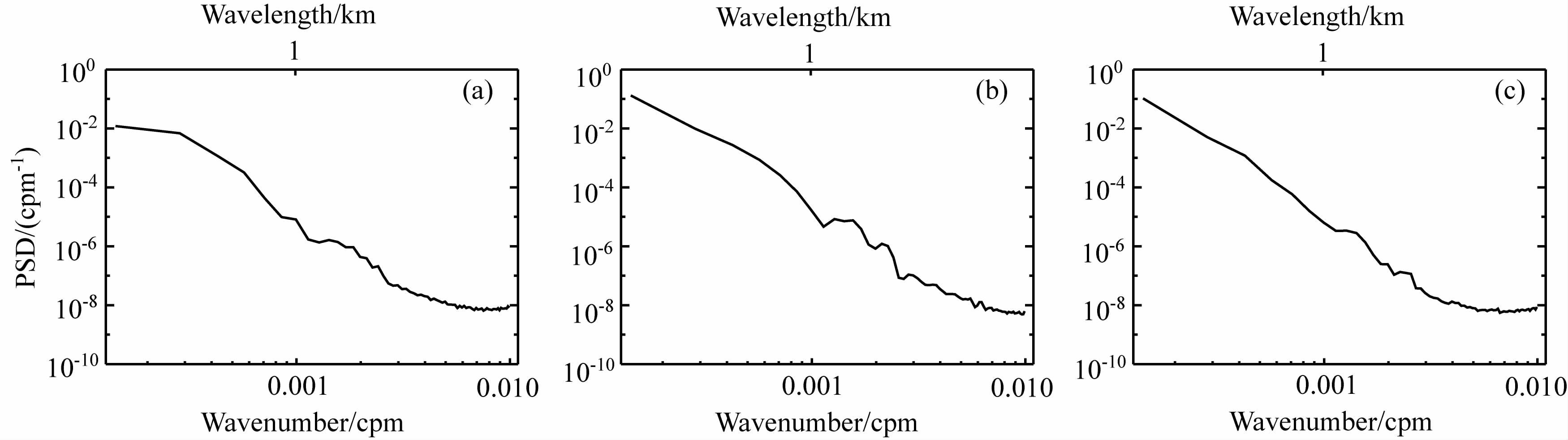
由图 9d可见,在整个暴雨过程中,垂直波长位于3~7km 之间,平均为5.83km.归一化温度扰动的垂直波数功率谱(图 10)表明垂直波长的大值往往集中在扰动能量大值区,且与能量成正比;后两个时段的垂直波数功率谱斜率相当,且明显大于暴雨前期,因此暴雨前期垂直波长较小,平均为4.67km, 后两个时段平均垂直波长较大,且非常接近,分别为6.28km 和6.55km.
|
图 10 各个时段暴雨中心区归一化温度扰动的垂直波数功率谱 (a) 4 日 11—18 时;(b) 4 日 18 时一5 日 01 时;()5 日 01—08 时. Fig. 10 The power spectra of vertical wavenumbers for the normalized temperatureperturbations over the rainstorm area for different period (a) 1100—1800UTC July 4;(b) 1800UTC July 4—0100UTC July 5 ; (c) 0100—0800UTC July 5. |
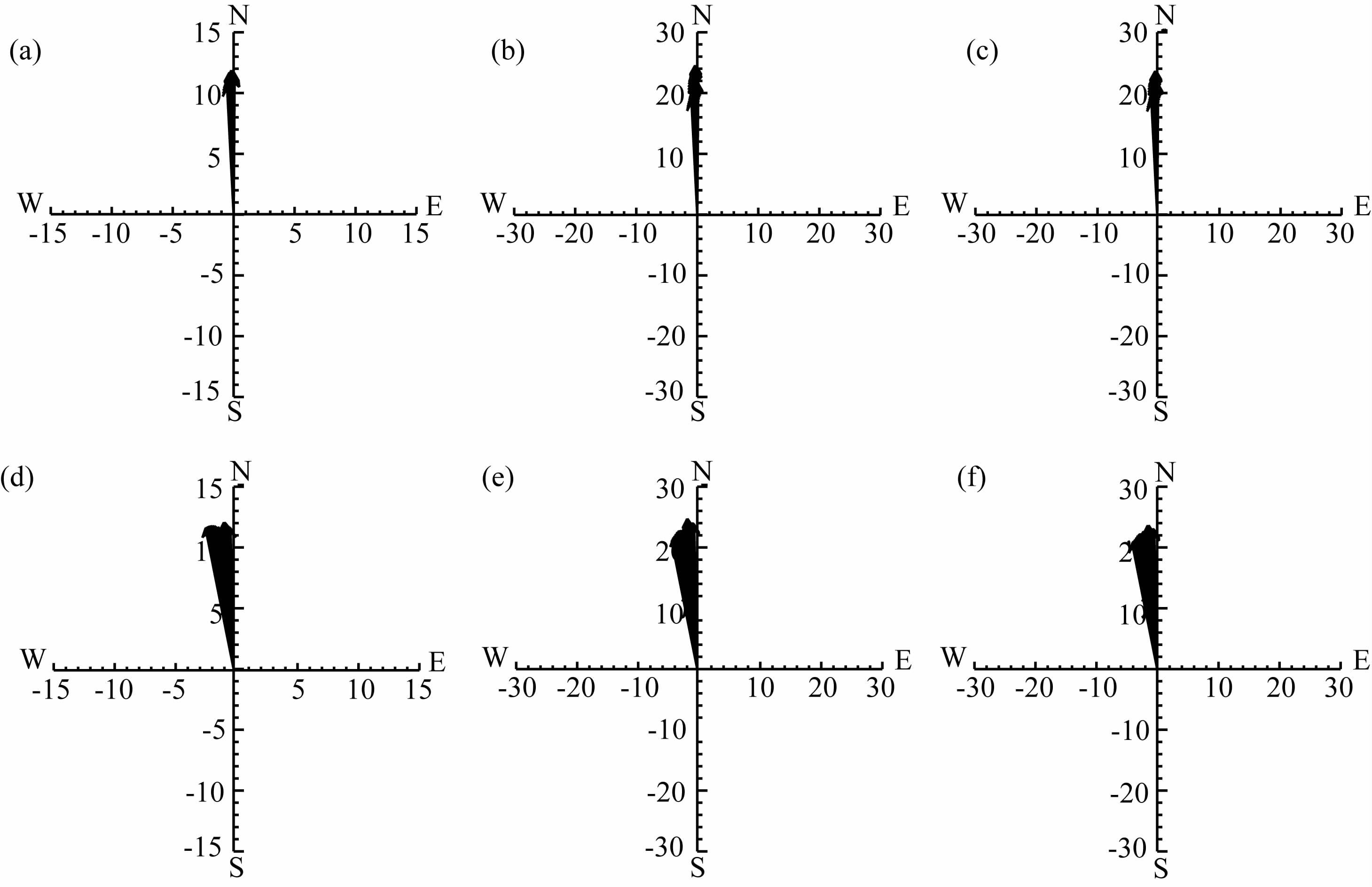
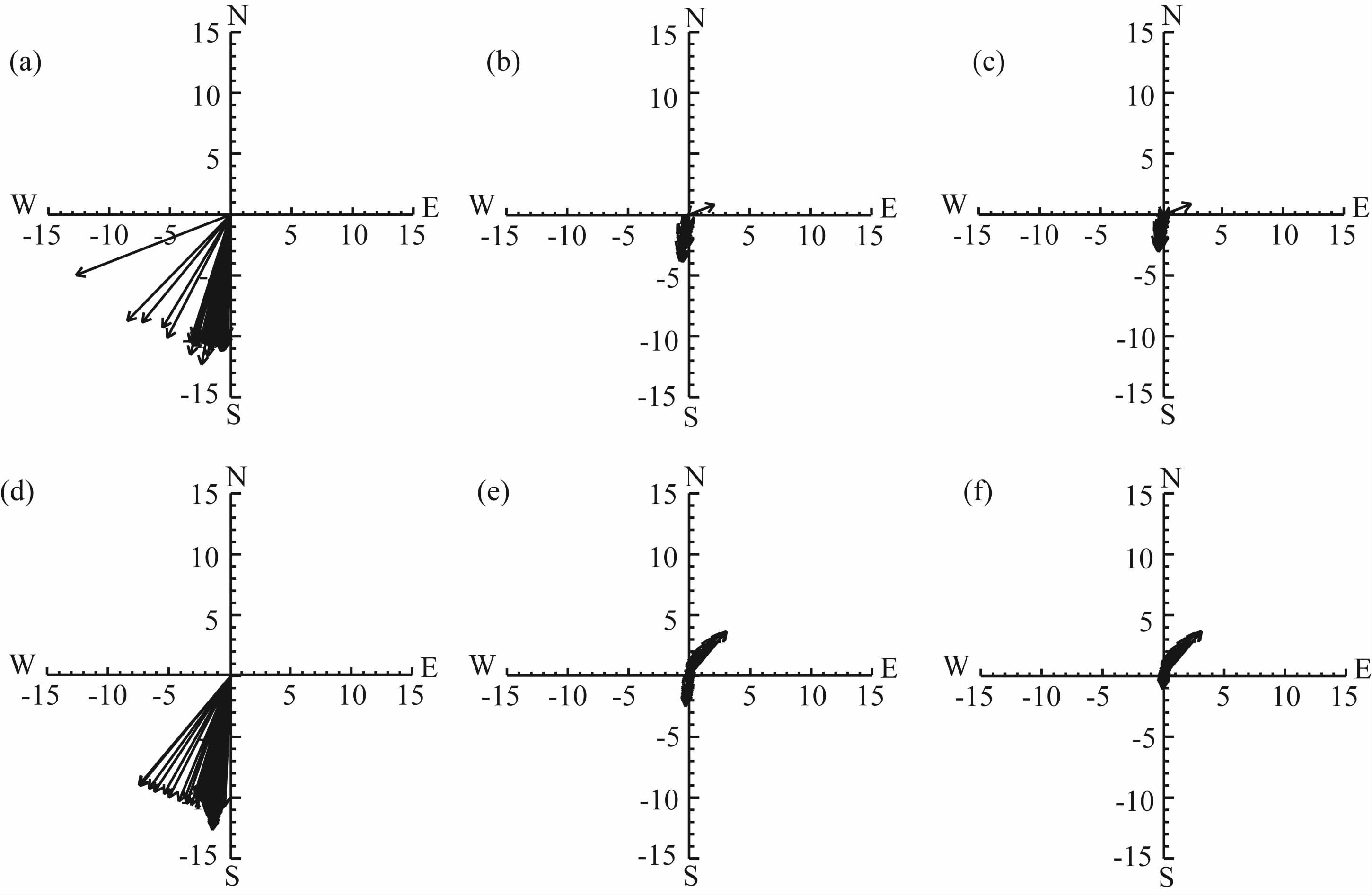
图 11a和图 11d分别为后两个时段重力波水平相速的矢量图,由图可见,当不考虑背景风场的作用时,水平相速矢量方向与前文所述重力波水平传播方向基本相同,且两个时段的水平相速相当,约为10m·s-1.由于在所研究的垂直范围内背景风场为西南风,且暴雨后期的风速大于强暴雨阶段(图略),因此叠加背景风场以后,水平相速发生了较大变化.强暴雨阶段的水平相速矢量方向变化不大,但相速明显减小,平均为4.2m·s-1(图 11b);暴雨后期原本向南偏西方向传播的重力波大都变为向东北方向传播,相速也明显减小,平均为2.8m·s-1(图 11e).后两个时段σ/f的平均值分别为3.61 和6.52,从而使得这两个时段的水平相速与群速非常接近,暴雨后期更是如此.比较考虑背景风场后的水平相速(图 11b和图 11e)和群速(图 11c和图 11f)矢量图可看〗出,叠加背景风场以后,后两个时段内的水平相速与群速都非常接近,强暴雨阶段平均水平群速为3.1m·s-1,而在暴雨后期为2.5m·s-1,更接近该时段的相速.
|
图 11 后两个时段暴雨中心区重力波水平相速(a, d)与考虑背景风场的水平相速(b, e)、水平群速(c, f)矢量图(单位:m. s-1) (a—c) 4 日 18 时一5 日 01 时;(d—f) 5 日 01—08 时. Fig. 11 Vector graph of gravity-wave horizontal phase velocity (a, d), ground-based horizontal phase velocity (b, e) andground-based horizontal group velocity (c, f) over the rainstorm area for the last two periods (units:m • s-1) (a—c) 1800UTC July 4—0100UTC July 5 ; (d—f) 0100—0800UTC July 5. |
为了揭示重力波对降水的影响,本文选取非降水区内距暴雨中心区较近的江苏宿迁(图 1b)附近区域(118.0°E—118.5°E,33.7°N—34.0°N)进行对比分析,研究时段和垂直范围选取与前文降水中心区相同.在获取背景廓线方法上也进行了诸多比较,最终选择利用四次多项式拟合获取背景廓线.图 12是非降水区扰动动能密度与位能密度之比随时间的演变,可见除部分时次该比值略大外,其他均位于1附近.
由非降水区上空垂直速度和扰动能量密度的时间-高度剖面图(图略)可知,无论在时间上还是空间上,非降水区上空垂直速度和能量的时空分布相对于暴雨中心区都很均匀,且明显小于暴雨中心区的值,表明非降水区上空上升气流较弱,存在稳定的小振幅波动.
从4日11时至5日08时,非降水区重力波椭圆偏振度d均大于0.7(图略),平均为0.9,表明其扰动场也主要是单频波.暴雨前期和暴雨后期偏振椭圆长短轴之比有部分时次大于10(图 13a),为了与暴雨中心区的重力波特征进行对比分析,本文只对后两个时段中偏振椭圆长短轴之比小于10 的模拟结果进行计算和分析.在这两个降水阶段,重力波周期位于2~8h之间(图 13b),平均为4.4h;水平波长为50~350km(图 13c),平均为184.8km, 属于中α 尺度波和中β 尺度波.整个暴雨过程中,垂直波长位于3~7km 之间(图 13d),平均为6km, 其演变趋势与暴雨中心区非常相似.后两个时段σ/f的平均值为5.6,使得水平相速与群速接近.当不考虑背景风场的作用时,强暴雨阶段,非降水区重力波向正北方向传播,暴雨后期传播方向略偏西,但两个时段的水平相速相当,约为11.5m·s-1(图 14a和图 14d).叠加背景风场以后,水平相速矢量方向基本不变,但相速增大到23m·s-1左右(图 14b和图 14e);水平群速矢量方向与相速基本相同,群速约为22m·s-1左右(图 14c和图 14f).与暴雨中心区的重力波参数相比,非降水区上空的重力波振幅偏小,周期偏短,频率偏高,水平波长减小,水平相速增大,但垂直波长相当.此外,非降水区重力波参数随时间变化缓慢,幅度小,不如暴雨中心区变化剧烈,这可能是因为暴雨中心区对流活动强,重力波不断生成、发展、破碎,而非降水区重力波受对流影响较小,相对稳定.上述分析表明,小振幅的中α 尺度波和中β尺度波若不发展,则对降水影响不大.
6 结论本文利用WRF模式对2003年7月4—5日淮河流域强降水过程的高时空分辨率模拟结果,采用动力学方法提取了此次暴雨过程中心区的重力波参数,并分析了重力波参数的演变特征,得到以下结论:
(1) 整个暴雨过程中,重力波椭圆偏振度均大于0.5,平均达到0.92,表明与暴雨过程相伴的扰动场主要由单频波组成,因此,在偏振椭圆长短轴之比小于10时利用该比值计算波动频率是可行的.
(2) 在降水增强的过程中,暴雨中心区上空的对流运动显著增强,重力波能量也显著增多,但主要集中在对流层上层;在降水减弱的过程中,对流迅速减弱,重力波能量也迅速减小,且在整个对流层分布趋于均匀.重力波强度和暴雨强度之间存在正相关关系.
(3) 此次暴雨过程中,重力波主要向南偏西方向传播,与背景风场方向相反,反向背景风场对重力波上传的促进作用使得强暴雨阶段和暴雨后期的能量上传比例高于暴雨前期.
(4) 暴雨过程相伴的重力波水平波长变化很大,小到50km, 大到600km, 属于中α尺度波和中β 尺度波;垂直波长介于3~7km 之间,与能量成正比;频率为1.66f~10f;周期为2.5~13.5h, 且与水平波长呈显著正相关关系.暴雨后期,随着重力波的频散,周期和水平波长有明显减小趋势,频率有增大趋势.
(5) 当不考虑背景风场的作用时,水平相速矢量方向与重力波水平传播方向基本相同,相速约为10m·s-1.叠加背景风场以后,强暴雨阶段的水平相速矢量方向变化不大,但相速明显减小;暴雨后期原本向南偏西方向传播的重力波大都变为向东北方向传播,相速也明显减小.由于暴雨过程相应的重力波频率较高,使得这两个时段的水平相速与群速非常接近.
(6) 非降水区重力波参数和暴雨中心区明显不同.非降水区上空也存在小振幅的中α尺度波和中β尺度波,但重力波参数随时间变化缓慢.与暴雨中心区的重力波参数相比,非降水区上空的重力波振幅偏小,周期偏短,频率偏高,水平波长减小,水平相速增大,但垂直波长相当.只有当小振幅的中α 尺度波和中β 尺度波得到发展才能对降水产生影响.
本文结论还需要利用更多个例结果进一步分析验证.
致谢澳大利亚Adelaide大学R.Vincent教授提供了相关分析程序.感谢两位审稿人提出详细修改建议.
| [1] | 李麦村. 重力波对特大暴雨的触发作用. 大气科学 , 1978, 2(3): 201–209. Li M C. Studies on the gravity wave initiation of the excessively heavy rainfall. Chinese Journal of Atmospheric Sciences (in Chinese) , 1978, 2(3): 201-209. |
| [2] | 马振锋. 大气中低频重力波指数与西南低涡发展及其暴雨的关系. 高原气象 , 1994, 13(1): 50–56. Ma Z F. The relations between the index of low-frequency gravitational wave and heavy rain proceed from development of southwest vortex. Plateau Meteorology (in Chinese) , 1994, 13(1): 50-56. |
| [3] | 陈金中, 黄荣辉. 中层大气重力波的一种激发机制及其数值模拟Ⅰ. 非地转不稳定和波结构. 大气科学 , 1995, 19(5): 554–562. Chen J Z, Huang R H. A possible mechanism for exciting gravity waves in middle atmosphere and its numerical simulation. Part I: Ageostrophic instability and wave structure. Chinese Journal of Atmospheric Sciences (in Chinese) , 1995, 19(5): 554-562. |
| [4] | Uccellini L W, Koch S E. The synoptic setting and possible energy sources for mesoscale wave disturbance. Mon. Wea. Rev. , 1987, 115(3): 721-729. DOI:10.1175/1520-0493(1987)115<0721:TSSAPE>2.0.CO;2 |
| [5] | 郭虎, 季崇萍, 张琳娜, 等. 北京地区2004年7月10日局地暴雨过程中的波动分析. 大气科学 , 2006, 30(4): 703–711. Guo H, Ji C P, Zhang L N, et al. A case study of local rainstorm in Beijing on 10 July 2004: the analysis of the gravity wave. Chinese Journal of Atmospheric Sciences (in Chinese) , 2006, 30(4): 703-711. |
| [6] | 龚佃利, 吴增茂, 傅刚. 一次华北强对流风暴的中尺度特征分析. 大气科学 , 2005, 29(3): 453–464. Gong D L, Wu Z M, Fu G. Analysis of the mesoscale characteristics about a severe thunderstorm in north China. Chinese Journal of Atmospheric Sciences (in Chinese) , 2005, 29(3): 453-464. |
| [7] | Allen S J, Vincent R A. Gravity wave activity in the lower atmosphere: Seasonal and latitudinal variations. J. Geophys. Res. , 1995, 100(D1): 1327-1350. DOI:10.1029/94JD02688 |
| [8] | Vincent R A, Allen S J, Eckermann S D. Gravity-wave parameters in the lower stratosphere. // Hamilton K ed. Gravity Wave Processes and Their Parameterization in Global Climate Models. Heidelberg: Springer-Verlag, 1997: 7-25. |
| [9] | Vincent R A, Alexander M J. Gravity waves in the tropical lower stratosphere: An observational study of seasonal and interannual variability. J. Geophys. Res. , 2000, 105(D14): 17971-17982. DOI:10.1029/2000JD900196 |
| [10] | Zink F, Vincent R A. Wavelet analysis of stratospheric gravity wave packets over Macquarie Island 1, wave parameters. J. Geophys. Res. , 2001, 106(D10): 10275-10288. DOI:10.1029/2000JD900847 |
| [11] | 卞建春, 陈洪滨, 吕达仁. 用垂直高分辨率探空资料分析北京上空下平流层重力波的统计特性. 中国科学D辑: 地球科学 , 2004, 34(8): 748–756. Bian J C, Chen H B, Lü D R. Analysis of characteristics of gravity wave under stratosphere by using the high-resolution data of radiosonde observation. Science in China Ser. D Earth Science (in Chinese) , 2004, 34(8): 748-756. |
| [12] | Wang L, Greller M A, Alexander M J. Spatial and temporal variations of gravity wave parameters. Part I: intrinsic frequency, wavelength, and vertical propagation direction. J. Atmos. Sci. , 2005, 62(1): 125-142. DOI:10.1175/JAS-3364.1 |
| [13] | Zhang S D, Yi F. A statistical study of gravity waves from radiosonde observations at Wuhan (30°N, 114°E), China. Annales Geographysicae , 2005, 23(3): 665-673. DOI:10.5194/angeo-23-665-2005 |
| [14] | Wang L, Geller M A. Morphology of gravity-wave energy as observed from 4 years (1998—2001) of high vertical resolution U. S. radiosonde data. J. Geophys. Res. , 2003, 108(D16): 4489. DOI:10.1029/2002JD002786 |
| [15] | Zhang S D, Yi F. Latitudinal and seasonal variations of inertial gravity wave activity in the lower atmosphere over central China. J. Geophys. Res. , 2007, 112: D05109. DOI:10.1029/2006JD007487 |
| [16] | Zhang S D, Yi F, Huang C M, et al. Intensive radiosonde observations of gravity waves in the lower atmosphere over Yichang (111°18'E, 30°42'N), China. Annales Geographysicae , 2008, 26(7): 2005-2018. DOI:10.5194/angeo-26-2005-2008 |
| [17] | Zhang S D, Yi F, Huang C M, et al. Latitudinal and seasonal variations of lower atmospheric inertial gravity wave energy revealed by US radiosonde data. Annales Geophysicae , 2010, 28(5): 1065-1074. DOI:10.5194/angeo-28-1065-2010 |
| [18] | 许小峰, 孙照渤. 非地转平衡流激发的重力惯性波对梅雨锋暴雨影响的动力学研究. 气象学报 , 2003, 61(6): 655–660. Xu X F, Sun Z B. Dynamic study on influence of gravity wave induced by unbalanced flow on Meiyu front heavy rain. Acta Meteorologica Sinica (in Chinese) , 2003, 61(6): 655-660. |
| [19] | 李俊, 张绍东, 易帆. 重力波包在中层大气温度波导中传播的数值模拟. 地球物理学报 , 2007, 50(4): 1030–1039. Li J, Zhang S D, Yi F. A numerical simulation on gravity waves propagation in mesospheric thermal duct. Chinese J. Geophys. (in Chinese) , 2007, 50(4): 1030-1039. |
| [20] | 李俊, 张绍东. 重力波在中层大气温度波导中的传播模式研究. 地球物理学报 , 2010, 53(2): 237–246. Li J, Zhang S D. Wave mode analyses of gravity waves propagating in the mesospheric thermal duct. Chinese J. Geophys. (in Chinese) , 2010, 53(2): 237-246. |
| [21] | 覃卫坚, 寿绍文, 高守亭, 等. 一次冰雹过程的惯性重力波观测及数值模拟. 地球物理学报 , 2010, 53(5): 1039–1049. Qin W J, Shou S W, Gao S T, et al. Numerical study of the dynamical mechanism of inertial gravity waves in hail storm process. Chinese J. Geophys. (in Chinese) , 2010, 53(5): 1039-1049. |
| [22] | 孙建华, 周海光, 赵思雄. 2003年7月4~5日淮河流域大暴雨中尺度对流系统的观测分析. 大气科学 , 2006, 30(6): 1103–1118. Sun J H, Zhou H G, Zhao S X. An observational study of mesoscale convective systems producing severe heavy rainfall in the Huaihe river basin during 3-4 July 2003. Chinese Journal of Atmospheric Sciences (in Chinese) , 2006, 30(6): 1103-1118. |
| [23] | 章国材. 美国WRF模式的进展和应用前景. 气象 , 2007, 30(12): 27–31. Zhang G C. Progress of weather research and forecast (WRF) model and application in the United States. Meteorological Monthly (in Chinese) , 2007, 30(12): 27-31. |
| [24] | Lin Y L, Farley R D, Orville H D. Bulk parameterization of the snow field in a cloud model. J. Appl. Meteor. , 1983, 22(6): 1065-1092. DOI:10.1175/1520-0450(1983)022<1065:BPOTSF>2.0.CO;2 |
| [25] | Gregory T, Rasmussen R M, Manning K. Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part I: Description and sensitivity analysis. Mon. Wea. Rev. , 2004, 132(2): 519-542. DOI:10.1175/1520-0493(2004)132<0519:EFOWPU>2.0.CO;2 |
| [26] | Kain J S. The Kain-Fritsch convective parameterization: An update. J. Appl. Meteor. , 2004, 43(1): 170-181. DOI:10.1175/1520-0450(2004)043<0170:TKCPAU>2.0.CO;2 |
| [27] | Hong S Y, Noh Y, Dudhia J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Wea. Rev. , 2006, 134(9): 2318-2341. DOI:10.1175/MWR3199.1 |
| [28] | Mlawer E J, Taubman S J, Brown P D, et al. Radiative transfer for inhomogeneous atmosphere: RRRTM, a validated correlated-k model for the longwave. J. Geophys. Res. , 1997, 102(D14): 16663-16682. DOI:10.1029/97JD00237 |
| [29] | Dudhia J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. , 1989, 46(20): 3077-3107. DOI:10.1175/1520-0469(1989)046<3077:NSOCOD>2.0.CO;2 |
| [30] | Hines C O. Tropopausal mountain waves over Arecibo: A case study. J. Atmos. Sci. , 1989, 46(4): 476-488. DOI:10.1175/1520-0469(1989)046<0476:TMWOAA>2.0.CO;2 |
| [31] | Holton J R. An Introduction to Dynamic Meteorology. Fourth Edition. San Diego: Elsevier Academic Press, 2004 . |
| [32] | Eckermann S D. Hodographic analysis of gravity waves: Relationships among Stokes parameters, rotary spectra and cross-spectral methods. J. Geophys. Res. , 1996, 101(D14): 19169-19174. DOI:10.1029/96JD01578 |
| [33] | 韦志刚, 陈文, 黄荣辉. 敦煌夏末大气垂直结构和边界层高度特征. 大气科学 , 2010, 34(5): 905–913. Wei Z G, Chen W, Huang R H. Vertical atmospheric structure and boundary layer height in the summer clear days over Dunhuang. Chinese Journal of Atmospheric Sciences (in Chinese) , 2010, 34(5): 905-913. |
| [34] | 刘晓, 徐寄遥. 重力波与不同背景风场之间的非线性相互作用. 自然科学进展 , 2006, 16(11): 1436–1441. Liu X, Xu J Y. Nonlinear interactions between gravity waves and background winds. Prog. Nat. Sci. (in Chinese) , 2006, 16(11): 1436-1441. |
 2012, Vol. 55
2012, Vol. 55