2. 中国科学院研究生院,北京 100049
2. Graduate University of Chinese Academy of Sciences, Beijing 100049, China
朗缪尔探针是目前国际上应用最广泛的一种空间等离子体环境就位探测技术,它质量小、结构简单、功耗低,可以就位测量空间等离子体的电子密度、电子温度等整体特性参数,以及航天器的表面电位及其变化情况,能够保障航天器的安全,为电离层模型和空间天气预报提供输入数据,并研究电离层的不规则性和分布特征.
早在1946年朗缪尔探针就被安装在V-2 火箭上[1],首次开始了电离层等离子体就位探测的实验.虽然过去半个多世纪了,朗缪尔探针技术仍是就位探测空间等离子体的重要手段,广泛被探空火箭和各种航天器采用,用来进行科学探测和为航天器的安全保障服务.例如:欧洲的ICI[2]系列和DEOS[3]系列探空火箭,美国的COQUI[4]系列和EQUIS[5]系列探空火箭等都载有朗缪尔探针,对电离层的各种精细结构和现象进行就位探测和研究;各种低轨卫星也把朗缪尔探针作为电离层就位探测的重要手段,如:国际太空站[6]使用朗缪尔探针对国际太空站的电位和空间等离子体环境进行监测;DMSP 和NPOESS[7]系列卫星使用朗缪尔探针对低轨空间等离子体环境进行探测和研究,C/NOFS[8]卫星利用朗缪尔探针测量空间等离子体参数对导航通讯中断进行预警,Demeter卫星利用朗缪尔探针研究地震和电离层扰动的相互关系.但目前,朗缪尔探针技术在我国空间环境探测领域仍是空白,随着我国航天任务的增多,朗缪尔探针的研制无论对于航天安全保障还是空间科学研究都具有非常重要的意义.
本文主要介绍一种基于探空火箭的朗缪尔探针方案设计及其初步测试的结果.
2 科学任务地球电离层距离地面高度低于300km 的区域,是电离层发生、发展的重要区域,有着复杂的分层结构(D、E、F1、F2 层等)和精细结构,存在复杂的热过程、化学过程、流体力学过程和电动力学过程,是研究电离层分布规律和动力学发生、发展的主要区域.
通常F2 层高度(约300km)以下,是人造卫星不能到达的区域,该区域的电离层测量以地基遥感测量为主,例如相干散射雷达、非相干散射雷达、电离层数字测高仪、GPS电离层TEC 监测仪等.但是这些遥感测量方法不能获得电离层小尺度的精细结构,这已不能完全满足日益发展的电离层研究的需求.箭载朗缪尔探针的最大优势就是能够进行从底部到高空的电离层垂直剖面的探测,并能对电离层的小尺度精细结构进行就位探测.
2.1 探测对象本朗缪尔探针的方案设计与研制以子午工程1)探空火箭为平台.首发探空火箭在我国中国科学院海南探空部(约19°N,109°E)发射,飞行高度约200km, 用来获取我国低纬电离层垂直高度精细结构的科学数据.可以利用国际电离层参考模型IRI-2007计算出该探测区域的电离层的基本特性参数.
1)子午工程是由中国科学院牵头多单位共同建设的国家重大科学研究和工程项目,在我国沿120°E,30°N 附近形成以地基为主的空间环境监测链,通过地磁、无线电、探空火箭等多种手段连续监测地球表面20~30km 以上高度的空间环境.
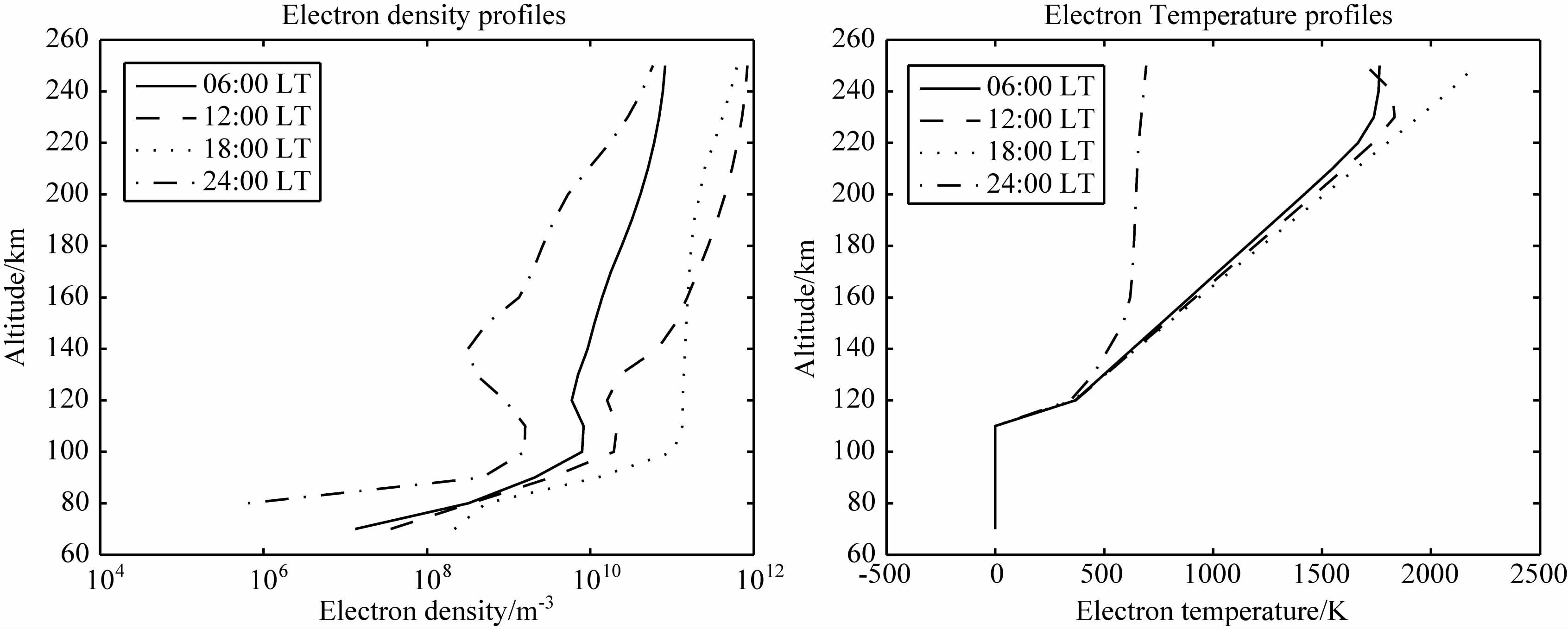
图 1 是利用IRI-2007 计算出的火箭发射地上空电离层分别在早晨(06∶00LT)、中午(12∶00LT)、黄昏(18∶00LT)、子夜(24∶00LT)四个时段70km到250km 高度电离层电子密度和电子温度剖面.考虑到在磁暴、亚暴等条件下,等离子体参数经常出现较大幅度的扰动,电子密度会有几个百分点到几十个百分点的变化,极严重时可能会有成倍的增长.因此,探空火箭等离子体测量仪器性能指标的基本需求如下:电子密度102~5×106cm-3,电子温度500~3000K.同时,为了满足电离层垂直高度精细结构的探测,朗缪尔探针在固定偏压模式下进行探测,时间分辨率约3.7ms, 空间分辨率优于10m.
|
图 1 火箭发射地上空等离子体特性参数 Fig. 1 The parameters of the ionosphere above the launch site |
我国子午工程首发探空火箭主要用来获取我国低纬电离层垂直高度精细结构的科学数据,以该探空火箭为平台的朗缪尔探针主要实现以下三方面的探测目标:
(1) 获取我国低纬电离层70km 到200km 的电子密度精细结构剖面,重点研究D 层及各层间过渡区域的精细结构特征.电离层D 层中性成分密度大,碰撞频率高,对电波吸收大,电波回波很弱甚至收不到回波,地面很难进行详细探测;电离层各层之间谷区,容易被下方电离区域所遮蔽,地面设备也很难进行详细探测[9].朗缪尔探针将在探空火箭上升段约65km 高度处开机工作,在火箭的上升段和下降段分别实现对70km 到200km 的电离层电子密度剖面的探测.
(2) 探测电离层突发E 层(Es 层)的精细结构.火箭飞行过程中有可能从Es 层中穿越,探测到Es 层的精细结构,用于研究Es 层的结构特征及其产生发展机制.Es 层是E 层中的不规则的电离密集薄层,电子密度超出邻近区域1倍以上,其发生高度约在110km 左右,厚度约几百米到数千米(多数1km左右).探空火箭朗缪尔探针在固定偏压模式下进行探测,时间分辨率约3.7ms, 空间分辨率优于10m, 可以对Es 层进行较为详尽的测量.
(3) 探测电离层不规则体或等离子体泡的精细结构.低纬电离层是电离层闪烁的多发区域和电离层不规则体、扩展F 等的发生区域.电离层闪烁主要是由于电离层不规则体对电波散射等作用造成的.由于火箭的最大飞行高度只有200km 左右,火箭飞行探测过程中有可能部分从电离层等离子体泡下部穿越,以探空火箭为平台的朗缪尔探针就位探测有可能部分探测电离层不规则体或等离子体泡的内部精细结构.
探空火箭发射期间,朗缪尔探针设备将和地面观测设备开展联合试验———天基协同探测.由于火箭飞行的最大高度低于电离层顶位置(300~400km 高度),因此,可以利用地面综合站的DPS-4 电离层测高仪进行比较测量.DPS-4 仪器通过电波传播实验(频率扫描范围1~40 MHz)可得到电离层等离子体电子密度剖面实时数据(虚高剖面)和等离子体不规则结构数据以及电波传播参数.因频率扫描工作方式的制约,DPS-4 高度空间分辨比较低(普通模式,高度空间分辨5km),通过调整频率扫描范围,可将高度空间分辨提高到2.5km.这样在箭载朗缪尔探针工作高度范围(上升过程),可得到大约50个有效数据点,可以与朗缪尔探针探测数据进行比较分析.
3 基本原理郎缪尔探针的基本原理是将一根金属电极(传感器)伸入到等离子体中,通过测量电极的电压和其收集的等离子体电流关系,来反演等离子体的特性参数.Irving Langmuir最初提出了朗缪尔探针的概念,并在1926年与Mott-Smith 一起推导出了朗缪尔探针理论公式[10],即公式(1)—(5):
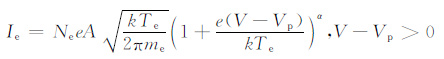
|
(1) |
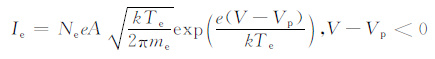
|
(2) |
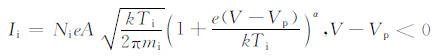
|
(3) |

|
(4) |
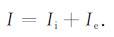
|
(5) |
α=1,球形传感器;α=1/2,圆柱形传感器;α=0,平板形传感器.
式中,I,Ie, Ii 分别是总电流、电子电流和离子电流;Ne, Ni 分别是电子密度和离子密度;e是电子电荷常量;A是传感器有效面积;k是玻耳兹曼常数;Te, Ti分别是电子温度和离子温度;me, mi分别是电子质量和离子质量;V是传感器的电位,Vp 是空间等离子体电位.
箭载朗缪尔探针通常分为固定偏压和扫描电压两种.固定偏压探针,可以高时空分辨率地测量电子密度的相对变化,可以测量小尺度的电离层精细结构,但是固定偏压探针不能获得电子温度的信息.扫描电压探针通过伏安特性曲线来反演电子密度、电子温度和火箭电位等参数,但是扫描电压时空分辨率远低于固定偏压探针.本朗缪尔探针采用扫描电压和固定偏压相结合的方式(具体见4.4节).
4 朗缪尔探针方案设计探空火箭朗缪尔探针系统包括两个电子探针和一个离子探针:电子探针是典型的朗缪尔探针,用于测量电子密度和温度;离子探针是一种特殊朗缪尔探针,用于测量离子的密度.本文朗缪尔探针专指电子探针,离子探针部分不在本文介绍.
朗缪尔探针由传感器、伸杆和电子学三部分组成,如图 2所示.传感器用来收集空间等离子体电流;伸杆用来消除火箭本体对测量的影响;电子学用来产生扫描电压和采集测量信号.

|
图 2 朗缪尔探针火箭安装示意图 Fig. 2 The Langmuir probe configurations on the rocke |
朗缪尔探针结构比较简单,但是朗缪尔探针的实际工程应用却要受到很多因素的制约,例如传感器的大小、形状,航天器(火箭)的鞘层、尾迹,航天器(火箭)的电位等.
4.1 传感器的设计朗缪尔探针传感器的设计包括传感器的形状、大小及其表面镀层等,它的设计受多种因素的制约,同时也影响着空间等离子体电流的收集.
朗缪尔探针传感器形状通常有平板形、圆柱形和球形三种.传感器形状的选取主要受探针电流收集理论制约和传感器边缘效应的影响.平板形探针的电子饱和电流为常数(在(1)式中,平板形探针α=0),但平板形探针有很强的边缘效应,电子饱和电流的实际大小需要数值模拟才能给出;圆柱形探针也有很强终端效应[11],且对于高速运动的航天器(火箭)需要考虑航天器(火箭)飞行速度方向与圆柱形探针的夹角对测量带来的影响[12];球形探针则具有各向同性的电场电位分布,没有终端效应,更利于带电粒子的收集.在空间环境探测领域,早期应用以圆柱形探针较多,近年来以球形探针应用较为广泛.
朗缪尔探针传感器大小主要由两方面决定:一方面,探针收集电流信号大小正比于传感器的表面积,为了提高载荷的信噪比,要求传感器尽可能的大;另一方面,探针传感器收集来的电流,要通过火箭表面和空间等离子体进行电荷交换返回到空间等离子体中去,形成一个闭合回路.由于物体在空间等离子体中收集的电子电流远大于离子电流,就要求当朗缪尔探针工作在电子饱和区时,火箭必须有足够大的外表面积吸收离子电流来补偿探针传感器收集来的电子电流.因此火箭本体的大小又限制了传感器的大小[13].
综合以上各方面因素,根据火箭的实际情况,朗缪尔探针传感器设计为一直径4cm 球形传感器,上半球为收集极,下半球为保护电极,球表面采用TiN镀层.该镀层机械强度高、功函数均一、化学性能稳定、耐腐蚀、耐氧化,已被国外很多试验机构所验证[14],同时在国外也被广泛应用到星载朗缪尔探针上,例如欧洲的Demeter卫星[15]、Cassini卫星[16]、Rossata卫星[17]等.
4.2 伸杆长度火箭与等离子体相互作用,火箭会处于悬浮电位(相对空间等离子体为负),并在其周围形成鞘层;火箭在等离子体中高速运动会在其尾部形成尾流区.为避免朗缪尔探针测量结果受到火箭电位、鞘层及其尾流的影响,朗缪尔探针的传感器应安装在火箭的头部或侧翼,并且通过伸杆远离火箭本体.伸杆长度主要受到火箭鞘层厚度的限制.火箭鞘层的厚度,主要由空间等离子体的德拜长度λD 决定(公式(6)),在距离火箭3到5 倍德拜长度的位置可以认为是未受火箭本体干扰的背景等离子体[18].在70km到200km 高度范围内,德拜半径约从几毫米到几厘米变化,因此20~30cm 长度的伸杆可以满足基本的测量需求.
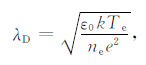
|
(6) |
式中参数都为国际单位制,其中ε0 为真空介电常数,k为玻耳兹曼常数,Te 为电子温度,ne 为电子密度,e为基本电荷.
4.3 双探针设计与安装朗缪尔探针采用两个球形传感器,安装在火箭平台头部径向对称的2 个位置,伸杆展开后两探针连线与火箭轴向垂直.火箭头体分离并抛掉整流罩后,朗缪尔电子探针伸杆展开.图 2为朗缪尔探针在火箭上安装位置示意图,图 2a为火箭发射状态,图 2b为火箭整流罩抛掉后,朗缪尔探针正常工作状态.
双探针的设计主要有三方面优点:一是保持火箭结构和质量对称,有利于火箭自旋稳定;二是两个探针的测量结果可以相互验证;三是,在火箭的下落过程郎缪尔探针的测量会受到火箭尾迹的影响[19],双探针对称设计可以保证火箭始终有一个探针工作在尾迹区以外.
4.4 工作模式扫描电压探针可以获取电离层等离子体电子密度和电子温度以及火箭电位等参数,固定偏压探针可以获取电离层精细结构的电子密度相对变化或扰动信息.其中,扫描电压的设计必须使朗缪尔伏安特性曲线包含离子饱和区、电子阻滞区和电子饱和区三个完整区域才能反演出等离子体的特性参数.固定偏压则需要使朗缪尔探针固定工作在电子饱和区或离子饱和区.理论上,朗缪尔探针扫描电压需要以等离子体电位Vp 作为中心基准进行扫描;在实际工程应用上朗缪尔探针只能以火箭结构地的电位Vsp作为基准.火箭在等离子体中将处于悬浮电位Vf, 该悬浮电位即是火箭相对于空间等离子体的电位Vsp.火箭悬浮电位可由(5)式I=Ii+Ie =0得出,根据70km 到200km 等离子体特性参数(见2.1节),Vsp约为-0.5V 左右.
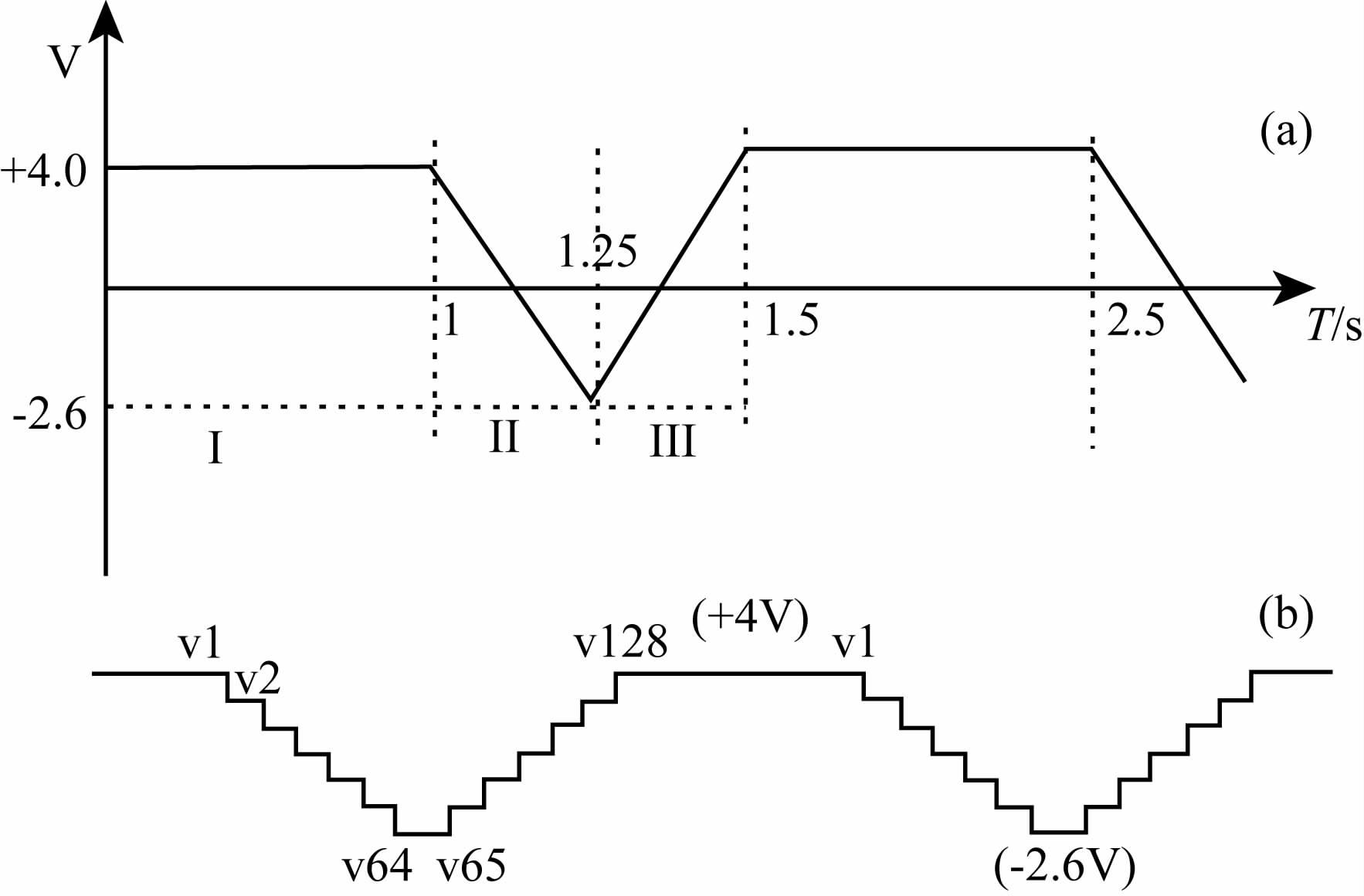
为了既能获取70km 到200km 电离层电子温度参数,又能获得电离层精细结构的信息,该朗缪尔探针采用扫描电压和固定偏压相结合的工作模式.朗缪尔探针两路探针同步工作,扫描电压的扫描周期为1.5s, 电压幅度为-2.6~+4V,图 3为扫描电压的示意图.扫描电压一个周期内共有三个阶段,分别为阶段Ⅰ、阶段Ⅱ和阶段Ⅲ.其中阶段Ⅰ为固定偏压4.0V,时间1s, 误差范围±5mV.阶段Ⅱ为下降段,时间0.25s, 其中有64步阶梯,每步时间等间隔.阶段Ⅲ为上升段,时间0.25s, 其中有64 步阶梯,每步时间等间隔.图 3b为阶段Ⅱ 和阶段Ⅲ 扫描阶梯的示意图.阶段Ⅱ 和阶段Ⅲ 扫描阶梯的扫描电压值如表 1.
|
图 3 扫描电压的示意图 Fig. 3 The sweeping voltage of the electron prob |
|
|
表 1 扫描电压阶梯的扫描电压值 Table 1 The steps of the sweeping voltage |
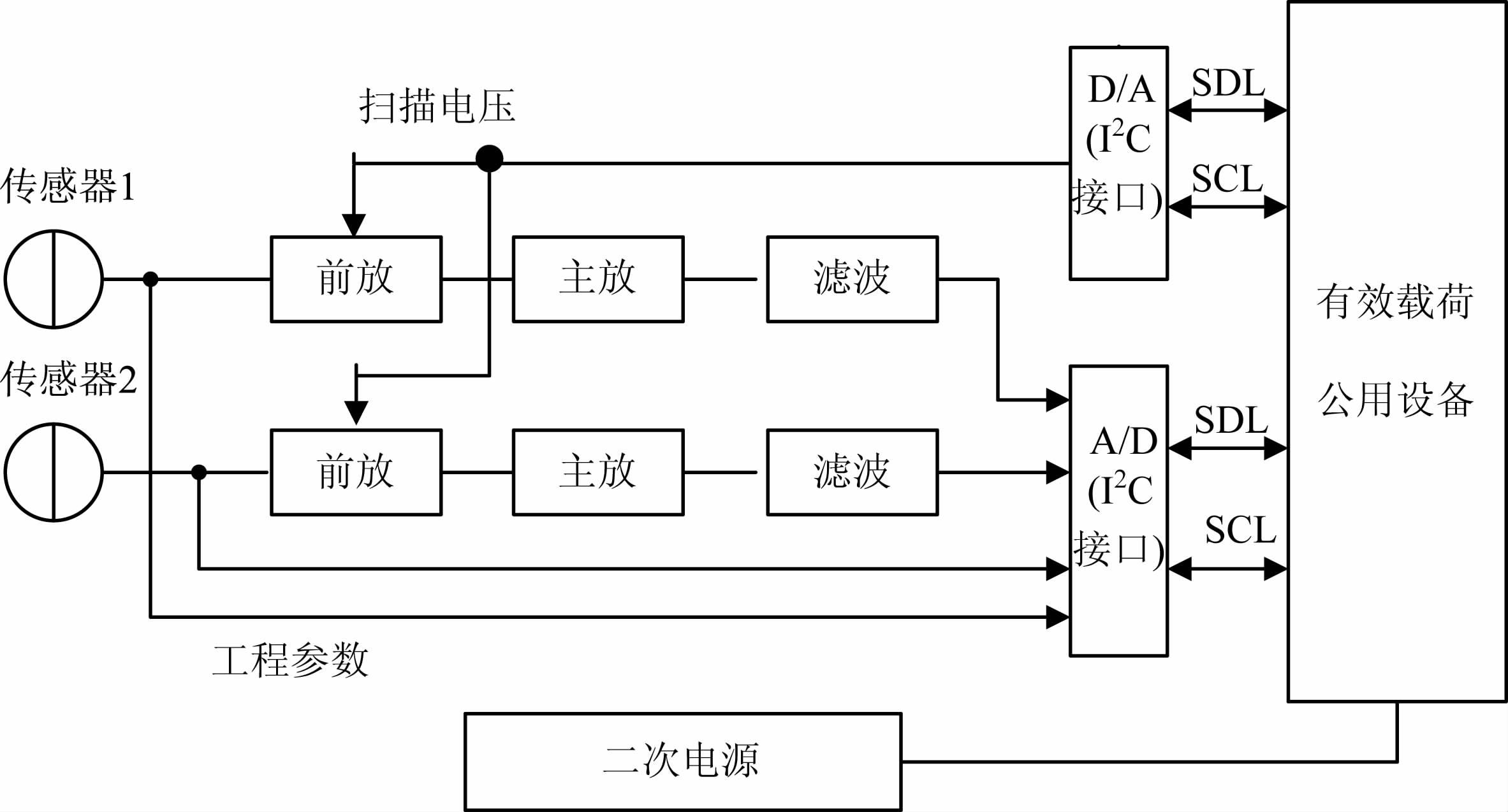
朗缪尔探针电子学包括两个电子测量电路,原理框图如图 4,两个电子测量电路同步工作,但各自具有独立的前放电路,独立完成测量.电子测量电路分别为两个电子传感器提供-2.6~ +4V 扫描电压,并测量电子传感器的收集电流.朗缪尔探针采用12位A/D 产生扫描电压,12 位D/A 采集科学数据,采样频率256 Hz.朗缪尔探针和箭载公用设备通过I2C 总线实现数据传输,其中箭载公用设备控制电子探针的扫描电压和工作时续,并接收朗缪尔探针的科学数据和工程参数.
|
图 4 朗缪尔探针电子、离子探测电子学原理框图 Fig. 4 The Langmuir probe functional block diagram |
朗缪尔探针属于微弱电流信号测量电路,测量电流信号小,动态范围大,其中电子探针电流测量动态范围:100pA~480uA.
5 测试结果朗缪尔探针实验室测试方法主要有两种:一是用模拟信号源进行测试,主要用来对其电子学进行测试定标;一是通过在真空罐内产生等离子体,模拟再现空间等离子体环境,对整个朗缪尔探针系统进行测试.
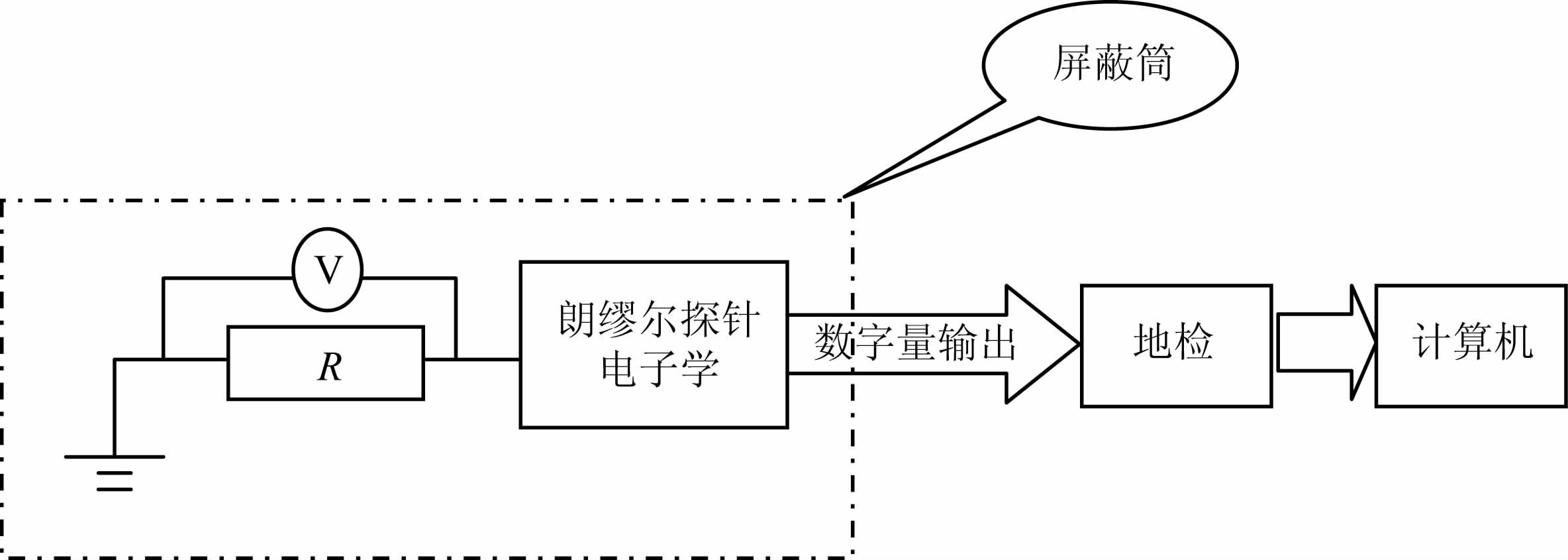
5.1 模拟信号源测试朗缪尔探针电子学主要用来给传感器提供扫描电压,并测量传感器收集的空间等离子体电流.因此对朗缪尔探针电子学的测试就是对其扫描电压和测量电流的准确性进行测试标定.图 5 为朗缪尔探针电子学测试定标原理框图:R为标准电阻,可以为朗缪尔探针提供一个等效负载,模拟产生一个标准电流输入信号;电压表用于测定朗缪尔探针的扫描电压(-2.6~+4V);地检设备用于采集朗缪尔探针数字量输出,并且转存到计算机.由于朗缪尔探针属于微弱信号测量设备,为保证测量的准确性,整个测试需要在良好的电磁屏蔽环境下进行.
|
图 5 朗缪尔探针电子学测试定标框图 Fig. 5 The calibration test functional block diagram for the Langmuir probe |
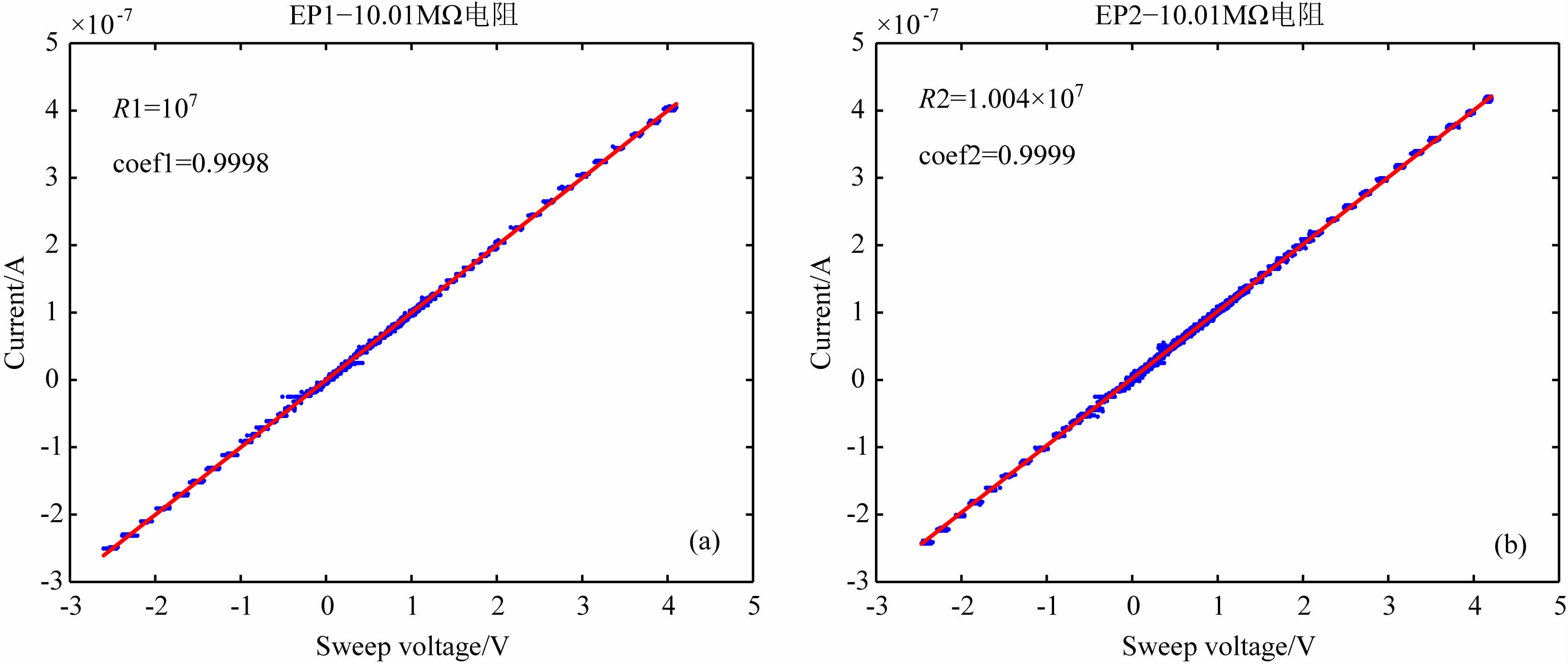
图 6 是电子探针在常温下测试定标的一组结果.采用高精度静电计测定标准电阻R的值为10.01 MΩ,可以认为是标准电阻的真实值.R1、R2分别是根据电子探针1和2实际测量结果拟合得出标准电阻值,其中R1=10.00MΩ,R2=10.04MΩ,相关系数分别为coef1=0.9998,coef2=0.9999.可见电子探针电子学的输出线性度接近于1,可以准确测定微弱电流信号.
|
图 6 电子探针电子学测试定标结果 Fig. 6 The calibration test results for the electron probe |
朗缪尔探针主要用来就位测量空间等离子体的电子密度、温度等.在地面对包含传感器在内的整个载荷进行测试,需要有一个空间等离子体模拟系统,模拟再现电离层空间等离子体状态和参数,为朗缪尔探针提供工作环境和探测对象.
意大利天体物理研究院行星际物理研究所(INAF-IFSI)拥有先进的低能等离子体模拟测试实验设备,以氩气(Ar)为工作介质,可以模拟再现电离层空间等离子体状态和参数.其中氩离子具有约8km/s的漂移速度,电子密度约在1012m-3的量级,电子温度约1000~3000K.
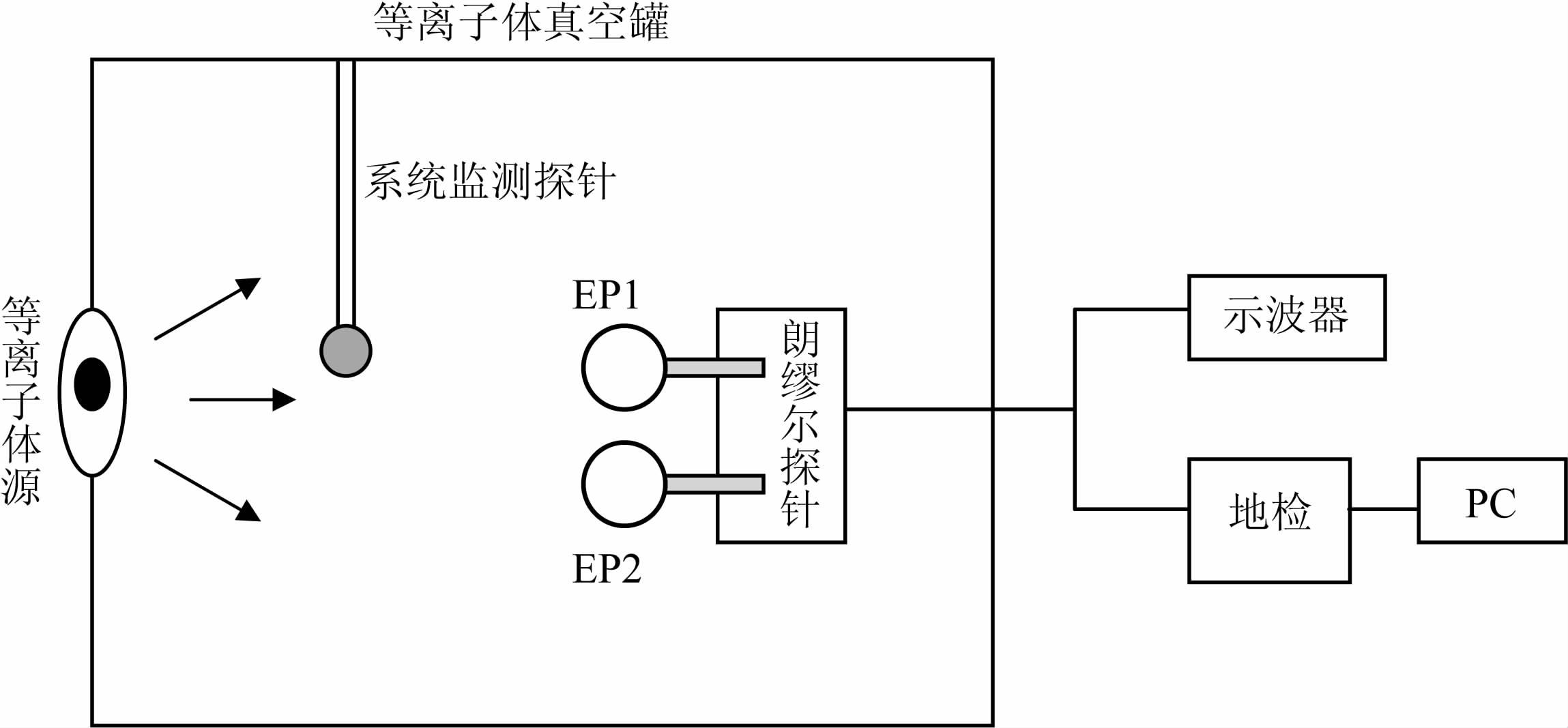
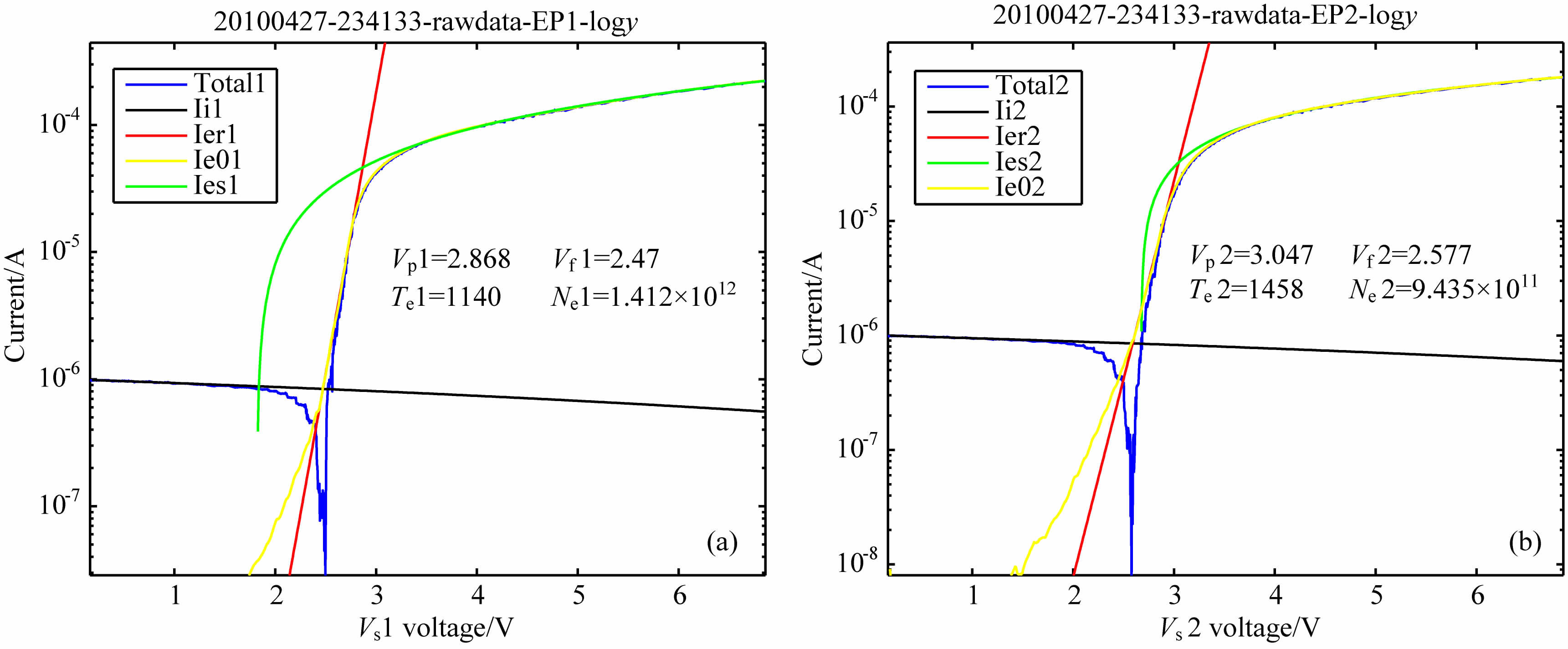
朗缪尔探针在意大利INAF-IFSI等离子体模拟系统内进行测试的原理框图如图 7,在磁场控制系统补偿掉地磁场的情况下,该系统将在真空罐中后部中心区域产生一个比较稳定的等离子体区域,朗缪尔探针电子探针传感器便放置在该区域.当系统监测探针确定等离子体正常工作后,朗缪尔探针便可开始进行测试(由于模拟系统产生的等离子体电位约3V 左右,为获得完整伏安特性曲线,将电子探针的扫描电压调整为:0.2~6V).电子探针的初步测量结果如图 8 所示,该图是朗缪尔探针的一组实测数据在半对数坐标下的伏安特性曲线及其结果.其中,图 8a为电子探针1测量结果;图 8b为电子探针2 测量结果.Vp1、Vp2 分别为电子探针1 和2 测得的等离子体电位;Vf1、Vf2分别为电子探针1和2 测得的悬浮电位;Te1和Te2分别为电子探针1和2测得的电子温度;Ne1、Ne2 分别为电子探针1和2 测得的电子密度.可以看出由于真空罐内等离子体分布不是十分均匀,处于不同位置的电子探针测得的等离子体参数有所不同.
|
图 7 电子探针等离子体源测试框图 Fig. 7 The schematic diagram for the electron probe test in the plasma chamber |
|
图 8 朗缪尔探针电子探针实测伏安特性曲线及其拟合反演结果 Fig. 8 The detected I-V curves of the electron probe in the plasma chamber and the results calculated from them |
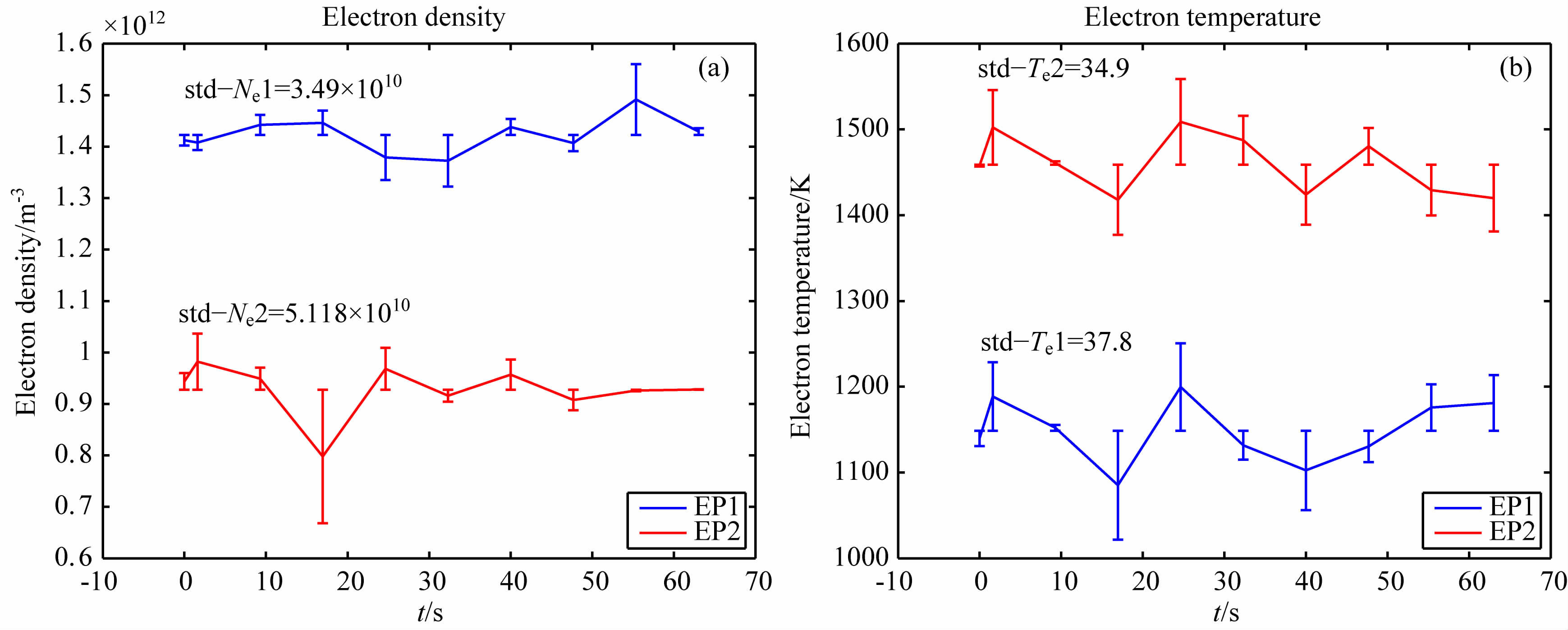
图 9是70s时间内电子探针测得的等离子体参数的变化情况.图 9a是电子密度测量结果,std_Ne1和std_Ne2分别是电子探针1(EP1)和2(EP2)测得电子密度的标准偏差;图 9b是电子温度测量结果,std_Te1和std_Te2 分别是电子探针1 和2 测得电子温度的标准偏差.在1min时间内,可以认为等离子体状态基本保持稳定,即认为等离子体的电子密度和电子温度基本保持不变,电子探针测得的电子密度和电子温度的相对变化可以认为是电子探针的测量相对误差(相对精密度),该误差主要来源于两个方面:一是电子学电路本身噪声带来的误差和外界环境电磁噪声耦合到电路带来的误差;一是等离子体参数的获得要通过对伏安特性曲线进行非线性拟合等数学处理,该处理过程会带来一定的误差.图 9的测试结果表明,电子探针的电子密度和电子温度的测量相对精密度优于10%,可以满足科学探测的需求.
|
图 9 70 s时间内电子探针测得的等离子体参数的相对变化 Fig. 9 The relative variety of the plasma parameters monitoredby the electron probe in 70 seconds |
本文主要介绍了基于子午工程探空火箭平台研制的朗缪尔探针,包括该探测任务的科学任务目标、探针基本原理、探针的方案的论证、基本测量方案设计以及探针测试实验的一些初步结果.电子学测试结果表明朗缪尔探针电子学工作状态良好,输出线性度接近于1;等离子体源初步测试结果表明,该朗缪尔探针可以满足科学探测的需求.
目前,子午工程探空火箭已经成功发射,朗缪尔探针获得有效的科学数据返回,相关探测结果将在后续论文中论述.在空间环境探测领域,朗缪尔探针是一种应用广泛的空间等离子体就位探测技术,在国外已有半个多世纪的历史,在此之前国内还未有成功应用的先例.子午工程探空火箭有效载荷朗缪尔探针的成功研制和成功科学探测,填补了我国此项空间载荷技术的空白.
| [1] | Kanal M. Theory of current collection of moving spherical probes. Scientific Report No. JS-5. Space Physics Research Lab: University of Michigan, 1962 . |
| [2] | Jacobsen K S, Pedersen A, Moen J I, et al. A new Langmuir probe concept for rapid sampling of space plasma electron density. Meas. Sci. Technol. , 2010, 21(8): 085902. DOI:10.1088/0957 |
| [3] | Hirt M, Steigies C T, Piel A. Plasma diagnostics with Langmuir probes in the equatorial ionosphere: II. Evaluation ofDEOS flight F06. J. Phys. D: Appl. Phys. , 2001, 34(7): 2650-2657. |
| [4] | Barjatya A, Swenson C M. Observations of triboelectric charging effects on Langmuir-type probes in dusty plasma. J. Geophys. Res. , 2006, 111: A10302. DOI:10.1029/2006JA011806 |
| [5] | Ilysell D L, Larsen M F, Swenson C M, et al. Onset conditions for equatorial spread F determined during EQUIS II. Geophysical Research LeUers , 2005, 32: L24104. DOI:10.1029/2005GL024743 |
| [6] | Swenson C M, Fish C, Thompson D. The floating potential measurement unit 41st Aerospace Sciences Meeting and Exhibit, 6-9january 2003, Reno, Nevada: AIAA 20031081. |
| [7] | Rich F J. Users guide for the topside ionospheric plasma monitor (SSIES, SSIES-2 and SSIES-3) on spacecratt of the Defense Meteorological Satellite Program. Air Force Phillips Laboratory, IlanscomAFB, MA, 1994, 1: 32. |
| [8] | de La Beaujardiere O, Jeong L, BasuB, et al. C/NOFS: a mission to forecast scintillations. Air Force Research Laboratory, IlanscomAFB, MA01731, 2003, 1: 28. |
| [9] | 熊年禄, 唐存琛, 李行健. 电离层物理概论. 武汉: 武汉大学出版社, 1999 . |
| [10] | Mott SmithII M, Langmuir I. The theory of collectors in gaseous discharges. Physical Review , 1926, 28(4): 727-763. DOI:10.1103/PhysRev.28.727 |
| [11] | Sanmartin J R. End effect in Langmuir probe response under ionospheric satellite conditions. The Physics of Fluids , 1972, 15(6): 1134-1143. DOI:10.1063/1.1694039 |
| [12] | Bettinger R T, Chen A A. An end effect associated with cylindrical Langmuir probes moving at satellite velocities. Journal of Geophysical Research, Space Physics , 1968, 73(7): 2513-2528. DOI:10.1029/JA073i007p02513 |
| [13] | Szuszczewicz EP. Area influences and floating potentials in Langmuir probe measurements. Journal of Applied Physics , 1972, 43(3): 874-880. DOI:10.1063/1.1661297 |
| [14] | Wahlstrom M K, Johansson E, Veszelti E, et al. Improved Langmuir probe surface coatings for the Cassini satellite. Thin Solid Films , 1992, 220(1-2): 315-320. DOI:10.1016/0040-6090(92)90591-X |
| [15] | Lebretona J P, Stverak S, Travnicek P, et al. The ISL Langmuir probe experiment processing onboard DEMETER: Scientific objectives, description and first results. Planeiary and Space Science , 2006, 54(5): 472-486. DOI:10.1016/j.pss.2005.10.017 |
| [16] | Gurnett D A, KuthWS, Kirchner D L, et al. The Cassini radio and plasma wave investigation. Space Science Reviews , 2004, 114(1-4): 395-463. DOI:10.1007/s11214-004-1434-0 |
| [17] | Eriksson A I, Boström R, Gil11 R, et al. RPC-LAP: The Rosetta Langmuir probe instrument. Space Science Reviews , 2007, 128(1-4): 729-744. DOI:10.1007/s11214-006-9003-3 |
| [18] | Hutchinson I II. Principles of Plasma Diagnostics. United Kingdom: Cambridge University Press, 2002 . |
| [19] | AaseJG. Development of a prototype Langmuir probe for the ICI-1 sounding rocket [Master's thesis]. University of Oslo: Department of Physics, 2005. |
 2012, Vol. 55
2012, Vol. 55


