2. 中国地质科学院矿产资源研究所,北京 100037
2. InsLiLuLe of Mineral Resources , Chinese Academy of Geological Sciences, Beijing 100037, China
大地电磁测深法(Nagnetotelluric, MT)自20世纪50年代诞生起,以野外施工简便、探测深度大、垂向分辨能力和水平分辨能力高等优点,在探测地壳深部结构方面已得到广泛应用,并已成为矿产资源勘查、地下水和地热勘探、油气普查、地震预报、岩石圈深部结构探测等领域不可或缺的重要地球物理方法之一[1].然而,由于天然电磁场信号弱、频带宽,矿区附近重工业密集等因素造成的环境噪声以及人类活动等人文电磁噪声日益严重,导致大地电磁测量数据受到严重污染,这给地球物理勘探工作带来巨大困难[2-3].因此,对大地电磁信号中的强噪声干扰进行有效压制,从而来改善大地电磁测量数据质量,获得无偏的阻抗估计是取得良好勘探结果的关键,也一直是大地电磁测深领域的研究前沿和热点之一.通过研究证明,实际观测的大地电磁信号是典型的非线性、非平稳信号[4-5].
分析国内外相关文献可知,目前的大地电磁去噪方法其能力都存在一定的局限性.互功率谱和加权平均功率谱法虽对不相关噪声具有一定的抑制能力,但电磁噪声往往是同时作用在各道电磁信号上,属于相关噪声,导致该方法失效[6-7];远参考道法虽能消除同一测点各道之间不相关的电磁噪声,并对各道之间同源电磁噪声也有较好的效果,但经远参考处理后,单点数据的误差棒不同程度地变大了,特别是在受电磁干扰污染严重、校正量较大的数据段,该现象尤为明显,且参考道距离的选择是一个比较实际的问题[8];Robust处理法对于MT 资料中的非高斯正态分布噪声的消除具有优越性,能有效减少视电阻率和相位的分散度,但Robust法无法消除输入端的噪声,且无法剔除噪声较多、能量较强时的近源电磁相关噪声对数据的干扰[9-10];小波变换虽能有效压制大地电磁局部相关噪声,但小波变换过分依赖于小波基函数的选取,有时随着尺度增大,相应正交基函数的频谱局部性变差,使其对大地电磁信号更精细分解受到限制[11-12];近年来,Hilbert-Huang变换应用到电法勘探,并能有效抑制大地电磁信号中的工频干扰,与小波变换相比不需要选择基函数,具有更强的时频刻画能力.但因经验模态分解(END)是自适应的,无法揭示每时段的频率特性和能量差异所具有的细微性变化,分解得到的固有模态函数(INF)具有多分辨性,对于每阶INF 分量在大地电磁信号中的物理意义还有待进一步探究,且该算法占用大量运算时间,不适合实测大地电磁信号处理[13-14];人机联作去噪法是基于可视化技术的思想,将MT 原始数据通过计算机图形界面显示处理,并使用人机联作的方式去除噪声.该方法虽能较好地降低噪声能量,改善测量数据质量,但操作时涉及了太多的人为因素,耗费了很多时间和精力,不适合处理观测周期长和噪声较多的数据,且操作者必须具备丰富的噪声识别经验,否则效果会适得其反[15].
2008年以来,我国开展了深部探测技术与实验研究,需要在矿集区进行大地电磁探测工作,尤其是我国东部和华南的矿集区,经济发达、矿山密布、人烟稠密、矿山开采的大功率直流电机车、高压电网、电视塔、各种金属管网、广播电台、雷达、通讯电缆及信号发射塔等造成的电磁干扰,严重污染了实际大地电磁信号,导致MT 数据采集与处理相当困难[16].由于矿集区电磁噪声类型复杂、能量大,相关性强,且频率覆盖范围极宽,现有在频率域的处理方法对该类强噪声干扰无能为力.因此,如何从矿集区微弱大地电磁信号中压制或分离强干扰是一项极具挑战性的工作.针对这一系列不利因素,鉴于国内对资源的强劲需求及快速处理矿集区海量MT 数据,我们另辟蹊径,考虑从时间域寻找有针对性的方法在矿集区获取有效、优质的MT 测量数据.这项工作的开展对矿集区电磁法探测结果的处理和解释具有重要意义,同时对探测地壳精细结构,寻找深部控矿构造具有非常重要的实际价值.
数学形态学(NathematicalNorphology,NN) 是基于积分几何、随机集合论等数学理论建立起来的一种非线性信号处理方法[17],形态滤波器是从数学形态学发展起来的一种新型的非线性滤波技术. 近年来,随着形态学理论的飞速发展,形态学滤波被逐步推广到一维信号处理领域[18-19].本文针对大地电磁信号的特点,尝试性地引入形态滤波技术对矿集区的大地电磁强干扰在时间域进行信噪分离,采用形态学中的开、闭运算,选择合理的结构元素,构造适合大地电磁信号的组合广义形态滤波器.实验结果表明,该方法能有效抑制大地电磁信号中的强噪声干扰,较好地还原了大地电磁信号的原始特征,改善了MT 测量数据质量.
2 形态学滤波数学形态学是1964年由法国数学家Natheron G 和SerraJ共同创立的一种信号分析方法.此后,两人通过详细阐述拓扑学、随机论、递增映射和凸性分析等问题,逐步建立并完善了数学形态学的理论体系[20-21].该方法最早是以图像的形态特征作为研究对象,现已成功应用于图像处理、图形分析、计算机视觉以及电能扰动等工程实践领域[22-25].方法的基本思想是通过集合来描述目标信号,集合各部分之间的关系则说明目标信号的结构特点,即设计一个称为结构元素的“探针”,通过探针在信号中不断移动来考察信号各部分之间的关联[26-28].该方法仅取决于待处理信号的局部特征,利用结构元素对信号的几何特征进行局部匹配或修正,同时保留目标信号主要的形状特征,以达到提取有用信息、抑制噪声的目的[29-30].
2.1 基本原理
数学形态学中的形态变换包括腐蚀、膨胀、形态开、形态闭以及形态开、闭线性组合.以一维离散信号为例,数学描述如下[21]:设输入信号f(n)为定义在F={0,1,…,N-1}上的离散函数,结构元素g(n)为定义在G={0,1,…,M-1}上的离散函数,且N
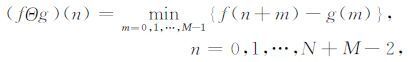
|
(1) |

|
(2) |
式中,符号Θ 和⊕ 分别表示腐蚀和膨胀运算.从以上定义可知,腐蚀和膨胀运算等价于离散函数在滑动滤波窗(相当于结构元素)内的最小值和最大值滤波.其中,腐蚀运算表示一个收缩过程,用来剔除边界不平滑的凸起部分,算法减少了峰值,加宽了谷域,使目标收缩,孔洞扩张;膨胀运算表示一个扩张过程,用来填平边界不平滑的凹陷部分,算法增大了谷值,扩展了峰顶,使目标扩张,孔洞收缩.
形态开、闭运算是在腐蚀和膨胀级联的基础上衍生而来的复合运算,从而组成数学形态学中最基本的形态滤波器.f(n)关于g(n)的形态开、闭运算分别定义为
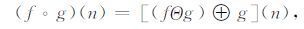
|
(3) |
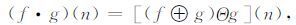
|
(4) |
式中,符号ο和·分别表示形态开和形态闭运算.其中,形态开运算是对同一结构元素进行先腐蚀后膨胀,目的是消除目标信号中的细节和毛刺,使目标信号的轮廓光滑,从而剔除尖峰,抑制正脉冲噪声;形态闭运算是对同一结构元素进行先膨胀后腐蚀,目的是填平目标信号中的小洞及裂缝,滤除低谷噪声,从而补偿谷底,抑制负脉冲噪声.因此,实际应用中常采用形态开、闭运算相结合来抑制正、负脉冲噪声.
Naragos[31-32]采用相同尺寸形状的结构元素,通过形态开、闭运算级联,定义了形态开-闭(OC)和闭-开(CO)滤波器:
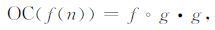
|
(5) |
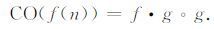
|
(6) |
由以上定义可知,形态开-闭(OC)和形态闭-开(CO)滤波器都能同时滤除目标信号中的正、负脉冲噪声,但由于形态开运算的收缩性导致形态开-闭滤波器输出偏小,而形态闭运算的扩张性导致形态闭-开滤波器输出偏大,以至滤波结果存在统计偏倚现象[33].因此,单独使用它们并不能取得较好的滤波效果.为了有效抑制各种噪声干扰和克服统计偏倚现象,常采用两者的平均值来逼近原信号,构造形态开-闭和形态闭-开的组合滤波器(OC-CO)如下:
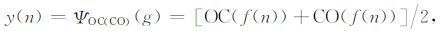
|
(7) |
式中,y(n)表示形态滤波器的输出结果,ΨOC(CO)(g) 表示形态滤波器的基本滤波运算单元.
2.2 结构元素的选取形态滤波的质量取决于所选择的形态变换和结构元素.其中,形态变换的选择必须满足一些基本的约束条件,而结构元素的选取则需要根据具体情况来确定.
结构元素在形态运算中的作用类似于一般信号处理时的滤波窗口或参考模板,其尺寸和形状都将对形态学运算产生很大影响.采用不同的结构元素可以提取出目标信号不同的形状特征,常见的结构元素有直线型、三角型、圆盘型、正弦型、抛物线型以及其他多边形组合.结构元素的设计通常取决于待处理信号的形状,一般一种结构元素对一种噪声有较好的滤除效果.待处理信号的形状不同,则应选用不同的结构元素才能达到噪声压制的目的.相对而言,结构元素越复杂,其滤除噪声的能力就越强,但所耗费的时间也就越长.
2.3 组合广义形态滤波器的构造由于大地电磁噪声类型复杂多样,为了能灵活应用不同形状和尺寸的结构元素以及修正标准形态算子所产生的统计偏倚现象,文中引入广义形态滤波器对大地电磁信号进行噪声压制[34].广义形态开-闭和形态闭-开滤波器的数学描述分别定义为
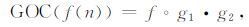
|
(8) |
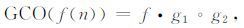
|
(9) |
式中,g1、g2 分别表示不同的结构元素.
广义形态滤波器的基本滤波运算单元ΨGOC(GCO)(g1,g2) 定义为
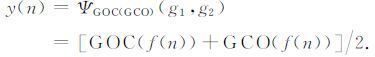
|
(10) |
采用广义形态开-闭和闭-开组合,能更好地保持目标信号的几何结构特征,修正标准形态算子所产生的统计偏倚现象[35].
由于圆盘型结构元素具有旋转不变性,避免了直线结构平滑程度不够的缺点,而抛物线型结构元素能有效抑制脉冲噪声干扰[36].因此,文中选用圆盘型和抛物线型两种结构元素相结合来设计广义形态滤波器.结构元素形状如图 1所示.
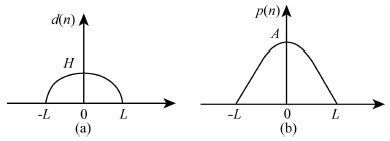
|
图 1 两种结构元素 (a)圆盘型结构元素;(b)抛物线型结构元素. Fig. 1 Two structuring elements (a) Disc type structuring element ; (b) Parabolic structuring element. |
圆盘型结构元素定义为
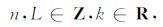
|
(11) |
抛物线型结构元素定义为
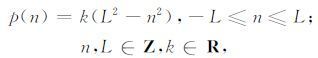
|
(12) |
以上两种结构元素只需改变参数k和L就能改变其幅度和宽度,从而控制结构元素的大小.
考虑到大地电磁信号的准对称性和克服基线漂移,文中将正、负结构元素级联组成如图 2所示的组合广义形态滤波器,其目的是进一步抑制目标信号中的各种噪声干扰和消除统计偏倚现象[37-38].
图 2中,ΨGOC(GCO)(-g1,-g2) 表示采用负的结构元素组成的广义形态基本滤波单元.
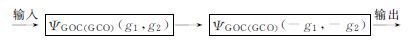
|
图 2 组合广义形态滤波器 Fig. 2 The combination generalized morphological filter |
经组合广义形态滤波后,重构的大地电磁有用信号定义为
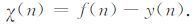
|
(13) |
图 3所示为安徽庐枞矿集区某测点的一段实测MT 原始数据.对该段数据的时间序列进行分析可知,电道和磁道均不同程度受到了周期性的突跳、波动等信号干扰,这些信号与稳定的天然电磁场信号相比,具有振幅大、能量强、周期性明显等特征.分析大量MT 信号的时间序列可知,矿集区中的强噪声干扰通常以方波噪声、脉冲噪声、三角波噪声和似充放电三角波噪声为主,这些噪声都是由于矿集区中复杂的外界因素和人文因素所造成的.
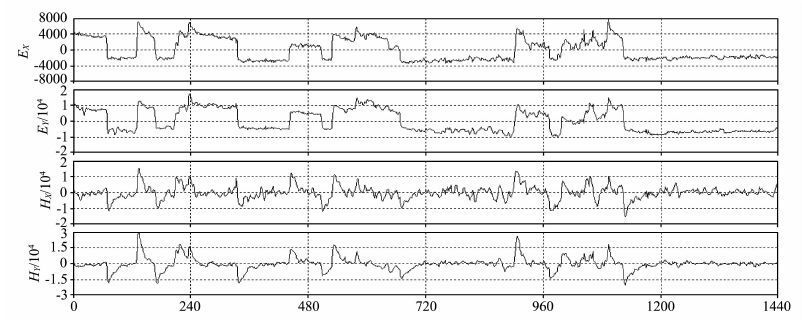
|
图 3 实测MT原始数据 Fig. 3 Original data of actual MT |
为了验证本文方法的实用性,对该矿集区中受强干扰严重的MT 数据进行数学形态滤波研究.鉴于大地电磁信号的数据量庞大、噪声类型极其复杂,文中仅选用具有以上典型干扰特征的电场分量EX 和EY运用形态滤波法进行讨论.
3.1 不同类型结构元素滤波效果对比图 4所示为采用不同类型的结构元素对实测大地电磁信号EX进行形态滤波的仿真效果图.
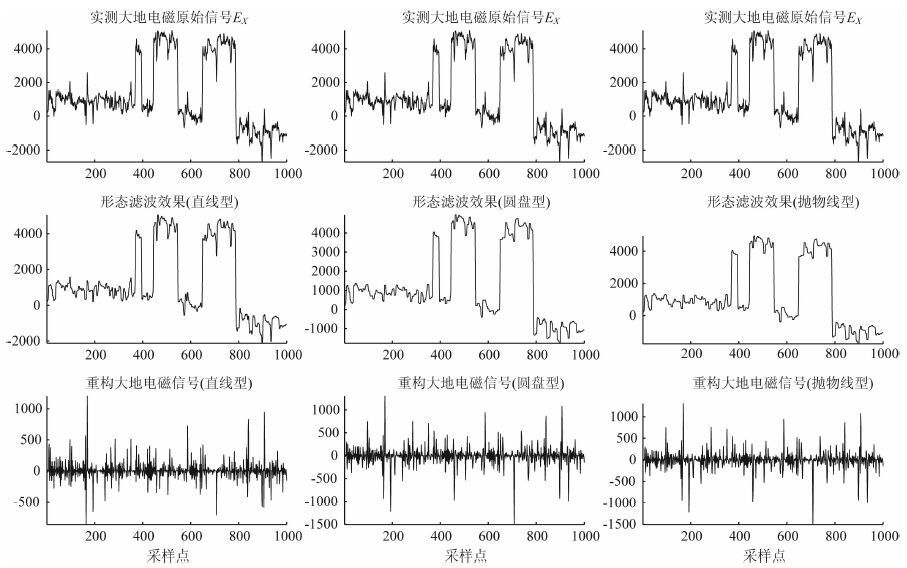
|
图 4 不同类型结构元素的滤波效果图 Fig. 4 Filtering effect chart of different kinds of structuring elements |
从图 4可知,含方波噪声的大地电磁信号分别经三种不同类型的结构元素的形态滤波器后,将小于或等于结构元素的信号进行了滤除,只保留了比结构元素大的信号单元.结果表明:数学形态滤波对大地电磁强干扰具有较好的去噪能力.比较图 4可知,圆盘型和抛物线型结构元素较直线型结构元素滤波效果明显,提取的形态轮廓清晰、平滑,重构的大地电磁信号有效地剔除了大尺度干扰和基线漂移,突出了MT 有用信号的相关局部特征.
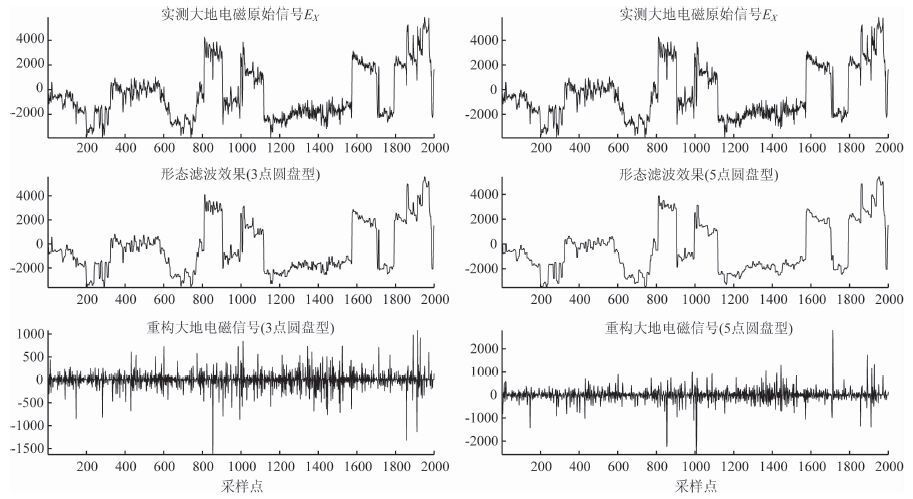
3.2 同一类型不同尺寸结构元素滤波效果对比图 5所示为采用不同尺寸的圆盘型结构元素对实测大地电磁信号EX的去噪效果图.其中,结构元素分别采用3点结构元和5点结构元.
|
图 5 不同尺寸的圆盘型结构元素形态滤波效果图 Fig. 5 Morphology filtering effect chart of different sizes of disc type structuring elements |
分析图 5可知,5 点圆盘型结构元素的滤波效果比3点结构元素的效果明显.去噪前,含大尺度方波噪声的能量达到正常信号的几十倍,完全把MT 正常信号湮没.经过5点形态滤波后,提取出大尺度方波噪声的形态曲线,且曲线轮廓较3 点结构元自然、光滑,较好地保持了原始信号的特征.重构后的MT 信号基本滤除了由噪声引起的突跳波形,强噪声干扰与MT 正常信号得到了有效分离.
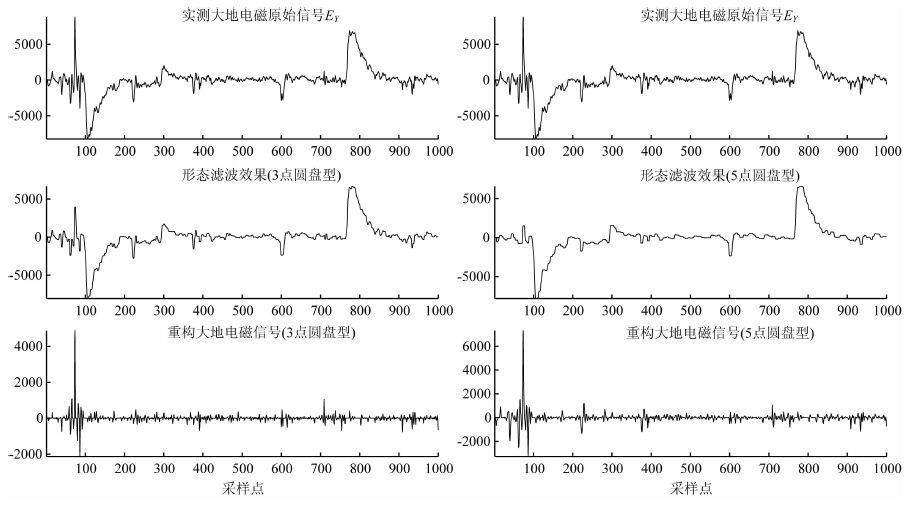
图 6所示为采用不同尺寸的抛物线型结构元素对实测大地电磁信号EY的去噪效果图.
|
图 6 不同尺寸的拋物线型结构元素形态滤波效果图 Fig. 6 Morphology filtering effect chart of different sizes of parabolic structuring elements |
对比图 6 可知,5 点抛物线型结构元素的滤波效果比3点结构元素好,通过形态滤波提取出的含大尺度似充放电三角波噪声的轮廓较3点结构元素光滑,重构的大地电磁信号波形较为平稳,且保留了丰富的细节成分.
通过以上分析可知,选择合适的结构元素的尺寸能较好地获取叠加在MT 有用信号上的噪声形态轮廓,重构后的MT 信号则基本还原了MT 有用信号的原始特征.
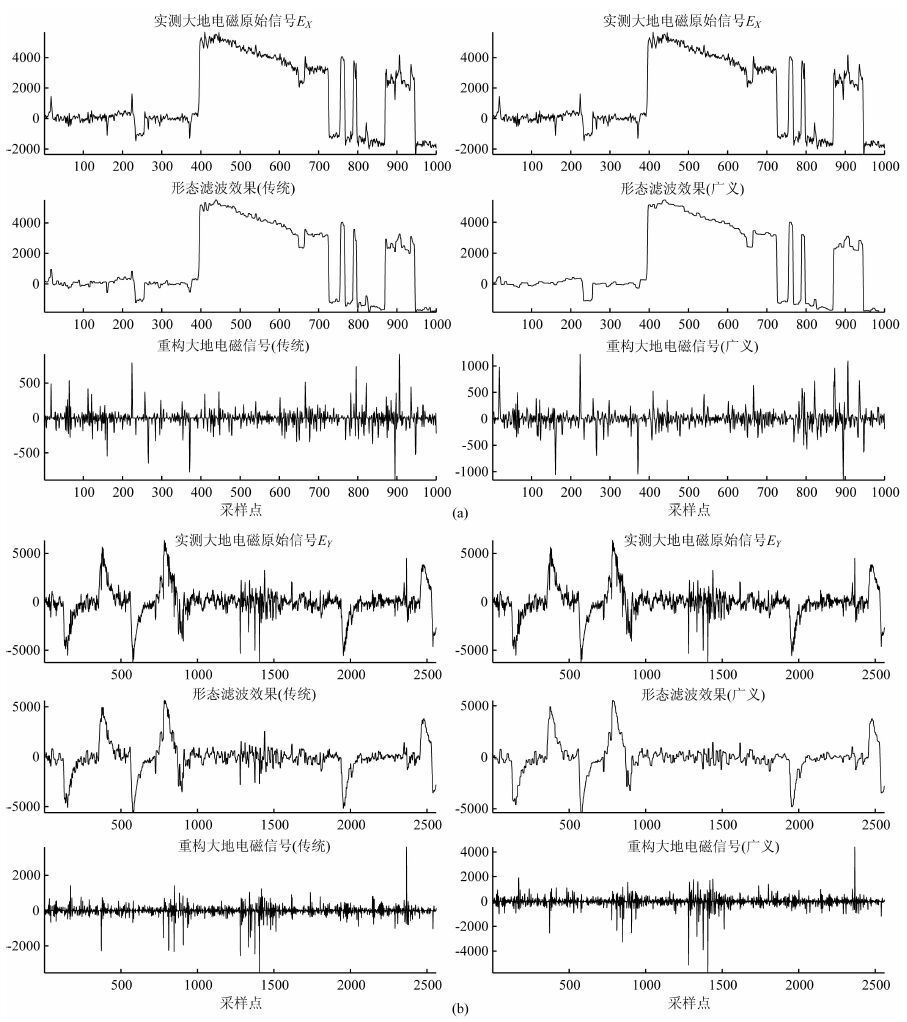
3.3 传统与组合广义形态滤波效果对比图 7所示为传统形态滤波和根据图 2设计的组合广义形态滤波的效果对比图.
|
图 7 两种算法的滤波效果对比 (a)EX分量;(b)EY分量. Fig. 7 Comparison of filtering effect chart for two algorithms (a)EX Component;(b)EV Component. |
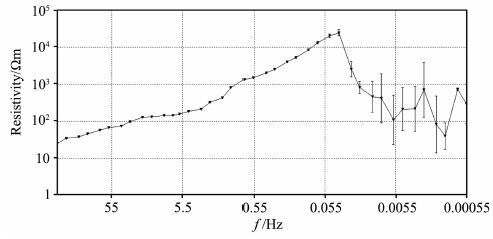
分析图 7可知,传统形态滤波在获取噪声轮廓上出现很严重的毛刺现象,曲线不光滑、连续性差,且在部分曲率最大处造成了信号的失真,而组合广义形态滤波几乎能完整地勾勒出整段大尺度噪声轮廓,曲线自然、光滑,重构的MT 信号则较好地保留了有用信号的细节信息,重现了原始MT 信号的基本特征,从而保证了MT 有用信号的可靠性与准确性.图 8所示为该矿集区某测点的MT 原始数据在TN 模式下的视电阻率曲线图.
|
图 8 原始数据视电阻率曲线 Fig. 8 Resistivity curve of original data |
从图 8可知,原始数据的视电阻率曲线整体连续性较差.在大于5.5 Hz时曲线形态较为平稳,5.5~0.055Hz处曲线呈45°左右渐近线快速上升,表现为典型的近源效应.在0.055 Hz左右时,视电阻率值超过10000Ωm,在0.0055 Hz时,视电阻率值快速下降至100Ωm,且低频段误差棒增大,并出现不同程度的突跳畸变,这些现象表明该测点数据受到了矿集区强噪声干扰.
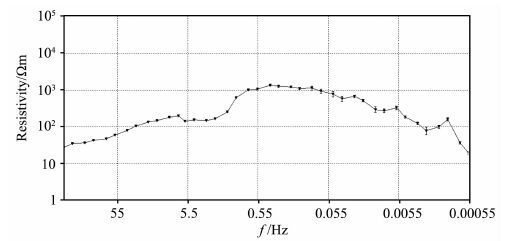
图 9 所示为组合广义形态滤波后重构的MT 数据的视电阻率曲线图.
|
图 9 滤波后视电阻率曲线 Fig. 9 Resistivity curve after filtering |
对比图 8 可知,5.5~0.055 Hz处的近源干扰基本消除,低频段突跳频点得到了有效恢复,0.055~0.0055Hz的低频误差棒明显减小,曲线形态光滑、平稳,整体连续性大为提高.实验结果表明,该测点经组合广义形态滤波后的数据质量较原始数据有明显改善,得到的视电阻率曲线为地下电性结构提供了资料的可解释性.
4 结论本文将数学形态滤波引入到大地电磁噪声压制领域,提出了一种基于数学形态滤波的大地电磁噪声压制方法,并应用到矿集区实测大地电磁信号与强干扰分离中.介绍了数学形态学的基本原理,分析了结构元素的选取方法,采用正、负结构元素级联构造了组合广义形态滤波器,比较了传统形态滤波和组合广义形态滤波的去噪效果.实验结果表明,形态学滤波能有效抑制大地电磁信号中的大尺度干扰和基线漂移,较好地保持了目标信号的局部特征;设计的组合广义形态滤波器在大地电磁噪声压制中的效果明显,进一步修正了由标准形态算子所产生的统计偏倚现象.方法的优势在于,不需考虑噪声干扰是何种类型,只要选择与目标信号相匹配的结构元素,设计合适的形态学滤波器,则能较好地还原大地电磁信号的原始特征.该方法较好地改善了MT测量数据品质,且计算速度快,适合矿集区海量MT 数据处理. 可以预测:形态学滤波在该领域将具有广阔的应用前景,为大地电磁信号与强干扰的有效分离以及开展大地电磁深部探测与深部找矿提供了新的解决途径.
由于结构元素的选取对形态滤波器的滤波效果至关重要,迄今为止,选取何种结构元素及其尺寸只能通过反复实验获得.因此,如何根据背景噪声和待处理信号的形状自适应地选取结构元素的类型和尺寸,以及合理运用形态变换的线性组合将有待进一步深入研究.
| [1] | 汤井田, 何继善. 可控源音频大地电磁法及其应用. 长沙: 中南大学出版社, 2005 . Tang J T, lie J S. Controllable Source Audio Magnetotelluric Method and Its Application (in Chinese) (in Chinese). Changsha: Central South University Press, 2005 . |
| [2] | Cai JII, Tang J T, IIuaR II, et al. An analysis method for magnetotelluric data based on the Ililbert-IIuang transform. ExploraLion Geophysics , 2009, 40(2): 197-205. DOI:10.1071/EG08124 |
| [3] | 肖晓, 汤井田, 周聪, 等. 庐枞矿集区大地电磁探测及电性结构初探. 地质学报 , 2011, 85(5): 873–886. Xiao X, Tang J T, Zhou C, et al. Magnetotelluric Sounding in the Lujiang-Zongyang ore-district and preliminary study of electrical structure. AcLa GeoLogica Sinica (in Chinese) (in Chinese) , 2011, 85(5): 873-886. |
| [4] | 王书明, 王家映. 关于大地电磁信号非最小相位性的讨论. 地球物理学进展 , 2004, 19(2): 216–221. Wang S M, Wang J Y. Discussion on the non-minimum phase of magnetotelluric signals. Progress in Geophysics (in Chinese) (in Chinese) , 2004, 19(2): 216-221. |
| [5] | 王书明, 王家映. 大地电磁信号统计特征分析. 地震学报 , 2004, 26(6): 669–674. Wang S M, Wang J Y. Analysis on statistic characteristics of magnetotelluric signal. AcLa Seismologica Sinica (in Chinese) (in Chinese) , 2004, 26(6): 669-674. |
| [6] | Kao D W, Rankin D. Enhancement of signal-to-noise ratio in magnetotelluric data. Geophysics , 1977, 42(1): 103-110. DOI:10.1190/1.1440703 |
| [7] | Goubau W M, Gamble T D, Clarke J. Magnetotelluric data analysis: removal of Bias. Geophysics , 1978, 43(6): 1157-1169. DOI:10.1190/1.1440885 |
| [8] | Gamble T D, Goubau W M, Clarke J. Error analysis for remote reference magnetotellurics. Geophysics , 1979, 44(5): 959-968. DOI:10.1190/1.1440988 |
| [9] | Egbert G D. Robust multiple-station magnetotelluric data processing. Geophysical Journal InLernaLional , 1997, 130(2): 475-496. DOI:10.1111/gji.1997.130.issue-2 |
| [10] | 柳建新, 严家斌, 何继善, 等. 基于相关系数的海底大地电磁阻抗Robust估算方法. 地球物理学报 , 2003, 46(2): 241–245. Liu J X, YanJB, IleJS, et al. Robust estimation method of sea magnetotelluric impedance based on correlative coefficient. Chinese J. Geophys. (in Chinese) (in Chinese) , 2003, 46(2): 241-245. |
| [11] | Trad D 0, Travassos J M. Wavelet filtering of magnetotelluric data. Geophysics , 2000, 65(2): 482-491. DOI:10.1190/1.1444742 |
| [12] | 范翠松, 李桐林, 王大勇. 小波变换对MT数据中方波噪声的处理. 吉林大学学报(地球科学版) , 2008, 38(Suppl.): 61–63. Fan C S, Li T L, Wang D Y. Treatment of wavelet transform for square wave noise in MT date. Journal of Jilin University (Earth Science Edition) (in Chinese) (in Chinese) , 2008, 38(Suppl.): 61-63. |
| [13] | 汤井田, 化希瑞, 曹哲民, 等. nilbert-IIuang变换与大地电磁噪声压制. 地球物理学报 , 2008, 51(2): 603–610. Tang J T, IIua X R, Cao Z M, et al. Ililbert-IIuang transformation and noise suppression of magnetotelluric sounding data. Chinese J. Geophys. (in Chinese) (in Chinese) , 2008, 51(2): 603-610. |
| [14] | 汤井田, 蔡剑华, 任政勇, 等. Itilben-IIuang变换与大地电磁信号的时频分析. 中南大学学报(自然科学版) , 2009, 40(5): 1399–1405. Tang J T, Cai J II, Ren Z Y, et al. Ililbert-IIuang transform and time frequency analysis of magnetotelluric signal. Journal of Central South University (Science and Technology) (in Chinese) (in Chinese) , 2009, 40(5): 1399-1405. |
| [15] | 王大勇.长江中下游矿集区综合地质地球物理研究——以九瑞、铜陵矿集区为例[博士论文].吉林:吉林大学,2010. Wang D Y. The integrated geophysical and geological study in the ore bett of the middle and lower reach of the Yangtze rive--The cases study of Tongling and Jiurui ore district [Ph. D. thesis] (in Chinese). Jilin: Jilin University,2010. |
| [16] | 吕庆田, 史大年, 汤井田, 等. 长江中下游成矿带及典型矿集区深部结构探测——Sin〇Probe03年度进展综述. 地球学报 , 2011, 32(3): 257–268. Lu Q T, Shi D N, Tang J T, et al. Probing on deep structure of middle and lower reaches of the Yangtze Metallogenic Bett and typical ore concentration area:a review of annual progress of SinoProbe-03. AcLa GeoscienLica Sinica (in Chinese) (in Chinese) , 2011, 32(3): 257-268. |
| [17] | 龚炜, 石青云. 数字空间中的数学形态学——理论及应用. 北京: 科学出版社, 1997 . Gong W, Shi Q Y. Mathematical Morphology in Digital Space (in Chinese) (in Chinese). Beijing: Science Press, 1997 . |
| [18] | 胡爰军, 唐贵基, 安连锁. 基于数学形态学的旋转机械振动信号降噪方法. 机械工程学报 , 2006, 42(4): 127–130. Hu A J, Tang G J, An L S. De-noising technique for vibration signals of rotating machinery based on mathematical morphology filter. Chinese Journal of Mechanical Engineering (in Chinese) (in Chinese) , 2006, 42(4): 127-130. DOI:10.3901/JME.2006.04.127 |
| [19] | 张文斌, 杨辰龙, 周晓军. 形态滤波方法在振动信号降噪中的应用. 浙江大学学报(工学版) , 2009, 43(11): 2096–2099. Zhang W B, Yang C L, Zhou X J. Application of morphology filtering method in vibration signal de-noising. Journal of Zhejiang University (Engineering Science) (in Chinese) (in Chinese) , 2009, 43(11): 2096-2099. |
| [20] | Matheron G Random Sets and Integral Geometry New York: Wiley Press,1975. |
| [21] | Serra J. Image Analysis and Mathematical Morphology. New York: Academic Press, 1982 . |
| [22] | 岳蔚,刘沛.基于数学形态学消噪的电能质量扰动检测方法.电力系统自动化,2002, 26(7): 13-17. Yue W,Liu P. Detection of power quality disturbances based Sensors and Actuators (in Chinese), 2007, 20 (4): 828-831. |
| [23] | 蒋立辉, 耿蒙, 赵春晖. 基于广义形态滤波和模糊逻辑的散 斑噪声抑制. 红外与激光工程 , 2005, 34(1): 80–83. JiangL II, Geng M, Zhao C II. Speckle suppressing based on generalized morphological filter and fuzzy logic. Infrared and Lasrr Engineering (in Chinese) (in Chinese) , 2005, 34(1): 80-83. |
| [24] | 张建成, 吴新杰. 形态滤波在实时信号处理中应用的研究. 传感技术学报 , 2007, 20(4): 828–831. Zhang J C, Wu X J. Research on applications of morphological filtering in real-time signal processing. Chinese Journal of Sensors and Actuators (in Chinese) (in Chinese) , 2007, 20(4): 828-831. |
| [25] | 李兵, 张培林, 任国全, 等. 基于数学形态学的分形维数计算及在轴承故障诊断中的应用. 振动与冲击 , 2010, 29(5): 191–194. Li B, Zhang P L, Ren GQ, et al. Mathematic morphology-based fractal dimension calculation and its application in fault diagnosis of roller bearings. Journal of Vibration and Shock (in Chinese) (in Chinese) , 2010, 29(5): 191-194. |
| [26] | 舒泓, 王毅. 基于数学形态滤波和Itilbert变换的电压闪变测量. 中国电机工程学报 , 2008, 28(1): 111–114. Shu II, Wang Y. Voltage flicker detection method based on mathematical morphology filter and Itilbert transform. Proceedings of Lhe Chinese Society for Electrical Engineering (in Chinese) (in Chinese) , 2008, 28(1): 111-114. |
| [27] | 李春枝, 何荣建, 田光明. 数学形态滤波在振动信号分析中的应用研究. 计算机工程与科学 , 2008, 30(9): 126–128. Li CZ, He R J, Tian G M. Research on the application of the mathematical morphology filtering in vibration signal analysis. Compuirr Engineering 牔 Science (in Chinese) (in Chinese) , 2008, 30(9): 126-128. |
| [28] | 程扬军, 黄纯, 何朝晖, 等. 基于自适应顺序形态滤波的电能质量去噪算法. 计算机仿真 , 2009, 26(12): 218–220. Cheng YJ, IIuang C, IIe Z II, et al. A de-nosing method of power quality signal based on adaptive order morphology. Compuirr Simulation (in Chinese) (in Chinese) , 2009, 26(12): 218-220. |
| [29] | 桕林, 刘小峰, 秦树人. 小波-形态-EMD综合分析法及其应用. 振动与冲击 , 2008, 27(5): 1–4. B oL, Liu X F, QinSR. Hybrid wavelet-morphology-EMD analysis and its application. Journal of Vibration and Shock (in Chinese) (in Chinese) , 2008, 27(5): 1-4. |
| [30] | 陈辉, 郭科, 胡英. 数学形态学在地震信号处理中的应用研究. 地球物理学进展 , 2009, 24(6): 1995–2002. Chen II, Guo K, IIu Y. A study on application of mathematical morphology to seismic signal processing. Progress in Geophysics (in Chinese) (in Chinese) , 2009, 24(6): 1995-2002. |
| [31] | Maragos P, Schafer R W. Morphological filters-Part I: Their set-theoretic analysis and relations to linear shitt-invariant filters. IEEE Trans, on ASSP , 1987, 35(8): 1153-1169. DOI:10.1109/TASSP.1987.1165259 |
| [32] | Maragos P, Schafer R W. Morphological filters-Part I : Their relations to median, order-statistic, and stack filters. IEEETrans. onASSP,1987, 35(8): 1170-1184. |
| [33] | 杜必强, 唐贵基, 石俊杰. 旋转机械振动信号形态滤波器的设计与分析. 振动与冲击 , 2009, 28(9): 79–81. Du B Q, Tang G J, Shi J J. Design and analysis of morphological filter for vibration signals of a rotating machinery. Journal of Vibration and Shock (in Chinese) (in Chinese) , 2009, 28(9): 79-81. |
| [34] | 沈路, 周晓军, 张文斌, 等. 广义数学形态滤波器的旋转机械振动信号降噪. 振动与冲击 , 2009, 28(9): 70–73. Shen L, Zhou X J, Zhang W B, et al. De-noising for vibration signals of a rotating machinery based on generalized mathematical morphological filter. Journal of Vibration and Shock (in Chinese) (in Chinese) , 2009, 28(9): 70-73. |
| [35] | 赵静, 何正友, 钱清泉. 利用广义形态滤波与差分熵的电能质量扰动检测. 中国电机工程学报 , 2009, 29(7): 121–126. Zhao J, IIe Z Y, Qian Q Q. Detection of power quality disturbances utilizing generalized morphological filter and difference-entropy. Proceedings of Lhe CSEE (in Chinese) (in Chinese) , 2009, 29(7): 121-126. |
| [36] | 赵晓群, 王津. 一种基于形态学的语音增强方法. 同济大学学报(自然科学版) , 2006, 34(10): 1394–1397. Zhao X Q, Wang J. A speech enhancement method based on morphology. Journal of Tongri University (Natural Science) (in Chinese) (in Chinese) , 2006, 34(10): 1394-1397. |
| [37] | Trahanias P E. An approach to QRS complex detection using mathematical morphology. IEEE Trans. on Biomedical Engineering,1993,40(2): 201-205. |
| [38] | Wang J, Xu G I, Zhang Q, et al. Application of improved morphological filter to the extraction of impulsive attenuation signals. Mechanical Systems and Signal Processing , 2009, 23(1): 236-245. DOI:10.1016/j.ymssp.2008.03.012 |
 2012, Vol. 55
2012, Vol. 55


