2. 北京大学地球与空间科学学院, 北京 100871
2. School of Earth and Space Science, Peking University, Beijing 100871, China
地下核试验是为了一定研究目的,在预定条件下于地下一定深度进行的核爆炸装置的爆炸实验,浅层地下核试验,地面形成弹坑,有大量放射性溢出.封闭式地下核试验,常称为深层地下核试验,不形成弹坑,大量放射性封闭于地下,是核武器试验的主要手段,某种意义上来讲,也是唯一的手段.封闭式地下核爆炸的力学效应是相当复杂的,包含有多种效应,如层裂(又称剥裂)现象及其诱发的构造地震断层的活动等.通过对岩体变形及其破坏效应的研究,如地表弹坑形成机制等研究结果表明,地下核爆炸过程中,冲击波产生和爆炸空腔的膨胀所涉及的物理过程,就其强度而言,远远超过其他任何一种物理过程[1],因此,通常将球对称爆炸震源作为地下封闭式核爆炸的主要震源机制,虽然球对称爆炸震源模式能够解释许多地下核爆炸地震现象,然而要解释近场和远场所观测到的地震波全部特征是远远不够的,如SH 横向运动分量的普遍存在,体现了传播路径的复杂性和震源的非球对称性成分的存在[2-6].简单源模型不能解释由地下核爆炸激发的地震面波,如N-N 源模型[7],可以较好地解释体波数据,但不能解释长周期面波数据.地下核爆炸激发的Lg波,在区域震相中,幅值往往很大,是估计当量、研究识别判据的重要震相[8-9],通常认为,爆炸源区附近的Rg波的散射,是Lg波形成的主要机制,按球对称理论,利用地表形成的Rg波解释不了Lg波波谱中的低谷点现象[10-12],但是,利用层裂机制,可以得到较好的解释.地震矩张量反演结果亦显示,除了球对称分量外,地下核爆炸震源矩张量中存在偏分量[8, 12].
由于上述原因,促使人们设计辅助源模式,来深入研究地下核爆炸震源过程中的非球对称机制.通过对面波资料的分析,表明层裂是地下核爆炸过程中最重要的二次源过程[9, 10, 13],理论上来讲,该二次源机制对体波也具有调制作用,但是,地表反射波往往会掩盖这种调制作用,本文利用经验格林函数方法,消除了路径的影响,对地下核爆炸地震波远场P 波的二次源特性进行了研究,这对深入理解地下核爆炸的震源机制以及完善识别判据[14-15]、提高当量估计精度,具有重要参考意义.
2 地下核爆炸震源时间函数的研究意义及主要手段震源的研究主要包括震源机制和震源时间函数两方面内容,震源机制描述震源的空间特征,主要体现了地震波各主要震相的相对激发特征和地震波辐射空间方向性特征,震源时间函数是描述震源的时间特征,它包括地震波的频率特征、强度特征等.
地下核爆炸的震源机制中,球对称压缩模式占据主导地位,而天然地震震源机制被认为是双力偶剪切破裂源.地下核爆炸和天然地震震源机制存在明显的差异,一般认为天然地震的震源过程包括多次破裂,其震源时间函数为多个在时间上有一定延迟的时间函数叠加组合.理论上讲,地下核爆炸的震源时间函数为简单脉冲时间函数,利用震源时间函数研究地下爆炸震源特性,立足于震源物理本质,理论依据可靠,被认为是地震核查识别技术发展的主要方向之一.
2.1 利用自由场数据反演震源时间函数自从进行地下核试验以来,关于地下核爆炸震源函数的研究,主要是利用近场地震测试数据来反演.早期的研究主要依赖于自由场的速度或加速度及径向应力的测试数据.本着这一目的,美国及其他核大国都投入了大量的人力和物力.由于测试技术的难度相当大,测试结果均不理想,由自由场数据获得的震源空间尺度非常小和持续时间非常短,测点局限于爆心附近小范围区域内,记录波形只包含很短的压缩波信息.加之地下核爆炸弹性响应区是一个具有争议的模糊概念,使得有些测试数据被怀疑是否处在弹性区范围内.因而人们对由自由场测试数据计算得到的震源函数有了争议,甚至对其准确性表示出怀疑.
2.2 经验格林函数方法利用远区或近区资料反演出震源时间函数是比较现实的,将小震级事件作为经验格林函数(EGF),反演相邻事件的震源时间函数[16-20],便可以做到这一点.这种方法的最大优点在于,经验格林函数中自然包含了路径效应及接收场地效应.缺点:经验格林函数的选取并不是一件容易的事情.通常利用余震记录作为经验格林函数来拟合大地震事件的波形,Frankel[17]利用该方法计算了天然地震的破裂尺度和应力降,并发展了谱比反卷积技术,反演了天然地震事件的震源时间函数并定量分析了震源的破裂尺度及破裂方向.Li[20]利用该方法运用远场地震观测资料分析了中国及哈萨克斯坦地下核爆炸的震源时间函数,结果符合远区爆炸源源时间函数的位移微分特征,实践证明,格林函数方法是研究地下核爆炸震源过程的重要手段之一.
3 地下核爆炸震源时间函数特征球对称爆炸源激发的地震波场可以描述为
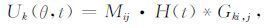
|
(1) |
Uk为位移的k分量,Gki,j为格林函数的空间导数,H(t)为阶跃函数,用来描述爆炸源时间过程,其定义为当t<0时等于0,当t≥0时等于1,其导数为δ(t).Mij取如下张量形式,表示球对称爆炸源:
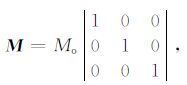
|
(2) |
Mo 为爆炸源标量地震矩.可见,用球对称模型来解释复杂的地下核爆炸过程,其局限性是显然的.对一些重要震相,如Lg波,所表现出来的特性,必须要考虑辅助震源模型.
地下核爆炸产生的力学效应中,普遍观测到层裂现象[9-10].层裂是爆炸荷载下表层岩体破坏的一种形式,是地下核试验过程中的一个重要的力学现象.在垂直方向,爆炸产生的冲击波从爆心出发向地表传播,经自由表面反射后由压缩波转变成拉伸波,并和继续向上传播的压缩波叠加,形成拉伸力.当拉伸力超过岩层的上覆压力与介质抗拉强度之和时,岩层则被拉断上抛飞出,然后经自由下落撞击地球介质,该震源机制产生的P 波在时间上稍微滞后于爆炸本身产生的直达P 波,极性为正.理论上来说,这样的二次源机制,对地下核爆炸激发的地震波必然有影响.
利用近场资料反演地下核爆炸源的特性,这类工作做得比较多,但多限于研究源的过冲[21-22]、拐角频率[7]、高频衰减特性[3, 23].对非线性层裂源过程的研究工作,多集中于对过程定量的数学描述[9, 23],Bakun[22]等首次将地下核爆炸直达P 波后面几秒钟到达的震相定义为“层裂相”.
在球对称源的基础上,给出含有层裂过程的地震波场的数学描述,是很有意义的,针对远区记录信号,可以用垂向点力模型来描述层裂[24-26],含有层裂机制的地下核爆炸激发的地震波场可以描述为
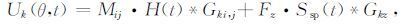
|
(3) |
Mij取(2) 式形式,Ssp(t)为层裂过程时间函数,Fz 描述层裂的单力强度,作用于爆炸源上方自由表面处,这里需要注意的是,对远场信号来说,对应地表单力的格林函数取与爆炸源处的格林函数相同形式,对于远场来说,爆炸源时间过程取阶跃函数是合适的.
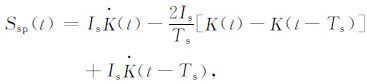
|
(4) |
其中
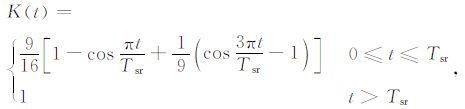
|
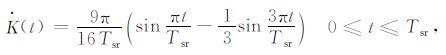
|
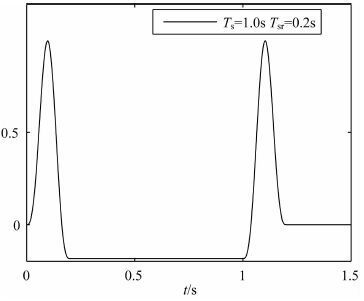
Ts 为层裂周期,Is 为层裂冲量,Tsr 为层裂起始时间.图 1为层裂起始时间Tsr=0.2s、层裂周期Ts=1.0s情况下的Ssp(t)函数示意图,具有明显的双脉冲形式,起始脉冲为爆炸所致,后面的脉冲为层裂物质回拍地球介质造成的[9].
考虑路径响应P(t)、观测点场地响应A(t)及记录仪器响应I(t),远场位移(垂向)可以写为分解形式[24]:
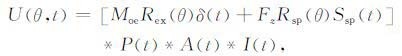
|
(5) |
|
图 1 层裂时间函数 Fig. 1 Equivalent point-force time function for spall process |
其中,Rex、Rsp 分别为相应震源辐射因子,此时,爆炸源时间函数取微分形式,得到一脉冲函数δ(t).
同一台站接收到的发生在同一地点的小地震事件,即经验格林函数事件表示为
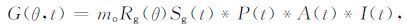
|
(6) |
其中,mo、Rg 和Sg 分别为小事件的标量地震矩、震源辐射因子和震源时间函数.小地震事件的震源时间函数可被看作δ 函数,响应谱Sg(ω)=1.由格林函数事件记录反褶积目标事件求得震源时间函数谱:
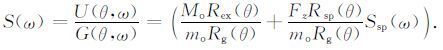
|
(7) |
采用高斯滤波与最低水准限制相结合的办法来优化反褶积过程[19],选择一已知较小的地下核爆炸事件作为EGF,相应地,Rg(θ)=1.如果目标事件是地下核爆炸,则Rex(θ)=1,(7) 式化为
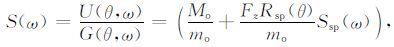
|
(8) |
反演回时间域中,有:
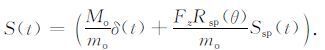
|
(9) |
爆炸源的脉冲函数,叠加在层裂源时间函数起始脉冲上,垂向点力的辐射因子Rsp(θ)不随方位角变化[26].总的效果为双脉冲形式,且形状不随方位角变化.由于爆炸强度要大于层裂强度,理论上讲,后面的脉冲相对要小一些,如果层裂效应显著,双脉冲形式可以存在于远场体波中.需要说明的是,所选格林函数尽管当量较小,本身也可能会含有层裂成分,这对二次脉冲的绝对幅值影响较大,但对其形状、以及形状随方位的变化影响较小.本文重点考察二次脉冲是否存在及其变化特征,故格林函数中的层裂成分不影响分析结果.
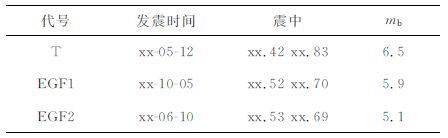
4 实际远场P波资料反演结果本文对发生在某地下核试验区域的3次地下核爆炸地震波数据进行了分析,将其中震级较大事件作为待求源时间函数的目标事件,另两次当量较小的事件作为EGF,表 1给出了这些事件的具体参数(因为涉及一些敏感数据,发震时刻中的年份及震中位置经纬度部分以xx 代替),T 表示目标事件,EGF 表示经验格林函数,mb 为震级.数据源自IRIS (Incorporated Research Institutions for Seismology).采用宽频带P波资料来获取震源时间函数;采样频率为每秒20点,时间窗取20s长.
|
|
表 1 事件基本参数列表 Table 1 Basic parameters of the underground nuclear explosions |
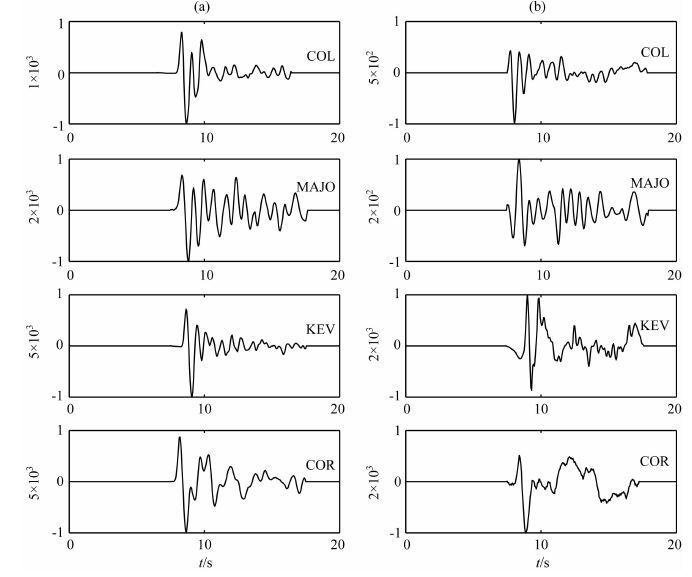
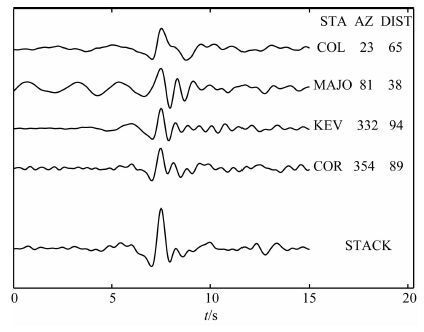
图 2为目标事件T 及EGF1 事件的地震记录波形图,右上角为记录台站名称.纵轴单位为点数(Counts).从该图中可以看出,相邻地下核爆炸在同一台站记录的波形具有较好的相似度,这也说明这两次地下核爆炸的震源特征是相似的.图 3 是以EGF1作为经验格林函数计算出来的事件T 的震源时间函数(幅值经归一化处理),“STA”代表记录台站名称,“AZ”代表方位角,“DIST”代表震中距,单位都为“°”,下边的“STACK”为叠加结果.可以看出,与理论预测结果相符,具有明显的双脉冲形式,虽然各个记录台站的方位角和震中距变化很大,分别从约23°到350°及38°到94°,反演出来的震源时间函数形式却很相近.
|
图 2 (a)目标事件T 垂向宽频带速度记录波形;(b)EGF1事件的垂向宽频带速度记录波形 Fig. 2 (a) Vertical components of broadband recordings of the target event T;b) Vertical components |
|
图 3 以EGF1作为经验格林函数反演的源时间函数及其叠加平均结果 Fig. 3 The estimates of the source time function of event T by usingEGFl as the empirical Green’s function |
脉冲间距约为1s,也就是说层裂周期Ts≈1.0s,符合一般层裂过程的周期范围.
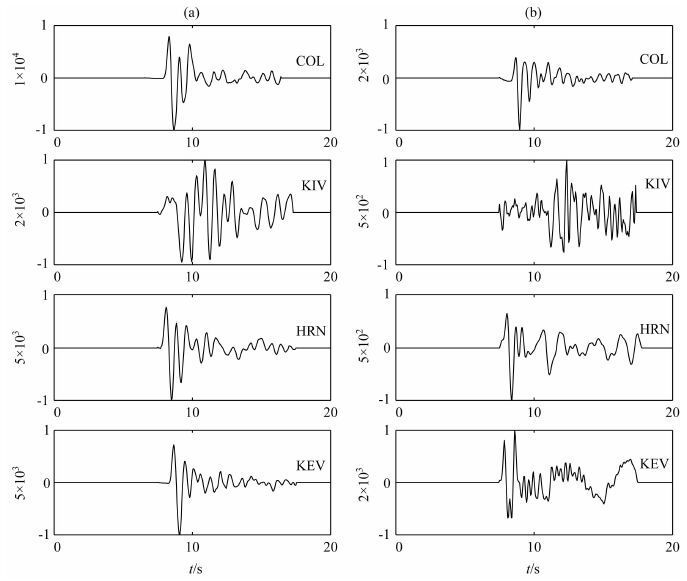
为检验格林函数方法的有效性,以EGF2 再次反演目标事件T,图 4和图 5为相应结果,其叠加平均结果与利用EGF1作为经验格林函数反演出来的结果非常相近,同样具有明显的双脉冲特征,形状基本不随方位角及震中距变化.这充分说明,该源时间函数反映了爆炸源及其附近二次源过程,并非传播路径所致,该时间函数特征与层裂物理机制相符.
|
图 4 (a)目标事件T 垂向宽频带速度记录波形;(b)EGF2事件的垂向宽频带速度记录波形 Fig. 4 (a) Vertical components of broadband recordings of the targetevent T; (b) Vertical components of broadband recordings of EGF2 at the same stations |

|
图 5 以EGF2作为经验格林函数反演源时间函数 及其叠加平均结果 Fig. 5 The estimates of the source time function of event T by using EGF2 as the empirical Green’s function |
地下核爆炸激发的地震波是一个十分复杂的物理过程,仅通过单纯爆炸源,去解释所观测到的地震波,几乎是不可能的.层裂是地下核爆炸过程中十分重要的非球对称源成分,在球对称源的基础上,叠加层裂源模型,是研究层裂对地震波调制作用的有力手段,利用远场P波数据反演地下核爆炸的震源时间函数,结果显示,具有不随方位角变化的双脉冲形式,与层裂机制相符,该结果支持层裂源是地下核爆炸的重要辅助源的结论.
利用经验格林函数方法反演震源时间函数,有可能对目标区域内发生的地震事件的震源特征,给出某种意义上的定量解释.利用反演可疑事件的震源时间函数的特征来作为识别手段,不仅理论依据充分,而且易于操作,不失为一种较好的判据.
经验格林函数选取的是否合理,是关键,如果所选取的经验格林函数中的层裂成分较大,那么,对反演结果的幅值影响较大.传统的识别判据及当量估计公式多基于球对称爆炸源的理论模式,考虑层裂对地震波的调制作用,对传统的当量估计公式进行修正,理论上来讲,可以提高估计精度.
| [1] | 陈剑杰. 封闭式地下核爆炸的地表变形与破坏. 中国地质大学, 1994. |
| [2] | Brune J, Espinosa A, Oliver J. Relative excitation of surface waves by earthquakes and underground explosions in the California-Nevada region. J. Geophys. Res. , 1963, 68(11): 3501-3513. DOI:10.1029/JZ068i011p03501 |
| [3] | Gupta I N, Chan W W, Wagner R A. A comparison of regional phases from underground nuclear explosions at East Kazakh and Nevada test sites. Bull. Seism. Soc. Am. , 1992, 82(1): 352-382. |
| [4] | Harkrider D G. Surface waves in multilayered elastic media I. Rayleigh and Love waves from buried sources in a multilayered elastic half-space. Bull. Seism. Soc. Am., 1964, 54(2): 627-679. |
| [5] | 靳平, 徐果明, 楼沩涛. 点力源在横向各向同性介质中激发的弹性波. 地球物理学报 , 1998, 41(4): 525–536. Jin P, Xu G M, Lou W T. Elastic waves from a point force in transversely isotropic media. Chinese J. Geophys. (in Chinese) (in Chinese) , 1998, 41(4): 525-536. |
| [6] | Burdick L J, Wallace T, Lay T. Modeling near-field and teleseismic observations from the Amchitka test site. J. Geophys. Res. , 1984, 89(B6): 4373-4388. DOI:10.1029/JB089iB06p04373 |
| [7] | Muller R A, Murphy R J. Seismic characteristics of underground nuclear detonations Part I. Seismic spectrum scaling. Bull. Seism. Soc. Am., 1971, 61(6): 1675-1692. |
| [8] | Stump B W, Reinke R E, Olsen K H, et al. Isotropic and deviatoric characterization of the COALORA nuclear explosion in Yucca flats. Geophys. J. , 1994, 116(3): 538-552. DOI:10.1111/gji.1994.116.issue-3 |
| [9] | Day S M, Rimer N, Cherry J T. Surface waves from underground explosions with spall: analysis of elastic and nonlinear source models. Bull. Seism. Soc. Am. , 1983, 73(1): 247-264. |
| [10] | Patton H J, Taylor R S. Analysis of Lg spectral ratios from NTS explosions: Implications for the source mechanisms of spall and the generation of Lg waves. Bull. Seism. Soc. Am. , 1995, 85(1): 220-236. |
| [11] | 徐恒垒, 靳平, 倪四道, 等. 谱元法数值模拟地表起伏对补偿线性矢量偶极源Rg波低谷点的影响. 地球物理学报 , 2011, 54(11): 2831–2837. Xu H L, Jin P, Ni S D, et al. Investigation of surface fluctuation effects on the spectral null of Rg waves generated by CLVD source with Spectral Element Method simulation. Chinese J. Geophys. (in Chinese) (in Chinese) , 2011, 54(11): 2831-2837. DOI:10.3969/j.issn.0001-5733.2011.11.013 |
| [12] | 何永锋, 陈晓非, 何耀明, 等. 地下爆炸Rg波低谷点激发机理. 地球物理学报 , 2005, 48(3): 643–648. He Y F, Chen X F, He Y M, et al. Generation of null in Rg wave by underground explosions. Chinese J. Geophys. (in Chinese) (in Chinese) , 2005, 48(3): 643-648. DOI:10.1002/cjg2.697 |
| [13] | He Y F, Chen X F, Zhang H M. The effect of spall on Lg waves. Acta Seismologica Sinica , 2005, 18(3): 331-337. DOI:10.1007/s11589-005-0082-0 |
| [14] | Hough S. Empirical Green's function analysis of recent moderate events in California. Bull.Seism.Soc.Am. , 2001, 91: 456-467. DOI:10.1785/0119970154 |
| [15] | 韩绍卿, 李夕海, 安跃文, 等. 核爆、化爆、地震识别研究综述. 地球物理学进展 , 2010, 25(4): 1206–1218. Han S Q, Li X H, An Y W, et al. A review on the identification of nuclear explosions, chemical explosions and natural earthquakes progress in geophysics. Progress in Geophysics (in Chinese) (in Chinese) , 2010, 25(4): 1206-1218. |
| [16] | Nicholas N. Empirical Green's functions: A comparison between pulse width measurements and deconvolution by spectral division. Bull. Seism. Soc. Am. , 1999, 89(1): 178-189. |
| [17] | Frankel A. Simulating strong motions of large earthquakes using recordings of small earthquakes: the Loma Prieta mainshock as a test case. Bull. Seism. Soc. Am. , 1995, 85(4): 1144-1160. |
| [18] | Atkinson G M, Silva W. An empirical study of earthquake source spectra for California earthquakes. Bull. Seism. Soc. Am. , 1997, 87(1): 97-113. |
| [19] | Li Y P, Toks?z M N, Rodi W. Investigation of source process of large earthquakes and nuclear explosions with the EGF method. Seismol. Res. Lett. , 1993, 64: 31-40. |
| [20] | Li Y P, Toks?z M N, William R. Source time functions of nuclear explosions and earthquakes in central Asia determined using empirical Green's functions. J. Geophys. Res. , 1995, 100(B1): 659-674. DOI:10.1029/94JB02465 |
| [21] | Taylor S R, Denny M D, Vergino E S, et al. Regional discrimination between NTS explosions and Western U. S. earthquakes. Bull. Seism. Soc. Am., 1989, 79(4): 1142-1176. |
| [22] | Bakun W H, Johnson L R. The deconvolution of teleseismic P waves from explosions Milrow and Cannikin. Geophys. J. , 1973, 34(3): 321-342. DOI:10.1111/j.1365-246X.1973.tb02399.x |
| [23] | Stump B W. Constraints on explosive sources with spall from near-source waveforms. Bull. Seism. Soc. Am. , 1985, 74(2): 361-377. |
| [24] | 何永锋, 赵克常, 张献兵. 地下核爆炸的主要非爆炸源机制. 地球物理学进展 , 2010, 25(3): 789–794. He Y F, Zhao K C, Zhang X B. Primary non-explosive source mechanisms for underground nuclear explosions progress in geophysics. Progress in Geophysics (in Chinese) (in Chinese) , 2010, 25(3): 789-794. |
| [25] | 何永锋, 陈晓非, 张海明. 地下核爆炸Lg波的激发机制. 地球物理学报 , 2005, 48(2): 367–369. He Y F, Chen X F, Zhang H M. The generation of Lg wave by underground nuclear explosions. Chinese J. Geophys. (in Chinese) (in Chinese) , 2005, 48(2): 367-369. |
| [26] | Aki K, Richards P G. Quantitative Seismology, Theory and Methods. San Francisco: Freeman W H and Company , 1980. |
 2012, Vol. 55
2012, Vol. 55