2. 中海石油研究总院, 北京 100027
2. CNOOC Research Institute, Beijing 100027, China
在石油天然气勘探开发中, 断层、通道和裂缝等结构特征以及河道砂体等沉积特征是发现和描述油藏的基础, 分辨和分析地震资料中这些结构特征具有重要的意义.然而, 由于这些区域地质形态的复杂性, 使得地震数据中这些区域易受噪声的干扰, 无论采用人工解释还是相干和边缘检测等自动检测算法来描述和刻画这些区域都变得较为困难.传统的地震资料去噪方法, 如F-K 域倾向滤波、f-x 域预测滤波和多道相干滤波等, 多是利用地震反射同相轴的横向一致性, 易造成对倾斜同相轴振幅的压制, 也会模糊小的断层和裂缝等不连续结构, 甚至会引起大的断层两侧同相轴的错误连接.如何能够较好地平衡地震噪声衰减和有效信号保护的关系受到了广泛的关注[1-6], 而能够保护和增强断裂等边缘结构的叠后噪声衰减技术尤其受到地震解释工作者的重视[7-9].
Luo等[10]基于次序统计的思想给出一种地震数据保边滤波(EPS, Edge-PreservingSmoothing) 算法, 该方法采用Kuwahara多窗分析技术, 计算当前分析点周围各个子窗内数据的均值和方差, 将最小方差对应的子窗的均值作为当前点的滤波输出.AlBinHassan等[11]发展了这种保边滤波思想, 给出了三维情况下的子窗剖分方法, 将EPS算法用于三维地震数据的保边滤波处理.Lu 等[12]基于多项式拟合的思想推广了一维的EPS算法, 该方法通过计算包含当前分析点的一系列平移子窗内信号对给定阶次的多项式拟合误差, 选择出最小拟合误差对应的子窗的信号估计值作为当前点的滤波输出.杨培杰等[13]也基于这种多窗分析思想给出一种方向性边界保持断层增强技术, 使得相干体中的断层图像得到更加清晰显示.Liu 等[14-15]应用图像处理中的二维多级中值滤波器消除地震随机噪声, 并分析了滤波器尺度参数选择对噪声衰减和信号细节保护的影响.此外, Fehmers等[16]引入微分方程滤波法用于地震资料的保边滤波处理, 该方法采用梯度结构张量估计地层方向, 度量地层的连续性, 以此约束扩散滤波方程的滤波方向和滤波程度.Lavialle等[17]结合线型和面型扩散滤波模型给出专门针对保护和增强断层构造的断层保持扩散滤波器.孙夕平等[18]和王旭松等[19]通过在扩散方程中引入二阶导数项、张尔华等[20]通过修正扩散方程中的保边约束项进一步改善非线性各向异性扩散滤波器的边缘保护性能.然而, 基于各向异性扩散方程的滤波方法以原始地震数据作为初始条件, 通过扩散时间的迭代推移形成滤波作用, 由于不好估计出获得最佳滤波效果的扩散时间, 导致不能准确预测其滤波性态[21].
经典的二维中值滤波法具有优异的噪声衰减性能, 尤其适用于消除非平稳信号中的峰值噪声.但是, 由于在滤波过程中其滤波窗口保持恒定, 且滤波操作没有方向特性, 使得采用中值滤波法处理具有层状结构的地震信号时, 必然会引起有用信号的损伤和不连续结构特征的模糊.一些改进的中值滤波方法如二维多级中值滤波器[14-15], 虽然有较强的信号细节保护能力, 但是其对噪声的衰减能力不够.本文结合微分方程滤波法中利用梯度结构张量刻画地震反射层局部结构特征的方法, 定义了带有能量变化强度信息的横向不连续性置信度量, 结合线型置信度量和横向不连续性置信度量, 给出一种二维结构自适应中值滤波方法, 使中值滤波操作窗函数根据信号局部结构特征自适应地作方向延伸和尺度伸缩, 从而既能最大限度地消除随机噪声, 又能有效保护有用信号和地层边缘等细节特征.
2 结构自适应中值滤波原理 2.1 地层倾向估计及横向不连续性度量有多种方法可用于地层结构的规则性分析[16, 22-25], 梯度结构张量法是其中一种简单而又有效的途径. 记二维地震剖面为u(x, t), 则该二维剖面对应的梯度结构张量由下式描述
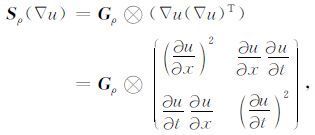
|
(1) |
其中, ∇和T分别为梯度算子和转置算子, ⊗ 表示卷积运算, Gρ 表示尺度为ρ的二维高斯函数Gρ(x, t)=exp(- (x2 +t2) /2ρ2) .在梯度结构张量的定义中, 由梯度向量Δu及其转置向量形成的张量矩阵与尺度为ρ 的高斯低通滤波器作用, 确定了梯度结构张量可度量的信号特征的最大尺度.将该对称半正定矩阵Sρ( ∇u)作矩阵特征分解
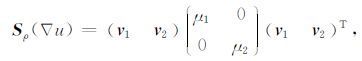
|
(2) |
其中, 特征值μ1 ≥μ2 ≥0反应了信号在位置(x, t) 的高斯邻域Gρ 内沿特征方向的振幅变化强度;特征向量v1 和v2 给出局部正交方位, v1 对应于局部振幅变化最大的方向, 即信号梯度方向, 而v2 对应于局部振幅变化最小的方向, 即反射同相轴的取向.根据梯度结构张量两个特征值的取值情况, 可分辨不同的信号结构特征, 文献[26]中引入线型信号结构的置信度量:
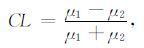
|
(3) |
该置信度量在区间[0, 1]之间取值, 衡量局部信号特征与线型结构的相似程度, 同时亦表征局部方位估计的准确程度.若CL→1, 则表示局部信号特征趋于线型结构, 估计的地层倾角的准确度越高;反之, 若CL→0, 则局部信号结构背离了线型假设, 这可能由干扰噪声和断层、裂缝等横向不连续性造成.根据线型结构置信度量可较好地识别局部呈线型结构的反射同相轴;但是, 由于该置信度量值判断的是信号能量的相对变化程度, 容易受到噪声的干扰, 并且在无明显信号结构的区域内取值没有意义, 从而很难从干扰背景中明确地识别断层、裂缝等横向不连续结构.
基于上述分析, 本文在线型结构置信度量的基础上, 给出一种含有信号横向能量变化强度信息的置信度量值, 用于识别断层、裂缝等横向不连续结构.
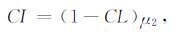
|
(4) |
(4) 式中(1-CL)项表示信号局部结构特征相对线型结构的背离程度, μ2 表征在给定度量邻域内在均方误差最小意义下信号沿局部一致方向的能量变化强度[24].在反射同相轴呈线型结构的区域, 由于CL→1, 即(1-CL)→0, 此时沿地层倾向的信号变化相对较小, 即μ2 →0, 从而使得CI→0.在含有断层、裂缝等横向不连续性的区域, 由于CL→0, 即(1-CL)→1;且在横向不连续区域, 由于信号结构背离了局部线型结构假设, 此处信号的一致性取向不明确, 因而沿局部一致性方向的信号变化强度也相对较大, 即μ2 

对于二维地震剖面u(x), 记x= (x, t)为采样点的空间、时间位置, 定义位置x处的结构自适应中值滤波操作为:
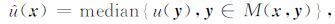
|
(5) |
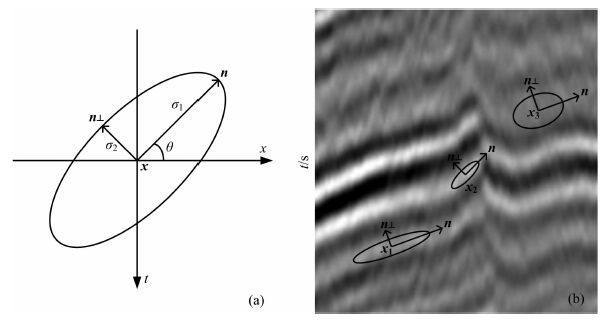
式中, M(x, y)表示位置x处的结构自适应滤波窗口(见图 1a), y为当前滤波窗口包含的采样点的空间、时间位置,
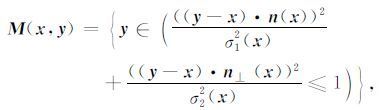
|
(6) |
其中, ·表示内积运算;n(x)和n⊥ (x)分别对应于x处的地层倾向及梯度方向, 取为梯度结构张量的两个特征向量, 即n(x)=v2(x), n⊥ (x)=v1(x);σ1(x)和σ2(x)分别表示椭圆形滤波窗口的长轴和短轴, 它们共同决定了结构自适应中值滤波器的滤波尺度以及滤波操作的方向选择性.滤波器尺度参数的设计是影响结构自适应中值滤波器性态的关键, 根据结构自适应滤波操作的要求, 本文结合线型结构置信度量CL和横向不连续性置信度量CI, 给出如下的滤波器尺度参数自适应选择策略:
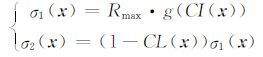
|
(7) |
式中Rmax 规定了椭圆形滤波窗口的最大尺寸, g(·) 为关于CI(x)的单调减函数, 其取值范围限定为(0, 1], 文中取g(·)为指数函数
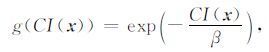
|
(8) |
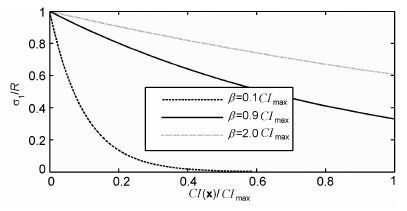
其中, β为针对CI(x)的阈值参数, 控制指数函数的衰减速度, β 取值越小, 指数函数的下降越快;反之, 指数函数的衰减变缓.
结构自适应中值滤波器根据信号的局部结构特征具有灵活的滤波尺度调节功能和方向选择特性, 控制最大滤波尺度的σ1(x)由横向不连续性置信度量CI(x)决定, 而调整方向选择特性的σ2(x)由线型结构置信度量CL(x)决定.在断层、裂缝等横向不连续区域由于CI(x)
联合式(7) 和(8) 可见, 结构自适应中值滤波器的滤波性能受到参数Rmax 和β 共同约束, 最大尺寸参数Rmax 控制滤波器的平滑性能, 阈值参数β 则调整滤波器对断层等边缘结构的保持程度.考虑到文中采用梯度结构张量估计地层的倾角和规则程度, 梯度结构张量的尺度参数ρ 决定了其对局部信号结构的度量孔径, 因此为了确保基于两种置信度量约束的滤波过程可信, 要求滤波窗口的最大尺寸Rmax 不超过2ρ, 即取Rmax ≤2ρ.对于阈值参数β, 由图 2 可见, 当β 取值偏小时, 稍大的横向不连续性置信度量CI(x)即引起滤波窗口的尺寸减小, 因而会使一些弱的断层、裂缝等边缘结构得到有效保护, 但同时也会减弱滤波器在横向不连续性区域的滤波效果;当β 取值偏大时, 只有很大的CI(x)才会导致滤波窗口萎缩到足够小, 因而在这种情况下滤波器的噪声衰减能力得到增强, 但在一定程度上会造成弱边缘结构的模糊和压制.
|
图 1 结构自适应中值滤波器窗口的构造 (a)滤波器窗口函数;(b)信号结构自适应滤波策略. Fig. 1 Filter window construction of structure-adaptive median filter (a) Filter window function; (b) Signal structure-consistent filtering mechanism. |
|
图 2 结构自适应中值滤波窗的长轴控制函数 Fig. 2 Controlling functions ofthe main axis of the structure-adaptive median filter kernel |
结构自适应中值滤波器的边缘结构保持性能受阈值参数β 控制, 选择合适的β 是保证滤波过程中能够有效保持断层、裂缝等地层边缘的关键.然而, 地震资料通常从浅层到深层, 即使在同一层段内信号横向能量变化的动态范围波动也很大, 很难统一地选择一个全局阈值参数β.本文给出一种区域分割的阈值参数自适应选择策略, 即根据待处理剖面内横向能量变化在时间和空间上的分布情况, 将剖面Ω 分割为若干具有一定边界重叠的子区域Ω =∪Ωi, 在每个子区域Ωi内取横向不连续性置信度量CI(x) 的极大值, 即
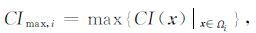
|
(9) |
从而通过下式得到该区域内的自适应阈值参数β 为
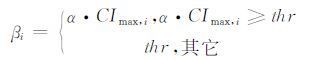
|
(10) |
式中α 为根据保边缘滤波要求而全局确定的百分比因子, thr是由剖面的整体噪声干扰水平所确定的基底噪声阈值.
通过将待处理剖面分割为若干子区域, 由(9) 和(10) 式将(8) 式中对阈值参数β 的绝对取值转化为对百分比因子α 的相对取值, 从而能够统一调整结构自适应中值滤波器的边缘保持性态.在实际资料处理中, 并不需要精确地确定子区域的大小, 一种典型的选择是每个子区域内包含100 道, 每道包含150个采样点, 即可满足滤波过程保持断层、裂缝等边缘特征的要求.
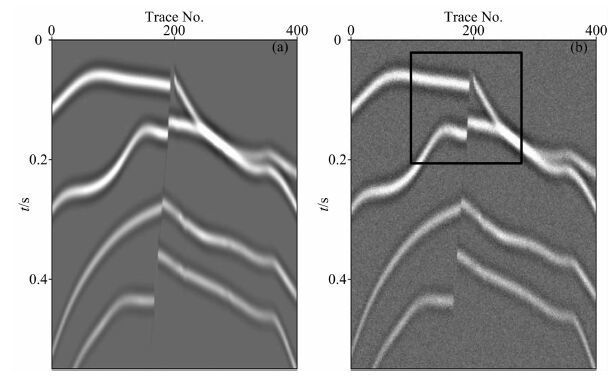
3 合成模型分析为了验证结构自适应中值滤波器的保护边缘去噪的有效性, 本文选取主频为20 Hz的Ricker子波, 采用射线追踪方法得到一个含有断层的复杂地层结构模型的合成地震数据(见图 3a), 在合成数据中加入5dB的带限高斯随机噪声, 得到图 3b的含噪数据.
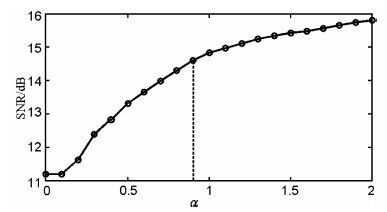
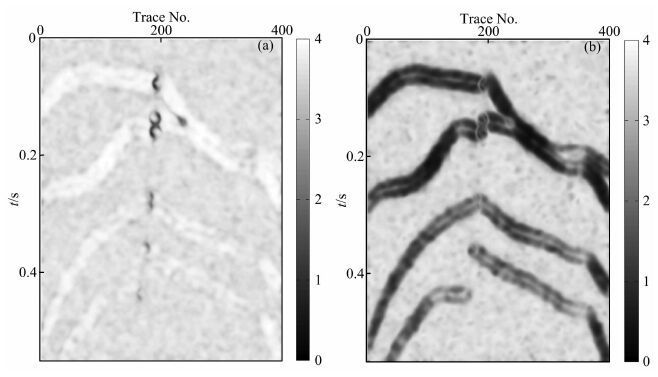
采用结构自适应中值滤波器处理加噪的合成数据, 考虑到合成数据的信噪比很低, 在梯度结构张量的计算中, 二维高斯低通滤波函数取较大的尺度参数ρ=4.0, 结构自适应中值滤波器的最大滤波尺寸取为Rmax =ρ =4.0, 即对应最大尺度为9点的滤波窗口.针对图 3b中黑色长方形框所选定的典型区域, 分析阈值百分比因子α 对滤波结果的影响.调整α 从10%开始以10%的间隔变化到200%, 记录每次滤波结果的信噪比, 得到该区域的滤波结果的信噪比随阈值百分比因子α 的变化曲线, 如图 4 所示.从图中可以看出, 信噪比曲线随α 的增大而升高, 且曲线在α=90%后升高逐渐变缓.这是由于随着α 的增加, 滤波器的保边缘性能减弱, 当α>90%后, 滤波过程已造成断面处波形的损伤, 在一定程度上抵消了滤波性能增强带来的信噪比增加.因而在处理该加噪的合成数据时, 选择阈值百分比因子α=90%, 此时对应的结构自适应中值滤波器的各向异性窗函数的长轴σ1 和短轴σ2 的取值分布如图 5所示.对比图 5a和图 5b可见, 结构自适应中值滤波器的尺度参数能够很好地匹配合成数据的信号结构特征, 在局部呈线型结构的同相轴区域椭圆形滤波窗口的长轴拉伸、短轴萎缩, 形成有强方向选择特性的各向异性窗口;在断层区域长轴和短轴同时萎缩, 形成小尺度分析窗口;而在无信号特征的区域, 长轴和短轴均被拉伸, 形成大尺度的各向同性窗口.
|
图 3 含有断层的复杂地层结构的合成地震数据 (a)原始数据;(b)加噪数据. Fig. 3 Synthetic seismic data of complex geology model with a fault (a) Clean data; (b) Noisy data. |
|
图 4 不同α 对应的结构自适应中值滤波结果的信噪比 Fig. 4 SNR of filtered results by structure-adaptive median filter using different α |
|
图 5 针对加噪合成数据的结构自适应中值滤波器的窗口参数 (a)椭圆形滤波窗口的长轴σ1;(b)椭圆形滤波窗口的短轴σ2. Fig. 5 Window parameters of structure-adaptive median filter corresponding to the noisy synthetic data (a) Main axes σ1 of the elliptic filter window; (b) The second axes 2 of the elliptic filter window. |
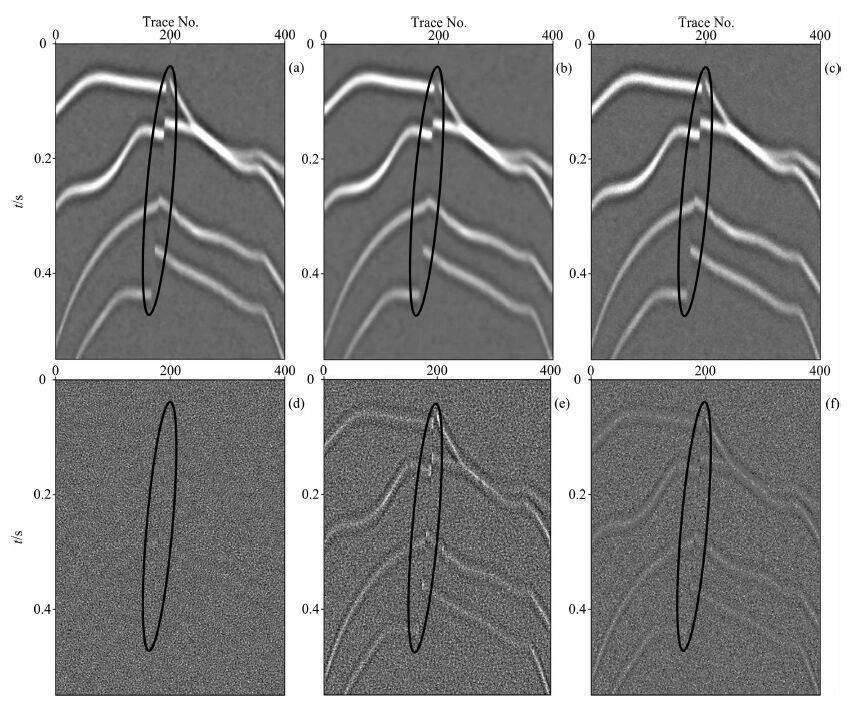
加噪合成数据的结构自适应中值滤波结果及其得到的噪声剖面分别如图 6a和图 6d所示.为了对比本文方法的处理效果, 使用经典的二维中值滤波器和具有信号细节保护能力的二维多级中值滤波器处理加噪合成数据.取两种中值滤波器的窗口尺寸与结构自适应中值滤波器的最大窗口尺寸相同, 即二维中值滤波器选择9×9的滤波窗口, 二维多级中值滤波器取9点的滤波长度, 两者对应的滤波结果以及得到的噪声剖面分别如图 6b-c和图 6e-f所示.
|
图 6 加噪合成数据的滤波结果比较 (a)结构自适应中值滤波结果;(b)二维中值滤波结果;(c)二维多级中值滤波结果;(d)结构自适应中值滤波器得到的噪声剖面;(e)二维中值滤波器得到的噪声剖面;(f)二维多级中值滤波器得到的噪声剖面. Fig. 6 Comparison of filtering results of the noisy synthetic data (a) Result obtained by structure-adaptive median filter; (b) Result obtained by 2D median filter; (c) Result obtained by 2D multistage median filter; (d) Noise removed by structure-adaptive median filter; (e) Noise removed by 2D median filter; (f) Noise removed by 2 D multistage median filter. |
从图 6a可见, 经过结构自适应中值滤波后, 随机噪声得到很大程度地衰减, 反射同相轴的一致性得到增强, 剖面整体变得非常干净;从图 6d可见, 结构自适应中值滤波器得到的噪声剖面中只有随机分布的干扰噪声, 无明显的有效信号结构, 断层结构在滤波过程中得到了有效保持.对比图 6b-c中两种中值滤波方法的滤波结果, 9×9的二维中值滤波器消除了大部分的随机噪声, 但也造成有效信号的损伤, 从其得到的噪声剖面图 6e可见, 滤波过程引起断层信息的模糊, 也造成反射同相轴的损伤, 尤其对倾斜反射结构的损伤更为明显;9 点滤波长度的二维多级中值滤波器虽然有较强的信号细节保护能力, 但是从其得到的噪声剖面图 6f可见, 二维多级中值滤波器对随机噪声衰减程度有限.
从上述分析、比较可以看出:在取相同滤波窗口尺度的条件下, 相比二维中值滤波器和二维多级中值滤波器, 结构自适应中值滤波器能够根据地震剖面的信号结构特征, 自适应地构造与信号结构相吻合的滤波窗口, 在消除随机噪声和保护断层等边缘结构之间找到了很好折中;结构自适应中值滤波器的噪声衰减性能接近9×9的二维中值滤波器, 而其对断层及有效信号保护能力又优于9点滤波长度的二维多级中值滤波器.
4 实际资料算例基于理论分析结果, 进一步将结构自适应中值滤波器用于叠后地震剖面的滤波处理.图 7中给出某油田的叠后纯波地震资料, 剖面中含有丰富的不连续结构特征, 除了两条主要的断层外, 在中央部位有一处杂乱反射区域, 在右侧偏下部有一处振幅异常区域.由于受到随机噪声和采集脚印的干扰, 同相轴的连续性受到一定影响, 不利于层位的横向追踪、不连续结构的自动检测和拾取等后继的解释和处理.运用本文的结构自适应中值滤波器处理该剖面, 选择100道、每道150个采样点的子区域分割;在梯度结构张量的计算中取高斯滤波器的尺度参数ρ=3.0;结构自适应中值滤波器的最大滤波尺寸取为Rmax =4.0, 即对应最大为9点的滤波窗口;为了达到较好的边缘保持性能, 取阈值百分比因子α =50%, 对应的滤波结果和得到的噪声剖面分别如图 8a和图 8d所示.作为对比, 同样采用两种中值滤波方法处理该剖面.由于二维中值滤波器的滤波窗口选择得过大, 对有效信号损伤严重, 而选择得过小, 会导致噪声衰减不够, 故此处取二维中值滤波器的窗口尺寸为5×5, 而二维多级中值滤波器采用9点滤波长度, 即与结构自适应中值滤波器的最大滤波尺寸相当, 对应的滤波结果和它们得到的噪声剖面分别如图 8b-c、e-f所示.

|
图 7 XX 油田实际地震剖面 Fig. 7 Real seismic profile from XX oil field |
|
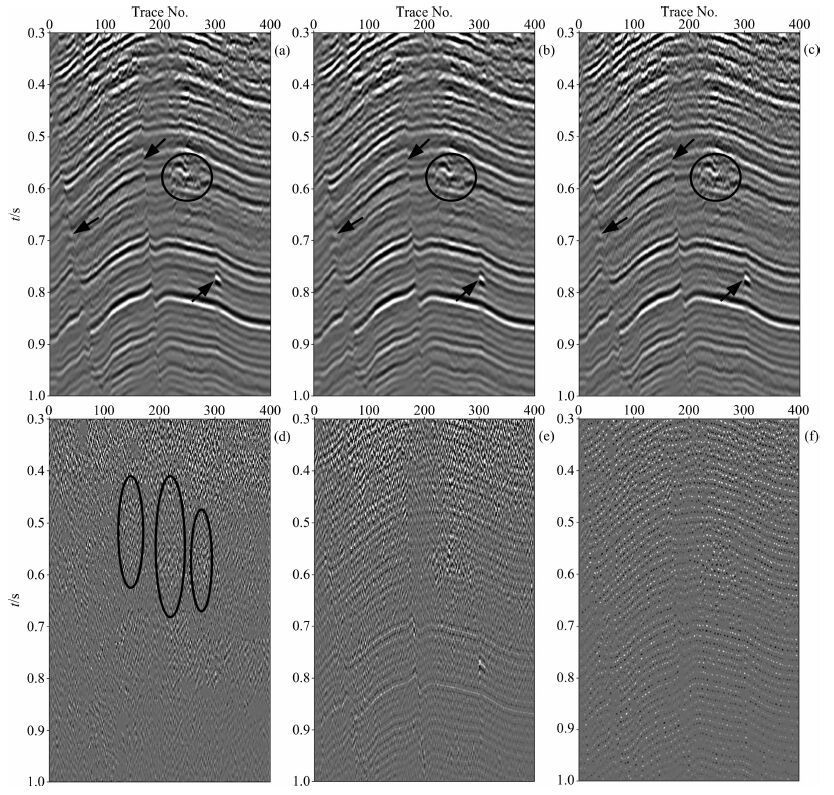
图 8 实际地震资料滤波结果比较 (a)结构自适应中值滤波结果;(b)二维中值滤波结果;(c)二维多级中值滤波结果;(d)结构自适应中值滤波器 得到的噪声剖面;(e)二维中值滤波器得到的噪声剖面;(f)二维多级中值滤波器得到的噪声剖面. Fig. 8 Comparison of filtering results of real seismic profile (a) Result obtained by structure-adaptive median filter; (b) Result obtained by 2D median filter; (c) Result obtained by 2D multistage median filter; (d) Noise removed by structur--adaptive median filter; (e ) Noise removed by 2D median filter; (f) Noise removed by 2D multistage median filter. |
对比结构自适应中值滤波前后的剖面图 7和图 8a可见, 结构自适应中值滤波过程消除了大部分的干扰噪声, 改善了反射同相轴的一致性, 断层构造得到增强, 振幅异常区域变得清晰.分析结构自适应中值滤波得到的噪声剖面(图 8d)可见, 浅层的干扰噪声非常强, 中深层的干扰噪声相对较弱, 剖面中除随机噪声外还有一些大角度的相干噪声;对比原始地震剖面图 7, 噪声剖面中看不到明显的有效信号结构.分析图 8b中二维中值滤波器的滤波结果, 从视觉上看噪声基本被压制, 信噪比得到很大的提高, 但是信号的边缘结构尤其断层、杂乱反射等被严重模糊, 这一点可以从其得到的噪声剖面(图 8e)得到印证.从图 8c和图 8f可见, 二维多级中值滤波器仅仅沿同相轴走向有微弱的噪声衰减作用, 滤波能力非常有限.以上结果表明, 结构自适应中值滤波器对浅层的强噪声和深层的弱噪声均能够有效压制, 不仅能够衰减随机噪声, 也能够消除部分相干噪声, 并且很好地保持了有效信号和断层、振幅异常等地层边缘和细节特征;结构自适应中值滤波器不仅具有二维中值滤波器优异的噪声衰减能力, 而且又不会因保护地层边缘和细节特征的需求而像二维多级中值滤波器那样引起滤波能力的明显降低.
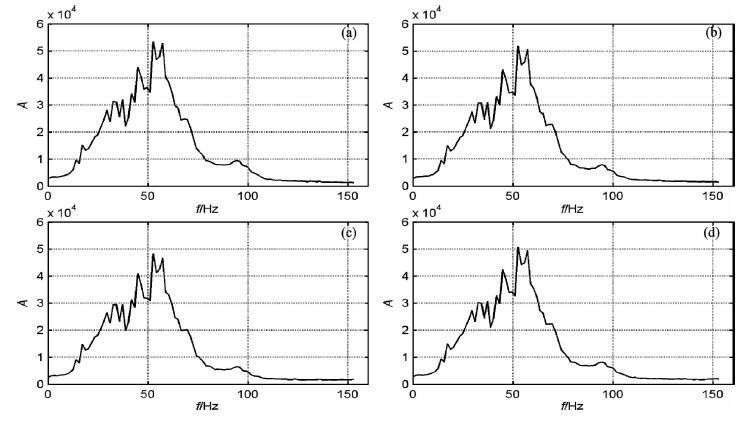
对原始地震剖面和三种滤波方法的处理结果进行频谱分析, 图 9给出相应剖面的平均振幅谱.对比处理前后的频谱发现, 三种方法处理后的高频段随机噪声幅度均要低于处理前, 且频谱的主要结构特点没有被破坏;然而结构自适应中值滤波器和二维多级中值滤波器均较好地保持了主频和有用信息频段的振幅谱, 而二维中值滤波器对主频和有用信息频段的振幅谱的损伤较为严重.以上结果说明结构自适应中值滤波器能够有效压制地震随机噪声, 并且几乎不损伤有用信息频段的频谱.
|
图 9 实际地震资料滤波结果平均振幅谱对比 (a)图 7的平均振幅谱;(b)图 8(a)的平均振幅谱;(c)图 8(b)的平均振幅谱;(d)图 8(c)的平均振幅谱. Fig. 9 Comparison of average spectrum of filtering results of real seismic profile (a) Average spectrum of Fig. 7 ; (b) Average spectrum of Fig. 8 (a ) ; (c) Average spectrum of Fig. 8 (b) ; (d) Average spectrum of Fig. 8 (c). |
在实际地震资料的处理中, 中值滤波器的应用已经比较成熟.本文针对现有的一些中值滤波方法在叠后地震资料随机噪声衰减方面存在的缺陷, 提出了一种结构自适应中值滤波器.该方法依据梯度结构张量对分析邻域内地层结构规则程度的估计情况, 引入了地震信号的两种结构特征的置信度量, 利用它们调控结构自适应中值滤波器的滤波窗口的尺度和形状, 使得滤波窗口能够最佳地匹配处理邻域内的地层结构特征.通过合成模型和实际地震资料的处理结果表明, 相比经典的二维中值滤波器及二维多级中值滤波器, 本文方法不仅能够有效地衰减随机噪声、提高剖面的信噪比, 而且能够较好地保持有效信号和断层、裂缝等地层边缘和细节特征.本文方法可作为一个预处理过程, 滤波结果进一步用于层位的自动追踪、对噪声敏感属性的提取等后继的解释和处理流程.
| [1] | 李月, 杨宝俊, 赵雪平, 等. 检测地震勘探微弱同相轴的混沌振子算法. 地球物理学报 , 2005, 48(6): 1428–1433. Li Y, Yang B J, Zhao X P, et al. An algorithm of chaotic vibrator to detect weak events in seismic prospecting records. Chinese J. Geophys. (in Chinese) (in Chinese) , 2005, 48(6): 1428-1433. |
| [2] | 高静怀, 毛剑, 满蔚仕, 等. 叠前地震资料噪声衰减的小波域方法研究. 地球物理学报 , 2006, 49(4): 1155–1163. Gao J H, Mao J, Man W S, et al. On the denoising method of prestack seismic data in wavelet domain. Chinese J. Geophys. (in Chinese) (in Chinese) , 2006, 49(4): 1155-1163. |
| [3] | Neelamani R, Baumstein A I, Gillard D G, et al. Coherent and random noise attenuation using the curvelet transform. The Leading Edge , 2008, 27(2): 240-248. DOI:10.1190/1.2840373 |
| [4] | 刘洋, FomelS, 刘财, 等. 高阶seislet变换及其在随机噪声消除中的应用. 地球物理学报 , 2009, 52(8): 2142–2151. Liu Y, Fomel S, Liu C, et al. High-order seislet transform and its application of random noise attenuation. Chinese J. Geophys. (in Chinese) (in Chinese) , 2009, 52(8): 2142-2151. |
| [5] | 陆文凯. 基于离散余弦变换的地震随机噪声压制技术. 石油地球物理勘探 , 2011, 46(2): 202–206. Lu W K. Seismic random noise suppression based on the discrete cosine transform. Oil Geophysical Prospecting (in Chinese) (in Chinese) , 2011, 46(2): 202-206. |
| [6] | 林红波, 李月, 徐学纯. 压制地震勘探随机噪声的分段时频峰值滤波方法. 地球物理学报 , 2011, 54(5): 1358–1366. Lin H B, Li Y, Xu X C. Segmenting time-frequency peak filtering method to attenuation of seismic random noise. Chinese J. Geophys. (in Chinese) (in Chinese) , 2011, 54(5): 1358-1366. |
| [7] | Chopra S, Marfurt K J. Seismic attributes–a historical perspective. Geophysics , 2005, 70(5): 3S-28SO. DOI:10.1190/1.2098670 |
| [8] | Chopra S, Marfurt K J. Emerging and future trends in seismic attributes. The Leading Edge , 2008, 27(3): 298-318. DOI:10.1190/1.2896620 |
| [9] | Chopra S, Misra S, Marfurt K J. Coherence and curvature attributes on preconditioned seismic data. The Leading Edge , 2011, 30(4): 386-393. DOI:10.1190/1.3575281 |
| [10] | Luo Y, Marhoon M, Al-Dossary S, et al. Acquistion Processing—Edge-preserving smoothing and applications. The Leading Edge , 2002, 21(2): 136-158. DOI:10.1190/1.1452603 |
| [11] | AlBinHassan N M, Luo Y, Al-Faraj M N. 3D edge-preserving smoothing and applications. Geophysics , 2006, 71(4): P5-P11. DOI:10.1190/1.2213050 |
| [12] | Lu Y H, Lu W K. Edge-preserving polynomial fitting method to suppress random seismic noise. Geophysics , 2009, 74(4): V69-V73. DOI:10.1190/1.3129907 |
| [13] | 杨培杰, 穆星, 张景涛. 方向性边界保持断层增强技术. 地球物理学报 , 2010, 53(12): 2992–2997. Yang P J, Mu X, Zhang J T. Orientational edge preserving fault enhance. Chinese J. Gephys. (in Chinese) (in Chinese) , 2010, 53(12): 2992-2997. |
| [14] | 刘财, 王典, 刘洋, 等. 二维多级中值滤波技术在随机噪声消除中的应用初探. 石油地球物理勘探 , 2005, 40(2): 163–167. Liu C, Wang D, Liu Y, et al. Preliminary study of using 2D multi-level median filtering technique to eliminate random noises. Oil Geophysical Prospecting (in Chinese) (in Chinese) , 2005, 40(2): 163-167. |
| [15] | Liu C, Liu Y, Yang B J, et al. A 2D multistage median filter to reduce random seismic noise. Geophysics , 2006, 71(5): V105-V110. DOI:10.1190/1.2236003 |
| [16] | Fehmers G C, H?cker C F W. Fast structural interpretation with structure-oriented filtering. Geophysics , 2003, 68(4): 1286-1293. DOI:10.1190/1.1598121 |
| [17] | Lavialle O, Pop S, Germain C, et al. Seismic fault preserving diffusion. Journal of Applied Geophysics , 2007, 61(2): 132-141. DOI:10.1016/j.jappgeo.2006.06.002 |
| [18] | 孙夕平, 杜世通, 汤磊. 相干增强各向异性扩散滤波技术. 石油地球物理勘探 , 2004, 39(6): 651–655. Sun X P, Du S T, Tang L. Coherent-enhancing anisotropic diffusion filtering technique. Oil Geophysical Prospecting (in Chinese) (in Chinese) , 2004, 39(6): 651-655. |
| [19] | 王旭松, 杨长春. 对地震图像进行保边滤波的非线性各向异性扩散算法. 地球物理学进展 , 2006, 21(2): 452–457. Wang X S, Yang C C. An edge-preserving smoothing algorithm of seismic image using nonlinear anisotropic diffusion equation. Progress in Geophys. (in Chinese) (in Chinese) , 2006, 21(2): 452-457. |
| [20] | 张尔华, 王伟, 高静怀, 等. 非线性各向异性扩散滤波器用于三维地震资料噪声衰减与结构特征增强. 地球物理学进展 , 2010, 25(3): 866–870. Zhang E H, Wang W, Gao J H, et al. Non-linear anisotropic diffusion filtering for 3D seismic noise removal and structure enhancement. Progress in Geophys. (in Chinese) (in Chinese) , 2010, 25(3): 866-870. |
| [21] | Gómez G. Local smoothness in terms of variance. Proceedings of the BMVC , 2000: 815-824. |
| [22] | Marfurt K J, Sudhaker V, Gersztenkorn A, et al. Coherency calculations in the presence of structural dip. Geophysics , 1999, 64(1): 104-111. DOI:10.1190/1.1444508 |
| [23] | Randen T, Monsen E, Signer C, et al. Three-dimensional texture attributes for seismic data analysis. 70th Annual International Meeting, SEG Expanded Abstracts , 2000: 668-671. |
| [24] | Wang Y E, Luo Y, Al-faraj M N. Inverse-vector approach for smoothing dips and azimuths. Geophysics , 2008, 73(6): P9-P14. DOI:10.1190/1.2976157 |
| [25] | Gao D L. Latest developments in seismic texture analysis for subsurface structure, facies, and reservoir characterization: A review. Geophysics , 2011, 76(2): W1-W13. DOI:10.1190/1.3553479 |
| [26] | Bakker P. Image structure analysis for seismic interpretation. Netherlands: Technische Universiteit Delft, 2002. |
 2012, Vol. 55
2012, Vol. 55

