2. 中国地震局地球物理研究所, 北京 100081
2. Institute of Geophysics, China Earthquake Administration, Beijing 100081, China
1972年11月16日在山西临汾召开“全国地震中期预报科研工作会议”上,国家地震局决定建立年度全国地震形势会商会制度,对近1、2 年地震形势进行评估,并指导协调近期的监测预报工作,这一措施推动全国地震监测预报工作进一步走向科学化与制度化[1]. 会商会根据地震学、地球物理学、大地测量等多学科信息,综合判定地震趋势并划定中国大陆年度地震危险区之后[2],形成的趋势性意见用于指导和加强地震监测、进行地震应急准备工作. 经过近四十年不间断的预测科学实践,作为一种真正的“向前”预测,中国的年度地震趋势会商会在国际上地震预测与预报研究领域有着独一无二的科学价值[3].
对年度地震危险区预测效能进行科学客观的评价是提高地震预测水平的关键之一,也是地震学家始终关注的科学问题[4-5]. 石耀霖等[6]和张国民等[7]对预测区域进行了空间网格化并利用R值评分法[8]对1990—1998年的年度预测作出评价,结果表明,中国年度地震危险区预测给出的结果只是略高于基于地震背景知识的随机预测,因此年度会商预测结果仍然是初步的、经验性的. 这一结论和史勇军等[9]用Pearson检验所得的结果是一致的. 然而这些工作中仍存在两个重要问题亟待解决:其一,由于危险区形状不规则、空间覆盖大小和预测震级不同,采用空间均匀网格化的R值评分实际上默认使用均匀泊松模型作为参考模型(零模型),这与实际的地震活动在空间上存在不均匀性的事实明显矛盾,进而影响对年度地震危险区预测效能及其显著性评价的科学性和客观性;其二,由于在划定年度危险区时,将不同学科信息进行综合实际上是一个复杂的科学问题,每个危险区包含的有效信息增益也各不相同. R值评分尽管能给出年度内所有危险区的整体评分结果,但不能反映单个危险区的信息增益. 提高年度危险区预测效能,离不开对有效信息增益的危险区预测经验的总结积累.
针对不连续的确定性“二元”预测(Yes/No prediction)和“黑箱”预测(blackbox)等各种复杂预测的显著性检验问题,Zhuang [10]提出了“博弈评分”(gamblingscoring)方法. 博弈评分首先利用选取好的“参考模型”计算每个危险区预测成功与否的概率作为“奖励”根据,然后根据实际地震的对应情况进行奖惩. 本文的目的就是利用博弈评分方法对中国年度地震危险区的预测效能和统计显著性进行重新评价.
2 博弈评分法年度地震危险区相应的预测不是以概率形式描述,而是圈定未来一年有可能发生“目标”震级以上地震的空间区域,并给出震级范围的确定性预测. 对这类预测目前常用R值评分法(也称Hanssen-Kuiper 技巧评分,参见文献[6, 11])来进行评价. 在均匀网格化的时空间区域上,R值的定义是预测有震格点数的命中率与预测无震格点数的误报率的差值,即

|
(1) |
其中a是预测“有震”的成功次数,b为错误的“无震”预测次数,c为误报的有震预测次数,d为正确的无震预测次数.
然而利用R值评分法对年度地震危险区进行评分是比较困难的,表现如下:(1) 年度危险区的形状不规则、大小不一. 石耀霖等[6]将中国大陆地区分为0.5°×0.5°的网格,根据每个方格上具体发震情况制成列联表. (2) 年度危险区预测的震级范围不同. 大体而言,中国大陆西部地区危险区的预测震级为6级左右或6~7级,东部危险区为5~6级. 在石耀霖等[6]的工作中,所有落入危险区的方格的预报震级一律为5级以上. 采用R值评分例如5级以上的统一标准对实际发生地震进行统计. 即使是严格按照预测震级范围进行评分,也无法客观反映预测不同震级大小和震级范围所面临的不同“风险”,以及预测成功和失败情况下的实际“效益”. 另一个办法是对震级和空间同时进行网格化. (3) 最重要的一点,由于不同地区地震活动强度存在差异,每个空间网格中发生5级以上地震的背景概率不同,R值评分采用均匀泊松模型的基本假设(零模型)明显不符合实际情况. 为解决这一问题,石耀霖等[6]先用均匀泊松模型为基本假设,对年度危险区结果进行评分;再以均匀泊松模型为基本假设,对非均匀泊松模型的预测结果进行评分,最后将两个评分进行对比. 其中,非均匀泊松模型采用如下方式实现:将危险区网格化后的“危险网格”随机排布,假定每个网格置为危险网格的几率与其地震活动强度成正比. 随机排布前后的R值之差被认为是年度会商结果和非均匀泊松模型的预报表现差异. 但是这种处理方法也带来了一些新的问题,我们将在后面章节中详加讨论.
Zhuang [10]提出的博弈评分(gamblingscore)方法着眼于预测者所冒的“风险”,即预测失败的概率,并对成功预测给予公平回报. 进行博弈评分的前提步骤是选取参照模型(referencemodel),实际操作中一般情况下可选取泊松模型,在对余震进行预测时则可使用大森/宇津公式. 如果参考模型给出在某时-空-强窗口内的发震概率为p0,在参考模型看来,对此窗口做出“有震”预测所冒风险(失败概率)为1-p0;进行“无震”预测所冒的风险(失败概率)则为p0. 约定预测者每次作“有震”预测时拿出1 点声望值作为抵押,如果预测成功,抵押将被退回,并奖励G=(1-p0) /p0 声望;如失败,抵押的1点声望值将被没收. “有震”预测回报率之所以定为G= (1-p0) /p0 是因为,如果参照模型是真实模型的话,预测者的期望收益为0,即ERGS=0;同样,“无震”预测的回报率应为1/G=p0/(1-p0) . Zhuang [10]还证明,如果参照模型是真实模型的无偏估计,预测者期望收益为正的必要条件是,所做预测和真实模型之间的相关性大于参照模型和真实模型之间的相关性.
采用与参考模型进行“声望分值”抵押和奖惩的方式进行评分,而对于“有震”或“无震”预测采用的具体方法则无任何限定. 因此博弈评分考虑到了危险区非均匀泊松模型的实际情况,并可适应“黑箱”式等复杂预测结果的检验. 此外,博弈评分还可以推广到概率预报和类似于图像信息学PI算法[12-14]用指标函数发布预报的情形[6].
目前,博弈评分方法已经逐渐开始得到应用,例如,Zechar和Zhuang [15]用博弈评分法对Shebalin 及其同事们根据“前兆逆向追踪法”(reversetracing ofprecursor,RTP)[16-17]发布的预测进行了显著性检验;Nolchan 和Rashkova[18]也用博弈评分法评测了M8算法的预报效果.
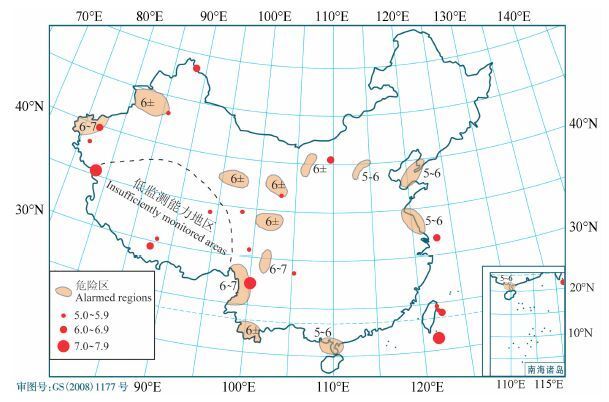
3 中国年度地震危险区预测效能的博弈评分 3.1 数据说明本研究选取中国大陆1990—2003 年度地震危险区[19-32]为研究对象. 图 1给出了中国大陆1996年度地震危险区预测图作为示例,各年度划定的危险区和预测震级情况如表 1 所示. 本节先对这些危险区进行博弈评分,然后与石耀霖等[6]和张国民等[7]的结果进行对比.
|
图 1 中国大陆1996年度地震危险区预测图.图中红色实心圆为1996年发生的Ms5.0以上地震,各危险区附近标出的数字为预测的震级范围 Fig. 1 The CEA annual earthquake predictions in 1996. The alarmed regions are marked in yellow and the earthquakes with magnitudes of 5 and above are represented by red dots. The numbers on the alarmed regions are the magnitude ranges of the expected future earthquakes |
|
|
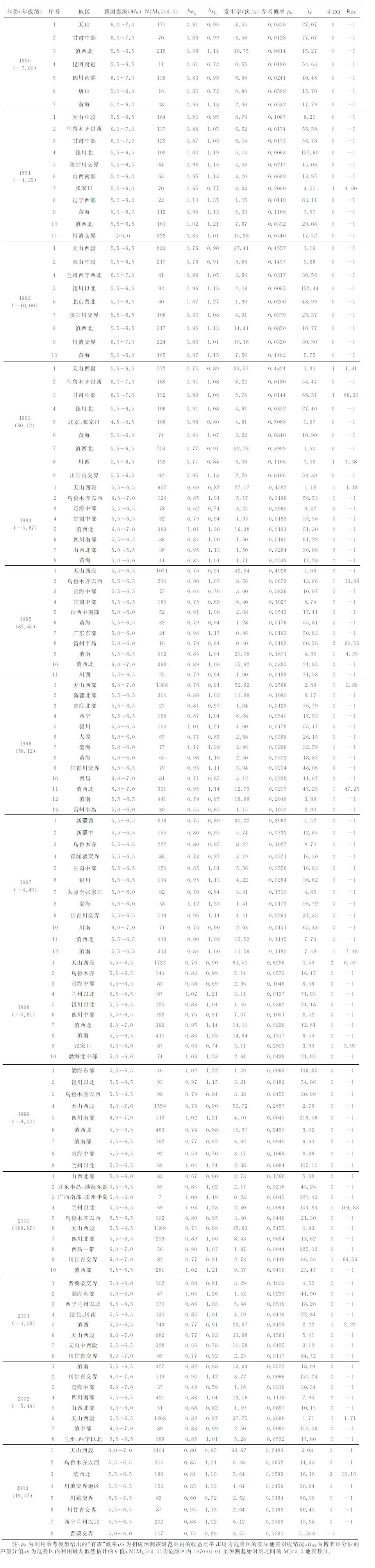
表 1 1990—2003年中国大陆年度地震危险区的博弈评分情况 Table 1 The gambling scores for each CEA prediction in the period of 1990—2003 |
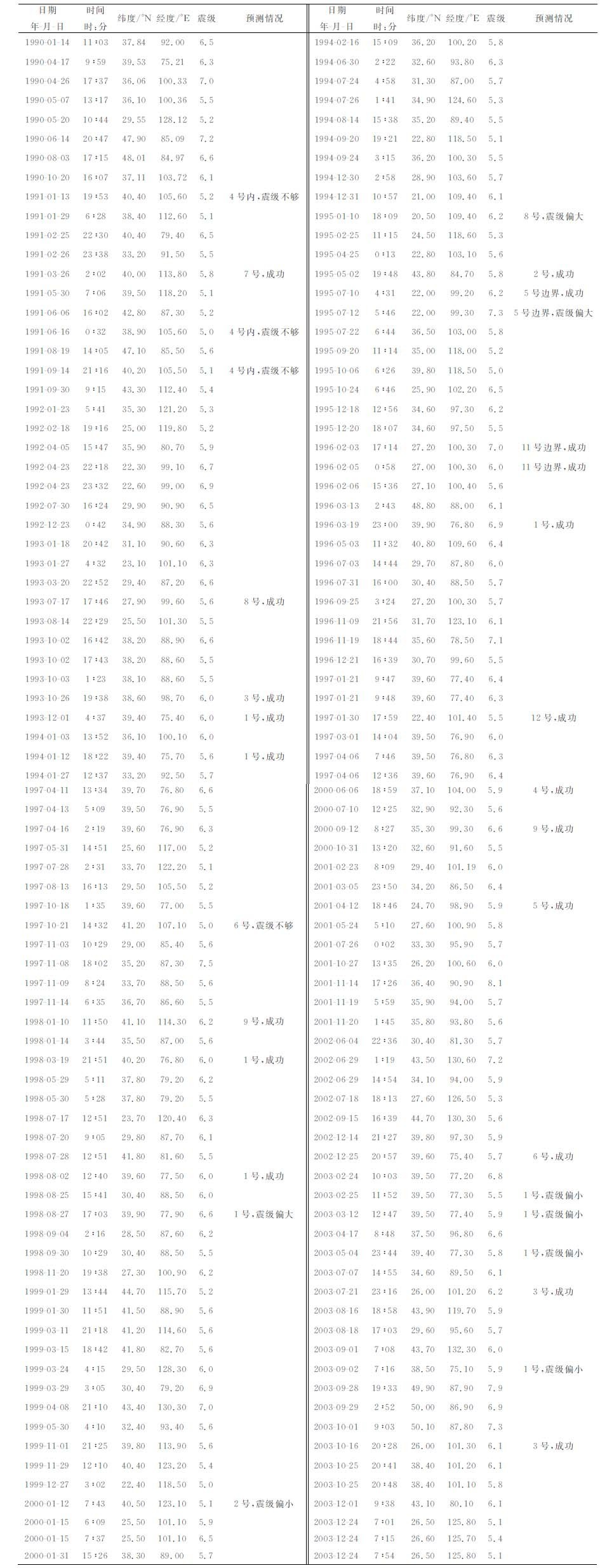
在参考模型计算时使用了中国地震台网中心提供的1970年以来ML3.5 以上地震的《中国地震月报目录》(http://www.csndmc.ac.cn/newweb/data.htm),该目录根据国家台网和各区域台网测定资料汇编而成,震级单位统一为地方震震级ML. 由于年度危险区预测效能评价是针对MS5.0 以上的中强地震,因此,本研究还采用了中国历史强震目录[33-34]和由中国地震台网中心提供的1991年1月1日至今的《中国大震速报目录》,用于确认预测与实际地震的对应情况. 表 2 列出1990—2003 年间《中国大震速报目录》所记录的中国大陆地区的MS5.0以上的所有中强地震.
3.2 参考模型的选取和参考概率的计算如前所述,博弈评分法的关键是根据参照模型求取的每个危险区内发震的参照概率. 这里选取时间上稳态空间上非均匀的泊松模型作为参照模型.
我们用
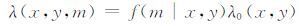
|
(2) |
来表示在地点(x,y)处震级为m的地震的发生率,也就是非均匀泊松参考模型的强度函数. 式中

|
是用概率密度函数的形式来表示的古登堡-里克特定律. 同时假定b值是地点的函数,而λ0(x,y)为所有m0 级以上地震的发生率. 在某区域B中发生震级在m1 到m2 之间地震的参考概率为

|
(3) |
其中T为预测时间段的长度. 将λ0(x,y)在区域S 上进行积分,可以得到S内地震发生率

|
设b在S内为常数b(S),p0(S,m1,m2) 可简化为
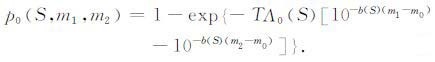
|
(4) |
区域S内的发生率Λ0 可以通过最大似然法进行估计,即

|
(5) |
其中T0 为地震目录起始时刻到预测时段的起始时刻之间的时间段. b值的最大似然估计为
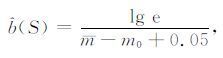
|
(6) |
其中m为时空窗S×T0 内ML3.5以上所有地震的平均震级. 在式(6) 中用m0 -0.05来代替震级下限m0 是为了消除对震级四舍五入到一位小数所带来的影响. 由此,预测区域S内在T时段内发生震级[m1,m2]的地震所对应的收益比为
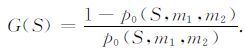
|
(7) |
在进行博弈评分时,首先由公式(4) 和(7) 分别计算参考概率p0 和有震预测收益比G,根据设定的“博弈”标准,以及对预测的时、空、强条件下实际地震发生情况的统计结果计算声望分值RGS.
在以上具体计算过程中,因为构筑参考模型使用的是以ML 为震级单位的全国地震目录,其中m0为3.5,而危险区的预测震级是以MS 为单位的,所以要做一些转换. 本研究采用了汪素云[35]最新的震级转换公式
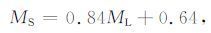
|
(8) |
由此,在MS 和ML 之间b值的关系为
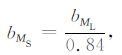
|
(9) |
而ML3.5对应的MS 震级下限为MS0=3.58. 而式(4) 相应变为
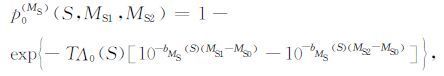
|
(10) |
即在区域S内发生面波震级MS1和MS2之间的地震的概率.
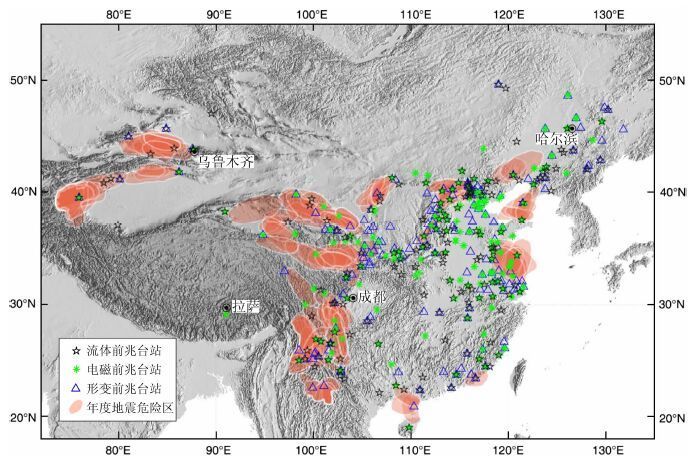
构建参考模型过程中,本研究未使用与前兆观测有关的信息. 为考察年度地震危险区划定与前兆观测可能的空间依赖关系,图 2 给出了年度地震危险区与前兆观测台站的分布图.2000年前后前兆台网“九五”数字化改造之前,中国大陆地震前兆观测主要包括流体、电磁和形变(包括重力)学科,且台站基本为模拟观测. 尽管2000—2003年期间前兆台站数量已有所增加,但由于仅为定性讨论,图 2仅给出了同时期前兆模拟台站的分布. 由图可见,一方面,各年度地震危险区本身存在较大重合,前兆台站东西部分布不均衡;另一方面,尽管东部地区的年度地震危险区周围和内部前兆台站分布较多,但年度危险区数量较多的西部地区则整体偏少. 因此,有相当数量的年度地震危险区的划定将主要依赖于地震活动分析,尽管本研究在计算参考概率时仅使用了地震发生率,但仍可较好反映大多数危险区的预测效能.
|
图 2 1990—2003年中国大陆年度地震危险区和同时期前兆台站分布 Fig. 2 The distributions of the alarmed regions and the precursor monitoring stations in the period 1990 to 2003 |
利用公式(4) 、(7) 分别计算每年度内各个地震危险区对应的参考概率p0 和预测震级范围[m1,m2]内的收益比率G,根据各个危险区的实际地震对应情况计算(参见表 2) 最终的声望分值RGS,相关结果如表 1所示. 表 1 中还列出了各危险区内的实际地震对应情况、b值和1970-01-01 至预测起始时刻之间的≥3.5级地震数目.
|
|
表 2 中国大陆1990—2003年期间Ms5.0以上地震列表 Table 2 A list of Ms≥5. 0 earthquakes in the Chinese Mainland |
从表 1中可以看出,年度地震危险区预测的总成绩往往由一些成功预测的个案决定. 例如,2000年第4号、1996年第11 号、2000 年第2 号和1993 年第3号危险区,是在地震活动水平很低(参考概率低于5%)的地区做出的成功预测,这些成功预测决定了当年的年成绩,也决定了年度会商的总成绩.
图 3给出了1990—2003 年度地震危险区预测的年度成绩的时间演化情况. 从年度总成绩来看,不同年度之间的预测效果差异很大,但中国大陆年度地震危险区的预测明显优于作为参考模型的非均匀泊松模型. 预测效果最好的三年是2000、1995 和1996年,分别为114.81、55.65 和41.28,而1990、1992和1999年则是负分,说明这三年的预测表现低于非均匀泊松模型.
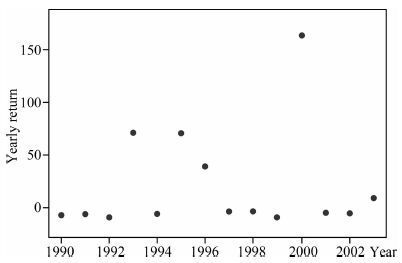
|
图 3 中国年度地震危险区预测的博弈评分年度成绩 Fig. 3 The yearly reputation return of the CEA predictions |
在以上结果中,总评分主要由几次低参考概率事件的成功预测所决定. 因此,参考概率的精度是影响博弈评分的关键. 由3.2节中的分析可以看出,影响参考概率的计算数值主要有以下两个因素:(1) 地震发生率的估计值及其误差,和(2) b值的估计值及其误差. 在本文中,地震发生率和b值均采用了最大似然估计. 根据最大似然估计的统计理论,
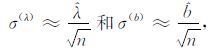
|
其中n为估计λ 或b值所用的地震数目. 为了估计以上因素对最终评分的影响,可以采用以下的模拟算法.
(1) 对于每一个危险区i,分别以
(2) 对于每一个i,生成以ΛiTi和(Λi×1年)为均值的两个服从泊松分布的随机数,记为N1 和N2,其中Ti为估计第i个危险区的发生率所用的地震目录的时间跨度.
(3) 对于每一个i,生成两个以Bi为参数,3.5 为下限值的指数分布的随机数组,其长度分别为N1 和N2.
(4) 对于每一个i,根据第一个指数分布的随机数组,按照本节中的分析方法,重新估计地震发生率和b值,然后计算参考概率和成功回报率.
(5) 对于每一个i,如果第二个数组中含符合第i个危险区所预测的地震,则此预报的评分为成功回报率,否则为-1.
(6) 记下所有危险区预测的总评分.
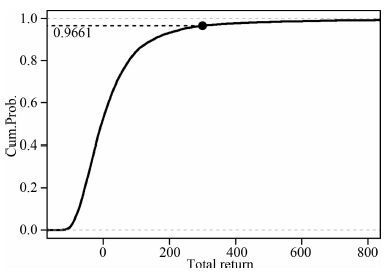
重复以上步骤很多次,得到总评分的随机分布,其累积概率分布函数如图 4所示. 从图中可以看出,年度会商的最终得分位于最上端的5%之内(96.61%),可见年度会商预测结果的显著性是明显的.
|
图 4 中国年度地震危险区预测的总博弈评分在随机情况下的累计概率曲线 Fig. 4 The cumulative probability function of the total reputation return for the CEA predictions under random conditions |
从理论上说,年度会商的预测的判据主要来源于两个部分,一是以往地震的平均活动水平,二是前兆异常信息. 在本研究中,地震活动的平均水平已经包含在参考模型中了,因此博弈评分法估算的是年度危险区预测中有多少地震活动背景知识之外的前兆信息. 当然,参考模型也可能含有预测所不具备的优点,但是对于本研究中这种只考虑有震预测的预设条件,博弈评分法是不计入参考模型的这些优点的.
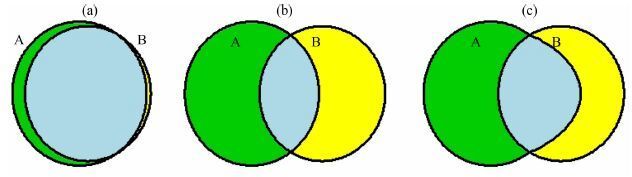
在此意义上,本文的分析和石耀霖等[6]有所不同. 石耀霖等[6]为了和非均匀泊松模型作对比,在保持年度危险区空间网格总数不变的情况下,按照和每个方格内地震活动强度成正比的机率随机生成新的危险区并进行R值评分. 年度会商结果和由非均匀泊松模型随机分配产生的预测的R值分别为0.184和0.150,由此认为年度会商结果只是略好于非均匀泊松模型. 实际上,两个R值分数之差(0.034) 不仅仅包含了年度会商预测中优于非均匀泊松模型的地方,同时也减掉了非均匀泊松模型优于会商结果的地方. 如图 5所示,如果A 和B 分别代表了会商结果和非均匀泊松模型优于均匀泊松模型的信息增益,本研究的博弈评分计算的是A 中不同于B的部分(绿色),而石耀霖等[6]给出的两个R值之差(0.034) 则为A 和B的面积之差. 由此可见,R值评分给出的年度会商预测的评分相对于非均匀泊松模型优势不明显的原因有以下两种:模式a,年度会商预测主要基于地震活动的背景知识产生,包含非常有限的前兆信息,如图 5a所示;模式b,年度会商预测含有非常少的地震活动的背景知识,但是所含有的前兆信息量和非均匀泊松模型超过非均匀泊松模型的信息量差别不大,如图 5b所示. 在表 1 列出的133个预测中,有10个成功预测(宽松标准)对应的参考概率小于10%,12个成功预测则大于10%,这说明模式b成立的可能性更大. 这一结论也可以从图 2中得到验证:历年的危险区多划在前兆观测台站密集地区附近. 由此可见,提高年度会商预测相对于非均匀泊松模型的R值评分的一个直接办法就是在会商结果中整合地震活动强度在空间上的分布,其原理如图 5c所示.
|
图 5 年度地震危险区预测和非均匀泊松模型的关系 (a)模式a;(b)模式b;(c)提高预测效果的方法之一. Fig. 5 An illustration of the relation between the R scores for the CEA annual predictions and the inhomogeneous Poisson model (a) Type a; (b) Type b; (c) A method for improving the R score of the CEA annual predictions. A and B represents,respectively, the R scores for the CEA predictions and the inhomogeneous Poisson model against the homogeneous Poisson model. |
此外,随机非均匀泊松模型的构建也导致了年度危险区预测R值评分不高. 由于年度危险区预测每年给出的空间网格总数不同,说明其认为地震活动在时间上是非稳态的. 石耀霖等[6]保持每年的危险区空间网格总数不变的条件下,随机创建危险区,相当于使用了非稳态的参考模型,也就是参考模型含有年度会商预测的以“年”为尺度的时间信息. 而在本文的博弈评分过程中,作为参考模型(零模型)的稳态非均匀泊松模型是显式给出的.
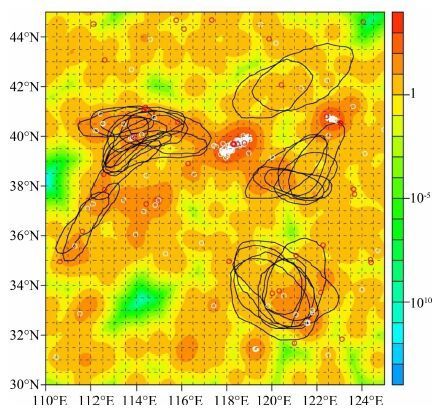
图 6给出了以华北地区为例的1990—2003 年间地震发生率与各年度地震危险区叠加情况. 由图可见,危险区覆盖了相当数目的0.5°×0.5°的网格,并形成一个连通区域. 随机生成危险区破坏了各个危险区内网格的连通性,大的危险区会被分割为多个小的网格. 如果某个危险区既包含了地震活跃区也包含了地震活动水平低的地区,重新分配时,高活动水平地区的网格很可能停留在原处,而低活动水平地区的网格则很可能分配到西部高活动水平地区,命中那里的5~6级地震并在统一考虑5级以上地震的情况下获得评分. 在年度会商中西部是不考虑5~5.5级的地震的,而在石耀霖等[6]的检验中,5 级以上的地震是整个范围内统一考虑的. 更为合理的可能的随机化检验的方法是,保持每个危险区的形状和大小不变,重新分配各个危险区的位置、主轴方向和所在的预测年度,分配的几率应该与每个危险区重定位后所覆盖的总体地震活动强度成正比,同时要求每年度的危险区不能重叠. 尽管这种模拟可通过马尔柯夫链蒙特卡罗方法(NarkovChain NonteCarlo)来实现,但技术上较为繁琐.
|
图 6 以华北地区为例的地震发生率与各年度地震危 险区叠加情况.图中的等值面给出了 1970—1989年以 来ML≥3. 5以上的地震发生率(/24a. deg2)计算中使 用了宽度0. 25°的核函数进行平滑,1989年前后的M4. 0 以上地震在图中分别用白色和红色空心圆表示 Fig. 6 Seimicity rates of earthquakes (ML≥3. 5, unit:events/ (24 a • deg2 ) during the time period from the beginning of 1966 to the end of 1989 in North China, obtained by smoothing seismicity of ML ≥3.5 events from 1966 to 1989 using kernel functions of bandwidth 0. 25 degree. Earthquakes of ML ≥4 0 before and after the end of 1989 were plotted in white and red circles,respectively |
为了简单起见,本研究把空白区简单处理为没有预测意见,预测者没有抵押声望点. 如果把这个作为抵押为1点的无震预测(东部5级以上,西部5.5 级以上),由于每年都会有2 到10 个5 级以上的地震发生在空白区内,用平均值为3 的泊松分布来作为非危险区上发生的地震数目(漏报地震数),那么无震预测失败的参考概率是1-exp(-3) =0.95,对应的预测预报回报比为19. 但如果把空白区无震预测的抵押声望值设为1,应该从每年的成绩里扣除1点,这对整体评分影响不大.
4.3 地震丛集的删除和保留在计算地震活动强度时,本研究未删除余震和前震. 不可否认,地震活动背景应该通过删除丛集后的地震目录来求取,而不是用整体地震活动强度. 但无论如何删除丛集,所得到的背景活动强度总是小于整体活动强度的. 对于有震预测而言,由背景活动强度给出的参考概率要低,也就是回报比变高. 因为年度会商结果给出的都是有震预测,删除丛集带来的效果是给出更高的博弈评分,所以使用整体活动强度为参考模型会压低年度会商预测的评分,正面的评分也就更为可信.
5 结论博弈评分法通过补偿成功预测所承受的风险来进行评分. 这一方法灵活易用,适合应用于像年度会商预测这种预测区不规则、震级范围不定、只有有震预测的预测. 本文把非均匀的稳态泊松模型作为参照模型,利用博弈评分检验了1990—2003年度中国大陆地震危险区预测结果的统计显著性. 结果表明,尽管各年度之间的预测评分差异很大,但1990-2003年的预测结果中明显含有优于非均匀泊松模型的成分. 由此可确定,中国的年度地震趋势会商给出的中国大陆地震危险区预测所依据的地震活动和其他前兆观测异常信息能够对地震预报所起到正面作用. 进一步分析还发现,年度危险区预测R值评分相对于非均匀泊松模型高出不多的原因是,年度会商结果在前兆观测资料和地震活动背景空间分布知识之间的整合不足,这可能是将来提高年度会商预测效能所需要关注的重点之一.
致谢研究过程中得到了吴忠良研究员的指导,刘杰研究员、李纲、晏锐等专家对本文提出诸多有益建议,作者谨表谢意.
| [1] | 孙其政, 吴书贵. 中国地震监测预报40年. 北京: 地震出版社, 2007 : 62 -63. Sun Q Z, Wu S G. China Earthquake Monitoring and Prediction 40 Years (in Chinese) (in Chinese). Beijing: Seismological Press, 2007 : 62 -63. |
| [2] | Wu F T. The annual earthquake prediction conference in China (National consultative meeting on seismic tendency). Pure Appl. Geophys. , 1997, 149(1): 249-264. DOI:10.1007/BF00945170 |
| [3] | Wu Z L, Liu J, Zhu C Z, et al. Annual consultation on the likelihood of earthquakes in continental China: Its scientific and practical merits. Earthquake Research in China , 2007, 21(4): 365-371. |
| [4] | 朱令人, 朱成熹, 洪时中等. 地震预报效能评价. // 国家地震局科技监测司. 中国地震预报方法研究. 北京: 地震出版社, 1991: 35-45. Zhu L R, Zhu C X, Hong S Z, et al. Evaluation of earthquake prediction. // Department of Science, Technology, and Monitoring, State Seismological Bureau ed. Study on Earthquake Prediction Method (in Chinese). Beijing: Seismological Press, 1991: 35-45. |
| [5] | 郑兆苾, 刘杰, 李罡风, 等. 全国年度地震重点危险区与地震相关性的统计模拟分析. 地震学报 , 2000, 13(5): 575–584. Zheng Z B, Liu J, Li G F, et al. Statistical simulation analysis of the correlation between the annual estimated key regions with a certain seismic risk and the earthquakes in China. Acta Seismologica Sinica (in Chinese) (in Chinese) , 2000, 13(5): 575-584. DOI:10.1007/s11589-000-0057-0 |
| [6] | 石耀霖, 刘杰, 张国民. 对我国90年代年度地震预报的评估. 中国科学院研究生院学报 , 2000, 17(1): 63–69. Shi Y L, Liu J, Zhang G M. The evaluation of Chinese annual earthquake prediction in the 90s. Journal of the Graduate School of the Chinese Academy of Sciences (in Chinese) (in Chinese) , 2000, 17(1): 63-69. |
| [7] | 张国民, 刘杰, 石耀霖. 年度地震预报能力的科学评价. 地震学报 , 2002, 15(5): 550–558. Zhang G M, Liu J, Shi Y L. An scientific evaluation of annual earthquake prediction ability. Acta Seismologica Sinica (in Chinese) (in Chinese) , 2002, 15(5): 550-558. DOI:10.1007/s11589-002-0024-z |
| [8] | 许绍燮. 地震预报能力评分. // 国家地震局科技监测司编. 地震预报方法实用化攻关文集(测震分册). 北京: 地震出版社, 1989: 586-589. Xu S X. The evaluation of earthquake prediction ability. // Department of Science, Technology and Monitoring, State. Seismological Bureau ed. The Practical Research Papers on Earthquake Prediction Methods (Seismicity Section) (in Chinese). Beijing: Seismological Press, 1989: 586-589. |
| [9] | 史勇军, 吴忠良, 白玲. 用皮尔逊检验分析年度地震趋势预测效果. 中国科学院研究生院学报 , 2004, 21(2): 248–253. Shi Y J, Wu Z L, Bai L. Evaluation of annual prediction of seismicity tendency using pearson test. Journal of the Graduate School of the Chinese Academy of Sciences (in Chinese) (in Chinese) , 2004, 21(2): 248-253. |
| [10] | Zhuang J C. Gambling scores for earthquake predictions and forecasts. Geophys. J. Int. , 2010, 181(1): 382-390. DOI:10.1111/gji.2010.181.issue-1 |
| [11] | Harte D, Vere-Jones D. The entropy score and its uses in earthquake forecasting. Pure Appl. Geophys. , 2005, 162(6): 1229-1253. |
| [12] | Rundle J B, Klein W, Turcotte D L, et al. Precursory seismic activation and critical-point phenomena. Pure Appl. Geophys. , 2000, 157(11-12): 2165-2182. |
| [13] | Rundle J B, Turcotte D L, Shcherbakov R, et al. Statistical physics approach to understanding the multiscale dynamics of earthquake fault systems. Rev. Geophys. , 2003, 41: 1019. DOI:10.1029/2003RG000135 |
| [14] | 蒋长胜, 吴忠良. 对地震预测的一个统计物理算法在川滇地区的回溯性预测检验. 中国科学: D辑 , 2008, 51(10): 1401–1410. Jiang C S, Wu Z L. Retrospective forecasting test of a statistical physics model for earthquakes in Sichuan-Yunnan region. Science in China Series D: Earth Sciences (in Chinese) (in Chinese) , 2008, 51(10): 1401-1410. DOI:10.1007/s11430-008-0112-6 |
| [15] | Zechar J D, Zhuang J C. Risk and return: evaluating reverse tracing of precursors earthquake predictions. Geophys. J. Int. , 2010, 182: 1319-1326. DOI:10.1111/j.1365-246X.2010.04666.x |
| [16] | Shebalin P, Keilis-Borok V, Zaliapin I, et al. Advance short-term prediction of the large Tokachi-oki earthquake, September 25, 2003, M=8.1:A case history. Earth Planets Space , 2004, 56: 715-724. DOI:10.1186/BF03353080 |
| [17] | Shebalin P, Zaliapin I, Keilis-Borok V I. Premonitory rise of the earthquake's correlation range: Lesser Antilles. Phys. Earth Planet. Inter. , 2000, 122: 241-249. DOI:10.1016/S0031-9201(00)00180-1 |
| [18] | Molchan G, Romashkova L. Gambling score in earthquake prediction analysis. Geophys. J. Int. , 2011, 184(3): 1445-1454. DOI:10.1111/gji.2011.184.issue-3 |
| [19] | 国家地震局分析预报中心. 中国地震趋势预测研究(1990年度). 北京: 地震出版社, 1989. Center for Analysis and Prediction, State Seismology Bureau. China Earthquake Administration. Study on the Seismic Tendency in China (for the year 1990) (in Chinese). Beijing: Seismological Press, 1989. |
| [20] | 国家地震局分析预报中心. 中国地震趋势预测研究(1991年度). 北京: 地震出版社, 1990. Center for Analysis and Prediction, State Seismology Bureau. Study on the Seismic Tendency in China (for the year 1991) (in Chinese). Beijing: Seismological Press, 1990. |
| [21] | 国家地震局分析预报中心. 中国地震趋势预测研究(1992年度). 北京: 地震出版社, 1991. Center for Analysis and Prediction, State Seismology Bureau. Study on the Seismic Tendency in China (for the year 1992) (in Chinese). Beijing: Seismological Press, 1991. |
| [22] | 国家地震局分析预报中心. 中国地震趋势预测研究(1993年度). 北京: 地震出版社, 1992. Center for Analysis and Prediction, State Seismology Bureau. Study on the Seismic Tendency in China (for the year 1993) (in Chinese). Beijing: Seismological Press, 1992. |
| [23] | 国家地震局分析预报中心. 中国地震趋势预测研究(1994年度). 北京: 地震出版社, 1993. Center for Analysis and Prediction, State Seismology Bureau. Study on the Seismic Tendency in China (for the year 1994) (in Chinese). Beijing: Seismological Press, 1993. |
| [24] | 国家地震局分析预报中心. 中国地震趋势预测研究(1995年度). 北京: 地震出版社, 1994. Center for Analysis and Prediction, State Seismology Bureau. Study on the Seismic Tendency in China (for the year 1995) (in Chinese). Beijing: Seismological Press, 1994. |
| [25] | 国家地震局分析预报中心. 中国地震趋势预测研究(1996年度). 北京: 地震出版社, 1995. Center for Analysis and Prediction, State Seismology Bureau. Study on the Seismic Tendency in China (for the year 1996) (in Chinese). Beijing: Seismological Press, 1995. |
| [26] | 国家地震局分析预报中心. 中国地震趋势预测研究(1997年度). 北京: 地震出版社, 1996. Center for Analysis and Prediction, State Seismology Bureau. Study on the Seismic Tendency in China (for the year 1997) (in Chinese). Beijing: Seismological Press, 1996. |
| [27] | 国家地震局分析预报中心. 中国地震趋势预测研究(1998年度). 北京: 地震出版社, 1997. Center for Analysis and Prediction, State Seismology Bureau. Study on the Seismic Tendency in China (for the year 1998) (in Chinese). Beijing: Seismological Press, 1997. |
| [28] | 中国地震局分析预报中心. 中国地震趋势预测研究(1999年度). 北京: 地震出版社, 1998. Center for Analysis and Prediction, China Earthquake Administration. Study on the Seismic Tendency in China (for the year 1999) (in Chinese). Beijing: Seismological Press, 1998. |
| [29] | 中国地震局分析预报中心. 中国地震趋势预测研究(2000年度). 北京: 地震出版社, 1999. Center for Analysis and Prediction, China Earthquake Administration. Study on the Seismic Tendency in China (for the year 2000) (in Chinese). Beijing: Seismological Press, 1999. |
| [30] | 中国地震局分析预报中心. 中国地震趋势预测研究(2001年度). 北京: 地震出版社, 2000. Center for Analysis and Prediction, China Earthquake Administration. Study on the Seismic Tendency in China (for the year 2001) (in Chinese). Beijing: Seismological Press, 2000. |
| [31] | 中国地震局分析预报中心. 中国地震趋势预测研究(2002年度). 北京: 地震出版社, 2001. Center for Analysis and Prediction, China Earthquake Administration. Study on the Seismic Tendency in China (for the year 2002) (in Chinese). Beijing: Seismological Press, 2001. |
| [32] | 中国地震局分析预报中心编. 中国地震趋势预测研究(2003年度). 北京: 地震出版社, 2002. Center for Analysis and Prediction, China Earthquake Administration. Study on the Seismic Tendency in China (for the year 2003) (in Chinese). Beijing: Seismological Press, 2002. |
| [33] | 国家地震局震害防御司. 中国历史强震目录(公元前23世纪—公元1911年). 北京: 地震出版社, 1995. Department of Earthquake Disaster Prevention, State Seismological Bureau. The Catalogue of Chinese Historical Strong Earthquakes (in Chinese). Beijing: Seismological Press, 1995. |
| [34] | 中国地震局震害防御司. 中国近代地震目录(公元1912—1990 MS≥4.7). 北京: 中国科学技术出版社, 1999. Department of Earthquake Disaster Prevention, China Earthquake Administration. The Catalogue of Chinese Modern Earthquakes (in Chinese). Beijing: China Science and Technology Press, 1999. |
| [35] | 汪素云, 高阿甲, 冯义钧, 等. 中国地震目录间的对比及标准化. 地震 , 2010, 30(2): 38–45. Wang S Y, Gao A J, Feng Y J, et al. Comparison and standardization of the Chinese earthquake catalogs. Earthquake (in Chinese) (in Chinese) , 2010, 30(2): 38-45. |
 2012, Vol. 55
2012, Vol. 55