2. Kochi Institute for Core Sample Research, Japan Agency for Marine-Earth Science and Technology (JAMSTEC), Nankoku, 783-8502, Japan;
3. 中国地质科学院地质研究所, 北京 100037;
4. 中国地质大学(北京)数理学院, 北京 100083
2. Kochi Institute for Core Sample Research, Japan Agency for Marine-Earth Science and Technology (JAMSTEC), Nankoku, 783-8502, Japan;
3. Institute of Geology, Chinese Academy of Geological Sciences, Beijing 100037, China;
4. School of Science, China University of Geosciences (Beijing), Beijing 100083, China
随着大陆动力学和地震科学研究的深入开展,特别是汶川5. 12大地震后,深部应力状态的研究愈来愈重要. 但目前尚没有既经济又简便的完善的深部地应力测量方法. 基于岩芯的非弹性应变恢复法(Anelastic Strain Recovery Nethod,简称ASR 法) 是近年来发展起来的深部应力测量的一种有效方法,它与钻孔崩落法、水压致裂法联合使用,可获得更丰富的地应力资料. 当钻孔崩落法和水压致裂法等不能使用时,ASR 法仍有可能得到比较可靠的资料,具有更广泛的适用性.
ASR 法首先由Voight[1]提出,并由Teufel[2]进行了一些实用性研究和进一步的发展. 但他们考虑的是二维问题. Natsuki[3]将其发展为三维问题. 近年来,ASR 法逐渐被应用于实际的深部三维地应力测量中[4-6]. 汶川5. 12 大地震后,我们将ASR 法应用于汶川地震断裂带科学钻的地应力测量. 这是我国大陆首次使用该方法进行的深部三维地应力测量.
本文对ASR 法的原理和计算方法进行了概述,并给出了汶川地震断裂带科学钻一号孔(Wenchuan Earthquake Fault Scientific Drilling Project, Hole-1,简称为WFSD-1) 的地应力测量典型结果.
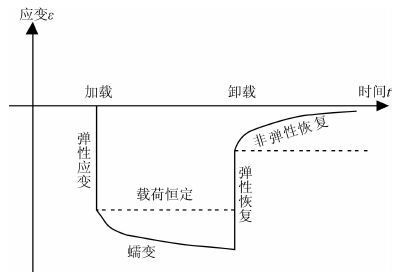
2 ASR 法的原理岩芯被钻出后,即脱离应力场的作用,岩芯卸荷. 由于岩石的黏弹性特性,岩芯除了立即发生弹性应变恢复以外,还随时间发生非弹性(滞弹性)应变恢复,根据岩芯表面不同方向非弹性应变恢复量,可以确定三维原地应力状态. 其原理基于岩石的流变性. 岩石是一种黏弹性体,具有流变性[7-8]. 当岩石施加载荷时,岩石立即产生弹性变形,然后产生蠕变. 当载荷去掉时,岩石变形立即发生弹性恢复,而后,随着时间的增加,非弹性应变慢慢恢复如图 1. 非弹性应变的恢复量与卸载之前的载荷量有关. 因而可以由岩芯的非弹性恢复量反演原地应力.
|
图 1 岩石流变性的模式图 Fig. 1 A schematic diagram of rock rheological property |
岩芯脱离应力场作用后,应变立即恢复,但岩芯由钻井深处到地面,再到井口实验室要一定时间,因而测量不能立即开始,而是滞后一段时间,一部分恢复量丢失. 然而,ASR法不要求测量非弹性应变恢复的全过程,只需一部分即可进行地应力的换算[5, 9]. 但是,为了保证精度,要求尽可能快地开始测量,捕捉更多的恢复量. 并使用稳定性好,精度高的仪器.
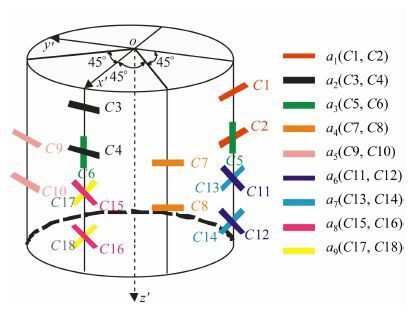
3 ASR 法应变计的布置由钻孔中取出的带有定向标志线的岩芯(长度约15cm),经清洗后,将应变计粘贴在岩芯表面. 沿基线(x′轴)以及与基线相隔45°、90°和-45°(顺时针方向为负)线粘贴应变计,共有18 个应变计,即C1,C2,…,C18,如图 2.
应变计长轴方向称为应变计的轴向. 共有9 个轴向,即由轴a1 到轴a9. 每个轴向有两个应变计,如轴向a1 的应变计为C1及C2.
|
图 2 岩芯表面应变计的布置 Fig. 2 The layout of strain gauges on the surface of a rock core |
9个轴向与坐标轴的关系为:轴a1 与x′轴平行,与y′,z′ 轴垂直;轴a2 与y′ 轴平行,与x′,z′ 轴垂直;轴a3 与z′轴平行,与x′,y′轴垂直;轴a4 与x′,y′ 轴斜交成45°;轴a5 与x′,y′ 轴斜交成正负45°,与z′ 轴垂直;轴a6,轴a7 与x′,z′轴斜交成45°,与y′ 轴垂直;轴a8,轴a9 与y′,z′轴斜交成45°,与x′轴垂直.
4 岩芯应变观测值与岩芯坐标系中应变分量的关系设岩芯坐标系为o-x′y′z′,z′轴与岩芯长轴平行(图 2) . 应变观测值b与岩芯坐标系中应变分量ε′x,ε′y,ε′z,ε′xy,ε′yz,ε′zx的关系式如下[8, 10]:
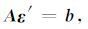
|
(1) |
式中:[ε′ = ε′x,ε′y,ε′z,ε′xy,ε′yz,ε′ zx ]T 为岩芯坐标系中的应变分量;b= [b1,b2,b3,b4,b5,b6,b7,b8,b9]T 为岩芯非弹性(滞弹性)应变恢复观测值. b1 为轴a1 的应变观测值,即与轴a1 对应的两个应变计的平均值;b2 为轴a2 的应变观测值,即与轴a2 对应的两个应变计的平均值;以此类推,直到b9. A为系数矩阵. A的展开式如下:
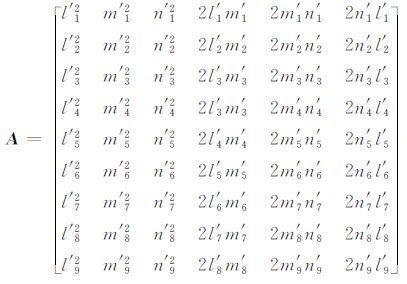
|
(2) |
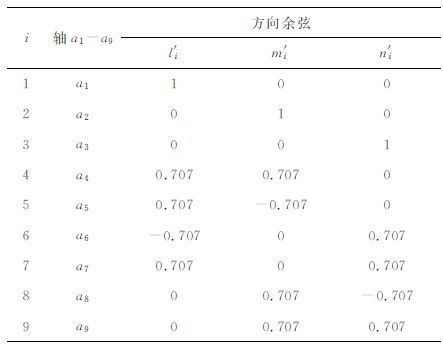
l′i,m′i,n′i(i=1,…,9) 是轴a1 到轴a9 相对o-x′y′z′轴的方向余弦. 由图 2可知,方向余弦的具体数值如表 1所示.
将表 1中的方向余弦数值代入式(2) ,可得:

|
(3) |
|
|
表 1 方向余弦 Table 1 方向余弦 Cosine of direction |
方程组(1) 中的未知数n=6,而方程数m=9. 方程数m大于未知数n,这时可用最小二乘法进行求解,得出最可信的答案. 按最小二乘法原理,解下面的方程组可得最小二乘法解答[11]
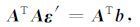
|
(4) |
(4) 式的解答如下:
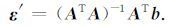
|
(5) |
设地理坐标系为o-xyz. x轴指向北,y轴指向东,z轴铅直向下. 因为岩芯坐标系是任意设定的,钻井(岩芯)有时是倾斜的,而且岩芯坐标系的o-x′轴的方位也不一定是向北的. 因此岩芯坐标系与地理坐标系通常是不重和的. 为了计算主应变(主应力)的方向、倾角和大小,需要将岩芯坐标系中的应变分量向地理坐标系转换. 坐标转换的表达式如下[8]:
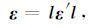
|
(6) |
其中
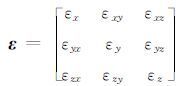
|
|
表 2 岩芯坐标轴与地理坐标轴的方向余弦 Table 2 Direction cosine between core coordinate axis and geographic coordinate axis |
知道了钻孔(岩芯)的倾向,倾角和岩芯坐标o-x′轴的方位则可以方便地求出方向余弦. 进而由方程(6) 得出地理坐标系中的应变张量ε.
7 主应变及主应力的计算 7. 1 主应变的计算由应变分量求主应变可通过解下列方程组得到[11]:
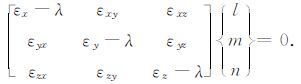
|
(7) |
上述方程组为齐次线性方程组,方程组非零解的必要和充分条件是系数行列式为零,即
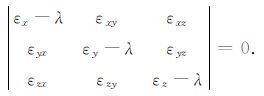
|
(8) |
行列式展开后为一元三次方程式. 解该方程式可得到三个根λ1,λ2,λ3,它们是三个主应变ε1,ε2,ε3. 将三个主应变逐个代回方程组(7) ,可求出三个主应变的方向余弦li,mi,ni(i=1,2,3) ,且li2 +mi2+ni2=1.
上述的求解实际是求应变分量矩阵的特征值及特征向量问题,特征值λi为主应变,特征向量为主应变的方向余弦. 主应变的方位和倾角可由方向余弦求得[9].
主应变εi(i= 1,2,3) 的方位角Di=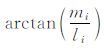
由非弹性应变计算主应力σi(i= 1,2,3) 的表达式如下[11]:
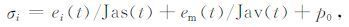
|
(9) |
式中ei(t)(i=1,2,3) 为非弹性偏应变,em(t)为非弹性体应变,Jas(t)为偏非弹性应变柔度,Jav(t) 为体积非弹性应变柔度,p0 为孔隙压力.
由(9) 式可以看出,只要求出Jas(t)及Jav(t),即可根据非弹性应变及孔隙压力求出三维地应力.
Jas(t)及Jav(t)可由实验得到,但这个实验比较复杂. 文献[5, 12]指出,可以近似地认为
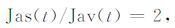
|
(10) |
于是铅直应力可表示为
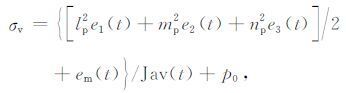
|
(11) |
式中,lp,mp,np 为铅直应力与三个应变主轴之间的方向余弦. 同时铅直应力可以按重力计算,

|
(12) |
如果已知测量的深度h,从地表到该深度的平均密度以及重力加速度g,则σv 可以由式(12) 得出,而由式(11) 可求出Jav(t),进而由式(10) 求出Jas(t),然后由式(9) 求出主应力σi(i=1,2,3) .
实际工作中,上述主应变和主应力的计算是通过专用软件进行的,是很方便的.
8 ASR 法的典型测量结果应用ASR 法在汶川地震断裂带科学钻探一号孔中进行了地应力测量,得到了满意的结果.
8. 1 汶川地震科学钻一号孔(WFSD-1) 的位置和地质简况汶川地震断裂带科学钻是汶川5. 12特大地震后快速反应的地震科学钻探工程项目(WFSD). 科学钻的一号孔(WFSD-1) 位于四川省都江堰市虹口镇,距5. 12地震震中约90km 如图 3. 与地表主断裂的水平距离约400m. 钻井深度1201m,(垂直孔深1179m)平均井斜11°,在589. 6m 深处穿过主断层. 地表至孔深176 m 为震旦系下统的变质火山岩,176~589. 2 m 为新元古代彭灌杂岩,589. 2 m 以下至终孔1201 m 为三叠系上统须家河组,主要为砂岩、砾岩、泥岩、页岩煤系地层. 孔深590 m 附近出现厚达70cm 的断层泥.

|
图 3 WFSD-1孔区地质简图 (a)平面图(据四川省1∶20万彭灌幅地质图编制);(b)剖面图. 1-三叠系上统须家河组上段;2- 三叠系上统须家河组中段;3-三叠系上统须家河组下段;4-三叠系下统;5-二叠系上统;6-二叠系下统;7-泥盆系上统;8- 泥盆系中统;9- 震旦系下统;10-元古代花岗岩;11- 逆冲断裂(a);12- 逆冲断裂(b);13-逆冲推覆体(a);14-飞来峰(b);15-钻孔;16-河流;17-道路;YBF-映秀—北川断裂. Fig. 3 Geological sketch map (a) of the WFSD-1 well site and tectonic profile (b) perpendicular to the YBF (a: compiled from the 1:200 000-scale Geologic Map of Sichuan Province,the Pengguan sheet) 1 - Upper member of Upper Triassic Xujiahe Formation; 2 -Middle member of Upper Triassic Xujiahe Formation; 3 -Lower member of Upper Triassic Xujiahe Formation; 4一Lower Triassic; 5 -Upper Permian; 6-Lower Permian; 7-Upper Devonian; 8一Middle Devonian; 9一Lower Sinian metavolcanite formation; 10一Proterozoic granite; 11 一Thrust fault (a) ; 12-Thrust fault (b) ; 13 -Thrust-nappe (a) ; 14-Klippe (b) ; 15-Borehole; 16-River; 17-Road; YBF-Yingxiu-Beichuan fault. |
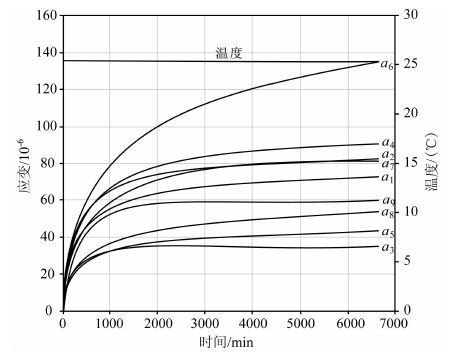
取自孔深746m(垂深)处的岩芯非弹性应变恢复曲线如图 4. 连续测量约5天. 测量期间温度变化小于±0. 1 ℃,测量结果显示,测量系统的漂移很小,可以忽略. 各个应变计的非弹性应变皆为拉张,说明原地的岩石承受着压应力. 曲线随时间平稳增加,初期非弹性应变增加较快,然后变缓,符合非弹性应变变化规律. 应变量达100多微应变,可满足测量的要求.
|
图 4 非弹性应变恢复曲线 (曲线编号与图 2相同) Fig. 4 Anelastic strain recovery curves |
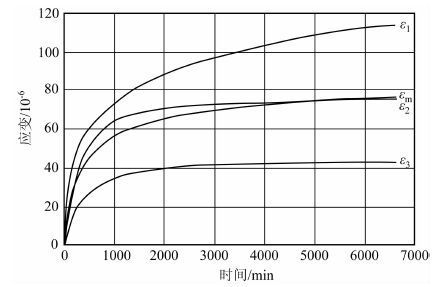
由9个方向的应变观测曲线使用前面叙述的最小二乘法并进行岩芯坐标轴的方位及井斜的校正后计算出三个主应变εi和平均主应变εm 如图 5. 三个非弹性主应变的方位和倾角如表 3. 如上所述,在均匀各向同性介质中,主应变的方位与主应力的方位是一样的. 因而,此主应变的方位也就是主应力的方位.
|
|
表 3 主应变(主应力)的方位和倾角 Table 3 Azimuth and dip angle of principal anelastic strain (principal stress) |
|
图 5 非弹性主应变曲线 Fig. 5 Anelastic principal strain recovery |
最大主应力σ1 和中间主应力σ2 近于水平,最小主应力σ3 近于铅直. 最大主应力σ1 的方位为北西49°. 这种应力状态可使龙门山断层产生逆冲兼右行走滑运动.
8. 4 应力的大小假定铅直应力等于上覆岩层的重量,则可用前面叙述的方法,近似计算主应力的大小. 根据上覆岩层的平均密度为2. 6g/cm3,得出三个主应力的大小分别为25. 2 NPa,21. 5 NPa,18. 5 NPa;铅直应力为19. 1NPa,水平最大主应力为25NPa,水平最小主应力为21. 1NPa.
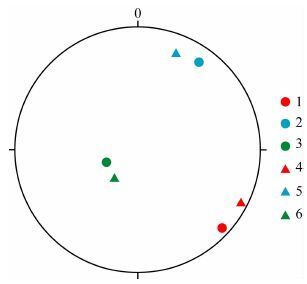
8. 5 与其他方法得到的结果的比较将汶川5. 12MS8. 0级地震的震源机制解主轴的方位如表 4[13],和WFSD-1的垂深746m 的ASR 结果画在同一个图上如图 6. 图中实心圆为ASR 测量结果,三角形为震源机制解主轴. 由表 3,表 4和图 6可见,ASR 测量得到的主应力σ1,σ2,σ3 的方位分别与P轴,T轴和B轴方位对应. 它们的方位和倾角都很接近.
|
图 6 ASR法得到的主应力与震源机制解主轴方位和倾角的对比 1-σ1;2-σ2;3-σ3;4-P轴;5-T轴;6-B轴 Fig. 6 Azimuth and dip angle of principal stress by ASR and principal axis of focal mechanism solutions 1-σ1;2-σ2;3-σ3;4-Axis P ; 5-Axis T ; 6-Axis B. |
|
|
表 4 2008年5月12日汶川Ms8. 0地震震源机制解[13] Table 4 Focal mechanism solutions for the Wenchuan earthquake of May 12,2008[13] |
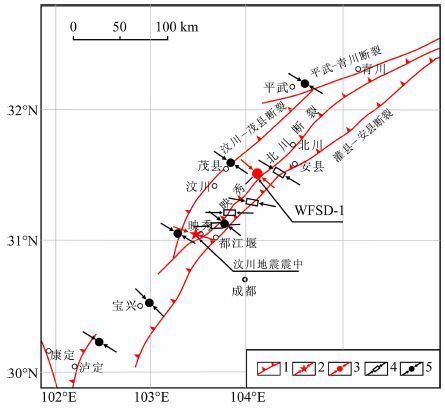
图 7为汶川地震区地应力测量结果[14-16]. 由图 7可以看出,WFSD-1的ASR得到的最大水平主应力的方位与附近地区的其他地应力测量方法得到的结果很一致,方位都在北西到北西西方向上.
|
图 7 汶川地震断裂带科学钻一号孔(WFSD-1)附近最大水 平主应力方向(其他方法得到主应力方向来自文献[14-16]) 1—断层;2—5.12 地震震中和震源机制解P轴方向;3— WFSD-1的位置和ASR 法得到的最大主应力方向;4—断层擦 痕法得到的最大水平主应力方向[16];5—水压致裂法得到的最 大水平主应力方向[15]. Fig. 7 The direction of maximum horizontal principal stress near WFSD-1 1一Fault; 2-5.12 Epicenter and Focal mechanism solution;3-Location of WFSD-1 and Maximum horizontal principal stress direction from ASR; 4-The direction of maximum horizontal principal stress from Fault slickenside analysis[16]; 5-The direction of maximum horizontal principal stress from hydrofracturing[15]. |
用非弹性应变恢复法(ASR 法)得到了汶川地震断裂带科学钻一号孔垂深746m 深处的三维地应力状态. 三个主应力的大小分别为25. 2NPa,21. 5NPa,18. 5 NPa. 最大主应力σ1 和中间主应力σ2 近于水平,最小主应力σ3 近于铅直. 最大主应力σ1 的方位为北西向与汶川地震断裂带走向近于正交. 这种地应力状态有利于汶川地震断裂带产生逆冲兼右行走滑运动,与汶川5. 12地震断层活动类型一致. 另外,ASR 法的测量结果与震源机制解和其他方法得到结果相近. 表明ASR 法是可信的,可用于深部的三维地应力测量.
9. 2 讨论ASR 法是建立在均质各向同性的基本假定之上的. 我们在选择岩芯试件时,依目视来挑选各向同性及均质的岩芯. 岩芯试件越是符合均匀各向同性条件,测量精度越高. ASR 法的测量精度,受岩芯的条件及定向精度的影响. 一般来说,方向角误差小于正负10°,应力值误差小于正负10%. 在应变测试时,我们还同时测量一个不变形的岩石样本,来监控测试系统的工作状态.
为了保证测量精度,应尽量保持岩芯试样环境不变. 岩芯试样由井口取出立即密封包装,保持含水率不变. 测试时,将密封好的岩芯试样放入恒温水槽内,测试过程中岩芯试样的温湿度不变(温度波动小于0. 1 ℃). 测试仪器也处于恒温的环境中. 采取这些措施,可防止岩芯试样的环境改变引起的体积变化.
另外,此方法比较适用于深井,不太适用于浅井. 因为深度越大,应力越大,非弹性应变量也大,测量误差相对较小. 一般测量深度至少大于300m. 在WFSD-1试验中,测量深度为746m,非弹性应变量达到了100微应变,能够保证其测试的精度.
岩芯越均匀完整,ASR 方法的效果越好. 在岩芯破碎的情况下,如能找到一段均匀完整的岩芯(长度不小于15cm),并能定向,则ASR 法还是可用的. 同钻孔崩落法、水压致裂法等其他方法比较起来,ASR 法能用的机率要大得多.
很多学者对震源机制解的P轴方位与主应力方位的关系进行了讨论,文献[17]给出讨论的情况. 一些学者认为震源机制解的P轴方位与主应力方位可能一致,也可能不一致,有时差别可能很大,它们的关系是不确定的. 尽管如此,震源机制解仍是当前测量地应力的主要方法之一[17-19]. 世界地应力图[20-21]和中国地应力图[22-23]都把震源机制解作为主要的资料来源,这些图中的主应力方向,50%以上的数据为地震震源机制解,其余为孔壁崩落分析、水压致裂应力测量等其他方法的结果,并将这些数据放在一起进行对比分析. Zoback等在研究美国北部断块地区的应力场时,将震源机制解P轴方位与其他方法得到的地应力方位(如水压致裂法、地质方法)进行对比,并指出,多个震源机制解的P轴平均方位与其他方法得到的地应力方位差别很小[24]. 因此,本文也将非弹性应变恢复法得到的主应力方位与震源机制解以及其他方法的结果进行对比,观察它们的一致性情况,为评价结果提供参考.
致谢工作中得到项目首席科学家许志琴院士、总地质师李海兵研究员、牛一雄研究员等的支持和帮助,评审专家提出了宝贵意见,在此表示感谢,林为人对日本学术振兴会(JSPS)的科研费资助(基盘B海外-22403008) 表示衷心的感谢.
| [1] | Voight B. Determination of the virgin state of stress in the vicinity of a borehole from measurements of a partial inelastic strain tensor in drill cores. Felsmechanik und Ingenieurgeologie , 1968, 6(4): 201-215. |
| [2] | Teufel L W. Determination of in-situ stress from anelastic strain recovery measurements of oriented core. // Rock Mechanics in Productivity and Protection-The 25th Symposium on Rock Mechanics. Denver, USA:, 1983: 421-430. |
| [3] | Matsuki K. Three-dimensional in-situ stress measurement with anelastic strain recovery of a rock core. // Wittke W ed. Proceedings of the 7th International Congress on Rock Mechanics. Aachen:, 1991: 557-560. |
| [4] | Matsuki K, Takeuchi K. Three-dimensional in situ stress determination by anelastic strain recovery of a rock core. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts , 1993, 30(7): 1019-1022. DOI:10.1016/0148-9062(93)90064-K |
| [5] | Lin W, Kwasniewski M, Imamura T, et al. Determination of three-dimensional in situ stresses from anelastic strain recovery measurement of cores at great depth. Tectonophysics , 2006, 426(1-2): 221-238. DOI:10.1016/j.tecto.2006.02.019 |
| [6] | Lin W, Yeh E C, Ito H, et al. Preliminary results of stress measurement using drill cores of TCDP Hole-A: an application of anelastic strain recovery method to three-dimensional in-situ stress determination. Terrestrial, Atmospheric and Oceanic Sciences , 2007, 18(2): 379-393. DOI:10.3319/TAO.2007.18.2.379(TCDP) |
| [7] | 尹祥础. 固体力学. 北京: 地震出版社, 1985 : 1 -512. Yin X C. Solid Mechanics (in Chinese) (in Chinese). Beijing: Seismological Press, 1985 : 1 -512. |
| [8] | 耶格 J C, 库克 N G W著. 中国科学院工程力学研究所译. 岩石力学基础. 北京: 地震出版社, 1981: 1-690. Jaeger J C, Cook N G W. Institute of Engineering Mechanics, Chinese Academy of Sciences Translated. Fundamentals of Rock Mechanics (in Chinese). Beijing: Seismological Press, 1981: 1-690. |
| [9] | Matsuki K. Anelastic strain recovery compliance of rocks and its application to in situ stress measurement. Int. J. Rock. Mech. Mining Sci. , 2008, 45(6): 952-965. DOI:10.1016/j.ijrmms.2007.10.005 |
| [10] | 王连捷, 潘立宙, 廖椿庭, 等. 地应力测量及其在工程中的应用. 北京: 地质出版社, 1991 : 1 -174. Wang L J, Pan L Z, Liao C T, et al. Crustal Stress Measurements and Their Application in Engineering (in Chinese) (in Chinese). Beijing: Geological Publishing House, 1991 : 1 -174. |
| [11] | 徐次达, 华伯浩. 固体力学有限元理论、方法及程序. 北京: 水利水电出版社, 1983 : 1 -508. Xu C D, Hua B H. Solid Mechanics Finite Element Theory, Methods and Procedures (in Chinese) (in Chinese). Beijing: Water Resources and Hydropower Press, 1983 : 1 -508. |
| [12] | 林为人. 基于岩芯非弹性应变恢复量测定的深孔三维地应力测试方法. 岩石力学与工程学报 , 2008, 27(12): 2387–2394. Lin W. A core-based method to determine three-dimensional in-situ stress in deep drilling wells: anelastic strain recovery technique. Chinese Journal of Rock Mechanics and Engineering (in Chinese) , 2008, 27(12): 2387-2394. |
| [13] | 陈运泰, 许力生, 张勇等. 2008 年5 月12 日汶川特大地震震源特性分析报告. http://www.csi.ac.cn/sichuan/chenyuntai.pdf. Chen Y T, Xu L S, Zhang Y, et al. Report of the great Wenchuan earthquake source of May 12, 2008 (in Chinese). http: //www.csi.ac.cn/sichuan/chenyuntai.pdf. |
| [14] | Wu M L, Zhang Y Q, Liao C T, et al. Preliminary results of in-situ stress measurements along the Longmenshan Fault Zone after the Wenchuan Ms8.0 Earthquake. Acta Geologica Sinica , 2009, 83(4): 746-753. DOI:10.1111/j.1755-6724.2009.00098.x |
| [15] | 安其美, 丁立丰, 王海忠, 等. 龙门山断裂带的性质与活动性 研究. 大地测量与地球动力学 , 2004, 24(2): 115–119. An Q M, Ding L F, Wang H Z, et al. Research of property and activity of Longmen Mountain fault zone. Journal of Geodesy and Geodynamics (in Chinese) (in Chinese) , 2004, 24(2): 115-119. |
| [16] | 杜义, 谢富仁, 张效亮, 等. 汶川Ms8.0级地震断层滑动机制研究. 地球物理学报 , 2009, 52(2): 464–473. Du Y, Xie F R, Zhang X L, et al. The mechanics of fault slip of Ms8.0 Wenchuan earthquake. Chinese J. Geophys. (in Chinese) (in Chinese) , 2009, 52(2): 464-473. |
| [17] | 陈颙. 地壳岩石的力学性能. 北京: 地震出版社, 1988 : 1 -400. Chen Y. Mechanical Properties of Crust Rock: Theoretical Foundation and Experimental Methods (in Chinese) (in Chinese). Beijing: Seismological Press, 1988 : 1 -400. |
| [18] | 许忠淮, 汪素云, 黄雨蕊, 等. 由大量的地震资料推断的我国大陆构造应力场. 地球物理学报 , 1989, 32(6): 636–647. Xu Z H, Wang S Y, Huang Y R, et al. The tectonic stress field of Chinese continent deduced from a great number of earthquakes. Chinese J. Geophys. (in Chinese) (in Chinese) , 1989, 32(6): 636-647. |
| [19] | 李志明, 张金珠. 地应力与油气勘探开发. 北京: 石油工业出版社, 1997 . Li Z M, Zhang J Z. In-Situ Stress and Petroleum Exploration & Development (in Chinese) (in Chinese). Beijing: Petroleum Industry Press, 1997 . |
| [20] | 许忠淮. 板内应力场研究新成果的总结——JGR世界应力图项目专辑简介. 地球物理学进展 , 1994, 9(1): 75–83. Xu Z H. An aggregation of new results of intraplate stress researches: A brief account of the JGR special issue on world stress map project. Progress in Geophysics (in Chinese) (in Chinese) , 1994, 9(1): 75-83. |
| [21] | Zoback M L. First and second order patterns of stress in the lithosphere: The World Stress Map Project. J. Geophys. Res. , 1992, 97(B8): 11703-11728. DOI:10.1029/92JB00132 |
| [22] | 谢富仁, 崔效锋, 赵建涛, 等. 中国大陆及邻区现代构造应力场分区. 地球物理学报 , 2004, 47(4): 654–662. Xie F R, Cui X F, Zhao J T, et al. Regional division of the recent tectonic stress field in China and adjacent areas. Chinese J. Geophys. (in Chinese) (in Chinese) , 2004, 47(4): 654-662. |
| [23] | 崔效锋, 谢富仁, 赵建涛. 中国及邻区震源机制解的分区特征. 地震地质 , 2005, 27(2): 298–307. Cui X F, Xie F R, Zhao J T. The regional characteristics of focal mechanism solutions in China and its adjacent areas. Seismology and Geology (in Chinese) (in Chinese) , 2005, 27(2): 298-307. |
| [24] | Zoback M L, Zoback M D. Faulting patterns in North-central Nevada and strength of the crust. J. Geophys. Res. , 1980, 85(B1): 275-284. DOI:10.1029/JB085iB01p00275 |
 2012, Vol. 55
2012, Vol. 55