天气预报的种类按时间长短可分为:几小时的短时天气预报,1—3天的短期天气预报,4—9 天的中期天气预报和10—30天的延伸期天气预报. 气候预测,分月—季的短期气候预测,以及年、十年和几十年的气候预测. 短期逐日天气预报的成功发端于大气长波(Rossby)理论的建立. 对一地的短期天气预报,预报员应用的正是长波理论中“槽来脊去”的外推方法进行对未来天气的预估. 随着计算机的发展,大气流体动力学方程组的数值解为天气预报扩展了空间范围并延长了预报时效.
对于天气预报,最早的方法是以天气图为信息来源的天气学方法,现在又与气象卫星云图和雷达回波图等资料共同使用,以提高几小时至1 天的预报水平;第二种方法是以计算机为工具的数值天气预报,它通过解流体力学、热力学方程组制作天气预报;第三种是以概率论数理统计为手段的统计预报方法.
自从1950年世界上第一次成功地做出数值天气预报以来,数值天气预报方法取得了长足的发展. 数值解法日益精确,对大气的描述越加细致,垂直方向可分解到20~30 层,水平方向可细划到10~20km. 预报的精度和时效也在不断地提高和延长,一般对3天以内的重要天气过程及其相应的强烈天气如大风、降温、暴雨等均可做出较准确的预测. 欧洲中期天气预报中心(ECNWF)和美国国家环境预报中心(NCEP)等气象业务预测机构发展的数值天气预报模式或全球预报系统(FGS),现在已经能够把环流形势的预报延长到了10 天左右. 毫无疑问,数值方法必将成为未来天气预报的重点发展方向.
逐日的数值天气预报受到可预报性的限制[1-3]. 所谓可预报性,是指天气预报在时效上的一种上限,理论上为2周左右. 一般认为,预报误差产生的来源是初始条件的不确定和预报模式的不完善,而理论上认为是大气过程的混沌本质[4]. 目前的天气形势预报,特别是极端天气预报时效与理论上限还有很大的距离,即预报还存在不确定性. 对数值天气预报而言,其不确定性由以下几种因素造成. 其一是,模式中表征物理过程或计算近似造成的不确定性,也称模式误差. 它反映的是模式物理过程与发生在大气中实际的物理过程之间的不一致. 其二是模式初值条件的不确定性,其误差来源于观测和资料同化系统的近似等. 简言之,这是由于大气实际的初始状态与用于模式初值之间的差别造成. 初始误差随时间增长,数值积分3~5 天时误差增倍,对于小的误差增长更快.
由于天气图方法和数值模式方法不能从根本上解决未来几天的天气预报问题,因而人们利用统计方法弥补不足. 从观测的天气资料和数值预报模式资料中使用降尺度方法,就是统计方法的解释应用[5]. 因此,天气图、数值模式和统计方法,仍然是未来相当长时期内天气预报的主要手段. 本文将从概念和理论上提出改进天气预报技巧和延长预报时效的出路,以及动力学模式与统计方法的有机互补.
2 天气与气候的分离天气图方法的基础是长波理论. 数值天气预报方法的理论基础是流体力学方程. 它们都是确定性的方法,其思想基础来自牛顿(1642—1727年)力学的确定论. 拉普拉斯(1749—1827年)是一位法国的机械决定论者,他把牛顿的质点运动确定论扩展到了无穷质点系统的确定论. 他在1814 年的《概率论的哲学试验》著作中写道:“如果有一种智慧,它能在某一瞬间知道支配着自然的一切力,知道大自然所有组成部分的相对位置,并能伟大到足以分析所有这些事物;它能用一个单独的公式,从最大的天体到最小的原子,都毫无例外悉数概括出宇宙万物的运动,而且对未来就像对于过去那样,都能一目了然;那么目前的宇宙整体,可以看作是它以前的状态的结果,以及以后发展的原因”. 拉普拉斯是希望找到一个独立的公式,把宇宙的万物运动描述清楚. 他提到,公式中要包含力、位置和原子状态等问题的描述. 这样,宇宙的前因后果都确定了,也都能回溯过去和预测未来.
可将拉普拉斯的文字转换成公式. 宇宙是由无穷的银河系和太阳系组成的. 每个银河系称为一个子系统. 系统总是由物质组成的,假定有足够多的R个变量就可以描述这个系统或子系统.
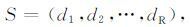
|
d1,d2,…,dR 等是R个变量,它们都是随时间变化的. R个变量构成和确定了系统随时间t变化的状态S(t).
系统有确定的空间范围,其大小依据确定的边界,边界分隔了系统内与系统外. 所谓系统动力学的描述不能缺少三个方面:一是它受系统外的强迫,即外强迫;二是系统内部存在某种制约机制;三是要能方便地描述系统的变化.一个理想的系统动力学预测模型[6]是
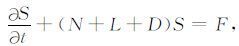
|
(1) |
这好似拉普拉斯文字描述的公式. 这里S是状态变量的全体,也是拉普拉斯考虑的每个原子的位置;F(t)是外界对系统的强迫,可以是时间的函数,也是拉普拉斯考虑的力;N为控制系统内部状态变化的复杂性(非线性),L为简单的线性作用关系,D为耗散作用;(N+L+D)就是这个系统的内部动力学.
如果上式中不考虑内部动力学(N+L+D)的作用,则有
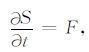
|
(2) |
问题变得非常的简单,如S= (u,v,w)只是一个质点的速度,则上式为
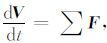
|
(3) |
这就是质点运动的牛顿第二定律. 即一个质点的加速度等于这个质点所受的合力. 拉普拉斯与牛顿的思想方法不同也体现在(1) 与(3) 式之间.
只要这个系统是由大于两个质点组成的外源强迫运动,就构成了天文上的三体或多体问题,此时就不能忽略系统内部动力学(N+L+D)的作用. 何况,大气和海洋,或全球气候系统是一个由无穷多个变量和质点组成的系统.
如果已经对某一系统有了完全的认识,也就是掌握了这个系统的内部动力学(N+L+D),外界对系统的作用F又有了确定和全面的描述,对t=0时的初值S0,可以精确地测量到每个分子的程度,利用容量无穷大和小数有效位无穷的计算机. 那么理论上,可以精确地得到任一时刻S在R维空间中的位置,其中也知道了每个分子的位置. 由此,就可以倒算,知道银河系和太阳系的形成,地球的形成,大气与海洋的过去运动和过去的气候变化. 也可以正算,无限期地预测它们的未来.
自然界中,层次是客观存在的,如银河系与太阳系,大气长波与短波,气候与天气等. 在一个时间内,系统中有嵌套的层次. 假定数学模型(1) 式是可以描述多个层次的. 在数学上,可以把系统的状态S(对外发布的要素)分成一个时间段上的气候部分S 和这个时间段上的天气扰动部分S′ 的和,即
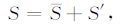
|
(4) |
这里有S 
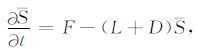
|
(5) |
则系统的天气扰动部分为
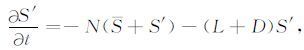
|
(6) |
可见,天气扰动部分依赖于系统内部的复杂性和线性与耗散的作用. 天气扰动部分与系统的非均匀性及内部动力学有关. 这样的确定是人为的,但有两点是清楚的. 一是,把一个可能完全混沌的问题,变成了至少两个层次的问题,其中一个层次上的问题可以用线性数学来描述,并可得到问题的解;二是,有一个数学上的气候定义,气候在一定时空尺度下状态(也称吸引子)随时间连续变化,仅依赖于系统的控制变量(外强迫),是一个线性过程. 反过来说,气候异常(天气扰动的总和)是这个线性过程上叠加在气候系统内部的复杂性或非线性作用的结果.
对线性部分,只要知道外强迫的控制变量,这一部分就是确定的. 由于复杂性的存在,就有很多的不确定性,称为随机的成分. 于是,可以认定:对任何复杂系统的状态,S(t)都可以写成确定性De 和随机性Ra 并存的方程:
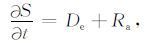
|
(7) |
其中,De =F-(L+D)S,Ra =-N(S+S′)-(L+D)S′. 从上述方程的分化,认识到:由于复杂性的存在,确定论的动力系统本质上是不确定的. 但在这个不确定性中,又蕴藏有确定的成分. 这一确定的成分在很多情况下是可以预报的. 另一部分中,存在对不确定部分的统计可预报性. 把确定性和随机性两者相联系. 这里的确定性是上一个层次研究的问题,随机性是下一个层次研究的问题. 即使在下一个层次中,我们会在后面分析到,仍然存在确定性的部分.
3 天气与气候的关系如果把系统限定为地球大气,那么根据定义,气候是在一定时空尺度下大气状态随时间的连续变化,仅依赖于系统的控制变量,是一个线性过程. 于是,最短时间的气候与最短时段的大气外强迫有关. 这个局地气候就是大气变量随太阳辐射的昼夜变化. 一地大气的温度、湿度、风等连续变量随太阳辐射昼夜变化的关系可用(5) 式描述. 在线性方程(5) 中,太阳辐射的昼夜变化与大气变量S (如气温、风等)不是同时的对应关系,而是有时间滞后项- (L +D)S 的作用. 显然,一地日内最强的太阳辐射是在午时,而当地的最高温度是在午后. 一地夜间接受不到太阳的直接辐射,大气放射地面长波辐射,最低温度出现在凌晨. 因此,有一地的最高温度与最低温度相对昼夜的不对称,但它们的出现是有规律的. 这种规则变化形成的物理原因是清楚的,是昼夜天气预报的气候部分. 这种昼夜气候是要认识的,并没有预报技巧. 预报员要做的是,明天的最高温度和最低温度是怎样偏离了昼夜气候变化的?在时间上和量值上偏离多少?把这个偏离预报出来,预报就称为是有技巧的. 温度偏离的原因是因为当地来了一个冷的(或暖的)大气扰动系统,改变了当地正常的昼夜气候. 于是,对那个扰动(高压或低压)系统的预报,成为预报当地温度偏差值(相对于气候)需要知道的前期信息. 对外发布的温度预报就是气候变化的温度部分与温度扰动部分的线性叠加.
我们又注意到,北半球或中国任一地方的地面与高空温度、湿度、风及地面降水的季节气候变化,总是落后太阳直射北回归线的时间一个多月[7-8]. 其原因就是在平均的线性方程(5) 中,外强迫F(太阳辐射季节变化)不是直接与大气变量S (如气温和风) 的同时对应关系,而是有时间滞后项- (L+D)S 的作用. 在季节循环过程中,一地的温度变化除了受到太阳辐射随季节作用外,还受到海陆地形分布、下垫面地貌状况、大气内部过程等的季节调节作用. 太阳(活动)辐射还存在10年和20年尺度的准周期性变化,海温还存在60—70年的周期性变化,它们对全球平均的气候变化也有滞后影响[9-10]. 如不考虑年代际和世纪变化,要发布的一地气候预报是太阳强迫的气候季节变化部分和海陆调节的气候季节变化部分与气候偏差的叠加. 这个偏差中还可分解为行星尺度的逐日偏差和天气尺度的逐日偏差两个部分. 于是,一个观测变量可以分解成四个部分[11],即

|
(8) |
分解式等号左边的变量S(λ,φ,t)Y 是第Y年从1月1日起算第t日随经度λ 和纬度φ 变化的过去的或当前的气象观测量. 分解式等号右端第一项是对应N年内第t日气候平均及沿纬圈平均后,只随纬度φ 变化的量,反映的是太阳辐射纬度变化的影响. 右边第二项,是相对第t日用第1年至第N年时间平均的空间格点变量,减去相对第t日太阳辐射纬圈平均季节变化后的气候逐日空间变量场,反映的是海陆、地形差异调节的逐日气候空间变量场. 第三项是用当日观测的大气变量,减去逐日太阳辐射气候变化分量后,再做纬圈平均得到的,反映的是大气中行星尺度纬圈距平扰动分量,与行星尺度的赤道和极地热力强迫有关. 第四项,是用当日观测的大气变量,减去逐日气候变化分量(前两项),和行星尺度纬圈距平扰动分量得到的,反映的是大气中的局地天气瞬时扰动分量.
天气与气候之间是什么关系?有没有必要人为地把天气与气候分离开?关系式(8) 表明,每天观测的气象变量中既有气候,又有天气. 按照(8) 式,气象部门可以做出下列分工:左边的项指示需要进行气象变量的观测,相当于需要有一个“探测中心”,为认识气候和异常天气及异常气候的预报提供资料支撑. 右边第一和第二项指示需要有一个“气候中心”,通过资料分析获得对年(季节)循环的和长期(年代和世纪)循环的气候变化的认识. 第三和第四项指示需要一个“气象中心”,从观测资料中去除气候和气候变化,获得不同时段偏差部分的大气运动及预报大气扰动对应的极端天气事件.
是否具有预报技巧,是看(6) 式和(8) 式中,带有右上角撇号的扰动量. 天气预报发布的要素量中囊括了气候和偏差. 这个偏差大于一个确定的值就是极端天气事件. 按理,大气变量中出现的偏差越大,对应的极端天气事件越严重. 目前,常规的天气图方法、数值模式和统计方法都没有在严格意义上把气候与偏差分开,可以说是用混沌的初值来预报混沌的终值. 于是有论断:超过5 天的极端天气事件预报,必然是大气科学中世界性的难题. 极端天气事件的预报是要寻找前期信号:1—15 天的大气变量偏差,是天气预报员做短期和中期天气预报需要寻找的前期信号;20 天以上的变量偏差,也是气候预报员需要寻找的前期信号. 根据(8) 式,天气预报员和气候预报员都离不开前两项的气候认识作为基础. 极端天气事件的时间长度为几天至几十天. 在这个时段内,偏差部分的大气变量变化幅度最大,年循环的气候变化幅度要小一个量级,十年至几十年和世纪循环的气候变化幅度更小. 因此,极端天气事件的预报需要寻找大气中几天至十几天前的扰动信号.
4 天气距平模式在变量的两个层次上,上一个层次是要认识的气候,而下一个层次相对上一个层次为偏差,也称为距平. 气候是在外源强迫下的规则变化,是时间的函数. 如果距平变量随时间不变,但它叠加上气候的绝对值是变化的. 自从有天气图和数值天气预报以来,预报员分析的是绝对值,而极端天气的信息就隐含在绝对值中. 一个预报员经过几十年的长期摸索,等到快退休的时候才积累了一些预报极端天气事件的经验. 然而,这些经验只可会意,不可言传. 预报不对,被人笑话. 预报对了,又说不上道理. 实际上,这些经验很大部分可能与(8) 式的各项分离有异曲同工之妙. 然而,最有经验的预报员进行的信息分离也是定性的和几个可记忆的模型,很难胜任预测多种形式的极端天气事件.
区域性暴雨,或持续性区域暴雨是国家和地区级气象业务部门每天极为关注的极端天气事件. 仅仅850hPa观测风场物理分解后的扰动气流辐合线就能指示这类区域性暴雨极端天气事件的出现位置. 扰动气流辐合线与区域性暴雨的配置关系就是一种“暴雨天气距平模式”[12]. 利用当前欧洲中期天气预报中心(ECNWF)预报的850hPa风场分解的扰动流场辐合线可以平均提前6—7 天预报区域性暴雨的落区[13].
热浪是夏半年经常出现的持续性高温极端天气事件. 传统天气学关注500hPa的高压环流形势,判断它是否控制一个地区. “热浪天气距平模式”中,250hPa层的天气尺度位势高度扰动和400hPa层的天气尺度温度扰动最有可能提前7天预报需要跟踪的前期信号[14]. 利用ECNWF 的预报产品与前期扰动信号的结合可以提前1—2 周预报热浪事件[15].
持续性低温和冬季的雨雪冰冻天气也是全球大气科学界的难题,即难以提前5 天做出这类极端天气事件的预报. 然而,利用“低温天气距平模式”中的前期观测的850hPa天气尺度温度扰动和300hPa 天气尺度高度扰动低值信号与ECNWF 模式产品物理分解的结合可以提前1—2 周做出持续性低温和区域性雨雪冰冻极端天气的预报[16].
持续性区域旱涝是多次天气尺度扰动与行星尺度纬圈平均扰动共同作用的结果,于是区域持续性旱涝也可以分解为气候部分和扰动部分. 旱涝的扰动部分与天气尺度扰动和行星尺度扰动的结合构成了“区域持续性旱涝距平模式”[17].
距平变量模式预报极端天气事件具有技巧. 传统的天气学原理更适用于扰动形势下的极端天气事件分析. 在气象部门的未来预报方法中,同时使用传统“槽来脊去”天气模式与距平天气模式相结合,会大大提高预报技巧.
数值天气预报的发展大大延长了环流形势预报的时效. 目前ECNWF 的可用环流形势预报信息,已达到10天左右. 中期数值天气预报使用的是大气环流模式,未来数日的形势预报依赖于观测的初值.
这些初值是由逐日气候和天气扰动偏差共同组成的. 大气环流模式是把初值中的气候部分和偏差部分都拿来做随时间的积分. 于是,数值天气预报模式会出现一个通病,即预报与未来的实况之间出现系统性的偏差. 这种偏差不完全是初值偏差的放大,还包含气候部分再分解后的截断误差. 这部分截断误差经过非线性相互作用,误差会随积分过程不断放大.
理论上短期和中期数值天气预报模式应该取用(1) 式进行积分运算. (1) 式中,模式积分不但要考虑线性与非线性及耗散动力学过程,还要考虑太阳辐射的昼夜强迫和太阳与海洋的季节强迫. 当今所有模式不能够把气候部分模拟(预报)得很好,可能反映了上述误差的积累作用. 为了避免这一不足,理论上应该取用(6) 式的形式进行积分运算. 形如(6) 式的数值天气预报模式中,气候部分不是预报量,也就没有了气候误差的累积和放大. 模式(6) 需要输入的是初值偏差和认识的气候部分,预报的是未来变量偏差演变及其对应的极端天气事件. 未来取用(6) 式研制中期天气预报模式,会进一步延长预报时效和提高预报技巧. 这是数值天气预报中的“天气距平模式”.
5 气候距平模式短期气候预报模式不但需要初值,也需要未来强迫量的信息. 简单的气候模式是大气环流模式. 以大气为系统,它的上界有来自太阳辐射的强迫,它的下边界有来自陆地和海洋的动力与热力的强迫. 最初的耦合模式是简单的热带太平洋海气耦合模式,后来又发展到全球大气与全球海洋耦合的模式. 全球气候系统五大圈层相互作用的耦合模式称为气候系统模式,现在又发展为包括大气化学和生物过程在内的气候系统模式. 在全球气候系统模式中,圈层与圈层之间都会发生相互作用与耦合的过程. 全球气候系统模式仅仅是对真实的全球气候系统耦合动力学的一种仿真,不可避免地存在各种误差,模式的多样性也在所难免. 模式包含的圈层越多,则是把本来的外部强迫问题转变成了内部的动力学问题.
包括固体地球角动量变化在内的气候系统模式可以称为地球系统模式. 在固体地球、海洋和大气构成的地球系统中,大气与其下垫面的地球和海洋之间存在动力和热力的耦合,形成了大气的异常运动和大气质量相对固体地球的再分布. 如果不考虑海洋角动量的变化,则全球大气西风相对角动量的变化ΔMr,以地球角速度旋转的地球上大气质量再分布引起的大气角动量的变化ΔMΩ,和固体地球角动量的变化ΔME 之和是守恒的,即
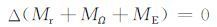
|
(9) |
称为地气角动量守恒,其中
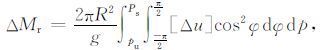
|
(10) |
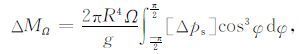
|
(11) |
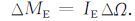
|
(12) |
上述式中,Ω 和ΔΩ 为地球自传角速度及其变率,R 为地球半径,g为重力加速度,φ 为纬度,p为气压从大气上层pu 到地面ps,[Δu]为西风距平的纬圈平均,IE 为固体地球的转动惯量.
在固体地球和大气之间,角动量的变化应该是它们之间力矩作用的结果,即
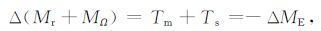
|
(12) |
其中,山脉力矩为
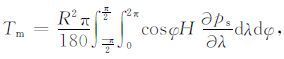
|
(13) |
摩擦力矩为
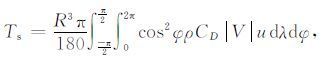
|
(14) |
式中,H为山脉高度,ρ为表面大气密度,CD为无量纲拖曳系数,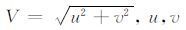
山脉力矩反映了表面气压分布相对山脉地形的作用. 在ElNiño海温距平位相时,南北美洲山脉地形的太平洋一侧气压偏低,山脉力矩使大气得到角动量,而固体地球失去角动量,即地球转动减慢.
Wendy和Smith[18]针对1982—1983 年的ElNiño 事件计算了3个大山脉的平均力矩,发现落基山山脉力矩最大,它的作用使全球总的大气角动量增加Δ(Mr +MΩ)>0. 摩擦力矩的计算非常困难,原因在于表面风的误差和拖曳系数的不确定. 虽然存在准确计算地气之间角动量交换和计算它们之间力矩的困难,但与ElNiño事件相联系的大气角动量变化和日长变化的事实已经得到了公认. 在ElNiño事件暖水位相时,大气西风角动量增加,而固体地球角动量减少,这就是海洋-大气-固体地球之间相互作用概念模型满足的观测事实[19]. 在年际时间尺度上,El Niño-SouthernOscillation (ENSO)事件的预测,除了海洋与大气的耦合外,固体地球也参与了耦合. 固体地球-大气-海洋角动量的守恒,也许是全球气候系统模式的一个约束条件.
无论是大气环流模式,还是海气耦合模式或全球气候系统模式,它们作长期数值积分时,除了距平值的积分外,还同时包含了对平均季节变化的模拟. 气候季节变化的模拟误差,会大大影响距平值的积分结果. 到目前为止,很多数值模式中的气候漂移和对气候季节进程的模拟,特别对东亚季风区气候特征和副热带高压强度的模拟仍然面临难以克服的困难. 几乎所有的耦合气候模式对中国梅雨期的气候模拟与实况气候的偏差可滞后2 个月,误差与梅雨本身的气候时段相当. 这样的模式当然难以用于梅雨异常的预测. 为此,早些年人们就提出要把预报对象分解为气候平均值及其距平值两部分的思路[3, 20],即把气候季节平均值的演变作为已知的,模式要预报的是距平值. 确切的,气候应该是逐日随季节变化的,如果用月平均值代替逐日气候变化也有误差. 把已知的气候季节演变值放进一个模式中,用格点差分或若干谱正交展开的方法积分下去,模式输出的气候与实际的气候之间就出现了差异,这个差异常常归并到了预报的距平值中了. 前面的理论(5和6式)和下面的过去实践都认为,气候距平模式优于普通的气候模式.
早在1970年代末,我国气候研究人员就建立了500hPa高度距平场和地表温度距平场的月预报方法,并认为这一尝试是长期数值天气预报有希望的一条途径[21]. 当时的长期数值天气预报就是现在所指的月和季节时间尺度的短期气候预测. 接着,邢如楠等[22-23]在1982年又发展了长期数值预报的三层滤波模式,用以预报地面温度和不同高度上环流的月距平. 后来,邱崇践和丑纪范[24]发展了一种相似-动力长期数值天气预报模式,黄建平和王绍武[25]利用这一模式做了季度预报试验. 这里,他们用历史相似场代替了气候平均场,初始场和预报场都是相对的距平场.
在ENSO 事件的预报历史上,Zebiak和Cane[26]发展的简单海气耦合模式,其大气变量和海洋变量都是距平量. 这样简单的模式成功地预报了1986—1987年的ENSO 事件. 后来该模式对1993—1995 年的海温距平进行的预报结果与观测结果并不一致. 尽管对这一模式有很多改进的版本,但总体上预报水平并没有很大的提高. 这一模式仅仅把研究的范围限定在20°S—20°N 的赤道太平洋上,他们认为ENSO 循环就在这个海气耦合的区域中. 尽管是一个非常简单的局地海气耦合的距平模式,但它运算方便,至今仍被人们用于理论研究. 随着观测现象的增多和复杂海气耦合模式的发展,人们逐渐认识到ENSO 事件是多尺度海气相互作用的结果[27].
当大气变量中的行星尺度纬圈平均扰动和天气尺度扰动在一个地区长期维持的时候就形成了所谓的旱涝异常. 大气环流异常是形成持续性极端天气和极端气候事件的直接原因. 我们的分析已经认识到,南方涛动(SO)、北极涛动(AO)、南极涛动(AAO)是行星尺度纬圈平均大气扰动形成的[28].
北大西洋涛动(NAO)、太平洋-北美型(PNA)遥相关和太平洋-日本涛动(PJO)等都是天气尺度扰动长期维持形成的[29].
6 统计预报模式1986年,丑纪范[3]对长期预报中的动力和统计两种方法有过精辟的论述. 动力方法是确定论的. 确定论认为天气的未来状态是现在状态和制约这种状态变化的物理规律所确定的必然结果. 形如(5) 式,现在的状态是跟随强迫的. 统计方法是以概率论为基础的. 概率论承认天气的未来状态有不确定性,期望依赖天气的现在状态和近期的演变情况,对未来作出概率的推断. 我们再把天气扰动(距平)场(6) 式分解成3个部分,即S′ =S′1+S′2+S′3.
第一部分是由气候平均场的非线性过程引起的,即
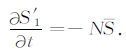
|
(15) |
如果不对气候变化场做格点差分和谱正交展开的积分,就不会出现这项偏差. 对其展开和积分是把人为形成的误差归并给了距平场. 其后果形成了无物理意义的扰动并由此出现了空报的极端天气事件. 现代气候模式中的极端天气事件增多也可能与此有关.
第二部分是扰动的线性过程,由
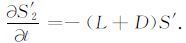
|
(16) |
可得到解. 在实际天气预报中,如果初始分离出了一个天气尺度扰动系统(扰动低压或扰动高压),这个扰动系统是可以外推做出一定时效预报的,滞后的时差依赖于大气内部线性动力学和耗散-(L+D).
这就是我们在本期几篇文章中,对极端高温热浪和极端低温冰冻事件寻找到的前期位势高度扰动和大气温度扰动表征的信号. 很多强的极端天气事件在出现之前,都可以提前4—10天找到天气扰动信号. (16) 式描述了在第二个层次上存在的确定性部分,它也是扰动(或距平)天气图预报方法的理论基础.
第三部分是扰动的非线性过程:

|
(17) |
如果有一个能够很好地描述非线性过程的动力学模式,这部分也可以积分下去,对线性项有一个补充. 如果现阶段不具备有可信的动力学模式,这项可用统计的方法做出预估. 如果大量试验认为动力模式和统计方法都不行,这项就没有必要考虑了. 95%的区域持续性高温热浪和低温事件能够找到前期信号[14, 30],这让我们相信,扰动非线性过程的增长是1 周或10天后的事.
在第二个层次,又可以把S′(t)写成确定性D′e 和随机性R′a 并存的方程:
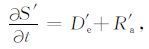
|
(18) |
其中,D′e=- (L+D)S′,R′a = -NS′.
从上述方程的分化认识到:自然系统中每个层次上都存在确定性的部分和不确定的随机部分. 统计学方法是要对动力学模式目前尚不能解决的部分做出估计.
7 结论与讨论气象观测已经积累了50—60年的逐日资料. 这些资料中包含气象要素受太阳辐射随季节的变化,也记录了海陆等地形分布的季节调节作用. 大气变量除了存在年代际和世纪变化外,还有昼夜循环和季节循环等气候规则变化. 这些并不需要预报,要预报的是观测变量减去太阳辐射强迫和海陆调节的气候变化后的偏差部分. 这个偏差部分还可分解为行星尺度和区域天气尺度的逐日偏差两个部分. 行星尺度逐日偏差部分与赤道海温异常(ENSO 事件)和两极涛动有关.
目前的常规天气图预报方法中包含了逐日气候变化的信息,也包含了天气扰动变化的信息. 然而,只有后者才是对区域极端天气事件预报有用的信息. 目前的天气图预报,应该同时给出传统天气图表达的信息和扰动(距平)天气图表达的信息,从而提高预报员对极端天气事件预报的技巧[31]. 数值天气预报产品中也要分离出扰动(距平)天气的要素.
寻找已发生的极端天气事件的前期信号称为倒向问题,而由扰动信号预测极端天气事件是所谓的正向问题. 倒向问题的研究是最终解决正向预报问题的基础. 在倒向问题中,特征层上大气扰动变量与极端天气事件(暴雨、热浪和低温)有高达95%的前期信号指示关系. 这是因为极端天气事件越强烈,大气扰动量的前期信号也越明显. 在正向问题中,重大的极端天气事件较少漏报,但一般的极端天气事件仍然有很多的空报. 目前估计的极端天气事件预报正确率大约在40% ~50%. 为了减少空报,不但需要给极端天气事件以适当的定义,还需要大量的“扰动量与极端天气事件”之间对应关系的总结与认识.
距平天气图将大大显现出未来极端天气事件发生的前期扰动信号. 扰动信号不仅仅在对流层中,多数会出现在对流层顶,甚至平流层中. 空间传播的扰动信号才具有预报意义,对流层顶是有利于天气尺度扰动信号传播的层次.
认识气候变化是天气预报的基础[32]. 同样,认识逐日的气候变化,是研制中期数值天气预报模式的基础. 认识年代际和世纪尺度的气候变化,也是研制气候模式的基础. 气候和气候变化是要认识的,要预报的是那些相对气候变化的偏差,或距平. 因此,距平模式是当前数值模式的发展方向,将会提高天气预报和气候预测的技巧.
| [1] | Lorenz E N. On the range of atmospheric predictability. Proc. First Statis. Meteor. Conf., Amer. Meteor. Soc., 1968: 11-19. |
| [2] | Lorenz E N. Atmospheric predictability as revealed by naturally occurring analogues. J. Atmos. Sci. , 1969, 26(4): 636-646. DOI:10.1175/1520-0469(1969)26<636:APARBN>2.0.CO;2 |
| [3] | 丑纪范. 长期数值天气预报. 北京: 气象出版社, 1986 . Chou J F. Long-Range Numerical Weather Prediction (in Chinese) (in Chinese). Beijing: China Meteorological Press, 1986 . |
| [4] | 卞建春, 杨培才. 关于大气过程可预报性问题的一些讨论. 高原气象 , 2003, 22(4): 315–323. Bian J C, Yang P C. Some remarks on the predictability of atmospheric processes. Plateau Meteorology (in Chinese) (in Chinese) , 2003, 22(4): 315-323. |
| [5] | Benestad R E, Hanssen-Bauer I, Chen D. Empirical-Statistical Downscaling. London: World Scientific Publishing , 2008. |
| [6] | 钱维宏. 全球气候系统. 北京: 北京大学出版社, 2009 . Qian W H. Global Climate System (in Chinese) (in Chinese). Beijing: Peking University Press, 2009 . |
| [7] | Qian W H, Tang S Q. Identifying global monsoon troughs and global atmospheric centers of action on a pentad scale. Atmos. Ocean. Sci. Lett. , 2010, 3(1): 1-6. DOI:10.1080/16742834.2010.11446841 |
| [8] | 钱维宏. 气候变化与中国极端气候事件图集. 北京: 气象出版社, 2011 . Qian W H. Atlas of Climate Change and China Extreme Climate Events (in Chinese) (in Chinese). Beijing: China Meteorological Press, 2011 . |
| [9] | 钱维宏, 陆波, 祝从文. 全球平均温度在21世纪将怎样变化?. 科学通报 , 2010, 55(19): 1963–1967. Qian W H, Lu B, Zhu C W. How would global-mean temperature change in the 21st century?. Chinese Sci. Bull. (in Chinese) (in Chinese) , 2010, 55(19): 1963-1967. |
| [10] | 钱维宏, 陆波. 千年全球气温中的周期性变化及其成因. 科学通报 , 2010, 55(35): 4052–4057. Qian W H, Lu B. Periodic oscillations in millennial global-mean temperature and their causes. Chinese Sci. Bull. (in Chinese) (in Chinese) , 2010, 55(35): 4052-4057. |
| [11] | Starr V P, White R M. Balance requirements of the general circulation. Cambridge, Mass: Geophysical Research , 1954, 12: 66. |
| [12] | 钱维宏, 单晓龙, 朱亚芬. 天气尺度扰动流场对区域暴雨的指示能力. 地球物理学报 , 2012, 55(5): 1513–1522. Qian W H, Shan X L, Zhu Y F. Capability of regional-scale transient wind anomalies to indicate regional heavy rains. Chinese J. Geophys. (in Chinese) (in Chinese) , 2012, 55(5): 1513-1522. DOI:10.6038/j.issn.0001-5733.2012.05.008 |
| [13] | 钱维宏. 中期-延伸期天气预报原理. 北京: 科学出版社, 2012 . Qian W H. Principles of Medium to Extended Range Weather Forecasts (in Chinese) (in Chinese). Beijing: Science Press, 2012 . |
| [14] | 丁婷, 钱维宏. 中国热浪前期信号及其模式预报. 地球物理学报 , 2012, 55(5): 1472–1486. Ding T, Qian W H. Statistical characteristics of heat wave precursors in China and model prediction. Chinese J. Geophys. (in Chinese) (in Chinese) , 2012, 55(5): 1472-1486. DOI:10.6038/j.issn.0001-5733.2012.05.005 |
| [15] | 钱维宏, 丁婷. 中国热浪事件的大气扰动结构及其稳定性分析. 地球物理学报 , 2012, 55(5): 1487–1500. Qian W H, Ding T. Atmospheric anomaly structures and stability associated with heat wave events in China. Chinese J. Geophys. (in Chinese) (in Chinese) , 2012, 55(5): 1487-1500. DOI:10.6038/j.issn.0001-5733.2012.05.006 |
| [16] | 钱维宏, 张宗婕. 南方持续低温冻雨事件预测的前期信号. 地球物理学报 , 2012, 55(5): 1501–1512. Qian W H, Zhang Z J. Precursors to predict low-temperature freezing-rain events in southern China. Chinese J. Geophys. (in Chinese) (in Chinese) , 2012, 55(5): 1501-1512. DOI:10.6038/j.issn.0001-5733.2012.05.007 |
| [17] | 钱维宏, 张宗婕. 西南区域持续性干旱事件的行星尺度和天气尺度扰动信号. 地球物理学报 , 2012, 55(5): 1462–1471. Qian W H, Zhang Z J. Planetary-scale and regional-scale anomaly signals for persistent drought events over Southwest China. Chinese J. Geophys. (in Chinese) (in Chinese) , 2012, 55(5): 1462-1471. DOI:10.6038/j.issn.0001-5733.2012.05.004 |
| [18] | Wendy L W, Smith R B. Length-of-day changes and mountain torque during El Nio. J. Atmos. Sci. , 1987, 44(24): 3656-3660. DOI:10.1175/1520-0469(1987)044<3656:LODCAM>2.0.CO;2 |
| [19] | 钱维宏, 丑纪范. 地气角动量交换与ENSO循环. 中国科学D辑 , 1996, 39(2): 215–224. Qian W H, Chou J F. Atmospheric-earth angular momentum exchange and ENSO cycle. Sci. China Ser. D (in Chinese) (in Chinese) , 1996, 39(2): 215-224. |
| [20] | Smagorinsky J. Problems and promises of deterministic extended range forecasting. B. Am. Meteorol. Soc. , 1969, 50(5): 286-311. |
| [21] | 长期数值天气预报研究小组. 长期数值天气预报的滤波方法. 中国科学A辑 , 1979(1): 75–84. Long-Range Numerical Weather Forecast Research Group. The filtering method of long-range numerical weather forecast. Sci. China Ser. A (in Chinese) (in Chinese) , 1979(1): 75-84. |
| [22] | 邢如楠, 巢纪平. 用三层滤波模式做季节预报的试验. 科学通报 , 1982(12): 738–740. Xing R N, Chao J P. The seasonal forecast experiments on three-layer filtering model. Chinese Science Bulletin (in Chinese) (in Chinese) , 1982(12): 738-740. |
| [23] | 邢如楠, 郭裕福, 巢纪平. 长期数值预报的三层滤波模式. 中国科学B辑 , 1982(2): 186–192. Xing R N, Guo Y F, Chao J P. The long-range numerical forecast three-layer model. Sci. China Ser. B (in Chinese) (in Chinese) , 1982(2): 186-192. |
| [24] | 邱崇践, 丑纪范. 天气预报的相似-动力方法. 大气科学 , 1989, 13(1): 22–28. Qiu C J, Chou J F. An analogue-dynamical method on numerical weather prediction. Chinese J. Atmos. Sci. (in Chinese) (in Chinese) , 1989, 13(1): 22-28. |
| [25] | 黄建平, 王绍武. 相似-动力模式的季节预报试验. 中国科学B辑 , 1991(2): 216–224. Huang J P, Wang S W. The seasonal forecast experiments of an analogue-dynamical model. Sci. China Ser. B (in Chinese) (in Chinese) , 1991(2): 216-224. |
| [26] | Zebiak S E, Cane M A. A model El Nio-Southern Oscillation. Mon. Wea. Rev. , 1987, 115: 2262-2278. DOI:10.1175/1520-0493(1987)115<2262:AMENO>2.0.CO;2 |
| [27] | 钱维宏, 王绍武. 多时空尺度海气相互作用与Zebick-Cane模式的改进. 中国科学D辑 , 1997, 27(6): 554–559. Qian W H, Wang S W. Multiple time-space scale atmosphere-ocean interaction and improvement of Zebiak-Cane model. Sci. China Ser. D (in Chinese) (in Chinese) , 1997, 27(6): 554-559. |
| [28] | Qian W H, Liang H Y. Propagation of planetary-scale zonalmean anomaly winds and polar oscillations. Chinese Sci. Bull. (in Chinese) , 2012. DOI:10.1007/s11434-012-5168-1 |
| [29] | 钱维宏, 梁浩原. 北半球大气遥相关型与区域尺度大气扰动. 地球物理学报 , 2012, 55(5): 1449–1461. Qian W H, Liang H Y. Atmospherical teleconnections and regional-scale atmospheric anomalies over the Northern Hemisphere. Chinese J. Geophys. (in Chinese) (in Chinese) , 2012, 55(5): 1449-1461. DOI:10.6038/j.issn.0001-5733.2012.05.003 |
| [30] | 张宗婕, 钱维宏. 中国冬半年区域持续性低温事件的前期信号. 大气科学 , 2012. |
| [31] | 钱维宏, 陆波. 我国汛期季度降水预报得分和预报技巧. 气象 , 2010, 36(10): 1–7. Qian W H, Lu B. Score and skill of seasonal forecasts of summer precipitation in China. Meteorological Monthly (in Chinese) (in Chinese) , 2010, 36(10): 1-7. |
| [32] | 钱维宏. 认识气候变化与极端气候预报. 科学 , 2008, 60(5): 12–15. Qian W H. Identifying climate changes and extreme climate forecast. Science (in Chinese) (in Chinese) , 2008, 60(5): 12-15. |
 2012, Vol. 55
2012, Vol. 55

