在气候学的发展过程中,1970—1980年代具有重要里程碑意义的发现,研究者提出了大气中的低频40~50d振荡[1-2]和大气遥相关型[3].用大气变量四部分物理分解中的第三部分可得到来自赤道对流层顶的行星尺度西风季节内(40~60d)振荡,并可以向赤道外传播到副热带和中-高纬度地区[4].这一向赤道外传播的行星尺度季节内振荡不同于Nadden和Julian[1-2]在1970 年代初提出的热带大气中向东传播的低频振荡.Nadden 和Julian 在热带大气中发现的低频40~50d振荡实际上是天气尺度扰动.1981年,Wallace 和Gutzler在总结了前人的工作之后,利用北半球冬季500hPa位势高度计算点相关,发现了5 种遥相关型,即东大西洋型(EA)、西大西洋型(WA)、西太平洋型(WP)、太平洋—北美型(PNA)和欧亚太平洋型(EUP).此外,在1986—1989 年期间,Nitta考虑夏季热带西太平洋对流活动激发的扰动对日本天气气候的影响,提出了太平洋—日本涛动(PJO)[5-7].与Wallace 和Gutzler[3]用冬季500hPa位势高度计算北半球遥相关不同,PJO 指数用的是850hPa位势高度[8].
显然,这些大气遥相关型的出现会连接着不同地区的异常天气和异常气候.大气的运动受到海洋和地形等的缓慢强迫作用及大气内部的非线性相互作用,必然会出现比较稳定的遥相关型.就像阻塞形势中的高压与低压的排列出现,也对应着相邻地区的异常天气和异常气候.因此,人们还会不断地提出一些大气遥相关型.遥相关型形成的物理本质以及不同遥相关型之间的关系仍然存在争议[9-10].那么,大气遥相关型的物理意义是什么?北半球大气中可能存在多少个稳定的遥相关型?我们将用行星尺度纬圈瞬变扰动和天气尺度瞬变扰动给予物理分解的解释.
2 资料和方法本文主要采用的大气变量是全球范围的850hPa、500和200hPa层的位势高度,资料来源于NCEP/NCARReanalysis1 的2.5°×2.5°格点资料[11],经度范围0°—360°,纬度范围90°S—90°N,时间为1980—2011年5月的逐日资料.北极涛动(AO)、北大西洋涛动(NAO)、太平洋—北美型(PNA)遥相关波列的月平均时间序列取自美国国家海洋和大气管理局(NOAA)网站(http://www.cpc.ncep.noaa.gov/data/teledoc/telecontents.shtml).
全球大气变量可以分解成纬圈-时间平均的气候对称部分、时间平均的气候非对称部分、纬圈平均的瞬时对称扰动和瞬时非对称扰动等四个部分[12].
前两个部分分别由太阳辐射和海陆分布热力调节的季节变化引起,并形成规则的逐日气候.第三部分是由极地与赤道热力强迫引起,可形成大气变量的行星尺度指数循环.第四部分是一些复杂的天气尺度瞬变波.我们关注第三和第四部分,也就是大气中的行星尺度纬圈平均扰动和天气尺度扰动分量的分离.具体的分离思路是,用历史观测的或当日观测的大气变量减去气候变化的逐日分量.以任一气压层的位势高度为例,第Y 年第t日的纬圈扰动分量是
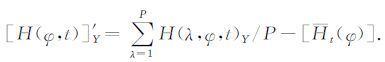
|
(1) |
天气尺度扰动在第Y 年第t日的分量为
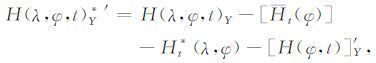
|
(2) |
该分量可以预示极端天气或异常气候事件.这一扰动分量的形成原因与多尺度地形和热力强迫以及大气中波动的非线性相互作用有关.
式(1)和(2)中,H(λ,φ,t)Y 是第Y年从1月1 日起算第t日随经度λ 和纬度φ 变化的历史的或当前的气象观测在空间上的位势高度.
珨[H t (φ)]是对应N 年内第t 日气候平均及纬圈平均后,只随纬度φ 变化的位势高度扰动分量,其数学表达式如下:
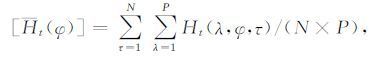
|
(3) |
该分量是太阳辐射季节变化确定的逐日气候变量,τ是第t日所用历史资料的年份(从第1年至第N年),λ是纬圈等距格点序号(从第1点至最后第P点).
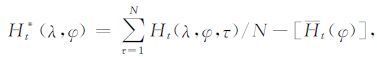
|
(4) |
该分量是海陆分布地形差异季节调节的逐日高度变化场,N取为30年(1981—2010年).
行星尺度纬圈平均扰动和天气尺度扰动还可以再做时间平均.当它们做3 天、5 天、7 天、9 天甚至一个月的时间平均后,存在的高度扰动就是稳定的大气异常环流,并在异常环流的不同部位出现异常天气和异常气候.为了得到不同地区上扰动之间的遥相关型,我们用旋转经验正交函数(REOF)展开的方法对月平均高度行星尺度纬圈平均扰动和月平均高度天气尺度扰动做分解.经验正交函数(EOF) 展开的作用,是把一个随时间变化的二维要素场分解成了若干个正交模态振幅随时间系数的演变.但EOF模态的结构依赖于选择的区域[13].在本文的计算中,除了赤道地区和北极点外,在北半球纬圈方向上无边界,REOF 的南北范围取为20°N—87.5°N (或赤道至87.5°N).与EOF 比较,REOF 的优点是其分解的分量能够反映出局地扰动的信息.大气中的扰动波列常常是在相邻地区出现相反的扰动趋势,REOF正好可以揭示这一特征.
3 遥相关型与天气扰动正交模态先给出Wallace和Gutzler[3]计算北半球冬季500hPa位势高度5 种遥相关型中的各个表达式.
PNA 遥相关型是人们最熟悉和研究得最多的大气遥相关型,其计算或定义式为
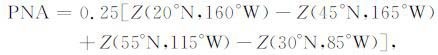
|
(5) |
这里,Z是四个不同位置上的标准化500hPa位势高度值.
西大西洋遥相关型(WA)、东大西洋遥相关型(WA)、西太平洋遥相关型(WP)和欧亚—太平洋遥相关型(EUP)的指数定义分别为
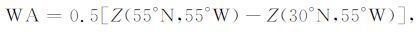
|
(6) |
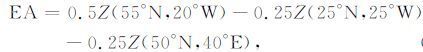
|
(7) |
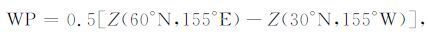
|
(8) |

|
(9) |
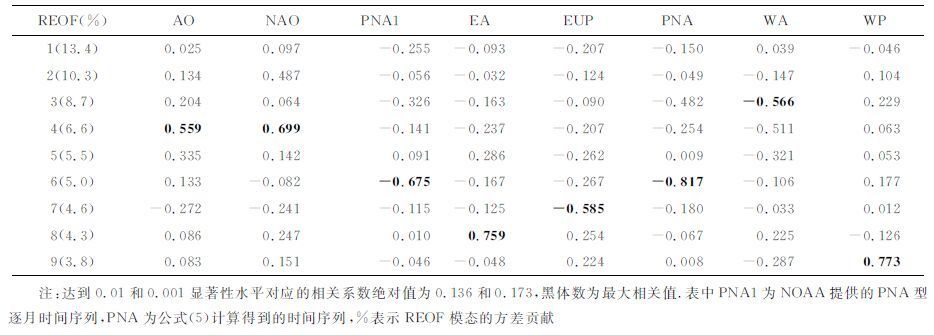
最初的5个大气遥相关型是用冬季500hPa高度定义和计算的,而后Barnston 和Livezey [14]对月平均的高度场使用旋转主分量方法分析其主要模态的年际变化,进而PNA、AO 和NAO 等指数序列也用月平均序列表达.利用1981—2010年的逐月北半球500hPa位势高度,表 1给出了根据上述定义计算的5种大气遥相关指数序列,与同期500hPa高度天气尺度扰动计算的REOF 时间序列之间的相关值.表 1 中还给出了同期NOAA 网页上AO、NAO、PNA 三个指数序列与500hPa高度天气尺度扰动REOF时间序列的相关值.
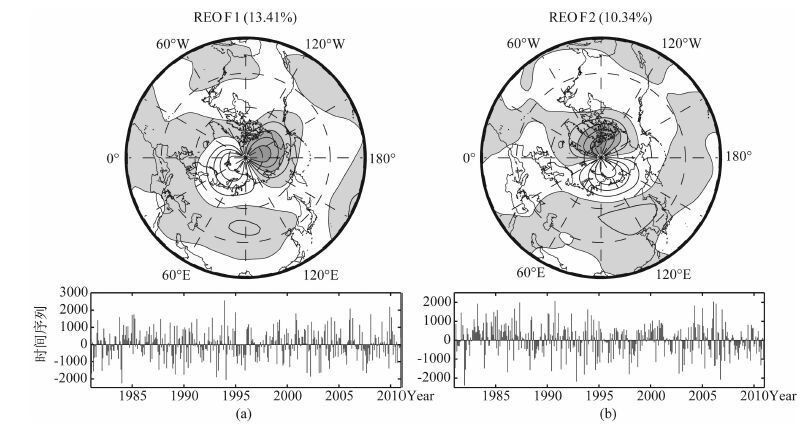
500hPa高度天气尺度扰动的REOF 第1和第2模态的空间分布如图 1 所示.这两个模态的方差百分比贡献分别为13.4%和10.3%,它们都有一对最大的相邻变化中心在北极(北冰洋)地区.第1 模态的一对中心在太平洋和大西洋以北的北极地区,第2模态的一对中心在欧亚大陆和北美大陆的北极地区.这两个遥相关型反映了极涡位置的偏极变化,也是常见的北极环流.这两个模态的时间系数序列中也存在季节内和年际时间尺度的变化.尽管表 1 中第1模态与EUP和PNA 达到0.001的显著性相关,但模态的中心不能反映EUP和PNA.同样的情况也反映在第2 模态与NAO 的相关系数中.北极地区的这两对相邻的偶极涛动,是独立存在的持续性天气尺度扰动环流异常形态.
|
|
表 1 1981—2010年500 hPa位势高度天气尺度扰动计算的REOF模态时间序列与各遥相关型指数序列的同期相关系数 Table 1 Simultaneous correlation coefficients between REOF time series of 500hPa geopotential height regional-scale anomalies and teleconnection indices for 1981 一2010 |
|
图 1 1981—2010年500hPa位势高度天气尺度扰动的月平均值计算的REOF第1和第2模态(阴影对应负值,等值线间隔为0.01)及其它们的时间系数序列 Fig. 1 The leading two REOF patterns (the shaded area corresponds to negative values,contour interval is 0. 01) of monthly mean of 500 hPa geopotential height regional-scale anomalies and the REOF time series for 1981—2010 |
第3模态的分布中心主要集中在西半球.它的分布形态像PNA(相关系数-0.48 和-0.33),更反映了WA 的分布(相关系数-0.57).由WA 指数定义得到的系数序列与REOF 第3 模态系数序列给出在图 2中,它们之间具有年际相反的距平变化,2009—2010年的冬季就经历了一次明显的年际振荡.

|
图 2 1981—2010年500hPa位势高度天气尺度扰动计算的REOF第3模态分布及其模态系数(灰色柱状线)与WA 指数序列(黑色实线) Fig. 2 The leading 3rd REOF mode pattern of 500 hPa geopotential height regiona--scale anomalies and the relationship between the mode time series (grey bars) and the WA index series (black solid line) for 1981—2010 |
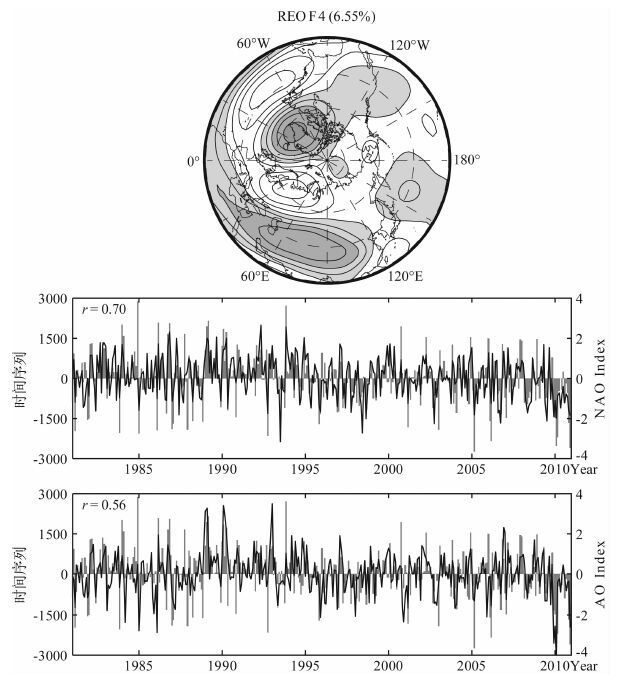
500hPa高度天气尺度扰动的REOF 第4模态系数与AO 和NAO 之间的相关系数分别达到0.6 和0.7(图 3).第4模态主要反映了北大西洋至欧亚地区的异常环流型.在北大西洋地区,南北的反向振荡正是NAO的结构.在欧亚地区也存在一个南北相反的振荡结构,于是可以在欧洲至亚洲地区定义一个南北方向的欧亚涛动(EAO).2008 年初和2011年初,中国南方持续性雨雪冰冻发生期间,对应的正是欧洲高度正异常与亚洲高度负异常.
|
图 3 同图 2但为第4模态及其系数序列与AO 和NAO 的系数序列 Fig. 3 Same as Fig. 2 but for the leading 4th REOF mode and time series of AO/NAO index |
第5模态反映了北大西洋至欧亚大陆上的500hPa 高度天气尺度扰动持续性结构,在中纬度地区有两对振荡中心(图 4).这是一种阻塞高压与截断低压的分布形势.当阻塞高压(截断低压)在东北亚的时候,截断低压(阻塞高压)在东欧,而在大西洋和西欧又有一对阻塞形势.由这样的四个振荡中心,我们也可以定义一种“大西洋—欧亚遥相关型”(AEA)并可构造它的指数序列.通过具体的例子分析发现,AEA 型时间序列在1988、1989、1991、1992、2006年的冬季与1983、2000、2004、2005、2008 年的冬季相反,对应欧洲,特别是中国南方与东南亚的降水距平相反分布(图略).
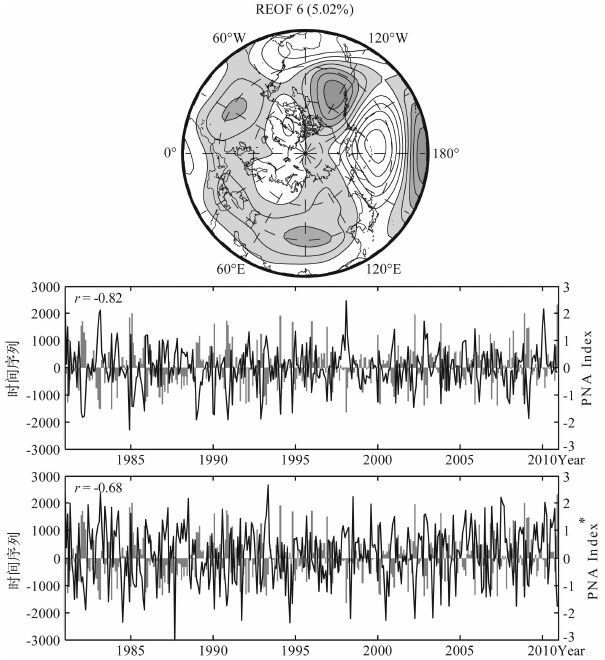
第6模态反映了北太平洋和北美地区的500hPa 高度天气尺度扰动结构(图 5).在北太平洋地区,扰动结构是南北方向上的涛动.在北美地区也几乎是南北方向的涛动.这两对涛动构成了所谓的太平洋—北美遥相关型(PNA).第6模态时间序列与式(5)和PNA(NOAA)序列都给出在图 5中,它们之间的相关值分别高达-0.82和-0.68.这些时间序列也都存在着年际变化和季节内变化.
|
图 5 同图 2但为第6模态及其系数序列与PNA 系数序列*为NOAA 提供的PNA 指数逐月序列 Fig. 5 Same as Fig. 2 but for the leading 6th REOF mode and time series of PNA index. Symbol * indicates the PNA index provided by NOAA |
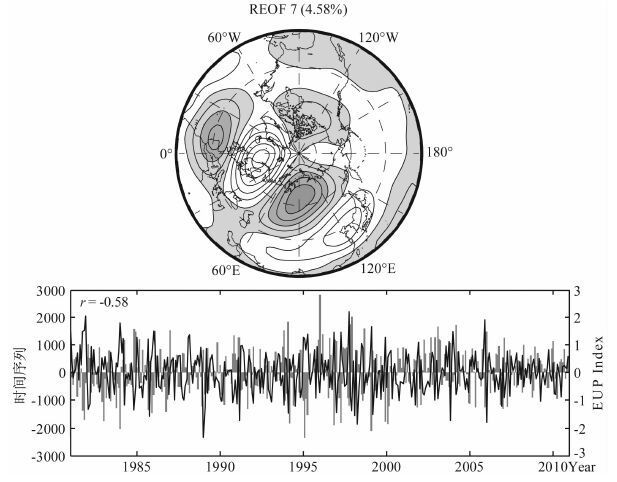
在表 1中,REOF第7模态与EUP之间有最高的相关值(-0.58).这个模态反映了中纬度欧亚地区的大气扰动,是另一类阻塞高压与截断低压的环流分布型(图 6),相当于阻塞高压在欧洲时,截断低压在北亚,下游的阻塞高压在东北亚.欧亚—太平洋遥相关型(EUP)明显的时期是在1980 年代前期和1990年代后期.
|
图 6 同图 2但为第7模态及其系数序列与EUP系数序列 Fig. 6 Same as Fig. 2 but for the leading 7 th REOF mode and time series of EUP index |
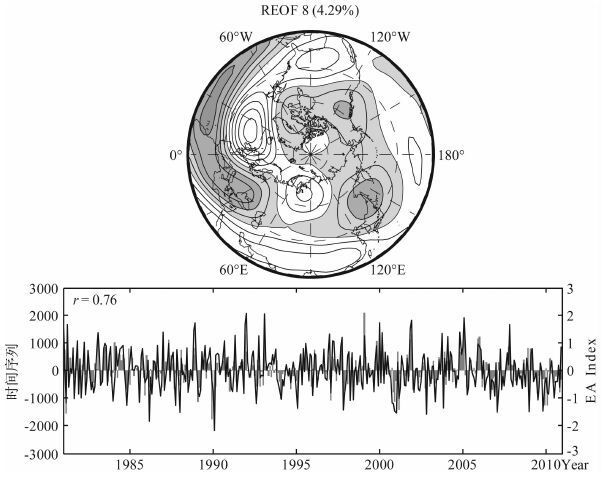
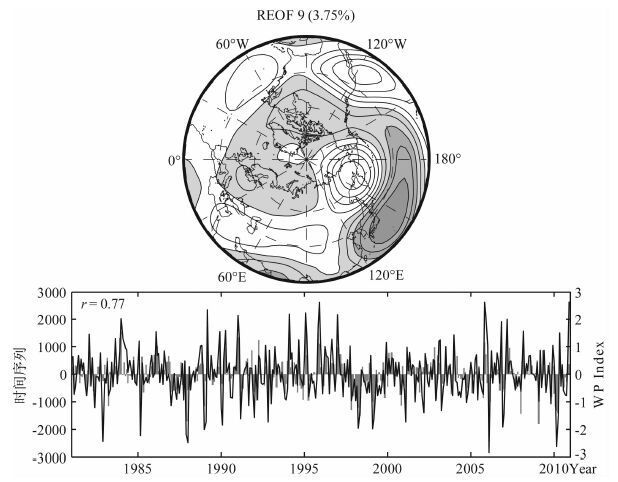
对于EA型和WP型,它们的指数序列与500hPa 高度天气尺度扰动中的第8和第9模态时间系数之间的相关值分别为0.76 和0.77.它们的模态分布及其时间序列与EA 和WP的时间序列分别给出在图 7和图 8中.第8 模态包含有东部北大西洋与冰岛之间的涛动,又含有东部北大西洋与欧洲中纬度之间的涛动.第9模态中有一对扰动中心正是在西太平洋的南北方向上,即西太平洋遥相关型(WP).
|
图 7 同图 2但为第8模态及其系数序列与EA 系数序列 Fig. 7 Same as Fig. 2 but for the leading 8th REOF mode and time series of EA index |
|
图 8 同图 2但为第9模态及其系数序列与WP系数序列 Fig. 8 Same as Fig. 2 but for the leading 9th REOF mode and time series of WP index |
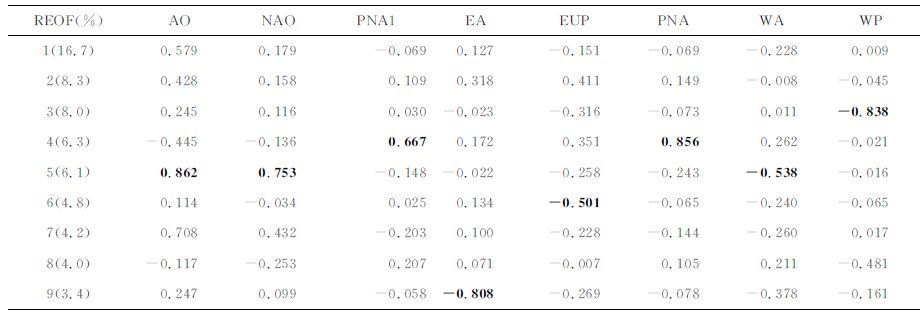
表 2是把表 1中的位势高度天气尺度扰动与位势高度行星尺度纬圈平均扰动叠加后,使用REOF 方法计算的相关结果.它们的前9 个模态与各个指数之间的相关值,与由天气尺度扰动REOF 计算的结果比较,在模态次序和相关值上都有了变化.除了EUP 和WA 型外,其他6 个遥相关指数系数与REOF模态系数之间的相关值都提高了.
|
|
表 2 同表 1但为天气尺度扰动与行星尺度纬圈平均高度扰动的叠加 Table 2 Same as Table 1,but the sum of planetary-scale zonal-mean and regional-scale height anomalies were used to calculate REOF modes |
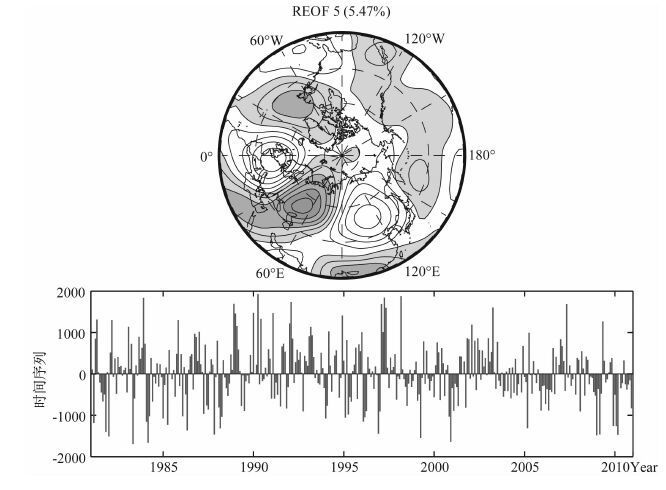
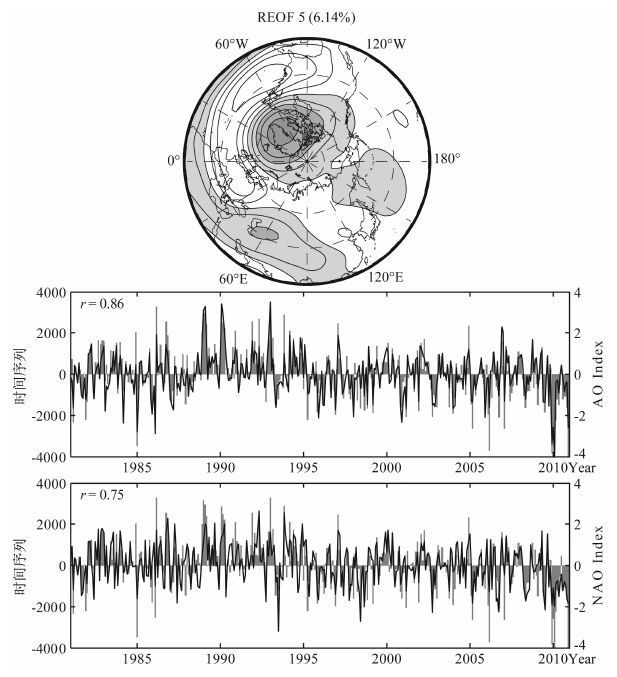
图 9中给出了天气尺度扰动叠加上行星尺度纬圈平均扰动后的500hPa位势高度REOF第5模态分布及其系数与NAO和AO的时间序列,它们之间的相关值高达0.75和0.86.模态分布中,北大西洋南北方向的涛动更加清楚了.它们的时间序列不但具有年际变化,还存在年代际变化.这部分年代际变化来自于纬圈平均扰动的长期贡献.
|
图 9 500hPa位势高度天气尺度扰动加行星尺度纬圈平均扰动后的REOF第5模态分布及其系数(灰色柱状线)与NAO 和AO 时间序列(黑色实线) Fig. 9 The leading 5th REOF mode of 500 hPa geopotential height planetary-scale zonal-mean and regional-scale anomalies combined, and the relationship between the mode time series (grey bars) and the NAO/AO index series (black solid line) for 1981—2010 |
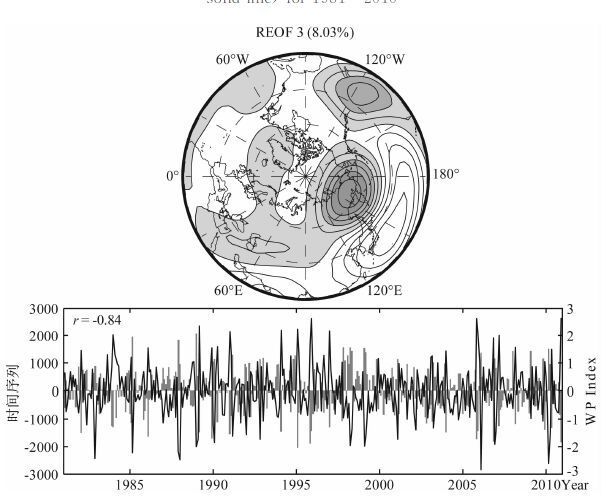
天气尺度高度扰动叠加上行星尺度纬圈平均高度扰动后的REOF第3模态,反映的西太平洋南北方向的波列结构给出在图 10中.第3模态时间系数与WP指数之间的相关值高达-0.84,具有年际和年代际的变化.与没有行星尺度纬圈平均高度扰动叠加的REOF模态分布比较,有纬圈平均高度扰动的叠加,加强了纬带结构的分布.
|
图 10 同图 9但为REOF3与WP时间序列 Fig. 10 Same as Fig. 9 but for the leading 3rd REOF mode and time series of WP index |
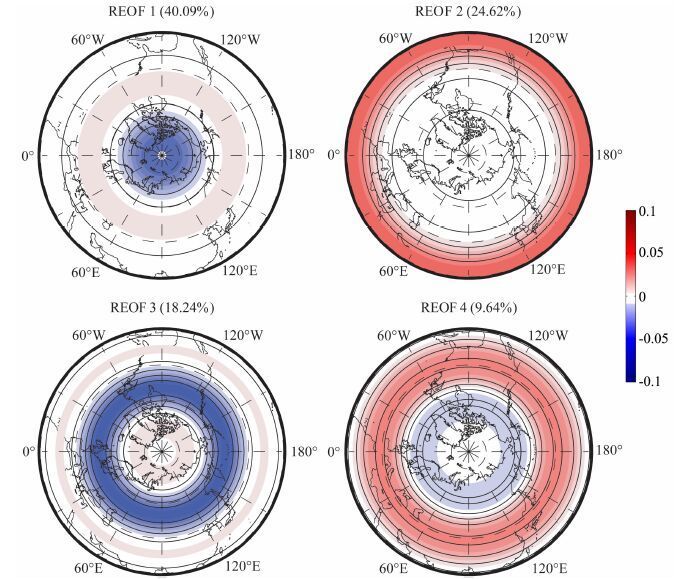
从文献[4]中,我们注意到起源于赤道地区的纬圈平均西风扰动,可以向赤道外地区传播到中高纬带,而起源于极地的西风扰动,也可以向极地外传播到高纬带地区.行星尺度纬圈平均大气扰动在各个气压层上都存在,只是在对流层顶的变幅最大.在前人计算的500hPa位势高度涛动中,包含了天气尺度高度扰动与纬圈平均高度扰动的叠加.于是,我们可以直接对500hPa 位势高度纬圈平均扰动做REOF展开.图 11中,前4个模态的方差百分比贡献已经占了93%,其中第1 和第2 模态分别占了40%和25%.第1模态反映了以北极为中心的行星尺度纬圈平均高度扰动,第2 模态反映了源自赤道带的高度扰动.第3和第4模态反映了高纬纬圈和中纬纬圈平均的高度扰动,它们对中-高纬地区的天气尺度高度扰动会有影响,使得模态结构在东西方向上拉长.1981—2010年期间,500hPa位势高度纬圈平均扰动前4个模态逐月时间系数如图 12所示.
|
图 11 500hPa位势高度行星尺度纬圈平均扰动前4个模态分布(虚线表示负值,等值线间隔0.01) Fig. 11 The leading 4 REOF patterns (the dashed lines correspond to negative values,contour interval is 0.01) of 500 hPa geopotential height planetary-scale zonal-mean anomalies |
|
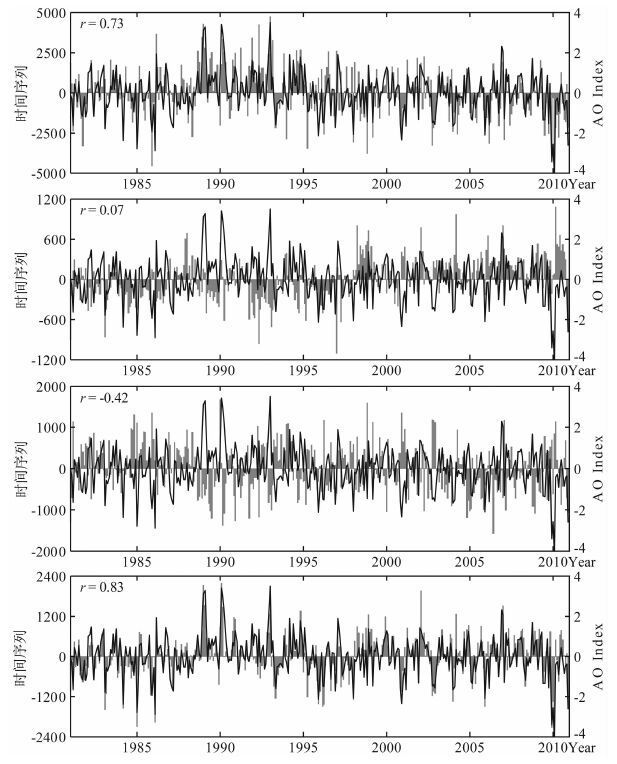
图 12 1981—2010年500hPa位势高度行星尺度纬圈平均扰动前4个模态逐月时间系数(灰色柱状线)与AO(黑色实线)的关系 Fig. 12 The relationship between the leading 4 REOF time series of 500hPa geopotential height planetary-scale zonal-mean anomalies (grey bars) and the AO index series (black solid line) |
北极和赤道的高度扰动都有长期增强的趋势和年际变化.中、高纬度纬圈平均高度扰动主要有年代际变化.第1至第4模态的时间序列与AO 指数的相关值,分别为0.73、0.07、-0.42和0.83,说明500hPa 位势高度的纬圈平均扰动第1和第3模态反映的是AO 结构,它们占总方差的58%.第2模态占(24%),反映的是源自热带的扰动,与AO 没有关系.
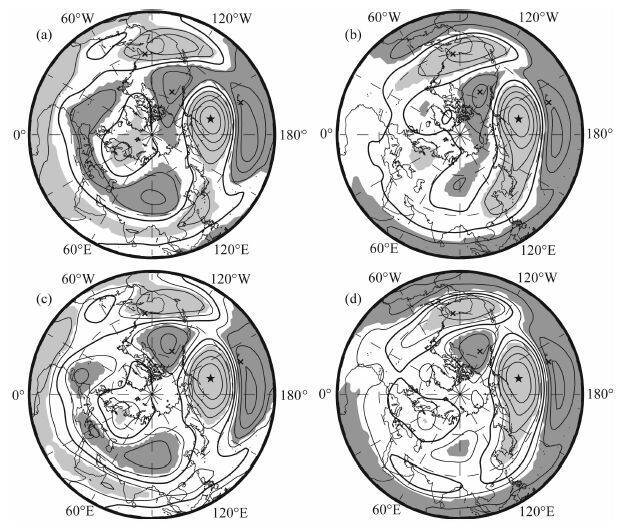
从图 13可以清楚地看出,无论是逐月相关,还是仅仅冬季相关,包含纬圈平均500hPa高度扰动叠加的点相关分布,比单纯的天气尺度高度扰动点相关分布在东西方向上大大拉长了,它们反映的都是PNA 遥相关型.这一比较说明,天气尺度扰动是PNA 遥相关波列形成的关键,纬圈平均扰动的叠加对PNA 波列有形态上的改变.
|
图 13 500 hPa位势高度点相关分布 (a)逐月天气尺度扰动;(b)逐月天气尺度扰动加行星尺度纬圈平均扰动;(c)冬季天气尺度扰动;(d)冬季天气尺度扰动加行星尺度纬圈平均扰动.星号(45°N,165°W)处为点相关中心,与X构成PNA型在式(5)中的位置.灰色阴影表示相关值达到0.01显著性水平,浅色与深 色分别指示正、负相关,等值线间隔为0.2,粗线为零相关. Fig. 13 One-point correlation maps for 500 hPa geipotential height (a) monthly regional-scale anomalies; (b) planetary-scale zonal-mean and regional-scale anomalies combined; (c) regional-scale anomalies in winter (DJF) months ; (d) planetary-scale zonal-mean anomalies plus regional-scale anomalies in winter (DJF) months. The grid points marked by asterisk and crosses “X ” represent the 4 center grids of PNA in formula (5). The shaded area indicates that the grid point’s correlation coefficient reaches the 0.01 significance level. Light and dark shadings indicate the positive and negative correlations, respectively,the interval of contour is 0. 2 and the heavy line denotes the zero correlation. |
除了500hPa的波列外,不同季节和不同高度上还存在另外一些波列.其中,太平洋—日本(PJ)遥相关型指数,是定义在850hPa上的位势高度场格点代数值的差[8]:
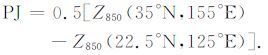
|
(10) |
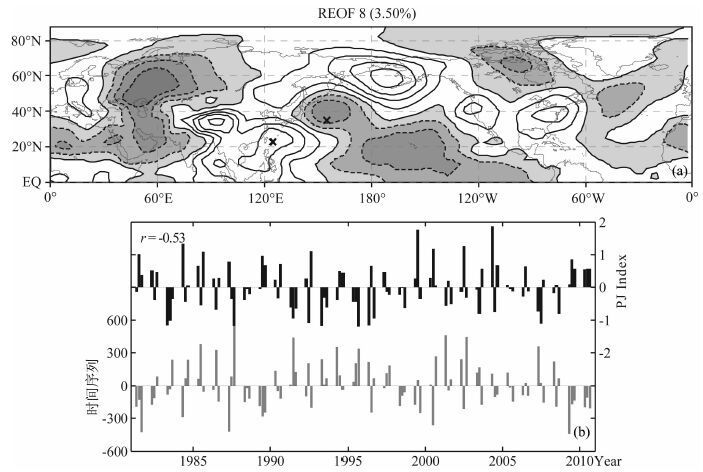
我们计算了四种850hPa位势高度REOF 分解,分别用天气尺度扰动和行星尺度纬圈平均扰动加天气尺度扰动做赤道至87.5°N 宽度带的REOF 分解,又分别用它们做20°N—87.5°N 宽度带的REOF分解.用展开的时间系数与PJ遥相关型指数时间序列计算相关.最高的相关值-0.53对应宽度带(EQ 至87.5°N)内的高度扰动,第2 高的相关值-0.42对应这一宽度带的行星尺度纬圈平均高度扰动加天气尺度高度扰动.第3高的相关值0.37对应宽度带(20°N—87.5°N)内的天气尺度高度扰动,第4高的相关值0.33 对应该宽度带的行星尺度纬圈平均高度扰动加天气尺度高度扰动.图 14 给出了850hPa夏季位势高度天气尺度扰动REOF 第8模态及其系数时间序列和PJ遥相关型系数时间序列.
|
图 14 850 hPa夏季位势高度天气尺度扰动REOF第8模态(a)及其系数时间序列(b)和PJ遥相关型系数时间序列,X的位置为PJ指数的取值点 Fig. 14 The leading 8th REOF mode of 850 hPa geopotential height regional-scale anomalies and the relationship between the mode time series and the PJ index time series, X denotes the points used to calculate PJ index |
PJ指数时间序列选取的两个点正是在(EQ 至87.5°N) REOF第8模态的邻近正、负中心处,因此它们之间的相关值也比较高.在EQ至87.5°N宽度带内的位势高度扰动REOF分解中,第3模态的一对中心分别位于亚洲大陆和中太平洋,用这对中心值可以很好的构造亚洲夏季风指数[15].
用200hPa和850hPa的位势高度天气尺度扰动也能得到REOF 的第1 和第2 模态在北极地区的一对振荡型分布.200hPa上第3 模态的分布就类似于PNA 型,850hPa上第4模态的分布也类似于PNA 型(图 15).200hPa和850hPa位势高度纬圈平均扰动的REOF前四个模态反映的也是北极、赤道和中、高纬带的带状扰动结构(图略).
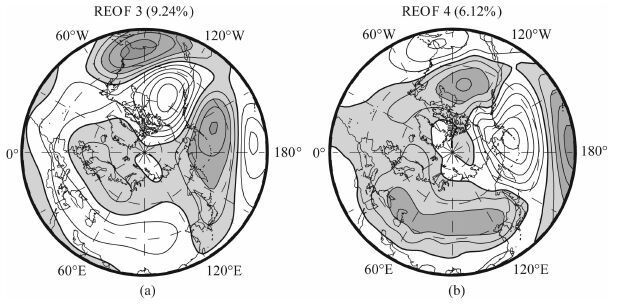
|
图 15 (a) 200 hPa和(b)850 hPa位势高度天气尺度扰动REOF对应的第3模态和第4模态 Fig. 15 The 3rd and 4th modes of REOF geopoltential height regional-scale anomalies at (a) 200 hPa and (b) 850 hPa |
到目前为止,人们已经发现和命名了大气中不同高度和不同地区的持续性涛动.这些涛动是大气行星尺度纬圈平均高度扰动和天气尺度高度扰动在一些地区持续性存在的结果.利用REOF 方法可以全面地揭示大气中经常出现的涛动,或遥相关型.
8 结 论根据球面大气变量的四分量物理分解,本文给出了行星尺度纬圈平均高度扰动和天气尺度高度扰动的点相关和REOF 分析,对北半球大气遥相关型,有了下列新认识:(1) 在月至季的时间尺度上,球面大气的一些固定地理位置会时常出现大气涛动,或遥相关型,如东大西洋型(EA)、西大西洋型(WA)、西太平洋型(WP)、太平洋—北美型(PNA)和欧亚太平洋型(EUP),它们主要来自持续性天气尺度扰动分量的贡献.
(2) EA 型和WA 型与北大西洋涛动(NAO)有着内在的联系,是NAO 的部分.北极涛动(AO),是北极地区与高纬带相反变化的持续性行星尺度纬圈平均扰动.NAO 是AO 的一部分.极地-高纬行星尺度纬圈平均高度扰动与赤道带高度扰动之间不具有相关关系,但它们都具有年际、年代际和长期变化的趋势.
(3) 除了已经认识和命名的大气中位势高度遥相关型外,北半球大气中还存在位于北极地区的两对偶极涛动、欧亚涛动(EAO)和“大西洋—欧亚型”(AEA)波列.EAO 和AEA 表现为欧亚地区稳定的环流形势和阻塞环流形势,对中国的持续性异常天气和异常气候具有较大的影响.
| [1] | Madden R D, Julian P. Detection of a 40-50 day oscillation in the zonal wind in the tropical Pacific. J. Atmos. Sci. , 1971, 28(5): 702-708. DOI:10.1175/1520-0469(1971)028<0702:DOADOI>2.0.CO;2 |
| [2] | Madden R D, Julian P. Description of global scale circulation cells in the tropics with 40-50 day period. J. Atmos. Sci. , 1972, 29(6): 1109-1123. DOI:10.1175/1520-0469(1972)029<1109:DOGSCC>2.0.CO;2 |
| [3] | Wallace J M, Gutzler D S. Teleconnections in the geopotential height field during the Northern Hemisphere winter. Mon. Wea. Rev. , 1981, 109(4): 784-812. DOI:10.1175/1520-0493(1981)109<0784:TITGHF>2.0.CO;2 |
| [4] | Qian W H, Liang H Y. Propagation of planetary-scale zonal mean wind anomalies and polar oscillations. Chinese Sci. Bull. , 2012. DOI:10.1007/s11434-012-5168-1 |
| [5] | Nitta T. Long-term variations of cloud amount in the western Pacific region. J. Meteorol. Soc. Jpn. , 1986, 64(3): 373-390. |
| [6] | Nitta T. Convective activities in the tropical western Pacific and their impact on the Northern Hemisphere summer circulation. J. Meteorol. Soc. Jpn. , 1987, 65: 373-390. |
| [7] | Nitta T. Global features of the Pacific-Japan oscillation. Meteorol. Atmos. Phys. , 1989, 41(1): 5-12. DOI:10.1007/BF01032585 |
| [8] | Wakabayashi S, Kawamura R. Extraction of major teleconnection patterns possibly associated with the anomalous summer climate in Japan. J. Meteorol. Soc. Jpn. , 2004, 82(6): 1577-1588. DOI:10.2151/jmsj.82.1577 |
| [9] | Feldstein S B, Franzke C. Are the North Atlantic Oscillation and the Northern Annular Mode distinguishable?. J. Atmos. Sci. , 2006, 63(11): 2915-2930. DOI:10.1175/JAS3798.1 |
| [10] | Itoh H. Reconsideration of the true versus apparent Arctic Oscillation. J. Climate , 2008, 21(10): 2047-2062. DOI:10.1175/2007JCLI2167.1 |
| [11] | Kalnay E, Kanamitsu M, Kistler R, et al. The NCEP/NCAR 40-year reanalysis project. B. Am. Meteorol. Soc. , 1996, 77(3): 437-472. DOI:10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2 |
| [12] | 钱维宏. 天气尺度瞬变扰动的物理分解原理. 地球物理学报 , 2012, 55(5): 1439–1448. Qian W H. Physical decomposition principle of regional-scale transient anomaly. Chinese J. Geophys. (in Chinese) (in Chinese) , 2012, 55(5): 1439-1448. DOI:10.6038/j.issn.0001-5733.2012.05.002 |
| [13] | Dommenget D, Latif M. A cautionary note on the interpretation of EOFs. J. Climate , 2002, 15: 216-225. DOI:10.1175/1520-0442(2002)015<0216:ACNOTI>2.0.CO;2 |
| [14] | Barnston A G, Livezey R E. Classification, seasonality and persistence of low-frequency atmospheric circulation patterns. Mon. Wea. Rev. , 1987, 115(6): 1083-1126. DOI:10.1175/1520-0493(1987)115<1083:CSAPOL>2.0.CO;2 |
| [15] | Zhao P, Zhu Y N, Zhang R H. An Asian-Pacific teleconnection in summer tropospheric temperature and associated Asian climate variability. Climate Dyn. , 2007, 29(2-3): 293-303. DOI:10.1007/s00382-007-0236-y |
 2012, Vol. 55
2012, Vol. 55