大气运动的根本原因是太阳辐射的日变化、年变化和更长时间长度的年代际和世纪变化.大气运动又可看成为不同时空尺度波或气旋与反气旋系统的叠加.这些系统大的如极涡、南亚高压、副热带高压等行星尺度系统,小的如台风、中纬度气旋等天气尺度系统.这些系统的强度和活动位置一旦反常就会导致极端天气事件的发生.极端天气事件预报的成功就归结为对这些天气系统异常的预报.
在天气动力学的发展历史上,最重大的成就是20世纪30—40年代以Rossby [1]为首的芝加哥学派创立的大气长波理论.他们发现高空天气图中北半球中纬度在自西向东的绕极环流之上,叠加有长达数千公里的波动.这些波动除有自身的结构和运动规律外,还与低空的锋面气旋存在内在的联系.对于这种现象,Rossby提出了位势涡度概念,从理论上证明是地转参数f=2Ωsinφ 随纬度变化,即β 效应而引起的一种涡旋性波动,从而创立了著名的长波(行星波)理论.长波理论需要满足在自由大气中的质量无辐散条件.满足这个条件的层次在500—600hPa附近,即在大气对流层的中部.在天气图上的表现就是500hPa上“槽来脊去”.根据长波理论,在确定的西风气流下,波长越长的波向东移动的速度越慢,甚至后退,而波长较短的波向东移动较快. 于是,1940—1950年代开始,预报员就掌握了长波移动的外推方法,预测未来时刻槽和脊的位置,从而做出未来短期(2—3天)内的天气(如降水)预报.超过这个期限,天气系统(槽和脊)就会发生很大的变化或调整,该方法的预报也就失去了意义.事实上,500hPa上的天气系统(槽和脊)不可能按照一种尺度的波动运动,而会受到多尺度波动和来自高低层波动的影响,一般3 天后的槽脊强度和位置就将发生明显的变化.
数值天气预报模式的优点就是能够包含大气中多尺度波动和多层次波动的相互作用.于是,目前欧洲中期天气预报模式[2]的环流形势预报已经达到了9—10天的可用信息.无论是天气形势实况,还是数值天气预报形势,一个槽脊到达东亚大槽的位置就会发生明显的强度变化,往往天气环流系统并不对应观测到的极端天气事件.在9月份,当有热带风暴移近到华南沿海,即将登陆时,还会迅速加深.对这些现象,资深预报员可以总结出很多的经验,但经验只可会意,难以言传.本文首先从极端天气事件和异常气候事件的定义出发,从大气变量物理分解的角度认识天气扰动对极端天气和异常气候事件发生的预示意义.
2 极端天气事件与异常气候事件天气是多气象要素(温度、气压、湿度、风等)随时间的连续变化及其产生的各种现象(如云、雨雪、雷暴、雾霾、沙尘暴等).天气是与中尺度—天气尺度(200~2000km)系统的生消和移动相联系的.因此,天气系统的移动速度和生命期决定了局地天气变化的时间尺度.
天气的一些要素,特别是气温、降水、能见度和风,在量值上不超过一定的限度,对人们的生产和生活不会构成威胁,这些天气都是正常的.它们的量值超过了一定的限度(阈值)就会给人们的生产和生活造成危害.随着经济发展速度的加快和人们活动范围的拓展与社会财富的累积,同样强度的异常天气,在过去没有损失,不等于现在就没有损失.
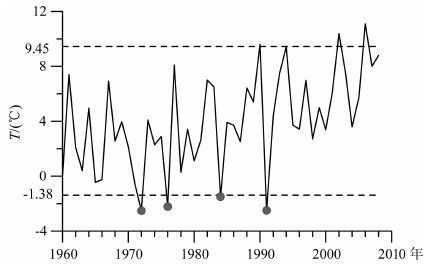
这里,我们只从气象上定义极端天气事件.以北京4月1日的日最低气温(夜间气温)为例.1960—2008年49年的4月1日最低气温平均值是4.04℃,第90个百分位的气温值是9.45 ℃,第10个百分位的气温值是-1.38 ℃.在49 年中有4 个4 月1 日的气温低于第10个百分位值.用于界定极端高温的第90个或第95个百分位温度值与用于界定极端低温的第10个或第5个百分位温度值,这些是人为确定的相对阈值.49年中,1972年的4月1日和1991 年的4月1日出现了两个最冷最低气温,称为最冷夜.它们可能是某一天的低温情况,但不一定是寒潮或低温天气过程中出现的最低气温.
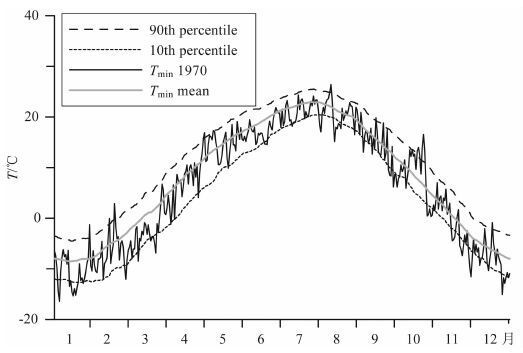
气候的一般定义是一段时间内(月以上)天气的总和特征.在统计上,它既包含了平均状态,也反映了极端情况,如极端高温和极端低温等.图 1只给出了北京49 年中所有4 月1 日的最低气温,和第10与第90百分位的最低气温值.用此方法,我们可以确定49年中4 月2 日、3 日,以至全年365 天的每日最低气温值和该日第10个及第90个百分位的最低气温值.把北京365 天逐日最低气温的多年平均值和两个阈值画在一起如图 2 所示.图 2 中的细曲线是1970年北京站的逐日最低气温.因为日最低气温出现在夜间,那些日最低气温值位于短虚线之下的称为冷夜,那些日最低气温值位于长虚线之上的称为暖夜.1970年的1 月份,有两次连续的日最低气温低于第10个百分位阈值的时段.第一次持续了2天,第二次持续了5天.第一次持续时间短于第二次,但强度大.它们反映了两个持续时间和强度各不相同的寒潮极端天气事件过程.因此,不同的极端天气事件要比较它们的持续时间、强度差异和区域范围.持续时间越长、影响范围越大和越强的极端天气事件,形成的危害会越大.
|
图 1 北京1960—2008年49年中4月1日最低气温(℃) 序列及其第10个百分位值和第90个百分位值线(虚线) Fig. 1 Daily minimum temperature (℃)in Beijing on April 1 from 1960 to 2008. The dashed lines indicate the 10 th and 90th percentiles of daily minimum temperature |
|
图 2 使用北京1960—2008年逐日最低气温计算的年循环(灰色实线)和用来确定相对温度极值的逐日第90百分位值(长虚线)与逐日第10百分位值(短虚线)的序列,细实线为1970年的逐日最低气温序列 Fig. 2 Annual cycle (grey solid line) and the 10th (short dashed line) and the 90th (long dashed line) percentiles for determining relative temperature extremes based on daily minimum temperature series in Beijing from 1960 to 2008. The thin solid line denotes the daily minimum temperature series from January 1 to December 31,1970 |
从图 2中可以看出,在1970年的7 月份,日最低气温都落在两条虚线之间,表明该月最低气温(气候)是正常的.可是,该年1 月份出现的2 次低温寒潮天气过程致使1 月平均最低气温比常年偏低,该年11月份出现了3 次低温寒潮天气过程,也使得11月平均最低气温比常年偏低.当月平均气温比常年偏低达到某一个确定的阈值,则可以认为发生了气候异常.可见,极端天气事件可以按天气过程的持续性(天数)而定,而异常气候事件可以定义由连续(或相连)出现的多次极端天气事件过程组成.经过时间平滑,相连的极端天气事件在平滑后极端值有所减小,过程也有所模糊,但在连续多次的极端天气事件平滑后的月尺度或数月尺度上气候异常事件更加明确了.这里也就清楚地给出了极端天气事件与异常气候事件之间的关系,即异常气候事件来自于多次或者持续的极端天气事件的积累.20个冷夜以单日均匀分布到一年中,与20个冷夜出现在一个月内,从异常气候事件的角度看是完全不同的.按上述定义,前者不是异常气候事件,后者是该年很强的月尺度异常气候冷事件.这是气候变化研究中需要考虑的一种确定异常气候事件的思路.
从图 1中可以看出,北京站在前20 年和后20年的平均最低气温是不同的,后者平均气温偏高,可能含有年代际变化.选择前20 年与后20 年的日最低气温做出图 2的分布也会不同.如果用前20年温度分布计算的百分位值,来确认后20年每年的冷暖日极端,冷夜必然减少,暖夜必然增多,但不等于极端天气事件和异常气候事件的增多.因此,极端天气和异常气候是比气候变化更受政府和公众关心的事件.
3 物理分解的意义为什么先要有极端天气事件和异常气候事件的定义呢?这是因为要追根溯源,即寻找发生这些事件的原因.一个气象站观测的连续变量,如温度、气压、湿度和风,或一个探空气象站观测的高空温度、位势高度、湿度和高空风(统称为大气变量)随时间变化的序列是一维的.连续几十年到百年的观测序列中包含变量的昼夜(日)循环变化、季节(年)循环变化、几十年和几百年的周期性变化,以及非规则强迫形成的大气内部天气尺度扰动和观测误差.寒潮、低温、热浪、区域持续性暴雨等都与天气尺度扰动有关.大气变量中的日变化、季节循环和各种时间尺度的周期性变化成份都是气候变化,如太阳辐射等周期性强迫引起的大气变化.这些气候变化是需要认识、掌握和利用的,而不需要预报.需要预报的是相对这些规则变化的扰动.
当前气象和气候要素场的分解有多种数学方法,如子波变换[3]、Fourier变换[4]、奇异谱分析(SSA)[5],以及经验模态分解(END)[6]和集合经验模态分解(EEND)[7]等方法.这些方法的特点是能够满足数学分解的正交性,其中END 和SSA 收敛的速度相对较快,但它们都需要分解成近十个或上百个正交分量.核心问题是,这些数学分解的分量难以明确对应的物理含义.根据气象时间序列变化的本质,我们可先从观测的气象序列中提取气候变化的规则(或周期)分量并用强迫量的序列做同样时间尺度的物理分解,从而确认气候变化的因果关系[8].两个简单又可理解的例子是,日变化的当地温度是在太阳正午最大辐射后的2—3个小时最高,季节变化的北半球中高纬度温度是在太阳直射北回归线(6 月22 日)40多天后的8 月初最高[9].这种因果关系的时间差就有了预报意义.
大气多变量在空间上随时间的变化和相互作用构成了大气运动的复杂形式.在简单的由二维空间和一维时间构成的系统中,一个大气变量如温度,区域上的数学分解方法可用经验正交函数展开(EOF),得到多个空间模态和对应的时间系数序列. 这些空间模态满足数学上的正交和收敛,但大部分模态不具有物理含义.大气是在球面三维空间中的无边界运动.大气变量的球谐函数展开方法是当前短期(1—3 天)和中期(4—9 天)-延伸期(10—30天),以及气候(月至年)预测模式中分解变量的基本方法.随着计算机容量和速度的提高,满足正交性的球谐函数变量展开波数会越来越多(可高达几百,如T639就有639个正交的谐波分量),相对于空间分辨率越来越高.这些分解的波也同样缺少物理含义. 由于大气运动的复杂性(非线性相互作用),无物理意义的波作为初始值进入计算机运算,可产生出新的虚假波,导致几天到10天后数值天气预报模式结果与实况相反,失去预报意义.
4 物理分解的方法根据大气环流的平衡特性[10],我们用最近10年以上(可用N大于10 年或至30 年)全球或北半球对流层至平流层大气观测的站点或格点温度T、位势高度H、风V和湿度Q等变量进行四分量物理分解,以温度T分解式为例:
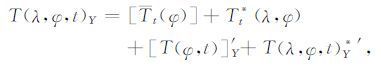
|
(1) |
(1) 式等号左边的变量T(λ,φ,t)Y是第Y年从1月1日起算第t日随经度λ 和纬度φ 变化的历史的、当前的气象观测温度场,或中期数值天气预报模式的温度场.
分解式等号右端第一项[Tt(φ)]是对应N 年内第t日气候平均及沿纬圈平均后只随纬度φ 变化的温度,其数学表达式如下:
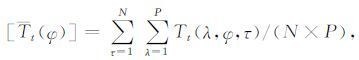
|
(2) |
该分量Tt[(φ)]是太阳辐射季节变化确定的气候变量(如温度)场,τ 是第t日从第1年至第N年,λ是纬圈等距格点数从第1点至最后第P点.
分解式等号右边第二项是相对第t日用第1年至第N年时间平均的空间格点温度减去相对第t日太阳辐射纬圈平均季节变化[Tt(φ)]后的气候逐日空间变量场,
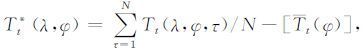
|
(3) |
该分量是海陆(地形)分布季节调节的逐日温度空间分布场.
第三项大气中行星尺度纬圈平均扰动分量的分离方法是:用历史观测的、当日观测的变量值,或中期数值天气预报模式的未来1 至10 天的大气变量的预报值,减去逐日纬圈平均气候分量得到.以温度扰动为例,分解式(1) 等号右边第三项是第Y年第t 日的纬圈平均行星尺度温度扰动分量,该分量是第t日行星尺度温度扰动循环所处的位相,与热带海洋或极地年代际、年际和季节内热力强迫变化有关.
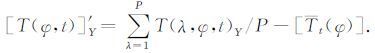
|
(4) |
第四项大气中的天气尺度瞬变扰动分量的分离方法是:用历史观测的、当日观测的变量值,或中期数值天气预报模式输出的未来1 至10 天的大气变量值,减去逐日气候分量和纬圈平均的瞬时扰动分量得到.以温度扰动为例,分解式(1) 等号右边第四项是第Y年第t日的天气尺度温度瞬变扰动分量,
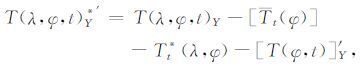
|
(5) |
该分量对极端天气事件有指示意义,称为天气尺度瞬变波分量,或天气尺度扰动,其形成原因是多尺度地形和热力强迫以及大气内部波动非线性相互作用的结果.最后两项在业务天气预报中可以有广泛的应用,是中期-延伸期极端天气事件预报的理论基础.
5 物理分解的比较常规天气图上混杂包含了天气尺度瞬变扰动信号和气候规则变化信号,而极端天气事件的发生是与天气尺度瞬变扰动联系的.在目前国内外的业务短期天气预报流程中,把气候变化分量与天气尺度瞬变扰动分量混在一起作为未来极端天气事件预报的信号,极大地削弱了大气中天气扰动对极端天气事件预报的信号指示能力.气象科研和业务预报中的区域大气或球面大气波动信号的获取仅仅满足正交收敛的数学分解,缺乏物理含义.在非线性数学模型,如短期和中期-延伸期天气预报模型以及气候预测模型中,无物理意义的波动必然产生出新的虚假波动,从而缩短可预报时效,或者产生气候漂移.
以温度场的分解为例,我们给出从原始观测场到四个分量物理分解的图示.图 3 是2002 年7 月15日北半球850hPa温度场T(λ,φ,t)Y分布.最大的高温区(高于300K)位于非洲至中东地区.第二大高于300K 的高温区在美国西部地区.第三大高于300K 的高温区在中国大陆的西部地区.图 3中存在几百公里的高、低温中心,但在视觉上已经被大陆和大洋尺度的高、低温中心掩盖了.
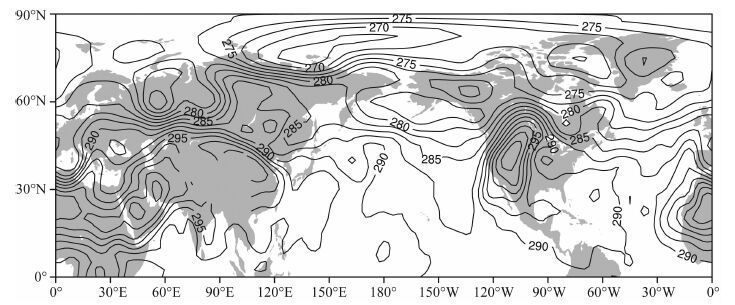
|
图 3 2002年7月15日北半球850hPa温度场T(λ,φ,t)Y分布(单位:K) 在地形高于1500m 处无等温线. Fig. 3 Distribution of the 850 hPa temperature (K) of the original observationT(λ,φ,t)Y July 15,2002 in the Northern Hemisphere There is no isotherm if the topography is higher than 1500 m.. |
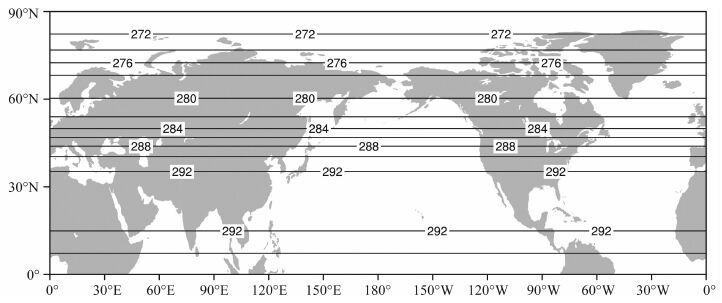
为了得到图 3中的那些天气尺度的瞬变高、低温中心,我们需要分离出图 3中的气候部分.图 4是用历史上30年(1971—2000年)7月15日850hPa 温度资料按照变量分解式展开的第一分量南北温差[Tt(φ)].温度分布呈纬圈条带:30°N 以南热带地区温度大于292K 并且均匀分布,35°N—55°N 之间温度从292K 下降到280K,70°N 以北地区温度进一步下降.这一分量反映了太阳辐射季节变化确定的气候变量(温度)场.气候上的7 月15 日,这一温度分量在中纬度地区(40°N—50°N)随纬度升高下降最快.
|
图 4 用历史30年(1971—2000年)7月15日观测的北半球850hPa 温度分解的纬圈-时间平均气候对称分量[Tt(φ)](单位:K) Fig. 4 Distribution of zonal time-averageclimate symmetric part[Tt(φ)]in the Northern Hemisphere based on the 850 hPa temperature (K) for the historical observations of 30 years (1971—2000) |
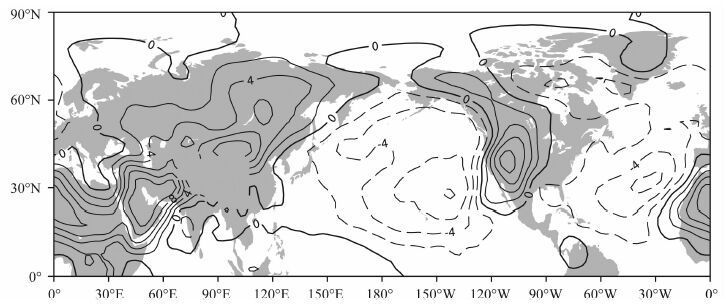
温度变化除了随太阳辐射有季节变化外,海陆分布的季节调节作用也是巨大的.图 5是用30年7 月15日850hPa历史多年温度按照变量分解式展开的第二分量,即分解出的海陆温差在该日的T*t(λ,φ)气候分布.图 3中,分别位于非洲-中东地区、美国西部地区和中国大陆西北地区的3个高温中心在图 5中更为清楚.可见,图 3中的3个850hPa高温中心主要来自海陆气候分量的贡献.北美大陆和欧亚-非洲大陆850hPa上的高温是海陆影响出的气候正距平,而太平洋和大西洋上为负距平,反映了海陆分布对大气低层气候温度的调节作用,由它们的温差可以构造热力气候(或季风)指数.Zhao 等[11]利用夏季亚洲与北太平洋这两个相邻区域上的温度年际变化构造了一个东亚夏季风指数,它能反映北半球多个区域的年际气候异常.
|
图 5 用历史30年(1971—2000年)7月15日观测的北半球850hPa温度分解的时间平均气候非对称部分T*t(λ,φ)(单位:K).在地形高于1500m 处无等温线 Fig. 5 Distribution of time-average climate asymmetric part Tt*(λ,φ)in the Northern Hemisphere based on the 850 hPa temperature (K ) for the historical observations of 30 years (1971—2000) .There is noisotherm if the topography is higher than 1500 m |
同样,用全球30年的850hPa位势高度也能计算出海陆引起的第二分量分布.比较第44候和第8 候850hPa上的位势高度H*t(λ,φ)分布,可以得到全球存在随季节变化的17个高压和低压系统[9],另外还有一个南极高压和一个南极低压[12].这些高压系统和低压系统被称为大气活动中心.但是,大气活动中心的变化不是孤立的,有时两个相邻的大气活动中心的气压(或高度)有此起彼伏的现象,Walker 把这种翘翘板式的变化称为涛动.Walker 和Bliss[13](1932) 提出了世界天气(worldweather)的概念并首次定义了下列3 大涛动.南太平洋与印度洋气压变化相反,称为南方涛动(SO).大西洋上,冰岛低压与其以南地区的北大西洋亚速尔高压,两个中心气压的变化称为北大西洋涛动(NAO).太平洋上,阿留申低压与夏威夷高压,它们之间的气压变化称为北太平洋涛动(NPO).对全球存在的19 个大气活动中心,Walker和Bliss提出的全球三大涛动只用到了6个大气活动中心,还有13个大气活动中心没有被用上.实际上,人们可以利用任意相邻的两个大气活动中心定义一个涛动,构造一个环流(气候)指数,或季风指数.
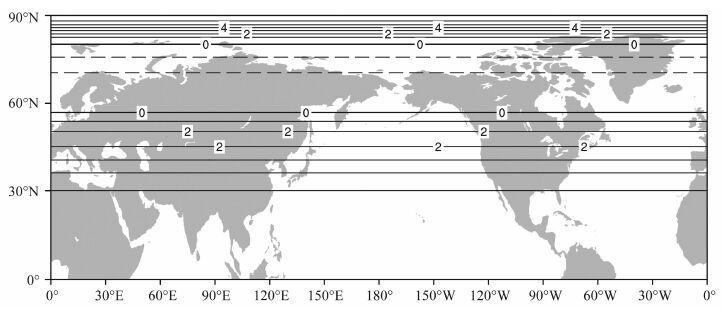
在季节内至年际时间尺度上,赤道内外下垫面,特别是海洋热力状况会发生明显的变化,从而引起大气环流和大气变量的瞬变扰动.图 6是2002年7 月15日观测温度计算的分解第三项,即南北多条带指数循环[T(φ,t)]′Y,30°N 至55°N 之间和80°N 以北为正异常扰动温度条带,而55°N 至80°N 之间为负异常扰动温度条带,反映了大气下垫面强迫引起的纬圈平均行星尺度大气瞬变扰动.
|
图 6 用2002年7月15日观测的北半球850hPa温度计算的行星尺度纬圈平均对称扰动[T(φ,t)]′Y(单位:K) Fig. 6 Distribution of the zonal-average planetary-scale transient symmetric anomaly[T(φ,t)]′Y in the Northern Hemisphere based the observational 850 hPa temperature (K) on July 15, 2002 |
早期,Rossby提出把35°和55°纬圈之间的平均地转西风定义为西风指数就是第三分量的数量描述.十年前,当Thompson和Wallace提出位势高度场和温度场的北极涛动(AO)信号[14]的一年后,Gong和Wang定义了南极涛动(AAO)指数[15],两个涛动也是南、北半球中高纬度地区第三分量的表现.
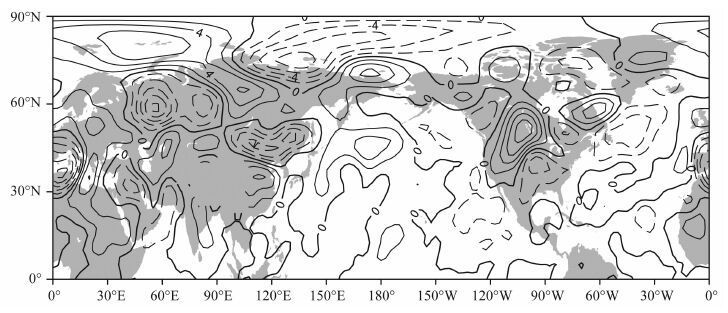
根据(5) 式,可得到某日的大气扰动量.图 7 是2002年7月15日观测的850hPa温度计算的分解第四项,反映了该日天气尺度瞬变温度扰动T(λ,φ,t)Y*′,华北至东北为负距平的温度扰动,而中国南方的正距平温度扰动对应7月7日至18日的热浪.位于中国的这一对南北温度扰动比原始温度场(图 3)更清楚,用天气尺度瞬变扰动更有利于极端天气事件的分析和预报.同样,在美国的中北部、加拿大中部和东部地区也各有一个高温扰动中心.这些高温扰动中心都对应有地面上的气温偏高.对天气尺度瞬变扰动也可以计算3 天、5 天、7 天、9 天,甚至1 个月的时间平均,从而分析和认识扰动系统的稳定与持续性.
|
图 7 用2002年7月15日观测的北半球850hPa温度计算的天气尺度瞬变非对称扰动T(λ,φ,t)Y*′(单位:K).在地形高于1500m 处无等温线 Fig. 7 Distribution of the regional-scale transient asymmetric anomaly T(λ,φ,t)Y*′in the Northern Hemisphere based the observational 850 hPa temperature (K) on July 15,2002. There is no isotherm if the topography is higher than 1500 m |
这些长时间平均仍然存在的天气尺度扰动,会在一些地方时常出现,并像波列那样排列[16-17].太平洋-北美遥相关型(PNA)、西大西洋遥相关型(WA)、东大西洋遥相关型(EA)、西太平洋遥相关型(WP)、欧亚-太平洋遥相关型(EUP)、日本-太平洋遥相关型(PJ)等,都是大气中经常出现的波列.显然,这些遥相关波列会带来不同地区的异常天气和异常气候.
6 物理分解分量随时间变化的相对值图 7是850hPa气压层上分解得到的天气尺度瞬变温度扰动分布.对应中国南方和北方的高温扰动和低温扰动中心,如果它们持续3天、5天、甚至7 天仍然存在,说明这是一个持续稳定的天气扰动,必然会形成持续异常的极端天气事件.统计上,我们可考察温度、高度和风在四项分解中每项各占总方差的相对百分率贡献及其随平均时间(天数)的变化.
图 8表示2003 年(365 天)850hPa的温度、高度和风在四项分解中各项占总方差的相对百分率贡献及其随平均时间(1—30 天平均)的变化.对温度场的分解(图 8a),第四项T(λ,φ,t)Y*′从1 天的52%下降到30 天平均的26%,而第二项T*t(λ,φ) 和第一项[Tt(φ)]分别从1 天的25% 和11% 增加到30天平均的40%和26%.15天以内的天气尺度温度扰动分量有着较强的信号.
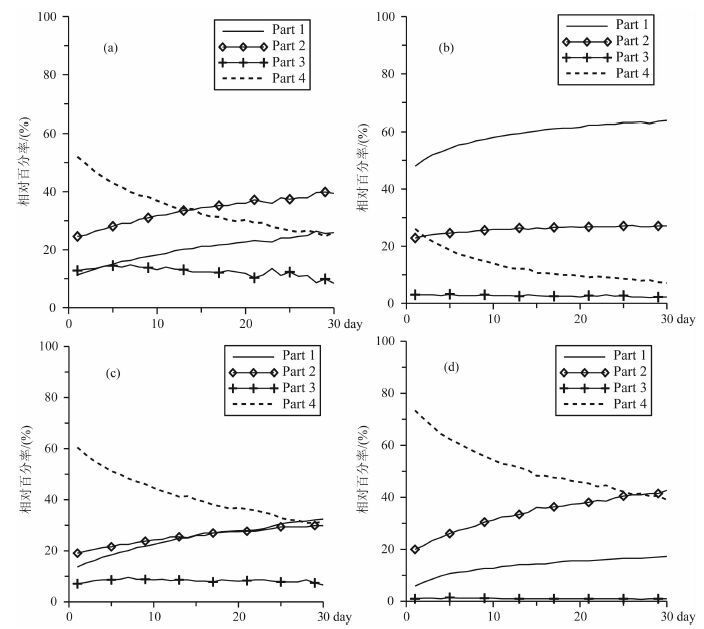
|
图 8 850hPa变量在四项分解中每项各占总方差的相对百分率贡献随平均时间(天数)的变化(a)温度;(b)高度;(c)西风U;(d)南风V. Fig. 8 Decomposition ratio (%) of four terms changed with average days for variables of (a) temperature, (b) geopotential height, (c) westerly wind U, and (d) southerly wind V at the 850 hPa level |
对高度场的分解(图 8b),第一项[珨Ht(φ)]在最初15天的平均从48%增大到60%,而第四项H(λ,φ,t)Y*′从1天的26%减小到30天平均的7%,第三项[H(φ,t)]′Y占的比例很小,第二项H*t(λ,φ)在1—30天维持在23%~27%.在几天内,分解的前两项气候分量占有相当大的比重,会掩盖与极端天气事件对应的天气尺度扰动分量信号的提取.
对西风U分量(图 8c)进行分解,天气尺度扰动分量U(λ,φ,t)Y*′从1天的61%下降到30天平均的31%,而第一、第二项从1天的14% 和19% 上升到30天平均的32%和30%.对南风V分量(图 8d)的分解,天气扰动分量V(λ,φ,t)Y*′从1天的73%下降到30天平均的40%,而第一、第二项从1 天的6%和20%上升到30天平均的17%和43%.四个变量中第三项占的比例很小,都不超过15%,温度场和南风V分量的第三项比例尤为小,分别为2%~3%和1%左右.在1 至20 天内的平均中,经向风天气尺度瞬变扰动分量对热量和水汽的输送有直接的贡献.因此,850hPa层的扰动风,对暴雨等极端天气事件的发生,能够提取重要的预报信息.
现有常规的天气预报方法所采用的极端天气事件(结果)与大气变量(原因)的对接关系,是极端天气事件与原始观测气象变量A(温度、高度、风等)的对接.气象变量A中包含有太阳辐射的季节变化和海陆分布季节调节对温度等大气变量的作用,它们不是产生极端天气事件的直接原因.四分量物理分解则建立了极端天气事件(结果)与天气尺度瞬变波动(扰动)变量A*′(原因)的直接对接关系[18].从这些图例看出,天气尺度瞬变扰动分量必须从观测资料中把气候变化分量分离开,这对极端天气事件的预报才有意义.
7 结果与讨论(1) 每天观测的全球大气变量中包含已知外源强迫的常规气候变化的分量和行星尺度与天气尺度瞬变扰动分量.通过四分量分解式可以清楚地得到有物理含义的气候变化分量与天气尺度瞬变扰动分量.第一分量是太阳辐射季节变化引起的逐日大气气候响应.第二分量反映了海陆热力和动力对比对气候的季节调节作用.第三分量反映了行星尺度大气瞬变扰动,是纬圈指数循环的季节、年际和长期变化.第四分量是瞬变天气尺度的大气波动,当稳定时间较长时就是一种异常扰动,对应有异常天气和异常气候.观测量和模式预报量的四分量物理分解可以把科研人员和业务预报员从长期混淆的经验积累中解放出来,增加人们对极端天气事件发生本质的认识,提高业务人员的预报技能.
(2) 用观测变量和模式产品物理分解的天气尺度瞬变扰动,与极端天气事件之间可能存在着紧密的物理因果关系.未来的短期和中期(或延伸期)预报系统中,如果增加天气尺度瞬变波动分量的扰动天气图参与预报会商,将会大大提高高温热浪、寒潮低温、暴雨、干旱和台风路径等的灾害性天气预报能力.
(3) 逐日气候与天气尺度瞬变波动的分解方法,在短期、中期(或延伸期)和气候预报模式中的应用,可极大地提高目前这些数值预报的水平和延长预报时效.因为没有物理意义的波动,被代入模式运算,必然产生出没有物理意义的结果,难以延长预报时效.同样,有物理意义的气候波动被分解为无物理意义的分量,也会产生没有意义的气候漂移.
(4) 利用1971—2000年(或1981—2010年)共30年的对流层至平流层的多变量大气观测资料,我们已经建立了大气逐日气候资料集.利用1950—2010年的逐日观测对流层至平流层的大气多变量资料,我们已经建立了天气尺度瞬变扰动(波动)的数据集.这些气候和天气扰动资料集是研究历史上极端天气事件成因和预报未来短、中期和延伸期极端天气事件的基础.
(5) 以温度分解为例,本方法在获得气候变化分量时取用了30年的历史逐日确定时刻观测变量的平均.实际上,逐日对应时刻的气候在30 年中也是随时间变化的.全球平均温度在最近30年的增暖趋势约为0.5 ℃.相对于最近30年,中国的极端低温[19-20]和极端高温[21]事件的平均温度变化强度为5~10 ℃.因此,单位时间内长期气候变化的幅度相对天气扰动的变化幅度要小几个量级.
| [1] | Rossby C G, Collaborators. Relation between variations in the intensity of the zonal circulation of the atmosphere and the displacements of the semi-permanent centers of action. J. Marine Res. , 1939, 2(1): 38-55. DOI:10.1357/002224039806649023 |
| [2] | Brankovic', Palmer T N, Molteni F, et al. Extended-range predictions with ECMWF models: Time-lagged ensemble forecasting. Q. J. R. Meteorol. Soc. , 1990, 116(494): 867-912. DOI:10.1002/(ISSN)1477-870X |
| [3] | Lau K M, Weng H. Climate signal detection using wavelet transform: How to make a time series sing. Bull. Am. Meteor. Soc. , 1995, 76(12): 2391-2402. DOI:10.1175/1520-0477(1995)076<2391:CSDUWT>2.0.CO;2 |
| [4] | Brook B G J. Applying wavelet and Fourier transform analysis to large geophysical datasets. Lecture Notes in Computer Science , 2009, 5549: 426-434. |
| [5] | Schlesinger M E, Ramankutty N. An oscillation in the global climate system of period 65~70 years. Nature , 1994, 367(6465): 723-726. DOI:10.1038/367723a0 |
| [6] | Wu Z, Huang N E, Long S R, et al. On the trend, detrending, and variability of nonlinear and nonstationary time series. Proceedings of the National Academy of Sciences, USA , 2007, 104(38): 14889-14894. DOI:10.1073/pnas.0701020104 |
| [7] | Wu Z, Huang N E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Advances in Adaptive Data Analysis , 2009, 1(1): 1-41. DOI:10.1142/S1793536909000047 |
| [8] | Qian W H, Lu B. Periodic oscillations in millennial global-mean temperature and their causes. Chinese Sci. Bull. , 2010, 55(35): 4052-4057. DOI:10.1007/s11434-010-4204-2 |
| [9] | Qian W H, Tang S Q. Identifying global monsoon troughs and global atmospheric centers of action on a pentad scale. Atmospheric and Oceanic Science Letters , 2010, 3(1): 1-6. DOI:10.1080/16742834.2010.11446841 |
| [10] | Starr V P, White R M. Balance requirements of the general circulation. Geophysical Research Paper , 1954, 12: 66. |
| [11] | Zhao P, Zhu Y, Zhang R. An Asian-Pacific teleconnection in summer tropospheric temperature and associated Asian climate variability. Clim. Dyn. , 2007, 29(2-3): 293-303. DOI:10.1007/s00382-007-0236-y |
| [12] | 钱维宏. 气候变化与中国极端气候事件图集. 北京: 气象出版社, 2011 . Qian W H. Atlas of Climate Change and China Extreme Climate Events (in Chinese) (in Chinese). Beijing: China Meteor. Press, 2011 . |
| [13] | Walker G T, Bliss E. World weather V. Mem. Roy. Meteor. Soc. , 1932, 4(36): 53-84. |
| [14] | Thompson D W J, Wallace J M. The Arctic Oscillation signature in the wintertime geopotential height and temperature fields. Geophys. Res. Lett. , 1998, 25(9): 1297-1300. DOI:10.1029/98GL00950 |
| [15] | Gong D Y, Wang S W. Definition of Antarctic Oscillation index. Geophys. Res. Lett. , 1999, 26(4): 459-462. DOI:10.1029/1999GL900003 |
| [16] | Wallace J M, Gutzler D S. Teleconnections in the geopotential height field during the Northern Hemisphere winter. Mon. Wea. Rev. , 1981, 109(4): 784-812. DOI:10.1175/1520-0493(1981)109<0784:TITGHF>2.0.CO;2 |
| [17] | Barnston A G, Livezey R E. Classification, seasonality and persistence of low-frequency atmospheric circulation patterns. Mon. Wea. Rev. , 1987, 115(6): 1083-1126. DOI:10.1175/1520-0493(1987)115<1083:CSAPOL>2.0.CO;2 |
| [18] | 钱维宏. 基于大气变量物理分解的低温雨雪冰冻天气的中期预报系统和方法: 中国, CN10222174A.2011-10-19. Qian W H. Middle-range forecast system and method of the low-temperature freezing rain based on the physical decomposition of atmospheric variables: China, CN10222174A.2011-10-19. |
| [19] | Ding T, Qian W H, Yan Z W. Characteristics and changes of cold surge events over China during 1960—2007. Atmospheric and Oceanic Science Letters , 2009, 2(6): 339-344. DOI:10.1080/16742834.2009.11446823 |
| [20] | Zhang Z J, Qian W H. Identifying regional prolonged low temperature events in China. Adv. Atmos. Sci. , 2011, 28(2): 338-351. DOI:10.1007/s00376-010-0048-6 |
| [21] | Ding T, Qian W H, Yan Z W. Changes of hot days and heat waves in China during 1961—2007. Int. J. Climatol. , 2009, 30(10): 1452-1462. |
 2012, Vol. 55
2012, Vol. 55

