2. 中国地质大学(北京)地球物理与信息技术学院,北京100083;
3. 中国石油大学(北京)地球物理与信息工程学院,北京102249;
4. 中国石油大学(华东)地球科学与技术学院,东营257096;
5. 中国海洋石油公司研究总院,北京100027
2. School of Geophysics and Information Technology,China University of Geosciences ,Beijing 100083,China;
3. College of Geophysics and Information Engineering,China University of Petroleum,Beijing 102249,China;
4. College of Geosciences and Technology,China University of Petroleum,Dongying 257096,China;
5. Research InsLLiLuLe of China NcLional Offshore Oil Corp. ,Beijing 100027,China
大斜度井/水平井(即定向井)对远距离或环境较敏感区域的油气开采有积极意义.定向井电阻率测井的影响主要包括相对井斜、围岩和层厚以及泥浆侵入等方面[1-4],而且,由于双侧向测井电极系参数不同,其测井响应也有差别.双侧向测井视电阻率影响的校正通常包括井眼校正、井斜-围岩/层厚校正和侵入校正等.传统的围岩/层厚影响校正图版是针对某一种双侧向测井仪器在井眼垂直地层条件下得到的,在定向井中原有的图版不能照搬使用.而且,从三维双侧向测井的数值模拟来看,在仪器倾斜条件下,尤其是井斜角超过30°后,测井视电阻率受围岩的影响较大.因此,要想获得准确的地层电阻率,必须同时考虑井斜、围岩和目的层厚度的变化来研究环境校正[5-10].
目前,国内外学者在电阻率测井的数值模拟和环境校正方面作了一些积极探索和研究,取得了一些成果.高杰等[11]针对理想模型采用正演和快速反褶积方法进行定向井的电测井曲线校正,但没有对实际测井数据进行校正.邓少贵等[12]针对水平井地层模型,利用有限元数值模拟方法建立了水平井双侧向测井层厚及围岩影响校正图版,并据此有效地实现了层厚及围岩影响校正方法.在径向泥浆侵入方面,泥浆侵入会造成电测井响应的动态变化[13-16],而且,在大斜度井/水平井中,由于井斜、层厚/围岩的影响,实际的泥浆侵入特性更为复杂,难以直接利用双侧向测井资料进行流体识别,因此,必须求取原状地层的电阻率.而且,石油测试工程也迫切需要知道泥浆侵入半径,为射孔枪选择和测试分析提供参考和依据.因此,针对定向井开展双侧向测井的环境影响校正是非常有意义的.
针对研究区的定向井测井环境、盐水泥浆以及地质特点,本文首先采用二维有限元方法(2DFEM)计算了不同尺寸井眼的电阻率响应,并绘制了井眼校正图版;然后,针对不同井斜的地层模型,采用三维有限元方法(3DFEM)计算了不同厚度地层的测井响应,构建了井斜-围岩/层厚图版,并利用图版的规律实现了井眼校正和井斜-围岩/层厚的电阻率校正.最后,针对泥浆侵入的影响,利用非线性最小二乘反演方法计算了侵入半径和地层真电阻率,最终实现了双侧向测井的环境校正.理想模型和实际测井数据的处理结果表明,该方法应用效果较好.
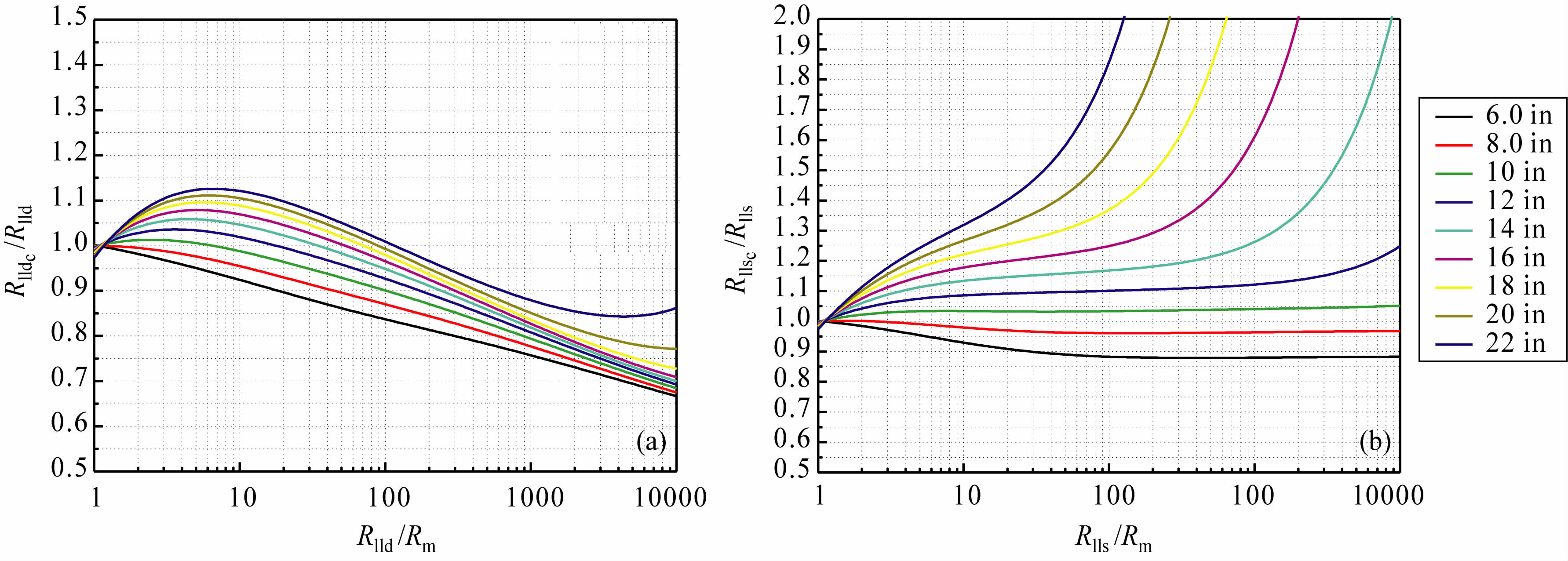
2 双侧向测井环境影响校正方法 2.1 井眼影响校正图版和校正方法利用有限元(FEM)开展双侧向测井井眼影响校正研究.在地层无限厚、井眼尺寸一定、无泥浆侵入条件下的地层模型,具有旋转轴对称性,因此,可用二维有限元方法(2D FEM )模拟电阻率响应[6, 17-18].利用上述方法对双侧向测井进行大量数值模拟,制作了研究区井眼校正图版(图 1).该图版的制作条件是:研究区泥浆电阻率(Rm )约为1.0Ωm,井眼的尺寸从6in(1in=2.54cm,下同)开始,以2in为步长,逐步递增至22in.以深侧向电阻率(Rlld)与泥浆电阻率的比值(Rlld/Rm)为横坐标,校正系数(Rlldc/Rlld)为纵坐标,井径(D)做模数.从图 1a可以看出,随着泥浆电阻率的降低或Rlld/Rm 的增大,校正量Rlldc/Rlld逐渐增大;当Rlld/Rm 大于一定数值时,校正量Rlldc/Rlld越来越小.对于浅侧向来说,随着泥浆电阻率的降低或Rlls/Rm 的增大,其校正量具有如下变化规律(图 1b):当井径大于8in时,校正量Rllsc/Rlls越来越大;当井径小于8in 时,校正量Rllsc/Rlls越来越小并逐渐趋于不变.
|
图 1 双侧向井眼校正图 (a)深侧向;(b)浅侧向. Fig. 1 Borehole correction charts for dual laterolog (a) Deep laterolog;(b) Shallow laterolog. |
利用该图版,将厚度无限大、无侵入地层的视电阻率乘上校正系数即可得到原状地层的电阻率.对图 1所示图版中不同井径的关系曲线进行回归,可得到深、浅侧向电阻率的具体校正公式.
不同井径的深侧向电阻率校正近似表达式如下:
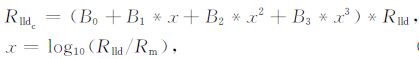
|
(1) |
式中,B0、B1、B2、B3 为系数,具体数值见表 1
|
|
表 1 Rlld井眼校正公式系数表 Table 1 Borehole correction formula coefficients for Rlld |
.不同井径的浅侧向电阻率校正近似表达式如下:
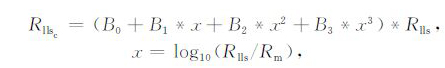
|
(2) |
式中,B0、B1、B2、B3,具体数值见表 2.
|
|
表 2 Rlls井眼校正公式系数表 Table 2 Borehole correction formula coefficients for Rlls |
进行井斜-围岩/层厚影响校正,需要制作不同井斜角和层厚的校正图版.在不考虑泥浆侵入影响的条件下,采用三层介质模型,上下为围岩(Rs),中间为目的层(Rt).图版具体制作方法:针对某一井斜角的三层介质模型,利用三维有限元(3D FEM)数值模拟方法[2, 4, 7]计算多组不同层厚(H)模型的深侧向和浅侧向视电阻率,记为Rlld和Rlls;然后,提取出不同层厚(H)下某一固定Rlld/Rs(或Rlls/Rs)的一组数据,绘出该井斜条件下的围岩/层厚校正图版;最后,改变井斜角,得到其他井斜角的一系列校正图版.图 2和图 3分别为井斜角15°、30°、45°、60°、75°、90°的围岩/层厚校正图版.

|
图 2 不同井斜角深侧向测井围岩/层厚校正图版 (a) 15°井斜角;(b) 30。井斜角;(c) 45。井斜角;(d) 60。井斜角;(e) 75。井斜角;(f)90。井斜角. Fig. 2 Bed-thickness correction charts for deep laterolog in different derivation angles (a) 15。deviation angle; (b)30。deviation angle; (c) 45。deviation angle;(d) 60。deviation angle; (e) 75。deviation angle; (f) 90。deviation angle. |

|
图 3 不同井斜角浅侧向测井围岩/层厚校正图版 (a) 15°井斜角;(b) 30。井斜角;(c) 45。井斜角;(d) 60。井斜角;(e) 75。井斜角;(f)90。井斜角. Fig. 3 Bed-thickness correction charts for shallow laterolog in different derivation angles (a) 15。deviation angle; (b) 30。deviation angle; (c) 45。deviation angle;(d) 60。deviation angle; (e)75。deviation angle; (f) 90。deviation angle. |
这一系列图版的制作条件是:三层地层模型,井径为0.045m(已经经过井眼校正,相当于紧贴仪器周围),研究区围岩(Rs)为3.0Ωm,仪器无偏心,无泥浆侵入.选定目的层厚度(H)为横坐标,深侧向校正系数(Rlldc/Rlld)和浅侧向校正系数(Rllsc/Rlls为纵坐标,视电阻率与围岩电阻率的比值(Rlld/Rs 或Rlls/Rs)为图版模数.
图 2所示为不同井斜角和层厚的深侧向校正图版,可以看出,深侧向电阻率校正系数(Rlldc/Rlld)随目的层厚度(H)的增大而起伏变化,其变化规律取决于围岩电阻率与目的层电阻率的比值.当围岩电阻率大于目的层电阻率时,校正系数Rlldc/Rlld大于1,说明校正后的电阻率大于原视电阻率;当围岩电阻率小于目的层电阻率时,校正系数Rlldc/Rlld小于1,说明校正后的电阻率小于原视电阻率.随着目的层厚度的增大,深侧向校正系数曲线Rlld/Rlls逐渐减小,当目的层厚度增大20m 时,该校正系数Rlld/Rlls趋近于1,可不必进行层厚校正.当井斜角较小时,如小于30°时,校正系数Rlldc/Rlld数值介于1.0~1.3之间,即不同层厚的校正系数不大;随着井斜角的增加,其校正系数逐渐增大,当井斜角为60°时,校正系数Rlldc/Rlld数值介于1.0~1.9之间,当井斜角逐渐增加到75°和90°后,校正系数Rlldc/Rlld持续增大,这说明井斜越大电阻率受的影响也越大,相应的校正系数也越大.总之,井斜越大、层厚越小校正系数越大.
对于浅侧向测井来说,图 3所示规律与图 2类似,只不过校正系数Rllsc/Rlls偏小.
为实现计算机的快速校正,根据图版所表达的规律,拟合了一系列校正公式.以图 2c所示为45°井斜校正图版为例,从图中得到不同的Rlld/Rs 对应的校正公式.当目的层厚度(H)为0.6~1.92m 时Rlldc= (B0+B1*H+B2*H2+B3*H3)*Rlld,(3)式中,B0、B1、B2、B3 的具体数值见表 3.
|
|
表 3 45°井斜Rlld围岩/层厚校正公式系数表(H=0.6〜1.92 m Table 3 Bed-thickness correction formula coefficients for Rlld with 45。deviation angle (H=0.6 〜1.92 m) |
当目的层厚度(H)为1.92~15.0m 时
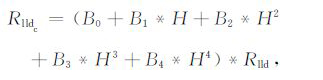
|
(4) |
式中,B0、B1、B2、B3、B4 的具体数值见表 4.
|
|
表 4 45°井斜Rlld围岩/层厚校正公式系数表(H=1.92〜15.0 m) Table 4 Bed-thickness correction formula coefficients for Rlldwith 45。deviation angle (H=1.92〜15.0 m) |
同理,从图 3c可得到Rlls的校正公式.当目的层厚度(H)为0.6~2.72m 时
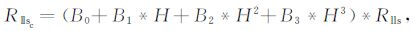
|
(5) |
式中,B0、B1、B2、B3 的具体数值见表 5.
|
|
表 5 45。井斜Rlls围岩/层厚校正公式系数表(H=0.6〜2.72 m) Table 5 Bed-thickness correction formula coefficients for Rllswith 45。deviation angle (H=0.6〜2.72 m) |
当目的层厚度(H)为2.72~15.0m 时
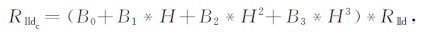
|
(6) |
式中,B0、B1、B2、B3 的具体数值见表 6.
|
|
表 6 45。井斜Rlls围岩/层厚校正公式系数表(H=2. 72〜15.0m) Table 6 Bed-thicknes correction formula coefficients for Rllswith 45。deviation angle (H=2.72〜15.0 m) |
根据上述不同井斜-围岩/层厚图版和校正公式,就可以对井眼校正后的双侧向测井曲线进行环境校正.具体校正步骤如下:首先,利用自然电位(SP)或自然伽马(GR)等进行分层,分别计算每层的平均电阻率和上下围岩的电阻率以及每层的厚度;然后,根据井斜角选择相应的图版及其相应的校正公式,采用插值的方法求得相应的校正系数;最后,利用上述公式对双侧向测井进行井斜、围岩/层厚校正.
2.3 泥浆侵入校正方法从理论上讲,利用三维有限元的方法可以构建不同侵入深度的校正图版(即旋风图版),通过查图版的方法可以读取地层真电阻率和侵入深度,但是这种办法费时费力.因此,为了实现泥浆侵入的计算机自动校正,拟采用反演的方法求取原状地层电阻率.
2.3.1 泥浆侵入校正反演方法双侧向测井响应是原状地层电阻率、冲洗带电阻率和侵入半径等模型参数向量(p)的非线性函数,记为Rth(p).双侧向测井电阻率反演问题是:利用双侧向测井数据(观测数据,Rai,i=1,2,…,m)求解原状地层电阻率(Rt)、冲洗带电阻率(Rxo)和侵入半径(Rin)等地层参数.但由于地层模型参数和测井响应之间没有明确的解析关系,求解上述地层模型参数(p)通常采用Marquardt优化算法.该方法是一种非线性优化方法,通常采用逐次线性化的方法进行最小二乘求解,其特点是通过多次迭代求解线性化后的法方程,逐步逼近最优解.为此,首先将其在地层模型参数向量的某个初值p0 处作Taylor展开,并略去二次项及二次以上项:
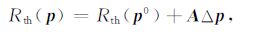
|
(7) |
式中,Rth(p)为计算的理论测井值构成的向量,即Rth(p)= (Rth1,Rth2,…,Rthm),m维;p= (ρ1,ρ2,…,ρn)T 为待反演的地层模型参数向量,n维;Δp=p-p0 是向量p的修正量向量,A为m×n阶的Jacobi矩阵:
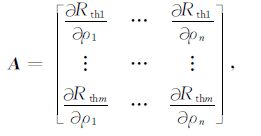
|
其中,\[{{a}_{ij}}=\frac{\partial {{R}_{\text{th}i}}}{\partial {{\rho }_{j}}}\left( i=1,2,\cdots ,m;j=1,2\cdots ,n \right)\]为Jacobi矩阵元素,是第i点的视电阻率理论计算值Rthi关于第j个模型参数ρj的一阶偏导数(常称Frechet导数).
根据(7)式得到理论测井值向量(Rth)与测井数据(Ra)的残差:
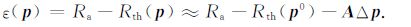
|
(8) |
记b=Ra-Rth(p0)为观测值向量Ra 与某个给定地层模型(参数向量为p0 )计算的理论测井值Rth(p0)之差,则(8)式变为
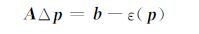
|
略去该式中的ε(p),得方程组
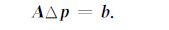
|
(9) |
该式为关于地层模型参数修正量向量Δp的m×n线性方程组.
通常情况下,测井反演时测量值个数m要大于待反演参数个数n,故(9)式为超定方程.由于该方程系数矩阵A的逆不存在或其部分奇异值为零,使得该方程可能无解或实际计算时解不稳定.Tikhonov和Arsenin把这种问题归为不适定问题,并提出了求解不适定问题的正则化方法(RegularizationMethod)[19,20],引入正则化因子(即阻尼因子),将(9)式修正为
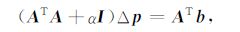
|
(10) |
此式即为利用Marquardt算法进行反演计算的方程.求解出Δp,则地层模型参数即为

|
由于在进行侵入校正之前已经进行了井眼、井斜-围岩/层厚校正,消除了上述影响因素,因此,待反演的观测数据是经过上述校正后的数据,待反演的模型参数向量为p= (Rt,Rxo,rin)T.
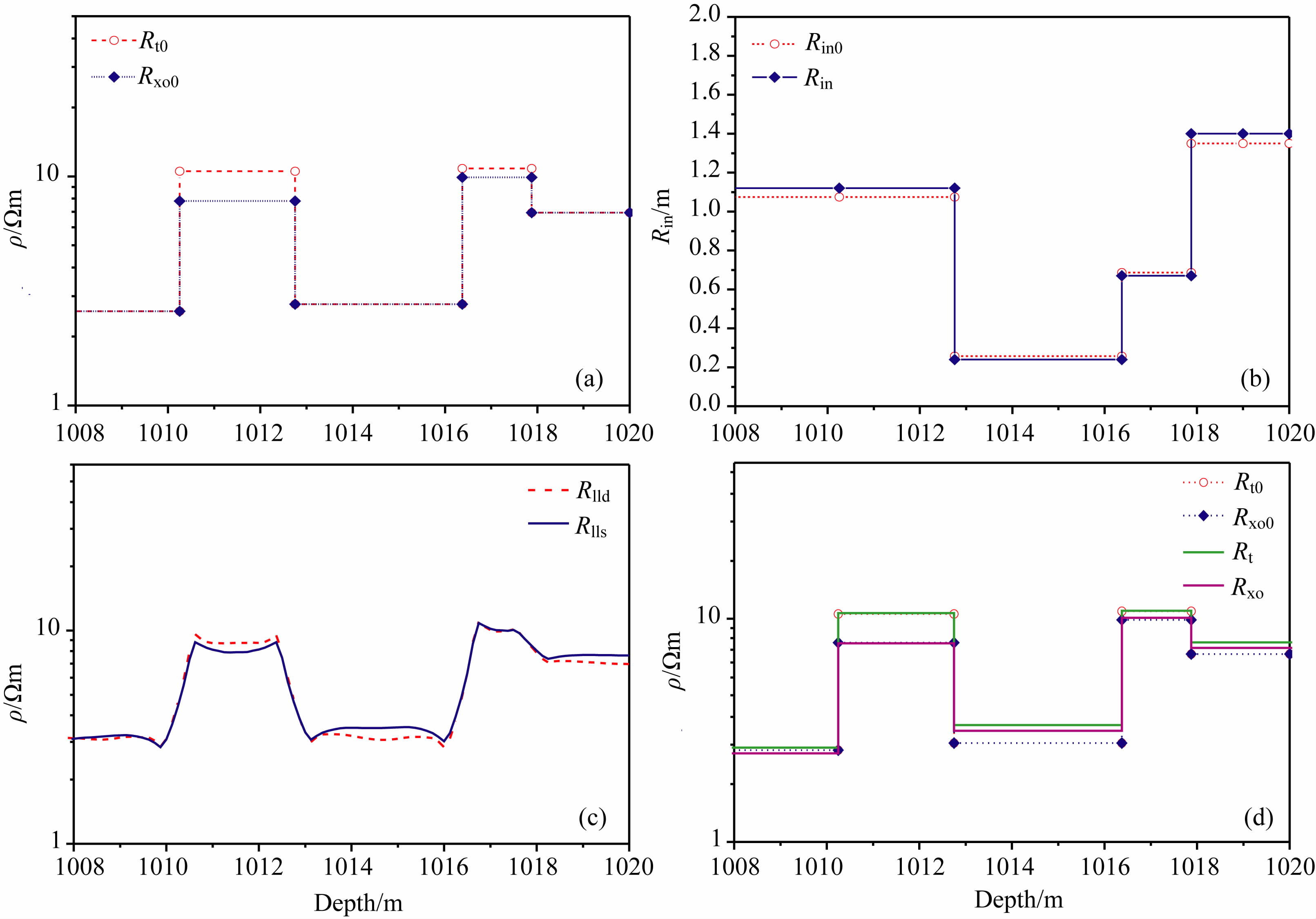
2.3.2 双侧向测井三参数反演模型验证为验证算法的可靠性,用理想模型(图 4a和图 4b)进行电阻率的正反演计算的相互验证.图 4a所示为5层的原状地层电阻率(Rt0)和冲洗带电阻率(Rxo0)模型,图 4b为相应的侵入半径模型(Rin0).首先,用三维有限元正演算法计算该地层模型的深侧向(Rlld)和浅侧向(Rlls)测井响应,作为待反演的观测数据(图 4c).然后,选取适当的原状地层电阻率、冲洗带电阻率和侵入半径初始值作为反演初始模型,用正演方法计算相应的测井数据,将之与观测数据进行比较,通过不断修正参数值使目标函数减小,直到取得极小值,此时的参数值即为求解结果,即反演得到原状地层电阻率(Rt)、冲洗带电阻率(Rxo)和侵入半径(Rin).从图 4d可以看出,反演结果与与设定地层模型的电阻率、侵入半径参数基本一致,说明该反演算法是可靠的.
|
图 4 双侧向测井正演模拟及反演实验 (a)地层电阻率模型;(b)侵入模型与反演的侵入半径;(c)地层模型的双侧向测井响应;(d)电阻率反演结果与模型对比. Fig. 4 Forward modeling and inversion tests of dual laterolog (a) Formation resistivity model; (b) Invasion model and invasion radius inverted;(c) Dual laterolog modeling results; (d) Comparisons of inversion results and model. |
经过井眼校正后的深、浅侧向测井曲线在进行人工或计算机自动分层后,分别计算每层的平均电阻率和上下围岩的电阻率以及每层的厚度.根据不同的井斜角,由双侧向电阻率的层厚校正图版得到具体的校正系数完成曲线校正.校正后的测井曲线作为输入,利用三参数反演方法实现地层真电阻率(Rt)、冲洗带电阻率(Rxo)和侵入半径(Rin)的计算.
3.1 实例A井A 井为研究区内一口开发井,泥浆电阻率为0.421Ωm@22 ℃和0.233Ωm@57 ℃;自然电位为正异常,说明泥浆相对地层水为盐水泥浆.本井采用常规CCLTDLL/MSFL 测井系列.
该本井段的井斜角为33°,对该井先后进行井眼、井斜-围岩/层厚、侵入校正,侵入校正采用反演方法.首先进行井眼校正,得到井眼校正后的深侧向电阻率(RLDB)和浅侧向电阻率(RLSB);然后,将RLDB 和RLSB 作为输入进行井斜-围岩/层厚校正,其校正结果为RLDP和RLSP;最后将RLDP和RLSP作为输入进行侵入校正,得到原状地层电阻率(Rt)、冲洗带电阻率(Rxo)以及侵入半径(Rin).
图 5为本井1500~1600m 的处理成果.从图中看出,井眼校正前后电阻率变化不大,但是井斜-围岩/层后校正后其电阻率具有明显的变化:深侧向电阻率(RLDP)变大,浅侧向电阻率(RLSP)几乎不变,说明低阻围岩对储层电阻率影响较大.在图示的层段中,有三个砂层,其中2号层(1520~1531.0m),原测量电阻率约为10 Ωm,反演的原状地层电阻率(Rt)约为14~15 Ωm,反演后电阻率升高约4~5Ωm,反演的冲洗带电阻率(Rxo)为6Ωm,比原浅侧向电阻率数值略小2.0Ωm,因此,双侧向测井正差异变大;同时,计算的侵入半径(Rin)为0.5~1.0m,泥浆侵入较深,可以推测该储层储集性能好,为高孔、高渗储层.在这三个储层中间的层段,自然电位和自然伽马测井曲线指示为泥岩,而且其反演的深侧向电阻率和冲洗带电阻率完全重合,无侵入.

|
图 5 A井电阻率环境校正处理结果 Fig. 5 Dual laterolog environment correction results for Well A |
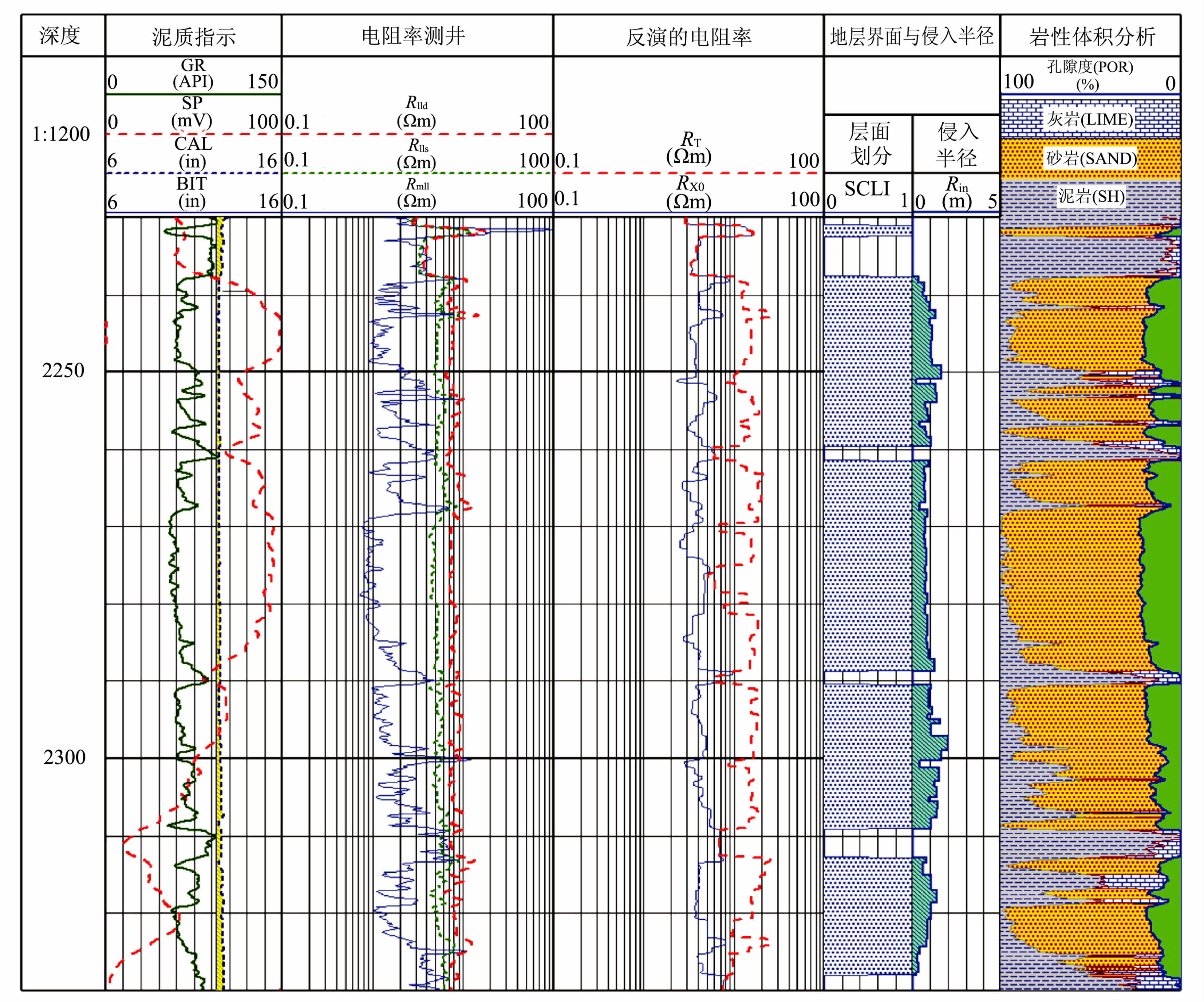
B井为研究区内另一口评价井,泥浆电阻率为0.1381Ωm@27 ℃和0.063Ωm@84 ℃;自然电位为正异常,说明泥浆相对地层水为盐水泥浆.该本井段的井斜角为10°,对该井进行了井眼和井斜-围岩/层厚校正处理,图 6显示了该井2230~2330m 段的数据处理结果.该段岩性为砂岩,测量的深侧向电阻率(Rlld)约为6Ωm,反演的原状地层电阻率(Rt)约为10Ωm,电阻率数值增高约4.0Ωm,而反演的冲洗带电阻率比浅侧向电阻率(Rlls)数值小1~2Ωm,此时,原状地层电阻率(Rt)与冲洗带电阻率(Rxo)的正差异比原双侧向差异大,电阻率数据得到了校正,而且计算的侵入半径(Rin)为1.0~1.5m.在未反演之前,储层与非储层的电阻率差异较小(本井泥岩段电阻率约为2~4Ωm)差异较小,很难分辨流体的性质和计算流体的饱和度,反演后地层电阻率(Rt)与冲洗带电阻率(Rxo)的比值约为2~5,解释为油层.2010年10 月测试日产油8m3,水0.3m3,测试结果证实了解释结论.
|
图 6 B井双侧向环境校正处理结果 Fig. 6 Dual Laterolog environment correction results for Well B |
本井说明在侵入较深且泥浆电阻率较小的情况下,地层视电阻率测量不准确,泥浆侵入校正是必不可少的.
3.3 实例C井C 井为研究区内另一口评价井,泥浆电阻率为0.421Ωm @22 ℃ 和0.233Ωm @57 ℃;自然电位为正异常,说明泥浆相对地层水为盐水泥浆.该本井段的井斜角为45°.图 7 为本井2260~2300 m 井段的处理成果为砂岩.在泥质砂岩段(2260~2288m),反演的深侧向电阻率(Rt)和冲洗带电阻率(R>xo)大多完全重合,计算得到大多层段侵入半径(Rin)为0m.而在砂岩段(2288~2300m),深侧向电阻率(Rlld)约为50~60Ωm,浅侧向电阻率(Rlls)约为40Ωm,两者呈明显正差异;反演后,原状地层真电阻率(Rt)约为80~120Ωm,比视电阻率大30~60Ωm,反演的冲洗带电阻率(Rxo)约为20Ωm,比原浅侧向电阻率数值略小,计算的侵入半径(Rin)为0.5~1.5m.原状地层电阻率与冲洗带之间的差异大,这说明储集性能好,与计算的孔隙度数据吻合.

|
图 7 C井双侧向环境校正处理结果 Fig. 7 Dual laterolog environment correction results for Well C |
与A 井、B井相比,C 井斜较大,校正量也较大;此外,由于本井的孔隙度比A 井和B 井孔隙度大,盐水泥浆的侵入对储层影响也较大,因此必须进行侵入校正.
4 结论与讨论此项研究针对盐水泥浆条件下定向井中井眼、泥浆、井斜、围岩等环境影响因素问题,针对双侧向测井提出了一套利用图版和反演理论相结合的环境校正思路和方法,形成了一套环境校正方法和程序,实现了定向井的双侧向测井环境校正.
(1) 井眼校正和井斜-围岩/层厚校正的图版法.针对研究区的双侧向测井系列、泥浆性能和围岩电阻率,利用有限元数值模拟方法分别研制了一系列不同井眼尺寸泥浆校正图版以及不同井斜的井斜-围岩/层厚校正图版,研究出了各个图版中的校正规律,利用计算机实现了井眼(泥浆)、井斜-围岩/层厚的快速校正,能够消除上述因素对测井的影响.从图版可以看出,井斜越大时薄层的校正量越大,井斜较小时可不必进行层厚校正;厚度越大校正量越小,当厚度大于20m 时可不必进行层厚校正.
(2) 采用非线性最小二乘反演方法开展了侵入校正方法研究.针对井眼(泥浆)、井斜-围岩/层厚的快速校正后的测井数据,利用非线性最小二乘反演方法计算得到了地层真电阻率和冲洗带电阻率以及侵入半径.针对预设地层模型计算了双侧向测井电阻率,并进行了反演实验,其反演结果与模型具有较高的一致性,说明基于此反演方法的侵入校正结果是可靠的;
(3) 对研究区的双侧向测井数据进行了数据处理,分析了研究区地层的侵入特征和电阻率校正情况.实例分析认为,环境校正后得到的地层真电阻率均比原视电阻率高,井斜角越大,其校正量越大,原视电阻率受井斜影响越大;计算的研究区侵入半径大约为0.5~1.5m,泥浆侵入校正是必不可少的.
总之,针对盐水泥浆条件下定向井中双侧向测井数据必须进行井眼(泥浆)、井斜-围岩、侵入等环境影响因素校正,才能得到地层的真电阻率.
| [1] | Chemali R, Gianzero S, Su S M. The Dual Laterolog In Common Complex Situations. SPWLA 29th Annual Logging Symposium, June 5-8, 1988. |
| [2] | 汪涵明, 张庚骥. 倾斜地层的双侧向测井响应. 测井技术 , 1994, 18(6): 408–412. Wang H M, Zhang G J. The dual Laterolog response in dipping beds. Well Logging Technology (in Chinese) , 1994, 18(6): 408-412. |
| [3] | 聂在平, 陈思渊. 复杂介质环境中双侧向测井响应的高效数值分析. 电子学报 , 1994, 22(6): 30–37. Nie Z P, Chen S Y. The numerical analysis for the response of dual lateral logging tool in a complex environment. Acta Electronica Sinica (in Chinese) , 1994, 22(6): 30-37. |
| [4] | 肖加奇, 张庚骥. 水平井和大斜度井中双侧向测井响应的正演. 石油大学学报 (自然科学版) , 1996, 20(1): 24–30. Xiao J Q, Zhang G J. Computation of dual laterolog responses in highly deviated and horizontal wells with 3-d finite element method. Journal of the University of Petroleum, China (in Chinese) , 1996, 20(1): 24-30. |
| [5] | Xiao J, Beard D L, Zhou Q. A practical dipping-effect correction for multlarray induction tools in deviated wells. SPWLA 37th annual logging symposium, June 16-19 1996. |
| [6] | Wang H M. Finite Element Analysis of Resistivity Logging. Dissertation of University of Houston , 1999. |
| [7] | Wang H M, Shen L C, Zhang G J. Dual laterolog Response in 3-D Environments. Petrophysics , 2000, 41(3): 234-241. |
| [8] | Cosmo C, Spalburg M R, Looyestijn W J. Fast deconvolution of laterologs by direct inverse filtering. SPWLA 32nd annual logging symposium, June 16-19, 1991. |
| [9] | Maurer H, Antonov Y, Corley B, et al. Advanced processing for a new array laterolog tool. SPWLA Fiftieth Annual Logging Symposium, June 21-24, 2009. |
| [10] | 谭茂金, 张庚骥, 运华云, 等. 非轴对称条件下用三维模式匹配法计算电阻率测井响应. 地球物理学报 , 2007, 50(3): 803–810. Tan M J, Zhang G J, Yun H Y, et al. 3-D numerical mode-matching (NMM) method for resistivity logging responses in nonsymmetric Conditions. Chinese J^ Geophys^ (in Chinese) , 2007, 50(3): 803-810. |
| [11] | 高杰, 谢然红. 大斜度井侧向测井三维正演数值模拟及曲线快速校正方法研究. 石油勘探与开发 , 2000, 27(2): 69–271. Gao J, Xie R H. 3D numerical forward modeling and fast correction of dual-laterolog for high angle deviated wells. Petrol Eum Exploration And Development (in Chinese) , 2000, 27(2): 69-271. |
| [12] | 邓少贵, 李竹强, 李智强. 水平井双侧向测井响应及层厚/围岩影响快速校正. 石油勘探与开发 , 2009, 36(6): 725–730. |
| [13] | 陈丽虹, 李舟波. 侵入带对视电阻率的影响. 长春科技大学学报 , 1999, 29(3): 295–298. Chen L H, Li Z B. Effect of the invaded zone on apparent resistivity. Journal of Changchun University of Science and Technology (in Chinese) , 1999, 29(3): 295-298. |
| [14] | 潘和平, 樊政军, 马勇. 电阻率测井的钻井液侵入校正方法. 天然气工业 , 2005, 25(7): 40–44. Pan H P, Fan Z J, Ma Y. Correction method of drilling fluid invasion of resistivity logging. Natural Gas Industry (in Chinese) , 2005, 25(7): 40-44. |
| [15] | 谢关宝, 范宜仁, 吴海燕, 等. 储层泥浆侵入深度预测方法研究. 测井技术 , 2006, 30(3): 240–243. |
| [16] | 李长喜, 李潮流, 周灿灿, 等. 淡水钻井液侵入对双感应和双侧向测井响应的影响. 石油勘探与开发 , 2007, 34(5): 603–608. Li C X, Li C L, Zhou C C, et al. Effects of fresh drilling mud invasion on logging responses of dual induction and dual lateral to reservoirs. Petroleum Exploration and Development (in Chinese) , 2007, 34(5): 603-608. |
| [17] | 李大潜, 等. 有限元素法在电法测井中的应用. 北京: 石油工业出版社, 1980 . Li D Q. Finite Element Method in Electrical Logging (in Chinese). Beijing: Petroleum Industry Press, 1980 . |
| [18] | 张庚骥. 电法测井(下册). 北京: 石油工业出版社, 1984 . Zhang G J. Electrical Logging (in Chinese). Beijing: Petroleum Industry Press, 1984 . |
 2012, Vol. 55
2012, Vol. 55


