2. 地质过程与矿产资源国家重点实验室, 武汉 430074;
3. 东方地球物理公司综合物化探事业部, 河北 涿州 072751
2. State Key Laboratory of Geological Processes and Mineral Resources, Wuhan 430074, China;
3. BGP, CNPC, Hebei Zhuozhou 072751, China
海洋可控源电磁法(MarineControlledSourceElectromagnetic,CSEM)被称为自三维反射地震出现以来最为重要的地球物理勘探技术[1],是海上油气勘探的有效方法,但在我国尚未开展系统的研究工作.早期,胡文宝[2]、杨梅霞等[3],杨进[4]等在海洋电磁法方面进行过1D 和2D 的数值模拟研究.近两年,魏文博等[5]、刘长胜等[6]开展了海洋电磁法的实验研究.为了在我国油气勘探领域推广这一方法技术,何展翔等[7-9]对CSEM 做了系统的调研工作,并在利用CSEM 参数识别海上油气田边界方面开展了前瞻性的研究[10].目前,CSEM 的研究和应用已经逐渐走向了三维勘探.在三维电磁场的正演模拟方面,国内外学者均做了大量重要的工作:Newman和Alumbaugh[11]给出了频率域的交错网格有限差分法;Smith[12, 13]对频率域的交错网格有限差分法进行了深入的探讨,提出了在迭代求解系统方程的过程中加入散度校正来加快收敛速度的方法;Badea等[14]给出了基于库仑标准势的有限元法;沈金松[15]也基于交错网格有限差分法计算了三维频率域的电磁响应;Weiss等[16]发展了Newman 的方法,引入了有限体积法;Maao[17]给出了时域的有限差分法;Streich[18]在现有频率域有限差分法的基础上,给出了提高计算精度的几种方法;Mittet[19] 在海洋CSEM 响应模拟中引入地震波场模拟中广为使用的高阶时域有限差分法;徐志锋和吴小平[20]给出了基于磁矢量位和电标量势的频率域有限元法;陈辉等[21]在三维大地电磁交错网格有限差分模拟中,进一步发展了散度校正方法.Mukherjee和Everett[22]给出了基于矢量有限元法的海洋CSEM 模拟方法.
对CSEM 的地形模拟,还未见三维情况下的工作公开发表,仅Li和Key 基于二维的自适应网格剖分有限元法[23-25]对一个二维的斜坡模型进行了模拟分析[26].
本文采用基于交错网格的三维有限体积法来模拟CSEM 响应,为了提高CSEM 地形响应的模型精度,对含地形界面网格单元的电导率进行加权平均处理,通过与有限元程序的计算结果对比,验证了方法的有效性.最后,计算了一个三维带地形的储层模型的CSEM 响应,并分析了地形变化的影响.
2 有限体积法基本原理 2.1 控制方程对于海洋可控源电磁法所使用的电流密度为Js,角频率为ω 的低频电偶极子场源,在似稳场假设下,忽略位移电流,其电场响应E满足如式(1)所示的二阶偏微分方程[16]:
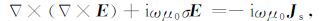
|
(1) |
式中,μ0 =4π×10-7H/m 为真空中的磁导率,σ为电导率,时谐因子取eiωt.对于一个电偶极子源,Js可以表示为[15]
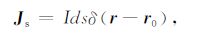
|
(2) |
(2)式中,δ(r)为单位冲激函数(即狄拉克函数,且有$\int_{-\infty }^{\infty }{\delta \left( r \right)}\left. \text{d}r=1 \right)$,其表达式为
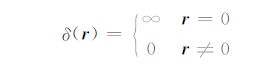
|
(3) |
从式(2)可以看出:当r=r0 时,即在场源点,电流密度Js 为无穷大.为了在数值模拟中解决场源点处的奇异性问题,引入一个参考电导率模型σ0(如电导率等于海水电导率3.3S/m 的全空间或者一维层状模型等),用解析法求偶极子源Js 对该简单模型的电场响应E0 (以下称为一次场或背景场),由于E0 满足(1)式,故有
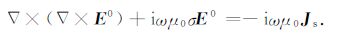
|
(4) |
将(1)式减去(4)式可得
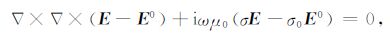
|
(5) |
引入二次场E′ = (E-E0)代入式(5)并整理可得

|
(6) |
式(6)即为待求的控制方程,该式中不含在场源点处奇异的电流源项Js,将其离散后得到一个大型线性方程组,解该方程组即可求得二次场E′,则总场E可由下式求得
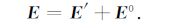
|
(7) |
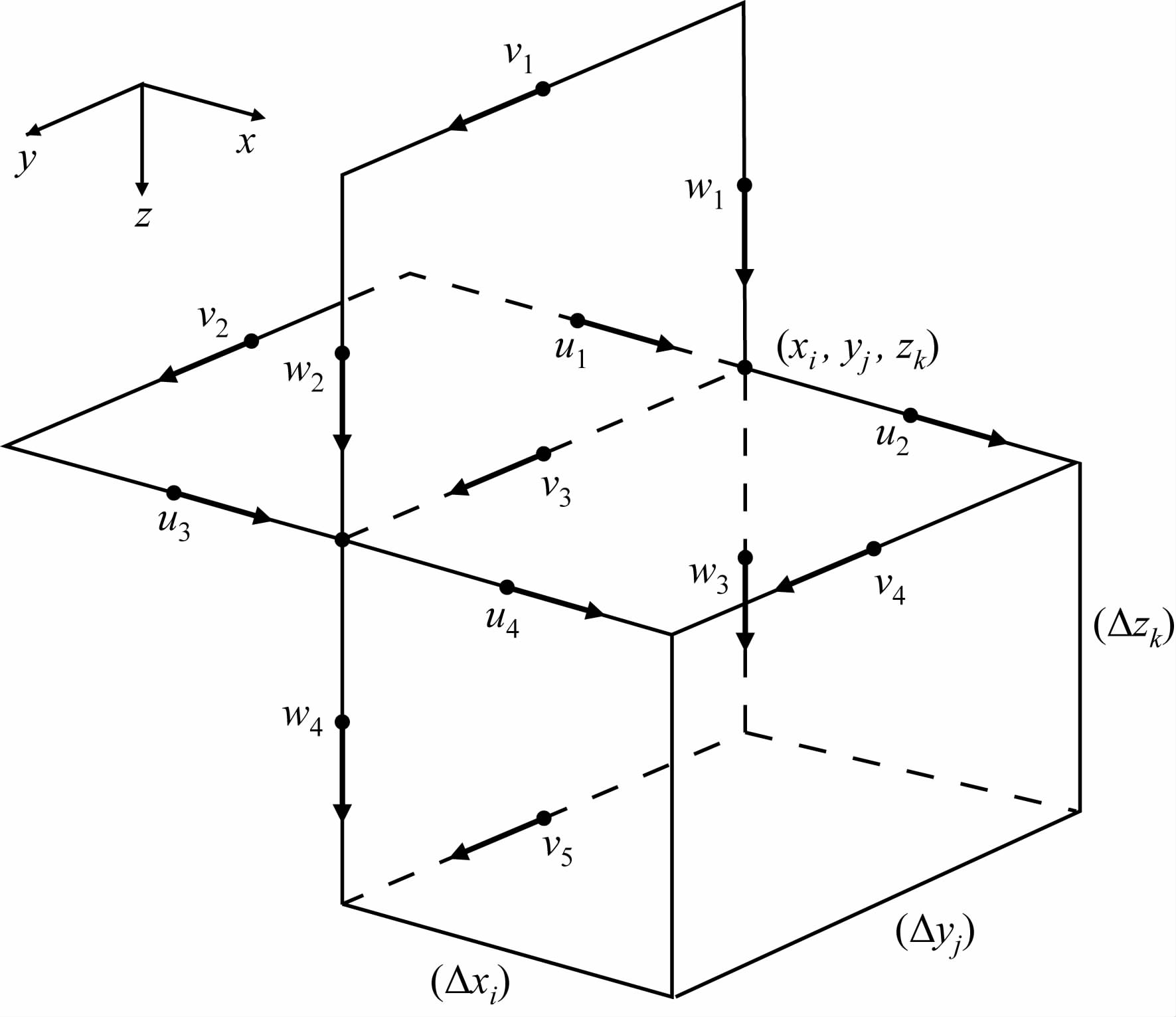
对待求解的偏微分方程(6)采用Yee格式对其进行离散化.对每一个网格单元,电场的采样位置位于网格单元每条棱边的中心点处,磁场的采样位置位于网格单元每个面的中心点位置.为了表达式的简明起见,将与(i,j+1/2,k)处的${\hat{y}}$向电场分量${{{{E}'}}_{y}}\left( i,j+1/2,k \right)$差分相关的各${\hat{x}}$,${\hat{y}}$和${\hat{z}}$向电场分量分别表示为${{u}_{p}}$,vp,${{\omega }_{p}}$,其中p= 1,2,3,4,而将${{{{E}'}}_{y}}\left( i,j+1/2,k \right)$表示为v3 (如图 1所示).
|
图 1 交错网格电场单元各分量位置示意图 (据Weiss 2006,有修改) Fig. 1 The position of electric componets on an electric staggered grid(Revised from Weiss 2006) |
将式(6)向${\hat{y}}$轴上投影可得如下的标量方程
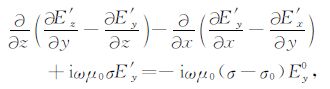
|
(8) |
则将式(8)直接用有限差分离散,可得
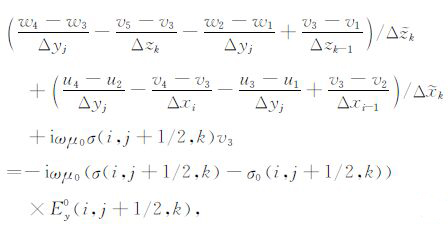
|
(9) |
(9)式中,$\sigma \left( i,j+1/2,k \right)$、${{\sigma }_{0}}\left( i,j+1/2,k \right)$和$E_{y}^{0}\left( i,j+1/2,k \right)$分别为电导率模型、参考电导率模型和一次场在点(i,j+ 1/2,k)处的取值,$\Delta {{{\tilde{x}}}_{i}}=1/2\left( \Delta {{x}_{i-1}}+\Delta {{x}_{i}} \right),\Delta {{{\tilde{z}}}_{k}}=1/2\left( \Delta {{z}_{k-1}}+\Delta {{z}_{k}} \right)$.式(9)即为有限差分离散的${\hat{y}}$轴上的标量方程,同理可以导出与上式形式相似的${\hat{x}}$和${\hat{z}}$轴上的标量方程.
为了导出式(6)的有限体积离散表达式,对每个待计算的电场分量构造一个体积单元(图 2).

|
图 2 控制体积单元(据Wdss 2006,有修改) Fig. 2 The control volume (Revised from Weiss 2006) |
在每个体积单元Ω 上对式(6)求积分有
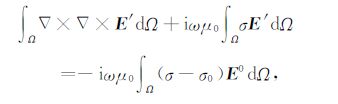
|
(10) |
根据高斯散度定理,如下恒等式成立:
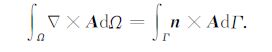
|
(11) |
由式(11),可以将式(10)中第一项对Ω 的体积分转化为对Γ 的面积分:
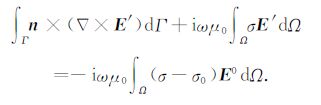
|
(12) |
(12)式中,n为Γ 面的外法向单位矢量.为了得到三个互相耦合的标量方程,将式(12)分别向${\hat{x}}$,${\hat{y}}$和${\hat{z}}$轴投影.取${\hat{y}}$轴上的分量为例,可得
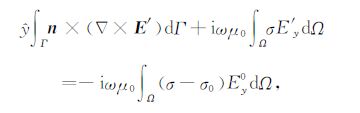
|
(13) |
将式(13)在图 1 所示的交错网格上离散,有
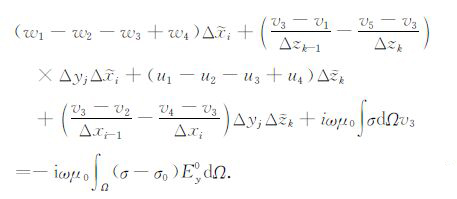
|
(14) |
同理,可以得到与(14)式相似的${\hat{x}}$和${\hat{z}}$轴上的分量所满足的标量方程.
为了比较有限体积法与有限差分法离散控制方程的差别,在式(9)的两端乘上图 2所示的控制体积单元的体积${{\Delta }_{\Omega }}=\Delta {{{\tilde{x}}}_{i}}\Delta {{y}_{i}}\Delta {{{\tilde{z}}}_{k}}$,则有
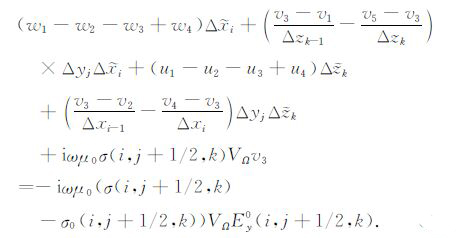
|
(15) |
表 1给出了式(14)和式(15)差异部分的比较.在场量的差分项,二者完全相同;在左端项求取体积电导及右项端对一次场求积分时,有限差分只取控制体积单元Ω 的中心点(i,j+1/2,k)处的值作为整个控制体积单元的平均值,而有限体积法则考虑了控制体积单元Ω 内的电导率和一次场的变化.这就是有限体积法较之有限差分法精度更高的原因所在.
|
|
表 1 有限差分与有限体积离散表达式差异比较表 Table 1 Comparison of the discrete formulae of FVM with FDM |
式(14)中的右端积分项可以应用数值积分法(如高斯积分法、牛顿-柯特斯积分法等)求其积分值.对边界上的网格单元应用Dirichlet边界条件,即将切向分量设置为零,则可形成复对称的方程组
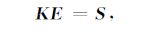
|
(16) |
式(16)中,E为离散网格节点上待求的电场值向量,S为离散后的右端项,K为刚度矩阵.
对方程组式(16)可以采用Krylov子空间迭代方法来求解[11],如双共轭梯度法(BICG)、拟最小残差法(QMR)等.
2.3 地形模拟与有限元法、边界元法等数值方法相比,采用规则矩形网格的有限差分和有限体积法不能对地形等不规则界面进行相对精确的模拟.为了提高海洋可控源电磁模拟的地形响应的精度,可以采取如下思路:一是在海底地形起伏区域加密网格,增强离散网格对该区域电性变化的刻画能力;二是对地形边界面上的网格单元的电导率值进行加权平均处理.
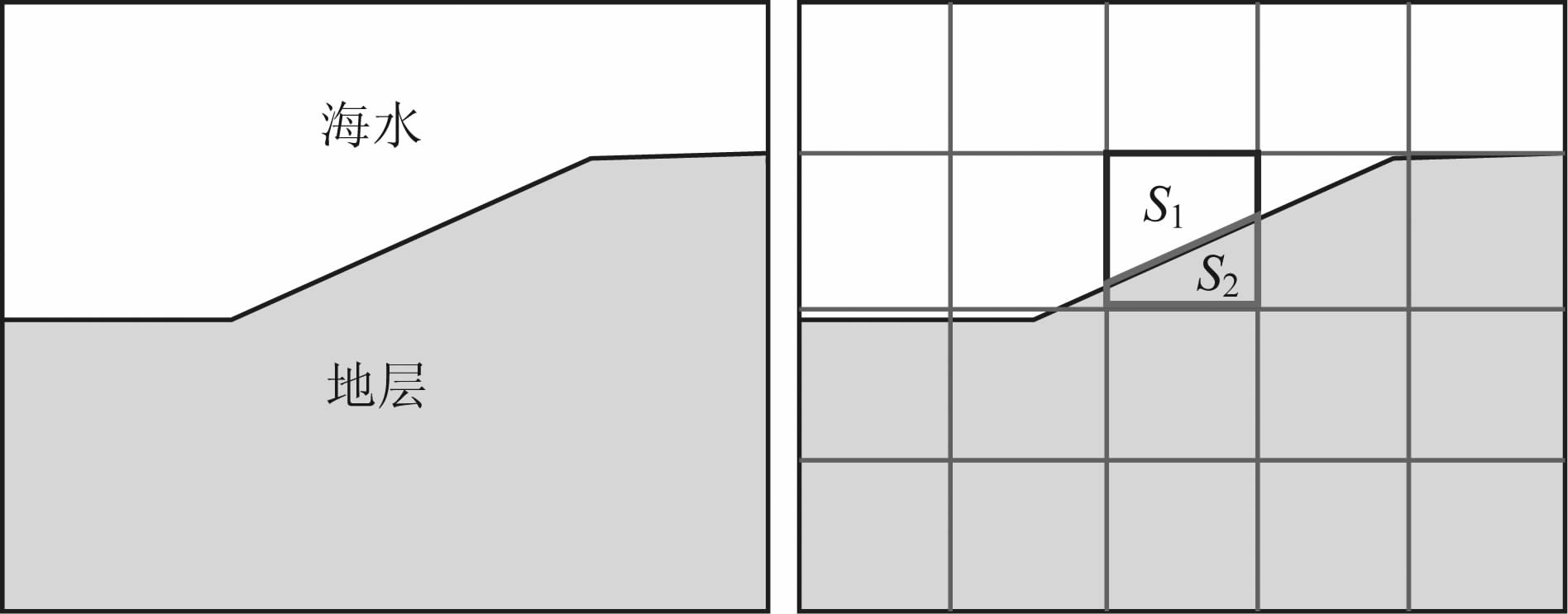
对于一个位于海底地形界面上的网格单元(如图 3b中加粗网格所示),在正演模拟时,其电导率σtopo 既不等于地层的电导率σ2 也不等于海水的电导率σ1,而是设置为由界面所分隔的体积S1 和S2 的加权平均,即
|
图 3 地形边界面网格单元物性加权平均原理示意图 Fig. 3 The conductivity weighting mean method for the cells on the terrain interface |
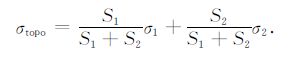
|
(17) |
规则矩形网格离散起伏地形界面本质上是空间局部化“以直代曲",由此产生的锯齿状台阶对电磁场的高精度模拟带来严重影响[27].电导率加权平均处理的实质是通过物性参数的平均化压制规则矩形网格剖分刻画物性参数分布不均匀的精度差所带来的影响,不仅适用于模拟地形起伏,也适用于模拟地下任意物性界面,在地震波场的模拟中已广为采用[28].采用界面电导率平均法可以有效地提高CSEM 地形响应的模拟精度,同时又不需要对原算法进行修改,只需要在建模时对地形界面的网格单元的电导率进行加权平均即可.
3 模型计算 3.1 一维层状模型为了评价三维有限体积算法的计算精度,设计了一个包含空气(电导率为10-12 S/m)、海水(电导率为3.3S/m)和沉积地层(电导率为1.0S/m)的一维层状模型.该层状模型存在解析解,解析解的计算采用加州大学圣地亚哥分校Scripps海洋研究所海洋电磁实验室(SIO)所开发的Dipole1D 进行计算.用于三维有限体积程序计算的层状模型的参数如表 2所示.
|
|
表 2 —维层状模型参数 Table 2 Parameters of the ID layered model |
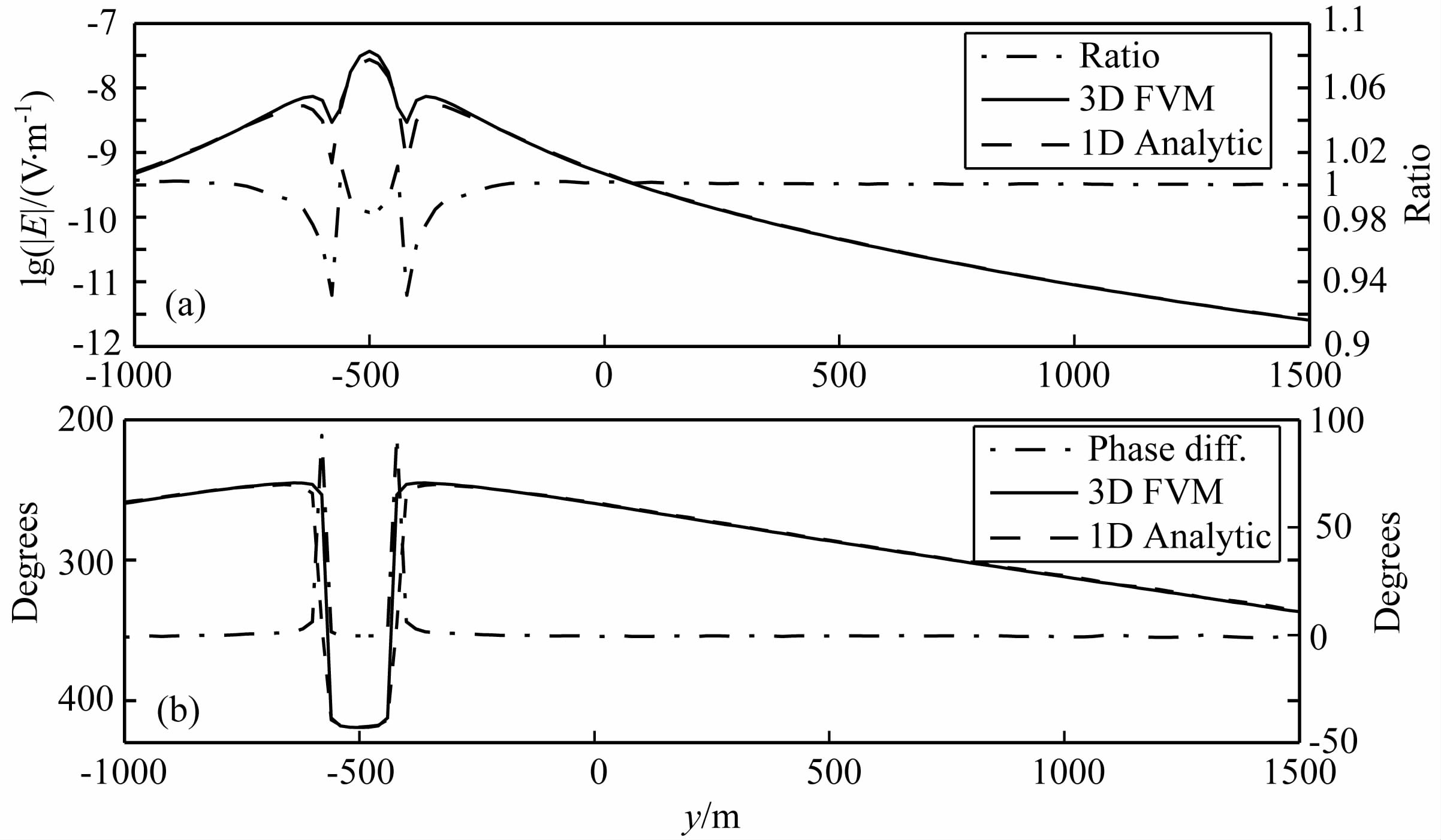
观测系统设置如下:(1)接收站分布于x=0m,y向从-1000~1500 m 的海底;接收点距为20 m,共126个接收点;(2)水平电偶极子(HED)场源位于(0,-500,900)m处,电偶极距为1Am,距海底100m,发射频率为0.25Hz,发射方向为y向.水平电场分量Ey的幅值和相位如图 4(a,b).
|
图 4 一维层状模型的CSEM水平电场幅值(a)及水平电场相位(b) Fig. 4 The amplitude curve (a) and the phase curve (b) of horizontal inline electric field of the 1D layered model |
图 4(a,b)中,实线为有限体积解,虚线为解析解,点划线为二者幅值的比值(图 4a)或相位差值(图 4b).从图中可以看出,除近场源区域外,二者的一致性很好,幅值的比值很接近于1,相位差值近似等于0.这验证了三维有限体积算法的正确性.另外,在近场源区域有限体积解和解析解之间存在较大差异的原因是有限体积解在场源附近区源的模型剖分较粗引起的,并不影响远区场的模拟精度.
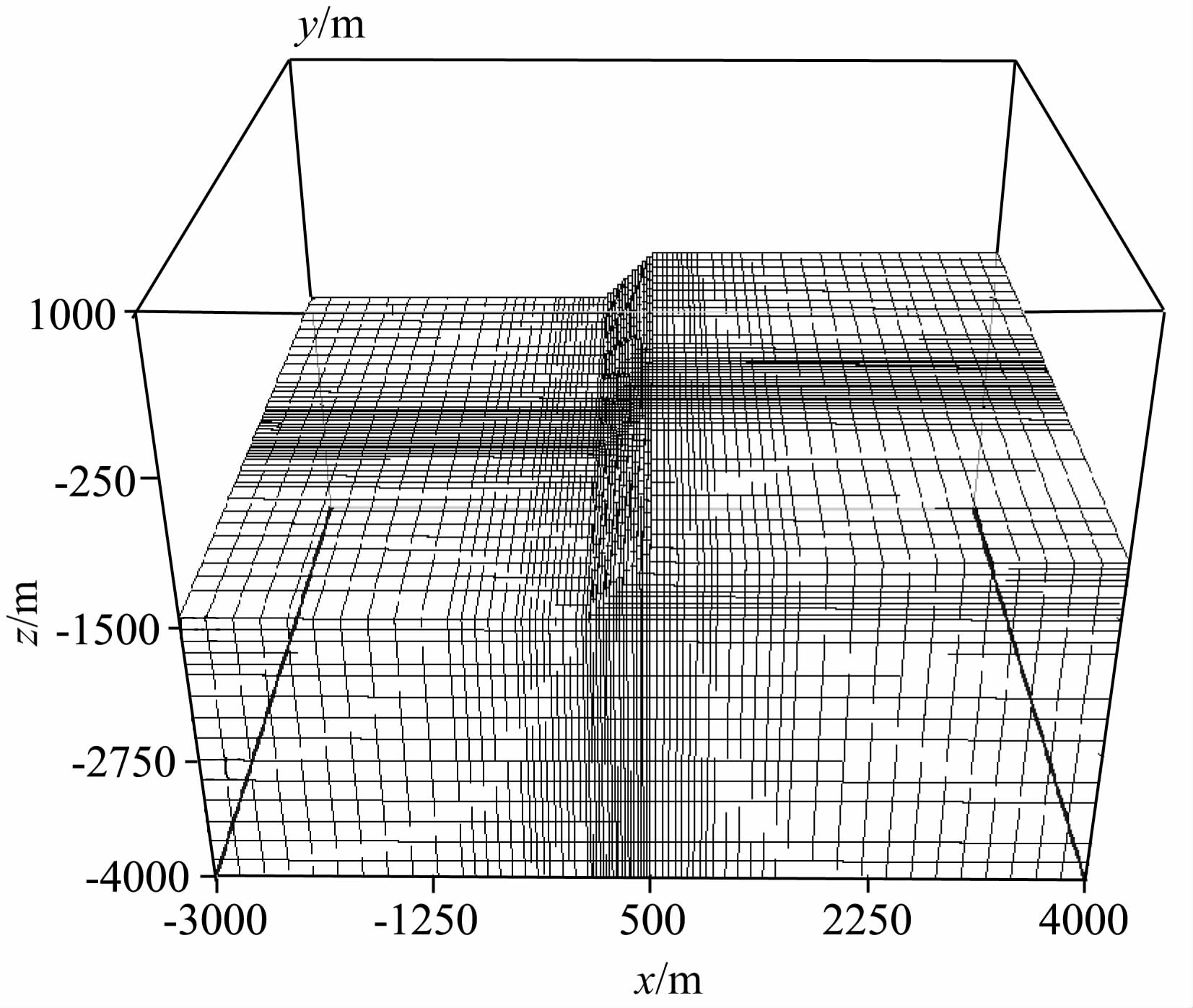
3.2 二维斜坡模型为了验证上述地形界面网格单元电导率加权平均处理对提高CSEM 地形响应模拟精度的有效性,设计了一个2D 的斜坡模型(如图 5所示):2D 斜坡模型由电导率为3.3S/m 的海水层和电导率为1.0S/m的沉积地层组成(图 5中剥离了海水层,只显示了沉积地层),海水深度在模型中部x方向上由2500m 变化到2000 m,斜坡的坡度为45°.图 5显示在地形变化的区域以及观测系统所在的区域,对网格剖分进行了加密.模型的范围及剖分参数如表 3所示.
|
图 5 二维斜坡模型的剖分示意图(图中坐标轴x轴向东,y轴向南,z轴向上,坐标单位为m) Fig. 5 Meshes and topography of the 2D slope model |
|
|
表 3 二维斜坡模型参数 Table 3 Parameters of the 2D slope model |
观测系统设置如下:(1)接收站分布于y=0m,x向从-1925~2025m 的海底;接收点距为50 m,共80 个接收点. (2)水平电偶极子场源位于(-800,0,1400)m处,电偶极距为1 Am,距海底100m,发射频率为1Hz,发射方向为x向.
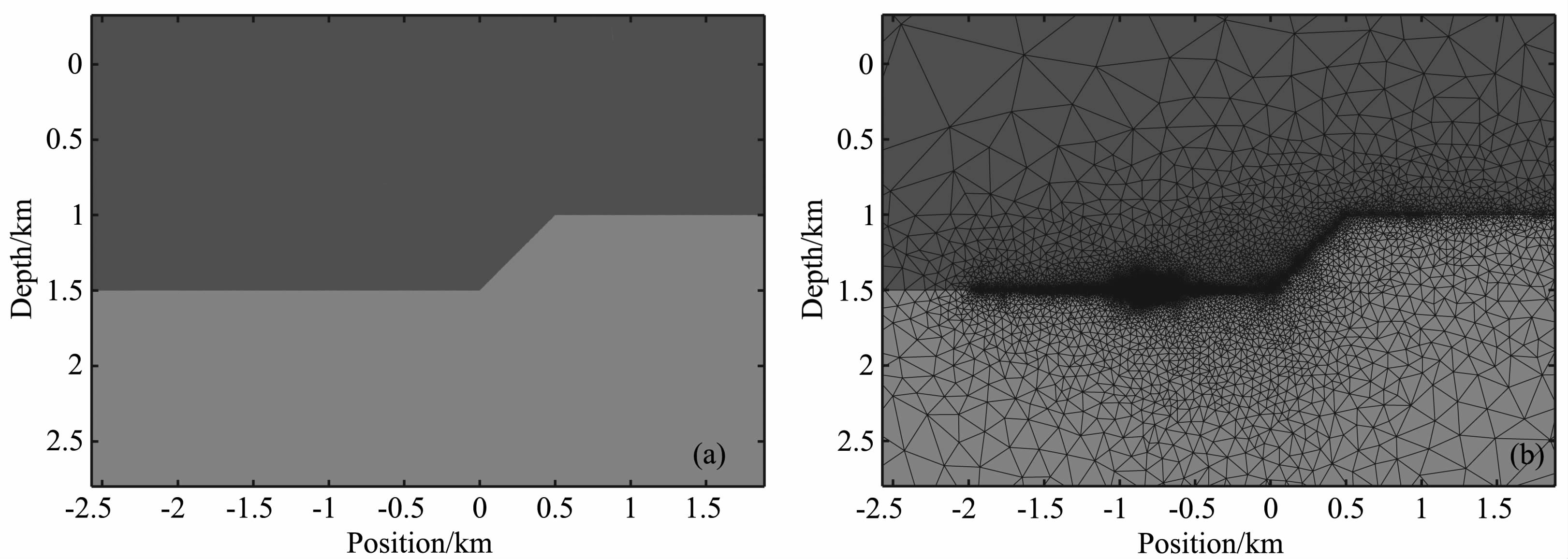
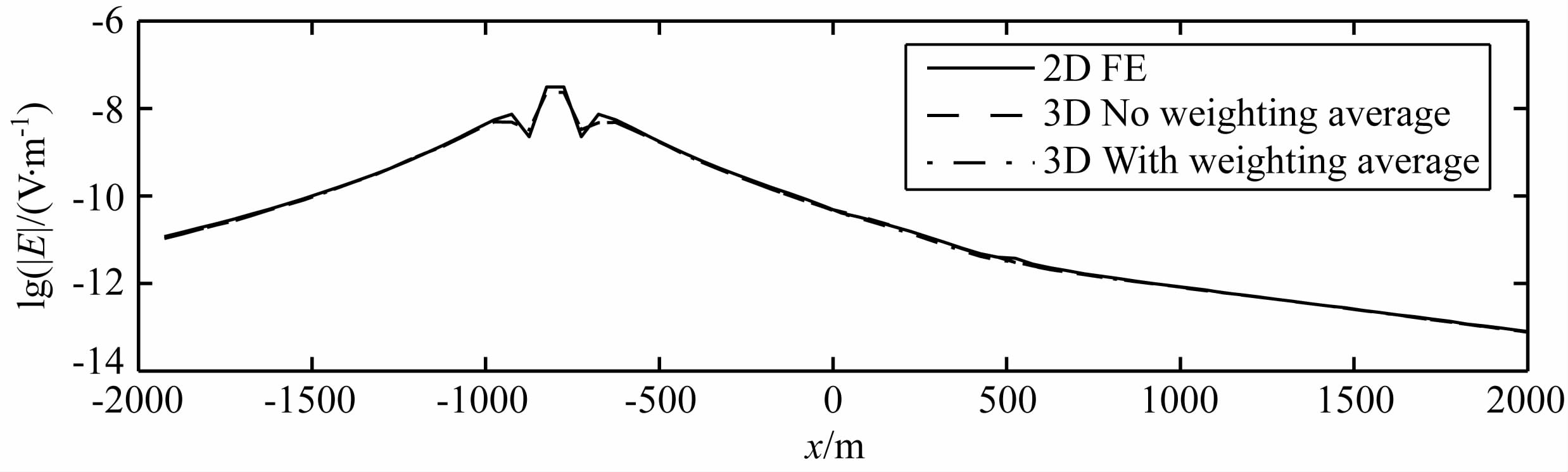
为了进行对比,对该二维斜坡模型进行了三次不同的正演:(1)采用SIO 开发的二维自适应网格有限元程序MARE2DCSEM,直接计算一个二维的斜坡模型(图 6a)的CSEM响应;(2)未做地形界面电导率加权平均处理的三维有限体积法CSEM 响应;(3)带电导率加权平均处理的三维有限体积法CSEM 响应.计算结果的Inline方向电场分量的幅值曲线如图 7所示.
|
图 6 二维斜坡模型局部 )及其剖分(b) Fig. 6 The 2D slope model segment (a) and its unstructured grids (b) |
|
图 7 二维斜坡模型的Inline方向水平电场响应幅值 Fig. 7 The amplitude curve of horizontal inline electric field of the 2D slope model |
在用MARE2DCSEM 程序进行计算时,模型区域的大小为100km×100km,经过39次自适应细化剖分,在场源附近、观测站附近及模型中电导率变化复杂的区域自动对网格进行了加密(图 6b),使得网格剖分数达到了30338个,且90%以上的网格分布于观测系统所在的区域.
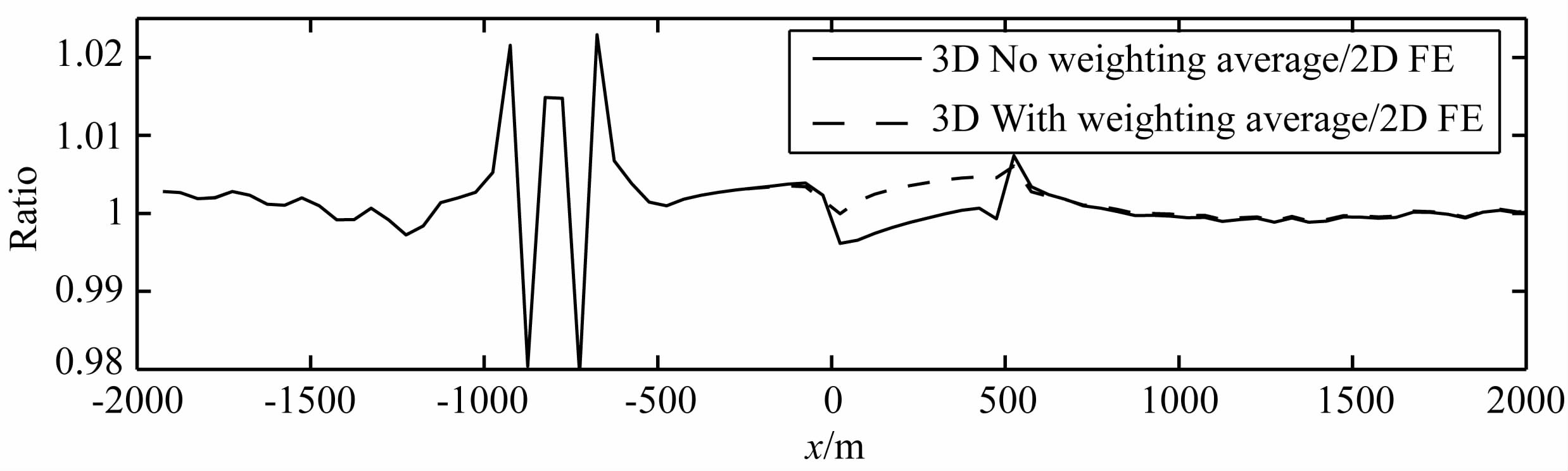
对二维斜坡模型的地形响应模拟的计算精度,从理论上来说,采用基于非结构三角网格自适应剖分二维有限元法应比采用基于规则网格剖分的三维有限体积法要高.因此,可将MARE2DCSEM 程序的计算结果作为一个近似的标准解来检验有限体积程序的解,并对三维有限体积解进行归一化处理(图 8).从图 7、8可以看出:(1)三个正演结果的CSEM响应曲线基本重合,归一化后的CSEM 响应比值基本在1附近波动,表明无论对电导率进行加权处理与否,三维有限体积解与二维有限元解均有很好的一致性,也验证了三维有限体积算法的正确性和有效性;(2)在地形变化的区域(y方向0~500 m),CSEM 响应出现了明显的畸变,表明CSEM 响应对地形变化比较敏感;(3)图 8显示经过加权平均处理后的CSEM 地形响应比未加权平均处理响应曲线在地形变化区域更接近于2D 有限元解,这表明经过加权平均处理后,地形响应的精度得到明显的提高;(4)在近场源区域(y方向-1000~-500m),同前所述,有限体积解与有限元解存在较明显差异的原因是有限体积解在近场源区域的剖分网格较粗造成的.
|
图 8 用2D有限元解归一化后的3D有限体积解 Fig. 8 Normalized 3D FVM solution by 2D FEM solution |
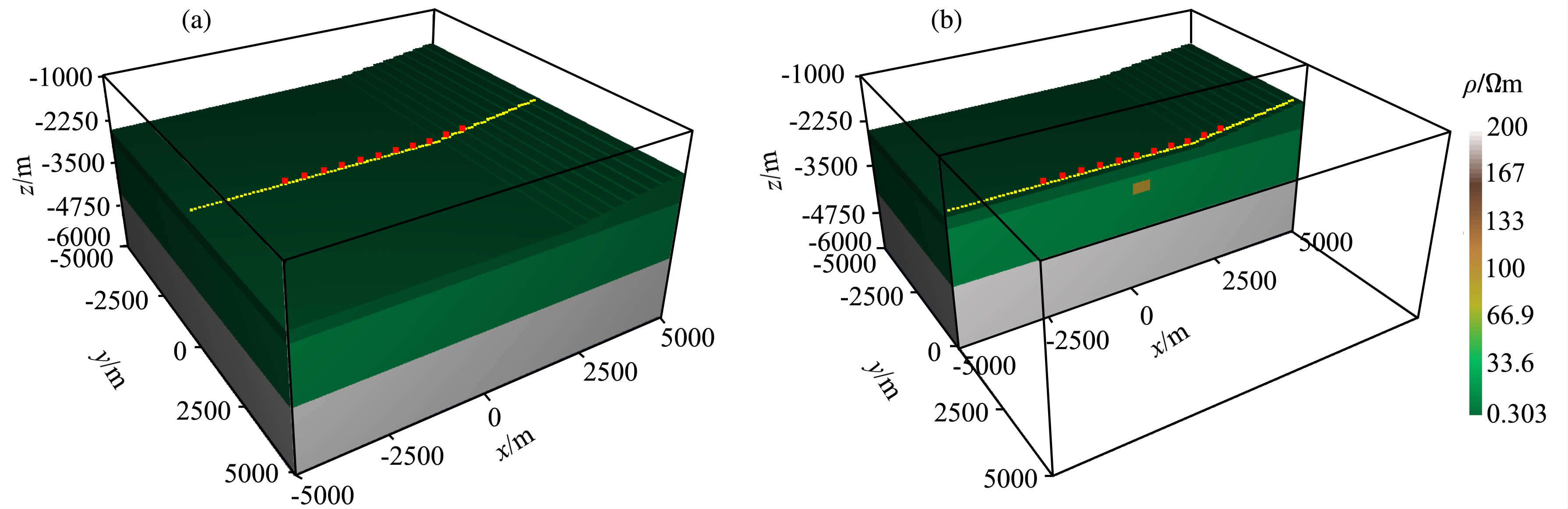
为探讨地形对储层模型的CSEM 响应的影响,设计了带地形的储层模型(图 9).图中,为了显示出设计的海底斜坡地形,剥离了海水层(图 9a).通过东西方向的垂直切片(图 9b),可以看到一个500m×500m×300m 大小的高阻(0.01S/m)储层赋存于电导率为0.05S/m 的地层之中,其上覆盖300m 至800m 厚的电导率为1.0S/m 的海底沉积物,其下伏地层为电导率为0.005S/m 的高阻基岩层.模型的剖分参数见表 4所示.
|
图 9 三维带地形储层模型(a)及观测系统设置(b)(图中黄点为测站位置,红点为场源激发时的位置) Fig. 9 The 3D reservior model with topography (a) and the observation system (b)(The yellow points are receivers,red points are the exciting position of transmiters) |
|
|
表 4 三维带地形储层模型参数 Table 4 Parameters of the 3D reservior model |
观测系统设置如下:(1)接收站分布于y=0 m的平面上,x向从-5000m 开始到5000m 终止,每100m 设置一个,共101个,狕向深度随着海底地形的起伏而变化;(2)水平电偶极子场源位于测线的正上方,狕向距海底100m,x向从-2500m 至2500m,每500m 激发一次,共激发11 次,偶极距为1Am,发射频率为0.25Hz,发射方向为y向.在上述观测系统设置下,测站所观测到的CSEM 响应如图 10所示.
|
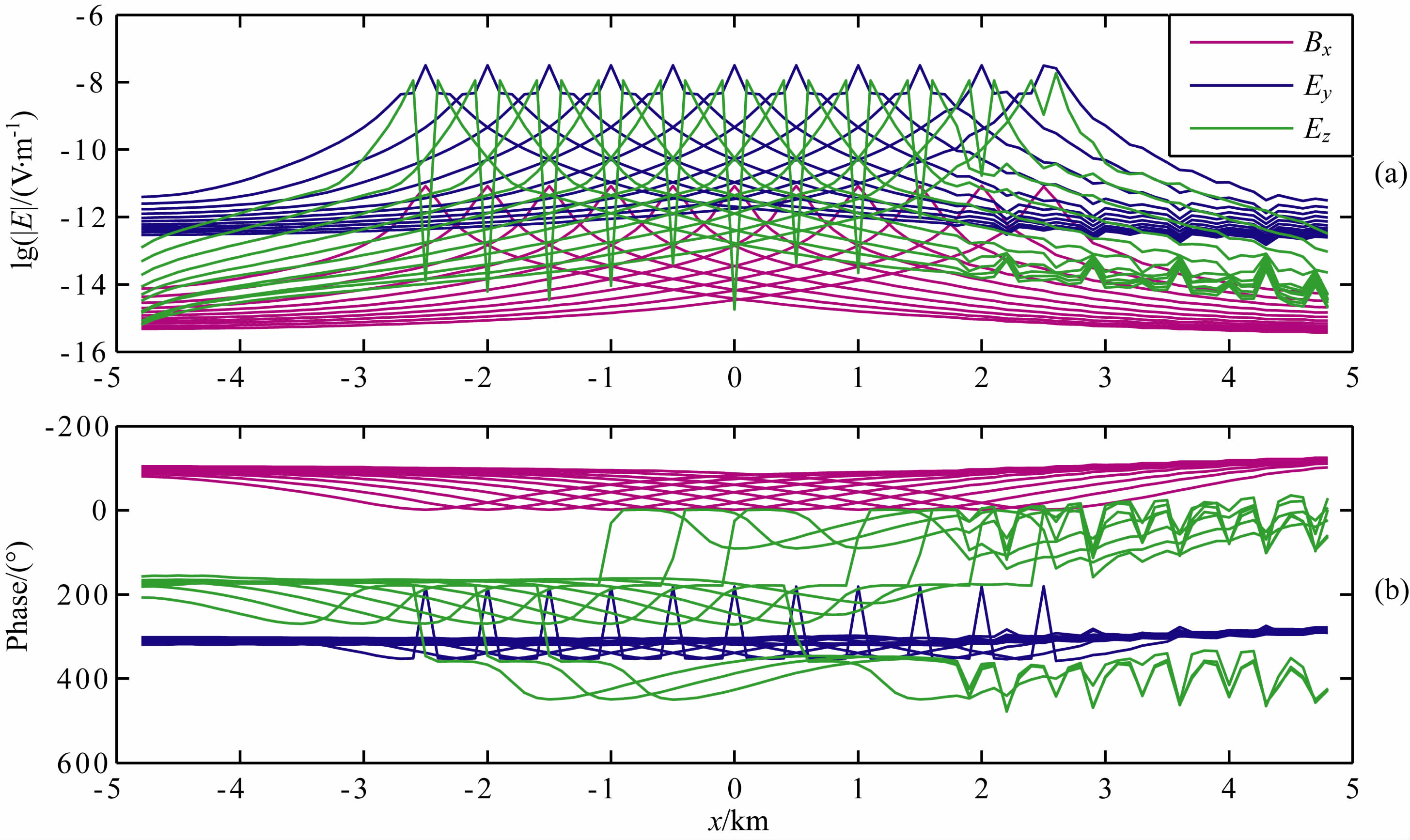
图 10 三维带地形储层模型CSEM响应 (a)幅值曲线;(b)相位曲线. Fig. 10 The magnitude versus oOfset(MVO) (a) curves and the phase versus oOfset(PVO) (b) curves of the reservior model |
从图 10 可以看出,斜坡地形的存在对CSEM的电场响应的影响非常明显,无论是幅值还是相位曲线都在斜坡地形区域(从图中1.5km 至5.0km处)产生较大的起伏跳跃,但磁场响应并未产生明显的变化.
为了突出高阻储层在CSEM 响应中的反映,取远离储层中心位置(0km,0km,1.1km)的位于(0km,-4.0km,0.5km)处的观测站的电磁响应来归一化位于储层正上方的观测站(0km,0km,0.5km)的电磁响应,得到如图 11所示的归一化后的电磁响应幅值和相位曲线.
|
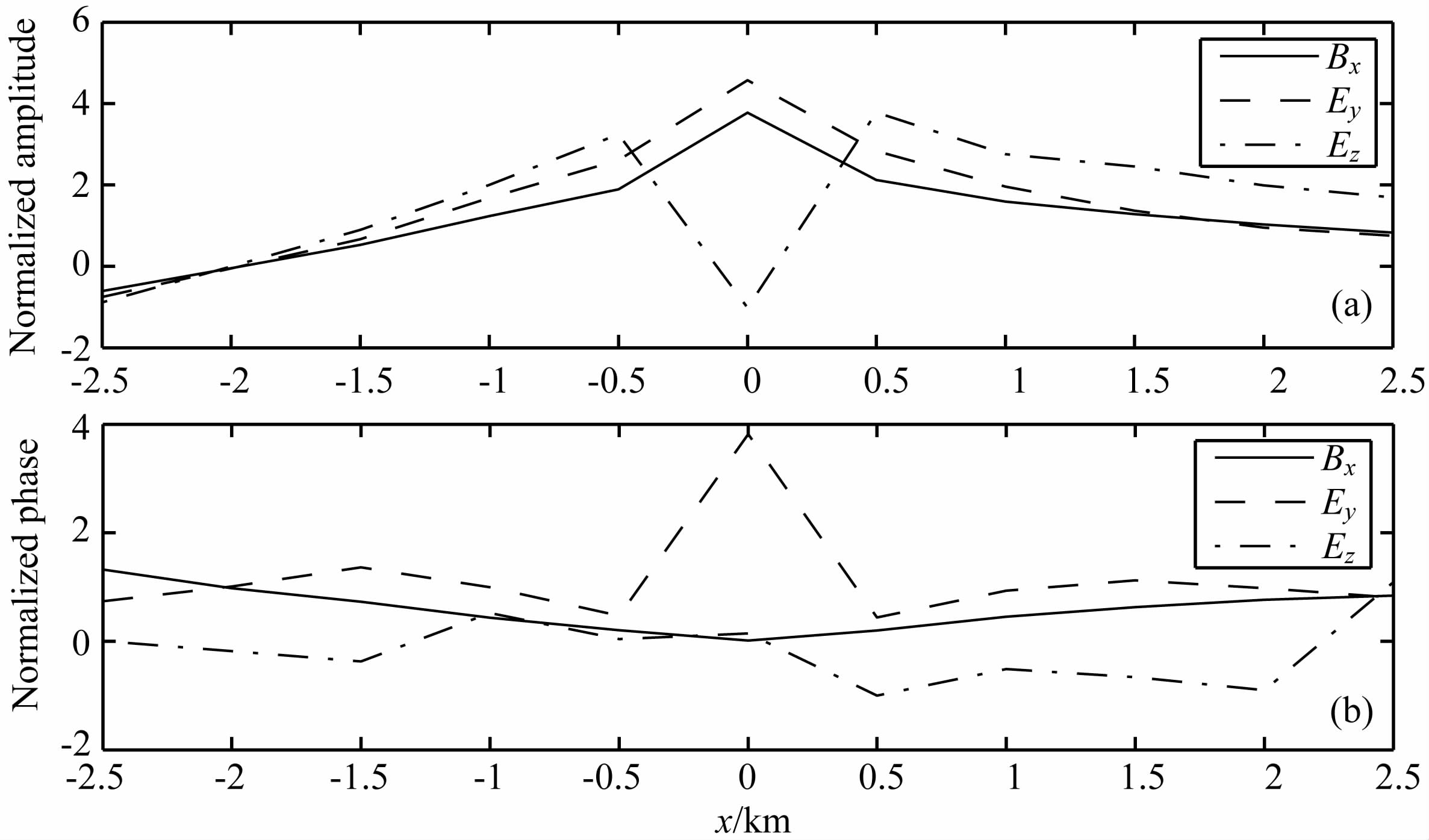
图 11 储层正上万测站归一化后响应幅值曲线(a)及响应相位曲线(b) Fig. 11 The normalized amplitude curves (a) and normalized phase curves(b) of the receiver over the reservior |
从图 11(a,b)可以看出:(1)储层上方的测站所观测到的归一化后的CSEM 电场和磁场响应比远离储层的测站所观测到的明显增大,其中Ey和Bx分量在储层正上方的幅值和相位均达到最大,Ey分量的相位在高阻储层与围岩接触带达到最小;Ey分量的幅值在储层正上方达到极小,而在储层与围岩的接触部位达到最大.Ez分量的相位变动频繁,与储层异常的对应关系不明显;说明电磁场水平方向分量对高阻储层中心的反映最明显,而垂向分量对高阻储层边界的反映最明显;(2)由于地形的影响,使得斜坡地形抬升区域归一化后的CSEM 电场和磁场响应比未抬升区域的明显增大(幅值曲线中正坐标部分明显大于负坐标部分).
为了研究地形的变化对CSEM 响应的影响,用远离地形变化处的位于(0km,-4.0km,0.5km)的观测站的电磁响应来归一化位于地形抬升区域的观测站(0km,3.0km,0.3km)的电磁响应,得到如图 12(a,b)所示的归一化后的电磁响应幅值和相位曲线.
|
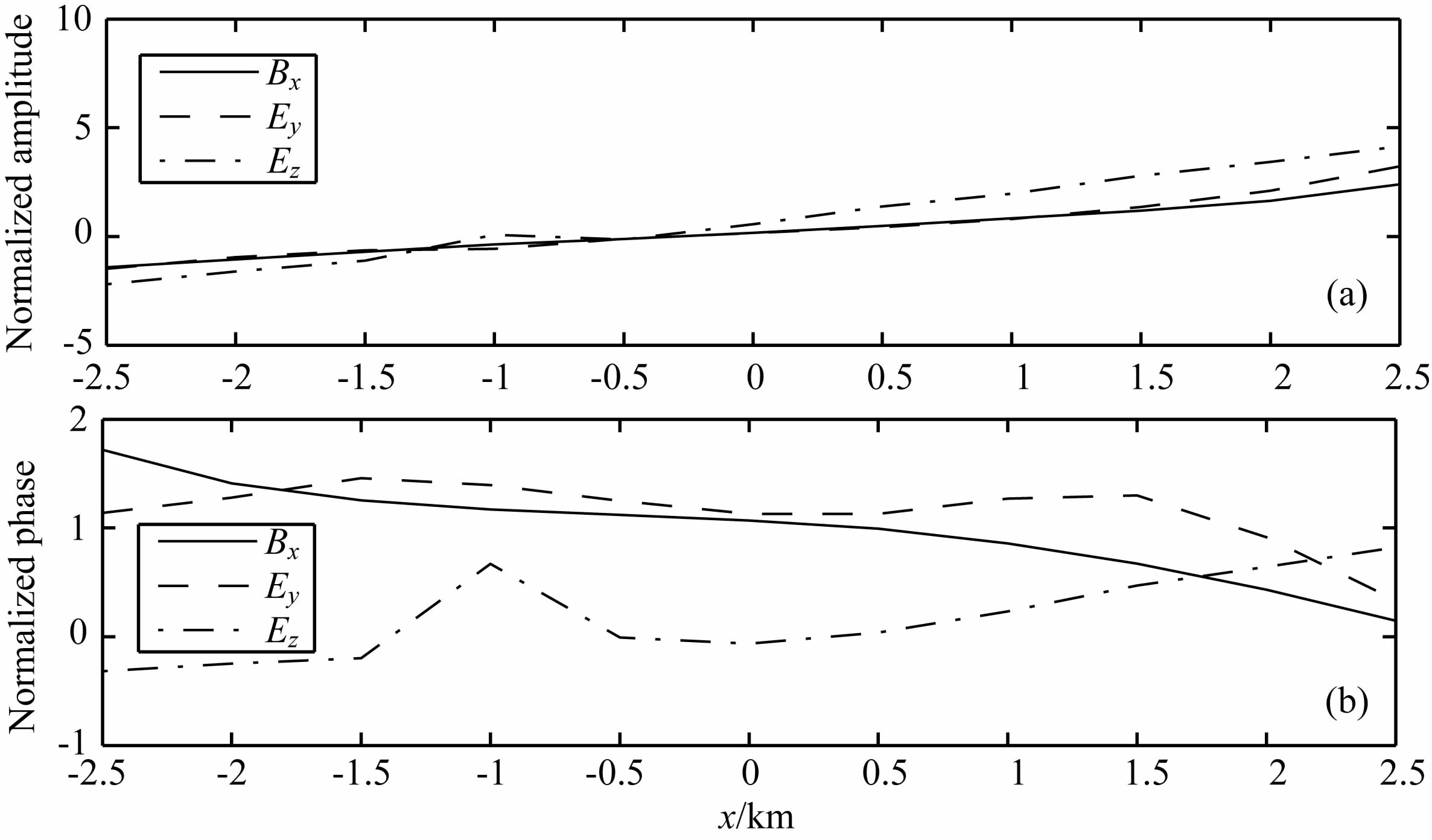
图 12 地形抬升区域测站归一化后响应幅值曲线(a)和响应相位曲线(b) Fig. 12 The normalized amplitude curves (a) and the normalized phase curves (b) of the receiver at the orographic uplitt area |
从图 12可以看出:地形抬升区域的归一化后的CSEM 响应各分量的幅值曲线均随着地形的抬升而增大,显示出与地形呈明显正相关;而归一化后的相位曲线并未反映出明显的规律.从以上的模拟结果也可以看出,地形的变化对CSEM 响应有着很明显的影响,更为复杂的地形起伏的响应规律还有待进一步的研究.
4 结 论本文探讨了应用有限体积法来模拟频率域海洋可控源电磁响应,推导并总结了采用有限差分法和有限体积法离散CSEM 控制方程的异同.有限体积法与有限差分法相比,增加了控制方程右端项对一次场的数值积分,显著提高了离散后形成的复对称线性方程组中场源项的精度,但并未增加迭代求解该大型方程组的计算量.因此,有限体积法较之有限差分法,不但具有更高的计算精度,同时也可获得与有限差分法相当的计算效率.
对离散化后的海底地形界面上的网格单元进行电导率的加权平均处理,可以有效地提高CSEM 地形响应的模拟精度.通过对一个带地形的储层模型的CSEM 响应进行模拟分析,表明海底地形变化对CSEM 的电场分量影响明显,磁场分量对地形的变化不敏感.
致 谢感谢东方地球物理公司对本项研究工作的资助.感谢美国加州大学圣地亚哥分校海洋学院海洋电磁实验室提供的Dipole1D 程序和MARE2DCSEM程序.感谢弗吉尼亚理工学院的Chester Weiss在程序编写等方面提供的帮助.
| [1] | Constable S, Srnka L J. An introduction to marine controlled-source electromagnetic methods for hydrocarbon exploration. Geophysics , 2007, 72(2): WA3-WA12. DOI:10.1190/1.2432483 |
| [2] | 胡文宝. 海洋地球物理中的电磁法. 地球物理学进展 , 1991(1): 1–8. Hu W B. The electromagnetic methods in marine geophysics. Progress in Geophysics (in Chinese) , 1991(1): 1-8. |
| [3] | 杨梅霞, 张胜业, 贾豫葛. 海洋大地电磁二维正演及结果分析. 现代地质 , 2001, 15(1): 98–102. Yang M X, Zhang S Y, Jia Y G. Marine magnetotelluric two dimension forward modeling. Geoscience (in Chinese) , 2001, 15(1): 98-102. |
| [4] | 杨进, 魏文博, 王光锷. 海水层对海洋大地电磁勘探的影响研究. 地学前缘 , 2008, 15(1): 217–221. Yang J, Wei W B, Wang G E. The effect of seawater in the marine magnetotelluric sounding. Earth Science Frontiers (in Chinese) , 2008, 15(1): 217-221. |
| [5] | 魏文博, 邓明, 温珍河, 等. 南黄海海底大地电磁测深试验研究. 地球物理学报 , 2009, 52(3): 740–749. Wei W B, Deng M, Wen Z H, et al. Experimental study of marine magnetotellurics in southern Huanghai. Chinese J. Geophys. (in Chinese) , 2009, 52(3): 740-749. |
| [6] | 刘长胜, EverettM, 林君, 等. 海底电性源频率域CSEM勘探建模及水深影响分析. 地球物理学报 , 2010, 53(8): 1940–1952. Liu C S, Everett M, Lin J, et al. Modeling of seafloor exploration using electric-source frequency-domain CSEM and the analysis of water depth effect. Chinese J. Geophys. (in Chinese) , 2010, 53(8): 1940-1952. |
| [7] | 何展翔, 孙卫斌, 孔繁恕, 等. 海洋电磁法. 石油地球物理勘探 , 2006(4): 451–457. He Z X, Sun W B, Kong F S. Marine electromagnetic approach. Oil Geophysical Prospecting (in Chinese) , 2006(4): 451-457. |
| [8] | 何展翔, 余刚. 海洋电磁勘探技术及新进展. 勘探地球物理进展 , 2008, 31(1): 2–9. He Z X, Yu G. Marine EM survey technology and its new advances. Progress in Exploration Geophysics (in Chinese) , 2008, 31(1): 2-9. |
| [9] | 何展翔, 王志刚, 孟翠贤, 等. 基于三维模拟的海洋CSEM资料处理. 地球物理学报 , 2009, 52(8): 2165–2173. He Z X, Wang Z G, Meng C X, et al. Data processing of marine CSEM based on 3D modeling. Chinese J. Geophys. (in Chinese) , 2009, 52(8): 2165-2173. |
| [10] | He Z X, Strack K, Yu G, et al. On reservoir boundary detection with marine CSEM. Applied Geophysics , 2008, 5(3): 181-188. DOI:10.1007/s11770-008-0026-2 |
| [11] | Newman G A, Alumbaugh D L. Frequency-domain modeling of airborne electromagnetic responses using staggered finite differences. Geophysical Prospecting , 1995, 43(8): 1021-1042. DOI:10.1111/gpr.1995.43.issue-8 |
| [12] | Smith J T. Conservative modeling of 3-D electromagnetic fields, Part I: Properties and error analysis. Geophysics , 1996, 61(5): 1308-1318. DOI:10.1190/1.1444054 |
| [13] | Smith J T. Conservative modeling of 3-D electromagnetic fields, Part II: Biconjugate gradient solution and an accelerator. Geophysics , 1996, 61(5): 1319-1324. DOI:10.1190/1.1444055 |
| [14] | Badea E A, Everett M E, Newman G A, et al. Finite-element analysis of controlled-source electromagnetic induction using Coulomb-gauged potentials. Geophysics , 2001, 66(3): 786-799. DOI:10.1190/1.1444968 |
| [15] | 沈金松. 用交错网格有限差分法计算三维频率域电磁响应. 地球物理学报 , 2003, 46(2): 280–288. Shen J S. Modeling of 3-D electromagnetic responses in frequency domain by using staggered grid finite difference method. Chinese J. Geophys. (in Chinese) , 2003, 46(2): 280-288. |
| [16] | Weiss C J, Constable S. Mapping thin resistors and hydrocarbons with marine EM methods, Part II—Modeling and analysis in 3D. Geophysics , 2006, 71(6): G321-G332.. DOI:10.1190/1.2356908 |
| [17] | Maao F A. Fast finite-difference time-domain modeling for marine-subsurface electromagnetic problems. Geophysics , 2007, 72(2): A19-A23. DOI:10.1190/1.2434781 |
| [18] | Streich R. 3D finite-difference frequency-domain modeling of controlled-source electromagnetic data: Direct solution and optimization for high accuracy. Geophysics , 2009, 74(5): F95-F105. DOI:10.1190/1.3196241 |
| [19] | Mittet R. High-order finite-difference simulations of marine CSEM surveys using a correspondence principle for wave and diffusion fields. Geophysics , 2010, 75(1): F33-F50. DOI:10.1190/1.3278525 |
| [20] | 徐志锋, 吴小平. 可控源电磁三维频率域有限元模拟. 地球物理学报 , 2010, 53(8): 1931–1939. Xu Z F, Wu X P. Controlled source electromagnetic 3-D modeling in frequency domain by finite element method. Chinese J. Geophys. (in Chinese) , 2010, 53(8): 1931-1939. |
| [21] | 陈辉, 邓居智, 谭捍东, 等. 大地电磁三维交错网格有限差分数值模拟中的散度校正方法研究. 地球物理学报 , 2011, 54(6): 1649–1659. Chen H, Deng J Z, Tan H D, et al. Study on divergence correction method in three-dimensional magnetotelluric modeling with staggered-grid finite difference method. Chinese J. Geophys. (in Chinese) , 2011, 54(6): 1649-1659. |
| [22] | Mukherjee S, Everett M. 3D controlled-source electromagnetic edge-based finite element modeling of conductive and permeable heterogeneities. Geophysics , 2011, 76(4): F215-F226. DOI:10.1190/1.3571045 |
| [23] | Li Y G, Key K. 2D marine controlled-source electromagnetic modeling: Part 1—An adaptive finite-element algorithm. Geophysics , 2007, 72(2): WA51-WA62. DOI:10.1190/1.2432262 |
| [24] | Li Y G, Dai S K. Finite element modelling of marine controlled-source electromagnetic responses in two-dimensional dipping anisotropic conductivity structures. Geophysical Journal International , 2011, 185(2): 622-636. DOI:10.1111/gji.2011.185.issue-2 |
| [25] | Key K, Ovall J. A parallel goal-oriented adaptive finite element method for 2.5D electromagnetic modeling. Geophysical Journal International , 2011, 186(1): 137-154. DOI:10.1111/gji.2011.186.issue-1 |
| [26] | Li Y, Constable S. 2D marine controlled-source electromagnetic modeling: Part 2——The effect of bathymetry. Geophysics , 2007, 72(2): WA63-WA71. DOI:10.1190/1.2430647 |
| [27] | Aprea C, Booker J R, Smith J T. The forward problem of electromagnetic induction: accurate finite-difference approximations for two-dimensional discrete boundaries with arbitrary geometry. Geophys. J. Int| , 1997, 129(1): 29-40. |
| [28] | Xu Y X, Xia J H, Miller R D. Numerical investigation of implementation of air-earth boundary by acoustic-elastic boundary approach. Geophysics , 2007, 72(5): SM147-SM153. DOI:10.1190/1.2753831 |
 2012, Vol. 55
2012, Vol. 55


