2. 中石油东方地球物理公司物探技术研究中心, 河北 涿州 072751
2. Geophysical Technique Research Centre, BGP Inc. of CNPC, Hebei Zhuozhou 072751, China
陆上地震勘探往往在山地、丘陵等复杂地表区域进行.此时,起伏的地表面以及近地表速度的横向变化对地震数据的采集和处理造成了很大的困难.虽然可以通过静校正来消除地表起伏的影响,然而,常规的静校正方法往往是基于地表一致性假设的,当基岩出露,地表高程变化较大,近地表速度横向变化剧烈时,地表一致性假设已经不再适用,此时,常规的静校正方法会使得地震波场产生畸变,并对后续的偏移成像处理造成不利影响.
波动方程基准面校正是解决复杂地表条件下偏移成像问题的有效方法.Berryhill(1979),Berryhill(1984)首先提出了该思想,并将其应用到了叠前数据[1-2].此后,Yilmaz和Lucas(1986),Schneider等(1995),Bevc(1997)以及Yang 等(1999)先后就波动方程基准面校正并结合层替代技术做了许多有益的尝试[3-6].同常规的静校正方法相比,波动方程基准面校正能够有效地消除起伏地表对同相轴造成的扭曲.然而,近地表速度的横向变化,往往对基准面的选取造成一定的困难,并且严重影响基准面校正的精度.基于波场延拓的偏移成像方法,也是解决复杂地表问题的有效途径.Beasley和Lynn(1992)提出的“零速层"法[7],Reshef(1991)提出的波场逐步累加“直接下延"法[8],以及何英等(2002)提出的“波场上延"法都能较好地消除起伏地表对地震偏移成像的影响[9].Shragge(2005)提出在黎曼坐标系下进行波场延拓,为解决复杂地表的问题提供了新的思路[10].然而,在复杂的地表条件下,观测系统往往是不规则的,波场延拓法很难适应非规则采集的地震数据,对地震数据进行插值等规则化处理往往需要巨大的额外计算量.
与上述方法不同,基于射线理论的地震成像方法(如Kirchhoff偏移、高斯束偏移)可以直接从起伏的地表面进行波场的偏移成像,且无需规则采集的地震数据,具有对复杂地表条件天然的适应性.Wiggins(1984)首先提出了适用于非水平地表地震数据的Kirchhoff积分延拓和偏移公式[11].Gray等(1995)证明直接在起伏地表进行Kirchhoff偏移的成像效果要优于首先进行基准面校正[12].Jager等(2003)提出了起伏地表条件下的真振幅Kirchhoff偏移方法[13].作为Kirchhoff偏移准确而有效的替代方法,高斯束偏移不但保留了Kirchhoff偏移灵活高效的特点,而且具有接近于波动方程偏移的成像精度.高斯束偏移最早由Hill(1990)提出,此后Hill,Gray等人对其进行了发展[14-18].Gray(2005)提出了一种适用于复杂地表条件的高斯束偏移方法[16],该方法通过局部高程静校正将单个高斯窗内的接收点高程校正到波束中心所在的基准面上,然后在此基准面上进行波场的延拓成像.然而,当地表高程及速度变化较大时,静校正对波场造成的畸变会对后续的偏移成像特别是近地表的成像造成不利影响.
基于前人的研究,本文提出了一种精度更高的,且具有振幅相对保持特点的复杂地表条件下的高斯束偏移方法.首先,通过RayleighII积分来近似描述复杂地表反向延拓的地震波场并结合基于高斯束表示的格林函数,推导了基于高斯束表示的波场反向延拓公式;接下来,结合反褶积成像条件并通过最速下降法将推导过程中的二维复值积分进行简化[18],得到了具有较高计算效率的保幅高斯束偏移公式.同Gray(2005)所提出的实现方法[16]相比,本文方法可以通过考虑起伏地表平面波的传播特点,直接在起伏地表进行局部平面波的分解,从而具有更高的成像精度(尤其是近地表部分),而且可以消除地震波几何扩散对成像振幅的影响,得到保幅的成像结果,有利于此后的AVO 以及岩性分析.
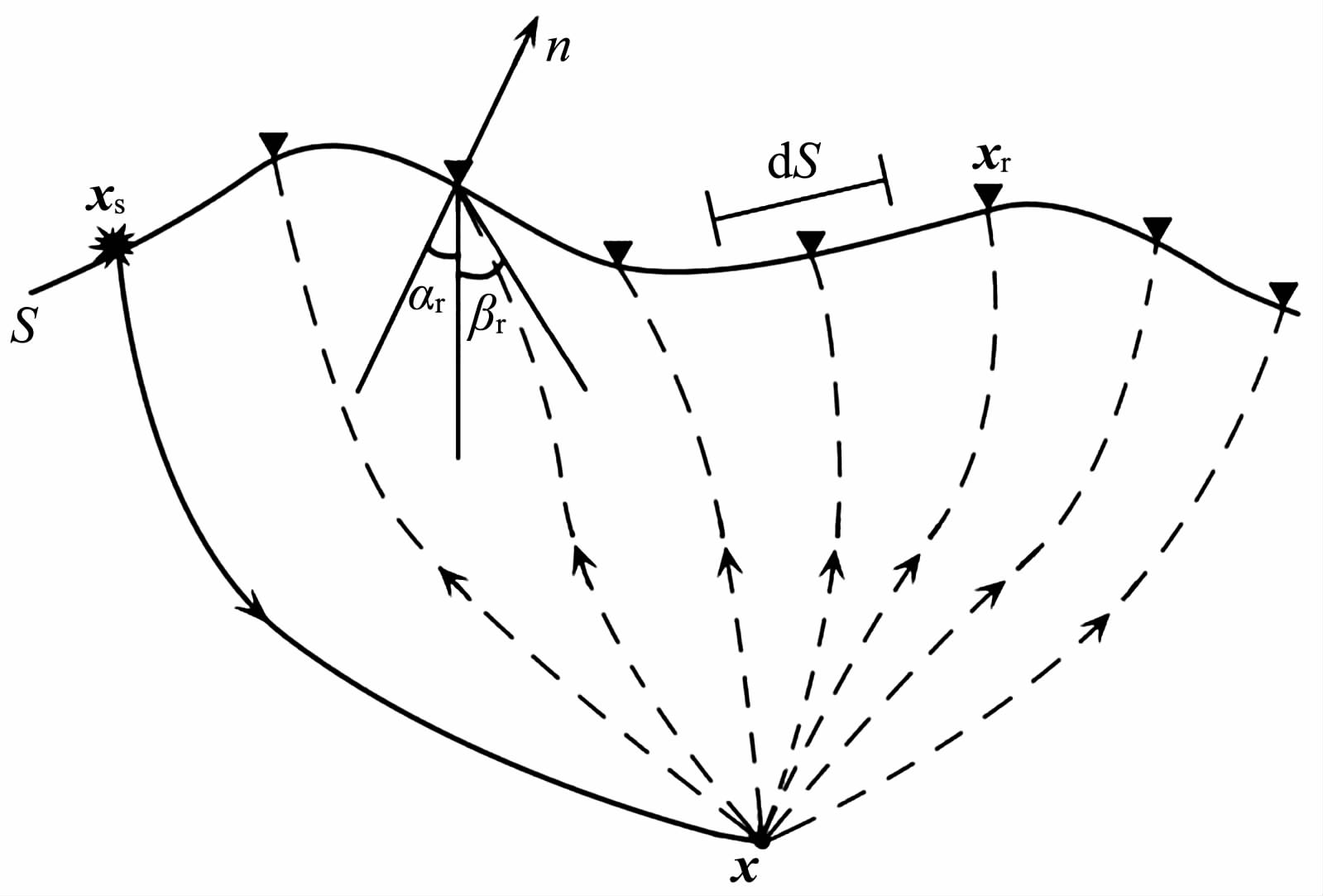
2 基本原理 2.1 基于高斯束表示的波场反向延拓公式考虑如图 1所示的二维起伏地表模型,假设S代表起伏地表面,xs = (xs,zs)为震源,xr = (xr,zr)为对应震源xs 的接收点,U(xr,xs,ω)为接收到的地震波场,x= (x,z)为地下成像点,则x点处反向延拓的地震波场U(x,xs,ω)可以通过Kirchhoff-Helmoholtz积分来表示[19-20]
|
图 1 复杂地表条件下的波场反向延拓 Fig. 1 Wavefield inverse extrapolation under complex topographic condition |
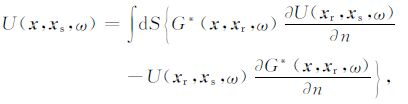
|
(1) |
其中,G(x,xr,ω)为接收点xr 到成像点x的格林函数,$\frac{\partial }{{\partial n}}$代表沿外法线方向求导,*代表复共轭.
当地表水平时,可以选取适当的格林函数来消除接收地震波场的法向导数项,此时式(1)简化为RayleighII积分[19-21].当地表的起伏在波长范围内变化不大时,反向延拓的地震波场U(x,xs,ω)依然可以通过RayleighII积分来近似表示[22-23]:
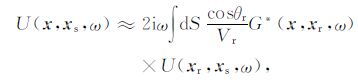
|
(2) |
其中,θr =βr-αr 为接收点xr 处射线出射方向同法线之间的角度,βr 和αr 分别为xr 处出射到达地下成像点x射线的出射角以及地表的倾角;Vr为xr处地表速度.(2)式也是Kirchhoff基准面校正的基本理论公式[1-2].接下来,我们以式(2)为基础,依据常规高斯束偏移的基本思想进行公式推导.
首先,对地震数据沿水平方向进行加窗处理,从而使其能同有限宽度的高斯束进行匹配.所选择的窗函数为高斯函数,具有以下性质:
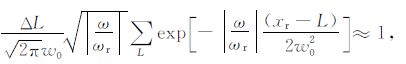
|
(3) |
其中,ωr,w0 分别为所选的参考频率以及高斯束的初始宽度;x=L为高斯窗的中心线,也是波束中心L的水平坐标;ΔL为其水平间隔.将式(3)代入式(2)得

|
(4) |
Hill所提出的动力学射线追踪方程组的初值可以使得高斯束的初始波前为平面的[11, 18],依据此特点,可以根据不同方向的平面波到达接收点xr 与波束中心L的走时延迟(如图 2所示),将接收点xr 的格林函数G(x,xr,ω)通过L处出射的高斯束uGB(x,L,ω)的积分来近似表示:

|
图 2 通过L处出射高斯束的积分 来近似格林函数G(x,xr,ω) Fig. 2 Approximate Green;s function G(x,xr,ω) by integral of Gaussian beams emanating from L |
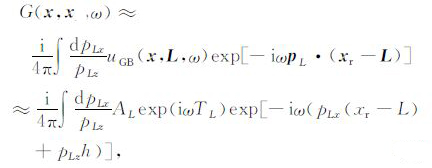
|
(5) |
其中,pL= (pLx,pLz)=$\left( {\frac{{\sin {\beta _L}}}{{{V_L}}},\frac{{\cos {\beta _L}}}{{{V_L}}}} \right)$为高斯束中心射线的初始慢度,βL为射线的出射角;h为xr 和L之间的高程差;TL,AL分别为高斯束uGB(x,L,ω)的复值走时和振幅;$\exp \left[ { - {\text{i}}\omega \left( {{P_{Lx}}\left( {{x_{\text{r}}} - L} \right) + {P_{Lz}}h} \right)} \right]$为补偿格林函数震源不同于高斯束出射点时相位变化的校正因子.当xr 距离L较远时,式(5)中的近似会存在一定的振幅误差,但由于高斯函数的衰减性质,上述近似并不足以对式(4)产生太大影响.
将式(5)代入式(4),得
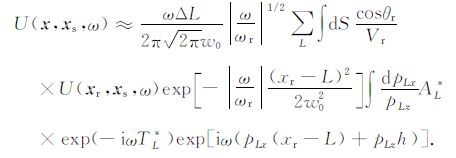
|
(6) |
对于出射角为βL的高斯束所经过的地下成像点,令Vr ≈VL,并通过βr ≈βL来近似表示由xr 到x射线的出射角,从而求得θr ≈βL-αr.交换式(6)的积分次序,得到基于高斯束表示的复杂地表波场反向延拓公式:
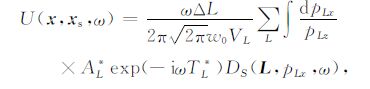
|
(7) |
其中
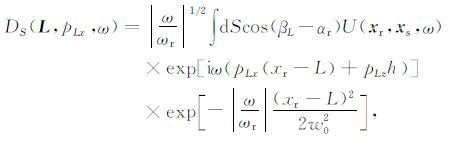
|
(8) |
为单个高斯窗内地震记录的倾斜叠加.
式(8)不同于常规的局部倾斜叠加[15]之处在于,其包含了地表的高程以及倾角信息,可以直接在起伏地表面进行平面波的分解.当近地表速度剧烈变化时,还可以通过接收点处的近地表速度来计算式(8)中的相移量$\exp \left[ {{\text{i}}\omega \left( {{p_{Lx}}\left( {{x_{\text{r}}} - L} \right) + {p_{Lz}}h} \right)} \right]$,来提高局部平面波的分解精度.此外,式(8)中积分间隔dS的选取会影响成像结果中的振幅信息,若要得到保幅的成像结果,需选择dS为实际的道间隔,本文的数值试算中将对此进行验证.
2.2 保幅成像公式对于炮域偏移,要得到真振幅意义上的偏移结果,需应用反褶积型的成像条件[11-13]:
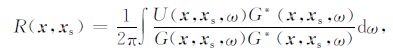
|
(9) |
其中,G(x,xs,ω)为正向传播的震源格林函数.将G(x,xs,ω)通过震源出射的高斯束来表示,并将式(7)代入式(9),得到初步的成像公式
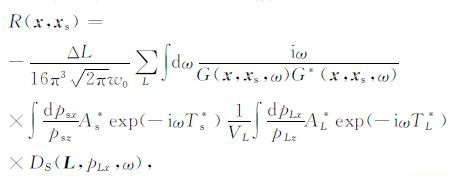
|
(10) |
(10)式包含关于psx和pLx的二维复值积分,直接进行求解计算量巨大.为提高其计算效率,利用最速下降法将上述二维复值积分简化为一维[5-8].
首先,将震源和波束中心射线参数的水平分量psx、pLx变换为中点和偏移距射线参数的水平分量pmx、phx,
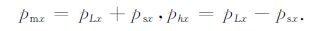
|
(11) |
变换的目的在于应用最速下降法后,可以对更多次的波至进行成像[15-16].此时,式(10)变为
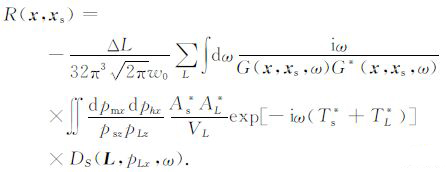
|
(12) |
接下来,利用最速下降法求取(12)式中关于phx的积分.Hill(2001)证明上述积分的鞍点对应着令走时Ts+TL虚部最小的phx0,Gray(2009)给出了此时积分以及震源照明项G(x,xs,ω)G*(x,xs,ω)的渐进解.在此利用上述结论,得到最终的复杂地表条件下保幅高斯束偏移的成像公式:
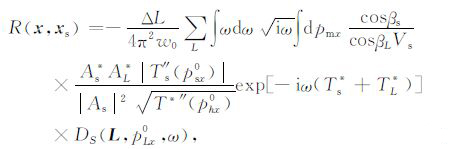
|
(13) |
其中,由于phx0以及pmx已知,psx0,pLx0可以通过式(11)求得;Vs 为震源处地表速度;βs 为对应着psx0的震源到成像点射线的出射角度;${{T''}_{\text{s}}}\left( {p_{{\text{s}}x}^0} \right),{T^{*''}}\left( {p_{hx}^0} \right)$为走时的二阶导数(其具体表达式可以参见文献[18]).
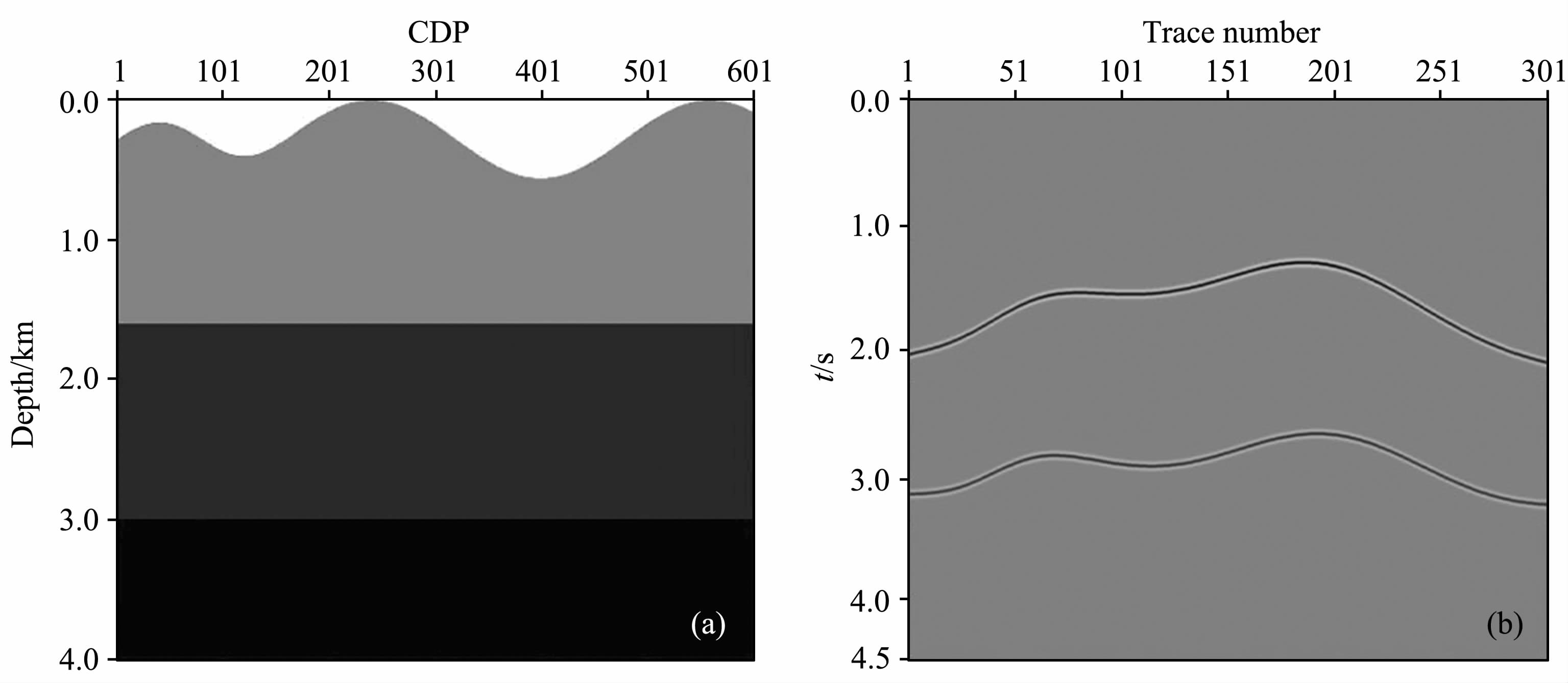
3 数值算例 3.1 保幅性测试通过对一个简单的起伏地表模型进行试算,验证本文方法的保幅性.设计了如图 3a所示的起伏地表速度模型,假设模型速度为2000 m/s,在深度为1.6km 以及3.0km 处存在密度差异造成的反射界面,令各层反射系数相同.模型网格为601×1000,纵横向采样间隔分别为10m 和4m,起伏地表最大高程差近600m.正演单炮记录如图 3b 所示,该炮记录共有301道,道与道之间的水平间距为20 m,炮点位于地表CDP=301处,图中可以看到地表起伏造成的非双曲线型的同相轴.
|
图 3 简单起伏地表模型 (a)三层起伏地表模型;(b)单炮记录. Fig. 3 A simple topographic model (a) The topographic model with three horizontal layers; (b) Single shot record. |
应用本文方法对上述模型进行试算.图 4a为选取dS为实际道间距时的单炮成像结果,图 4c为沿各反射界面所提取的归一化振幅,可以看到本文方法不但有效地消除了起伏地表的影响对各个反射层进行正确的成像,并且在一定的偏移距范围内基本上正确地恢复了界面真实的反射率.图 4b 为选取dS为常数时(所有道间距的几何平均)的单炮成像结果,图 4d为沿各反射界面所提取的归一化振幅,可以看到此时虽然模型的水平反射层得到了正确的成像,但其成像振幅同理论值有着较大的误差,由此可知,式(8)中dS的选择,对成像振幅有着明显的影响.

|
图 4 简单起伏地表模型偏移试算结果 (a) dS为实际道间距时成像结果;(b) dS为常数时成像结果;(c)(a)中各反射层的归一化振幅;(d)(b)中各反射层的归一化振幅. Fig. 4 Migrated results of the simple topographic model (a) Image with actual trace spacing dS; (b) Image with constant dS; (c) Normalized amplitudes along the reflectors in (a); (d) Normalized amplitudes along the reflectors in (b). |
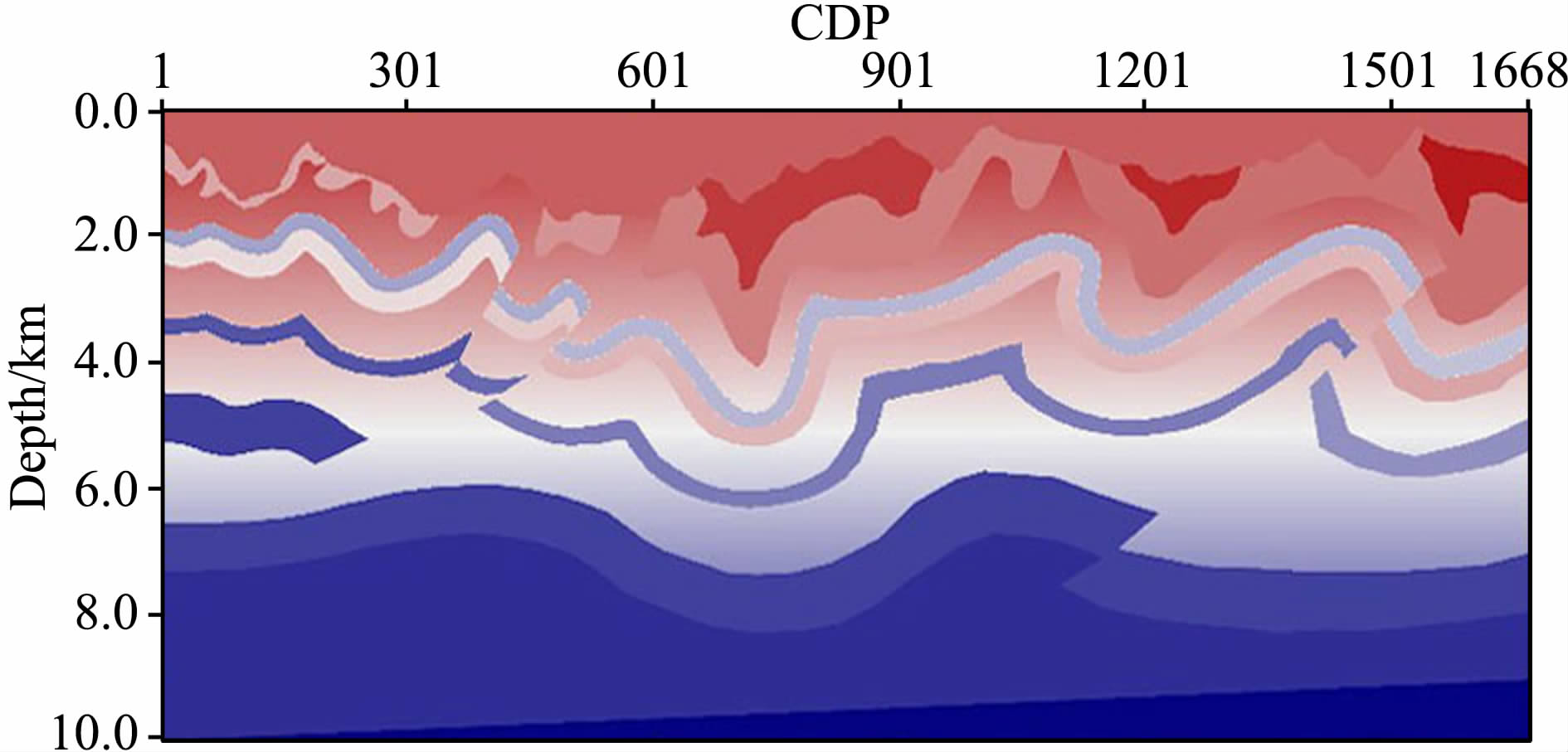
应用SEG 起伏地表模型进行试算,测试本文方法对复杂模型的成像效果.该模型具有典型的复杂地表和地下地质构造,由图 5 可以看到其地表高程变化剧烈,最大高程差接近1600 m,且近地表速度变化明显.模型网格为1668×1000,纵横向采样间隔分别为10m 和15m.模拟数据共有277炮,最大道数为480道,每道2000个采样点,4 ms采样,道间距为15m,炮间距为90 m,偏移距范围为15~3600m.
|
图 5 SEG起伏地表模型 Fig. 5 SEG topographic model |
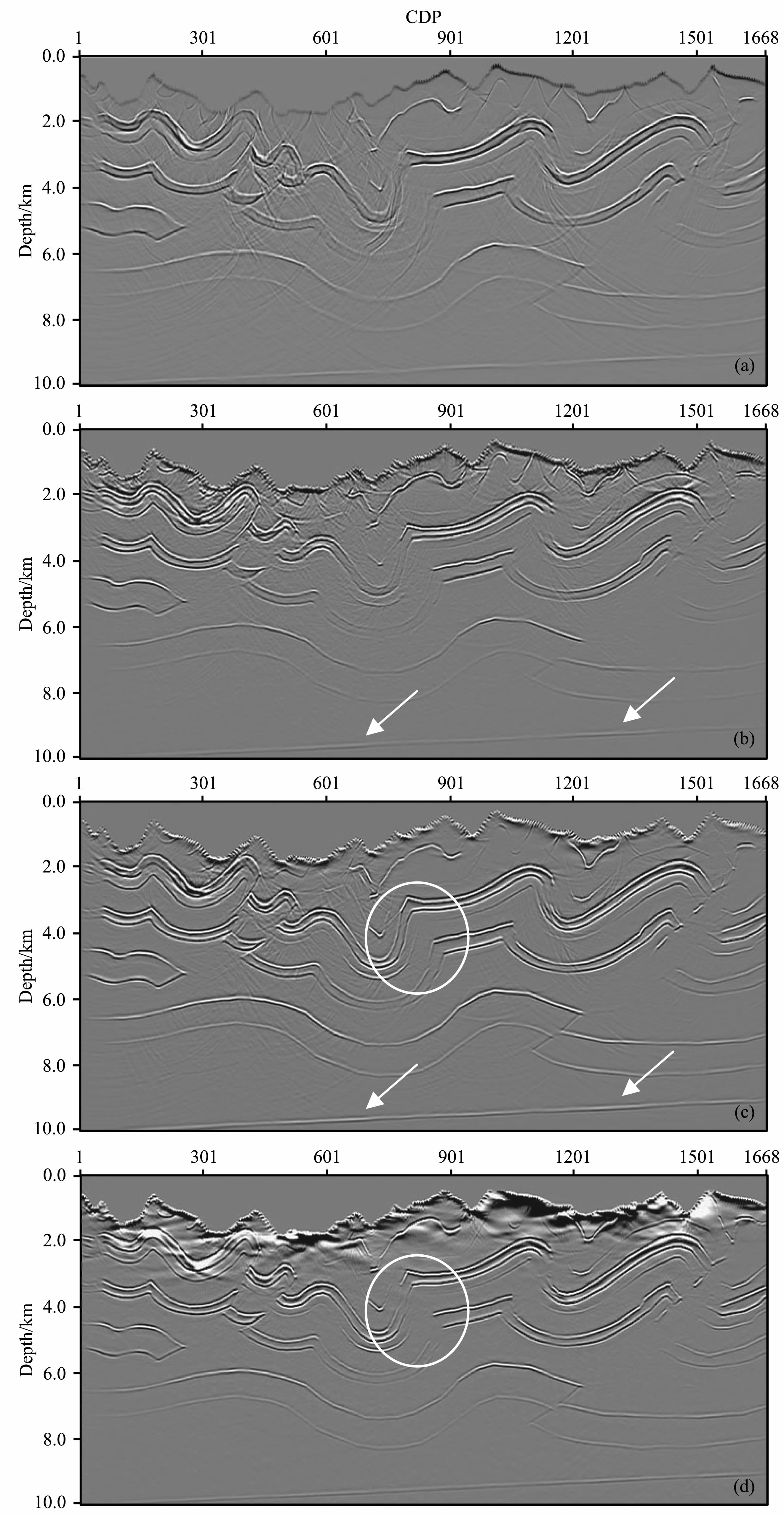
分别采用不同的成像方法对该模型进行试算并进行对比.图 6a为Kirchhoff偏移成像结果,图中可以看出,虽然模型的基本构造得到成像,但是剖面中含有大量的偏移噪声.图 6b为基于Gray所提出的复杂地表条件下高斯束偏移成像结果,同Kirchhoff偏移相比,其成像结果信噪比明显提高,但是其浅层成像效果不够理想,含有大量的噪声.图 6c为本文方法的成像结果,可以看到同Gray 所提出的方法相比,本文方法不但有效地压制了Gray 方法中局部静校正所造成的浅层噪声,提高了近地表的成像精度,且深层构造更为清晰,能量更为均衡.同图 6d所示的“直接下延"频率-空间域有限差分法波动方程偏移相比,本文方法虽引入少量偏移噪声,但是可以对圆圈所标识的陡倾构造进行有效的成像,且不存在浅层的低频干扰.
|
图 6 基于不同成像方法的SEG起伏地表模型叠前深度偏移结果 (a) Kirchhoff偏移;(b) Gray所提出高斯束偏移;(c)本文所提出高斯束偏移;(d)波动方程偏移. Fig. 6 Migrated results of SEG topographic model with different depth imaging methods (a) Kirchhoff migration; (b) Gaussian beam migration proposed by Gray;(c) Gaussian beam migration in this paper; (d) Wave equation migration. |
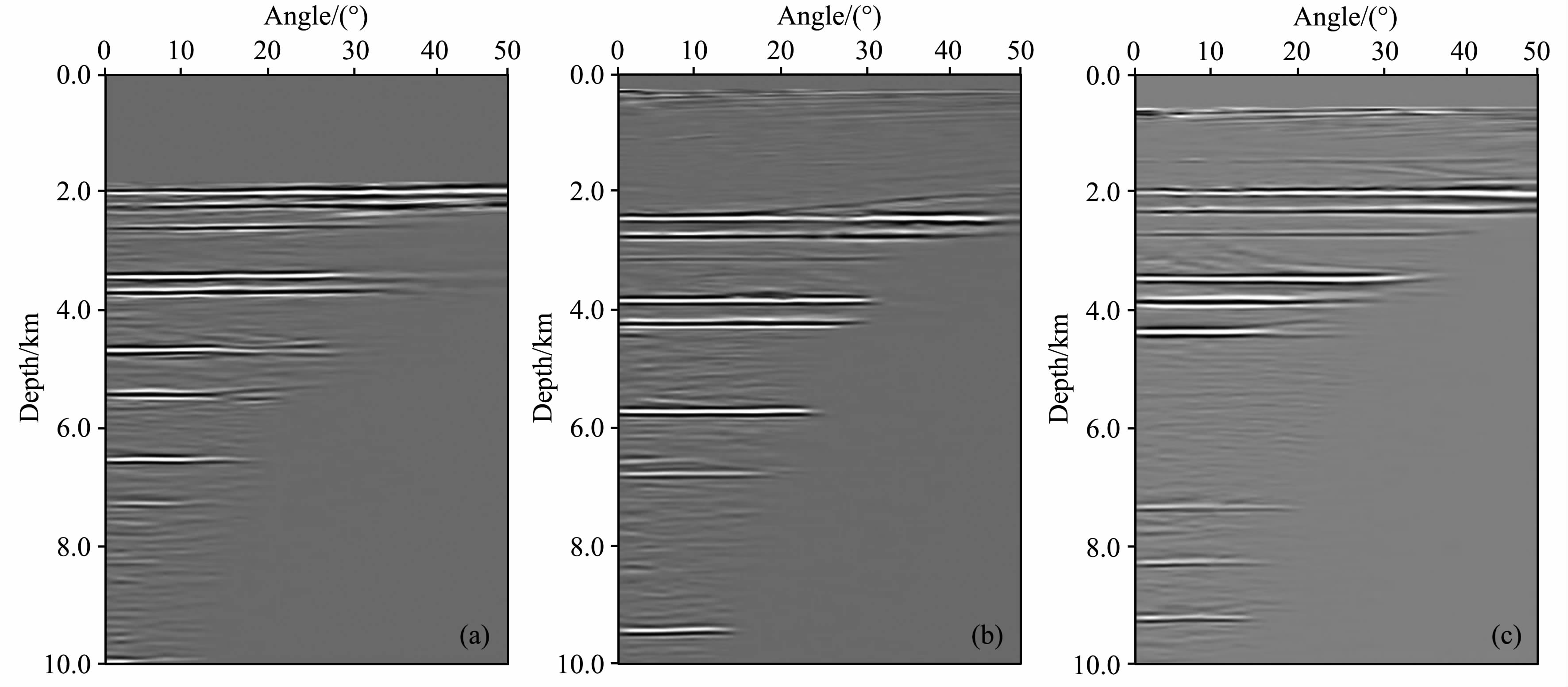
在进行深度偏移时,若速度模型准确且成像方法正确,所提取的角度域共成像点道集(ADCIGs)应为平直的.由于偏移测试中所用速度模型准确,因而可以通过判断ADCIGs是否拉平来验证本文所提出的成像方法的正确性.高斯束偏移的过程中,包含了地下射线的传播角度信息,可以利用此信息直接提取ADCIGs[24].我们在成像过程中提取了角度范围为0°~50°的ADCIGs,图 7a—7c 分别为CDP=100,1000,1400 处的ADCIGs,可以看到对应各个反射层的同相轴均比较平直,从而证明了本文所提出的复杂地表条件下高斯束偏移的正确性.
|
图 7 不同CDP处的ADCIGs (a) CDP=100; (b) CDP=1000; (c) CDP=1400. Fig. 7 ADCIGs of different CDP |
本文所提出的复杂地表条件下的保幅高斯束偏移不但可以有效地消除复杂地表对偏移成像的影响,并且可以得到反映地下随角度变化反射系数的偏移结果.数值模型的试算对上述结论进行了验证,并得到以下三个方面的认识:
(1) 倾斜叠加本质上是对根据平面波在接收点和束中心之间的传播时差,对地震记录施以对应的相移.式(8)所描述的局部倾斜叠加公式,考虑了地表的高程以及倾角等信息,可以直接在起伏地表进行局部平面波的分解,并且可以考虑近地表速度的变化从而进一步提高所分解平面波的精度;
(2) 高斯束偏移本质上是一种近似的平面波偏移方法,通过提高平面波分解的精度,本文方法可以有效地提高高斯束偏移的成像精度.此外,若要获得具有近似保幅的成像结果,还需考虑地表的倾角以及道间距信息;
(3) 本文方法还可以在成像的过程中,直接输出角度域共成像点道集,用以判断速度模型的准确性以及起伏地表条件下的偏移速度分析.
| [1] | Berryhill J R. Wave-equation datuming. Geophysics , 1979, 44(8): 1329-1341. DOI:10.1190/1.1441010 |
| [2] | Berryhill J R. Wave-equation datuming before stack. Geophysics , 1984, 49(11): 2064-2066. DOI:10.1190/1.1441620 |
| [3] | Yilmaz W, Lucas D. Prestack layer replacement. Geophysics , 1986, 51(7): 1355-1369. DOI:10.1190/1.1442186 |
| [4] | Schneider W A, Phillip L D, Paal E F. Wave-equation velocity replacement of the low-velocity layer for overthrust-belt data. Geophysics , 1995, 60(2): 573-579. DOI:10.1190/1.1443795 |
| [5] | Bevc D. Flooding the topography: Wave-equation datuming of land data with rugged acquisition topography. Geophysics , 1997, 62(5): 1558-1569. DOI:10.1190/1.1444258 |
| [6] | Yang K, Wang H Z, Ma Z T. Wave equation datuming from irregular surfaces using finite difference scheme. Expanded Abstracts of 69th Annual Internat SEG Mtg , 1999: 1842-1846. |
| [7] | Beasley C, Lynn W. The zero-velocity layer: Migration from irregular surfaces. Geophysics , 1992, 57(11): 1435-1443. DOI:10.1190/1.1443211 |
| [8] | Reshef M. Depth migration from irregular surfaces with depth extrapolation methods. Geophysics , 1991, 56(1): 119-122. DOI:10.1190/1.1442947 |
| [9] | 何英, 王华忠, 马在田, 等. 复杂地形条件下波动方程叠前深度成像. 勘探地球物理进展 , 2002, 25(3): 13–19. He Y, Wang H Z, Ma Z T, et al. Pre-stack wave equation depth migration for irregular topography. Progress in Exploration Geophysics (in Chinese) , 2002, 25(3): 13-19. |
| [10] | Shragge J, Paul S. Wave-equation migration from topography. Expanded Abstracts of 75th Annual Internat SEG Mtg , 2005: 1842-1846. |
| [11] | Wiggins J W. Kirchhoff integral extrapolation and migration of nonplanar data. Geophysics , 1984, 49(8): 1239-1248. DOI:10.1190/1.1441752 |
| [12] | Gray S H, Marfurt K J. Migration from topography: Improving the near-surface image. Canadian Journal of Exploration Geophysics , 1995, 31(1-2): 18-24. |
| [13] | Jager C, Hertweck T, Spiner M. True-amplitude Kirchhoff migration from topography. Expanded Abstracts of 73th Annual Internat SEG Mtg , 2003: 909-913. |
| [14] | Hill N R. Gaussian beam migration. Geophysics , 1990, 55(11): 1416-1428. DOI:10.1190/1.1442788 |
| [15] | Hill N R. Prestack Gaussian-beam depth migration. Geophysics , 2001, 66(4): 1240-1250. DOI:10.1190/1.1487071 |
| [16] | Gray S H. Gaussian beam migration of common-shot records. Geophysics , 2005, 70(4): S71-S77. DOI:10.1190/1.1988186 |
| [17] | Zhu T F, Gray S H, Wang D L. Prestack Gaussian-beam depth migration in anisotropic media. Geophysics , 2007, 72(3): S133-S138. DOI:10.1190/1.2711423 |
| [18] | Gray S H, Bleistein N. True-amplitude Gaussian-beam migration. Geophysics , 2009, 74(2): S11-S23. DOI:10.1190/1.3052116 |
| [19] | Schneider W A. Integral formulation for migration in two and three dimensions. Geophysics , 1978, 43(1): 49-76. DOI:10.1190/1.1440828 |
| [20] | Wapenarr C P A, Peels G L, Budejicky V, et al. Inverse extrapolation of primary seismic waves. Geophysics , 1989, 54(7): 853-863. DOI:10.1190/1.1442714 |
| [21] | Claerbout J F. Toward a unified theory of reflector mapping. Geophysics , 1971, 36(3): 467-481. DOI:10.1190/1.1440185 |
| [22] | Docherty P. A brief comparison of some Kirchhoff integral formulas for migration and inversion. Geophysics , 1991, 56(8): 1164-1169. DOI:10.1190/1.1443136 |
| [23] | Geiger H D. Relative-amplitude-preserving prestack time migration by the equivalent offset method. Calgary: University of Calgary , 2001. |
| [24] | 李振春, 岳玉波, 郭朝斌, 等. 高斯波束共角度保幅深度偏移. 石油地球物理勘探 , 2010, 45(3): 360–365. Li Z C, Yue Y B, Guo C B, et al. Gaussian beam common angle preserved-amplitude migration. Oil Geophysical Prospecting (in Chinese) , 2010, 45(3): 360-365. |
 2012, Vol. 55
2012, Vol. 55

