2. 中国石油大学(北京)CNPC物探重点实验室, 北京 102249
2. CNPC Key Laboratory of Geophysical Exploration, China University of Petroleum, Beijing 102249, China
地震波在地下介质中传播时,不仅受介质的各向异性影响,还受地层介质内在的黏滞性影响[1].因此,为了准确地描述地震波在地下介质中的传播特征和更精确地指导地震数据采集、处理和解释,应选取能够同时模拟地层各向异性特征和黏滞性特征的黏弹各向异性介质模型来进行波场数值模拟与分析.
目前,黏弹各向异性介质的地震波场数值模拟研究已经取得了一些进展.Carcione[1-3]基于广义线性固体模型引入新的黏弹性各向异性本构关系,建立了黏弹各向异性介质中随时间而变化的松弛矩阵,而且推导出了黏弹VTI介质的波动方程,并模拟了纵波、横波的各向异性和衰减特征.张忠杰等[4-5]用近似解析分析法模拟了黏弹EDA 介质中的波场.杜启振等[6-8]在Carcione的基础上给出了以各向异性主轴方位为参数的各向异性黏弹性介质波动方程,并先后采用有限元法、伪谱法和有限差分法对方位各向异性黏弹性介质中的波场进行了模拟与分析.郭智奇等[9]利用伪谱法模拟了黏弹VTI介质中的波场.谭未一等[10]采用规则网格有限差分法模拟了黏弹VTI介质中的波场.李军等[11]利用交错网格高阶有限差分对黏弹性VTI介质中的波场进行了数值模拟.然而,这些研究对黏弹各向异性介质的波场模拟主要针对两种特殊情况:黏弹VTI介质或黏弹HTI介质.而具有任意倾斜对称轴横向各向同性(TTI)介质在实际地层各向异性的表现中更具有广泛性[12-14].因此,如果能给出黏弹TTI介质波动方程,并针对其进行波场数值模拟与分析,则更具有一般性.
黏弹TTI介质可以看成是黏弹VTI介质经过旋转一定的角度后得到的,其对称轴与在地面建立的观测坐标系存有一定的夹角,如果利用普通交错网格法求解二维三分量的黏弹TTI介质波动方程,为计算应力而求质点振动速度的空间偏导数时,有些偏导不能直接求解,需要进行漂移或借助辅助网格.而且在普通交错网格中,要求弹性模量定义在所有的半网格点和整网格点上,而实际中通常只定义在半网格点上,这就需要对弹性模量进行插值[15].因此,当弹性模量变化很大时,普通交错网格法就容易出现计算不稳定的问题[16].Saengere等[17-18]首先提出了旋转交错网格有限差分算法,并指出其可以克服普通交错网格差分的上述缺陷.而后,一些学者利用旋转交错网格有限差分法分别对孔隙介质、各向异性介质等的波场进行了数值模拟[19-21].
旋转交错网格有限差分的所有物理量只定义在两个不同的位置.其中,应力(或质点振动速度)定义在离散网格单元的中心,质点振动速度(或应力)定义在离散网格单元的顶点,故可将所有的弹性模量定义在相同的位置,且可与应力所在的位置相同[17, 19].因此,采用旋转交错网格有限差分法,在模拟非均匀介质时,弹性模量不需要进行平均;在模拟TTI介质时,计算应力的所有物理量的空间偏导数可以直接求解,且弹性模量也不再需要进行插值处理[19].所以旋转交错网格差分法更适合黏弹TTI介质的波场模拟,并且相对于普通交错网格差分法,旋转交错网格差分法可以得到更加稳定、更可信的解.
本文在Carcione[1-2]提出的黏弹各向异性本构关系基础上,给出黏弹TTI介质的二维三分量一阶速度-应力方程,然后采用旋转交错网格任意偶数阶精度有限差分格式求解该方程,并将PML 引入到黏弹TTI介质波动方程的旋转交错网格差分数值模拟中,实现了该类介质波场的旋转交错网格高阶有限差分数值模拟,并且根据模拟结果具体分析了地震波在传播过程中所表现出的各向异性和黏弹性特征.
2 黏弹TTI介质波动方程 2.1 观测坐标系内的本构关系Carcione的黏弹各向异性理论认为介质对地震波的吸收衰减作用是由大量耗散机制引起的,且各种耗散机制可以用黏弹性的本构关系进行描述,采用其建立的应力应变关系[1],即
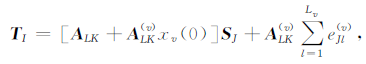
|
(1) |
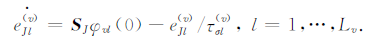
|
(2) |
其中,xv(0)(v= 1,2)表示0 时刻的弛豫模量,当v=1时,对应于纵波,当v=2时,对应于横波;TT =(T1,T2,T3,T4,T5,T6)= (σxx,σyy,σzz,σyz,σzx,σxy)表示应力向量;ST = (S1,S2,S3,S4,S5,S6)= (εxx,εyy,εzz,εyz,εzx,εxy)表示应变向量;ALK和A(v)LK(L,K=1,2,…,6;v=1,2)分别表示非弛豫空间函数和弛豫空间函数,并且其与弹性参数有关;Lv(v=1,2)表示纵波或横波弛豫机制的总数;e(v)Jl为记忆变量,e(v)Jl·是记忆变量的时间导数;φvl(0)(l=1,2,…,6;v= 1,2)表示第l个弛豫机制的响应函数;τ(v)σl(l=1,2,…,6;v=1,2)表示第l个机制的应力弛豫时间.上述变量及函数的具体表达式可以参见参考文献[1].
根据黏弹各向异性介质的本构关系,坐标旋转以后,可以得到观测坐标系下以任意方位角和倾角为参数的应力应变关系方程[1],即
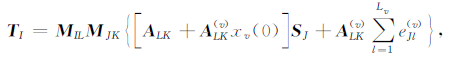
|
(3) |
式中,M为旋转变换矩阵[12],且
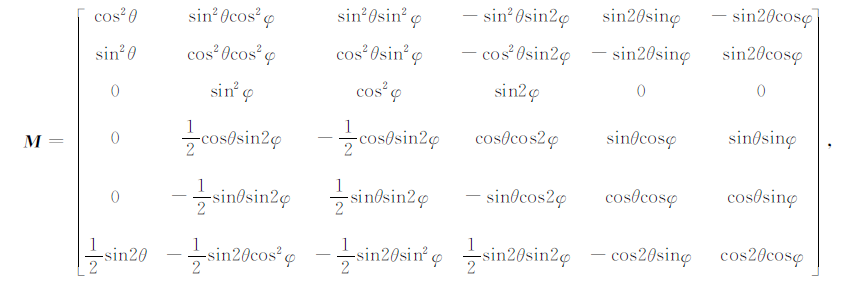
|
(4) |
其中,θ和φ 分别为在观测坐标系下的方位角和倾角.
将式(3)变形可得
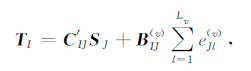
|
(5) |
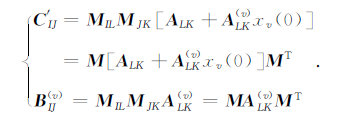
|
(6) |
由黏弹性各向异性介质的本构关系,给出黏弹TTI介质的二维三分量一阶速度-应力方程[1, 2].
运动方程:
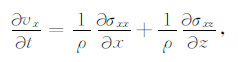
|
(7a) |
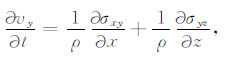
|
(7b) |
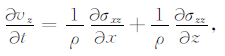
|
(7c) |
其中,ρ为介质的密度,vx、vy、vz分别是质点速度x、y、z的分量,σxx、σzz为正应力,σxz、σxy、σyz为切应力.
应力-速度关系:
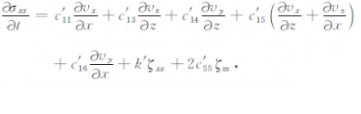
|
(8a) |
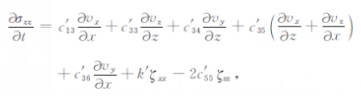
|
(8b) |
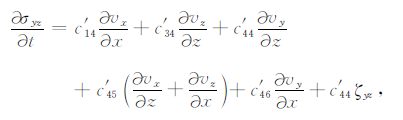
|
(8c) |
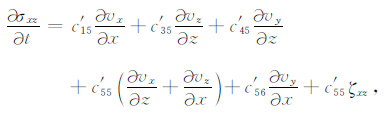
|
(8d) |
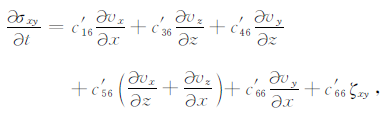
|
(8e) |
其中,c′ij为介质的弹性系数,ζxx、ζzz、ζyz、ζxz、ζxy是记忆变量的导数,并且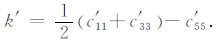
记忆变量方程:
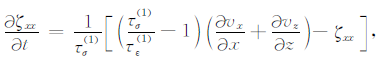
|
(9a) |
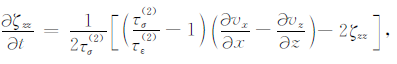
|
(9b) |
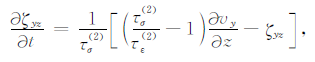
|
(9c) |
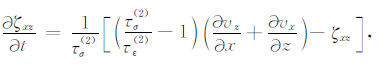
|
(9d) |
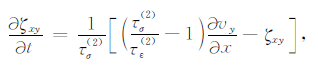
|
(9e) |
其中,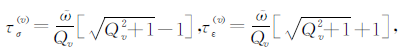
v=1、2分别对应两种耗散机制;τσ(v) 、τε(v) 分别是两种耗散机制的应力和应变的松弛时间;Q1、Q2 分别为纵波、横波的品质因子;$\tilde \omega $为中心频率的倒数.
由式(7)、(8)、(9)构成黏弹TTI介质中波动方程组,以此为基础对黏弹TTI介质做二维三分量波场数值模拟.
3 旋转交错网格有限差分格式图 1解释了旋转交错网格有限差分算法的二维空间交错方法.在旋转交错网格中,所有的速度分量都被定义在同一位置,而所有的应力分量位于另外的同一位置(黏弹TTI介质波动方程中的记忆变量的导数都定义在与应力分量相同的位置),因此,也可以将介质密度和弹性模量定义在相同的位置[19],本文中将它们定义在与应力分量相同的位置上.
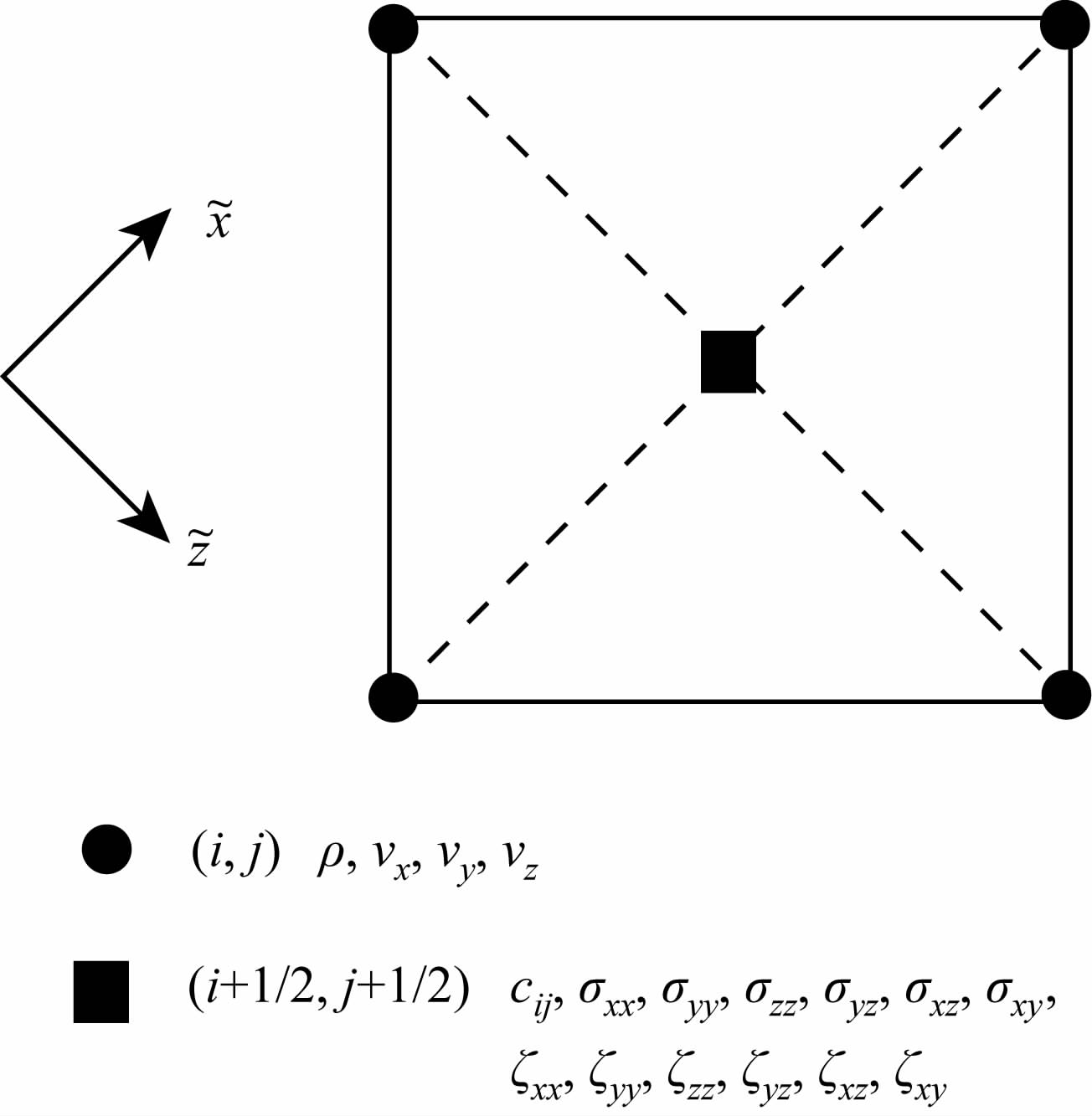
|
图 1 旋转交错网格的二维网格单元示意图[17] Fig. 1 Stencil of discretization scheme in rotated staggered grid scheme in 2D |
旋转交错网格有限差分法是先沿网格对角线方向计算相关物理量的空间导数,然后再将这些对角线方向的计算结果进行线性叠加来得到沿坐标轴方向的空间导数[19].在二维空间的情形下,旋转交错网格有限差分沿坐标轴方向的差分算子的计算表达式为[17]
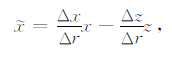
|
(10) |
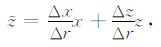
|
(11) |
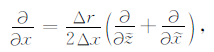
|
(12) |
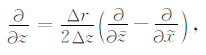
|
(13) |
式中$\tilde x$和$\tilde z$分别代表两个对角线的方向,Δx和Δz分别是沿坐标轴x、z方向的空间步长,Δr是对角线的长度,且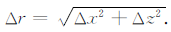
假定${D_{\tilde x}}$和${D_{\tilde z}}$分别表示∂/∂$\tilde x$和∂/∂$\tilde z$在$\tilde x$和$\tilde z$方向的任意偶数阶偏导数,设函数u(x,z,t)连续,且具有2N+1阶导数,则
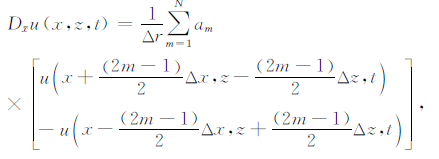
|
(14) |
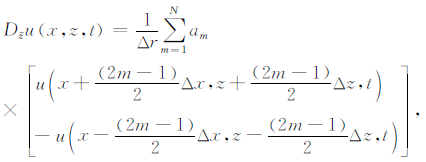
|
(15) |
式中,N为差分阶数的一半;m=1,2,…,N;am为差分系数,其值详细推导与普通交错网格的差分系数的推导是一致的,详见参考文献[22].
由式(12)-(15)可以推导出在x和z方向的偏导数,即
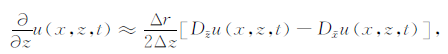
|
(16) |
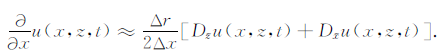
|
(17) |
利用式(14)-(17)直接求解黏弹TTI介质的波动方程组,可以得到方程的旋转交错网格任意偶数阶精度差分格式.
结合各向异性介质中弹性波方程差分算法的稳定性条件和旋转交错网格的特性,给出黏弹TTI介质中二维一阶速度-应力方程的时间二阶精度、空间2N阶精度的旋转交错网格差分稳定性条件近似表达式[23],即
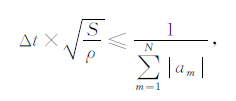
|
(18) |
式中,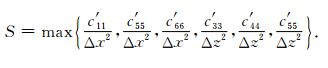
Berenger于1994 年首次提出了PML 吸收边界条件,并将其运用来消除电磁波场数值模拟中的人为截断边界所产生的反射波[24].随后许多学者将此方法引入到了地震波场的数值模拟中,并取得了比较好的效果[25].本文将PML 引入到用旋转交错网格高阶有限差分求解的黏弹TTI介质波动方程中.在二维空间情形下,旋转交错网格有限差分法中实现PML 的思路,与普通交错网格有限差分中PML 算法的基本思路是相同的.根据PML 吸收边界条件的基本原理,采用时间域变量分裂的方法,对一阶速度-应力黏弹TTI介质波动方程进行波场变量分离,可以得到应用于黏弹TTI介质波动方程的PML 吸收边界条件.在二维空间的条件下,对于式(7)、(8)、(9),每一个波场变量可分为两部分,即
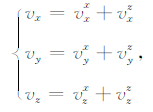
|
(19) |
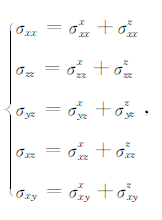
|
(20) |

|
(21) |
式中上标x和z代表该项只与相应的空间导数有关.同时,可以得到分裂后的PML 吸收边界中带有衰减因子的波动方程(下面只以σxx为例,逐步推导给出其吸收层边界方程的具体形式),即
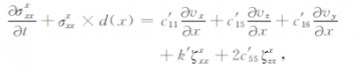
|
(22) |
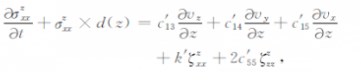
|
(23) |
其中,函数d(x)和d(z)是与x和z方向有关的衰减因子[25].
在数值模拟过程中PML 吸收层被分成了不同的区域,如图 2所示,不同区域的衰减因子的取值是不同的.在b1 和b3 代表的吸收层区域,d(x)=0,d(z)>0;在b2 和b4 代表的吸收层区域,d(x)>0,d(z)=0;在a1、a2、a3 和a4 代表的PML 吸收层区域,d(x)>0,d(z)>0.
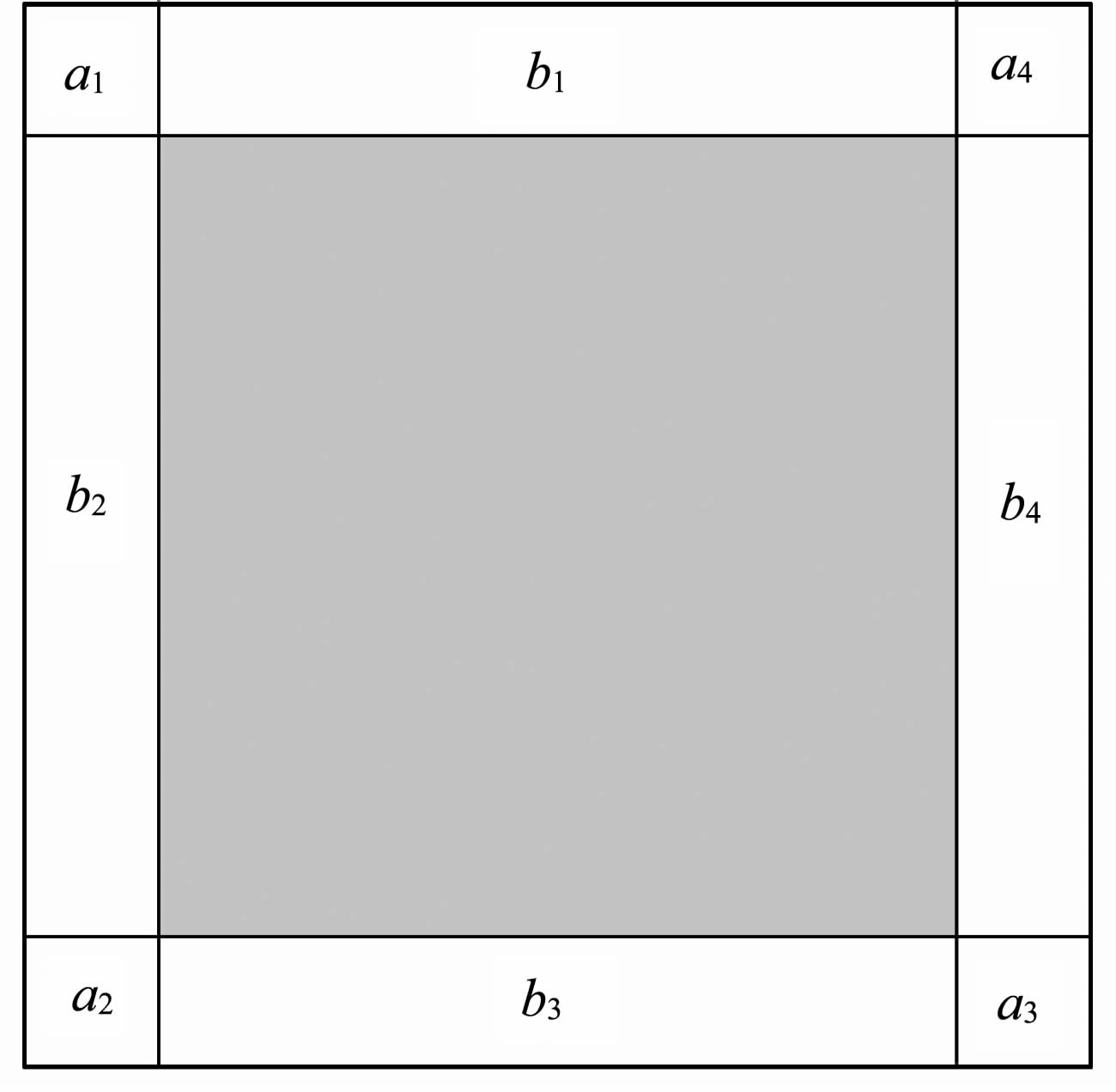
|
图 2 完全匹配层吸收边界示意图[25] Fig. 2 Stencil of perfectly matched layer absorbing boundary conditions |
限于篇幅,仅以式(20)中σxx分量和式(22)为例进行差分离散,给出其二阶时间差分精度、高阶空间差分的旋转交错网格有限差分格式,即
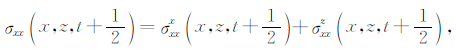
|
(24) |
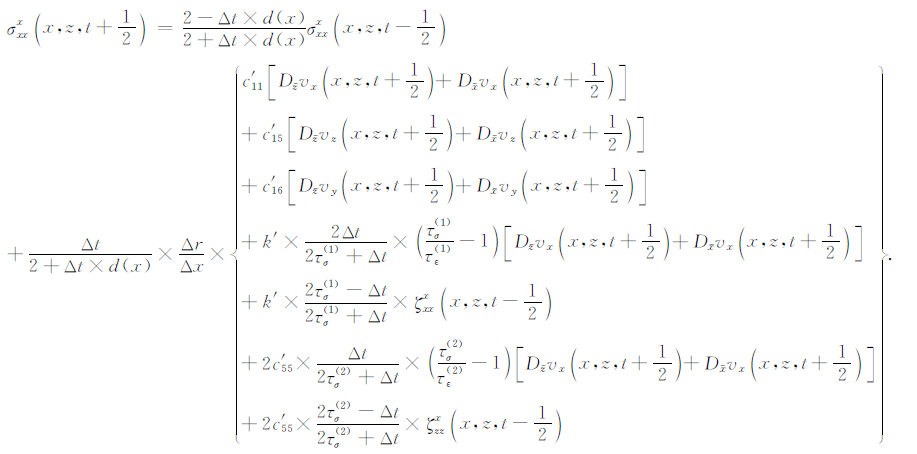
|
(25) |
${D_{\tilde x}}$和${D_{\tilde z}}$分别表示∂/∂$\tilde x$和∂/∂$\tilde z$在$\tilde x$和$\tilde z$方向的任意偶数阶偏导数式,故将式(14)和式(15)代入式(25)中,其余分裂变量采用同样的方式推导,即可求得PML边界条件的任意偶数阶旋转交错网格有限差分格式.
5 数值模拟与分析 5.1 PML吸收边界条件效果验证为了验证PML 吸收边界的效果,设计了一个大小为2000m×2000m、方位角为45°、对称轴倾角为60°的均匀黏弹TTI介质模型,空间采样间隔Δx=Δz=5m, 时间步长为1ms.模型介质在自然坐标系下的弹性参数如表 1,模型的纵波Q值为80,横波Q值为60.震源子波采用Ricker子波,震源位置(1000m, 1000m),主频为20Hz, 震源为x方向的横波源.
|
|
表 1 均匀黏弹性T1介质在自然坐标系下的弹性参数 Table 1 The elastic parameters of the homogeneous viscoelastic TTI media in the normal axis |
在数值模拟过程中采用二十阶空间差分精度、二阶时间差分精度的旋转交错网格有限差分格式对上述模型做二维三分量波场数值模拟.图 3(a, b, c)分别是考虑吸收边界条件时模拟得到的x、y、z三个分量的波场快照,在每个分量,四个波场快照从左到右对应的时间依次为600ms、840ms、1200ms和1800ms.从图 3可以看出,x、y、z三个分量入射到截断边界处的各类外行波都被完全吸收,这表明本文在用旋转交错网格差分法模拟黏弹TTI介质中波场时所采用的PML 边界条件对各类外行波都具有良好的吸收性能.
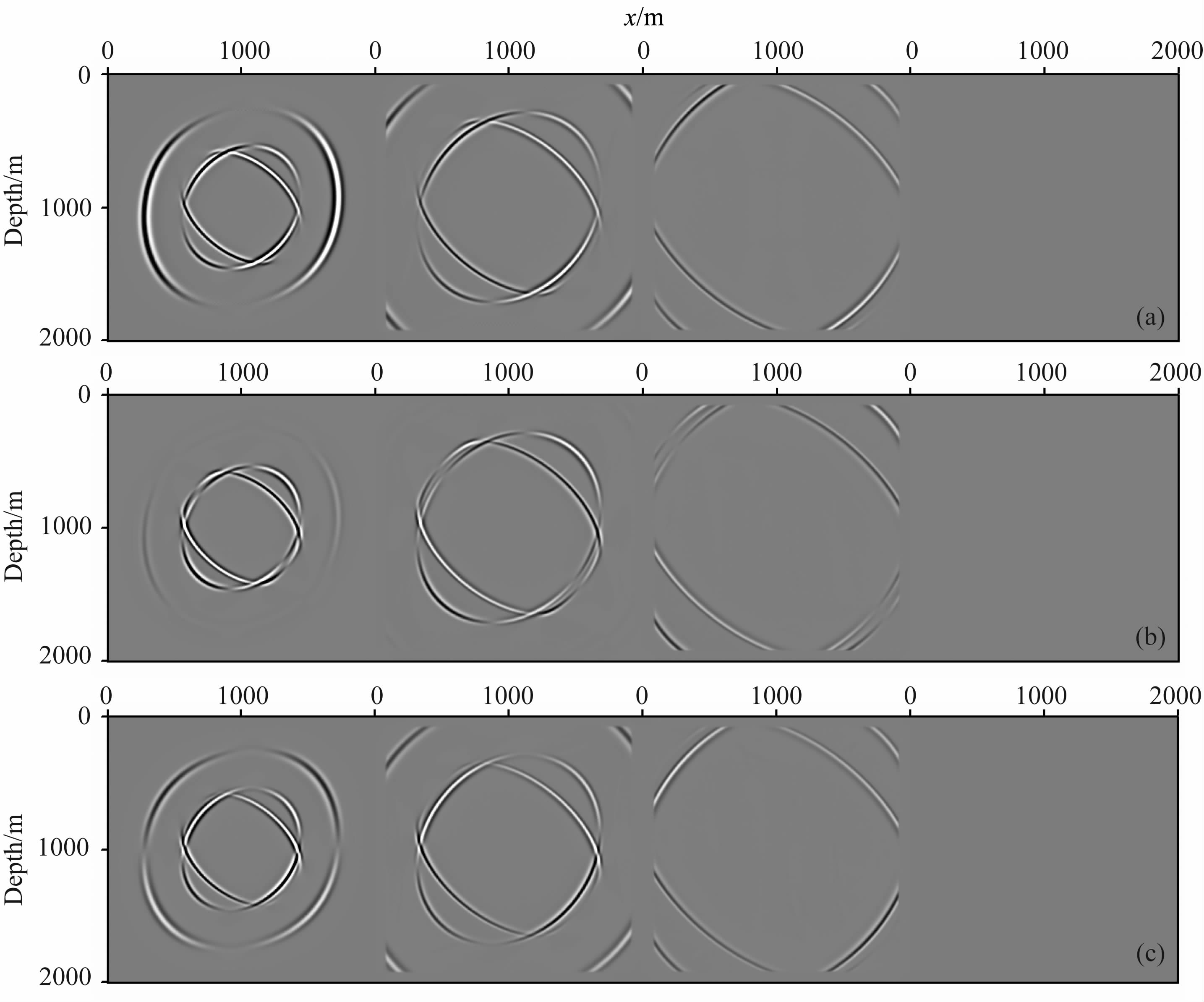
|
图 3 黏弹TTI介质中加PML 吸收边界的波场快照 (a)x分量;(b)y分量;(c)z分量. Fig. 3 Snapshots of wavefield in viscoelastic TTI media with PML absorbing boundary conditions Snapshots of wavefield in viscoelastic TTI media with PML absorbing boundary conditions (a)x-component;(b)y-component;(c)z-component. |
设计了一个大小为2000m×2000m 均匀黏弹TI介质模型,空间采样间隔Δx=Δz=5 m, 时间步长为1ms.模型的纵波Q值为80,横波Q值为60,模型介质在自然坐标系下的弹性参数如表 1.震源子波采用Ricker子波,震源位置(1000m, 1000m),主频为20Hz, 震源为x方向的横波源.数值模拟差分精度为:十八阶空间差分精度、二阶时间差分精度.图 4是黏弹TTI介质在方位角和对称轴倾角都为0时模拟得到的波场快照和单炮记录.图 5 是黏弹TTI介质在方位角为45°、对称轴倾角为60°时模拟得到的波场快照和单炮记录.
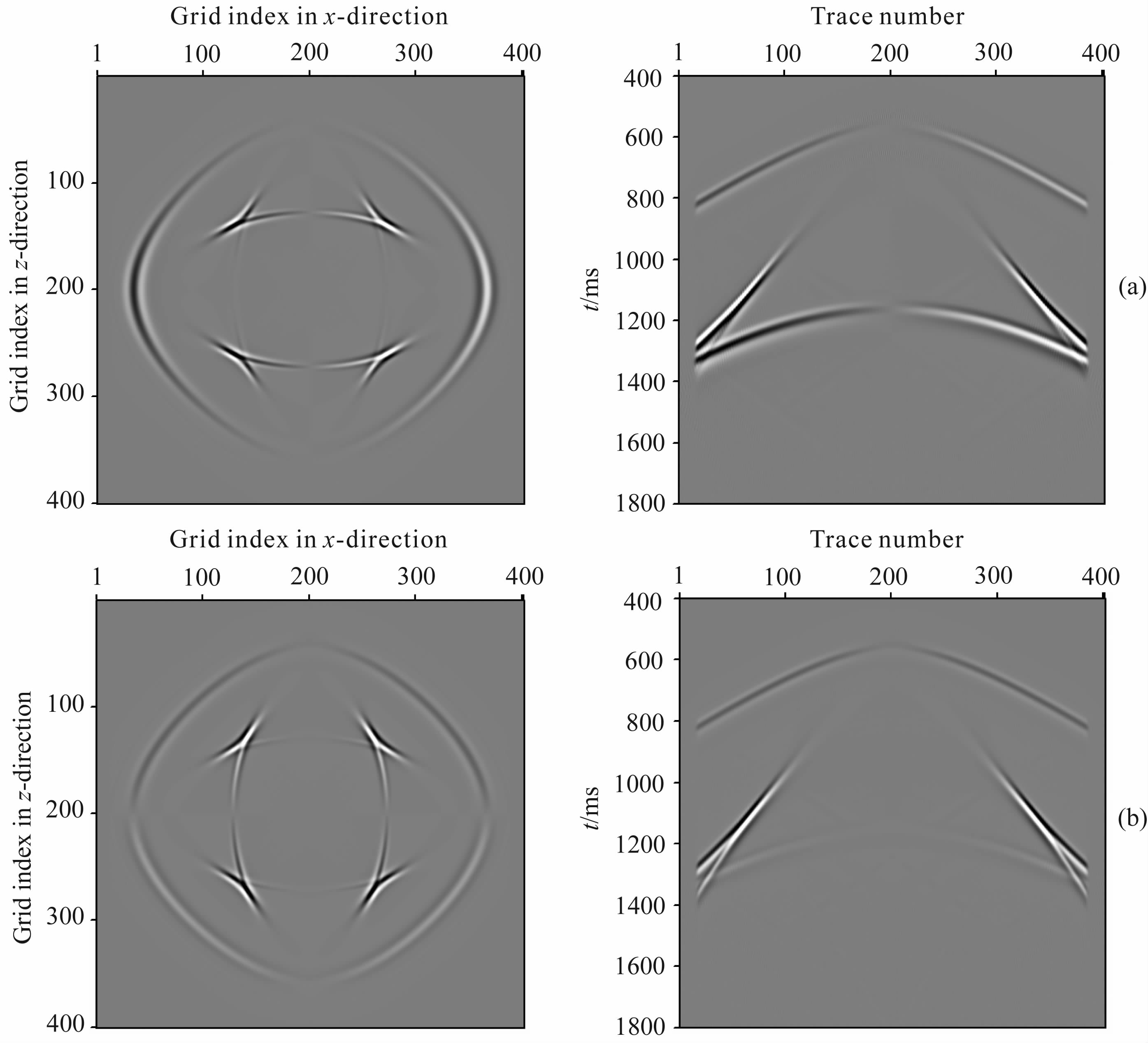
|
图 4 黏弹各向异性介质中地震波波场快照(左图)和传播记录(右图)介质方位角和倾角都为0,(a)x分量;(b)z分量. Fig. 4 Snapshots (left) and records(right) of seismic wave caused in viscoelastic and anisotropic media Media azimuth and dip angle are both zero degree(a)x-component,(b)z-component. |
从图 4中的各个分量可以看出:当黏弹TTI介质的对称轴倾角和方位角都等于0时,均匀黏弹TI介中的地震波记录包括拟纵波qP 波波形和拟横波qS波波形;波场快照中qS 波波前面的形状与单炮传播记录中qS波波形初至所形成的三叉区很相似,qS波波形及同相轴三叉区的出现导致波场变得更加复杂化;且单炮记录和波场快照中y分量均为0.
从图 5中的各个分量可以看到:当黏弹TTI介质的对称轴倾角不为0时,均匀黏弹TTI介质中地震波记录的三个分量中都有qP波波形、快横波qS1波形和慢横波qS2波形,即存在横波分裂现象;从单炮传播记录中也可以看到,各类波的同相轴变得不对称,且不一定是双曲线形态,并且随着偏移距的增大,在其对称轴上倾的方向上,qP 波形的初至时间要逐渐小于下倾向上qP 波形的初至时间,而两类qS波的情况则相反[27].
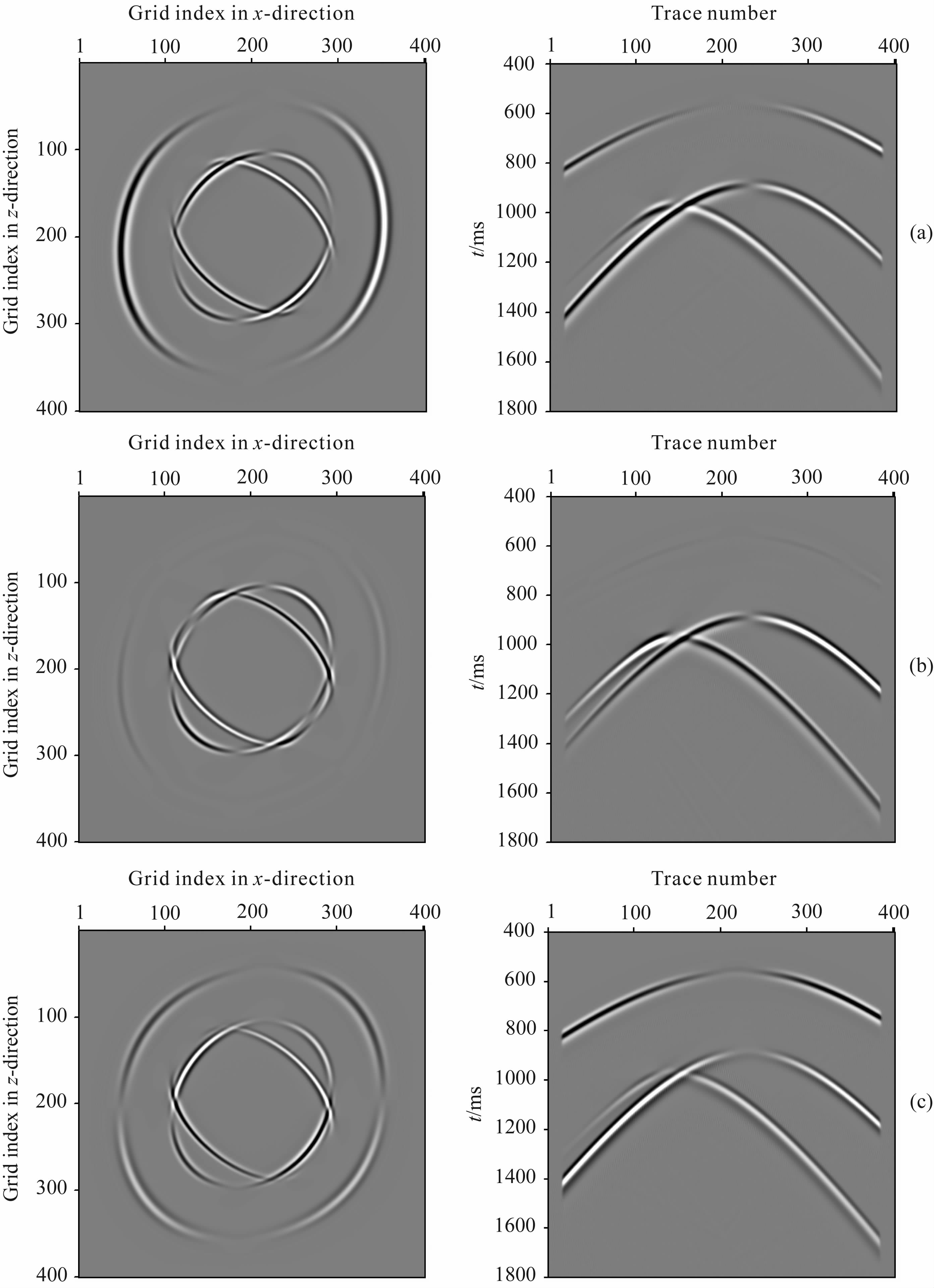
|
图 5 黏弹TTI介质中地震波波场快照(左图)和单炮传播记录(右图)介质方位角为45°、对称轴倾角为60°;(a)x分量;(b)y分量;(c)z分量. Fig. 5 Snapshots (left)and records (right) of seismic wave caused in viscoelastic and anisotropic media Media azimuth is 45 degree and dip angle of symmetry axis is 60 degree(a)x-component;(b)y-component;(c)z-component. |
为了简明地分析黏弹TTI介质中地震波的反射特征,设计了一个大小为5000 m×3000 m 两层介质模型.模型上层为黏弹TTI介质,其方位角为45°、对称轴倾角为60°;下层为黏弹各向同性介质,空间采样间隔Δx=Δz=5 m, 时间步长为1ms.模型介质参数如表 2.震源子波采用Ricker子波,震源位置(2500m, 1200m),主频为25 Hz, 震源为胀缩源.数值模拟差分精度为二十阶空间差分精度、二阶时间差分精度.
|
|
表 2 两层模型介质在自然坐标系下的介质参数 Table 2 The media's parameters of the double layers in the normal axis |
图 6是采用表 2中介质参数模拟得到的波场快照和单炮记录.从图 6 中可以看到,当上层黏弹TI介质的方位角和对称轴倾角都不为0时:(1)经过黏弹TTI介质与黏弹各向同性介质分界面的反射和透射后,其中地震反射波包括:拟纵波qP 波、转换的快横波qPS1 波、转换的慢横波qPS2 波、拟快横波qS1波、拟慢横波qS2波、转换的拟纵波qSP 波,且可看到明显的横波分裂现象;而在下层黏弹各向同性介质中的透射波只存在P 波、S 波、转换波SP波和转换波PS波;(2)在黏弹TTI介质中,qS波的波形初至会形成三叉区[26],这种特殊现象使地震波场变得更为复杂化,并特别容易引起误解;(3)黏弹TTI介质中,单炮记录上各类反射波的同相轴不再是双曲线型,且qS反射波的同相轴偏离最为明显.
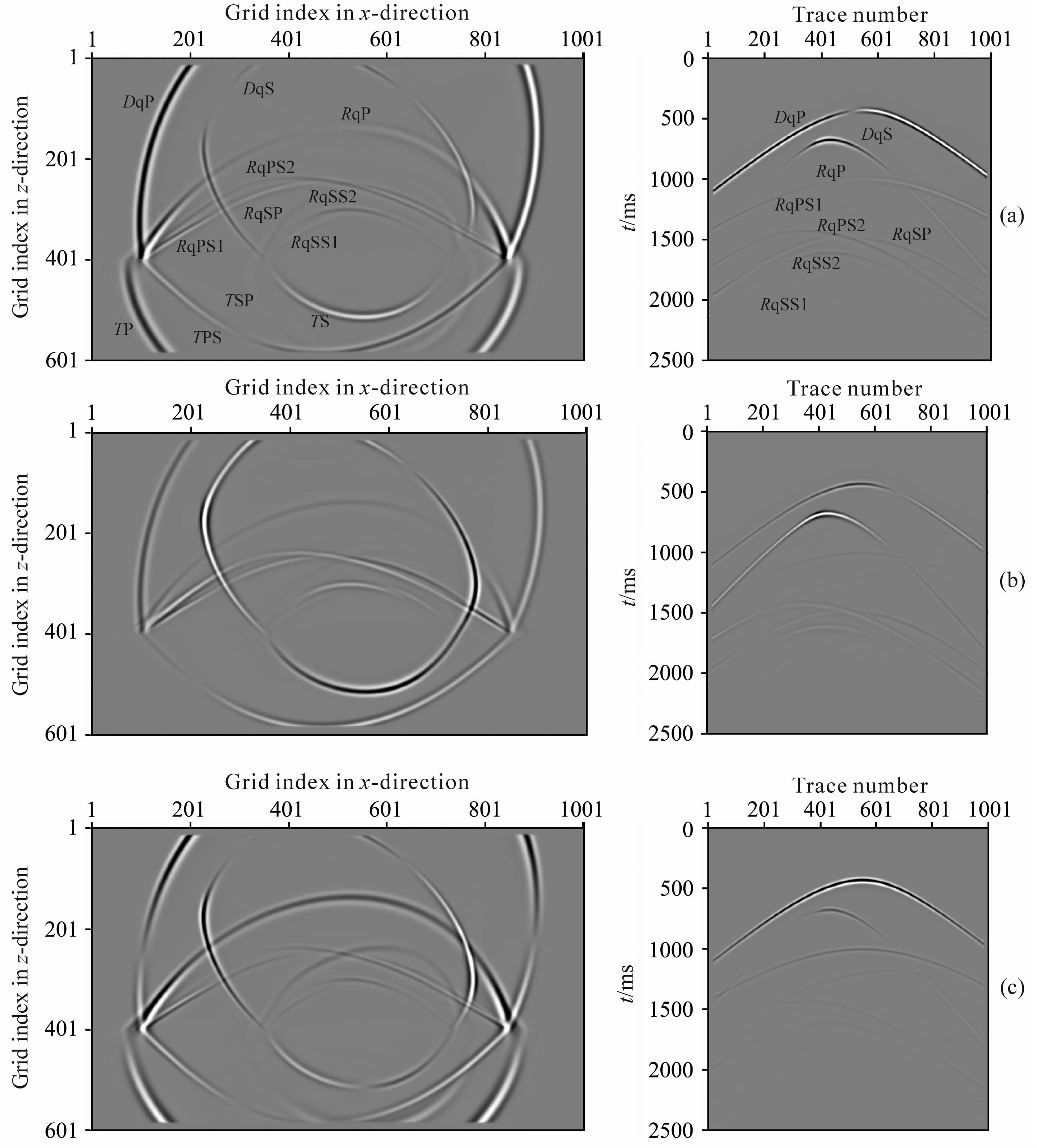
|
图 6 利用表2中介质参数模拟得到的地震波波场快照(左图)和单炮记录(右图)介质方位角为45°、对称轴倾角为60°;(a)为x分量,(b)为y分量,(c)为z分量;图中各种波前的字母:D、R和T分别表示直达波、反射波和透射波. Fig. 6 Snapshots (left) and records (right) of seismic wave simulated by media parameters according to table 2 Media azimuth is 45 degree and dip angle of symmetry axisis 60 degree (a) x-component;(b)y-component;(c)z-component;D,R and T stand for directed wave,reflected wave and transmitted wave,respectively. |
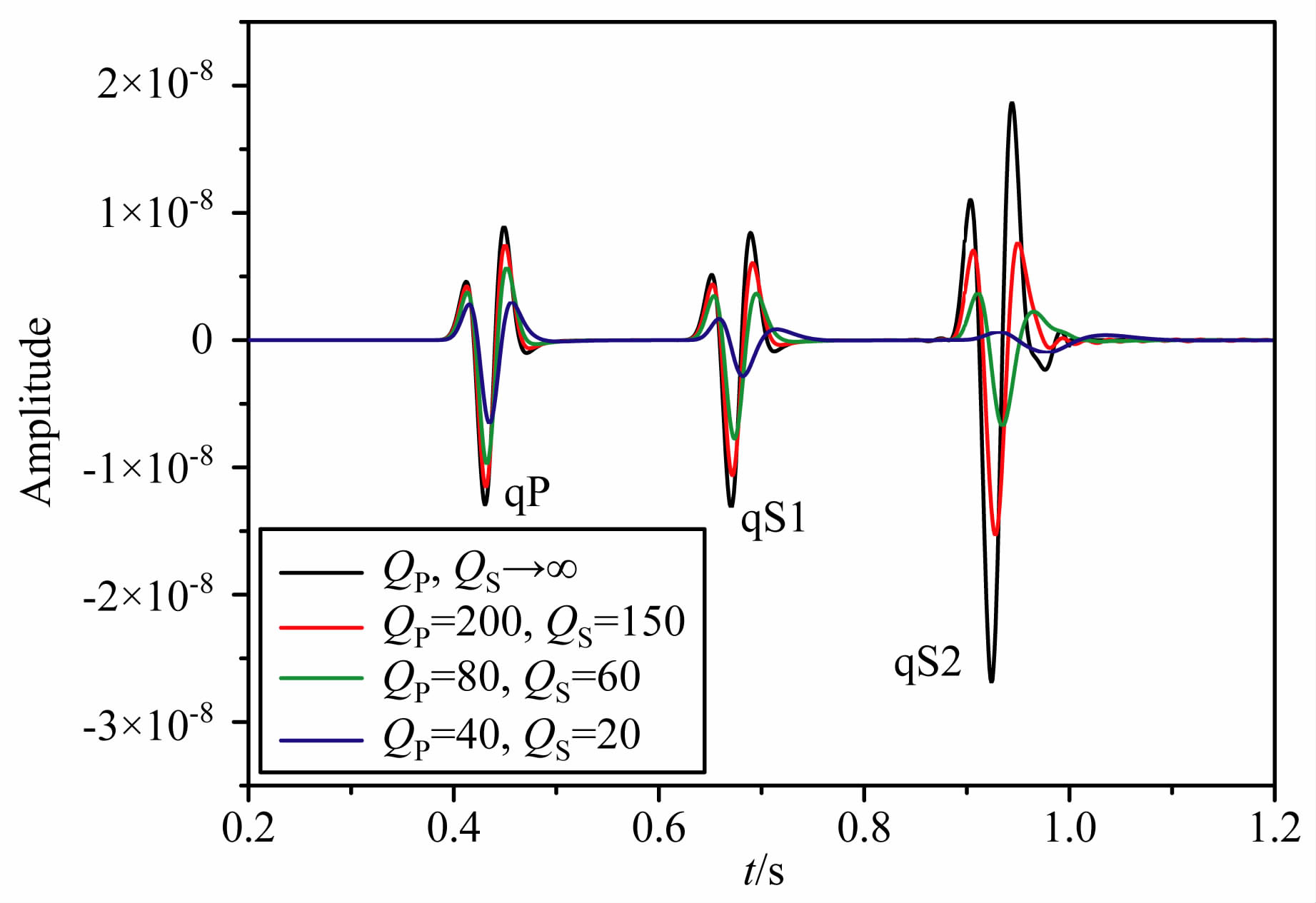
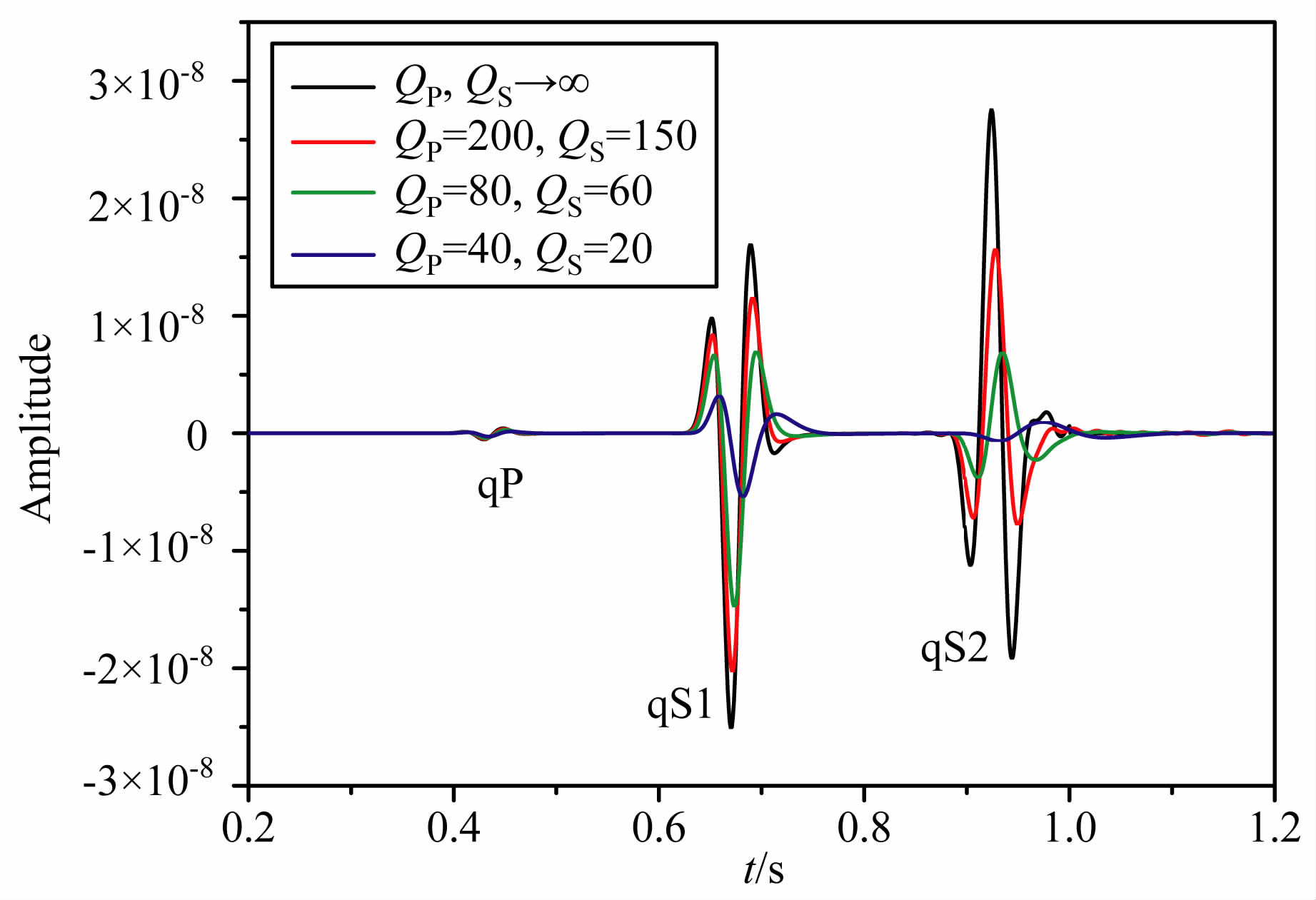
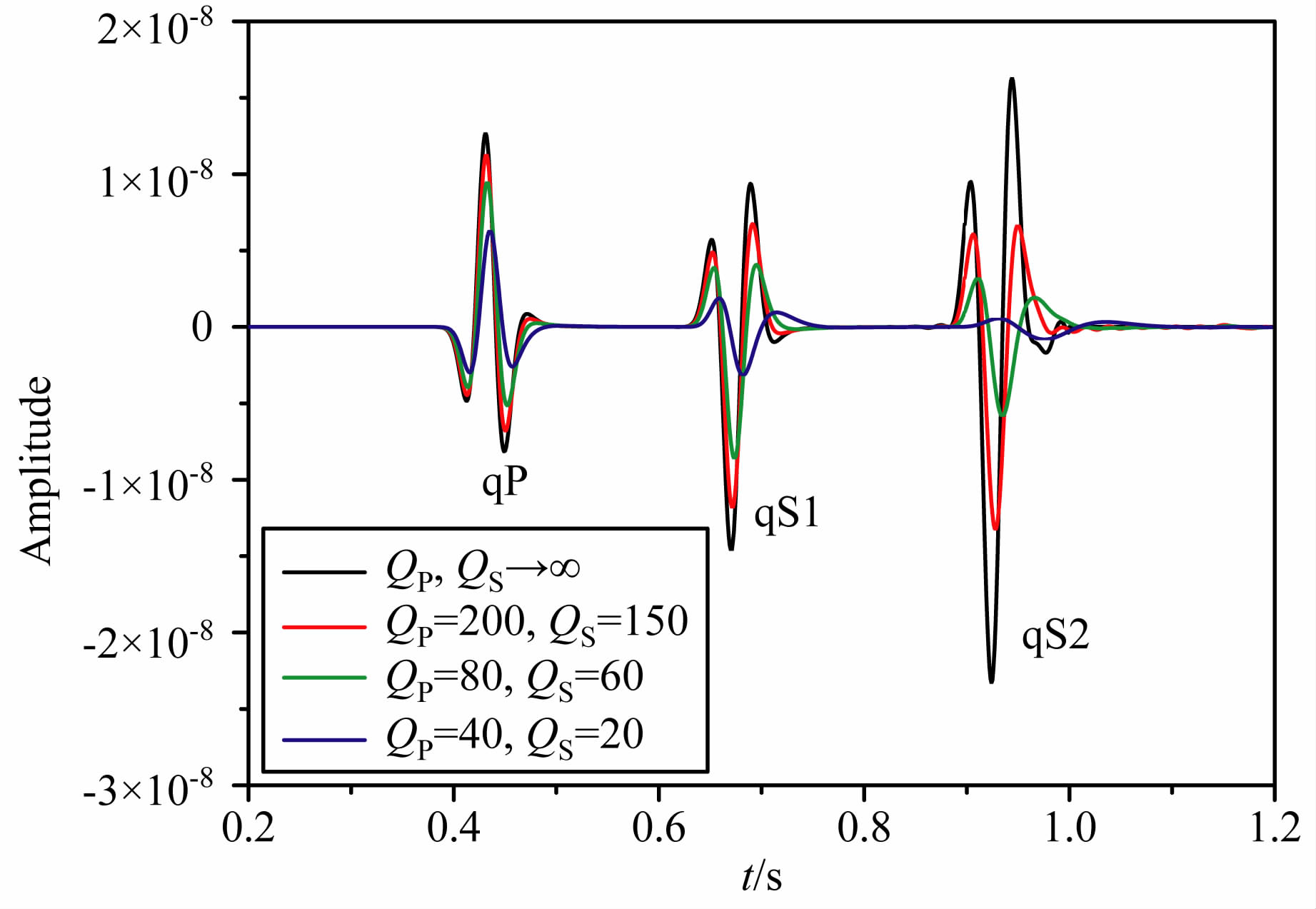
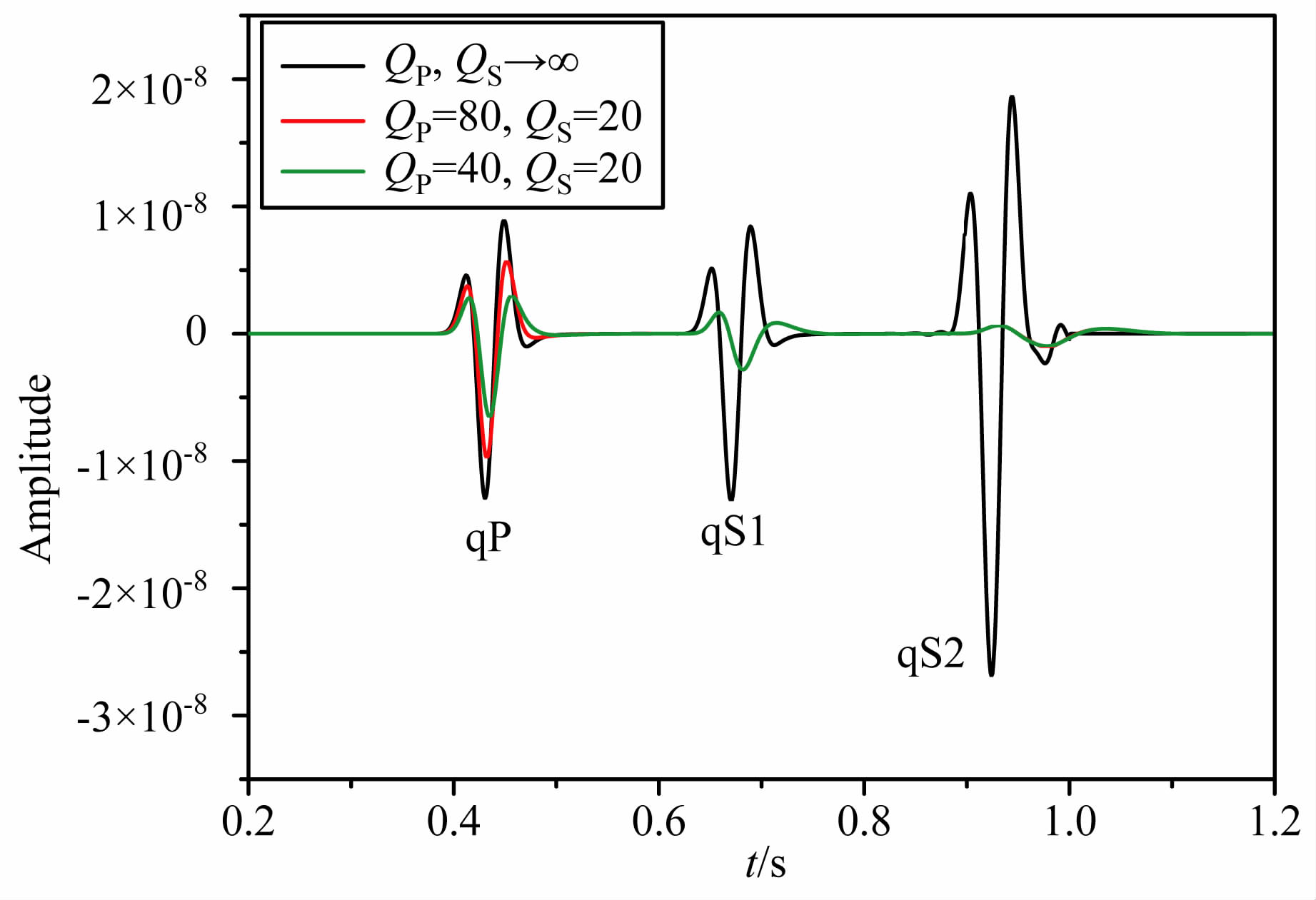
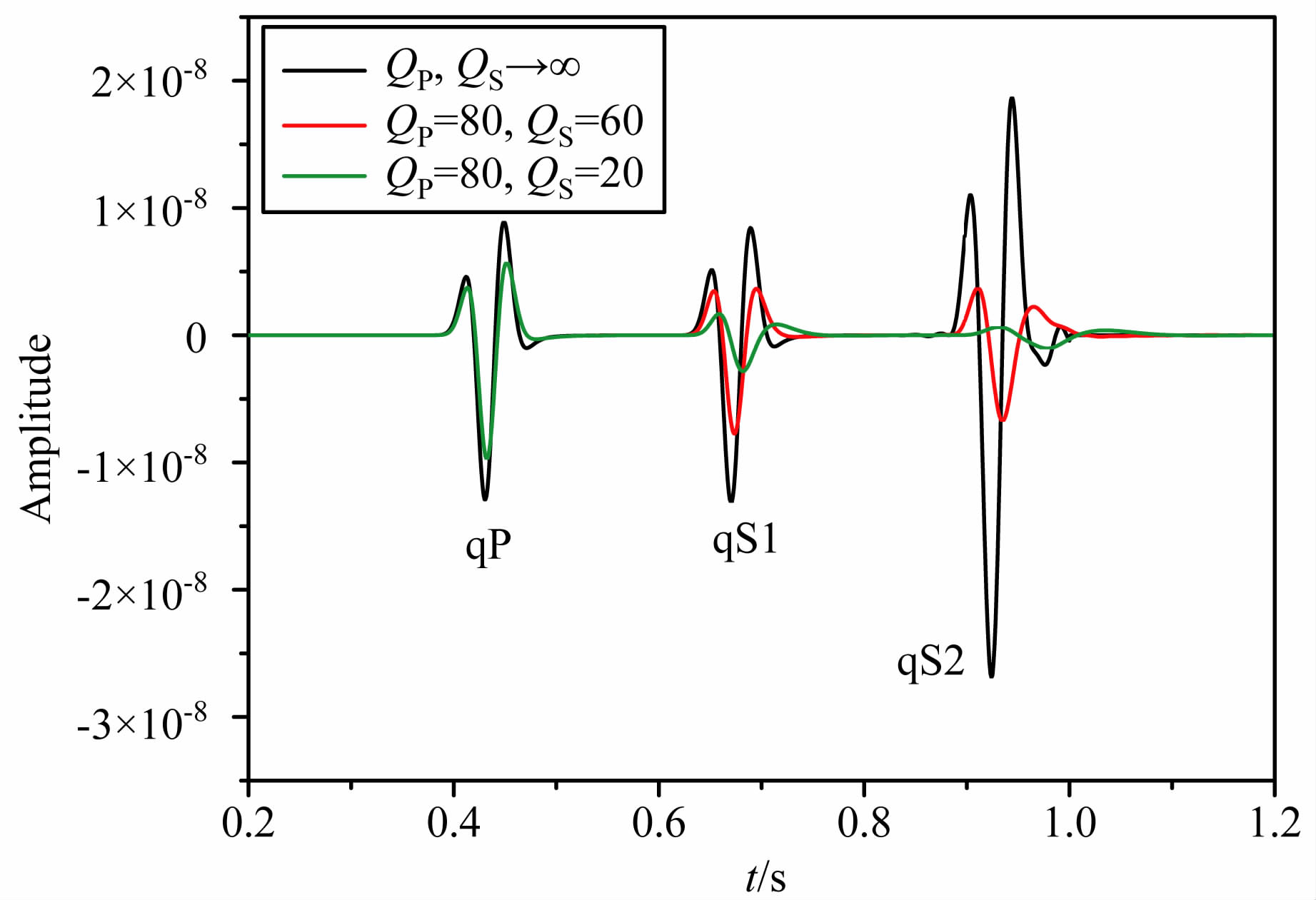
保持介质的弹性参数不变,但改变其纵波和横波的Q值,设计四种黏弹TTI介质模型以及一个TTI弹性介质模型(Q值无穷大),具体的介质参数如表 3.设计模型的大小为2000m×2000m、方位角为45°、对称轴倾角为60°,空间采样间隔Δx=Δz=5m, 时间步长为1ms.震源子波采用Ricker子波,震源位置(1000m, 1000m),主频为20 Hz, 震源为x方向的横波源.利用二十阶空间差分精度、二阶时间差分精度对四个模型分别做正演模拟,取(1500m, 500m)处质点的x、y、z三个分量振动记录进行分析.图 7、图 8、图 9分别是对表 3中介质1、2、3、4模拟得到的质点(1500m, 500m)处的x、y、z分量记录.图 10是对表 3 中介质1、5、4 分别模拟得到的质点(1500m, 500 m)处的x分量记录对比图.而图 11是对表 3中介质1、5、3分别模拟得到的质点(1500m, 500m)处的x分量记录对比图.
|
|
表 3 黏弹TT1介质在自然坐标系下的介质参数 Table 3 The media's parameters of the viscoelastic TT1 media in the normal axis |
|
图 7 对表 3中介质1、2、3、4分别模拟得到的质点(1500m,500m)处的x分量记录 Fig. 7 Records of x-component in point (1500m,500m) simulated by media 1,2,3 and 4 according to table 3 |
|
图 8 对表 3中介质1、2、3、4分别模拟得到的质点(1500m,500m)处的y分量记录 Fig. 8 Records of y-component in point (1500m,500m) simulated by media 1,2,3 and 4 according to table 3 |
|
图 9 对表 3中介质1、2、3、4分别模拟得到的质点(1500m,500m)处的z分量记录 Fig. 9 Records of z-component in point (1500m,500m) simulated by media 1,2,3 and 4 according to table 3 |
|
图 10 对表 3中介质1、5、4分别模拟得到的质点(1500m,500m)处的x分量记录 Fig. 10 Records of x-component in point (1500m,500m) simulated by media 1,5,4 according to table 3 |
|
图 11 对表 3中介质1、5、3分别模拟得到的质点(1500m,500m)处的x分量记录 Fig. 11 Records of x-component in point (1500m,500m) simulated by media 1,5,3 according to table 3 |
从图 7、图 8、图 9中可以看到,无论是x、y、z任一分量,由于介质的黏滞性而使质点的振动振幅都明显衰减,并且qS 波比qP 波的衰减幅度要大,而且品质因子越小,振幅衰减的越多,接收到的子波的峰值时间越往后延迟,并且波形变宽、畸变也越严重.从图 10中可以看出,纵波品质因子QP 对应于膨胀滞弹性的形变,且QP 越小qP 波振幅衰减越严重.从图 11中可以看出,横波品质因子QS 对应于剪切滞弹性的形变,且QS 越小qS波振幅衰减越严重.
6 结 论采用旋转交错网格高阶有限差分法模拟黏弹TTI介质中地震波场的传播过程,模拟精度较高,且易于实现.同时,将完全匹配层吸收边界条件应用到黏弹TTI介质旋转交错网格高阶有限差分模拟中,能有效地消除人工边界所产生的反射.
对模拟得到的波场进行分析表明:
(1) 黏弹TTI介质的各向异性主要影响波前面的形态,并且波前面形态复杂;qS 波波前面和同相轴的三分叉现象普遍,且其同相轴一般不再是双曲线型;当TI介质倾斜时,三个分量上均能够观测到横波分裂现象,而且各类波形的同相轴变得不对称;并且TI介质倾斜时,地震波通过界面反射后,其反射特征变得更为复杂,能够观测到反射横波的分裂现象.
(2) 黏弹TTI介质的黏弹性主要影响地震波的振幅衰减和波形畸变,对应于膨胀滞弹性形变的纵波品质因子主要影响qP 波的振幅衰减和波形畸变,对应于剪切滞弹性形变的横波品质因子主要影响qS波的振幅衰减和波形畸变;而且,当品质因子越小时,地震波振幅衰减的越多,接收到的子波的峰值时间越往后延迟,且其波形变宽、畸变也越严重.
| [1] | Carcione J M. Wave propagation in anisotropic linear viscoelastic media: Theory and simulated wavefields. Geophysical Journal International , 1990, 101(3): 739-750. DOI:10.1111/gji.1990.101.issue-3 |
| [2] | Carcione J M. Constitutive model and wave equations for linear, viscoelastic, anisotropic media. Geophysics , 1995, 60(2): 537-548. DOI:10.1190/1.1443791 |
| [3] | Carcione J M. Staggered mesh for the anisotropic and viscoelastic wave equation. Geophysics , 1999, 64(6): 1863-1866. DOI:10.1190/1.1444692 |
| [4] | Zhang Z J, Wang G J, Harris J M. Multi-component wavefield simulation in viscous extensively dilatancy anisotropic media. Physics of the Earth and Planetary Interiors , 1999, 114(1-2): 25-38. DOI:10.1016/S0031-9201(99)00043-6 |
| [5] | 张忠杰, 滕吉文, 贺振华. EDA介质中地震波速度、衰减与品质因子方位异性研究. 中国科学(E辑) , 1999, 29(6): 569–574. Zhang Z J, Teng J W, He Z H. Azimuthal anisotropy of seismic velocity, attenuation and Q value in viscous EDA media. Science in China (Series E) (in Chinese) , 1999, 29(6): 569-574. |
| [6] | 杜启振, 杨慧珠. 方位各向异性黏弹性介质波场有限元模拟. 物理学报 , 2003, 52(8): 2010–2014. Du Q Z, Yang H Z. Finite-element methods for viscoelastic and azimuthally anisotropic media. Acta Physica Sinica (in Chinese) , 2003, 52(8): 2010-2014. |
| [7] | 杜启振. 各向异性黏弹性介质伪谱法波场模拟. 物理学报 , 2004, 53(12): 4428–4434. Du Q Z. Wavefield forward modeling with the pseudo-spectral method in viscoelastic and azimuthally anisotropic media. Acta Physica Sinica (in Chinese) , 2004, 53(12): 4428-4434. |
| [8] | 杜启振, 王延光, 付水华. 方位各向异性黏弹性介质波场数值模拟. 地球物理学进展 , 2006, 21(2): 502–504. Du Q Z, Wang Y G, Fu S H. Wavefield forward modeling with the pseudo-spectral method in viscoelastic and azimuthally anisotropic media. Progress in Geophysics (in Chinese) , 2006, 21(2): 502-504. |
| [9] | 郭智奇, 刘财, 杨宝俊, 等. 黏弹各向异性介质中地震波场模拟与特征. 地球物理学进展 , 2007, 22(3): 804–810. Guo Z Q, Liu C, Yang B J. Seismic wave fields modeling and feature in viscoelastic anisotropic media. Progress in Geophysics (in Chinese) , 2007, 22(3): 804-810. |
| [10] | 谭未一, 赵兵, 张中杰. 黏弹性VTI介质地震波模拟特征分析. 地球物理学进展 , 2007, 22(4): 1305–1311. Tan W Y, Zhao B, Zhang Z J. The analysis of the wave field characteristics in viscoelastic VTI medium. Progress in Geophysics (in Chinese) , 2007, 22(4): 1305-1311. |
| [11] | 李军, 苏云, 李录明. 各向异性黏弹性介质波场数值模拟. 大庆石油学院学报 , 2009, 33(6): 38–42. Li J, Su Y, Li L M. Wavefield numeric simulation in anisotropic viscoelastic media. Journal of Daqing Petroleum Institute (in Chinese) , 2009, 33(6): 38-42. |
| [12] | 刘洋, 李承楚, 牟永光. 具有倾斜对称轴的横向各向同性介质中的弹性波. 石油地球物理勘探 , 1998, 33(2): 161–169. Liu Y, Li C C, Mou Y G. Elastic wave in transverse isotropic media with dipping symmetric axis. Oil Geophysical Prospecting (in Chinese) , 1998, 33(2): 161-169. |
| [13] | Qin Y L, Zhang Z J, Li S L. CDP mapping in tilted transversely isotropic (TTI) media. Part I: Method and effectiveness. Geophysical Prospecting , 2003, 51(4): 315-324. |
| [14] | Qin Y L, Zhang Z J, Xu S H. CDP mapping in tilted transversely isotropic (TTI) media. Part II: Velocity analysis by combining CDP mapping with a genetic algorithm. Geophysical Prospecting , 2003, 51(4): 325-332. |
| [15] | Virieux J. P-SV wave propagation in heterogeneous media: velocity-stress finite-difference method. Geophysics , 1986, 51(4): 889-901. DOI:10.1190/1.1442147 |
| [16] | 冯英杰, 杨长春, 吴萍. 地震波有限差分模拟综述. 地球物理学进展 , 2007, 22(2): 487–491. Feng Y J, Yang C C, Wu P. The review of the finite-difference elastic wave motion modeling. Progress in Geophysics (in Chinese) , 2007, 22(2): 487-491. |
| [17] | Saenger E H, Gold N, Shapiro S A. Modeling the propagation of elastic waves using a modified finite-difference grid. Wave Motion , 2000, 31(1): 77-92. DOI:10.1016/S0165-2125(99)00023-2 |
| [18] | Saenger E H, Bohlen T. Finite-difference modeling of viscoelastic and anisotropic wave propagation using the rotated staggered grid. Geophysics , 2004, 69(2): 583-591. DOI:10.1190/1.1707078 |
| [19] | 陈浩, 王秀明, 赵海波. 旋转交错网格有限差分及其完全匹配层吸收边界条件. 科学通报 , 2006, 51(17): 1985–1994. Chen H, Wang X M, Zhao H B. Rotated staggered grid finite-difference and the perfectly matched layer. Chinese Science Bulletin (in Chinese) , 2006, 51(17): 1985-1994. |
| [20] | 张鲁新, 符力耘, 裴正林. 不分裂卷积完全匹配层与旋转交错网格有限差分在孔隙弹性介质模拟中的应用. 地球物理学报 , 2010, 53(10): 2470–2483. Zhang L X, Fu L Y, Pei Z L. Finite difference modeling of Biot's poroelastic equations with unsplit convolutional PML and rotated staggered grid. Chinese J. Geophys. (in Chinese) , 2010, 53(10): 2470-2483. |
| [21] | 杜启振, 孙瑞艳, 张强. 组合边界条件下二维三分量TTI介质波场数值模拟. 石油地球物理勘探 , 2011, 46(2): 187–195. Du Q Z, Sun R Y, Zhang Q. Numerical simulation of three-component elastic wavefield in 2D TTI media in the condition of the combined boundary. Oil Geophysical Prospecting (in Chinese) , 2011, 46(2): 187-195. |
| [22] | Liu Y, Sen M K. An implicit staggered-grid finite-difference method for seismic modelling. Geophysical Journal International , 2009, 179(1): 459-474. DOI:10.1111/gji.2009.179.issue-1 |
| [23] | Igel H, Mora P, Riollet B. Anisotropic wave propagation through finite-difference grids. Geophysics , 1995, 60(4): 1203-1216. DOI:10.1190/1.1443849 |
| [24] | Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves. Journal of Computational Physics , 1994, 114(2): 185-200. DOI:10.1006/jcph.1994.1159 |
| [25] | Collino F, Tsogka C. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media. Geophysics , 2001, 66(1): 294-307. DOI:10.1190/1.1444908 |
| [26] | Zhang Z J, Teng J W, Wan Z C. Establishment of parameteric equations of seismic wave fronts in 2-D anisotropic media. Chinese Science Bulletin , 1994, 39(22): 1890-1894. |
| [27] | 裴正林, 王尚旭. 任意倾斜各向异性介质中弹性波波场交错网格高阶有限差分法模拟. 地震学报 , 2005, 27(4): 441–451. Pei Z L, Wang S X. A staggered-grid high-order finite-difference modeling for elastic wave field in arbitrary title aniotropic media. Acta Seismologica Sinica (in Chinese) , 2005, 27(4): 441-451. |
 2012, Vol. 55
2012, Vol. 55


